2025年中考数学二轮专题复习 大单元整合专题二 巧用“转化化归”求面积与最值 课件(共61张PPT)
文档属性
| 名称 | 2025年中考数学二轮专题复习 大单元整合专题二 巧用“转化化归”求面积与最值 课件(共61张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 41.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 14:12:18 | ||
图片预览



文档简介
(共61张PPT)
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
大单元整合专题二
巧用“转化化归”求面积与最值
类型1 反比例函数中|k|的几何意义
PART 01
问题1
单个反比例函数图象
模型 相关结论
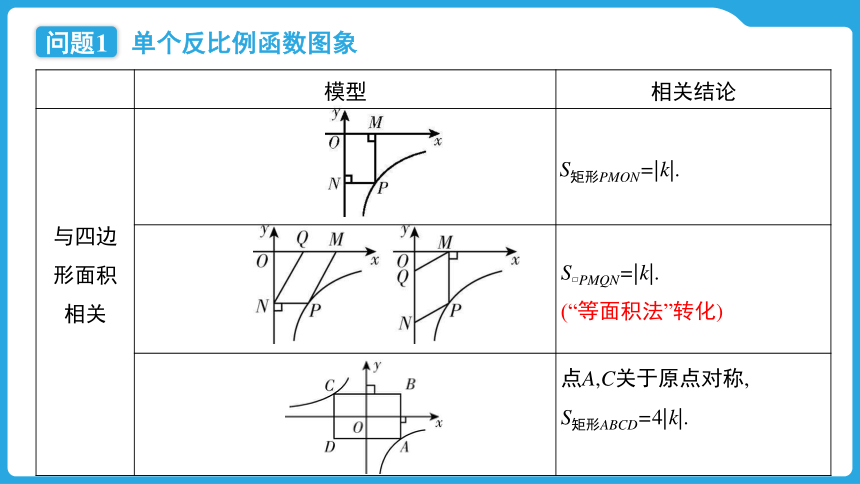
与四边 形面积 相关 S矩形PMON=|k|.
S PMQN=|k|.
(“等面积法”转化)
点A,C关于原点对称,
S矩形ABCD=4|k|.
问题1
单个反比例函数图象
模型 相关结论
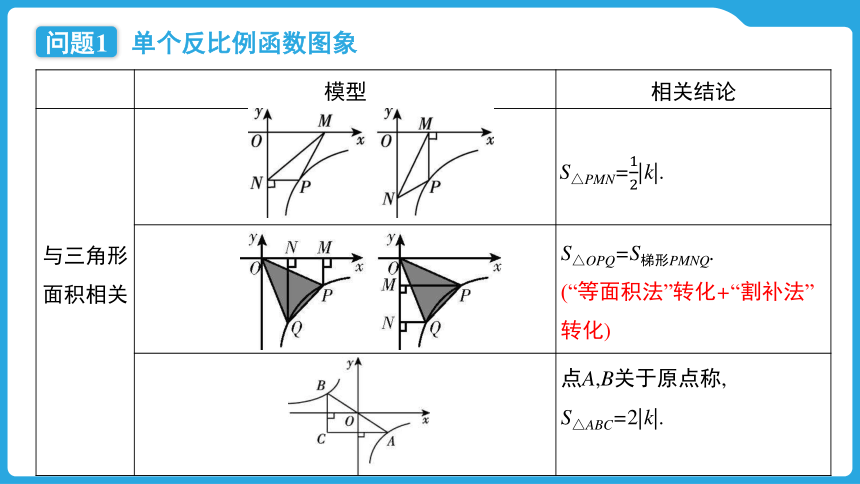
与三角形面积相关 S△PMN=|k|.
S△OPQ=S梯形PMNQ.
(“等面积法”转化+“割补法”转化)
点A,B关于原点称,
S△ABC=2|k|.
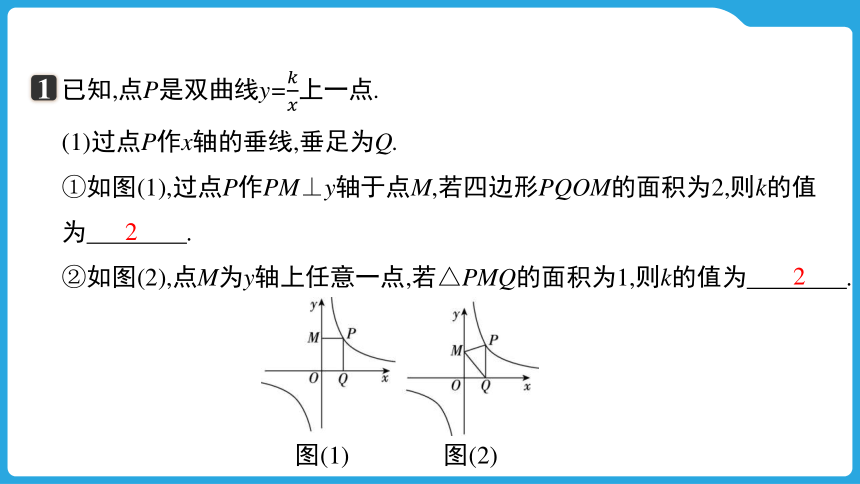
已知,点P是双曲线y=上一点.
(1)过点P作x轴的垂线,垂足为Q.
①如图(1),过点P作PM⊥y轴于点M,若四边形PQOM的面积为2,则k的值为 .
②如图(2),点M为y轴上任意一点,若△PMQ的面积为1,则k的值为 .
1
图(1) 图(2)
2
2
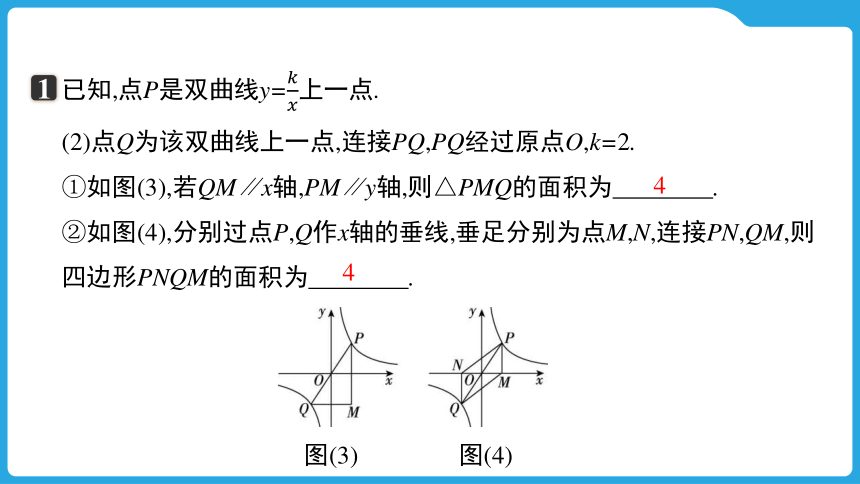
已知,点P是双曲线y=上一点.
(2)点Q为该双曲线上一点,连接PQ,PQ经过原点O,k=2.
①如图(3),若QM∥x轴,PM∥y轴,则△PMQ的面积为 .
②如图(4),分别过点P,Q作x轴的垂线,垂足分别为点M,N,连接PN,QM,则四边形PNQM的面积为 .
1
图(3) 图(4)
4
4
问题2
两个反比例函数图象
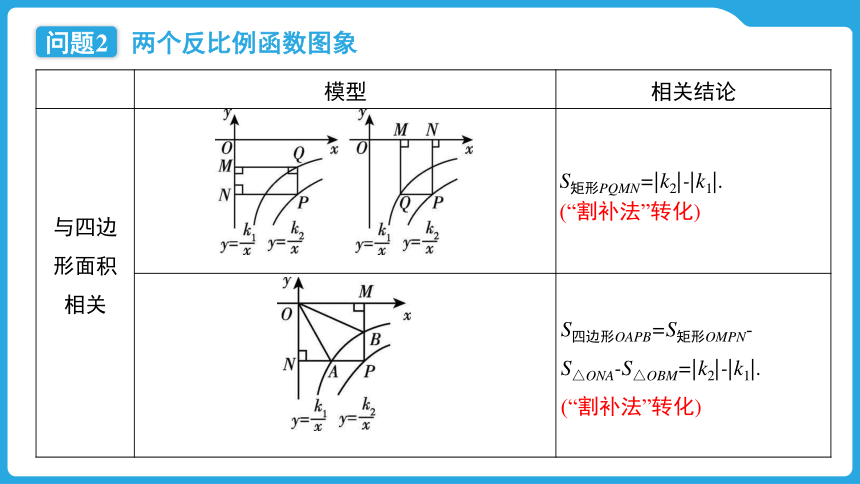
模型 相关结论
与四边 形面积 相关 S矩形PQMN=|k2|-|k1|.
(“割补法”转化)
S四边形OAPB=S矩形OMPN-
S△ONA-S△OBM=|k2|-|k1|.
(“割补法”转化)
问题2
两个反比例函数图象
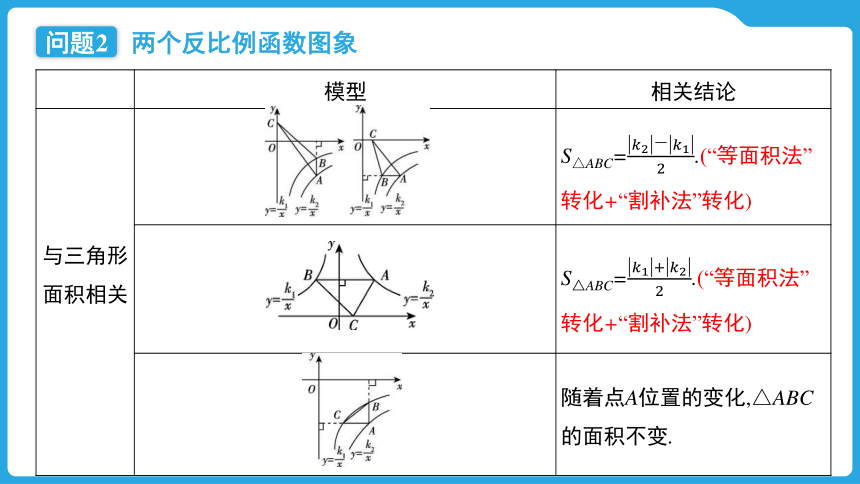
模型 相关结论
与三角形面积相关 S△ABC=.(“等面积法”
转化+“割补法”转化)
S△ABC=.(“等面积法”
转化+“割补法”转化)
随着点A位置的变化,△ABC的面积不变.
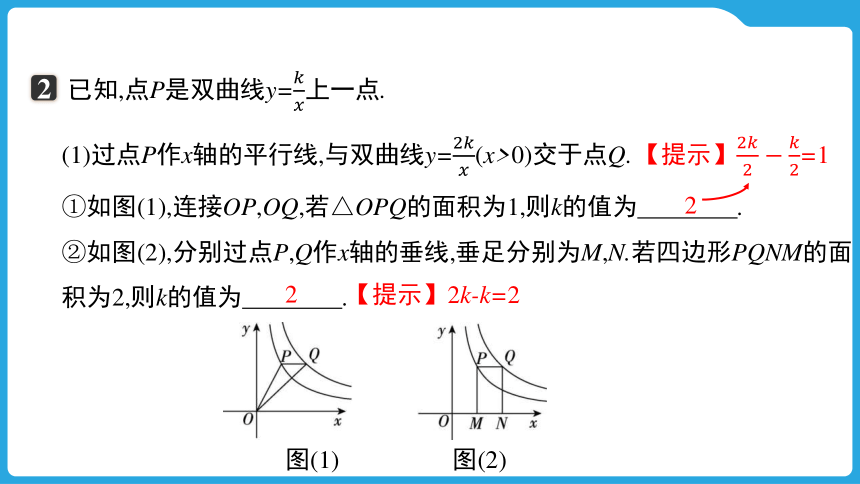
已知,点P是双曲线y=上一点.
(1)过点P作x轴的平行线,与双曲线y=(x>0)交于点Q.
①如图(1),连接OP,OQ,若△OPQ的面积为1,则k的值为 .
②如图(2),分别过点P,Q作x轴的垂线,垂足分别为M,N.若四边形PQNM的面积为2,则k的值为 .
2
图(1) 图(2)
2
2
【提示】=1
【提示】2k-k=2
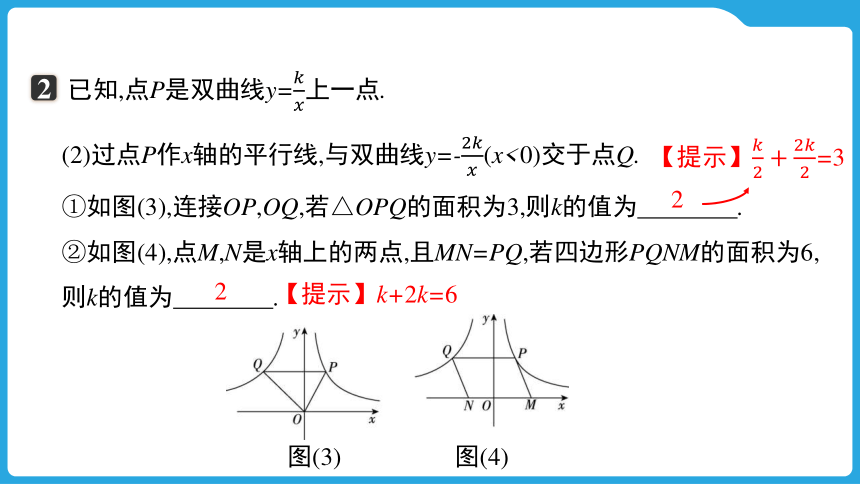
已知,点P是双曲线y=上一点.
(2)过点P作x轴的平行线,与双曲线y=-(x<0)交于点Q.
①如图(3),连接OP,OQ,若△OPQ的面积为3,则k的值为 .
②如图(4),点M,N是x轴上的两点,且MN=PQ,若四边形PQNM的面积为6,则k的值为 .
2
图(3) 图(4)
2
2
【提示】=3
【提示】k+2k=6
类型2 “垂线段最短”求最值
PART 02
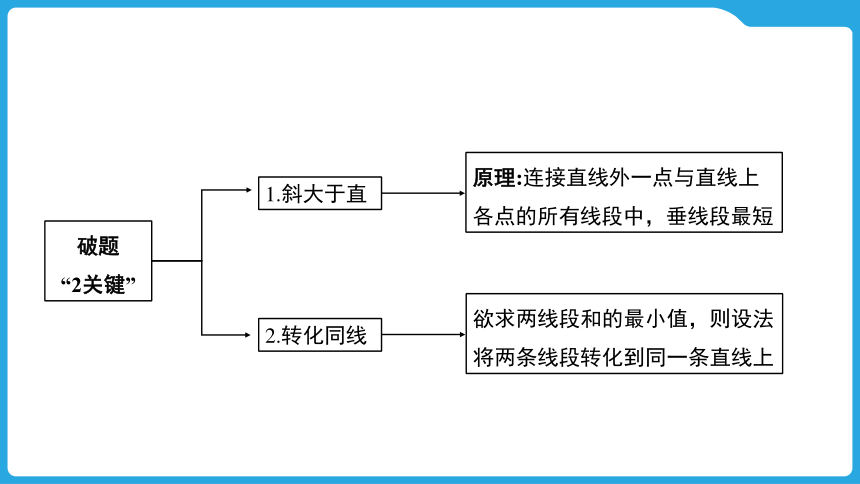
破题
“2关键”
1.斜大于直
2.转化同线
原理:连接直线外一点与直线上各点的所有线段中,垂线段最短
欲求两线段和的最小值,则设法将两条线段转化到同一条直线上
问题1
“ 一定一动”型
已知,如图,定点A在直线l外,点P为直线l上一动点,当AP最短时,确定点P的位置.
构图
过点A作AP⊥l于点P,点P即为所求.
模型分析
如图,BO平分∠ABC,OD⊥BC于点D,点E为射线BA上一动点,若OD=6,则OE的最小值为 .
1
6
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,点P为AB的中点,点F为线段BC上的动点.
(1)连接PF,则PF的最小值为 ;
(2)若BD是△ABC的角平分线,点E是线段BD上的动点,连接PE,EF,则PE+EF的最小值为 .
2
2
2
已知,如图,点P在∠AOB的内部,在OA上求作一点C,在OB上求作一点D,使PD+CD的值最小.
构图
作点P关于OB的对称点P',过点P'作P'C⊥OA于点C,交OB于点D,此时PD+CD的值最小,最小值即为P'C的长.
问题2
“一定两动”型
(注:若点P在∠AOB的边上时,构图方法与上同)
模型分析
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD平分∠ABC交AC于点D,点M是BD上一点,且BM=4,点F,G分别为线段BC,AB上的动点,连接MF,FG.
(1)当MF+FG的值最小时,在图中作出点F,G的位置;
3
(1)点F,G的位置如图所示(注:点M'是点M关于BC的对称点,M'G⊥AB).
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD平分∠ABC交AC于点D,点M是BD上一点,且BM=4,点F,G分别为线段BC,AB上的动点,连接MF,FG.
(2)MF+FG的最小值为 .
3
2
如图,在Rt△ACB中,∠C=90°,∠ABC=75°,AB=5,点E为边AC上的动点,点F为边AB上的动点,则FE+EB的最小值是( )
A.
B.
C.
D.
4
B
点拨 如图,作点F关于AC的对称点F ' ,连接AF ' ,EF ',延长AF ',BC交于点 B ' ,作 BD ⊥AB'于点D.当B,E,F'三点共线且与AB'垂直时,BE+EF的长度最小,即等于BD的长
构图
①作角:如图,以点A为顶点作∠NAD,使sin∠NAD=k(kAP=PE);
②作垂线:过点B作BE⊥AN于点E,交直线CD于点P,此时kAP+BP的值最小,最小值为BE的长.
问题3
“胡不归”模型
已知,如图,点A 为直线CD上一定点,点B为直线CD外一定点,点P 为直线CD上一动点,当kAP+BP(0时,确定点P的位置.
模型分析
如图,在△ABC中,AB=5,AC=4,sin A=,BD⊥AC于点D.点P为线段BD上的动点,则PC+PB的最小值为 .
5
【大招点拨】①过点P作PE垂直AB于点E,将PB等量转化为PE的长; ②将PC,PE转化在同一条直线上;③根据“垂线段最短”求出最小值.
[2024北京人大附中期中]如图,在平行四边形ABCD中,AB=3,BC=4,
∠ABC=60°,在线段AD上取一点E,使DE=1,连接BE,点M,N分别是线段AE,BE上的动点,连接MN,则MN+BN的最小值为 .
6
点拨 如图,过点N作NF⊥BC于点F,连接 MF,过点A作AH ⊥ BC于点H,易得∠EBC =30°,∴MN +BN = MN +NF ≥ MF≥AH = AB
类型3 “两点之间,线段最短”求最值
PART 03
(1)最小值——两定点在异侧
如图(1),在直线l两侧各有一个定点A,B,在直线l上求作点P,使得PA+PB的值最小.
图(1)
图(2)
作法:如图(2),连接AB,AB与直线l的交点即为点P.
问题1
“一动两定”型(含“将军饮马”模型)
问题1
“一动两定”型(含“将军饮马”模型)
在平面直角坐标系中,A(2,1),B(3,2),C(4,1),点P为x轴上一动点,连接PA,PB,PC.
(1)当PA+PC的值最小时,在图(1)中作出点P的位置,PA+PC的最小值为 .
1
图(1)
2
(2)最小值——两定点在同侧
如图(3),在直线l同侧有两个定点A,B,在直线l上求作点P,使得PA+PB的值最小.
图(3)
图(4)
作法:如图(4),作点A关于直线l的对称点A',连接A'B,A'B与直线l的交点即为点P.
问题1
“一动两定”型(含“将军饮马”模型)
在平面直角坐标系中,A(2,1),B(3,2),C(4,1),点P为x轴上一动点,连接PA,PB,PC.
(2)“将军饮马”模型 当PA+PB的值最小时,在图(2)中作出点P的位置,PA+PB的最小值为 .
1
图(2)
(3)最大值——两定点在同侧
如图(5),在直线l同侧有两个定点A,B,在直线l上求作点P,使得|PA-PB|的值最大.
图(5)
图(6)
作法:如图(6),连接BA并延长,BA的延长线与直线l的交点即为点P.
问题1
“一动两定”型(含“将军饮马”模型)
在平面直角坐标系中,A(2,1),B(3,2),C(4,1),点P为x轴上一动点,连接PA,PB,PC.
(3)当|PAPB|的值最大时,在图(3)中作出点P的位置,|PAPB|的最大值为 ,此时点P的坐标为 .
1
图(3)
(1,0)
(4)最大值——两定点在异侧
如图(7),在直线l两侧各有一个定点A,B,在直线l上求作点P,使得|PA-PB|的值最大.
图(7)
图(8)
作法:如图(8),作点B关于直线l的对称点B',连接AB'并延长,AB'的延长线与直线l的交点即为点P.
问题1
“一动两定”型(含“将军饮马”模型)
在平面直角坐标系中,A(2,1),B(3,2),C(4,1),点P为x轴上一动点,连接PA,PB,PC.
(4)当|PBPC|的值最大时,在图(4)中作出点P的位置,|PBPC|的最大值为 ,此时点P的坐标为 .
1
图(4)
(5,0)
如图,A,B两点的坐标分别为A(4,3),B(0,3),在x轴上找一点P,使线段PA+PB的值最小,则点P的坐标是 .
2
(2,0)
如图,在△ABC中,AB=3,AC=4,BC=5,EF是边BC的垂直平分线.点P是EF上的动点,则|PAPB|的最大值为 .
3
3
如图,点E,F是正方形ABCD的边AB的三等分点,P是对角线AC上的动点,当 PE+PF取得最小值时,的值是 .
4
点拨 如图,作点E关于AC的对称点E',连接PE ' ,E ' F,E ' F与AC交于点P ' ,过点F作 FG⊥AB交 AC于点G,∴PE +PF≥E ' F,易得 AE ' =AE,AF = GF,由△E ' AP ' ∽△FGP '可得,AP ' =AC,P ' C= AC
(1)“两动一定”型
如图(1),点P在∠AOB的内部,在OA,OB上分别求作点C,D,使△PCD的周长最小.
图(1)
图(2)
作法:如图(2),分别作点P关于OA,OB的对称点P',P″,连接P'P″,分别交OA,OB于点C,D,此时△PCD的周长最小,最小值为P'P″的长.
问题2
“两动一定”或“两动两定”型
问题2
“两动一定”或“两动两定”型
点P,Q在等边三角形ABC内部,且∠ABP=∠CBQ=15°,
BP=3,BQ=4.点M,N分别是边AB,BC上的动点.
(1)连接PM,PN,MN.①当△PMN的周长最小时,在图(1)中作出点M,N的位置;
②△PMN周长的最小值为 .
5
图(1)
3
(注:点P1,P2分别是点P关于AB,BC的对称点)
(2)“两动两定”型
如图(3),定点P,Q在∠AOB的内部,在OA,OB上分别求作点C,D,使得四边形PCDQ的周长最小.
图(3)
图(4)
作法:如图(4),作点P关于OA的对称点P',作点Q关于OB的对称点Q',连接 P'Q',分别交OA,OB于点C,D,此时四边形PCDQ的周长最小,最小值为PQ+P'Q'的长.
问题2
“两动一定”或“两动两定”型
点P,Q在等边三角形ABC内部,且∠ABP=∠CBQ=15°,
BP=3,BQ=4.点M,N分别是边AB,BC上的动点.
(2)连接PM,QN,MN.
①当PM+MN+NQ的值最小时,在图(2)中作出点M,N的位置;
②PM+MN+NQ的最小值为 .
5
图(2)
5
(注:点P'是点P关于AB的对称点,点Q'是点Q关于BC的对称点)
如图,已知∠AOB的大小为α,点P是∠AOB内部的一个定点,且OP=5,点E,F分别是OA,OB上的动点.若△PEF周长的最小值为5,则α= °.
6
45
点拨 如图,分别作点Р关于射线OA,OB的对称点C,D,连接OC,OD,CD,PC,PD.易得△PEF周长的最小值=CD=5,由OA垂直平分PC,OB垂直平分PD得∠COD =2α , OC=OD = OP =5,可得△COD是等腰直角三角形,即可得α 的值
如图,在矩形ABCD中,AB=3,AD=6,AE=4,AF=2,点G,H分别是边BC,CD上的动点,则四边形EFGH周长的最小值为 .
7
6
提示 如图,四边形EFGH周长的最小值=E'F'+EF
如图(1),定点A,B在两条平行线a,b两侧,在直线a,b上分别找点P,Q,使PQ与直线a,b垂直,且AP+PQ+QB的值最小.
图(1)
图(2)
作法:如图(2),将点A向下平移到点A'处,使AA'=PQ,连接A'B交直线b于点Q,作QP⊥b交直线a于点P,此时AP+PQ+QB的值最小.
问题3
“建桥选址”模型
问题3
“建桥选址”模型
如图,在菱形ABCD中,AB=4,∠ABC=60°,线段EF在BD上运动且EF=1,则AE+CF的最小值为( )
A.4
B.
C.-1
D.
8
B
点拨 如图,连接AC,过点A 作AM// BD,且AM =EF=1,连接CM , FM,易得四边形AMFE是平行四边形,∴AE +CF= FM+FC≥MC =
如图,在平面直角坐标系中,A(0,),B(3,-1),点C,D分别是直线y=1,x轴上的动点,且CD∥y轴,当AC+BD的值最小时,点D的坐标为 .
9
(,0)
类型4 “隐形圆”的应用
PART 04
问题1
“一动两定”型(含“将军饮马”模型)
模型分析
知识依据:到定点的距离等于定长的点的集合叫做圆(圆的定义),如图(1).
图(1) 图(2)
模型说明:如图(2),若AB=AC=AD,则点B,C,D在以点A为圆心、AB的长为半径的圆上.
如图,在矩形ABCD中,AB=3,AD=5,点E是折线ABC上的动点,连接DE,将矩形沿DE折叠,点A的对应点为点P[1].在点E运动过程中,
(1)点B,P之间的最小距离为 ;
(2)点C,P之间的最小距离为 .
1
【大招点拨】由[1]得DP=DA=5,为定长,∴点P在以点D为圆心,5为半径的圆上运动,画出隐形圆进而求出BP,CP的最小值.
2
-5
问题2
“直角对直径”作圆
知识依据:90°的圆周角所对的弦是直径(圆周角定理的推论).
模型说明:
(1)如图(1),在△ABC中,∠C=90°,若AB的长固
定,则点C的运动轨迹为以AB为直径的☉O(不含点A,B).
(2)如图(2),Rt△ABC和Rt△ABD共斜边AB,则A,B,C,D四点共圆,均在以AB为直径的☉O上.(确定四点共圆后,可根据圆周角定理的推论得到角相等,完成角度的等量转化)
图(1)
图(2)
模型分析
如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点[1],∠ADM=∠BAP[2].
在点P运动的过程中:
(1)点M到直线BC的最小距离为 ;
(2)连接BM,BM的最小值为 .
2
【大招点拨】由[1]得点M为动点,由[2]得∠AMD=90°为定角,
∴点M在以线段AD为直径的圆上运动,直径AD的长度为4,画出隐形圆即可求解.
1
-2
知识依据:在同圆或等圆中,同弧或等弧所对的圆周角相等(圆周角定理的推论).如图(1),∠C=∠D=∠E.
模型说明:在△ABC中,若AB的长度及∠C的大小固定,则点C在确定的圆上,AB为该定圆的弦,当∠C为锐角时,点C在优弧AB上(不含点A,B);当∠C为钝角时,点C在劣弧AB上(不含点A,B),如图
(2).其中,我们称AB为“定弦”,∠C为“定角”.
图(1)
图(2)
问题3
“定弦对定角”作圆
模型分析
如图,在边长为6的等边三角形ABC中[1],点E,F分别是边AC,BC上的动点[2],且AE=CF[3],连接BE,AF交于点P[4],连接CP.
(1)∠APB= °;
(2)CP的最小值为 .
3
【大招点拨】由[1][3]证得△ACF≌△BAE,可得∠APB的度数.由[2][4]得点P为动点,∴点P是在以线段AB为弦,且所对圆心角为120°的圆上运动(利用“定弦对定角”),画出隐形圆进而求出线段CP的最小值.
120
2
类型5 “主从联动”求轨迹与最值
PART 05
“主从联动模型”也叫“瓜豆模型”,出自成语“种瓜得瓜,种豆得豆”.这类动点问题中,存在两个相关联的动点,主动运动的点称为主动点,因主动点运动而“被动”运动的点称为从动点.
问题1
点在直线上运动
模型特点:①点A是直线l外一定点,点P是直线l上的主动点,点Q是从动点(点P运动到点P'处停止,线段PP'为主动点的运动轨迹,QQ'为从动点的运动轨迹).②AQ∶AP=k(k为定值).③∠PAQ=α(α为定角).此类问题有两种类型,构图如下:
结论:①点Q的运动轨迹是线段QQ';②∠Q'MP'=α;③△AQQ'∽△APP'(当k=1时,△AQQ'≌△APP');④QQ'=kPP'.
位似型(α=0°)
旋转型(α≠0°
,延长Q'Q,交PP'于点M)
模型分析
如图,长方形ABCD中,AB=3,BC=4,E为BC上一点,且BE=1,F为AB边上的一个动点[1],连接EF,将EF绕点E顺时针旋转45°到EG的位置[2],连接FG和CG,则CG的最小值为 .
1
1+
1
【大招点拨】①找主动点轨迹:由[1]得主动点为点F,且在AB上运动.②找从动点与主动点间的关系:由[2]得从动点为点G,定角为45°.③找主动点的起点和终点:将线段BE,AE分别绕点E顺时针旋转45°得到线段EG',EG″.④确定从动点轨迹:连接G'G″,则点G在线段G'G″上运动.当CG⊥G'G″时,CG的值最小,过点E作ET⊥CG于点T,计算可得结果.
(大招点拨)
问题2
点在圆上运动
模型特点:①点P是☉O上的主动点,A为定点,连接AP,点Q是从动点(从动点Q的运动轨迹也为圆,记为☉M).②AQ∶AP=k(k为定值).③∠PAQ=α(α为定角).此类问题有两种类型,构图如下:
位似型(α=0°)
旋转型(α≠0°)
模型分析
问题2
点在圆上运动
作图步骤:①先利用∠OAM=∠PAQ确定圆心M所在的直线.②再利用=确定AM的长. ③最后利用=确定☉M的半径.
位似型(α=0°)
旋转型(α≠0°)
结论:①点Q的运动轨迹是圆,且点P,Q的运动轨迹长度之比为k.②点Q的运动轨迹圆的半径=k·OP.③△AMQ∽△AOP,相似比为k.
模型分析
如图,在等腰直角三角形ABC中,AC=BC=2,点P在以斜边AB为直径的半圆上[1],M为PC的中点[2],当点P沿半圆从点A运动至点B时[3],点M运动的路径长是( )
A.π B.π
C.π D.2
2
【大招点拨】①找主动点轨迹:由[1][3]得主动点为点P,主动点的运动轨迹为半圆.②找从动点与主动点间的关系:由[2]得从动点为点M,且CM=PC.③找主动点的起点和终点:取AC的中点E,BC的中点F,连接EF.④确定从动点轨迹:点M的运动路径是以EF为直径的半圆弧.
C
(大招点拨)
如图,M是正方形ABCD的边CD的中点,P是正方形内一点,连接BP[1],线段BP以B为中心逆时针旋转90°得到线段BQ[2],连接MQ,MP.若AB=4,MP=1,则MQ的最小值为 .
3
2-1
3
(大招点拨)
【大招点拨】①找主动点轨迹:由[1]得主动点为点P,在以点M为圆心,1为半径的半圆上运动.②找从动点与主动点间的关系:由[2]得从动点为点Q,定角为∠PBQ=90°.③找主动点的起点和终点:连接BM,DB,将BD,BM,BC分别绕点B逆时针旋转90°得到BT,BF,BE.④确定从动点轨迹:可得FQ=1,即点Q的运动轨迹是以点F为圆心,1为半径的半圆弧.
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
大单元整合专题二
巧用“转化化归”求面积与最值
类型1 反比例函数中|k|的几何意义
PART 01
问题1
单个反比例函数图象
模型 相关结论
与四边 形面积 相关 S矩形PMON=|k|.
S PMQN=|k|.
(“等面积法”转化)
点A,C关于原点对称,
S矩形ABCD=4|k|.
问题1
单个反比例函数图象
模型 相关结论
与三角形面积相关 S△PMN=|k|.
S△OPQ=S梯形PMNQ.
(“等面积法”转化+“割补法”转化)
点A,B关于原点称,
S△ABC=2|k|.
已知,点P是双曲线y=上一点.
(1)过点P作x轴的垂线,垂足为Q.
①如图(1),过点P作PM⊥y轴于点M,若四边形PQOM的面积为2,则k的值为 .
②如图(2),点M为y轴上任意一点,若△PMQ的面积为1,则k的值为 .
1
图(1) 图(2)
2
2
已知,点P是双曲线y=上一点.
(2)点Q为该双曲线上一点,连接PQ,PQ经过原点O,k=2.
①如图(3),若QM∥x轴,PM∥y轴,则△PMQ的面积为 .
②如图(4),分别过点P,Q作x轴的垂线,垂足分别为点M,N,连接PN,QM,则四边形PNQM的面积为 .
1
图(3) 图(4)
4
4
问题2
两个反比例函数图象
模型 相关结论
与四边 形面积 相关 S矩形PQMN=|k2|-|k1|.
(“割补法”转化)
S四边形OAPB=S矩形OMPN-
S△ONA-S△OBM=|k2|-|k1|.
(“割补法”转化)
问题2
两个反比例函数图象
模型 相关结论
与三角形面积相关 S△ABC=.(“等面积法”
转化+“割补法”转化)
S△ABC=.(“等面积法”
转化+“割补法”转化)
随着点A位置的变化,△ABC的面积不变.
已知,点P是双曲线y=上一点.
(1)过点P作x轴的平行线,与双曲线y=(x>0)交于点Q.
①如图(1),连接OP,OQ,若△OPQ的面积为1,则k的值为 .
②如图(2),分别过点P,Q作x轴的垂线,垂足分别为M,N.若四边形PQNM的面积为2,则k的值为 .
2
图(1) 图(2)
2
2
【提示】=1
【提示】2k-k=2
已知,点P是双曲线y=上一点.
(2)过点P作x轴的平行线,与双曲线y=-(x<0)交于点Q.
①如图(3),连接OP,OQ,若△OPQ的面积为3,则k的值为 .
②如图(4),点M,N是x轴上的两点,且MN=PQ,若四边形PQNM的面积为6,则k的值为 .
2
图(3) 图(4)
2
2
【提示】=3
【提示】k+2k=6
类型2 “垂线段最短”求最值
PART 02
破题
“2关键”
1.斜大于直
2.转化同线
原理:连接直线外一点与直线上各点的所有线段中,垂线段最短
欲求两线段和的最小值,则设法将两条线段转化到同一条直线上
问题1
“ 一定一动”型
已知,如图,定点A在直线l外,点P为直线l上一动点,当AP最短时,确定点P的位置.
构图
过点A作AP⊥l于点P,点P即为所求.
模型分析
如图,BO平分∠ABC,OD⊥BC于点D,点E为射线BA上一动点,若OD=6,则OE的最小值为 .
1
6
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,点P为AB的中点,点F为线段BC上的动点.
(1)连接PF,则PF的最小值为 ;
(2)若BD是△ABC的角平分线,点E是线段BD上的动点,连接PE,EF,则PE+EF的最小值为 .
2
2
2
已知,如图,点P在∠AOB的内部,在OA上求作一点C,在OB上求作一点D,使PD+CD的值最小.
构图
作点P关于OB的对称点P',过点P'作P'C⊥OA于点C,交OB于点D,此时PD+CD的值最小,最小值即为P'C的长.
问题2
“一定两动”型
(注:若点P在∠AOB的边上时,构图方法与上同)
模型分析
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD平分∠ABC交AC于点D,点M是BD上一点,且BM=4,点F,G分别为线段BC,AB上的动点,连接MF,FG.
(1)当MF+FG的值最小时,在图中作出点F,G的位置;
3
(1)点F,G的位置如图所示(注:点M'是点M关于BC的对称点,M'G⊥AB).
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD平分∠ABC交AC于点D,点M是BD上一点,且BM=4,点F,G分别为线段BC,AB上的动点,连接MF,FG.
(2)MF+FG的最小值为 .
3
2
如图,在Rt△ACB中,∠C=90°,∠ABC=75°,AB=5,点E为边AC上的动点,点F为边AB上的动点,则FE+EB的最小值是( )
A.
B.
C.
D.
4
B
点拨 如图,作点F关于AC的对称点F ' ,连接AF ' ,EF ',延长AF ',BC交于点 B ' ,作 BD ⊥AB'于点D.当B,E,F'三点共线且与AB'垂直时,BE+EF的长度最小,即等于BD的长
构图
①作角:如图,以点A为顶点作∠NAD,使sin∠NAD=k(kAP=PE);
②作垂线:过点B作BE⊥AN于点E,交直线CD于点P,此时kAP+BP的值最小,最小值为BE的长.
问题3
“胡不归”模型
已知,如图,点A 为直线CD上一定点,点B为直线CD外一定点,点P 为直线CD上一动点,当kAP+BP(0
模型分析
如图,在△ABC中,AB=5,AC=4,sin A=,BD⊥AC于点D.点P为线段BD上的动点,则PC+PB的最小值为 .
5
【大招点拨】①过点P作PE垂直AB于点E,将PB等量转化为PE的长; ②将PC,PE转化在同一条直线上;③根据“垂线段最短”求出最小值.
[2024北京人大附中期中]如图,在平行四边形ABCD中,AB=3,BC=4,
∠ABC=60°,在线段AD上取一点E,使DE=1,连接BE,点M,N分别是线段AE,BE上的动点,连接MN,则MN+BN的最小值为 .
6
点拨 如图,过点N作NF⊥BC于点F,连接 MF,过点A作AH ⊥ BC于点H,易得∠EBC =30°,∴MN +BN = MN +NF ≥ MF≥AH = AB
类型3 “两点之间,线段最短”求最值
PART 03
(1)最小值——两定点在异侧
如图(1),在直线l两侧各有一个定点A,B,在直线l上求作点P,使得PA+PB的值最小.
图(1)
图(2)
作法:如图(2),连接AB,AB与直线l的交点即为点P.
问题1
“一动两定”型(含“将军饮马”模型)
问题1
“一动两定”型(含“将军饮马”模型)
在平面直角坐标系中,A(2,1),B(3,2),C(4,1),点P为x轴上一动点,连接PA,PB,PC.
(1)当PA+PC的值最小时,在图(1)中作出点P的位置,PA+PC的最小值为 .
1
图(1)
2
(2)最小值——两定点在同侧
如图(3),在直线l同侧有两个定点A,B,在直线l上求作点P,使得PA+PB的值最小.
图(3)
图(4)
作法:如图(4),作点A关于直线l的对称点A',连接A'B,A'B与直线l的交点即为点P.
问题1
“一动两定”型(含“将军饮马”模型)
在平面直角坐标系中,A(2,1),B(3,2),C(4,1),点P为x轴上一动点,连接PA,PB,PC.
(2)“将军饮马”模型 当PA+PB的值最小时,在图(2)中作出点P的位置,PA+PB的最小值为 .
1
图(2)
(3)最大值——两定点在同侧
如图(5),在直线l同侧有两个定点A,B,在直线l上求作点P,使得|PA-PB|的值最大.
图(5)
图(6)
作法:如图(6),连接BA并延长,BA的延长线与直线l的交点即为点P.
问题1
“一动两定”型(含“将军饮马”模型)
在平面直角坐标系中,A(2,1),B(3,2),C(4,1),点P为x轴上一动点,连接PA,PB,PC.
(3)当|PAPB|的值最大时,在图(3)中作出点P的位置,|PAPB|的最大值为 ,此时点P的坐标为 .
1
图(3)
(1,0)
(4)最大值——两定点在异侧
如图(7),在直线l两侧各有一个定点A,B,在直线l上求作点P,使得|PA-PB|的值最大.
图(7)
图(8)
作法:如图(8),作点B关于直线l的对称点B',连接AB'并延长,AB'的延长线与直线l的交点即为点P.
问题1
“一动两定”型(含“将军饮马”模型)
在平面直角坐标系中,A(2,1),B(3,2),C(4,1),点P为x轴上一动点,连接PA,PB,PC.
(4)当|PBPC|的值最大时,在图(4)中作出点P的位置,|PBPC|的最大值为 ,此时点P的坐标为 .
1
图(4)
(5,0)
如图,A,B两点的坐标分别为A(4,3),B(0,3),在x轴上找一点P,使线段PA+PB的值最小,则点P的坐标是 .
2
(2,0)
如图,在△ABC中,AB=3,AC=4,BC=5,EF是边BC的垂直平分线.点P是EF上的动点,则|PAPB|的最大值为 .
3
3
如图,点E,F是正方形ABCD的边AB的三等分点,P是对角线AC上的动点,当 PE+PF取得最小值时,的值是 .
4
点拨 如图,作点E关于AC的对称点E',连接PE ' ,E ' F,E ' F与AC交于点P ' ,过点F作 FG⊥AB交 AC于点G,∴PE +PF≥E ' F,易得 AE ' =AE,AF = GF,由△E ' AP ' ∽△FGP '可得,AP ' =AC,P ' C= AC
(1)“两动一定”型
如图(1),点P在∠AOB的内部,在OA,OB上分别求作点C,D,使△PCD的周长最小.
图(1)
图(2)
作法:如图(2),分别作点P关于OA,OB的对称点P',P″,连接P'P″,分别交OA,OB于点C,D,此时△PCD的周长最小,最小值为P'P″的长.
问题2
“两动一定”或“两动两定”型
问题2
“两动一定”或“两动两定”型
点P,Q在等边三角形ABC内部,且∠ABP=∠CBQ=15°,
BP=3,BQ=4.点M,N分别是边AB,BC上的动点.
(1)连接PM,PN,MN.①当△PMN的周长最小时,在图(1)中作出点M,N的位置;
②△PMN周长的最小值为 .
5
图(1)
3
(注:点P1,P2分别是点P关于AB,BC的对称点)
(2)“两动两定”型
如图(3),定点P,Q在∠AOB的内部,在OA,OB上分别求作点C,D,使得四边形PCDQ的周长最小.
图(3)
图(4)
作法:如图(4),作点P关于OA的对称点P',作点Q关于OB的对称点Q',连接 P'Q',分别交OA,OB于点C,D,此时四边形PCDQ的周长最小,最小值为PQ+P'Q'的长.
问题2
“两动一定”或“两动两定”型
点P,Q在等边三角形ABC内部,且∠ABP=∠CBQ=15°,
BP=3,BQ=4.点M,N分别是边AB,BC上的动点.
(2)连接PM,QN,MN.
①当PM+MN+NQ的值最小时,在图(2)中作出点M,N的位置;
②PM+MN+NQ的最小值为 .
5
图(2)
5
(注:点P'是点P关于AB的对称点,点Q'是点Q关于BC的对称点)
如图,已知∠AOB的大小为α,点P是∠AOB内部的一个定点,且OP=5,点E,F分别是OA,OB上的动点.若△PEF周长的最小值为5,则α= °.
6
45
点拨 如图,分别作点Р关于射线OA,OB的对称点C,D,连接OC,OD,CD,PC,PD.易得△PEF周长的最小值=CD=5,由OA垂直平分PC,OB垂直平分PD得∠COD =2α , OC=OD = OP =5,可得△COD是等腰直角三角形,即可得α 的值
如图,在矩形ABCD中,AB=3,AD=6,AE=4,AF=2,点G,H分别是边BC,CD上的动点,则四边形EFGH周长的最小值为 .
7
6
提示 如图,四边形EFGH周长的最小值=E'F'+EF
如图(1),定点A,B在两条平行线a,b两侧,在直线a,b上分别找点P,Q,使PQ与直线a,b垂直,且AP+PQ+QB的值最小.
图(1)
图(2)
作法:如图(2),将点A向下平移到点A'处,使AA'=PQ,连接A'B交直线b于点Q,作QP⊥b交直线a于点P,此时AP+PQ+QB的值最小.
问题3
“建桥选址”模型
问题3
“建桥选址”模型
如图,在菱形ABCD中,AB=4,∠ABC=60°,线段EF在BD上运动且EF=1,则AE+CF的最小值为( )
A.4
B.
C.-1
D.
8
B
点拨 如图,连接AC,过点A 作AM// BD,且AM =EF=1,连接CM , FM,易得四边形AMFE是平行四边形,∴AE +CF= FM+FC≥MC =
如图,在平面直角坐标系中,A(0,),B(3,-1),点C,D分别是直线y=1,x轴上的动点,且CD∥y轴,当AC+BD的值最小时,点D的坐标为 .
9
(,0)
类型4 “隐形圆”的应用
PART 04
问题1
“一动两定”型(含“将军饮马”模型)
模型分析
知识依据:到定点的距离等于定长的点的集合叫做圆(圆的定义),如图(1).
图(1) 图(2)
模型说明:如图(2),若AB=AC=AD,则点B,C,D在以点A为圆心、AB的长为半径的圆上.
如图,在矩形ABCD中,AB=3,AD=5,点E是折线ABC上的动点,连接DE,将矩形沿DE折叠,点A的对应点为点P[1].在点E运动过程中,
(1)点B,P之间的最小距离为 ;
(2)点C,P之间的最小距离为 .
1
【大招点拨】由[1]得DP=DA=5,为定长,∴点P在以点D为圆心,5为半径的圆上运动,画出隐形圆进而求出BP,CP的最小值.
2
-5
问题2
“直角对直径”作圆
知识依据:90°的圆周角所对的弦是直径(圆周角定理的推论).
模型说明:
(1)如图(1),在△ABC中,∠C=90°,若AB的长固
定,则点C的运动轨迹为以AB为直径的☉O(不含点A,B).
(2)如图(2),Rt△ABC和Rt△ABD共斜边AB,则A,B,C,D四点共圆,均在以AB为直径的☉O上.(确定四点共圆后,可根据圆周角定理的推论得到角相等,完成角度的等量转化)
图(1)
图(2)
模型分析
如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点[1],∠ADM=∠BAP[2].
在点P运动的过程中:
(1)点M到直线BC的最小距离为 ;
(2)连接BM,BM的最小值为 .
2
【大招点拨】由[1]得点M为动点,由[2]得∠AMD=90°为定角,
∴点M在以线段AD为直径的圆上运动,直径AD的长度为4,画出隐形圆即可求解.
1
-2
知识依据:在同圆或等圆中,同弧或等弧所对的圆周角相等(圆周角定理的推论).如图(1),∠C=∠D=∠E.
模型说明:在△ABC中,若AB的长度及∠C的大小固定,则点C在确定的圆上,AB为该定圆的弦,当∠C为锐角时,点C在优弧AB上(不含点A,B);当∠C为钝角时,点C在劣弧AB上(不含点A,B),如图
(2).其中,我们称AB为“定弦”,∠C为“定角”.
图(1)
图(2)
问题3
“定弦对定角”作圆
模型分析
如图,在边长为6的等边三角形ABC中[1],点E,F分别是边AC,BC上的动点[2],且AE=CF[3],连接BE,AF交于点P[4],连接CP.
(1)∠APB= °;
(2)CP的最小值为 .
3
【大招点拨】由[1][3]证得△ACF≌△BAE,可得∠APB的度数.由[2][4]得点P为动点,∴点P是在以线段AB为弦,且所对圆心角为120°的圆上运动(利用“定弦对定角”),画出隐形圆进而求出线段CP的最小值.
120
2
类型5 “主从联动”求轨迹与最值
PART 05
“主从联动模型”也叫“瓜豆模型”,出自成语“种瓜得瓜,种豆得豆”.这类动点问题中,存在两个相关联的动点,主动运动的点称为主动点,因主动点运动而“被动”运动的点称为从动点.
问题1
点在直线上运动
模型特点:①点A是直线l外一定点,点P是直线l上的主动点,点Q是从动点(点P运动到点P'处停止,线段PP'为主动点的运动轨迹,QQ'为从动点的运动轨迹).②AQ∶AP=k(k为定值).③∠PAQ=α(α为定角).此类问题有两种类型,构图如下:
结论:①点Q的运动轨迹是线段QQ';②∠Q'MP'=α;③△AQQ'∽△APP'(当k=1时,△AQQ'≌△APP');④QQ'=kPP'.
位似型(α=0°)
旋转型(α≠0°
,延长Q'Q,交PP'于点M)
模型分析
如图,长方形ABCD中,AB=3,BC=4,E为BC上一点,且BE=1,F为AB边上的一个动点[1],连接EF,将EF绕点E顺时针旋转45°到EG的位置[2],连接FG和CG,则CG的最小值为 .
1
1+
1
【大招点拨】①找主动点轨迹:由[1]得主动点为点F,且在AB上运动.②找从动点与主动点间的关系:由[2]得从动点为点G,定角为45°.③找主动点的起点和终点:将线段BE,AE分别绕点E顺时针旋转45°得到线段EG',EG″.④确定从动点轨迹:连接G'G″,则点G在线段G'G″上运动.当CG⊥G'G″时,CG的值最小,过点E作ET⊥CG于点T,计算可得结果.
(大招点拨)
问题2
点在圆上运动
模型特点:①点P是☉O上的主动点,A为定点,连接AP,点Q是从动点(从动点Q的运动轨迹也为圆,记为☉M).②AQ∶AP=k(k为定值).③∠PAQ=α(α为定角).此类问题有两种类型,构图如下:
位似型(α=0°)
旋转型(α≠0°)
模型分析
问题2
点在圆上运动
作图步骤:①先利用∠OAM=∠PAQ确定圆心M所在的直线.②再利用=确定AM的长. ③最后利用=确定☉M的半径.
位似型(α=0°)
旋转型(α≠0°)
结论:①点Q的运动轨迹是圆,且点P,Q的运动轨迹长度之比为k.②点Q的运动轨迹圆的半径=k·OP.③△AMQ∽△AOP,相似比为k.
模型分析
如图,在等腰直角三角形ABC中,AC=BC=2,点P在以斜边AB为直径的半圆上[1],M为PC的中点[2],当点P沿半圆从点A运动至点B时[3],点M运动的路径长是( )
A.π B.π
C.π D.2
2
【大招点拨】①找主动点轨迹:由[1][3]得主动点为点P,主动点的运动轨迹为半圆.②找从动点与主动点间的关系:由[2]得从动点为点M,且CM=PC.③找主动点的起点和终点:取AC的中点E,BC的中点F,连接EF.④确定从动点轨迹:点M的运动路径是以EF为直径的半圆弧.
C
(大招点拨)
如图,M是正方形ABCD的边CD的中点,P是正方形内一点,连接BP[1],线段BP以B为中心逆时针旋转90°得到线段BQ[2],连接MQ,MP.若AB=4,MP=1,则MQ的最小值为 .
3
2-1
3
(大招点拨)
【大招点拨】①找主动点轨迹:由[1]得主动点为点P,在以点M为圆心,1为半径的半圆上运动.②找从动点与主动点间的关系:由[2]得从动点为点Q,定角为∠PBQ=90°.③找主动点的起点和终点:连接BM,DB,将BD,BM,BC分别绕点B逆时针旋转90°得到BT,BF,BE.④确定从动点轨迹:可得FQ=1,即点Q的运动轨迹是以点F为圆心,1为半径的半圆弧.
同课章节目录
