2025年中考数学二轮专题复习 题型二-圆的综合题 课件(共24张PPT)
文档属性
| 名称 | 2025年中考数学二轮专题复习 题型二-圆的综合题 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 14:10:38 | ||
图片预览



文档简介
(共24张PPT)
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
题型二 圆的综合题
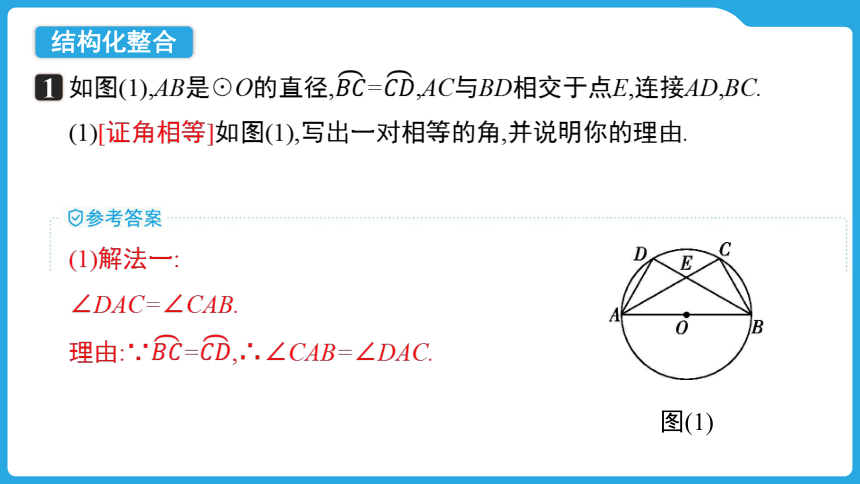
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(1)[证角相等]如图(1),写出一对相等的角,并说明你的理由.
1
结构化整合
图(1)
(1)解法一:
∠DAC=∠CAB.
理由:∵=,∴∠CAB=∠DAC.
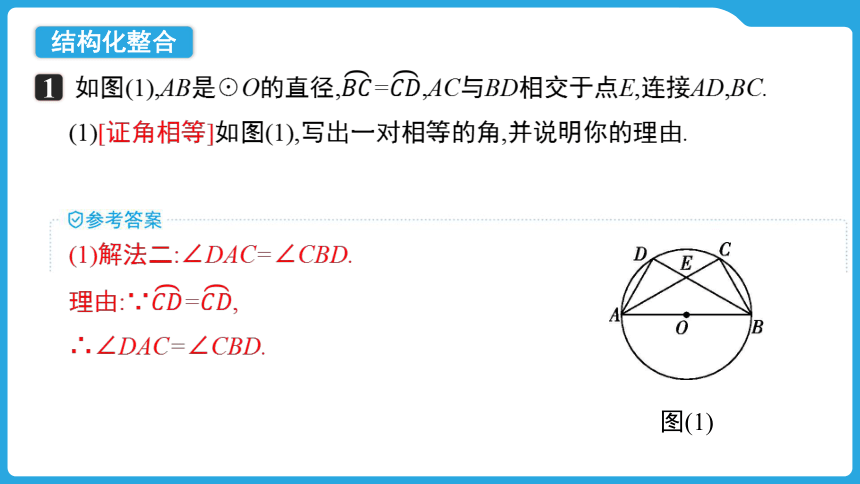
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(1)[证角相等]如图(1),写出一对相等的角,并说明你的理由.
1
结构化整合
图(1)
(1)解法二:∠DAC=∠CBD.
理由:∵=,
∴∠DAC=∠CBD.
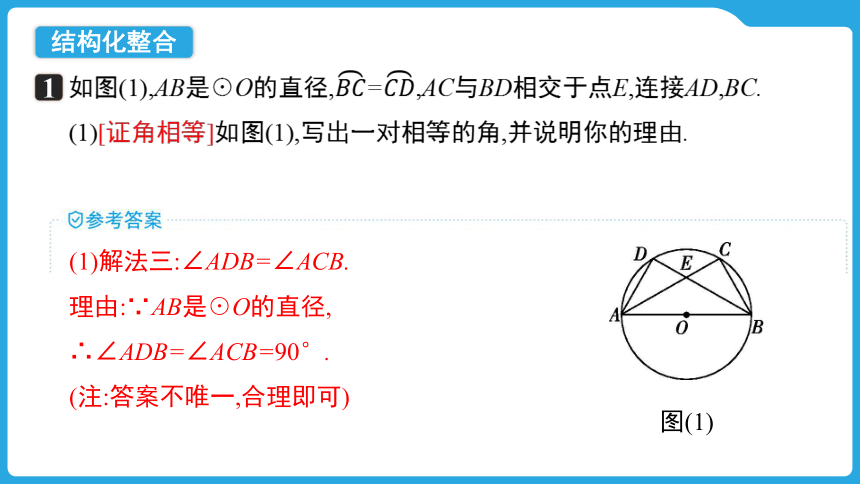
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(1)[证角相等]如图(1),写出一对相等的角,并说明你的理由.
1
结构化整合
图(1)
(1)解法三:∠ADB=∠ACB.
理由:∵AB是☉O的直径,
∴∠ADB=∠ACB=90°.
(注:答案不唯一,合理即可)
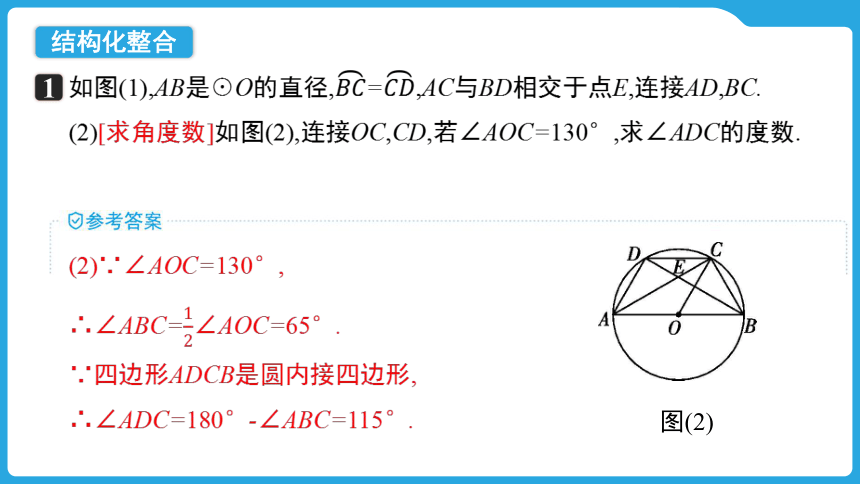
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(2)[求角度数]如图(2),连接OC,CD,若∠AOC=130°,求∠ADC的度数.
1
结构化整合
图(2)
(2)∵∠AOC=130°,
∴∠ABC=∠AOC=65°.
∵四边形ADCB是圆内接四边形,
∴∠ADC=180°-∠ABC=115°.
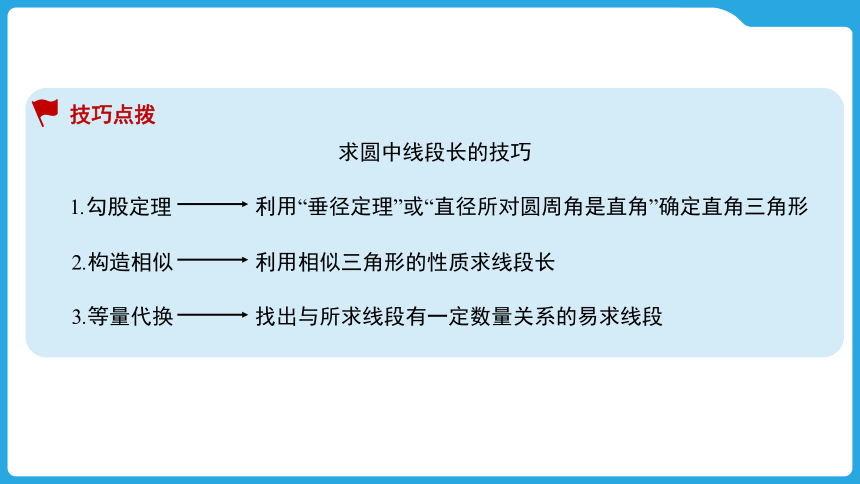
技巧点拨
遇:圆中求角度
想:圆中常用性质、定理
①圆周角是圆心角的一半
②圆内接四边形对角互补
③直径所对的圆周角是90°
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(3)[求线段长]如图(3),若CE=2,AE=6,求☉O的半径.
1
结构化整合
图(3)
(3)∵CE=2,AE=6,∴AC=8.
∵=,∴∠CAB=∠CBD.
∵∠ACB=∠BCE,
∴△ACB∽△BCE,
∴=,即=,
解得BC=4(负值已舍去).
∵AB是☉O的直径,∴∠ACB=90°,
∴AB===4,
∴OA=AB=2,
∴☉O的半径为2.
技巧点拨
求圆中线段长的技巧
1.勾股定理
利用“垂径定理”或“直径所对圆周角是直角”确定直角三角形
2.构造相似
利用相似三角形的性质求线段长
3.等量代换
找出与所求线段有一定数量关系的易求线段
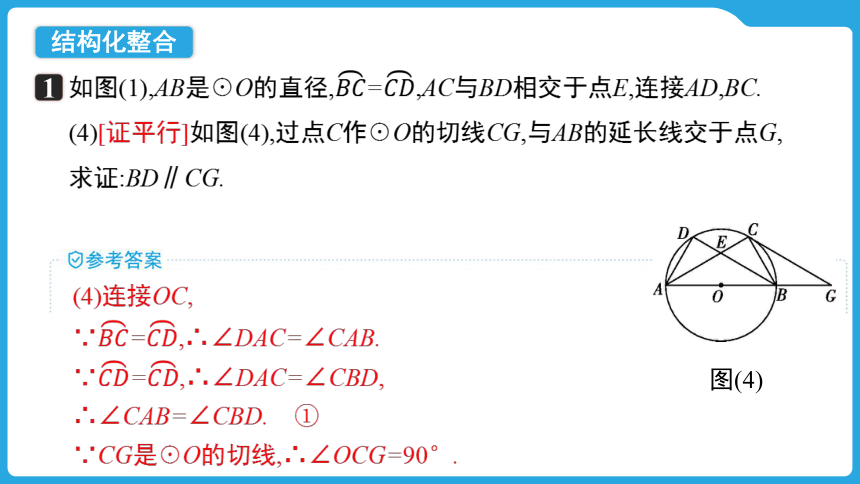
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(4)[证平行]如图(4),过点C作☉O的切线CG,与AB的延长线交于点G,求证:BD∥CG.
1
结构化整合
图(4)
(4)连接OC,
∵=,∴∠DAC=∠CAB.
∵=,∴∠DAC=∠CBD,
∴∠CAB=∠CBD. ①
∵CG是☉O的切线,∴∠OCG=90°.
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(4)[证平行]如图(4),过点C作☉O的切线CG,与AB的延长线交于点G,求证:BD∥CG.
1
结构化整合
图(4)
∵AB是☉O的直径,∴∠ACB=90°,
∴∠OCG=∠ACB,∴∠ACO=∠GCB.
∵OA=OC,∴∠CAB=∠ACO,
∴∠CAB=∠GCB. ②
由①②得,∠DBC=∠GCB,∴BD∥CG.
审题关键
关键1:遇到切线,连半径(切点与圆心的连线)
关键2:利用直角三角形,本题是指Rt△OCG
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(5)[证相似]如图(5),过点C作☉O的切线CG,与AB的延长线交于点G,连接CD,求证:△ADC∽△CBG.
1
结构化整合
图(5)
(5)连接OC,由(4)知,∠DAC=∠CAB,
∠CAB=∠GCB,∴∠DAC=∠GCB. ③
由(4)得,BD∥CG,∴∠DBA=∠CGA.
∵=,∴∠DCA=∠DBA,
∴∠DCA=∠CGB, ④ ∴由③④得,△ADC∽△CBG.
解题通法
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(6)[求阴影部分面积]如图(6),过点C作☉O的切线CG,与AB的延长线交于点G,若∠GCB=30°,BG=3,求阴影部分的面积.
1
结构化整合
图(6)
(6)连接OC,∵CG是☉O的切线,∴∠OCG=90°.
∵∠BCG=30°,∴∠OCB=60°.
又OC=OB,∴△COB是等边三角形,
∴∠COB=∠OBC=60°,∴∠G=∠GCB=30°,∴OB=CB=BG=3,
∴S阴影=S扇形COB-S△COB=-×3×=-.
解题通法
①求阴影部分的面积,联想“割补法”
②有“弧”找扇形,有“弦”找三角形
③判断各部分是加还是减
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(7)[判断四边形的形状]如图(7),过点C作☉O的切线CG,与AB的延长线交于点G,连接CD,OD,若∠GCB=30°,试判断四边形OBCD的形状,并说明理由.
1
结构化整合
图(7)
(7)四边形OBCD是菱形.
理由:连接OC,由(6)知,△OCB是等边三角形,
∴CB=OB.∵=,∴BC=CD.
∵OD=OB,∴OD=CD=CB=OB,∴四边形OBCD是菱形.
解题通法
改编自2023年贵州省中考第23题的设问
判定一个四边形是菱形的思路
2
[2024贵阳观山湖区模拟]如图,在△ABC的边BC上取一点O,以O为圆心,OC长为半径画☉O,☉O与边AB相切于点D,AC=AD,连接OA交☉O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是☉O的切线.
(2)若BC=6,cos B=,求☉O的半径长.
(3)在(2)的条件下,若F是AB的中点,求CE·CF的值.
2
[2024贵阳观山湖区模拟]如图,在△ABC的边BC上取一点O,以O为圆心,OC长为半径画☉O,☉O与边AB相切于点D,AC=AD,连接OA交☉O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是☉O的切线.
(1)证明:如图, 连接OD,
∵☉O与边AB相切于点D,∴OD⊥AB, 即∠ADO =90°.
在△ACO和△ADO中,∴△ACO≌△ADO(SSS),
∴∠ACO=∠ADO=90°.又∵OC是☉O的半径,∴AC是☉O的切线.
2
[2024贵阳观山湖区模拟]如图,在△ABC的边BC上取一点O,以O为圆心,OC长为半径画☉O,☉O与边AB相切于点D,AC=AD,连接OA交☉O于点E,连接CE,并延长交线段AB于点F.
(2)若BC=6,cos B=,求☉O的半径长.
(2)∵在Rt△ACB中,BC=6,cos B==,
∴AB=10,AC==8,
∴BD=10-8=2.
∵在Rt△ODB中,OB2=OD2+BD2,
∴(6-OC)2=OC2+4,解得OC=,∴☉O的半径长为 .
2
(3)在(2)的条件下,若F是AB的中点,求CE·CF的值.
(3)由(1)易得,∠AOC =∠AOD.
∵F是AB的中点, ∠ACB =90°,
∴AF =CF = BF,∴∠FCB=∠FBC.
∵OC=OE=,∴∠OCE=∠CEO,∴∠OEC=∠B.
∵∠OCE=∠FCB,∴ △OCE∽△FCB,
∴=,即=,∴CE·CF=OE·BC,∴CE·CF=16.
3
[2024遵义播州区模拟]如图,AB为☉O的直径,过☉O上一点D作切线CD,与AB的延长线交于点C,点E为☉O上一点,且=,连接DE交AB于点H,连接AD,DB,BE.
(1)写出图中一个与∠A相等的角: .
(2)求证:∠E=∠BDC.
(3)已知CD=4,CB=2,cos∠BDC=,求BE的长.
∠BDE(答案不唯一)
3
如图,AB为☉O的直径,过☉O上一点D作切线CD,与AB的延长线交于点C,点E为☉O上一点,且=,连接DE交AB于点H,连接AD,DB,BE.
(2)求证:∠E=∠BDC.
(2)证明:如图,连接OD,
∵CD为☉O的切线,∴OD⊥CD,∴∠ODC=90°.
∵AB为☉O的直径,∴∠ADB=90°.
∵∠ODA+∠ODB=90°,∠BDC+∠ODB=90°,
∴∠ODA=∠BDC.∵OD=OA,∴∠ODA=∠A,∴∠A=∠BDC.
∵∠E=∠A,∴∠E=∠BDC.
3
如图,AB为☉O的直径,过☉O上一点D作切线CD,与AB的延长线交于点C,点E为☉O上一点,且=,连接DE交AB于点H,连接AD,DB,BE.
(3)已知CD=4,CB=2,cos∠BDC=,求BE的长.
(3)设☉O的半径为r,则OD=OB=r,在Rt△OCD中,OD2+CD2=OC2,
即r2+42=(r+2)2,解得r=3,∴AB=6.
∵由(2)知,∠A=∠BDC,∴cos A=cos∠BDC=.
在Rt△ABD中,cos A==,∴AD=×6=,
∴BD==.∵=,∴BE=BD=.
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
题型二 圆的综合题
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(1)[证角相等]如图(1),写出一对相等的角,并说明你的理由.
1
结构化整合
图(1)
(1)解法一:
∠DAC=∠CAB.
理由:∵=,∴∠CAB=∠DAC.
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(1)[证角相等]如图(1),写出一对相等的角,并说明你的理由.
1
结构化整合
图(1)
(1)解法二:∠DAC=∠CBD.
理由:∵=,
∴∠DAC=∠CBD.
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(1)[证角相等]如图(1),写出一对相等的角,并说明你的理由.
1
结构化整合
图(1)
(1)解法三:∠ADB=∠ACB.
理由:∵AB是☉O的直径,
∴∠ADB=∠ACB=90°.
(注:答案不唯一,合理即可)
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(2)[求角度数]如图(2),连接OC,CD,若∠AOC=130°,求∠ADC的度数.
1
结构化整合
图(2)
(2)∵∠AOC=130°,
∴∠ABC=∠AOC=65°.
∵四边形ADCB是圆内接四边形,
∴∠ADC=180°-∠ABC=115°.
技巧点拨
遇:圆中求角度
想:圆中常用性质、定理
①圆周角是圆心角的一半
②圆内接四边形对角互补
③直径所对的圆周角是90°
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(3)[求线段长]如图(3),若CE=2,AE=6,求☉O的半径.
1
结构化整合
图(3)
(3)∵CE=2,AE=6,∴AC=8.
∵=,∴∠CAB=∠CBD.
∵∠ACB=∠BCE,
∴△ACB∽△BCE,
∴=,即=,
解得BC=4(负值已舍去).
∵AB是☉O的直径,∴∠ACB=90°,
∴AB===4,
∴OA=AB=2,
∴☉O的半径为2.
技巧点拨
求圆中线段长的技巧
1.勾股定理
利用“垂径定理”或“直径所对圆周角是直角”确定直角三角形
2.构造相似
利用相似三角形的性质求线段长
3.等量代换
找出与所求线段有一定数量关系的易求线段
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(4)[证平行]如图(4),过点C作☉O的切线CG,与AB的延长线交于点G,求证:BD∥CG.
1
结构化整合
图(4)
(4)连接OC,
∵=,∴∠DAC=∠CAB.
∵=,∴∠DAC=∠CBD,
∴∠CAB=∠CBD. ①
∵CG是☉O的切线,∴∠OCG=90°.
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(4)[证平行]如图(4),过点C作☉O的切线CG,与AB的延长线交于点G,求证:BD∥CG.
1
结构化整合
图(4)
∵AB是☉O的直径,∴∠ACB=90°,
∴∠OCG=∠ACB,∴∠ACO=∠GCB.
∵OA=OC,∴∠CAB=∠ACO,
∴∠CAB=∠GCB. ②
由①②得,∠DBC=∠GCB,∴BD∥CG.
审题关键
关键1:遇到切线,连半径(切点与圆心的连线)
关键2:利用直角三角形,本题是指Rt△OCG
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(5)[证相似]如图(5),过点C作☉O的切线CG,与AB的延长线交于点G,连接CD,求证:△ADC∽△CBG.
1
结构化整合
图(5)
(5)连接OC,由(4)知,∠DAC=∠CAB,
∠CAB=∠GCB,∴∠DAC=∠GCB. ③
由(4)得,BD∥CG,∴∠DBA=∠CGA.
∵=,∴∠DCA=∠DBA,
∴∠DCA=∠CGB, ④ ∴由③④得,△ADC∽△CBG.
解题通法
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(6)[求阴影部分面积]如图(6),过点C作☉O的切线CG,与AB的延长线交于点G,若∠GCB=30°,BG=3,求阴影部分的面积.
1
结构化整合
图(6)
(6)连接OC,∵CG是☉O的切线,∴∠OCG=90°.
∵∠BCG=30°,∴∠OCB=60°.
又OC=OB,∴△COB是等边三角形,
∴∠COB=∠OBC=60°,∴∠G=∠GCB=30°,∴OB=CB=BG=3,
∴S阴影=S扇形COB-S△COB=-×3×=-.
解题通法
①求阴影部分的面积,联想“割补法”
②有“弧”找扇形,有“弦”找三角形
③判断各部分是加还是减
如图(1),AB是☉O的直径,=,AC与BD相交于点E,连接AD,BC.
(7)[判断四边形的形状]如图(7),过点C作☉O的切线CG,与AB的延长线交于点G,连接CD,OD,若∠GCB=30°,试判断四边形OBCD的形状,并说明理由.
1
结构化整合
图(7)
(7)四边形OBCD是菱形.
理由:连接OC,由(6)知,△OCB是等边三角形,
∴CB=OB.∵=,∴BC=CD.
∵OD=OB,∴OD=CD=CB=OB,∴四边形OBCD是菱形.
解题通法
改编自2023年贵州省中考第23题的设问
判定一个四边形是菱形的思路
2
[2024贵阳观山湖区模拟]如图,在△ABC的边BC上取一点O,以O为圆心,OC长为半径画☉O,☉O与边AB相切于点D,AC=AD,连接OA交☉O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是☉O的切线.
(2)若BC=6,cos B=,求☉O的半径长.
(3)在(2)的条件下,若F是AB的中点,求CE·CF的值.
2
[2024贵阳观山湖区模拟]如图,在△ABC的边BC上取一点O,以O为圆心,OC长为半径画☉O,☉O与边AB相切于点D,AC=AD,连接OA交☉O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是☉O的切线.
(1)证明:如图, 连接OD,
∵☉O与边AB相切于点D,∴OD⊥AB, 即∠ADO =90°.
在△ACO和△ADO中,∴△ACO≌△ADO(SSS),
∴∠ACO=∠ADO=90°.又∵OC是☉O的半径,∴AC是☉O的切线.
2
[2024贵阳观山湖区模拟]如图,在△ABC的边BC上取一点O,以O为圆心,OC长为半径画☉O,☉O与边AB相切于点D,AC=AD,连接OA交☉O于点E,连接CE,并延长交线段AB于点F.
(2)若BC=6,cos B=,求☉O的半径长.
(2)∵在Rt△ACB中,BC=6,cos B==,
∴AB=10,AC==8,
∴BD=10-8=2.
∵在Rt△ODB中,OB2=OD2+BD2,
∴(6-OC)2=OC2+4,解得OC=,∴☉O的半径长为 .
2
(3)在(2)的条件下,若F是AB的中点,求CE·CF的值.
(3)由(1)易得,∠AOC =∠AOD.
∵F是AB的中点, ∠ACB =90°,
∴AF =CF = BF,∴∠FCB=∠FBC.
∵OC=OE=,∴∠OCE=∠CEO,∴∠OEC=∠B.
∵∠OCE=∠FCB,∴ △OCE∽△FCB,
∴=,即=,∴CE·CF=OE·BC,∴CE·CF=16.
3
[2024遵义播州区模拟]如图,AB为☉O的直径,过☉O上一点D作切线CD,与AB的延长线交于点C,点E为☉O上一点,且=,连接DE交AB于点H,连接AD,DB,BE.
(1)写出图中一个与∠A相等的角: .
(2)求证:∠E=∠BDC.
(3)已知CD=4,CB=2,cos∠BDC=,求BE的长.
∠BDE(答案不唯一)
3
如图,AB为☉O的直径,过☉O上一点D作切线CD,与AB的延长线交于点C,点E为☉O上一点,且=,连接DE交AB于点H,连接AD,DB,BE.
(2)求证:∠E=∠BDC.
(2)证明:如图,连接OD,
∵CD为☉O的切线,∴OD⊥CD,∴∠ODC=90°.
∵AB为☉O的直径,∴∠ADB=90°.
∵∠ODA+∠ODB=90°,∠BDC+∠ODB=90°,
∴∠ODA=∠BDC.∵OD=OA,∴∠ODA=∠A,∴∠A=∠BDC.
∵∠E=∠A,∴∠E=∠BDC.
3
如图,AB为☉O的直径,过☉O上一点D作切线CD,与AB的延长线交于点C,点E为☉O上一点,且=,连接DE交AB于点H,连接AD,DB,BE.
(3)已知CD=4,CB=2,cos∠BDC=,求BE的长.
(3)设☉O的半径为r,则OD=OB=r,在Rt△OCD中,OD2+CD2=OC2,
即r2+42=(r+2)2,解得r=3,∴AB=6.
∵由(2)知,∠A=∠BDC,∴cos A=cos∠BDC=.
在Rt△ABD中,cos A==,∴AD=×6=,
∴BD==.∵=,∴BE=BD=.
同课章节目录
