2025年中考数学二轮专题复习 大单元整合专题一 “见招出招”攻破常考几何模型 课件(共73张PPT)
文档属性
| 名称 | 2025年中考数学二轮专题复习 大单元整合专题一 “见招出招”攻破常考几何模型 课件(共73张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 29.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 00:00:00 | ||
图片预览







文档简介
(共73张PPT)
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
大单元整合专题一
“见招出招”攻破常考几何模型
类型1 中点模型
PART 01
问题1
与中位线有关
(见一个或两个中点)
(考虑中位线)
(1)见两个中点.
如图,点D,E分别是边
AB,AC的中点.
(2)见一个中点.
如图,点D是边AB的中点.
结论: ①DE∥BC,②DE=BC,③△ADE∽△ABC,
④S△ADE=S△ABC.
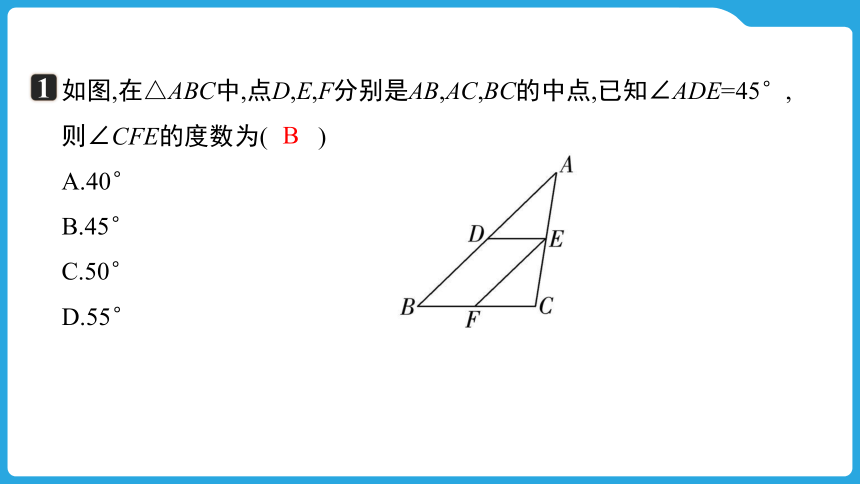
如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,已知∠ADE=45°,则∠CFE的度数为( )
A.40°
B.45°
C.50°
D.55°
1
B
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D,E分别为CN,MN的中点,则DE的最小值是 .
2
问题2
与直角三角形斜边上中点有关
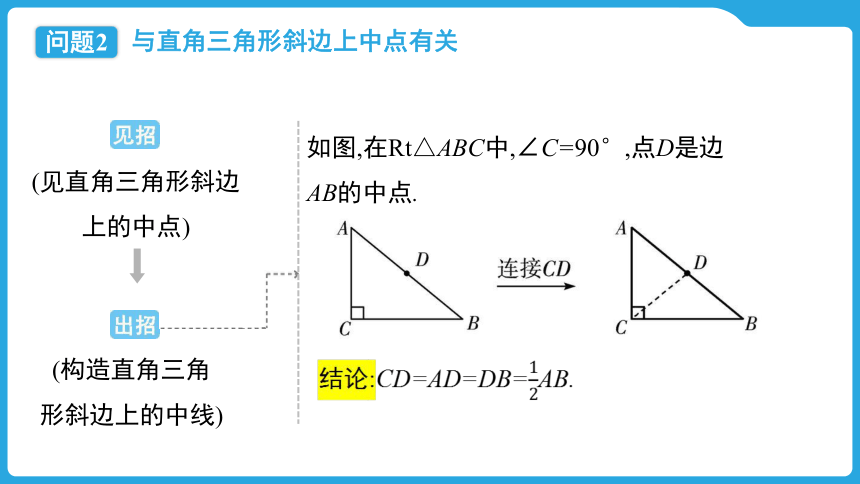
如图,在Rt△ABC中,∠C=90°,点D是边AB的中点.
结论:CD=AD=DB=AB.
(见直角三角形斜边上的中点)
(构造直角三角形斜边上的中线)
如图,一根木棍AB斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.变小
B.不变
C.变大
D.无法判断
3
B
如图,在△ABC中,∠BAC=90°,AB=AC=4,D是斜边BC的中点,E,F分别是AB,AC边上的点,且CF=AE,则四边形AEDF的面积为 .
4
4
提示 如图,S四边形AEDF =S△ADC
问题3
与等腰三角形底边上中点有关
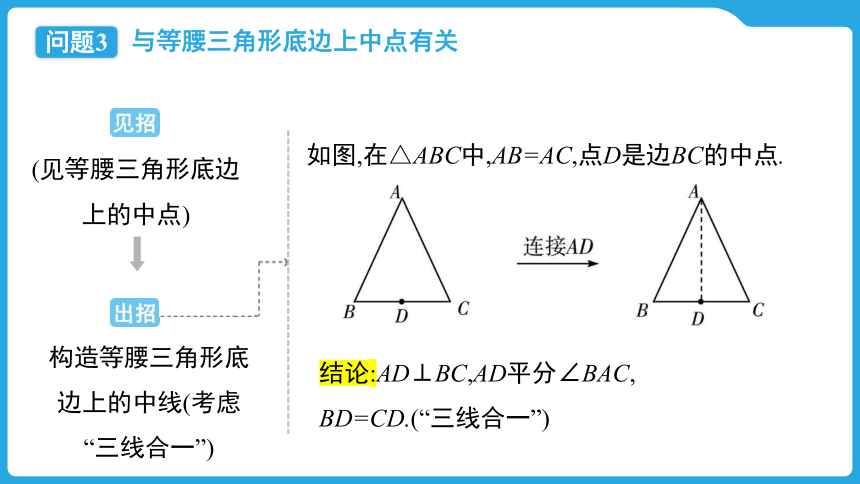
如图,在△ABC中,AB=AC,点D是边BC的中点.
结论:AD⊥BC,AD平分∠BAC,
BD=CD.(“三线合一”)
(见等腰三角形底边上的中点)
构造等腰三角形底边上的中线(考虑“三线合一”)
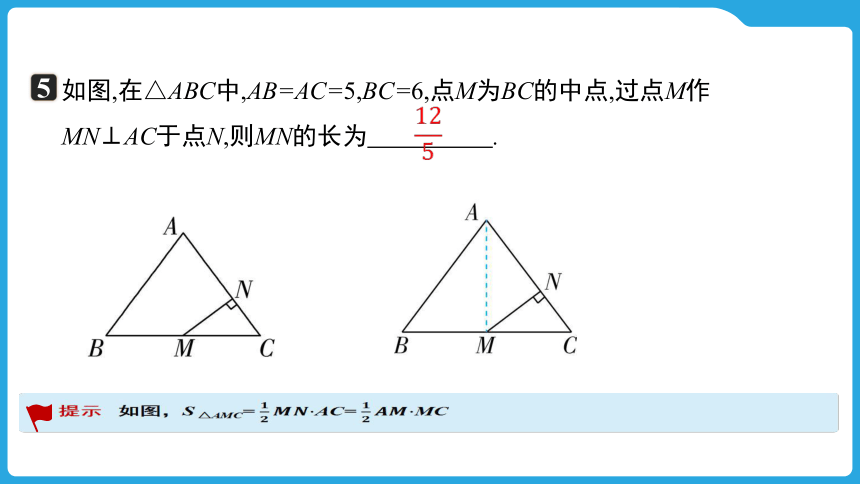
如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,过点M作MN⊥AC于点N,则MN的长为 .
5
提示 如图,S △AMC= AC= MC
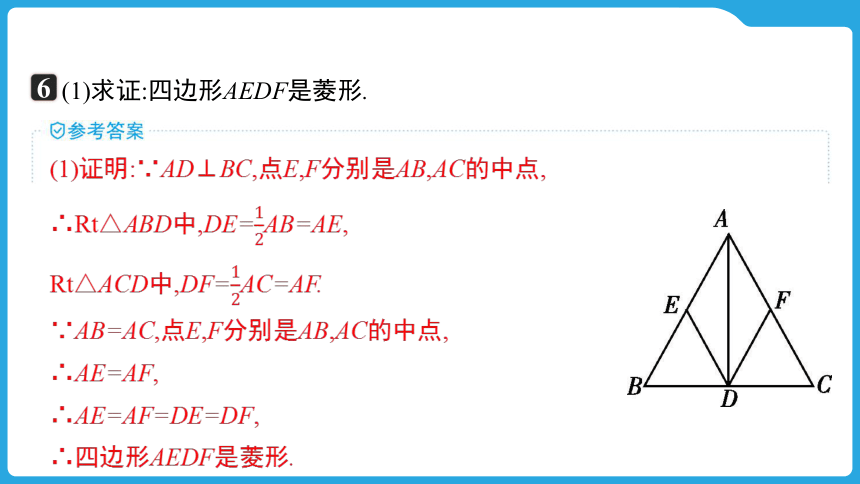
如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E,F分别是AB,AC的中点.
(1)求证:四边形AEDF是菱形.
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积.
6
(1)求证:四边形AEDF是菱形.
6
(1)证明:∵AD⊥BC,点E,F分别是AB,AC的中点,
∴Rt△ABD中,DE=AB=AE,
Rt△ACD中,DF=AC=AF.
∵AB=AC,点E,F分别是AB,AC的中点,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF是菱形.
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积.
6
(2)如图,连接EF交AD于点O,
∵菱形AEDF的周长为12,
∴AE=3.
设EF=x,AD=y,则x+y=7,
∴x2+2xy+y2=49.①
在Rt△AOE中,AO2+EO2=AE2,
∴(y)2+(x)2=32,
即x2+y2=36,②
把②代入①,可得2xy=13,
∴xy=,
∴菱形AEDF的面积为xy=.
问题4
与倍长中线、类中线有关
(1)倍长中线:如图,AD是△ABC的中线
结论:△ABD≌△ECD
(见中线、类中线)
(倍长中线、倍长类中线)
问题4
与倍长中线、类中线有关
(2)倍长类中线:如图,在△ABC中,D是BC的中点,E是AB上一点.
结论:△EBD≌△FCD
(见中线、类中线)
(倍长中线、倍长类中线)
如图,在△ABC中,∠ACB=120°,BC=4,点D为AB的中点,DC⊥BC,则△ABC的面积是 .
7
8
[2017贵阳24题节选(总12分)]
(1)阅读理解:如图(1),在四边形ABCD中,AB∥
DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB,AD,DC之间的等量关系为 .
8
图(1)
AD=AB+DC
(2)问题探究:如图(2),在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
8
图(2)
8
(2)AB=AF+CF.
证明:如图,延长AE交DF的延长线于点G,
∵E是BC的中点,
∴CE=BE.
∵AB∥DC,
∴∠BAE=∠G.
在△AEB和△GEC中,,
∴△AEB≌△GEC,
∴AB=GC.
∵AE是∠BAF的平分线,
∴∠BAG=∠FAG.
∵∠BAG=∠G,
∴∠FAG=∠G,
∴FA=FG,
∴AB=CG=GF+CF=AF+CF.
类型2 角平分线模型
PART 02
问题1
见角平分线,用性质定理
(见角平分线)
(用性质定理)
已知:如图,AP是∠MAN的平分线,OC⊥AN于点C.
作法:过点O作OB⊥AM于点B.
结论:①△ABO≌△ACO;②OB=OC;③AB=AC.
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E,再分别以点D,E为圆心,大于DE的长为半径画弧,两弧交于点F,作射线AF交边BC于点G.若CG=3,AB=10,则△ABG的面积是( )
A.15
B.10
C.3
D.30
1
A
问题2
角平分线+垂直,考虑三线合一
已知:如图,AP是∠MAN的平分线,BO⊥AP于点O.作法:延长BO交AN于点C.
结论:①AB=AC;②OB=OC;③∠ABC=∠ACB;
④△AOB≌△AOC.
(见角平分线+垂直)
(考虑三线合一)
如图,AD是△ABC的角平分线,过点B作AD的垂线[1],垂足为F,过点F作FG∥AB,交AC于点G,若AB=4,求线段FG的长.
2
【大招点拨】①见招:提取[1]中的信息得“角平分线+垂直”.②出招:辅助线的作法为延长BF交AC于点E.
如图,AD是△ABC的角平分线,过点B作AD的垂线[1],垂足为F,过点F作FG∥AB,交AC于点G,若AB=4,求线段FG的长.
2
如图,延长BF交AC于点E.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵BF⊥AD,∴∠AFB=∠AFE=90°.
∵AF=AF,∴△ABF≌△AEF(ASA),
∴AE=AB=4.
∵FG∥AB,∴∠BAF=∠AFG,
∴∠GAF=∠AFG,∴AG=FG.
∵∠FAG+∠AEF=∠AFG+∠EFG=90°,
∴∠GFE=∠GEF,∴FG=GE,
∴FG=AE=2.
问题3
角平分线+平行线,考虑等腰三角形
已知:如图,BD平分∠ABC,AD∥BC.
结论:AB=AD.
注:角平分线+平行四边形,考虑菱形.
(见角平分线+平行线)
(考虑等腰三角形)
如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧,交AN于点C,交AB于点D;②分别以点C,D为圆心、大于CD的长为半径作弧,两弧在∠NAB内交于点E;③作射线AE,交PQ于点F.若AB=2,
∠ABP=60°,则线段AF的长为 .
3
2
问题4
考虑截长补短构造对称图形
结论:△BOE≌△BOA, △BOD≌△BOC.
(见角平分线+求线段间
数量关系)
(考虑截长补短构造
对称图形)
已知:如图,△ABC中,BC>AB,BO平分∠ABC.
作法
如图,在△ABC中,AD平分∠BAC交BC于点D,且
∠B=2∠C,求证:AB+BD=AC.
4
截长法:
在AC上截取AE=AB,连接DE.
∵AD平分∠BAC,∴∠BAD=∠DAC.
在△ABD和△AED中,
∴△ABD≌△AED(SAS),
∴∠B=∠AED,BD=DE.
又∠B=2∠C,∴∠AED=2∠C.
而∠AED=∠C+∠EDC=2∠C,
∴∠C=∠EDC,∴DE=CE,
∴AB+BD=AE+CE=AC.
如图,在△ABC中,AD平分∠BAC交BC于点D,且
∠B=2∠C,求证:AB+BD=AC.
4
补短法:
延长AB到点F,使BF=BD,连接DF.
∵BF=BD,∴∠F=∠BDF,
∴∠ABC=∠F+∠BDF=2∠F.
又∠ABC=2∠C,
∴∠C=∠F.
在△ADF和△ADC中,
∴△ADF≌△ADC.
∴AC=AF,
∴AC=AF=AB+BF=AB+BD.
类型3 “一线三等角”模型
PART 03
(一条直线上有三个相等
的锐角、直角或钝角)
(构造“一线三等角”模型)
1.同侧型“一线三等角”(∠A=∠CED=∠B)
锐角“一线三等角” 直角“一线三等角”(“K”型图) 钝角“一线三等角”
结论: ①△ACE∽△BED;②若任一对应边相等,则△ACE≌△BED.
(一条直线上有三个相等
的锐角、直角或钝角)
(构造“一线三等角”模型)
2.异侧型“一线三等角”(∠FAC=∠ABD=∠CED)
锐角“一线三等角” 直角“一线三等角” 钝角“一线三等角”
结论: ①△ACE∽△BED;②若任一对应边相等,则△ACE≌△BED.
如图,一块含45°的三角板的一个顶点A与矩形ABCD的顶点重合,直角顶点E落在边BC上,另一顶点F恰好落在边CD的中点处,若BC=12,则AB的长为 .
1
问题1
与全等三角形结合
8
提示 如图,易得△ABE≌ △ECF,利用12-x=2x解得x
已知CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F分别是直线CD上的两点,连接AF,BE,∠BEC=∠CFA=α.
(1)如图(1),若直线CD经过∠BCA的内部,
且点E,F在射线CD上,∠BCA+α=180°.
求证:EF=BE-AF.
(2)如图(2),若直线CD不经过∠BCA的内部,
∠BCA=α,猜想线段EF,BE,AF之间的数量
关系,并加以证明.
2
图(1) 图(2)
问题1
与全等三角形结合
已知CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F分别是直线CD上的两点,连接AF,BE,∠BEC=∠CFA=α.
(1)如图(1),若直线CD经过∠BCA的内部,且点E,F在射线CD上,∠BCA+α=180°.求证:EF=BE-AF.
2
图(1)
问题1
与全等三角形结合
(1)证明:在△BCE中,∠CBE+∠BCE=180°-α.
∵∠BCA+α=180°,
∴∠BCA=180°-α,
∴∠CBE+∠BCE=∠BCA.
∵∠BCE+∠ACF=∠BCA,
∴∠CBE=∠ACF.
又∠BEC=∠CFA,CB=AC,
∴△BCE≌△CAF,
∴BE=CF,CE=AF.
∵EF=CF-CE,∴EF=BE-AF.
已知CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F分别是直线CD上的两点,连接AF,BE,∠BEC=∠CFA=α.
(2)如图(2),若直线CD不经过∠BCA的内部,∠BCA=α,猜想
线段EF,BE,AF之间的数量关系,并加以证明.
2
图(2)
问题1
与全等三角形结合
(2)猜想:EF=BE+AF.
证明:∵∠BCE+∠BCA+∠ACF=180°,
∴∠BCE+∠ACF=180°-α.
在△BCE中,∠CBE+∠BCE=180°-α,
∴∠CBE=∠ACF.
又∠BEC=∠CFA,CB=AC,
∴△BCE≌△CAF,
∴BE=CF,CE=AF.
∵EF=CF+CE,∴EF=BE+AF.
如图,沿直线DE折叠等边三角形纸片ABC,使点A落在BC边上任意一点F处(不与点B,C重合),已知△ABC的边长为9,D为AB上一点,BD=5,BF=2,则CE= .
3
问题2
与相似三角形结合
提示 如图,△DBF∽△FCE,即
【感知】如图(1),在正方形ABCD中,E为AB边上一点,连接DE,过点E作EF⊥DE交BC于点F.易证:△AED∽△BFE.(不需要证明)
【探究】
如图(2),在矩形ABCD中,E为AB边上一
点,连接DE,过点E作EF⊥DE交BC于点F.
(1)求证:△AED∽△BFE.
(2)若AB=10,AD=6,E为AB的中点,求BF
的长.
4
问题2
与相似三角形结合
图(1) 图(2)
如图(2),在矩形ABCD中,E为AB边上一点,连接DE,过点E作EF⊥DE交BC于点F.
(1)求证:△AED∽△BFE.
4
问题2
与相似三角形结合
图(1)
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴∠ADE+∠AED=90°.
∵DE⊥EF,
∴∠DEF=90°,
∴∠BEF+∠AED=90°,
∴∠ADE=∠BEF.
∵∠A=∠B,
∴△AED∽△BFE.
如图(2),在矩形ABCD中,E为AB边上一点,连接DE,过点E作EF⊥DE交BC于点F.
(2)若AB=10,AD=6,E为AB的中点,求BF的长.
4
问题2
与相似三角形结合
图(2)
(2)∵E为AB的中点,
∴AE=BE=5.
由(1)知,△AED∽△BFE,
∴=,即=, ∴BF=.
【应用】
如图(3),在△ABC中,∠ACB=90°,AC=BC,AB=4.E为AB边上一点(点E不与点A,B重合),连接CE,过点E作∠CEF=45°交BC于点F.当△CEF为等腰三角形时,BE的长为 ..
4
问题2
与相似三角形结合
图(3)
2或2
类型4 “手拉手”模型
PART 04
问题1
与全等三角形结合
(见双等腰、共顶点、
顶角相等、有旋转)
(连接“拉手线”,
利用全等)
如图,△ABC和△ADE是等腰三角形,∠BAC=
∠DAE,将△ADE绕点A旋转一定角度后,连接BD,CE.
结论: △ADB≌△AEC.
→
如图,△ACB和△ECD都是等腰直角三角形[1],∠ACB=∠ECD=90°,连接AE,D为AB边上一点,若AD=5,BD=12,则DE的长为( )
A.11
B.13
C.12
D.25
1
【大招点拨】①见招:由[1]判断出“手拉手”模型.②出招:可推出△ACE≌△BCD,再利用全等三角形的性质和勾股定理求DE的长.
B
如图(1),在等腰三角形ABC中,AB=AC,∠BAC=α,点D,E分别为AB,AC上的点,且AD=AE.将△ADE绕点A旋转,连接BD,CE,如图(2).
(1)图(1)中,BD与CE的数量关系为 .
2
图(1)
BD=CE
如图(1),在等腰三角形ABC中,AB=AC,∠BAC=α,点D,E分别为AB,AC上的点,且AD=AE.将△ADE绕点A旋转,连接BD,CE,如图(2).
(2)在图(2)的情形下,求证:BD=CE.
2
图(2)
证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE.
又AB=AC,AD=AE,∴△ABD≌△ACE,
∴BD=CE.
如图(1),在等腰三角形ABC中,AB=AC,∠BAC=α,点D,E分别为AB,AC上的点,且AD=AE.将△ADE绕点A旋转,连接BD,CE,如图(2).
(3)图(2)中,延长BD交CE于点F,求∠BFC的度数.(用含α的式子表示)
2
图(2)
(3)设BD,AC交于点O.
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
又∠BOA=∠COF,
∴∠BFC=∠BAC=α.
如图(1),在等腰三角形ABC中,AB=AC,∠BAC=α,点D,E分别为AB,AC上的点,且AD=AE.将△ADE绕点A旋转,连接BD,CE,如图(2).
(4)当α=60°时,如图(3).
①BD与CE的数量关系为 .
②延长CE,BD交于点F,则∠BFC的度数为 .
2
图(3)
BD=CE
60°
如图(1),在等腰三角形ABC中,AB=AC,∠BAC=α,点D,E分别为AB,AC上的点,且AD=AE.将△ADE绕点A旋转,连接BD,CE,如图(2).
(5)当α=90°时,如图(4).
①BD与CE的数量关系为 .
②设CE,BD交于点F,求∠BFC的度数.
2
图(4)
BD=CE
②设AB,CE交于点P,由题易得△EAC≌△DAB,
则∠ACE=∠ABD.
∵∠APC=∠FPB,
∴∠BFC=∠BAC=90°.
问题2
与相似三角形结合
已知△AOB和△COD是直角三角形,∠AOB=∠COD
=90°,点C,D分别在边OA,OB上,且CD∥AB,将△COD绕点O旋转一定角度后,直线AC,DB交于点E.
结论: ①当旋转过程中点A,O,C不共线时,有△AOC∽
△BOD;②AC⊥BD;③点E在△OAB的外接圆上.
(见非等腰、共顶点、
顶角相等、有旋转)
(连接“拉手线”,
利用相似)
如图,△ABC∽△ADE[1],∠BAC=∠DAE=90°[2],连接CE,AB=3,AC=4,点D在线段BC上运动,P为线段DE的中点[3],在点D的运动过程中,CP的最小值是 .
3
【大招点拨】由[1]得=,结合[2]推出△BAD∽△CAE,进而得∠DCE=90°,结合[3]可得CP=DE,再利用相似三角形的性质和“垂线段最短”求得CP的最小值.
2
如图(1),在△ABC中,=k,∠BAC=α,点D,E分别为AB,AC的中点.将△ADE绕点A旋转,连接BD,CE,如图(2).
(1)图(1)中,BD,CE的数量关系为 .
4
图(1)
=k
如图(1),在△ABC中,=k,∠BAC=α,点D,E分别为AB,AC的中点.将△ADE绕点A旋转,连接BD,CE,如图(2).
(2)在图(2)的情形下,(1)中结论是否仍然成立 若成立,请加以证明;若不成立,请说明理由.
4
图(2)
(2)成立.
证明:∵==,∴=.
又∠DAB=∠DAE-∠BAE=∠BAC-∠BAE=∠EAC,∴△DAB∽△EAC,∴==k.
如图(1),在△ABC中,=k,∠BAC=α,点D,E分别为AB,AC的中点.将△ADE绕点A旋转,连接BD,CE,如图(2).
(3)图(2)中,延长CE交BD于点F,求∠BFC的度数.
4
图(2)
(3)设AB,EF交于点O.
∵△DAB∽△EAC,∴∠ABD=∠ACE.
又∵∠BFC+∠ABD+∠BOF=180°,∠BAC+∠AC
E+∠AOC=180°,∠BOF=∠AOC,
∴∠BFC=∠BAC=α.
如图(1),在△ABC中,=k,∠BAC=α,点D,E分别为AB,AC的中点.将△ADE绕点A旋转,连接BD,CE,如图(2).
(4)当α=90°时,如图(3).
①BD与CE的数量关系为 .
②延长CE交BD于点F,则∠BFC的度数为 .
4
图(3)
=k
90°
如图(1),在△ABC中,=k,∠BAC=α,点D,E分别为AB,AC的中点.将△ADE绕点A旋转,连接BD,CE,如图(2).
(5)当α=45°,BA=BC时,如图(4).
①BD与CE的数量关系为 .
②设CE,BD交于点F,求∠BFC的度数.
4
图(4)
=
②设AB,CE交于点P,由题意易得△DAB∽△EAC,
∴∠DBA=∠ECA.
∵∠FPB=∠APC,∴∠BFC=∠BAC=45°.
类型5 “半角”模型
PART 05
问题1
120°角夹60°角
(见120°角夹60°角)
(利用旋转构造辅助线)
已知: 如图,①在四边形ABCD中,∠BAD=120°,∠B=
∠D=90°,AB=AD;②∠EAF=60°(内嵌的半角等于
两旁两个小角之和,即∠EAF=∠BAE+∠DAF=60°).
结论:①△ABE≌△ADG;②△AEF≌△AGF;
③BE+DF=EF.
构图: 如图,旋转△ABE至△ADG的位置,使AB与AD重合.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠BAD=
120°,AB=AD.∠MAN=60°,射线AM交线段BC于点E,射线AN交线段CD于点F,连接EF.
(1)判断BE,DF,EF之间的数量关系,并加以证明.
(2)若∠AEB=60°,则∠AFE= °.
1
如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠BAD=
120°,AB=AD.∠MAN=60°,射线AM交线段BC于点E,射线AN交线段CD于点F,连接EF.
(1)判断BE,DF,EF之间的数量关系,并加以证明.
1
(1)EF=BE+DF.
证明:将△ABE绕点A逆时针旋转120°,得到△ADK,如图,
则AK=AE,DK=BE,∠BAE=∠DAK,
∴∠KAF=∠DAK+∠DAF=∠BAE+∠DAF
=120°-60°=60°=∠EAF.
又AF=AF,∴△AKF≌△AEF,∴EF=KF=DK+DF=BE+DF.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠BAD=
120°,AB=AD.∠MAN=60°,射线AM交线段BC于点E,射线AN交线段CD于点F,连接EF.
(2)若∠AEB=60°,则∠AFE= °.
1
60
问题2
90°角夹45°角
已知: 如图,①四边形ABCD是正方形;
②∠EAF=45°(内嵌的半角等于两旁两个小角之和,即∠EAF=∠BAE+∠DAF=45°).
结论:①△ABE≌△ADG;②△AEF≌△AGF;
③BE+DF=EF.
(见90°角夹45°角)
(利用旋转或对称
构造辅助线)
构图:旋转△ABE至△ADG的位置,使AB与AD重合
问题2
90°角夹45°角
已知: 如图,①在Rt△PAB中,∠APB=90°,PA=PB;
②∠CPD=45°(内嵌的半角等于两旁两个小角之和,即∠CPD=∠APC+∠BPD=45°).
结论:AC2+BD2=CD2.
(见90°角夹45°角)
(利用旋转或对称
构造辅助线)
构图1: 旋转△PAC至△PBE的位置,使PA与PB重合,连接DE.
构图2: 先作△PAC关于直线PC的对称图形,再作△PBD关
于直线PD的对称图形,点A,B的对应点重合,为点A'.
如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN= .
2
点拨 如图,将△AMB沿点A逆时针旋转90°得到△AFC,连接NF,则△MAN≌△FAN,
MN=NF,结合勾股定理求解
3
如图(1),点M,N分别在正方形ABCD的边BC,CD上,∠MAN=45°,连接MN.
(1)求证:MN=BM+DN.请将下面的解题思路补充完整.
如图(2),把△ADN绕点A顺时针旋转 °至△ABE,使AD与AB重合.由∠ABE+∠ABC=180°,可知E,B,C三点共线,从而可证△AEM≌
,进而可得MN=BM+DN.
90
△ANM
3
(2)如图(3),当点M,N分别在正方形ABCD的边CB,DC的延长线上时,∠MAN=45°,连接MN.线段BM,DN和MN之间有怎样的数量关系 请写出你的猜想,并证明.
(2)MN=DN-BM,证明如下:如图,在DC上取一点G,使DG=BM.
3
(2)如图(3),当点M,N分别在正方形ABCD的边CB,DC的延长线上时,∠MAN=45°,连接MN.线段BM,DN和MN之间有怎样的数量关系 请写出你的猜想,并证明.
∵四边形ABCD是正方形,∴AD=AB,∠ADG=∠ABM=90°.
∵DG=BM,∴△ABM≌△ADG(SAS),∴AM=AG,∠MAB=∠GAD.
∵∠MAN=∠BAM+∠BAN=45°,∴∠GAD+∠BAN=45°,
∴∠GAN=45°,即∠MAN=∠GAN.
∵AN=AN,∴△MAN≌△GAN(SAS),
∴MN=NG=DN-DG=DN-BM,即MN=DN-BM.
类型6 “对角互补”模型
PART 05
类型6
“对角互补”模型
(见有一组对
角互为补角)
(构造辅助线:
作垂线或旋转)
特殊地,如图,∠AOB=90°,点C在∠AOB的平分线上,∠AOB+∠DCE=180°.
注:也可以是将△CFE绕点C旋转得到△CGD
结论:①△CGD≌△CFE;②CD=CE;③OD+
OE=OC;④若OC=a,则S四边形ODCE=
如图,已知∠AOB=60°,点P是∠AOB的平分线上的一个定点,点M,N分别在射线OA,OB上,且∠MPN与∠AOB互补[1].设OP=a,则四边形PMON的面积为 .
1
【大招点拨】①见招:由[1]得存在一组对角互为补角.②出招:过点P作PE⊥OA于点E,PF⊥OB于点F,可得△PFN≌△PEM,∴S四边形PMON=
S四边形PEOF=2S△POE,进而可求得面积.
a2
如图,在四边形ABCD中,∠BAD=∠BCD=90°[1],CA平分∠BCD[2],若BC =2,CD=4,则AC的长为 .
2
【大招点拨】①见招:由[1]得存在一组对角互为补角.②出招:结合[2],过点A分别向射线CB和射线CD作垂线,再利用全等三角形的判定与性质和勾股定理可求出AC的长.
3
如图,在等腰直角三角形ABC中,∠B=90°,BC=4,点D是AB的中点,点E为BC上一点,且BE=1,点F为AC上一点,若∠FDE=135°,则DF的长度为 .
3
点拨 作辅助线如图,易得∠MDB=∠FDE=135°,由△FMD∽△EBD可得DF的长
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
大单元整合专题一
“见招出招”攻破常考几何模型
类型1 中点模型
PART 01
问题1
与中位线有关
(见一个或两个中点)
(考虑中位线)
(1)见两个中点.
如图,点D,E分别是边
AB,AC的中点.
(2)见一个中点.
如图,点D是边AB的中点.
结论: ①DE∥BC,②DE=BC,③△ADE∽△ABC,
④S△ADE=S△ABC.
如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,已知∠ADE=45°,则∠CFE的度数为( )
A.40°
B.45°
C.50°
D.55°
1
B
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D,E分别为CN,MN的中点,则DE的最小值是 .
2
问题2
与直角三角形斜边上中点有关
如图,在Rt△ABC中,∠C=90°,点D是边AB的中点.
结论:CD=AD=DB=AB.
(见直角三角形斜边上的中点)
(构造直角三角形斜边上的中线)
如图,一根木棍AB斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.变小
B.不变
C.变大
D.无法判断
3
B
如图,在△ABC中,∠BAC=90°,AB=AC=4,D是斜边BC的中点,E,F分别是AB,AC边上的点,且CF=AE,则四边形AEDF的面积为 .
4
4
提示 如图,S四边形AEDF =S△ADC
问题3
与等腰三角形底边上中点有关
如图,在△ABC中,AB=AC,点D是边BC的中点.
结论:AD⊥BC,AD平分∠BAC,
BD=CD.(“三线合一”)
(见等腰三角形底边上的中点)
构造等腰三角形底边上的中线(考虑“三线合一”)
如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,过点M作MN⊥AC于点N,则MN的长为 .
5
提示 如图,S △AMC= AC= MC
如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E,F分别是AB,AC的中点.
(1)求证:四边形AEDF是菱形.
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积.
6
(1)求证:四边形AEDF是菱形.
6
(1)证明:∵AD⊥BC,点E,F分别是AB,AC的中点,
∴Rt△ABD中,DE=AB=AE,
Rt△ACD中,DF=AC=AF.
∵AB=AC,点E,F分别是AB,AC的中点,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF是菱形.
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积.
6
(2)如图,连接EF交AD于点O,
∵菱形AEDF的周长为12,
∴AE=3.
设EF=x,AD=y,则x+y=7,
∴x2+2xy+y2=49.①
在Rt△AOE中,AO2+EO2=AE2,
∴(y)2+(x)2=32,
即x2+y2=36,②
把②代入①,可得2xy=13,
∴xy=,
∴菱形AEDF的面积为xy=.
问题4
与倍长中线、类中线有关
(1)倍长中线:如图,AD是△ABC的中线
结论:△ABD≌△ECD
(见中线、类中线)
(倍长中线、倍长类中线)
问题4
与倍长中线、类中线有关
(2)倍长类中线:如图,在△ABC中,D是BC的中点,E是AB上一点.
结论:△EBD≌△FCD
(见中线、类中线)
(倍长中线、倍长类中线)
如图,在△ABC中,∠ACB=120°,BC=4,点D为AB的中点,DC⊥BC,则△ABC的面积是 .
7
8
[2017贵阳24题节选(总12分)]
(1)阅读理解:如图(1),在四边形ABCD中,AB∥
DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB,AD,DC之间的等量关系为 .
8
图(1)
AD=AB+DC
(2)问题探究:如图(2),在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
8
图(2)
8
(2)AB=AF+CF.
证明:如图,延长AE交DF的延长线于点G,
∵E是BC的中点,
∴CE=BE.
∵AB∥DC,
∴∠BAE=∠G.
在△AEB和△GEC中,,
∴△AEB≌△GEC,
∴AB=GC.
∵AE是∠BAF的平分线,
∴∠BAG=∠FAG.
∵∠BAG=∠G,
∴∠FAG=∠G,
∴FA=FG,
∴AB=CG=GF+CF=AF+CF.
类型2 角平分线模型
PART 02
问题1
见角平分线,用性质定理
(见角平分线)
(用性质定理)
已知:如图,AP是∠MAN的平分线,OC⊥AN于点C.
作法:过点O作OB⊥AM于点B.
结论:①△ABO≌△ACO;②OB=OC;③AB=AC.
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E,再分别以点D,E为圆心,大于DE的长为半径画弧,两弧交于点F,作射线AF交边BC于点G.若CG=3,AB=10,则△ABG的面积是( )
A.15
B.10
C.3
D.30
1
A
问题2
角平分线+垂直,考虑三线合一
已知:如图,AP是∠MAN的平分线,BO⊥AP于点O.作法:延长BO交AN于点C.
结论:①AB=AC;②OB=OC;③∠ABC=∠ACB;
④△AOB≌△AOC.
(见角平分线+垂直)
(考虑三线合一)
如图,AD是△ABC的角平分线,过点B作AD的垂线[1],垂足为F,过点F作FG∥AB,交AC于点G,若AB=4,求线段FG的长.
2
【大招点拨】①见招:提取[1]中的信息得“角平分线+垂直”.②出招:辅助线的作法为延长BF交AC于点E.
如图,AD是△ABC的角平分线,过点B作AD的垂线[1],垂足为F,过点F作FG∥AB,交AC于点G,若AB=4,求线段FG的长.
2
如图,延长BF交AC于点E.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵BF⊥AD,∴∠AFB=∠AFE=90°.
∵AF=AF,∴△ABF≌△AEF(ASA),
∴AE=AB=4.
∵FG∥AB,∴∠BAF=∠AFG,
∴∠GAF=∠AFG,∴AG=FG.
∵∠FAG+∠AEF=∠AFG+∠EFG=90°,
∴∠GFE=∠GEF,∴FG=GE,
∴FG=AE=2.
问题3
角平分线+平行线,考虑等腰三角形
已知:如图,BD平分∠ABC,AD∥BC.
结论:AB=AD.
注:角平分线+平行四边形,考虑菱形.
(见角平分线+平行线)
(考虑等腰三角形)
如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧,交AN于点C,交AB于点D;②分别以点C,D为圆心、大于CD的长为半径作弧,两弧在∠NAB内交于点E;③作射线AE,交PQ于点F.若AB=2,
∠ABP=60°,则线段AF的长为 .
3
2
问题4
考虑截长补短构造对称图形
结论:△BOE≌△BOA, △BOD≌△BOC.
(见角平分线+求线段间
数量关系)
(考虑截长补短构造
对称图形)
已知:如图,△ABC中,BC>AB,BO平分∠ABC.
作法
如图,在△ABC中,AD平分∠BAC交BC于点D,且
∠B=2∠C,求证:AB+BD=AC.
4
截长法:
在AC上截取AE=AB,连接DE.
∵AD平分∠BAC,∴∠BAD=∠DAC.
在△ABD和△AED中,
∴△ABD≌△AED(SAS),
∴∠B=∠AED,BD=DE.
又∠B=2∠C,∴∠AED=2∠C.
而∠AED=∠C+∠EDC=2∠C,
∴∠C=∠EDC,∴DE=CE,
∴AB+BD=AE+CE=AC.
如图,在△ABC中,AD平分∠BAC交BC于点D,且
∠B=2∠C,求证:AB+BD=AC.
4
补短法:
延长AB到点F,使BF=BD,连接DF.
∵BF=BD,∴∠F=∠BDF,
∴∠ABC=∠F+∠BDF=2∠F.
又∠ABC=2∠C,
∴∠C=∠F.
在△ADF和△ADC中,
∴△ADF≌△ADC.
∴AC=AF,
∴AC=AF=AB+BF=AB+BD.
类型3 “一线三等角”模型
PART 03
(一条直线上有三个相等
的锐角、直角或钝角)
(构造“一线三等角”模型)
1.同侧型“一线三等角”(∠A=∠CED=∠B)
锐角“一线三等角” 直角“一线三等角”(“K”型图) 钝角“一线三等角”
结论: ①△ACE∽△BED;②若任一对应边相等,则△ACE≌△BED.
(一条直线上有三个相等
的锐角、直角或钝角)
(构造“一线三等角”模型)
2.异侧型“一线三等角”(∠FAC=∠ABD=∠CED)
锐角“一线三等角” 直角“一线三等角” 钝角“一线三等角”
结论: ①△ACE∽△BED;②若任一对应边相等,则△ACE≌△BED.
如图,一块含45°的三角板的一个顶点A与矩形ABCD的顶点重合,直角顶点E落在边BC上,另一顶点F恰好落在边CD的中点处,若BC=12,则AB的长为 .
1
问题1
与全等三角形结合
8
提示 如图,易得△ABE≌ △ECF,利用12-x=2x解得x
已知CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F分别是直线CD上的两点,连接AF,BE,∠BEC=∠CFA=α.
(1)如图(1),若直线CD经过∠BCA的内部,
且点E,F在射线CD上,∠BCA+α=180°.
求证:EF=BE-AF.
(2)如图(2),若直线CD不经过∠BCA的内部,
∠BCA=α,猜想线段EF,BE,AF之间的数量
关系,并加以证明.
2
图(1) 图(2)
问题1
与全等三角形结合
已知CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F分别是直线CD上的两点,连接AF,BE,∠BEC=∠CFA=α.
(1)如图(1),若直线CD经过∠BCA的内部,且点E,F在射线CD上,∠BCA+α=180°.求证:EF=BE-AF.
2
图(1)
问题1
与全等三角形结合
(1)证明:在△BCE中,∠CBE+∠BCE=180°-α.
∵∠BCA+α=180°,
∴∠BCA=180°-α,
∴∠CBE+∠BCE=∠BCA.
∵∠BCE+∠ACF=∠BCA,
∴∠CBE=∠ACF.
又∠BEC=∠CFA,CB=AC,
∴△BCE≌△CAF,
∴BE=CF,CE=AF.
∵EF=CF-CE,∴EF=BE-AF.
已知CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F分别是直线CD上的两点,连接AF,BE,∠BEC=∠CFA=α.
(2)如图(2),若直线CD不经过∠BCA的内部,∠BCA=α,猜想
线段EF,BE,AF之间的数量关系,并加以证明.
2
图(2)
问题1
与全等三角形结合
(2)猜想:EF=BE+AF.
证明:∵∠BCE+∠BCA+∠ACF=180°,
∴∠BCE+∠ACF=180°-α.
在△BCE中,∠CBE+∠BCE=180°-α,
∴∠CBE=∠ACF.
又∠BEC=∠CFA,CB=AC,
∴△BCE≌△CAF,
∴BE=CF,CE=AF.
∵EF=CF+CE,∴EF=BE+AF.
如图,沿直线DE折叠等边三角形纸片ABC,使点A落在BC边上任意一点F处(不与点B,C重合),已知△ABC的边长为9,D为AB上一点,BD=5,BF=2,则CE= .
3
问题2
与相似三角形结合
提示 如图,△DBF∽△FCE,即
【感知】如图(1),在正方形ABCD中,E为AB边上一点,连接DE,过点E作EF⊥DE交BC于点F.易证:△AED∽△BFE.(不需要证明)
【探究】
如图(2),在矩形ABCD中,E为AB边上一
点,连接DE,过点E作EF⊥DE交BC于点F.
(1)求证:△AED∽△BFE.
(2)若AB=10,AD=6,E为AB的中点,求BF
的长.
4
问题2
与相似三角形结合
图(1) 图(2)
如图(2),在矩形ABCD中,E为AB边上一点,连接DE,过点E作EF⊥DE交BC于点F.
(1)求证:△AED∽△BFE.
4
问题2
与相似三角形结合
图(1)
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴∠ADE+∠AED=90°.
∵DE⊥EF,
∴∠DEF=90°,
∴∠BEF+∠AED=90°,
∴∠ADE=∠BEF.
∵∠A=∠B,
∴△AED∽△BFE.
如图(2),在矩形ABCD中,E为AB边上一点,连接DE,过点E作EF⊥DE交BC于点F.
(2)若AB=10,AD=6,E为AB的中点,求BF的长.
4
问题2
与相似三角形结合
图(2)
(2)∵E为AB的中点,
∴AE=BE=5.
由(1)知,△AED∽△BFE,
∴=,即=, ∴BF=.
【应用】
如图(3),在△ABC中,∠ACB=90°,AC=BC,AB=4.E为AB边上一点(点E不与点A,B重合),连接CE,过点E作∠CEF=45°交BC于点F.当△CEF为等腰三角形时,BE的长为 ..
4
问题2
与相似三角形结合
图(3)
2或2
类型4 “手拉手”模型
PART 04
问题1
与全等三角形结合
(见双等腰、共顶点、
顶角相等、有旋转)
(连接“拉手线”,
利用全等)
如图,△ABC和△ADE是等腰三角形,∠BAC=
∠DAE,将△ADE绕点A旋转一定角度后,连接BD,CE.
结论: △ADB≌△AEC.
→
如图,△ACB和△ECD都是等腰直角三角形[1],∠ACB=∠ECD=90°,连接AE,D为AB边上一点,若AD=5,BD=12,则DE的长为( )
A.11
B.13
C.12
D.25
1
【大招点拨】①见招:由[1]判断出“手拉手”模型.②出招:可推出△ACE≌△BCD,再利用全等三角形的性质和勾股定理求DE的长.
B
如图(1),在等腰三角形ABC中,AB=AC,∠BAC=α,点D,E分别为AB,AC上的点,且AD=AE.将△ADE绕点A旋转,连接BD,CE,如图(2).
(1)图(1)中,BD与CE的数量关系为 .
2
图(1)
BD=CE
如图(1),在等腰三角形ABC中,AB=AC,∠BAC=α,点D,E分别为AB,AC上的点,且AD=AE.将△ADE绕点A旋转,连接BD,CE,如图(2).
(2)在图(2)的情形下,求证:BD=CE.
2
图(2)
证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE.
又AB=AC,AD=AE,∴△ABD≌△ACE,
∴BD=CE.
如图(1),在等腰三角形ABC中,AB=AC,∠BAC=α,点D,E分别为AB,AC上的点,且AD=AE.将△ADE绕点A旋转,连接BD,CE,如图(2).
(3)图(2)中,延长BD交CE于点F,求∠BFC的度数.(用含α的式子表示)
2
图(2)
(3)设BD,AC交于点O.
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
又∠BOA=∠COF,
∴∠BFC=∠BAC=α.
如图(1),在等腰三角形ABC中,AB=AC,∠BAC=α,点D,E分别为AB,AC上的点,且AD=AE.将△ADE绕点A旋转,连接BD,CE,如图(2).
(4)当α=60°时,如图(3).
①BD与CE的数量关系为 .
②延长CE,BD交于点F,则∠BFC的度数为 .
2
图(3)
BD=CE
60°
如图(1),在等腰三角形ABC中,AB=AC,∠BAC=α,点D,E分别为AB,AC上的点,且AD=AE.将△ADE绕点A旋转,连接BD,CE,如图(2).
(5)当α=90°时,如图(4).
①BD与CE的数量关系为 .
②设CE,BD交于点F,求∠BFC的度数.
2
图(4)
BD=CE
②设AB,CE交于点P,由题易得△EAC≌△DAB,
则∠ACE=∠ABD.
∵∠APC=∠FPB,
∴∠BFC=∠BAC=90°.
问题2
与相似三角形结合
已知△AOB和△COD是直角三角形,∠AOB=∠COD
=90°,点C,D分别在边OA,OB上,且CD∥AB,将△COD绕点O旋转一定角度后,直线AC,DB交于点E.
结论: ①当旋转过程中点A,O,C不共线时,有△AOC∽
△BOD;②AC⊥BD;③点E在△OAB的外接圆上.
(见非等腰、共顶点、
顶角相等、有旋转)
(连接“拉手线”,
利用相似)
如图,△ABC∽△ADE[1],∠BAC=∠DAE=90°[2],连接CE,AB=3,AC=4,点D在线段BC上运动,P为线段DE的中点[3],在点D的运动过程中,CP的最小值是 .
3
【大招点拨】由[1]得=,结合[2]推出△BAD∽△CAE,进而得∠DCE=90°,结合[3]可得CP=DE,再利用相似三角形的性质和“垂线段最短”求得CP的最小值.
2
如图(1),在△ABC中,=k,∠BAC=α,点D,E分别为AB,AC的中点.将△ADE绕点A旋转,连接BD,CE,如图(2).
(1)图(1)中,BD,CE的数量关系为 .
4
图(1)
=k
如图(1),在△ABC中,=k,∠BAC=α,点D,E分别为AB,AC的中点.将△ADE绕点A旋转,连接BD,CE,如图(2).
(2)在图(2)的情形下,(1)中结论是否仍然成立 若成立,请加以证明;若不成立,请说明理由.
4
图(2)
(2)成立.
证明:∵==,∴=.
又∠DAB=∠DAE-∠BAE=∠BAC-∠BAE=∠EAC,∴△DAB∽△EAC,∴==k.
如图(1),在△ABC中,=k,∠BAC=α,点D,E分别为AB,AC的中点.将△ADE绕点A旋转,连接BD,CE,如图(2).
(3)图(2)中,延长CE交BD于点F,求∠BFC的度数.
4
图(2)
(3)设AB,EF交于点O.
∵△DAB∽△EAC,∴∠ABD=∠ACE.
又∵∠BFC+∠ABD+∠BOF=180°,∠BAC+∠AC
E+∠AOC=180°,∠BOF=∠AOC,
∴∠BFC=∠BAC=α.
如图(1),在△ABC中,=k,∠BAC=α,点D,E分别为AB,AC的中点.将△ADE绕点A旋转,连接BD,CE,如图(2).
(4)当α=90°时,如图(3).
①BD与CE的数量关系为 .
②延长CE交BD于点F,则∠BFC的度数为 .
4
图(3)
=k
90°
如图(1),在△ABC中,=k,∠BAC=α,点D,E分别为AB,AC的中点.将△ADE绕点A旋转,连接BD,CE,如图(2).
(5)当α=45°,BA=BC时,如图(4).
①BD与CE的数量关系为 .
②设CE,BD交于点F,求∠BFC的度数.
4
图(4)
=
②设AB,CE交于点P,由题意易得△DAB∽△EAC,
∴∠DBA=∠ECA.
∵∠FPB=∠APC,∴∠BFC=∠BAC=45°.
类型5 “半角”模型
PART 05
问题1
120°角夹60°角
(见120°角夹60°角)
(利用旋转构造辅助线)
已知: 如图,①在四边形ABCD中,∠BAD=120°,∠B=
∠D=90°,AB=AD;②∠EAF=60°(内嵌的半角等于
两旁两个小角之和,即∠EAF=∠BAE+∠DAF=60°).
结论:①△ABE≌△ADG;②△AEF≌△AGF;
③BE+DF=EF.
构图: 如图,旋转△ABE至△ADG的位置,使AB与AD重合.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠BAD=
120°,AB=AD.∠MAN=60°,射线AM交线段BC于点E,射线AN交线段CD于点F,连接EF.
(1)判断BE,DF,EF之间的数量关系,并加以证明.
(2)若∠AEB=60°,则∠AFE= °.
1
如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠BAD=
120°,AB=AD.∠MAN=60°,射线AM交线段BC于点E,射线AN交线段CD于点F,连接EF.
(1)判断BE,DF,EF之间的数量关系,并加以证明.
1
(1)EF=BE+DF.
证明:将△ABE绕点A逆时针旋转120°,得到△ADK,如图,
则AK=AE,DK=BE,∠BAE=∠DAK,
∴∠KAF=∠DAK+∠DAF=∠BAE+∠DAF
=120°-60°=60°=∠EAF.
又AF=AF,∴△AKF≌△AEF,∴EF=KF=DK+DF=BE+DF.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠BAD=
120°,AB=AD.∠MAN=60°,射线AM交线段BC于点E,射线AN交线段CD于点F,连接EF.
(2)若∠AEB=60°,则∠AFE= °.
1
60
问题2
90°角夹45°角
已知: 如图,①四边形ABCD是正方形;
②∠EAF=45°(内嵌的半角等于两旁两个小角之和,即∠EAF=∠BAE+∠DAF=45°).
结论:①△ABE≌△ADG;②△AEF≌△AGF;
③BE+DF=EF.
(见90°角夹45°角)
(利用旋转或对称
构造辅助线)
构图:旋转△ABE至△ADG的位置,使AB与AD重合
问题2
90°角夹45°角
已知: 如图,①在Rt△PAB中,∠APB=90°,PA=PB;
②∠CPD=45°(内嵌的半角等于两旁两个小角之和,即∠CPD=∠APC+∠BPD=45°).
结论:AC2+BD2=CD2.
(见90°角夹45°角)
(利用旋转或对称
构造辅助线)
构图1: 旋转△PAC至△PBE的位置,使PA与PB重合,连接DE.
构图2: 先作△PAC关于直线PC的对称图形,再作△PBD关
于直线PD的对称图形,点A,B的对应点重合,为点A'.
如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN= .
2
点拨 如图,将△AMB沿点A逆时针旋转90°得到△AFC,连接NF,则△MAN≌△FAN,
MN=NF,结合勾股定理求解
3
如图(1),点M,N分别在正方形ABCD的边BC,CD上,∠MAN=45°,连接MN.
(1)求证:MN=BM+DN.请将下面的解题思路补充完整.
如图(2),把△ADN绕点A顺时针旋转 °至△ABE,使AD与AB重合.由∠ABE+∠ABC=180°,可知E,B,C三点共线,从而可证△AEM≌
,进而可得MN=BM+DN.
90
△ANM
3
(2)如图(3),当点M,N分别在正方形ABCD的边CB,DC的延长线上时,∠MAN=45°,连接MN.线段BM,DN和MN之间有怎样的数量关系 请写出你的猜想,并证明.
(2)MN=DN-BM,证明如下:如图,在DC上取一点G,使DG=BM.
3
(2)如图(3),当点M,N分别在正方形ABCD的边CB,DC的延长线上时,∠MAN=45°,连接MN.线段BM,DN和MN之间有怎样的数量关系 请写出你的猜想,并证明.
∵四边形ABCD是正方形,∴AD=AB,∠ADG=∠ABM=90°.
∵DG=BM,∴△ABM≌△ADG(SAS),∴AM=AG,∠MAB=∠GAD.
∵∠MAN=∠BAM+∠BAN=45°,∴∠GAD+∠BAN=45°,
∴∠GAN=45°,即∠MAN=∠GAN.
∵AN=AN,∴△MAN≌△GAN(SAS),
∴MN=NG=DN-DG=DN-BM,即MN=DN-BM.
类型6 “对角互补”模型
PART 05
类型6
“对角互补”模型
(见有一组对
角互为补角)
(构造辅助线:
作垂线或旋转)
特殊地,如图,∠AOB=90°,点C在∠AOB的平分线上,∠AOB+∠DCE=180°.
注:也可以是将△CFE绕点C旋转得到△CGD
结论:①△CGD≌△CFE;②CD=CE;③OD+
OE=OC;④若OC=a,则S四边形ODCE=
如图,已知∠AOB=60°,点P是∠AOB的平分线上的一个定点,点M,N分别在射线OA,OB上,且∠MPN与∠AOB互补[1].设OP=a,则四边形PMON的面积为 .
1
【大招点拨】①见招:由[1]得存在一组对角互为补角.②出招:过点P作PE⊥OA于点E,PF⊥OB于点F,可得△PFN≌△PEM,∴S四边形PMON=
S四边形PEOF=2S△POE,进而可求得面积.
a2
如图,在四边形ABCD中,∠BAD=∠BCD=90°[1],CA平分∠BCD[2],若BC =2,CD=4,则AC的长为 .
2
【大招点拨】①见招:由[1]得存在一组对角互为补角.②出招:结合[2],过点A分别向射线CB和射线CD作垂线,再利用全等三角形的判定与性质和勾股定理可求出AC的长.
3
如图,在等腰直角三角形ABC中,∠B=90°,BC=4,点D是AB的中点,点E为BC上一点,且BE=1,点F为AC上一点,若∠FDE=135°,则DF的长度为 .
3
点拨 作辅助线如图,易得∠MDB=∠FDE=135°,由△FMD∽△EBD可得DF的长
同课章节目录
