2025年中考数学二轮专题复习 题型三-二次函数的实际应用 课件(共24张PPT)
文档属性
| 名称 | 2025年中考数学二轮专题复习 题型三-二次函数的实际应用 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 26.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
题型三 二次函数的实际应用
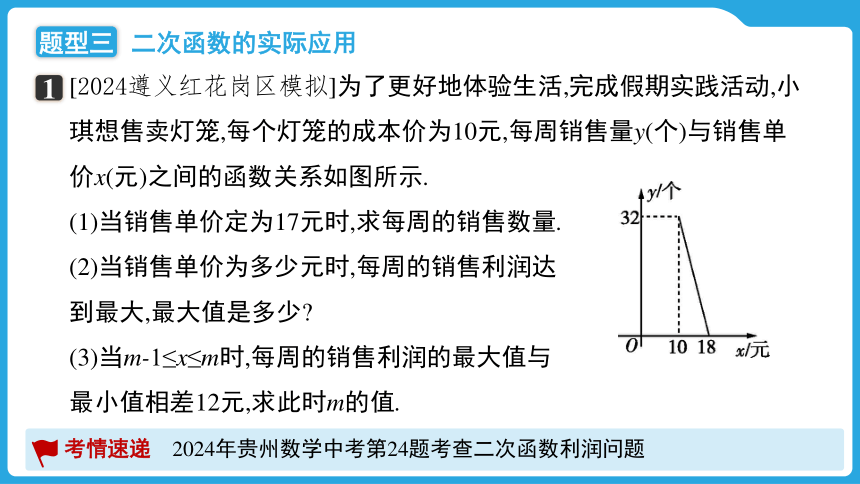
[2024遵义红花岗区模拟]为了更好地体验生活,完成假期实践活动,小琪想售卖灯笼,每个灯笼的成本价为10元,每周销售量y(个)与销售单价x(元)之间的函数关系如图所示.
(1)当销售单价定为17元时,求每周的销售数量.
(2)当销售单价为多少元时,每周的销售利润达
到最大,最大值是多少
(3)当m-1≤x≤m时,每周的销售利润的最大值与
最小值相差12元,求此时m的值.
1
题型三
二次函数的实际应用
考情速递 2024年贵州数学中考第24题考查二次函数利润问题
(1)当销售单价定为17元时,求每周的销售数量.
1
题型三
二次函数的实际应用
(1)设y=kx+b(k≠0).
∵一次函数的图象经过点(10,32),(18,0),
∴解得
∴y=-4x+72.
当x=17时,y=4.
答:当销售单价定为17元时,每周的销售数量是4个.
(2)当销售单价为多少元时,每周的销售利润达到最大,最大值是多少
1
题型三
二次函数的实际应用
(2)设每周的销售利润为w元,
根据题意得w=(x-10)(-4x+72)=-4x2+112x-720=-4(x-14)2+64.
∴当x=14时,w有最大值,最大值为64.
答:当销售单价为14元时,每周的销售利润达到最大,最大值是64元.
(3)当m-1≤x≤m时,每周的销售利润的最大值与最小值相差12元,求此时m的值.
1
题型三
二次函数的实际应用
(3)∵w=-4(x-14)2+64,
∴抛物线的对称轴为直线x=14,且抛物线上的点离对称轴越远,函数值越小.
分以下四种情况讨论.
①当m<14时,由题意,得-4m2+112m-720+4(m-1)2-112(m-1)+720=12,解得m=13.
(3)当m-1≤x≤m时,每周的销售利润的最大值与最小值相差12元,求此时m的值.
1
题型三
二次函数的实际应用
②当m-1>14时,由题意,得-4(m-1)2+112(m-1)-720+4m2-112m+720=12,解得m=16.
③当即由题意,得64+4m2-112m+720=12,
解得m=14+(舍去)或m=14-(舍去).
(3)当m-1≤x≤m时,每周的销售利润的最大值与最小值相差12元,求此时m的值.
1
题型三
二次函数的实际应用
④当
即14由题意,得64+4(m-1)2-112(m-1)+720=12,
解得m=15+(舍去)或m=15-(舍去).
综上,m=13或m=16.
利用二次函数的性质求最大利润的一般思路
1.根据“总利润=(售价-进价)×销售量”或“总利润=售价×销售量-总成本”列出二次函数表达式,并根据自变量的实际意义,确定自变量的取值范围.
2.将二次函数表达式化为顶点式,在自变量的取值范围内,利用二次函数的性质求最值,求解时应注意:
(1)若顶点的横坐标在自变量的取值范围内,则一般在顶点处取得最值(注意结合函数图象及题意具体情况具体分析);
(2)若顶点的横坐标不在自变量的取值范围内,则需结合二次函数的图象,利用二次函数的增减性,在自变量的取值范围内求出函数的最值.
注意:在售价变化引起销量变化的问题中,要弄清楚自变量x代表的是售价还是上涨(下降)的量.
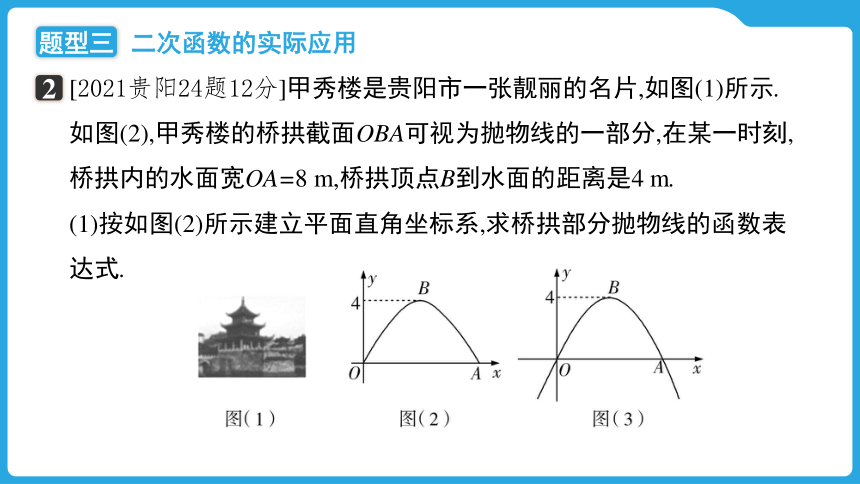
[2021贵阳24题12分]甲秀楼是贵阳市一张靓丽的名片,如图(1)所示.如图(2),甲秀楼的桥拱截面OBA可视为抛物线的一部分,在某一时刻,桥拱内的水面宽OA=8 m,桥拱顶点B到水面的距离是4 m.
(1)按如图(2)所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式.
2
题型三
二次函数的实际应用
(1)按如图(2)所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式.
2
题型三
二次函数的实际应用
(1)由题意知水面宽OA是8 m,桥拱顶点B到水面的距离是4 m,
结合函数图象可知B(4,4),O(0,0),
设二次函数的表达式为y=a(x-4)2+4,
将O(0,0)代入二次函数的表达式,可得a=-,
∴二次函数的表达式为y=-(x-4)2+4,
∴桥拱部分抛物线的函数表达式是y=-x2+2x(0≤x≤8).
(2)一只宽为1.2 m的打捞船径直向桥驶来,当船驶到桥拱下方且距O点0.4 m时,桥下水位刚好在OA处,有一名身高1.68 m的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱 请说明理由.(假设船底与水面齐平)
2
题型三
二次函数的实际应用
(2)他的头顶不会触碰到桥拱.理由如下:
由题意得此时工人距O点的距离为0.4+×1.2=1(m),
将x=1代入y=-x2+2x,解得y=1.75.
∵1.75 m>1.68 m,∴此时他的头顶不会触碰到桥拱.
(3)如图(3),桥拱所在的函数图象是抛物线y=ax2+bx+c(a≠0),该抛物线在x轴下方部分与桥拱OBA在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移m(m>0)个单位长度,平移后的函数图象在8≤x≤9时,y的值随x值的增大而减小,结合函数图象,求m的取值范围.
2
题型三
二次函数的实际应用
题型三
二次函数的实际应用
图(1)
(3)抛物线y=-x2+2x在x轴上方的部分与桥拱在平静水面中的倒影关于x轴成轴对称,如图(1)所示,
则新函数图象的对称轴也是直线x=4,
此时,当0≤x≤4或x≥8时,y的值随x值的增大而减小,
将新函数图象向右平移m个单位长度,可得平移后的函数图象,如图(2)所示,
∵平移不改变图形的形状和大小,
∴平移后新函数图象的对称轴是直线x=4+m,
图(2)
题型三
二次函数的实际应用
(3) ∴当m≤x≤4+m或x≥8+m时,y的值随x值的增大而减小.
当8≤x≤9时,y的值随x值的增大而减小,结合函数图象可知:
①m≤8且4+m≥9,得5≤m≤8;
②8+m≤8,得m≤0.
又∵m>0,
∴m≤0不符合题意,舍去.
综上所述,m的取值范围是5≤m≤8.
利用二次函数的性质求抛物线形问题的一般思路
1.从问题情境入手,建立适当的平面直角坐标系,将实际问题抽象成二次函数模型,即将题干中的信息转化为抛物线中的相关信息,在图中标注相应各点的坐标.
2.设出合适的解析式,将题中已知点的坐标代入解析式,求出抛物线的完整解析式(常用待定系数法).
3.利用二次函数解析式求出目标点的坐标,进而解决实际问题.
3
[2024山东滨州经开区二模]某公园内人工湖上有一座拱桥(横截面如图(1)所示),跨度AB为4米.在距点A水平距离为d米的地点处,拱桥距离水面的高度为h米.小红根据学习函数的经验,对d和h之间的关系进行了探究.
图(1) 图(2) 图(3)
3
下面是小红的探究过程:
(1)经过测量,得出了d和h的几组对应值,如表.
在d和h这两个变量中, 是自变量, 是这个变量的函数.
d/米 0 0.6 1 1.8 2.4 3 3.6 4
h/米 0.88 1.90 2.38 2.86 2.80 2.38 1.60 0.88
(2)如图(2),在平面直角坐标系中,画出(1)中所确定的函数的图象.
d
h
3
(3)结合表格数据和函数图象,解决下列问题:
①桥墩露出水面的高度AE为 米;
②如图(3),公园欲开设游船项目,现有长为3.5米,宽为1.5米,露出水面高度为2米的游船.为安全起见,公园要在水面上的C,D两处设置警戒线,并且CE=DF,要求游船能从C,D两点之间安全通过,求C处距桥墩的距离CE至少为多少米.(精确到0.1米)
0.88
(3) ②设h=ad2+bd+c,把(0,0.88),(1,2.38),(3,2.38)代入得,
解得
∴h=-0.5d2+2d+0.88,
对称轴为直线d=2.
令h=2,则2=-0.5d2+2d+0.88,
解得d1≈3.3(不合题意,舍去)或d2≈0.7.
答:C处距桥墩的距离CE至少为0.7米.
[2024贵州24题12分]某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(单位:盒)与销售单价x(单位:元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
日销售量y/盒 … 56 52 48 44 40 …
(1)求y与x的函数表达式.
(2)当糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品[1],赠送礼品后,为确保该种糖果日销售获得的最大利润为392元[2],求m的值.
解:(1)设y=kx+b(k≠0),(1分) 得分点1:正确设出一次函数表达式,得1分
将(12,56),(14,52)代入,得(2分)
得分点2:根据表格中数据正确列出方程组,得1分
解得(3分) 得分点3:正确解方程组,得1分
∴y=-2x+80.(4分) 得分点4:正确写出y与x的函数表达式,得1分
(2)设日销售利润为w元.
w=(x-10)(-2x+80)(6分) 得分点5:正确列出关系式,得2分
=-2x2+100x-800
=-2(x-25)2+450.(7分) 得分点6:正确写出顶点式,得1分
∵-2<0,∴二次函数图象开口向下,∴当x=25时,w有最大值为450.
答:当糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元.(8分)
得分点7:正确写出结论,得1分
(3)第1步:理解[1],即每赠送一件价值为m元的礼品=每件糖果的销售利润减少m元,列出有关日销售利润的二次函数
依题意得,w=(x-10-m)(-2x+80)(9分) 得分点8:根据题意正确列出关系式,得1分
=-2x2+(100+2m)x-800-80m.
第2步:根据[2],列出关于m的一元二次方程,并求解
∵最大利润为392元,∴当x=-=时,取得最大值392,
∴=392,(10分)
得分点9:根据顶点坐标公式建立方程正确,得1分
整理得,m2-60m+116=0,
解得m1=2,m2=58.(11分) 得分点10:解m的两个值都正确,得1分
第3步:结合实际意义,对m的值进行取舍
当m=58时,x==54,
∴此时每盒糖果的利润=54-10-58=-14(元),∴m=58不符合题意,舍去,
∴m=2.(12分) 得分点11:结果取舍正确,得1分
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
题型三 二次函数的实际应用
[2024遵义红花岗区模拟]为了更好地体验生活,完成假期实践活动,小琪想售卖灯笼,每个灯笼的成本价为10元,每周销售量y(个)与销售单价x(元)之间的函数关系如图所示.
(1)当销售单价定为17元时,求每周的销售数量.
(2)当销售单价为多少元时,每周的销售利润达
到最大,最大值是多少
(3)当m-1≤x≤m时,每周的销售利润的最大值与
最小值相差12元,求此时m的值.
1
题型三
二次函数的实际应用
考情速递 2024年贵州数学中考第24题考查二次函数利润问题
(1)当销售单价定为17元时,求每周的销售数量.
1
题型三
二次函数的实际应用
(1)设y=kx+b(k≠0).
∵一次函数的图象经过点(10,32),(18,0),
∴解得
∴y=-4x+72.
当x=17时,y=4.
答:当销售单价定为17元时,每周的销售数量是4个.
(2)当销售单价为多少元时,每周的销售利润达到最大,最大值是多少
1
题型三
二次函数的实际应用
(2)设每周的销售利润为w元,
根据题意得w=(x-10)(-4x+72)=-4x2+112x-720=-4(x-14)2+64.
∴当x=14时,w有最大值,最大值为64.
答:当销售单价为14元时,每周的销售利润达到最大,最大值是64元.
(3)当m-1≤x≤m时,每周的销售利润的最大值与最小值相差12元,求此时m的值.
1
题型三
二次函数的实际应用
(3)∵w=-4(x-14)2+64,
∴抛物线的对称轴为直线x=14,且抛物线上的点离对称轴越远,函数值越小.
分以下四种情况讨论.
①当m<14时,由题意,得-4m2+112m-720+4(m-1)2-112(m-1)+720=12,解得m=13.
(3)当m-1≤x≤m时,每周的销售利润的最大值与最小值相差12元,求此时m的值.
1
题型三
二次函数的实际应用
②当m-1>14时,由题意,得-4(m-1)2+112(m-1)-720+4m2-112m+720=12,解得m=16.
③当即
解得m=14+(舍去)或m=14-(舍去).
(3)当m-1≤x≤m时,每周的销售利润的最大值与最小值相差12元,求此时m的值.
1
题型三
二次函数的实际应用
④当
即14
解得m=15+(舍去)或m=15-(舍去).
综上,m=13或m=16.
利用二次函数的性质求最大利润的一般思路
1.根据“总利润=(售价-进价)×销售量”或“总利润=售价×销售量-总成本”列出二次函数表达式,并根据自变量的实际意义,确定自变量的取值范围.
2.将二次函数表达式化为顶点式,在自变量的取值范围内,利用二次函数的性质求最值,求解时应注意:
(1)若顶点的横坐标在自变量的取值范围内,则一般在顶点处取得最值(注意结合函数图象及题意具体情况具体分析);
(2)若顶点的横坐标不在自变量的取值范围内,则需结合二次函数的图象,利用二次函数的增减性,在自变量的取值范围内求出函数的最值.
注意:在售价变化引起销量变化的问题中,要弄清楚自变量x代表的是售价还是上涨(下降)的量.
[2021贵阳24题12分]甲秀楼是贵阳市一张靓丽的名片,如图(1)所示.如图(2),甲秀楼的桥拱截面OBA可视为抛物线的一部分,在某一时刻,桥拱内的水面宽OA=8 m,桥拱顶点B到水面的距离是4 m.
(1)按如图(2)所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式.
2
题型三
二次函数的实际应用
(1)按如图(2)所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式.
2
题型三
二次函数的实际应用
(1)由题意知水面宽OA是8 m,桥拱顶点B到水面的距离是4 m,
结合函数图象可知B(4,4),O(0,0),
设二次函数的表达式为y=a(x-4)2+4,
将O(0,0)代入二次函数的表达式,可得a=-,
∴二次函数的表达式为y=-(x-4)2+4,
∴桥拱部分抛物线的函数表达式是y=-x2+2x(0≤x≤8).
(2)一只宽为1.2 m的打捞船径直向桥驶来,当船驶到桥拱下方且距O点0.4 m时,桥下水位刚好在OA处,有一名身高1.68 m的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱 请说明理由.(假设船底与水面齐平)
2
题型三
二次函数的实际应用
(2)他的头顶不会触碰到桥拱.理由如下:
由题意得此时工人距O点的距离为0.4+×1.2=1(m),
将x=1代入y=-x2+2x,解得y=1.75.
∵1.75 m>1.68 m,∴此时他的头顶不会触碰到桥拱.
(3)如图(3),桥拱所在的函数图象是抛物线y=ax2+bx+c(a≠0),该抛物线在x轴下方部分与桥拱OBA在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移m(m>0)个单位长度,平移后的函数图象在8≤x≤9时,y的值随x值的增大而减小,结合函数图象,求m的取值范围.
2
题型三
二次函数的实际应用
题型三
二次函数的实际应用
图(1)
(3)抛物线y=-x2+2x在x轴上方的部分与桥拱在平静水面中的倒影关于x轴成轴对称,如图(1)所示,
则新函数图象的对称轴也是直线x=4,
此时,当0≤x≤4或x≥8时,y的值随x值的增大而减小,
将新函数图象向右平移m个单位长度,可得平移后的函数图象,如图(2)所示,
∵平移不改变图形的形状和大小,
∴平移后新函数图象的对称轴是直线x=4+m,
图(2)
题型三
二次函数的实际应用
(3) ∴当m≤x≤4+m或x≥8+m时,y的值随x值的增大而减小.
当8≤x≤9时,y的值随x值的增大而减小,结合函数图象可知:
①m≤8且4+m≥9,得5≤m≤8;
②8+m≤8,得m≤0.
又∵m>0,
∴m≤0不符合题意,舍去.
综上所述,m的取值范围是5≤m≤8.
利用二次函数的性质求抛物线形问题的一般思路
1.从问题情境入手,建立适当的平面直角坐标系,将实际问题抽象成二次函数模型,即将题干中的信息转化为抛物线中的相关信息,在图中标注相应各点的坐标.
2.设出合适的解析式,将题中已知点的坐标代入解析式,求出抛物线的完整解析式(常用待定系数法).
3.利用二次函数解析式求出目标点的坐标,进而解决实际问题.
3
[2024山东滨州经开区二模]某公园内人工湖上有一座拱桥(横截面如图(1)所示),跨度AB为4米.在距点A水平距离为d米的地点处,拱桥距离水面的高度为h米.小红根据学习函数的经验,对d和h之间的关系进行了探究.
图(1) 图(2) 图(3)
3
下面是小红的探究过程:
(1)经过测量,得出了d和h的几组对应值,如表.
在d和h这两个变量中, 是自变量, 是这个变量的函数.
d/米 0 0.6 1 1.8 2.4 3 3.6 4
h/米 0.88 1.90 2.38 2.86 2.80 2.38 1.60 0.88
(2)如图(2),在平面直角坐标系中,画出(1)中所确定的函数的图象.
d
h
3
(3)结合表格数据和函数图象,解决下列问题:
①桥墩露出水面的高度AE为 米;
②如图(3),公园欲开设游船项目,现有长为3.5米,宽为1.5米,露出水面高度为2米的游船.为安全起见,公园要在水面上的C,D两处设置警戒线,并且CE=DF,要求游船能从C,D两点之间安全通过,求C处距桥墩的距离CE至少为多少米.(精确到0.1米)
0.88
(3) ②设h=ad2+bd+c,把(0,0.88),(1,2.38),(3,2.38)代入得,
解得
∴h=-0.5d2+2d+0.88,
对称轴为直线d=2.
令h=2,则2=-0.5d2+2d+0.88,
解得d1≈3.3(不合题意,舍去)或d2≈0.7.
答:C处距桥墩的距离CE至少为0.7米.
[2024贵州24题12分]某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(单位:盒)与销售单价x(单位:元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
日销售量y/盒 … 56 52 48 44 40 …
(1)求y与x的函数表达式.
(2)当糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品[1],赠送礼品后,为确保该种糖果日销售获得的最大利润为392元[2],求m的值.
解:(1)设y=kx+b(k≠0),(1分) 得分点1:正确设出一次函数表达式,得1分
将(12,56),(14,52)代入,得(2分)
得分点2:根据表格中数据正确列出方程组,得1分
解得(3分) 得分点3:正确解方程组,得1分
∴y=-2x+80.(4分) 得分点4:正确写出y与x的函数表达式,得1分
(2)设日销售利润为w元.
w=(x-10)(-2x+80)(6分) 得分点5:正确列出关系式,得2分
=-2x2+100x-800
=-2(x-25)2+450.(7分) 得分点6:正确写出顶点式,得1分
∵-2<0,∴二次函数图象开口向下,∴当x=25时,w有最大值为450.
答:当糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元.(8分)
得分点7:正确写出结论,得1分
(3)第1步:理解[1],即每赠送一件价值为m元的礼品=每件糖果的销售利润减少m元,列出有关日销售利润的二次函数
依题意得,w=(x-10-m)(-2x+80)(9分) 得分点8:根据题意正确列出关系式,得1分
=-2x2+(100+2m)x-800-80m.
第2步:根据[2],列出关于m的一元二次方程,并求解
∵最大利润为392元,∴当x=-=时,取得最大值392,
∴=392,(10分)
得分点9:根据顶点坐标公式建立方程正确,得1分
整理得,m2-60m+116=0,
解得m1=2,m2=58.(11分) 得分点10:解m的两个值都正确,得1分
第3步:结合实际意义,对m的值进行取舍
当m=58时,x==54,
∴此时每盒糖果的利润=54-10-58=-14(元),∴m=58不符合题意,舍去,
∴m=2.(12分) 得分点11:结果取舍正确,得1分
同课章节目录
