2025年中考数学二轮专题复习 题型四-二次函数图象与性质综合题 课件(共29张PPT)
文档属性
| 名称 | 2025年中考数学二轮专题复习 题型四-二次函数图象与性质综合题 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 28.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
题型四 二次函数图象与性质综合题
已知二次函数y=-x2+2bx+c.
(1)二次函数图象的对称轴是直线x= .(用含b的代数式表示)
(2)当b=1时,若抛物线经过点M(2,3),求这个二次函数的表达式.
1
结构化整合
b
(2)当b=1时,二次函数的表达式是y=-x2+2x+c,
将点M(2,3)代入得,
3=-22+4+c,解得c=3,
∴当b=1时,二次函数的表达式是y=-x2+2x+3.
已知二次函数y=-x2+2bx+c.
(3)在(2)的条件下,抛物线上分别有两点(-,y1),(t,y2),若y1
1
结构化整合
(3)当b=1时,二次函数的对称轴是直线x=1,
∴点(-,y1)关于直线x=1的对称点是(,y1),
∴当y1图示速解
拓展:已知二次函数y=ax2+bx+c(a≠0)图象上的两点A(x1,y0),B(x2,y0),则二次函数图象的对称轴为直线x=.
已知二次函数y=-x2+2bx+c.
(4)在(2)的条件下,对于一切实数x,若函数值y
1
结构化整合
(4)∵对于一切实数x,函数值y∴二次函数y=-x2+2x+3的图象与直线y=x+k没有交点.
当二次函数y=-x2+2x+3的图象与直线y=x+k只有一个交点时,
即关于x的方程-x2+2x+3=x+k只有一个解,
整理方程得,-x2+x+3-k=0,∴Δ=12-4×(-1)×(3-k)=1+12-4k=13-4k=0,
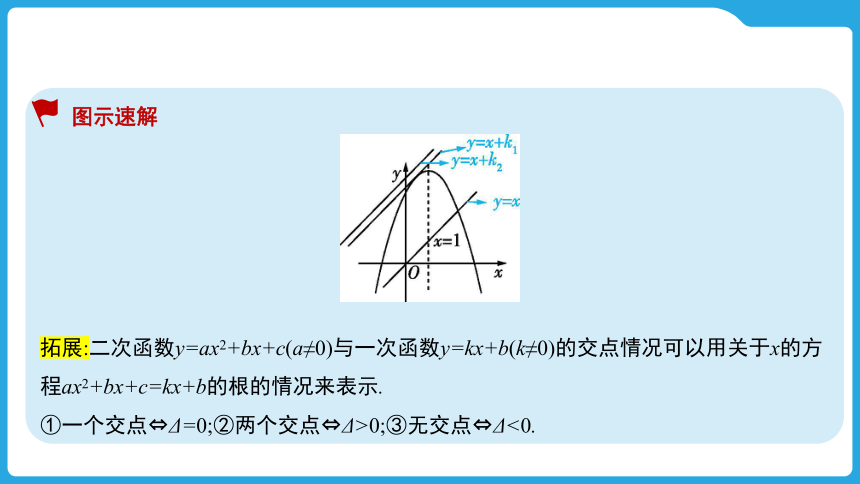
∴解得k=,∴当k>时,对于一切实数x,函数值y图示速解
拓展:二次函数y=ax2+bx+c(a≠0)与一次函数y=kx+b(k≠0)的交点情况可以用关于x的方程ax2+bx+c=kx+b的根的情况来表示.
①一个交点 Δ=0;②两个交点 Δ>0;③无交点 Δ<0.
已知二次函数y=-x2+2bx+c.
(5)在(2)的条件下,当m-2≤x≤m时,二次函数的最大值是-2m,求m的值.
1
结构化整合
(5)∵二次函数y=-x2+2x+3的图象开口向下,对称轴是直线x=1,
∴分以下3种情况进行讨论.①当m<1时,-m2+2m+3=-2m,
解得m=-+2或m=+2(舍去).
②当m-2>1,即m>3时,有-(m-2)2+2(m-2)+3=-2m,
解得m=+4或m=-+4(舍去).
③当m-2<1-1+2+3=-2m,解得m=-2,不符合题意,舍去.综上,m=-+2或m=+4.
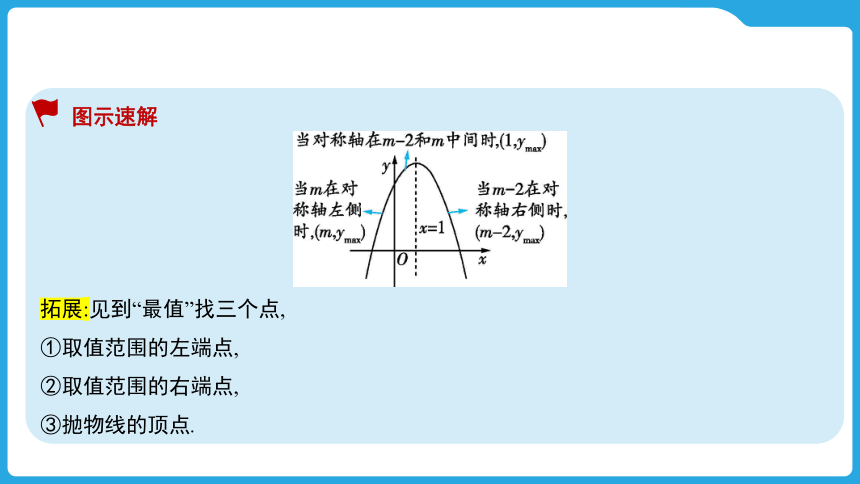
图示速解
拓展:见到“最值”找三个点,
①取值范围的左端点,
②取值范围的右端点,
③抛物线的顶点.
已知二次函数y=-x2+2bx+c.
(6)若c=1,当2≤x≤4时,函数y的值总大于等于1,求b的取值范围.
1
结构化整合
(6)当c=1时,二次函数的表达式是y=-x2+2bx+1,
∴二次函数的图象开口向下,对称轴是直线x=b.
∵当2≤x≤4时,函数y的值总大于等于1,
∴当x=2时,y=-22+4b+1≥1,解得b≥1.
当x=4时,y=-42+8b+1≥1,解得b≥2.
∴b的取值范围是b≥2.
图示速解
已知二次函数y=-x2+2bx+c.
(7)若c=1,是否存在实数b(b>1),使得当1≤x≤4时,二次函数的最大值比最小值大3,若存在,求出b的值;若不存在,请说明理由.
1
结构化整合
(7)存在.∵当c=1时,二次函数的表达式是y=-x2+2bx+1,
∴二次函数的图象开口向下,对称轴是直线x=b,顶点坐标是(b,b2+1).
当x=1时,y=-1+2b+1=2b,
当x=4时,y=-16+8b+1=-15+8b.
∵当1≤x≤4时,二次函数的最大值比最小值大3,
∴当b>1时,分以下3种情况讨论.
已知二次函数y=-x2+2bx+c.
(7)若c=1,是否存在实数b(b>1),使得当1≤x≤4时,二次函数的最大值比最小值大3,若存在,求出b的值;若不存在,请说明理由.
1
结构化整合
①若b>4,此时x=4,y有最大值,x=1,y有最小值,
∴-15+8b-2b=3,解得b=3(舍去).
②若1∴b2+1-(-15+8b)=3,解得b=-+4或b=+4(舍去).
③若2.5解得b=+1或b=-+1(舍去).综上,b的值为-+4或+1.
图示速解
拓展:抛物线开口向下,到对称轴距离越远的点函数值越小;抛物线开口向上,到对称轴距离越远的点,函数值越大.
已知二次函数y=-x2+2bx+c.
(8)在(2)的条件下,若二次函数的图象分别交x轴于点A,B,且点A在点B的左侧,与y轴交于点C,则对称轴上是否存在一点P,使得PA+PC的值最小,若存在,求出点P的坐标;若不存在,请说明理由.
1
结构化整合
(8)存在.
由(2)知,二次函数的表达式为y=-x2+2x+3,
∴点C的坐标是(0,3),对称轴是直线x=1.
当y=0时,解得x=3或x=-1,∴点A的坐标是(-1,0),点B的坐标是(3,0).
∵点A,B关于直线x=1对称,∴PA+PC=PB+PC≥BC.
已知二次函数y=-x2+2bx+c.
(8)在(2)的条件下,若二次函数的图象分别交x轴于点A,B,且点A在点B的左侧,与y轴交于点C,则对称轴上是否存在一点P,使得PA+PC的值最小,若存在,求出点P的坐标;若不存在,请说明理由.
1
结构化整合
(8)设直线BC的表达式为y=tx+n,分别代入点B,C的坐标,
得解得
∴直线BC的表达式是y=-x+3,∴当x=1时,y=2,
∴当PA+PC的值最小时,点P的坐标是(1,2).
图示速解
“将军饮马”模型链接 大单元整合专题二-类型3-问题1
改编自2023年贵州省中考第24题的设问
已知二次函数y=-x2+2bx+c.
(9)在(8)的条件下,若点Q为抛物线BC上一动点(不与点B,C重合),求点Q到直线BC的最大距离.
1
结构化整合
(9)过点Q作QE∥y轴交直线BC于点E,交x轴于点F,作QG⊥BC于点G,
由(8)知,直线BC的表达式是y=-x+3,
设Q(a,-a2+2a+3),则E(a,-a+3),
∴QE=-a2+2a+3-(-a+3)=-a2+3a=-(a-)2+,∴当a=时,QE有最大值,为.
由(8)知,OB=3,OC=3,∴∠CBO=45°,
已知二次函数y=-x2+2bx+c.
(9)在(8)的条件下,若点Q为抛物线BC上一动点(不与点B,C重合),求点Q到直线BC的最大距离.
1
结构化整合
(9) ∴∠QEG=∠BEF=45°,
∴QG=QE×sin 45°==,
∴点Q到直线BC的最大距离为.
图示速解
拓展:本问利用到转化思想,将“求QG的最大值”转化为“求QE的最大值”,其中45°角是本问隐含的关键条件.
已知二次函数y=-x2+2bx+c.
(10)在(2)的条件下,平移抛物线y=-x2+2bx+c,使平移后的抛物线的顶点在直线y=x+1上,求平移后的抛物线与y轴交点纵坐标的最大值.
1
结构化整合
(10)由(2)知,抛物线的表达式是y=-x2+2x+3,
∵平移后的抛物线的顶点在直线y=x+1上,
∴设平移后的抛物线的表达式为y=-(x-h)2+h+1,∴y=-x2+2hx-h2+h+1.
设平移后的抛物线与y轴交点的纵坐标为d,则d=-h2+h+1=-(h-)2+,
∴当h=时,平移后的抛物线与y轴交点纵坐标的最大值为.
2
[2024遵义汇川区模拟]已知点P(m,n)在抛物线y=a(x-1)2+3(a为常数,a≠0)上.
(1)若m=2,n=4,
①求抛物线的解析式;
②若点A(t-1,y1),B(t,y2)在该二次函数的图象上,且点A在对称轴左侧、点B在对称轴右侧,若y1(2)当-1≤m≤0时,总有n≥-2,且当3≤m<4时,总有n≤-2,求a的值.
2
(1)若m=2,n=4,
①求抛物线的解析式;
(1)①当m=2,n=4时,P(2,4),
把P(2,4)代入y=a(x-1)2+3得,
4=a(2-1)2+3,解得a=1,
∴y=(x-1)2+3.
2
(1)若m=2,n=4,
②若点A(t-1,y1),B(t,y2)在该二次函数的图象上,且点A在对称轴左侧、点B在对称轴右侧,若y1②∵y=(x-1)2+3,
∴抛物线的开口向上,对称轴为直线x=1,抛物线上的点离对称轴越远,函数值越大,由题意,得
解得2
(2)当-1≤m≤0时,总有n≥-2,且当3≤m<4时,总有n≤-2,求a的值.
(2)当a>0时,y>3,与题意不符,∴a<0,
∴抛物线的开口向下,对称轴为直线x=1,
∴当x≤1时,y随x的增大而增大;当x≥1时,y随x的增大而减小,
∴当m=-1时,n=-2.
把P(-1,-2)代入y=a(x-1)2+3,
得-2=a(-1-1)2+3,
解得a=-.
3
[2024六盘水二模]已知二次函数图象的顶点坐标为(1,-4),且图象经过点(3,0),(0,-3).
(1)求二次函数的表达式.
(2)将二次函数的图象向右平移m(m>0)个单位长度后,图象经过点
(1,-),求m的值.
(3)结合(2),在平移后的图象上,当n-2≤x≤n+1时,函数的最小值为-3,求n的值.
3
(1)求二次函数的表达式.
(1)∵二次函数图象的顶点坐标为(1,-4),
∴设二次函数的表达式为y=a(x-1)2-4.
∵图象过点(3,0),
∴0=4a-4,
解得a=1,
∴二次函数的表达式为y=(x-1)2-4.
3
(2)将二次函数的图象向右平移m(m>0)个单位长度后,图象经过点(1,-),求m的值.
(2)由题意,将二次函数的图象向右平移m(m>0)个单位长度得,
y=(x-1-m)2-4.
∵平移后的图象过点(1,-),∴-=m2-4,
解得m=或m=-(舍去),
∴m=.
3
(3)结合(2),在平移后的图象上,当n-2≤x≤n+1时,函数的最小值为-3,求n的值.
(3)由(2)得平移后的二次函数表达式为y=(x-)2-4.
∴抛物线的开口向上,对称轴是直线x=.当x<时,y随x的增大而减小;当x>时,y随x的增大而增大;当x=时,y取得最小值为-4.
∵当n-2≤x≤n+1时,函数的最小值为-3,
∴分以下两种情况进行讨论.
3
(3)结合(2),在平移后的图象上,当n-2≤x≤n+1时,函数的最小值为-3,求n的值.
①当n+1<,即n<时,有(n+1-)2-4=-3,
解得n=-或n=(舍去).
②当n-2>,即n>时,有(n-2-)2-4=-3.
解得n=或n=(舍去).
综上,n=-或n=.
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
题型四 二次函数图象与性质综合题
已知二次函数y=-x2+2bx+c.
(1)二次函数图象的对称轴是直线x= .(用含b的代数式表示)
(2)当b=1时,若抛物线经过点M(2,3),求这个二次函数的表达式.
1
结构化整合
b
(2)当b=1时,二次函数的表达式是y=-x2+2x+c,
将点M(2,3)代入得,
3=-22+4+c,解得c=3,
∴当b=1时,二次函数的表达式是y=-x2+2x+3.
已知二次函数y=-x2+2bx+c.
(3)在(2)的条件下,抛物线上分别有两点(-,y1),(t,y2),若y1
1
结构化整合
(3)当b=1时,二次函数的对称轴是直线x=1,
∴点(-,y1)关于直线x=1的对称点是(,y1),
∴当y1
拓展:已知二次函数y=ax2+bx+c(a≠0)图象上的两点A(x1,y0),B(x2,y0),则二次函数图象的对称轴为直线x=.
已知二次函数y=-x2+2bx+c.
(4)在(2)的条件下,对于一切实数x,若函数值y
1
结构化整合
(4)∵对于一切实数x,函数值y
当二次函数y=-x2+2x+3的图象与直线y=x+k只有一个交点时,
即关于x的方程-x2+2x+3=x+k只有一个解,
整理方程得,-x2+x+3-k=0,∴Δ=12-4×(-1)×(3-k)=1+12-4k=13-4k=0,
∴解得k=,∴当k>时,对于一切实数x,函数值y
拓展:二次函数y=ax2+bx+c(a≠0)与一次函数y=kx+b(k≠0)的交点情况可以用关于x的方程ax2+bx+c=kx+b的根的情况来表示.
①一个交点 Δ=0;②两个交点 Δ>0;③无交点 Δ<0.
已知二次函数y=-x2+2bx+c.
(5)在(2)的条件下,当m-2≤x≤m时,二次函数的最大值是-2m,求m的值.
1
结构化整合
(5)∵二次函数y=-x2+2x+3的图象开口向下,对称轴是直线x=1,
∴分以下3种情况进行讨论.①当m<1时,-m2+2m+3=-2m,
解得m=-+2或m=+2(舍去).
②当m-2>1,即m>3时,有-(m-2)2+2(m-2)+3=-2m,
解得m=+4或m=-+4(舍去).
③当m-2<1
图示速解
拓展:见到“最值”找三个点,
①取值范围的左端点,
②取值范围的右端点,
③抛物线的顶点.
已知二次函数y=-x2+2bx+c.
(6)若c=1,当2≤x≤4时,函数y的值总大于等于1,求b的取值范围.
1
结构化整合
(6)当c=1时,二次函数的表达式是y=-x2+2bx+1,
∴二次函数的图象开口向下,对称轴是直线x=b.
∵当2≤x≤4时,函数y的值总大于等于1,
∴当x=2时,y=-22+4b+1≥1,解得b≥1.
当x=4时,y=-42+8b+1≥1,解得b≥2.
∴b的取值范围是b≥2.
图示速解
已知二次函数y=-x2+2bx+c.
(7)若c=1,是否存在实数b(b>1),使得当1≤x≤4时,二次函数的最大值比最小值大3,若存在,求出b的值;若不存在,请说明理由.
1
结构化整合
(7)存在.∵当c=1时,二次函数的表达式是y=-x2+2bx+1,
∴二次函数的图象开口向下,对称轴是直线x=b,顶点坐标是(b,b2+1).
当x=1时,y=-1+2b+1=2b,
当x=4时,y=-16+8b+1=-15+8b.
∵当1≤x≤4时,二次函数的最大值比最小值大3,
∴当b>1时,分以下3种情况讨论.
已知二次函数y=-x2+2bx+c.
(7)若c=1,是否存在实数b(b>1),使得当1≤x≤4时,二次函数的最大值比最小值大3,若存在,求出b的值;若不存在,请说明理由.
1
结构化整合
①若b>4,此时x=4,y有最大值,x=1,y有最小值,
∴-15+8b-2b=3,解得b=3(舍去).
②若1
③若2.5
图示速解
拓展:抛物线开口向下,到对称轴距离越远的点函数值越小;抛物线开口向上,到对称轴距离越远的点,函数值越大.
已知二次函数y=-x2+2bx+c.
(8)在(2)的条件下,若二次函数的图象分别交x轴于点A,B,且点A在点B的左侧,与y轴交于点C,则对称轴上是否存在一点P,使得PA+PC的值最小,若存在,求出点P的坐标;若不存在,请说明理由.
1
结构化整合
(8)存在.
由(2)知,二次函数的表达式为y=-x2+2x+3,
∴点C的坐标是(0,3),对称轴是直线x=1.
当y=0时,解得x=3或x=-1,∴点A的坐标是(-1,0),点B的坐标是(3,0).
∵点A,B关于直线x=1对称,∴PA+PC=PB+PC≥BC.
已知二次函数y=-x2+2bx+c.
(8)在(2)的条件下,若二次函数的图象分别交x轴于点A,B,且点A在点B的左侧,与y轴交于点C,则对称轴上是否存在一点P,使得PA+PC的值最小,若存在,求出点P的坐标;若不存在,请说明理由.
1
结构化整合
(8)设直线BC的表达式为y=tx+n,分别代入点B,C的坐标,
得解得
∴直线BC的表达式是y=-x+3,∴当x=1时,y=2,
∴当PA+PC的值最小时,点P的坐标是(1,2).
图示速解
“将军饮马”模型链接 大单元整合专题二-类型3-问题1
改编自2023年贵州省中考第24题的设问
已知二次函数y=-x2+2bx+c.
(9)在(8)的条件下,若点Q为抛物线BC上一动点(不与点B,C重合),求点Q到直线BC的最大距离.
1
结构化整合
(9)过点Q作QE∥y轴交直线BC于点E,交x轴于点F,作QG⊥BC于点G,
由(8)知,直线BC的表达式是y=-x+3,
设Q(a,-a2+2a+3),则E(a,-a+3),
∴QE=-a2+2a+3-(-a+3)=-a2+3a=-(a-)2+,∴当a=时,QE有最大值,为.
由(8)知,OB=3,OC=3,∴∠CBO=45°,
已知二次函数y=-x2+2bx+c.
(9)在(8)的条件下,若点Q为抛物线BC上一动点(不与点B,C重合),求点Q到直线BC的最大距离.
1
结构化整合
(9) ∴∠QEG=∠BEF=45°,
∴QG=QE×sin 45°==,
∴点Q到直线BC的最大距离为.
图示速解
拓展:本问利用到转化思想,将“求QG的最大值”转化为“求QE的最大值”,其中45°角是本问隐含的关键条件.
已知二次函数y=-x2+2bx+c.
(10)在(2)的条件下,平移抛物线y=-x2+2bx+c,使平移后的抛物线的顶点在直线y=x+1上,求平移后的抛物线与y轴交点纵坐标的最大值.
1
结构化整合
(10)由(2)知,抛物线的表达式是y=-x2+2x+3,
∵平移后的抛物线的顶点在直线y=x+1上,
∴设平移后的抛物线的表达式为y=-(x-h)2+h+1,∴y=-x2+2hx-h2+h+1.
设平移后的抛物线与y轴交点的纵坐标为d,则d=-h2+h+1=-(h-)2+,
∴当h=时,平移后的抛物线与y轴交点纵坐标的最大值为.
2
[2024遵义汇川区模拟]已知点P(m,n)在抛物线y=a(x-1)2+3(a为常数,a≠0)上.
(1)若m=2,n=4,
①求抛物线的解析式;
②若点A(t-1,y1),B(t,y2)在该二次函数的图象上,且点A在对称轴左侧、点B在对称轴右侧,若y1
2
(1)若m=2,n=4,
①求抛物线的解析式;
(1)①当m=2,n=4时,P(2,4),
把P(2,4)代入y=a(x-1)2+3得,
4=a(2-1)2+3,解得a=1,
∴y=(x-1)2+3.
2
(1)若m=2,n=4,
②若点A(t-1,y1),B(t,y2)在该二次函数的图象上,且点A在对称轴左侧、点B在对称轴右侧,若y1
∴抛物线的开口向上,对称轴为直线x=1,抛物线上的点离对称轴越远,函数值越大,由题意,得
解得
(2)当-1≤m≤0时,总有n≥-2,且当3≤m<4时,总有n≤-2,求a的值.
(2)当a>0时,y>3,与题意不符,∴a<0,
∴抛物线的开口向下,对称轴为直线x=1,
∴当x≤1时,y随x的增大而增大;当x≥1时,y随x的增大而减小,
∴当m=-1时,n=-2.
把P(-1,-2)代入y=a(x-1)2+3,
得-2=a(-1-1)2+3,
解得a=-.
3
[2024六盘水二模]已知二次函数图象的顶点坐标为(1,-4),且图象经过点(3,0),(0,-3).
(1)求二次函数的表达式.
(2)将二次函数的图象向右平移m(m>0)个单位长度后,图象经过点
(1,-),求m的值.
(3)结合(2),在平移后的图象上,当n-2≤x≤n+1时,函数的最小值为-3,求n的值.
3
(1)求二次函数的表达式.
(1)∵二次函数图象的顶点坐标为(1,-4),
∴设二次函数的表达式为y=a(x-1)2-4.
∵图象过点(3,0),
∴0=4a-4,
解得a=1,
∴二次函数的表达式为y=(x-1)2-4.
3
(2)将二次函数的图象向右平移m(m>0)个单位长度后,图象经过点(1,-),求m的值.
(2)由题意,将二次函数的图象向右平移m(m>0)个单位长度得,
y=(x-1-m)2-4.
∵平移后的图象过点(1,-),∴-=m2-4,
解得m=或m=-(舍去),
∴m=.
3
(3)结合(2),在平移后的图象上,当n-2≤x≤n+1时,函数的最小值为-3,求n的值.
(3)由(2)得平移后的二次函数表达式为y=(x-)2-4.
∴抛物线的开口向上,对称轴是直线x=.当x<时,y随x的增大而减小;当x>时,y随x的增大而增大;当x=时,y取得最小值为-4.
∵当n-2≤x≤n+1时,函数的最小值为-3,
∴分以下两种情况进行讨论.
3
(3)结合(2),在平移后的图象上,当n-2≤x≤n+1时,函数的最小值为-3,求n的值.
①当n+1<,即n<时,有(n+1-)2-4=-3,
解得n=-或n=(舍去).
②当n-2>,即n>时,有(n-2-)2-4=-3.
解得n=或n=(舍去).
综上,n=-或n=.
同课章节目录
