2025年中考数学二轮专题复习 题型五-几何探究题 课件(共23张PPT)
文档属性
| 名称 | 2025年中考数学二轮专题复习 题型五-几何探究题 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 22.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 14:15:12 | ||
图片预览






文档简介
(共23张PPT)
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
题型五 几何探究题
[2024烟台中考改编]在等腰直角三角形ABC中,∠ACB=90°,AC=BC,
D为直线BC上任意一点,连接AD,将线段AD绕点D按顺时针方向旋转[1]
90°得线段ED,连接BE.
【尝试发现】
(1)如图(1),当点D在线段BC上时,线段BE与CD的数量关系为 .
1
题型五
几何探究题
图(1)
BE=CD
[2024烟台中考改编]在等腰直角三角形ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD,将线段AD绕点D按顺时针方向旋转[2]90°得线段ED,连接BE.
【类比探究】
(2)当点D在线段BC的延长线上时,先在图(2)中补全图形[2],再探究线段BE与CD的数量关系并证明.
(3)若AC=BC=1,CD=2,求sin∠ECD的值.
1
题型五
几何探究题
图(2)
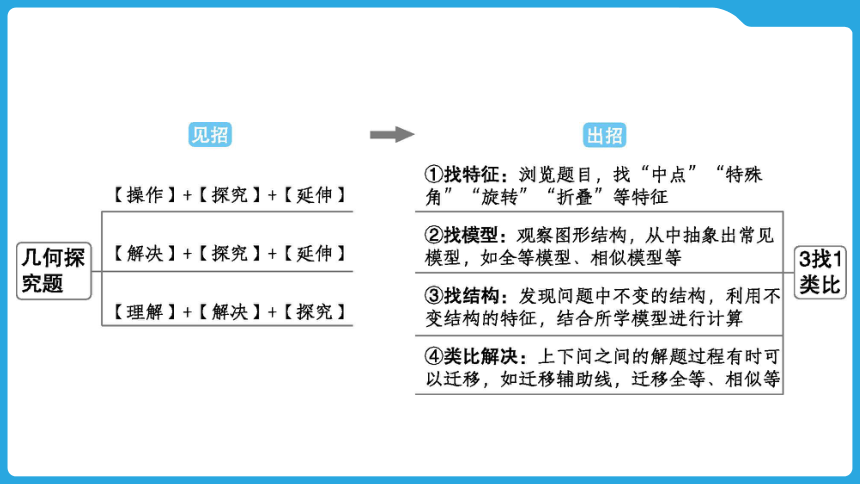
【大招点拨】识别题干信息:【发现】+【探究】+【拓展】
①找特征:根据[1]和[2],判断该题的特征是“旋转+操作”.
②找模型:旋转找全等模型,解答(1)和(2)的关键是作辅助线:过点E作EM⊥CB于点M,构造“一线三垂直”全等模型
③找结构:本题中的“不变结构”是等腰直角三角形ABC和线段AD绕点D按顺时针方向旋转90°.
④类比解决:结合(1)和(2)的解题思路,在解答(3)时,利用到的数学思想是分类讨论思想.
【自主解答】
1
题型五
几何探究题
(2)当点D在线段BC的延长线上时,先在图(2)中补全图形[2],再探究线段BE与CD的数量关系并证明.
1
题型五
几何探究题
图(1)
(2)补全图形如图(1).BE=CD.
证明:如图,过点E作EM⊥CB于点M.
由旋转,得AD=DE,∠ADE=90°,∴∠ADC+∠EDM=90°.
∵∠ACD=90°,∴∠ADC+∠CAD=90°,∴∠CAD=∠EDM.
又∵∠ACD=∠EMD=90°,∴△ACD≌△DME,
∴CD=EM,AC=DM.
又∵AC=BC,∴DM=BC,∴BM=DC,∴BM=EM,
∴在Rt△BME中,BE==EM=CD.
[2024烟台中考改编]在等腰直角三角形ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD,将线段AD绕点D按顺时针方向旋转[1]90°得线段ED,连接BE.
【联系拓展】
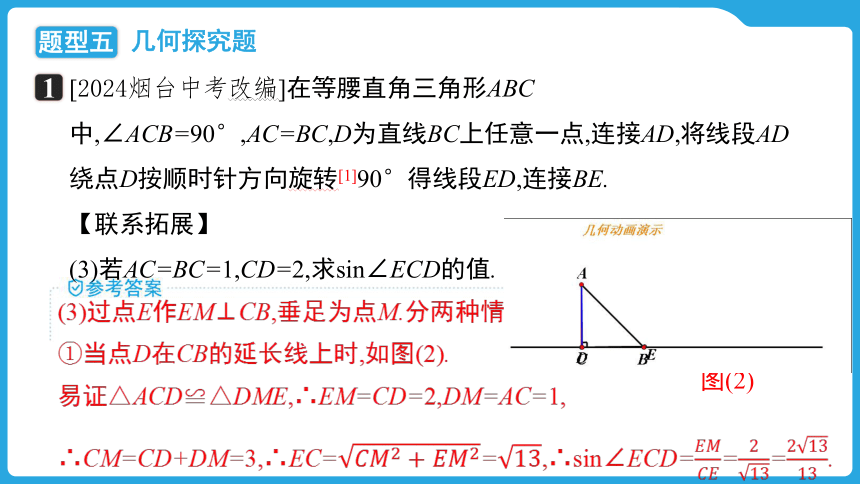
(3)若AC=BC=1,CD=2,求sin∠ECD的值.
1
题型五
几何探究题
(3)过点E作EM⊥CB,垂足为点M.分两种情况讨论.
①当点D在CB的延长线上时,如图(2).
易证△ACD≌△DME,∴EM=CD=2,DM=AC=1,
∴CM=CD+DM=3,∴EC==,∴sin∠ECD===.
图(2)
(3)若AC=BC=1,CD=2,求sin∠ECD的值.
1
题型五
几何探究题
图(3)
②当点D在BC的延长线上时,如图(3).
易证△ACD≌△DME,
∴EM=CD=2,DM=AC=1,
∴CM=CD-DM=1,∴EC==,
∴sin∠ECD===.
∴sin∠ECD的值为或.
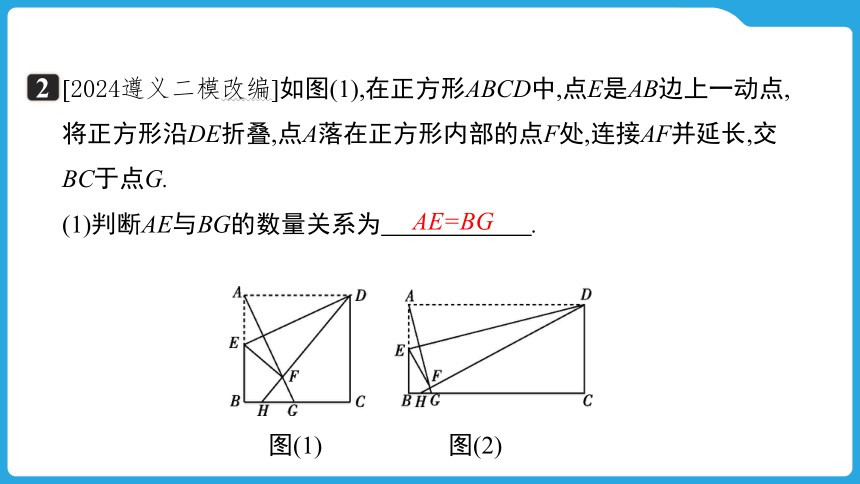
[2024遵义二模改编]如图(1),在正方形ABCD中,点E是AB边上一动点,将正方形沿DE折叠,点A落在正方形内部的点F处,连接AF并延长,交BC于点G.
(1)判断AE与BG的数量关系为 .
2
图(1) 图(2)
AE=BG
(2)【应用】如图(1),延长DF交BC于点H.
①证明:∠HFG=∠FGH;
2
图(1)
(2)①证明:∵AD∥BC,
∴∠DAF=∠AGH.
由折叠可知,DA=DF,
∴∠DAF=∠AFD,
∴∠AFD=∠AGH.
∵∠AFD=∠HFG,
∴∠AGH=∠HFG.
(2)【应用】如图(1),延长DF交BC于点H.
②若HB=3a,HF=5a,AE=8,求BE的长度.
2
图(1)
②由①知,∠FGH=∠HFG,则HG=FH=5a,
∵BH=3a,∴BG=BH+HF=8a.
由折叠可得,AF⊥DE,∴∠BAG+∠AED=90°.
∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠ABG=90°,
∴∠AED+∠ADE=90°,
∴∠BAG=∠ADE,
∴△ADE≌△BAG,
(2)【应用】如图(1),延长DF交BC于点H.
②若HB=3a,HF=5a,AE=8,求BE的长度.
2
图(1)
∴AE=BG=8a=8,∴a=1,
∴BH=3,HF=5,EF=AE=8.
连接EH,△EBH与△EFH都是直角三角形,
∴BE2+BH2=EF2+FH2,
即BE2+32=82+52,
∴BE=4(负值已舍去).
(3)【拓展】如图(2),将正方形改成矩形,其中AD=2CD,将矩形沿DE折叠,使点A落在点F处(矩形内部),连接AF并延长,交BC于点G,延长DF交直线BC于点H.若HB=3a,HF=5a,求的值.
2
图(1) 图(2)
(3)分两种情况讨论:①如图(1),当点H在线段BC上时,
易知,∠AGH=∠HFG,∴HG=HF=5a,∴BG=8a.
易证得△ADE∽△BAG,∴=,∴2=,∴AE=16a.
设BE=x,则AB=16a+x,∴DF=AD=32a+2x,
∴CD=AB=16a+x,DH=32a+2x+5a=37a+2x,CH=32a+2x-3a=29a+2x.
在Rt△DCH中,∵CH2+CD2=DH2,
∴(29a+2x)2+(16a+x)2=(37a+2x)2,∴x=4a(负值已舍去),
∴==.
图(1)
②如图(2),当点H在线段CB的延长线上时,易知,∠AGH=∠HFG,
∴HF=HG=5a,∴BG=2a.易证得△ADE∽△BAG,
∴=,∴2=,∴AE=4a.
设BE=y,则AB=4a+y,∴DF=AD=8a+2y,
∴CD=AB=4a+y,DH=8a+2y+5a=13a+2y,CH=8a+2y+3a=11a+2y.
在Rt△DCH中,∵CH2+CD2=DH2,∴(11a+2y)2+(4a+y)2=(13a+2y)2,
∴y=4a(负值已舍去),∴==.
综上所述,=或=.
图(2)
[2024贵州25题12分]
综合与探究:如图,∠AOB=90°,点P在∠AOB的平分线上,PA⊥OA于点A.
(1)【操作判断】
如图(1),过点P作PC⊥OB于点C,根据题意在图(1)中画出PC,图中∠APC的度数
为 度.
(2)【问题探究】
如图(2),点M在线段AO上,连接PM,过点P作PN⊥PM
交射线OB于点N.求证:OM+ON=2PA.
图(1) 图(2)
(3)【拓展延伸】
点M在射线AO上,连接PM,过点P作PN⊥PM交射线OB于点N,射线NM与射线PO相交于点F,若ON=3OM,求的值.
图(1) 图(2)
解:(1)如图(1),PC即为所求.(2分) 得分点1:作图正确,得2分
图(1) 图(2)
90 (4分) 得分点2:正确写出∠APC的度数,得2分
(2)证明:如图(2),过点P作PC⊥OB于点C.
由题意知,四边形OAPC是矩形,
∵点P在∠AOB的平分线上,PA⊥OA,PC⊥OB,
∴PA=PC,(5分) 得分点3:根据角平分线的性质得出PA=PC,得1分
∴矩形OAPC是正方形,(6分) 得分点4:正确判定四边形OAPC是正方形,得1分
∴OA=AP=PC=OC,∠APC=90°.
∵PN⊥PM,∴∠APM=∠CPN=90°-∠MPC.
∵∠MAP=∠NCP=90°,
∴△APM≌△CPN(ASA),(7分) 得分点5:正确证明△APM≌△CPN,得1分
∴AM=CN,
∴OM+ON=OM+OC+CN=OM+AM+OC=OA+OC=2PA,
∴OM+ON=2PA.(8分) 得分点6:通过等量代换得出正确结论,得1分
(3)第1步:考虑“点M在线段AO上”这一种情况,并作辅助线
①当点M在线段AO上时,如图(3),延长NM,PA交于点G.
图(3)
第2步:利用线段关系找全等三角形
由(2)知,OM+ON=2AP,设OM=x,则ON=3x,OA=AP=2x.
∴AM=AO-OM=x=OM.
∵∠MON=∠MAG=90°,∠OMN=∠AMG,∴△MON≌△MAG(ASA),
∴AG=ON=3x.(9分) 得分点7:通过三角形全等得出AG与ON的关系,得1分
第3步:在相似三角形中,利用线段间的数量关系,得出结论
易得AP∥OB,∴△ONF∽△PGF,
∴===,
∴=,∴=.(10分) 得分点8:正确计算出 的值,得1分
第4步:考虑“点M在AO的延长线上”这一情况,并作辅助线
②当点M在AO的延长线上时,如图(4),过点P作
PC⊥OB于点C,并延长交MN于点G.
图(4)
第5步:类比第2步,找全等三角形
由(2)知,四边形OAPC是正方形,
∴OA=AP=PC=OC,∠APC=90°,PC∥AO.
∵PN⊥PM,
∴∠APM=∠CPN=90°-∠MPC.
∵∠A=∠PCN=90°,
∴△APM≌△CPN(ASA),
∴AM=CN,(11分) 得分点9:通过三角形全等得出AM与CN的关系,得1分
∴ON-OM=OC+CN-OM=AO+AM-OM=2AO.
设OM=y,则ON=3OM=3y,∴AO=y,CN=AM=2y.
图(4)
第6步:类比第3步,在相似三角形中,利用线段间的数量关系,得出结论
∵PC∥AO,∴△CGN∽△OMN,∴=,即=,∴CG=.
∵PC∥AO,∴△OMF∽△PGF,∴===,∴=,
∴=.(12分) 得分点10:正确计算出的值,得1分
综上,的值为或.
【注意】第(3)问解法较多,用其他解法,只要方法正确,得出正确结果,即可参照关键步骤给分.
第1讲 Unit 1—Unit 3
(含Starter Units)
七年级上册
2025年中考数学二轮专题复习
题型五 几何探究题
[2024烟台中考改编]在等腰直角三角形ABC中,∠ACB=90°,AC=BC,
D为直线BC上任意一点,连接AD,将线段AD绕点D按顺时针方向旋转[1]
90°得线段ED,连接BE.
【尝试发现】
(1)如图(1),当点D在线段BC上时,线段BE与CD的数量关系为 .
1
题型五
几何探究题
图(1)
BE=CD
[2024烟台中考改编]在等腰直角三角形ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD,将线段AD绕点D按顺时针方向旋转[2]90°得线段ED,连接BE.
【类比探究】
(2)当点D在线段BC的延长线上时,先在图(2)中补全图形[2],再探究线段BE与CD的数量关系并证明.
(3)若AC=BC=1,CD=2,求sin∠ECD的值.
1
题型五
几何探究题
图(2)
【大招点拨】识别题干信息:【发现】+【探究】+【拓展】
①找特征:根据[1]和[2],判断该题的特征是“旋转+操作”.
②找模型:旋转找全等模型,解答(1)和(2)的关键是作辅助线:过点E作EM⊥CB于点M,构造“一线三垂直”全等模型
③找结构:本题中的“不变结构”是等腰直角三角形ABC和线段AD绕点D按顺时针方向旋转90°.
④类比解决:结合(1)和(2)的解题思路,在解答(3)时,利用到的数学思想是分类讨论思想.
【自主解答】
1
题型五
几何探究题
(2)当点D在线段BC的延长线上时,先在图(2)中补全图形[2],再探究线段BE与CD的数量关系并证明.
1
题型五
几何探究题
图(1)
(2)补全图形如图(1).BE=CD.
证明:如图,过点E作EM⊥CB于点M.
由旋转,得AD=DE,∠ADE=90°,∴∠ADC+∠EDM=90°.
∵∠ACD=90°,∴∠ADC+∠CAD=90°,∴∠CAD=∠EDM.
又∵∠ACD=∠EMD=90°,∴△ACD≌△DME,
∴CD=EM,AC=DM.
又∵AC=BC,∴DM=BC,∴BM=DC,∴BM=EM,
∴在Rt△BME中,BE==EM=CD.
[2024烟台中考改编]在等腰直角三角形ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD,将线段AD绕点D按顺时针方向旋转[1]90°得线段ED,连接BE.
【联系拓展】
(3)若AC=BC=1,CD=2,求sin∠ECD的值.
1
题型五
几何探究题
(3)过点E作EM⊥CB,垂足为点M.分两种情况讨论.
①当点D在CB的延长线上时,如图(2).
易证△ACD≌△DME,∴EM=CD=2,DM=AC=1,
∴CM=CD+DM=3,∴EC==,∴sin∠ECD===.
图(2)
(3)若AC=BC=1,CD=2,求sin∠ECD的值.
1
题型五
几何探究题
图(3)
②当点D在BC的延长线上时,如图(3).
易证△ACD≌△DME,
∴EM=CD=2,DM=AC=1,
∴CM=CD-DM=1,∴EC==,
∴sin∠ECD===.
∴sin∠ECD的值为或.
[2024遵义二模改编]如图(1),在正方形ABCD中,点E是AB边上一动点,将正方形沿DE折叠,点A落在正方形内部的点F处,连接AF并延长,交BC于点G.
(1)判断AE与BG的数量关系为 .
2
图(1) 图(2)
AE=BG
(2)【应用】如图(1),延长DF交BC于点H.
①证明:∠HFG=∠FGH;
2
图(1)
(2)①证明:∵AD∥BC,
∴∠DAF=∠AGH.
由折叠可知,DA=DF,
∴∠DAF=∠AFD,
∴∠AFD=∠AGH.
∵∠AFD=∠HFG,
∴∠AGH=∠HFG.
(2)【应用】如图(1),延长DF交BC于点H.
②若HB=3a,HF=5a,AE=8,求BE的长度.
2
图(1)
②由①知,∠FGH=∠HFG,则HG=FH=5a,
∵BH=3a,∴BG=BH+HF=8a.
由折叠可得,AF⊥DE,∴∠BAG+∠AED=90°.
∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠ABG=90°,
∴∠AED+∠ADE=90°,
∴∠BAG=∠ADE,
∴△ADE≌△BAG,
(2)【应用】如图(1),延长DF交BC于点H.
②若HB=3a,HF=5a,AE=8,求BE的长度.
2
图(1)
∴AE=BG=8a=8,∴a=1,
∴BH=3,HF=5,EF=AE=8.
连接EH,△EBH与△EFH都是直角三角形,
∴BE2+BH2=EF2+FH2,
即BE2+32=82+52,
∴BE=4(负值已舍去).
(3)【拓展】如图(2),将正方形改成矩形,其中AD=2CD,将矩形沿DE折叠,使点A落在点F处(矩形内部),连接AF并延长,交BC于点G,延长DF交直线BC于点H.若HB=3a,HF=5a,求的值.
2
图(1) 图(2)
(3)分两种情况讨论:①如图(1),当点H在线段BC上时,
易知,∠AGH=∠HFG,∴HG=HF=5a,∴BG=8a.
易证得△ADE∽△BAG,∴=,∴2=,∴AE=16a.
设BE=x,则AB=16a+x,∴DF=AD=32a+2x,
∴CD=AB=16a+x,DH=32a+2x+5a=37a+2x,CH=32a+2x-3a=29a+2x.
在Rt△DCH中,∵CH2+CD2=DH2,
∴(29a+2x)2+(16a+x)2=(37a+2x)2,∴x=4a(负值已舍去),
∴==.
图(1)
②如图(2),当点H在线段CB的延长线上时,易知,∠AGH=∠HFG,
∴HF=HG=5a,∴BG=2a.易证得△ADE∽△BAG,
∴=,∴2=,∴AE=4a.
设BE=y,则AB=4a+y,∴DF=AD=8a+2y,
∴CD=AB=4a+y,DH=8a+2y+5a=13a+2y,CH=8a+2y+3a=11a+2y.
在Rt△DCH中,∵CH2+CD2=DH2,∴(11a+2y)2+(4a+y)2=(13a+2y)2,
∴y=4a(负值已舍去),∴==.
综上所述,=或=.
图(2)
[2024贵州25题12分]
综合与探究:如图,∠AOB=90°,点P在∠AOB的平分线上,PA⊥OA于点A.
(1)【操作判断】
如图(1),过点P作PC⊥OB于点C,根据题意在图(1)中画出PC,图中∠APC的度数
为 度.
(2)【问题探究】
如图(2),点M在线段AO上,连接PM,过点P作PN⊥PM
交射线OB于点N.求证:OM+ON=2PA.
图(1) 图(2)
(3)【拓展延伸】
点M在射线AO上,连接PM,过点P作PN⊥PM交射线OB于点N,射线NM与射线PO相交于点F,若ON=3OM,求的值.
图(1) 图(2)
解:(1)如图(1),PC即为所求.(2分) 得分点1:作图正确,得2分
图(1) 图(2)
90 (4分) 得分点2:正确写出∠APC的度数,得2分
(2)证明:如图(2),过点P作PC⊥OB于点C.
由题意知,四边形OAPC是矩形,
∵点P在∠AOB的平分线上,PA⊥OA,PC⊥OB,
∴PA=PC,(5分) 得分点3:根据角平分线的性质得出PA=PC,得1分
∴矩形OAPC是正方形,(6分) 得分点4:正确判定四边形OAPC是正方形,得1分
∴OA=AP=PC=OC,∠APC=90°.
∵PN⊥PM,∴∠APM=∠CPN=90°-∠MPC.
∵∠MAP=∠NCP=90°,
∴△APM≌△CPN(ASA),(7分) 得分点5:正确证明△APM≌△CPN,得1分
∴AM=CN,
∴OM+ON=OM+OC+CN=OM+AM+OC=OA+OC=2PA,
∴OM+ON=2PA.(8分) 得分点6:通过等量代换得出正确结论,得1分
(3)第1步:考虑“点M在线段AO上”这一种情况,并作辅助线
①当点M在线段AO上时,如图(3),延长NM,PA交于点G.
图(3)
第2步:利用线段关系找全等三角形
由(2)知,OM+ON=2AP,设OM=x,则ON=3x,OA=AP=2x.
∴AM=AO-OM=x=OM.
∵∠MON=∠MAG=90°,∠OMN=∠AMG,∴△MON≌△MAG(ASA),
∴AG=ON=3x.(9分) 得分点7:通过三角形全等得出AG与ON的关系,得1分
第3步:在相似三角形中,利用线段间的数量关系,得出结论
易得AP∥OB,∴△ONF∽△PGF,
∴===,
∴=,∴=.(10分) 得分点8:正确计算出 的值,得1分
第4步:考虑“点M在AO的延长线上”这一情况,并作辅助线
②当点M在AO的延长线上时,如图(4),过点P作
PC⊥OB于点C,并延长交MN于点G.
图(4)
第5步:类比第2步,找全等三角形
由(2)知,四边形OAPC是正方形,
∴OA=AP=PC=OC,∠APC=90°,PC∥AO.
∵PN⊥PM,
∴∠APM=∠CPN=90°-∠MPC.
∵∠A=∠PCN=90°,
∴△APM≌△CPN(ASA),
∴AM=CN,(11分) 得分点9:通过三角形全等得出AM与CN的关系,得1分
∴ON-OM=OC+CN-OM=AO+AM-OM=2AO.
设OM=y,则ON=3OM=3y,∴AO=y,CN=AM=2y.
图(4)
第6步:类比第3步,在相似三角形中,利用线段间的数量关系,得出结论
∵PC∥AO,∴△CGN∽△OMN,∴=,即=,∴CG=.
∵PC∥AO,∴△OMF∽△PGF,∴===,∴=,
∴=.(12分) 得分点10:正确计算出的值,得1分
综上,的值为或.
【注意】第(3)问解法较多,用其他解法,只要方法正确,得出正确结果,即可参照关键步骤给分.
同课章节目录
