数学六年级下北师大版3.1图形的旋转(二)课件
文档属性
| 名称 | 数学六年级下北师大版3.1图形的旋转(二)课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-07 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
1 图形的旋转二
1.了解生活中旋转现象的广泛存在。
2.掌握旋转的有关概念,理解旋转变换也是图形的一种基本变换。
3.会找出旋转前后图形中的对应点、对应线段、对应角、旋转中心、旋 转角。
学习目标
情境导入
自转与公转
情境导入
情境导入
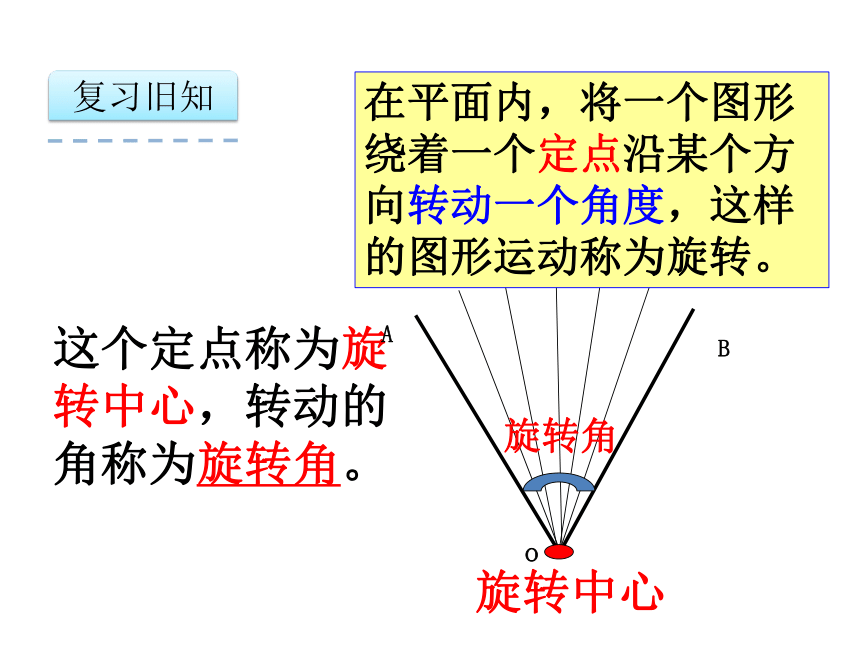
这个定点称为旋转中心,转动的角称为旋转角。
旋转角
旋转中心
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
A
o
B
复习旧知
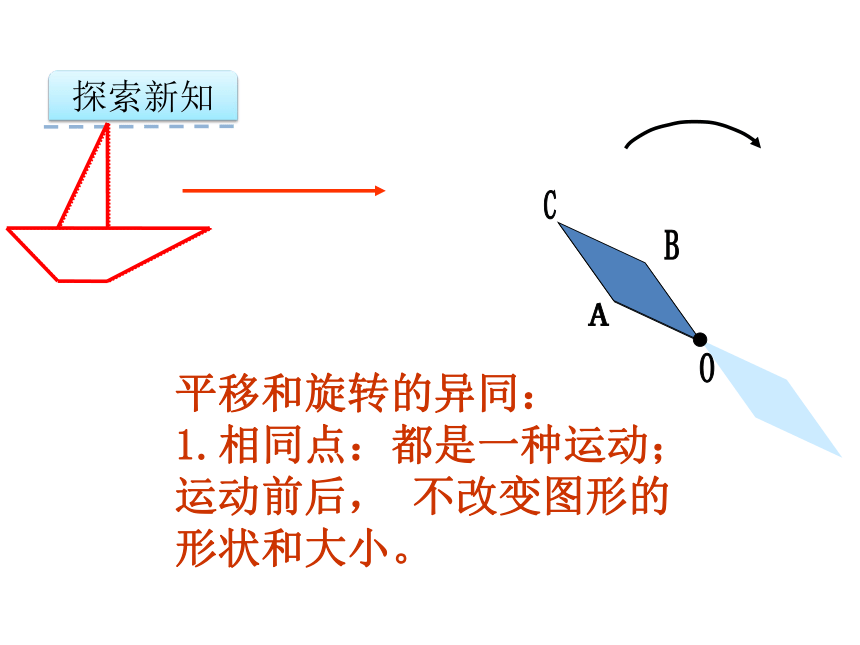
平移和旋转的异同:
1.相同点:都是一种运动;运动前后, 不改变图形的形状和大小。
探索新知
2.不同点。
运动方向 运动量
的衡量
平移 直线 移动一定距离
旋转 顺时针
逆时针 转动一定的角度
探索新知
1.如图,如果把钟表的指针看作四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是__旋转角___
(2)经过旋转,点A、B分别移动到什么位置?
o
o
900
A移动到D;B移动到E
探索新知
o
风车旋转前后,每个三角形的形状、大小、位置有什么变化?
性质1:旋转前、后的图形形状和大小都没变。
探索新知
(4)对应点到旋转中心的距离相等。
旋转的基本性质
(1)旋转不改变图形的大小和形状。
(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度。
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角。
探索新知
1.画出三角形AOB 绕点O顺时针旋转900后的图形。
B
A
O
A`
B`
旋转时要注意旋转的角度和距离。
说一说你是怎样画的
学以致用
2.下列现象中属于旋转的有( )。
①飞机螺旋桨的转动 ②电梯上下移动 ③开教室里的窗户 ④旋转木马 ⑤摩天轮 ⑥小朋友滑滑梯
3.四边形AD′C′B′是由正方形ABCD旋转而成。
(1)旋转中心是______
(2)旋转的角度是______
点A
45°
C'
D'
B'
B
A
C
D
①③④⑤
学以致用
4. 如图,已知□ABCD的对角线BD=4cm,将□ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )。
A
B
C
D
O
A.4π cm B.3π cm C.2π cm D.π cm
C
学以致用
课堂回顾:这节课,主要学习了什么?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
旋转的概念:
课堂小结
旋转的性质:
1、旋转不改变图形的大小和形状。
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等。
3、对应点到旋转中心的距离相等。
课堂小结
1 图形的旋转二
1.了解生活中旋转现象的广泛存在。
2.掌握旋转的有关概念,理解旋转变换也是图形的一种基本变换。
3.会找出旋转前后图形中的对应点、对应线段、对应角、旋转中心、旋 转角。
学习目标
情境导入
自转与公转
情境导入
情境导入
这个定点称为旋转中心,转动的角称为旋转角。
旋转角
旋转中心
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
A
o
B
复习旧知
平移和旋转的异同:
1.相同点:都是一种运动;运动前后, 不改变图形的形状和大小。
探索新知
2.不同点。
运动方向 运动量
的衡量
平移 直线 移动一定距离
旋转 顺时针
逆时针 转动一定的角度
探索新知
1.如图,如果把钟表的指针看作四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是__旋转角___
(2)经过旋转,点A、B分别移动到什么位置?
o
o
900
A移动到D;B移动到E
探索新知
o
风车旋转前后,每个三角形的形状、大小、位置有什么变化?
性质1:旋转前、后的图形形状和大小都没变。
探索新知
(4)对应点到旋转中心的距离相等。
旋转的基本性质
(1)旋转不改变图形的大小和形状。
(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度。
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角。
探索新知
1.画出三角形AOB 绕点O顺时针旋转900后的图形。
B
A
O
A`
B`
旋转时要注意旋转的角度和距离。
说一说你是怎样画的
学以致用
2.下列现象中属于旋转的有( )。
①飞机螺旋桨的转动 ②电梯上下移动 ③开教室里的窗户 ④旋转木马 ⑤摩天轮 ⑥小朋友滑滑梯
3.四边形AD′C′B′是由正方形ABCD旋转而成。
(1)旋转中心是______
(2)旋转的角度是______
点A
45°
C'
D'
B'
B
A
C
D
①③④⑤
学以致用
4. 如图,已知□ABCD的对角线BD=4cm,将□ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )。
A
B
C
D
O
A.4π cm B.3π cm C.2π cm D.π cm
C
学以致用
课堂回顾:这节课,主要学习了什么?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
旋转的概念:
课堂小结
旋转的性质:
1、旋转不改变图形的大小和形状。
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等。
3、对应点到旋转中心的距离相等。
课堂小结
