辽宁省盘锦市2025届九年级上学期期中考试数学试卷(含答案)
文档属性
| 名称 | 辽宁省盘锦市2025届九年级上学期期中考试数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 00:00:00 | ||
图片预览



文档简介
辽宁省盘锦市2025届九年级上学期期中考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.中国新能源汽车产销量连续9年位居全球第一,下列新能源汽车的车标中,为中心对称图形的是( )
A. B.
C. D.
2.如图,与相切于A点,,则( )
A.20° B.35° C.70° D.110°
3.用配方法解方程时,原方程应变形为( )
A. B. C. D.
4.剪纸是我国的民间传统艺术,能为节日增加许多喜庆的氛围.剪纸中有一种“抛物线剪纸”艺术,即作品的外轮廓在抛物线上,体现了一种曲线美,如图,这是利用“抛物线剪纸”艺术剪出的蝴蝶,建立适当的平面直角坐标系,使外轮廓上的A,B,C,D四点落在抛物线上,则下列结论正确的是( )
A. B. C. D.
5.已知点,,都在二次函数的图象上,则,,的大小关系为( )
A. B. C. D.
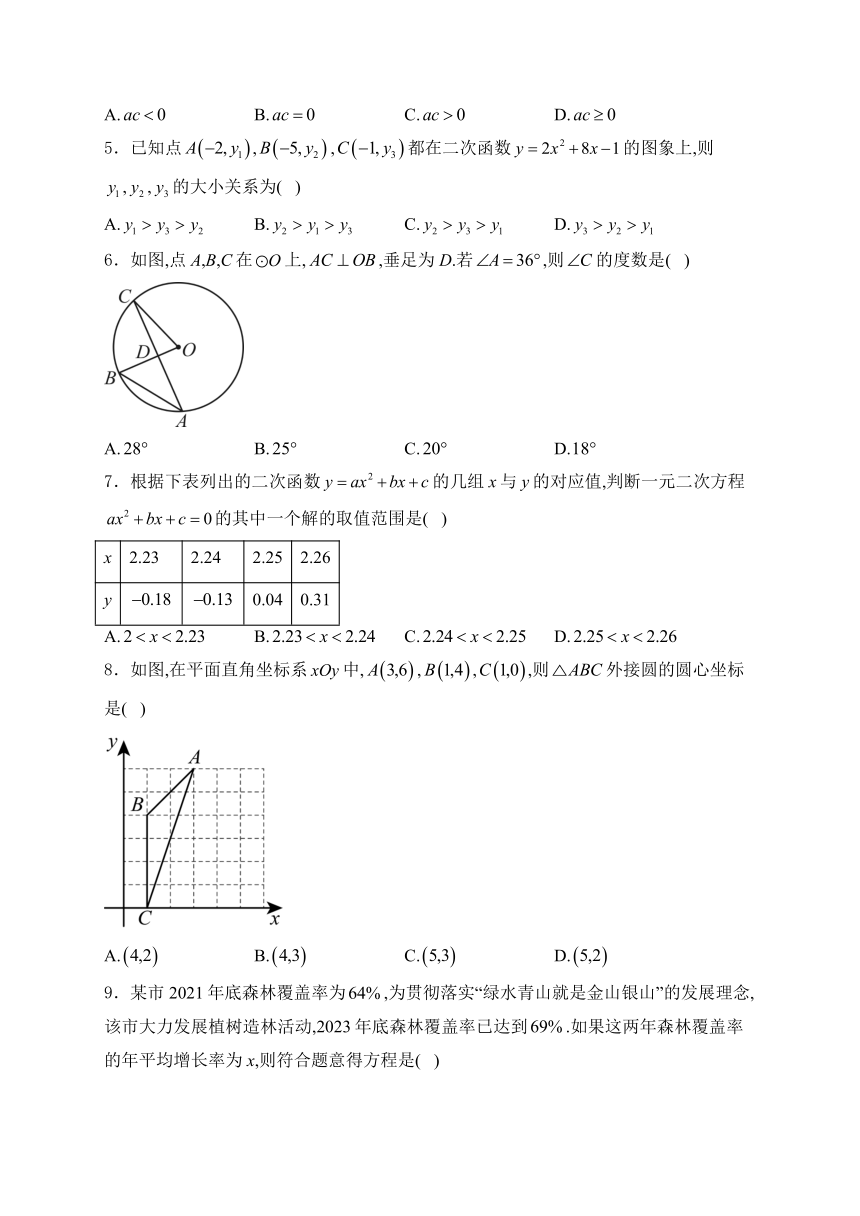
6.如图,点A,B,C在上,,垂足为D.若,则的度数是( )
A. B. C. D.
7.根据下表列出的二次函数的几组x与y的对应值,判断一元二次方程的其中一个解的取值范围是( )
x 2.23 2.24 2.25 2.26
y 0.04 0.31
A. B. C. D.
8.如图,在平面直角坐标系中,,,,则外接圆的圆心坐标是( )
A. B. C. D.
9.某市2021年底森林覆盖率为,为贯彻落实“绿水青山就是金山银山”的发展理念,该市大力发展植树造林活动,2023年底森林覆盖率已达到.如果这两年森林覆盖率的年平均增长率为x,则符合题意得方程是( )
A. B.
C. D.
10.将抛物线的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )
A. B. C. D.
二、填空题
11.已知的半径为6,点P在外,则点P到圆心O的距离d的取值范围是______.
12.二次函数的图象的顶点坐标是______.
13.关于x的一元二次方程有两个不相等的实数根,则k的取值范围是______.
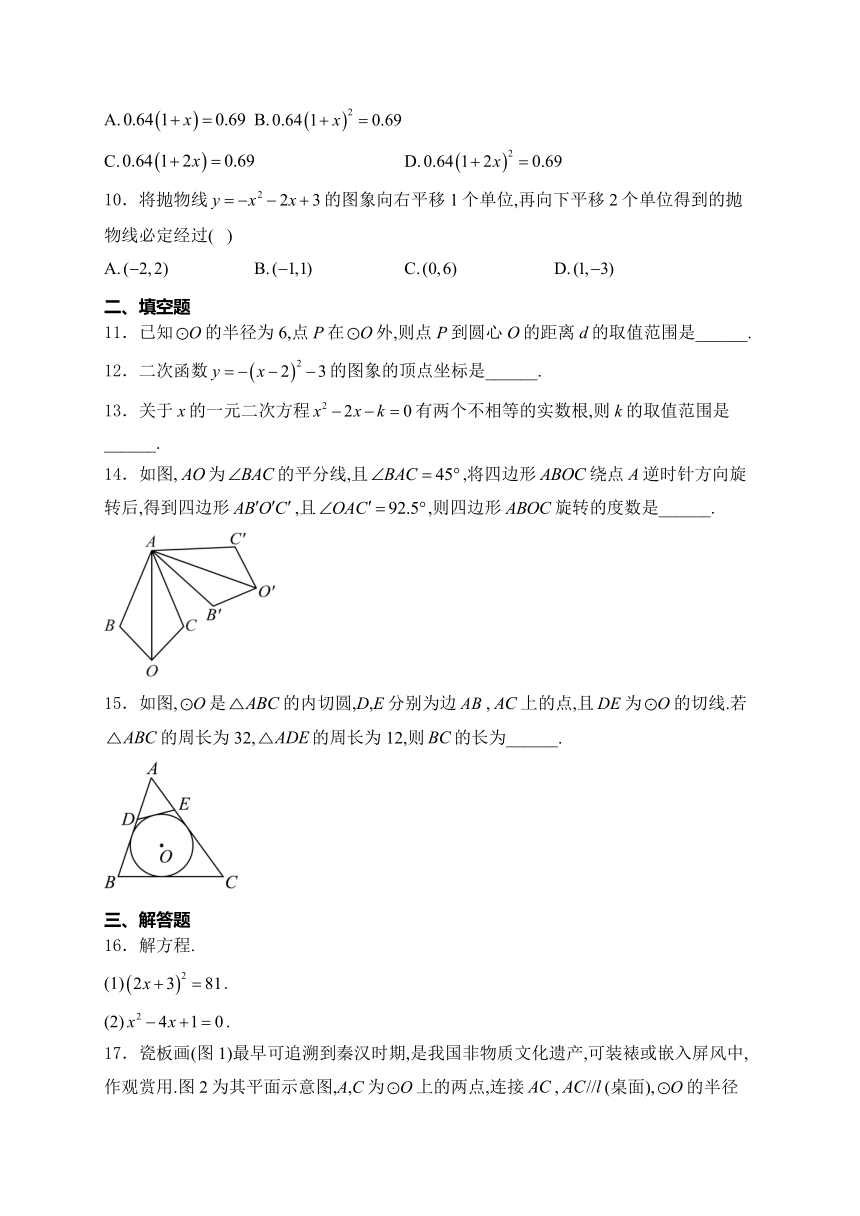
14.如图,为的平分线,且,将四边形绕点A逆时针方向旋转后,得到四边形,且,则四边形旋转的度数是______.
15.如图,是的内切圆,D,E分别为边,上的点,且为的切线.若的周长为32,的周长为12,则的长为______.
三、解答题
16.解方程.
(1).
(2).
17.瓷板画(图1)最早可追溯到秦汉时期,是我国非物质文化遗产,可装裱或嵌入屏风中,作观赏用.图2为其平面示意图,A,C为上的两点,连接,(桌面),的半径,,分别与直线l垂直于B,D两点,,,过点O作于点E,交于点F,求圆心O到桌面l的距离.
18.在下面的网格图中,每个小正方形的边长均为1个单位长度.在中,,,.
(1)在图中作出以点A为旋转中心,沿顺时针方向旋转后的图形.
(2)若点A的坐标为,点B的坐标为,请在图中画出平面直角坐标系,并写出点C的坐标.
(3)根据(2)中的平面直角坐标系,作出与关于原点对称的.
19.已知抛物线的解析式为.
(1)若抛物线的对称轴为,求a的值.
(2)若抛物线经过点,求此时抛物线与x轴的两个交点之间的距离.
20.实践教学
向阳中学在劳动课上自制月饼销售.
数据采集
一盒月饼的成本共40元,第一天按每盒60元销售,销售了100盒;第二天共制作月饼150盒.若第二天按第一天的价格出售,预计同样可售出第一天的数量,若每盒每降价1元,则可多售出10盒.
数据应用
若计划第二天降价销售,且利润为2240元,每盒月饼应降价多少元?
21.如图,在中,C为的中点,于点D,于点E.
(1)求证:.
(2)若,,求四边形的面积.
22.张老师善于通过合适的主题整合教学内容,帮助同学们用整体的、联系的、发展的眼光看问题,形成科学的思维习惯.下面是张老师在“矩形纸片的剪拼”主题下设计的问题,请你解答.
(1)观察发现
将为,为的矩形纸片沿对角线剪开,得到和.如图1,将以点A为旋转中心,按逆时针方向旋转,,得到,过点C作,交的延长线于点E,则四边形的形状是______.
(2)探究迁移
如图2,若将以点A为旋转中心逆时针旋转,得到的,若B,A,三点在同一条直线上,连接,取的中点F,连接AF并延长至点G,使,连接CG,,得到四边形,请你判断四边形的形状,并加以证明.
(3)拓展应用
如图3,在(2)的条件下,将沿着方向平移,使点B与点A重合,此时A点平移至点,与相交于点H,连接,求的值.
23.综合与探究
如图,在平面直角坐标系中,抛物线经过点,,连接,为抛物线部分上一动点(可与A,B两点重合),过点P作轴交直线于点M,交x轴于点N.
(1)求抛物线和直线的解析式.
(2)①求线段的最大值.
②连接,当为等腰三角形时,求m的值.
参考答案
1.答案:D
解析:A.不是中心对称图形,故此选项错误;
B.不是中心对称图形,故此选项错误;
C.不是中心对称图形,故此选项错误;
D.是中心对称图形,故此选项正确.
故选D.
2.答案:A
解析:∵与相切于A点,
∴.
又∵,
∴中,,
故选A.
3.答案:C
解析:方程两边同时加上4,得,
即.
故选:C.
4.答案:A
解析:∵根据抛物线开口向上,与y轴交于负半轴,
∴,,则,
故选:A.
5.答案:C
解析:二次函数的对称轴为直线,
,
∴该二次函数图象的开口向上,图象上的点离对称轴越近,对应的函数值越小,
∵,,,且
.
故选:C.
6.答案:D
解析:∵,
∴,
∵,
∴,
∴.
故选:D.
7.答案:C
解析:由表可以看出,当x取2.24与2.25之间的某个数时,,即这个数是的一个根.
故关于x的一元二次方程的一个解的大致范围是.
故选:C.
8.答案:D
解析:如图所示:点P即为所求;
所以点P的坐标为.
故选:D.
9.答案:B
解析:根据题意,得
即,
故选:B.
10.答案:B
解析:将抛物线化为顶点式,
即:
,
将抛物线的图象向右平移1个单位,再向下平移2个单位,
根据函数图像平移性质:左加右减,上加下减得:
,
A选项代入,,不符合;
B选项代入,,符合;
C选项代入,,不符合;
D选项代入,,不符合;
故选:B.
11.答案:
解析:∵的半径为6,点P在外,
∴点到圆心的距离d的取值范围是.
故答案为:.
12.答案:
解析:二次函数图象的顶点坐标是.
故答案为:.
13.答案:/
解析:关于x的一元二次方程有两个不相等的实数根,
,
解得.
故答案为:.
14.答案:/70度
解析:∵为的平分线,且,
∴,
∵将四边形绕点A逆时针方向旋转后,得到四边形,
∴,,
∴.
故答案为:.
15.答案:10
解析:如图:
由切线长定理得:,,,,
,
,
,
故答案为:10.
16.答案:(1),
(2),
解析:(1)
解得:,;
(2)
.
解得:,.
17.答案:27cm
解析:∵,,,分别垂直于点B,D,
∴,.
∵,
∴.
在中,根据勾股定理得,
∴.
18.答案:(1)见解析
(2)建立平面直角坐标系见解析.点C的坐标为
(3)见解析
解析:(1)如图,即为所求.
(2)建立平面直角坐标系如图所示.点C的坐标为.
(3)如图,即为所求.
19.答案:(1)
(2)4
解析:(1)抛物线的对称轴为,
,解得,
经检验,是该分式方程的解.
(2)∵抛物线经过点,
∴,解得,
∴抛物线解析式为.
当,即时,
,解得,,
抛物线与x轴的两个交点的坐标分别为,,
两个交点之间的距离为.
20.答案:每盒月饼应降价4元
解析:设每盒月饼降价x元.
,则,
根据题意,得,
整理得:,
解得,(舍去).
答:每盒月饼应降价4元.
21.答案:(1)见解析
(2)
解析:(1)证明:如图,连接.
为的中点,
,
,
平分.
又,,
.
(2)如图,连接
由(1)得,
,
.
∵,
∴,
.
,
在中,,
,
.
同理,可得,
.
22.答案:(1)菱形
(2)是正方形,理由见解析
(3)
解析:(1)四边形是菱形,证明如下:
由图1可知,是矩形的对角线,,,
,
在图2中,由旋转知,,,
,
,
,
,
,
四边形是平行四边形,
又,
是菱形,
故答案为:菱形;
(2)是正方形,证明如下:
图1中,四边形是矩形,
,
,,
,
在图3中,由旋转知,,
,
,
点D,A,B在同一条直线上,
,
由旋转知,,
点F是的中点,
,,
,
四边形是平行四边形,
,
是菱形,
又,
菱形是正方形;
(3)在中,,,
,,
由(2)结合平移知,,
在中,,
,
.
23.答案:(1)抛物线的解析式为,直线的解析式为
(2)①的最大值为1②或或
解析:(1)∵抛物线经过点,
∴.
将点代入,得,解得,
抛物线的解析式为.
设直线AB的解析式为,
将点代入,得,解得,
∴直线AB的解析式为.
(2)①将代入中,得.
将代入中,得.
∴,
即的最大值为1.
②∵点M在直线上,且点,
∴点M的坐标为.
∵点,
∴,
∴,
.
当为等腰三角形时,
(ⅰ)若,则,
即,解得.
(ⅱ)若,则,
即,解得或(舍去).
(ⅲ)若,则,
即,解得或(舍去).
综上所述,或或.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.中国新能源汽车产销量连续9年位居全球第一,下列新能源汽车的车标中,为中心对称图形的是( )
A. B.
C. D.
2.如图,与相切于A点,,则( )
A.20° B.35° C.70° D.110°
3.用配方法解方程时,原方程应变形为( )
A. B. C. D.
4.剪纸是我国的民间传统艺术,能为节日增加许多喜庆的氛围.剪纸中有一种“抛物线剪纸”艺术,即作品的外轮廓在抛物线上,体现了一种曲线美,如图,这是利用“抛物线剪纸”艺术剪出的蝴蝶,建立适当的平面直角坐标系,使外轮廓上的A,B,C,D四点落在抛物线上,则下列结论正确的是( )
A. B. C. D.
5.已知点,,都在二次函数的图象上,则,,的大小关系为( )
A. B. C. D.
6.如图,点A,B,C在上,,垂足为D.若,则的度数是( )
A. B. C. D.
7.根据下表列出的二次函数的几组x与y的对应值,判断一元二次方程的其中一个解的取值范围是( )
x 2.23 2.24 2.25 2.26
y 0.04 0.31
A. B. C. D.
8.如图,在平面直角坐标系中,,,,则外接圆的圆心坐标是( )
A. B. C. D.
9.某市2021年底森林覆盖率为,为贯彻落实“绿水青山就是金山银山”的发展理念,该市大力发展植树造林活动,2023年底森林覆盖率已达到.如果这两年森林覆盖率的年平均增长率为x,则符合题意得方程是( )
A. B.
C. D.
10.将抛物线的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )
A. B. C. D.
二、填空题
11.已知的半径为6,点P在外,则点P到圆心O的距离d的取值范围是______.
12.二次函数的图象的顶点坐标是______.
13.关于x的一元二次方程有两个不相等的实数根,则k的取值范围是______.
14.如图,为的平分线,且,将四边形绕点A逆时针方向旋转后,得到四边形,且,则四边形旋转的度数是______.
15.如图,是的内切圆,D,E分别为边,上的点,且为的切线.若的周长为32,的周长为12,则的长为______.
三、解答题
16.解方程.
(1).
(2).
17.瓷板画(图1)最早可追溯到秦汉时期,是我国非物质文化遗产,可装裱或嵌入屏风中,作观赏用.图2为其平面示意图,A,C为上的两点,连接,(桌面),的半径,,分别与直线l垂直于B,D两点,,,过点O作于点E,交于点F,求圆心O到桌面l的距离.
18.在下面的网格图中,每个小正方形的边长均为1个单位长度.在中,,,.
(1)在图中作出以点A为旋转中心,沿顺时针方向旋转后的图形.
(2)若点A的坐标为,点B的坐标为,请在图中画出平面直角坐标系,并写出点C的坐标.
(3)根据(2)中的平面直角坐标系,作出与关于原点对称的.
19.已知抛物线的解析式为.
(1)若抛物线的对称轴为,求a的值.
(2)若抛物线经过点,求此时抛物线与x轴的两个交点之间的距离.
20.实践教学
向阳中学在劳动课上自制月饼销售.
数据采集
一盒月饼的成本共40元,第一天按每盒60元销售,销售了100盒;第二天共制作月饼150盒.若第二天按第一天的价格出售,预计同样可售出第一天的数量,若每盒每降价1元,则可多售出10盒.
数据应用
若计划第二天降价销售,且利润为2240元,每盒月饼应降价多少元?
21.如图,在中,C为的中点,于点D,于点E.
(1)求证:.
(2)若,,求四边形的面积.
22.张老师善于通过合适的主题整合教学内容,帮助同学们用整体的、联系的、发展的眼光看问题,形成科学的思维习惯.下面是张老师在“矩形纸片的剪拼”主题下设计的问题,请你解答.
(1)观察发现
将为,为的矩形纸片沿对角线剪开,得到和.如图1,将以点A为旋转中心,按逆时针方向旋转,,得到,过点C作,交的延长线于点E,则四边形的形状是______.
(2)探究迁移
如图2,若将以点A为旋转中心逆时针旋转,得到的,若B,A,三点在同一条直线上,连接,取的中点F,连接AF并延长至点G,使,连接CG,,得到四边形,请你判断四边形的形状,并加以证明.
(3)拓展应用
如图3,在(2)的条件下,将沿着方向平移,使点B与点A重合,此时A点平移至点,与相交于点H,连接,求的值.
23.综合与探究
如图,在平面直角坐标系中,抛物线经过点,,连接,为抛物线部分上一动点(可与A,B两点重合),过点P作轴交直线于点M,交x轴于点N.
(1)求抛物线和直线的解析式.
(2)①求线段的最大值.
②连接,当为等腰三角形时,求m的值.
参考答案
1.答案:D
解析:A.不是中心对称图形,故此选项错误;
B.不是中心对称图形,故此选项错误;
C.不是中心对称图形,故此选项错误;
D.是中心对称图形,故此选项正确.
故选D.
2.答案:A
解析:∵与相切于A点,
∴.
又∵,
∴中,,
故选A.
3.答案:C
解析:方程两边同时加上4,得,
即.
故选:C.
4.答案:A
解析:∵根据抛物线开口向上,与y轴交于负半轴,
∴,,则,
故选:A.
5.答案:C
解析:二次函数的对称轴为直线,
,
∴该二次函数图象的开口向上,图象上的点离对称轴越近,对应的函数值越小,
∵,,,且
.
故选:C.
6.答案:D
解析:∵,
∴,
∵,
∴,
∴.
故选:D.
7.答案:C
解析:由表可以看出,当x取2.24与2.25之间的某个数时,,即这个数是的一个根.
故关于x的一元二次方程的一个解的大致范围是.
故选:C.
8.答案:D
解析:如图所示:点P即为所求;
所以点P的坐标为.
故选:D.
9.答案:B
解析:根据题意,得
即,
故选:B.
10.答案:B
解析:将抛物线化为顶点式,
即:
,
将抛物线的图象向右平移1个单位,再向下平移2个单位,
根据函数图像平移性质:左加右减,上加下减得:
,
A选项代入,,不符合;
B选项代入,,符合;
C选项代入,,不符合;
D选项代入,,不符合;
故选:B.
11.答案:
解析:∵的半径为6,点P在外,
∴点到圆心的距离d的取值范围是.
故答案为:.
12.答案:
解析:二次函数图象的顶点坐标是.
故答案为:.
13.答案:/
解析:关于x的一元二次方程有两个不相等的实数根,
,
解得.
故答案为:.
14.答案:/70度
解析:∵为的平分线,且,
∴,
∵将四边形绕点A逆时针方向旋转后,得到四边形,
∴,,
∴.
故答案为:.
15.答案:10
解析:如图:
由切线长定理得:,,,,
,
,
,
故答案为:10.
16.答案:(1),
(2),
解析:(1)
解得:,;
(2)
.
解得:,.
17.答案:27cm
解析:∵,,,分别垂直于点B,D,
∴,.
∵,
∴.
在中,根据勾股定理得,
∴.
18.答案:(1)见解析
(2)建立平面直角坐标系见解析.点C的坐标为
(3)见解析
解析:(1)如图,即为所求.
(2)建立平面直角坐标系如图所示.点C的坐标为.
(3)如图,即为所求.
19.答案:(1)
(2)4
解析:(1)抛物线的对称轴为,
,解得,
经检验,是该分式方程的解.
(2)∵抛物线经过点,
∴,解得,
∴抛物线解析式为.
当,即时,
,解得,,
抛物线与x轴的两个交点的坐标分别为,,
两个交点之间的距离为.
20.答案:每盒月饼应降价4元
解析:设每盒月饼降价x元.
,则,
根据题意,得,
整理得:,
解得,(舍去).
答:每盒月饼应降价4元.
21.答案:(1)见解析
(2)
解析:(1)证明:如图,连接.
为的中点,
,
,
平分.
又,,
.
(2)如图,连接
由(1)得,
,
.
∵,
∴,
.
,
在中,,
,
.
同理,可得,
.
22.答案:(1)菱形
(2)是正方形,理由见解析
(3)
解析:(1)四边形是菱形,证明如下:
由图1可知,是矩形的对角线,,,
,
在图2中,由旋转知,,,
,
,
,
,
,
四边形是平行四边形,
又,
是菱形,
故答案为:菱形;
(2)是正方形,证明如下:
图1中,四边形是矩形,
,
,,
,
在图3中,由旋转知,,
,
,
点D,A,B在同一条直线上,
,
由旋转知,,
点F是的中点,
,,
,
四边形是平行四边形,
,
是菱形,
又,
菱形是正方形;
(3)在中,,,
,,
由(2)结合平移知,,
在中,,
,
.
23.答案:(1)抛物线的解析式为,直线的解析式为
(2)①的最大值为1②或或
解析:(1)∵抛物线经过点,
∴.
将点代入,得,解得,
抛物线的解析式为.
设直线AB的解析式为,
将点代入,得,解得,
∴直线AB的解析式为.
(2)①将代入中,得.
将代入中,得.
∴,
即的最大值为1.
②∵点M在直线上,且点,
∴点M的坐标为.
∵点,
∴,
∴,
.
当为等腰三角形时,
(ⅰ)若,则,
即,解得.
(ⅱ)若,则,
即,解得或(舍去).
(ⅲ)若,则,
即,解得或(舍去).
综上所述,或或.
同课章节目录
