2024-2025学年湖南省“金太阳联考”高一年级12月联考数学试题(含答案)
文档属性
| 名称 | 2024-2025学年湖南省“金太阳联考”高一年级12月联考数学试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 84.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 00:00:00 | ||
图片预览




文档简介
2024-2025学年湖南省“金太阳联考”高一年级12月联考数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.“”是“为指数函数”的( )
A. 充要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分也不必要条件
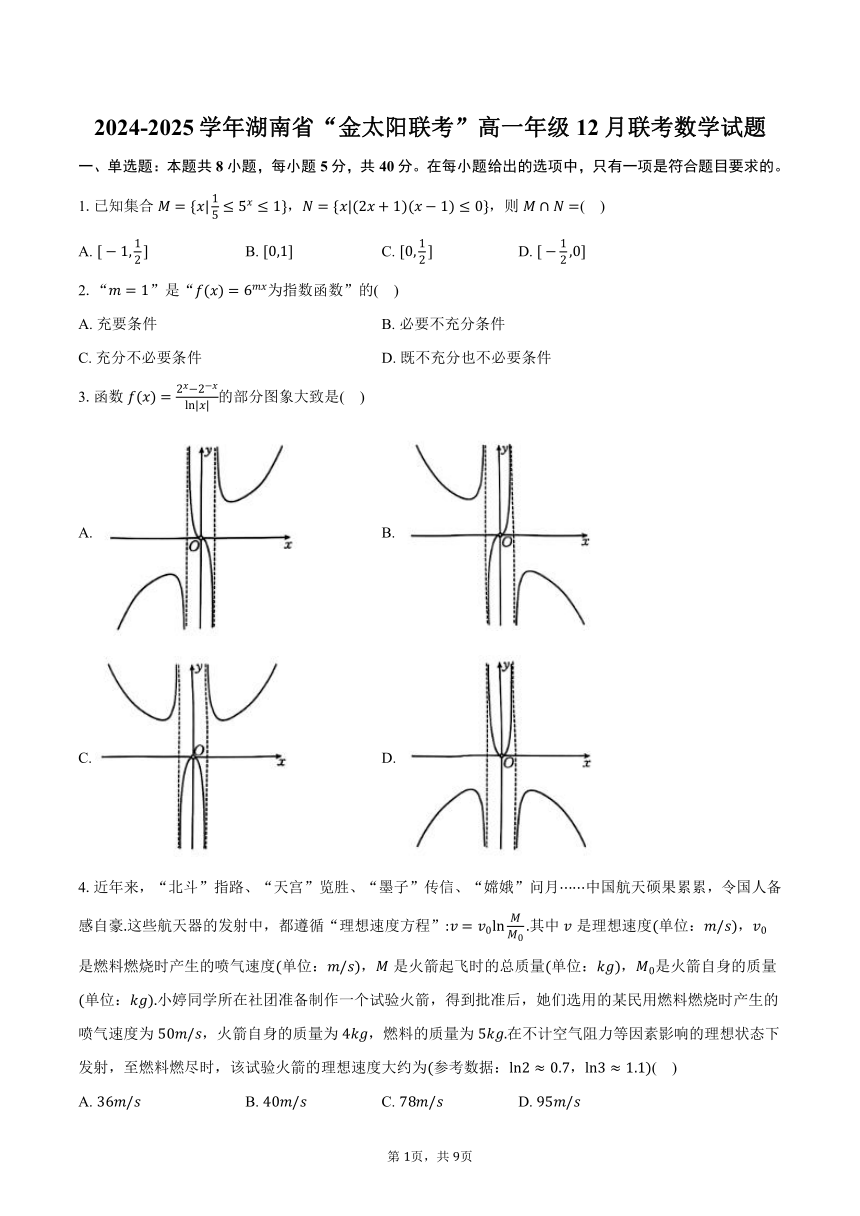
3.函数的部分图象大致是( )
A. B.
C. D.
4.近年来,“北斗”指路、“天宫”览胜、“墨子”传信、“嫦娥”问月中国航天硕果累累,令国人备感自豪这些航天器的发射中,都遵循“理想速度方程”其中是理想速度单位:,是燃料燃烧时产生的喷气速度单位:,是火箭起飞时的总质量单位:,是火箭自身的质量单位:小婷同学所在社团准备制作一个试验火箭,得到批准后,她们选用的某民用燃料燃烧时产生的喷气速度为,火箭自身的质量为,燃料的质量为在不计空气阻力等因素影响的理想状态下发射,至燃料燃尽时,该试验火箭的理想速度大约为参考数据:,( )
A. B. C. D.
5.下列函数中,既是奇函数又在上单调递增的是( )
A. B.
C. D.
6.若函数的最小值是,则实数的值为( )
A. 或 B. 或 C. 或 D. 或
7.已知函数的零点为,的零点为,则下列结论错误的是( )
A. B. C. D.
8.设,若函数有个不同的零点,,,,且,则的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列关于不等式的说法正确的是( )
A. ,
B. 若,,则
C. 若,,,则
D. ,,
10.下列关于对数运算正确的是( )
A. 设,,均为正实数,且,则
B. 若方程的两根为,,则
C. 已知,则
D.
11.定义“正对数”现有四个命题,其中是真命题的有( )
A. 若,,则
B. 若,,则
C. 若,,则
D. 若,,则
三、填空题:本题共3小题,每小题5分,共15分。
12.已知函数在上具有单调性,则实数的取值范围是 .
13.已知定义在上的函数满足是偶函数在上为增函数若不等式成立,则实数的取值范围是 .
14.设是定义在上的奇函数,当时,若对任意的,不等式恒成立,则实数的取值范围是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知关于的不等式.
若,,且,试求它的解集
若,,试求它的解集.
16.本小题分
已知函数.
若,求的最小值
若,存在实数,,使得当的定义域为时,的值域为,求实数的取值范围.
17.本小题分
年全年,中国新能源汽车产量、销量分别达到万辆和万辆,同比分别增长和我国新能源汽车产销量占全球比重超过,连续年位居世界第一新能源汽车出口万辆,同比增长,均创历史新高年中国数家车企推出多款电动新能源汽车,引起市场轰动,电动新能源汽车逐步成为人们购车的热门选择有关部门在高速公路上对某型号电动汽车进行测试,得到了该电动汽车每小时耗电量单位:与速度单位:的数据,如下表所示:
经画图研究可知该电动汽车在高速公路上行驶时每小时耗电量与速度的关系为.
求出函数的函数解析式.
张某驾驶一辆同型号电动汽车从地出发,经高速公路最低限速,最高限速匀速行驶到距离为的地出发前,汽车电池存量为,汽车到达地后至少要保留的保障电量假设该电动汽车从静止加速到速度为的过程中消耗的电量与行驶的路程都忽略不计已知该高速公路上服务区有功率为的充电桩充电量充电功率充电时间若不充电,该电动汽车能否到达地并说明理由若需要充电,求该电动汽车从地到达地所用时间即行驶时间与充电时间之和的最小值结果保留一位小数.
18.本小题分
已知函数为偶函数.
求的值
求的最小值
若对任意恒成立,求实数的取值范围.
19.本小题分
设,是非空实数集,如果对于集合中的任意两个实数,,按照某种确定的关系,在中都有唯一确定的数和它对应,那么就称为从集合到集合的一个二元函数,记作,,,其中称为二元函数的定义域.
已知,若,,,求
设二元函数的定义域为,如果存在实数满足,,都有,,,使得,那么我们称是二元函数的下确界若,,且,判断函数是否存在下确界若存在,求出此函数的下确界若不存在,说明理由.
设的定义域为,若,,,,则称在上关于单调递增已知在上关于单调递增,求实数的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:把,代入不等式,得.
因为,所以,即,解得,
所以所求不等式的解集是.
把,代入不等式,得即.
若,则不等式为一个一元一次不等式
若,则其对应的函数零点是,,
需根据零点大小与的正负进行讨论.
当时,原不等式变为,解集是
当时,原不等式变为,解集是
当时,原不等式变为,解集是
当时,原不等式变为,解集是
当时,原不等式变为,解集是或
16.解:若,则,
令,,则,,
该二次函数开口向上,其图象的对称轴为直线,
所以当时,.
因为,所以在上单调递增,
则当的定义域为时,的值域为,
所以即在上有两个不同的实数解,
即在上有两个不同的实数解.
令,,所以在上有两个不同的实数解,
所以解得
所以实数的取值范围为
17.解析:由题意,
所以..
设耗电量为,则.
任取,..
,
由,,,得,即,
所以函数在上单调递增,
故,即最小耗电量大于电池存量减去保障电量,
所以该车不在服务区充电不能到达地.
设行驶时间与充电时间分别为,,总和为单位:,
若能到达地,则初始电量充电电量一消耗电量保障电量,
即,解得,
所以总时间,
当且仅当,即时,等号成立,
所以该汽车到达地的最少用时约为.
18.解:因为 为偶函数,
所以 ,则 ,
所以 ,即 恒成立,
因为 不恒为 ,所以 ,故 .
由得,
,
因为 ,则 ,当且仅当 ,即 时,等号成立,
所以 ,故 最小值为 .
因为 ,
任取 且 ,
所以,
因为 且 ,所以 ,
所以 ,即 ,
所以 ,则 在 上为增函数,
又因为 为偶函数, ,
所以 ,
当 时, 恒成立,则 ;
当 时, ,所以 ,
设 ,
当且仅当 ,即 时,等号成立,
由复合函数的单调性易得 在 上单调递增,
且当 时, ,当 时, ,
所以 有解,即 有解,所以等号能成立,
所以 ,故 ,则 ;
综上, .
所以实数的取值范围为
19.解:由可得,,
由可得,
由
又,
所以
由可得,,
由,可得,所以,
当且仅当时取等号.
,
当且仅当,即时取等号.
因为在上是关于单调递增,
所以,
即存在,对于任意的,,都有,
化简可得,即,
下面求函数的最小值,
设,,
,
所以函数在递增,,
即存在,使得,设,,
当时,,
当时,,
设,,
所以,
综上,,
所以的取值范围是
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.“”是“为指数函数”的( )
A. 充要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分也不必要条件
3.函数的部分图象大致是( )
A. B.
C. D.
4.近年来,“北斗”指路、“天宫”览胜、“墨子”传信、“嫦娥”问月中国航天硕果累累,令国人备感自豪这些航天器的发射中,都遵循“理想速度方程”其中是理想速度单位:,是燃料燃烧时产生的喷气速度单位:,是火箭起飞时的总质量单位:,是火箭自身的质量单位:小婷同学所在社团准备制作一个试验火箭,得到批准后,她们选用的某民用燃料燃烧时产生的喷气速度为,火箭自身的质量为,燃料的质量为在不计空气阻力等因素影响的理想状态下发射,至燃料燃尽时,该试验火箭的理想速度大约为参考数据:,( )
A. B. C. D.
5.下列函数中,既是奇函数又在上单调递增的是( )
A. B.
C. D.
6.若函数的最小值是,则实数的值为( )
A. 或 B. 或 C. 或 D. 或
7.已知函数的零点为,的零点为,则下列结论错误的是( )
A. B. C. D.
8.设,若函数有个不同的零点,,,,且,则的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列关于不等式的说法正确的是( )
A. ,
B. 若,,则
C. 若,,,则
D. ,,
10.下列关于对数运算正确的是( )
A. 设,,均为正实数,且,则
B. 若方程的两根为,,则
C. 已知,则
D.
11.定义“正对数”现有四个命题,其中是真命题的有( )
A. 若,,则
B. 若,,则
C. 若,,则
D. 若,,则
三、填空题:本题共3小题,每小题5分,共15分。
12.已知函数在上具有单调性,则实数的取值范围是 .
13.已知定义在上的函数满足是偶函数在上为增函数若不等式成立,则实数的取值范围是 .
14.设是定义在上的奇函数,当时,若对任意的,不等式恒成立,则实数的取值范围是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知关于的不等式.
若,,且,试求它的解集
若,,试求它的解集.
16.本小题分
已知函数.
若,求的最小值
若,存在实数,,使得当的定义域为时,的值域为,求实数的取值范围.
17.本小题分
年全年,中国新能源汽车产量、销量分别达到万辆和万辆,同比分别增长和我国新能源汽车产销量占全球比重超过,连续年位居世界第一新能源汽车出口万辆,同比增长,均创历史新高年中国数家车企推出多款电动新能源汽车,引起市场轰动,电动新能源汽车逐步成为人们购车的热门选择有关部门在高速公路上对某型号电动汽车进行测试,得到了该电动汽车每小时耗电量单位:与速度单位:的数据,如下表所示:
经画图研究可知该电动汽车在高速公路上行驶时每小时耗电量与速度的关系为.
求出函数的函数解析式.
张某驾驶一辆同型号电动汽车从地出发,经高速公路最低限速,最高限速匀速行驶到距离为的地出发前,汽车电池存量为,汽车到达地后至少要保留的保障电量假设该电动汽车从静止加速到速度为的过程中消耗的电量与行驶的路程都忽略不计已知该高速公路上服务区有功率为的充电桩充电量充电功率充电时间若不充电,该电动汽车能否到达地并说明理由若需要充电,求该电动汽车从地到达地所用时间即行驶时间与充电时间之和的最小值结果保留一位小数.
18.本小题分
已知函数为偶函数.
求的值
求的最小值
若对任意恒成立,求实数的取值范围.
19.本小题分
设,是非空实数集,如果对于集合中的任意两个实数,,按照某种确定的关系,在中都有唯一确定的数和它对应,那么就称为从集合到集合的一个二元函数,记作,,,其中称为二元函数的定义域.
已知,若,,,求
设二元函数的定义域为,如果存在实数满足,,都有,,,使得,那么我们称是二元函数的下确界若,,且,判断函数是否存在下确界若存在,求出此函数的下确界若不存在,说明理由.
设的定义域为,若,,,,则称在上关于单调递增已知在上关于单调递增,求实数的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:把,代入不等式,得.
因为,所以,即,解得,
所以所求不等式的解集是.
把,代入不等式,得即.
若,则不等式为一个一元一次不等式
若,则其对应的函数零点是,,
需根据零点大小与的正负进行讨论.
当时,原不等式变为,解集是
当时,原不等式变为,解集是
当时,原不等式变为,解集是
当时,原不等式变为,解集是
当时,原不等式变为,解集是或
16.解:若,则,
令,,则,,
该二次函数开口向上,其图象的对称轴为直线,
所以当时,.
因为,所以在上单调递增,
则当的定义域为时,的值域为,
所以即在上有两个不同的实数解,
即在上有两个不同的实数解.
令,,所以在上有两个不同的实数解,
所以解得
所以实数的取值范围为
17.解析:由题意,
所以..
设耗电量为,则.
任取,..
,
由,,,得,即,
所以函数在上单调递增,
故,即最小耗电量大于电池存量减去保障电量,
所以该车不在服务区充电不能到达地.
设行驶时间与充电时间分别为,,总和为单位:,
若能到达地,则初始电量充电电量一消耗电量保障电量,
即,解得,
所以总时间,
当且仅当,即时,等号成立,
所以该汽车到达地的最少用时约为.
18.解:因为 为偶函数,
所以 ,则 ,
所以 ,即 恒成立,
因为 不恒为 ,所以 ,故 .
由得,
,
因为 ,则 ,当且仅当 ,即 时,等号成立,
所以 ,故 最小值为 .
因为 ,
任取 且 ,
所以,
因为 且 ,所以 ,
所以 ,即 ,
所以 ,则 在 上为增函数,
又因为 为偶函数, ,
所以 ,
当 时, 恒成立,则 ;
当 时, ,所以 ,
设 ,
当且仅当 ,即 时,等号成立,
由复合函数的单调性易得 在 上单调递增,
且当 时, ,当 时, ,
所以 有解,即 有解,所以等号能成立,
所以 ,故 ,则 ;
综上, .
所以实数的取值范围为
19.解:由可得,,
由可得,
由
又,
所以
由可得,,
由,可得,所以,
当且仅当时取等号.
,
当且仅当,即时取等号.
因为在上是关于单调递增,
所以,
即存在,对于任意的,,都有,
化简可得,即,
下面求函数的最小值,
设,,
,
所以函数在递增,,
即存在,使得,设,,
当时,,
当时,,
设,,
所以,
综上,,
所以的取值范围是
第1页,共1页
同课章节目录
