26.2 实际问题与反比例函数 同步练 初中数学人教版九年级下册
文档属性
| 名称 | 26.2 实际问题与反比例函数 同步练 初中数学人教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 598.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
26.2 实际问题与反比例函数 同步练
2024-2025学年初中数学人教版九年级下册
一、单选题
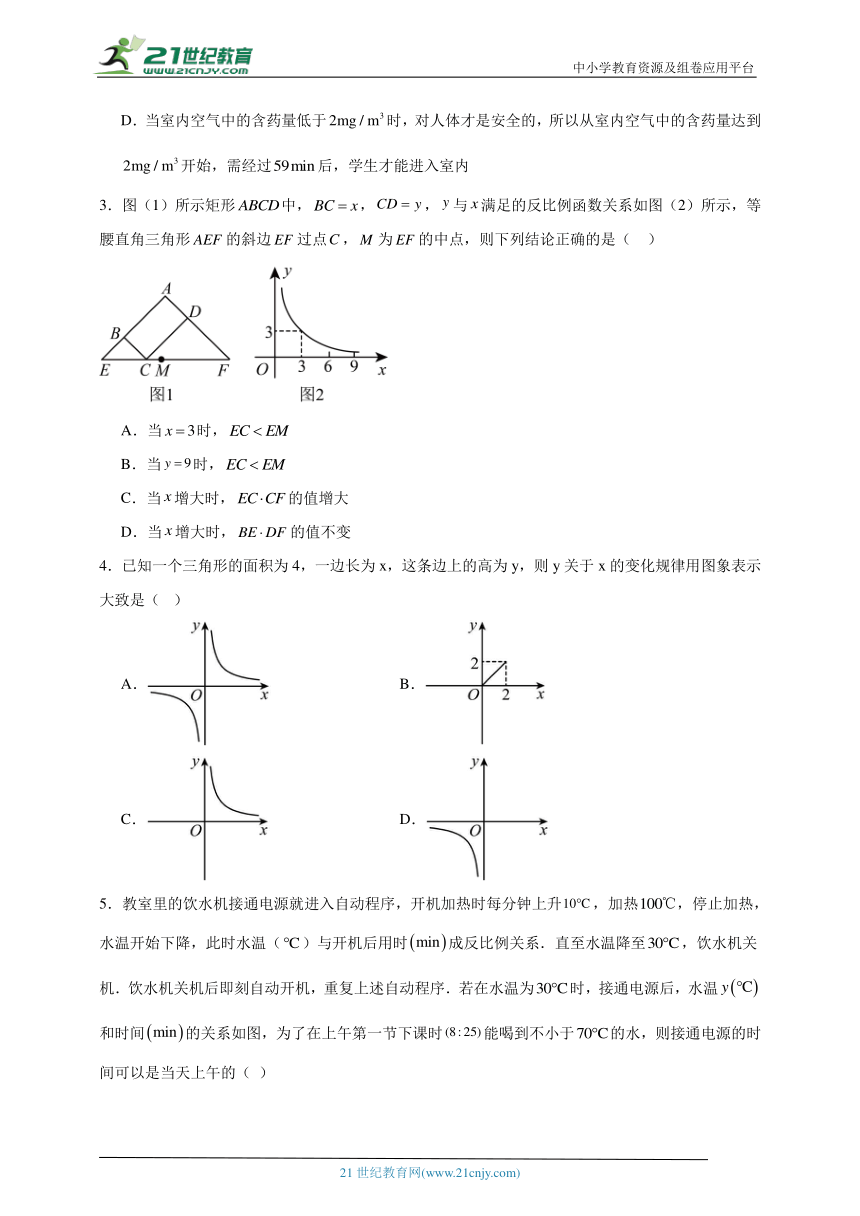
1.为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:V=Sh(V≠0),则S关于h的函数图象大致是
A.B.
C.D.
2.春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过的集中药物喷洒,再封闭宿舍,然后打开门窗进行通风,室内每立方米空气中含药量与药物在空气中的持续时间之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
A.经过集中喷洒药物,室内空气中的含药量最高达到
B.室内空气中的含药量不低于的持续时间达到了
C.当室内空气中的含药量不低于且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D.当室内空气中的含药量低于时,对人体才是安全的,所以从室内空气中的含药量达到开始,需经过后,学生才能进入室内
3.图(1)所示矩形中,,,与满足的反比例函数关系如图(2)所示,等腰直角三角形的斜边过点,为的中点,则下列结论正确的是( )
A.当时,
B.当时,
C.当增大时,的值增大
D.当增大时,的值不变
4.已知一个三角形的面积为4,一边长为x,这条边上的高为y,则y关于x的变化规律用图象表示大致是( )
A. B.
C. D.
5.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升,加热,停止加热,水温开始下降,此时水温()与开机后用时成反比例关系.直至水温降至,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为时,接通电源后,水温和时间的关系如图,为了在上午第一节下课时能喝到不小于的水,则接通电源的时间可以是当天上午的( )
A. B. C. D.
6.今年,某公司推出一款的新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9688元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A.y=+2000 B.y=﹣2000
C.y= D.y=
7.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷
8.随着私家车的增多,交通也越来越拥挤,通常情况下,某段公路上汽车的行驶速度y(千米/时)与路上每百米拥有车的数量x(辆)的关系如图所示,当时,y与x成反比例关系,当车速低于20千米/时时,交通就会拥堵,为避免出现交通拥堵,公路上每百米拥有车的数量x应该满足的范围是( )
A. B. C. D..
二、填空题
9.根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
10.电流通过导线时会产生热量,电流I(单位:A)、导线电阻R(单位:Ω)、通电时间t(单位:s)与产生的热量Q(单位:J)满足关系式.已知导线的电阻为10Ω,通电2s时间导线产生90J的热量,则电流I为 A.
11.近视眼镜的度数度与镜片焦距米呈反比例,其函数关系式为如果近似眼镜镜片的焦距米,那么近视眼镜的度数y为 .
12.将油箱注满升油后,轿车行驶的总路程(单位:千米)与平均耗油量(单位:升/千米)之间是反比例函数关系是常数,.已知某轿车油箱注满油后,以平均耗油量为每千米耗油升的速度行驶,可行驶千米,当平均耗油量为升/千米时,该轿车可以行驶 千米.
13.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:y=(k≠0),其图象为如图的一段曲线,若这段公路行驶速度不得超过60km/h,则该汽车通过这段公路最少需要 h.
三、解答题
14.某工厂生产化肥的总任务一定,平均每天化肥产量y(吨)与完成生产任务所需要的时间x(天)之间成反比例关系,如果每天生产化肥125吨,那么完成总任务需要7天.
(1)求y关于x的函数表达式,并指出比例系数;
(2)若要5天完成总任务,则每天产量应达到多少?
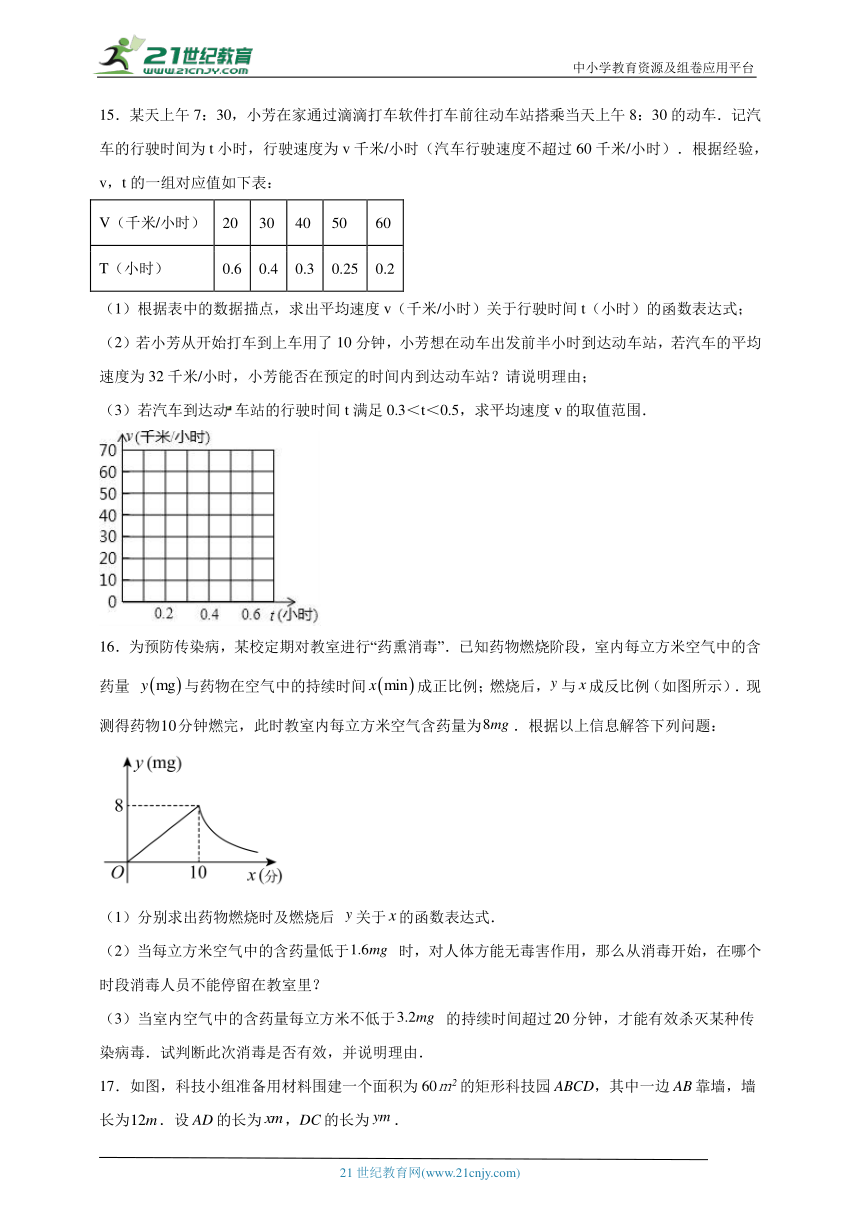
15.某天上午7:30,小芳在家通过滴滴打车软件打车前往动车站搭乘当天上午8:30的动车.记汽车的行驶时间为t小时,行驶速度为v千米/小时(汽车行驶速度不超过60千米/小时).根据经验,v,t的一组对应值如下表:
V(千米/小时) 20 30 40 50 60
T(小时) 0.6 0.4 0.3 0.25 0.2
(1)根据表中的数据描点,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)若小芳从开始打车到上车用了10分钟,小芳想在动车出发前半小时到达动车站,若汽车的平均速度为32千米/小时,小芳能否在预定的时间内到达动车站?请说明理由;
(3)若汽车到达动车站的行驶时间t满足0.3<t<0.5,求平均速度v的取值范围.
16.为预防传染病,某校定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量 与药物在空气中的持续时间成正比例;燃烧后,与成反比例(如图所示).现测得药物分钟燃完,此时教室内每立方米空气含药量为.根据以上信息解答下列问题:
(1)分别求出药物燃烧时及燃烧后 关于的函数表达式.
(2)当每立方米空气中的含药量低于 时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
(3)当室内空气中的含药量每立方米不低于 的持续时间超过分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
17.如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为.设AD的长为,DC的长为.
(1)求与之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.
18.某汽车销售商推出分期付款购车促销活动,交首付款后,余额要在30个月内结清,不计算利息,王先生在活动期间购买了价格为12万元的汽车,交了首付款后平均每月付款万元,个月结清.与的函数关系如图所示,根据图像回答下列问题:
(1)确定与的函数解析式,并求出首付款的数目;
(2)王先生若用20个月结清,平均每月应付多少万元?
(3)如果打算每月付款不超过4000元,王先生至少要几个月才能结清余额?
参考答案:
1.C
∵V=Sh(V为不等于0的常数),∴(h≠0),S是h的反比例函数.
根据反比例函数的图象和性质可知,图象为反比例函数在第一象限内的部分.
2.C
解∶由图象可知,经过集中喷洒药物,室内空气中的含药量最高达到,故A选项正确.不符合题意.
设0把(5,10)代入得,k1=2,
∴y1=2x,
∴y1=8时,x=4,
15-4=11,
∴室内空气中的含药量不低于8mg/m3的持续时间达到了11min,故B选项正确,不符合题意;
由图象可知,y=5时,x<5或x>15,
设反比例函数解析式为y2=,
把(15,8)代入得:8=,
解得:,
∴,
当y1=5时,x1=2.5,当y2=5时,x2=24,
24-2.5=21.5<35,故C选项错误,符合题意;
当y1=2时,x1=1,当y2=2时,x2=60,
60-1=59,故D选项正确.不符合题意,
3.D
解:因为等腰直角三角形AEF的斜边EF过C点,M为EF的中点,所以△BEC和△DCF都是直角三角形;观察反比例函数图像得x=3,y=3,则反比例解析式为y=.
A、当x=3时,y=3,即BC=CD=3,所以CE=BC=3,CF=CD=3,C点与M点重合,则EC=EM,所以A选项错误;
B、当y=9时,x=1,即BC=1,CD=9,所以EC=,EF=10,EM=5,所以B选项错误;
C、因为EC CF=x y=2×xy=18,所以,EC CF为定值,所以C选项错误;
D、因为BE DF=BC CD=xy=9,即BE DF的值不变,所以D选项正确.
4.C
解:∵三角形的面积为4, 一边长为x,这条边上的高为y,
∴,所以.
5.B
解:开机加热时每分钟上升,
从到需要7分钟,
设一次函数关系式为:,
将,代入得,,
,令,解得;
设反比例函数关系式为:,
将代入,
得,
,
将代入,
解得;
,令,解得.
所以,饮水机的一个循环周期为分钟.每一个循环周期内,在时间段内,水温不小于.
逐一分析如下:
选项至之间有85分钟.,不在时间段内,故不可行;
选项至之间有75分钟.,位于时间段内,故可行;
选项至之间有60分钟.,不在时间段内,故不可行;
选项至之间有50分钟.,不在时间段内,故不可行.
综上所述,四个选项中,唯有符合题意.
6.C
由题意可得:y= .
7.D
如图所示,人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数关系是反比例函数,它的图象在第一象限,
∴y随x的增大而减小,
∴A,B错误,
设y=(k>0,x>0),把x=50时,y=1代入得:k=50,
∴y=,
把y=2代入上式得:x=25,
∴C错误,
把x=50代入上式得:y=1,
∴D正确,
8.B
设反比例函数的表达式为,将代入,得,所以当车速为20千米/时,,解得,故为避免出现交通拥堵,公路上每百米拥有车的数量x应该满足的范围是.
9.300
解:设
∴.
∴.
设售价为m元,则销量为,于是,
解得,
经检验是方程的解.
所以,售价应定为300元.
故答案为:300.
10./
解:∵,
∴,
∴;
故答案为.
11.400
把代入,
,
故答案为400.
12.950
∵以平均耗油量为每千米耗油0.1升的速度行驶,可行驶760千米,
∴760=,解得:k=76,
∴当平均耗油量为0.08升/千米时,该轿车可以行驶的路程S==950(千米)
故答案为950.
13.
解:由题意可得:k=xy=40,
则y≥=,
即该汽车通过这段公路最少需要h.
故答案为.
14.(1)y=,875;(2)若要5天完成总任务,则每天产量应达到175吨.
解:(1)设y=,
根据题意得:k=xy=125×7=875,
∴每天生产化肥产量y(吨)与完成生产任务所需要的时间x(天)之间的函数解析式为y=,比例系数为875;
(2)当x=5时,y==175(吨),
即若要5天完成总任务,则每天产量应达到175吨.
15.(1)v=;(2)若汽车的平均速度为32千米/小时,小芳不能在预定的时间内到达动车站;(3)平均速度v的取值范围是24<v<40
(1)根据表格中数据,可知v=,
∵v=20时,t=0.6,
∴k=20×0.6=12,
∴v= (t≥0.2).
(2)∵1﹣-=,
∴t=时,v==36>32,
∴若汽车的平均速度为32千米/小时,小芳不能在预定的时间内到达动车站;
(3)∵0.3<t<0.5,
∴24<v<40,
答:平均速度v的取值范围是24<v<40.
16.(1),;(2)第分至分内消毒人员不可以留在教室里;(3)本次消毒有效.
(1)设燃烧时药物燃烧后y与x之间的解析式y=ax,点(10,8)代入,得
10a=8,
∴a=,
∴;
药物燃烧后y与x之间的解析式y=,把点(10,8)代入,得
k=80,
∴;
(2)把代入可得
把代入可得
根据图象,当时,
即从消毒开始后的第分至分内消毒人员不可以留在教室里.
(3)把代入可得
把代入可得
本次消毒有效.
17.(1);(2)满足条件的所有围建方案:AD=5m,DC=12m或AD=6m,DC=10m或AD=10m,DC=6m.
解:(1)如图,AD的长为,DC的长为,
根据题意,得,即.
∴与之间的函数关系式为.
(2)由,且都为正整数,
∴x可取1,2,3,4,5,6,10,12,15,20,30,60.
∵
∴符合条件的有:时,;时,;时,.
答:满足条件的所有围建方案:AD=5m,DC=12m或AD=6m,DC=10m或AD=10m,DC=6m.
18.(1)y=,3万元;(2)0.45万元;(3)23个月才能结清余款
解:(1)由图像可知y与x成反比例,
设y与x的函数关系式为y=,
把(5,1.8)代入关系式得1.8=,
∴k=9,∴y=,
∴12﹣9=3(万元).
答:首付款为3万元;
(2)当x=20时,y==0.45(万元),
答:每月应付0.45万元;
(3)当y=0.4时,0.4=,
解得:x=,
又∵k>0,在第一象限内,y随x的增大而减小,
∴当y≤4000时,x≥,
又x取整数,∴x的最小值为23.
答:王先生至少要23个月才能结清余额.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
26.2 实际问题与反比例函数 同步练
2024-2025学年初中数学人教版九年级下册
一、单选题
1.为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:V=Sh(V≠0),则S关于h的函数图象大致是
A.B.
C.D.
2.春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过的集中药物喷洒,再封闭宿舍,然后打开门窗进行通风,室内每立方米空气中含药量与药物在空气中的持续时间之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
A.经过集中喷洒药物,室内空气中的含药量最高达到
B.室内空气中的含药量不低于的持续时间达到了
C.当室内空气中的含药量不低于且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D.当室内空气中的含药量低于时,对人体才是安全的,所以从室内空气中的含药量达到开始,需经过后,学生才能进入室内
3.图(1)所示矩形中,,,与满足的反比例函数关系如图(2)所示,等腰直角三角形的斜边过点,为的中点,则下列结论正确的是( )
A.当时,
B.当时,
C.当增大时,的值增大
D.当增大时,的值不变
4.已知一个三角形的面积为4,一边长为x,这条边上的高为y,则y关于x的变化规律用图象表示大致是( )
A. B.
C. D.
5.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升,加热,停止加热,水温开始下降,此时水温()与开机后用时成反比例关系.直至水温降至,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为时,接通电源后,水温和时间的关系如图,为了在上午第一节下课时能喝到不小于的水,则接通电源的时间可以是当天上午的( )
A. B. C. D.
6.今年,某公司推出一款的新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9688元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A.y=+2000 B.y=﹣2000
C.y= D.y=
7.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷
8.随着私家车的增多,交通也越来越拥挤,通常情况下,某段公路上汽车的行驶速度y(千米/时)与路上每百米拥有车的数量x(辆)的关系如图所示,当时,y与x成反比例关系,当车速低于20千米/时时,交通就会拥堵,为避免出现交通拥堵,公路上每百米拥有车的数量x应该满足的范围是( )
A. B. C. D..
二、填空题
9.根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
10.电流通过导线时会产生热量,电流I(单位:A)、导线电阻R(单位:Ω)、通电时间t(单位:s)与产生的热量Q(单位:J)满足关系式.已知导线的电阻为10Ω,通电2s时间导线产生90J的热量,则电流I为 A.
11.近视眼镜的度数度与镜片焦距米呈反比例,其函数关系式为如果近似眼镜镜片的焦距米,那么近视眼镜的度数y为 .
12.将油箱注满升油后,轿车行驶的总路程(单位:千米)与平均耗油量(单位:升/千米)之间是反比例函数关系是常数,.已知某轿车油箱注满油后,以平均耗油量为每千米耗油升的速度行驶,可行驶千米,当平均耗油量为升/千米时,该轿车可以行驶 千米.
13.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:y=(k≠0),其图象为如图的一段曲线,若这段公路行驶速度不得超过60km/h,则该汽车通过这段公路最少需要 h.
三、解答题
14.某工厂生产化肥的总任务一定,平均每天化肥产量y(吨)与完成生产任务所需要的时间x(天)之间成反比例关系,如果每天生产化肥125吨,那么完成总任务需要7天.
(1)求y关于x的函数表达式,并指出比例系数;
(2)若要5天完成总任务,则每天产量应达到多少?
15.某天上午7:30,小芳在家通过滴滴打车软件打车前往动车站搭乘当天上午8:30的动车.记汽车的行驶时间为t小时,行驶速度为v千米/小时(汽车行驶速度不超过60千米/小时).根据经验,v,t的一组对应值如下表:
V(千米/小时) 20 30 40 50 60
T(小时) 0.6 0.4 0.3 0.25 0.2
(1)根据表中的数据描点,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)若小芳从开始打车到上车用了10分钟,小芳想在动车出发前半小时到达动车站,若汽车的平均速度为32千米/小时,小芳能否在预定的时间内到达动车站?请说明理由;
(3)若汽车到达动车站的行驶时间t满足0.3<t<0.5,求平均速度v的取值范围.
16.为预防传染病,某校定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量 与药物在空气中的持续时间成正比例;燃烧后,与成反比例(如图所示).现测得药物分钟燃完,此时教室内每立方米空气含药量为.根据以上信息解答下列问题:
(1)分别求出药物燃烧时及燃烧后 关于的函数表达式.
(2)当每立方米空气中的含药量低于 时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
(3)当室内空气中的含药量每立方米不低于 的持续时间超过分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
17.如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为.设AD的长为,DC的长为.
(1)求与之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.
18.某汽车销售商推出分期付款购车促销活动,交首付款后,余额要在30个月内结清,不计算利息,王先生在活动期间购买了价格为12万元的汽车,交了首付款后平均每月付款万元,个月结清.与的函数关系如图所示,根据图像回答下列问题:
(1)确定与的函数解析式,并求出首付款的数目;
(2)王先生若用20个月结清,平均每月应付多少万元?
(3)如果打算每月付款不超过4000元,王先生至少要几个月才能结清余额?
参考答案:
1.C
∵V=Sh(V为不等于0的常数),∴(h≠0),S是h的反比例函数.
根据反比例函数的图象和性质可知,图象为反比例函数在第一象限内的部分.
2.C
解∶由图象可知,经过集中喷洒药物,室内空气中的含药量最高达到,故A选项正确.不符合题意.
设0
∴y1=2x,
∴y1=8时,x=4,
15-4=11,
∴室内空气中的含药量不低于8mg/m3的持续时间达到了11min,故B选项正确,不符合题意;
由图象可知,y=5时,x<5或x>15,
设反比例函数解析式为y2=,
把(15,8)代入得:8=,
解得:,
∴,
当y1=5时,x1=2.5,当y2=5时,x2=24,
24-2.5=21.5<35,故C选项错误,符合题意;
当y1=2时,x1=1,当y2=2时,x2=60,
60-1=59,故D选项正确.不符合题意,
3.D
解:因为等腰直角三角形AEF的斜边EF过C点,M为EF的中点,所以△BEC和△DCF都是直角三角形;观察反比例函数图像得x=3,y=3,则反比例解析式为y=.
A、当x=3时,y=3,即BC=CD=3,所以CE=BC=3,CF=CD=3,C点与M点重合,则EC=EM,所以A选项错误;
B、当y=9时,x=1,即BC=1,CD=9,所以EC=,EF=10,EM=5,所以B选项错误;
C、因为EC CF=x y=2×xy=18,所以,EC CF为定值,所以C选项错误;
D、因为BE DF=BC CD=xy=9,即BE DF的值不变,所以D选项正确.
4.C
解:∵三角形的面积为4, 一边长为x,这条边上的高为y,
∴,所以.
5.B
解:开机加热时每分钟上升,
从到需要7分钟,
设一次函数关系式为:,
将,代入得,,
,令,解得;
设反比例函数关系式为:,
将代入,
得,
,
将代入,
解得;
,令,解得.
所以,饮水机的一个循环周期为分钟.每一个循环周期内,在时间段内,水温不小于.
逐一分析如下:
选项至之间有85分钟.,不在时间段内,故不可行;
选项至之间有75分钟.,位于时间段内,故可行;
选项至之间有60分钟.,不在时间段内,故不可行;
选项至之间有50分钟.,不在时间段内,故不可行.
综上所述,四个选项中,唯有符合题意.
6.C
由题意可得:y= .
7.D
如图所示,人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数关系是反比例函数,它的图象在第一象限,
∴y随x的增大而减小,
∴A,B错误,
设y=(k>0,x>0),把x=50时,y=1代入得:k=50,
∴y=,
把y=2代入上式得:x=25,
∴C错误,
把x=50代入上式得:y=1,
∴D正确,
8.B
设反比例函数的表达式为,将代入,得,所以当车速为20千米/时,,解得,故为避免出现交通拥堵,公路上每百米拥有车的数量x应该满足的范围是.
9.300
解:设
∴.
∴.
设售价为m元,则销量为,于是,
解得,
经检验是方程的解.
所以,售价应定为300元.
故答案为:300.
10./
解:∵,
∴,
∴;
故答案为.
11.400
把代入,
,
故答案为400.
12.950
∵以平均耗油量为每千米耗油0.1升的速度行驶,可行驶760千米,
∴760=,解得:k=76,
∴当平均耗油量为0.08升/千米时,该轿车可以行驶的路程S==950(千米)
故答案为950.
13.
解:由题意可得:k=xy=40,
则y≥=,
即该汽车通过这段公路最少需要h.
故答案为.
14.(1)y=,875;(2)若要5天完成总任务,则每天产量应达到175吨.
解:(1)设y=,
根据题意得:k=xy=125×7=875,
∴每天生产化肥产量y(吨)与完成生产任务所需要的时间x(天)之间的函数解析式为y=,比例系数为875;
(2)当x=5时,y==175(吨),
即若要5天完成总任务,则每天产量应达到175吨.
15.(1)v=;(2)若汽车的平均速度为32千米/小时,小芳不能在预定的时间内到达动车站;(3)平均速度v的取值范围是24<v<40
(1)根据表格中数据,可知v=,
∵v=20时,t=0.6,
∴k=20×0.6=12,
∴v= (t≥0.2).
(2)∵1﹣-=,
∴t=时,v==36>32,
∴若汽车的平均速度为32千米/小时,小芳不能在预定的时间内到达动车站;
(3)∵0.3<t<0.5,
∴24<v<40,
答:平均速度v的取值范围是24<v<40.
16.(1),;(2)第分至分内消毒人员不可以留在教室里;(3)本次消毒有效.
(1)设燃烧时药物燃烧后y与x之间的解析式y=ax,点(10,8)代入,得
10a=8,
∴a=,
∴;
药物燃烧后y与x之间的解析式y=,把点(10,8)代入,得
k=80,
∴;
(2)把代入可得
把代入可得
根据图象,当时,
即从消毒开始后的第分至分内消毒人员不可以留在教室里.
(3)把代入可得
把代入可得
本次消毒有效.
17.(1);(2)满足条件的所有围建方案:AD=5m,DC=12m或AD=6m,DC=10m或AD=10m,DC=6m.
解:(1)如图,AD的长为,DC的长为,
根据题意,得,即.
∴与之间的函数关系式为.
(2)由,且都为正整数,
∴x可取1,2,3,4,5,6,10,12,15,20,30,60.
∵
∴符合条件的有:时,;时,;时,.
答:满足条件的所有围建方案:AD=5m,DC=12m或AD=6m,DC=10m或AD=10m,DC=6m.
18.(1)y=,3万元;(2)0.45万元;(3)23个月才能结清余款
解:(1)由图像可知y与x成反比例,
设y与x的函数关系式为y=,
把(5,1.8)代入关系式得1.8=,
∴k=9,∴y=,
∴12﹣9=3(万元).
答:首付款为3万元;
(2)当x=20时,y==0.45(万元),
答:每月应付0.45万元;
(3)当y=0.4时,0.4=,
解得:x=,
又∵k>0,在第一象限内,y随x的增大而减小,
∴当y≤4000时,x≥,
又x取整数,∴x的最小值为23.
答:王先生至少要23个月才能结清余额.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
