【培优集训】2024年浙江省宁波市近2年九年级期末精选考试压轴真题集训60题(含解析)
文档属性
| 名称 | 【培优集训】2024年浙江省宁波市近2年九年级期末精选考试压轴真题集训60题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 17:52:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024年浙江省宁波市近2年九年级期末精选考试压轴真题集训
一.选择题
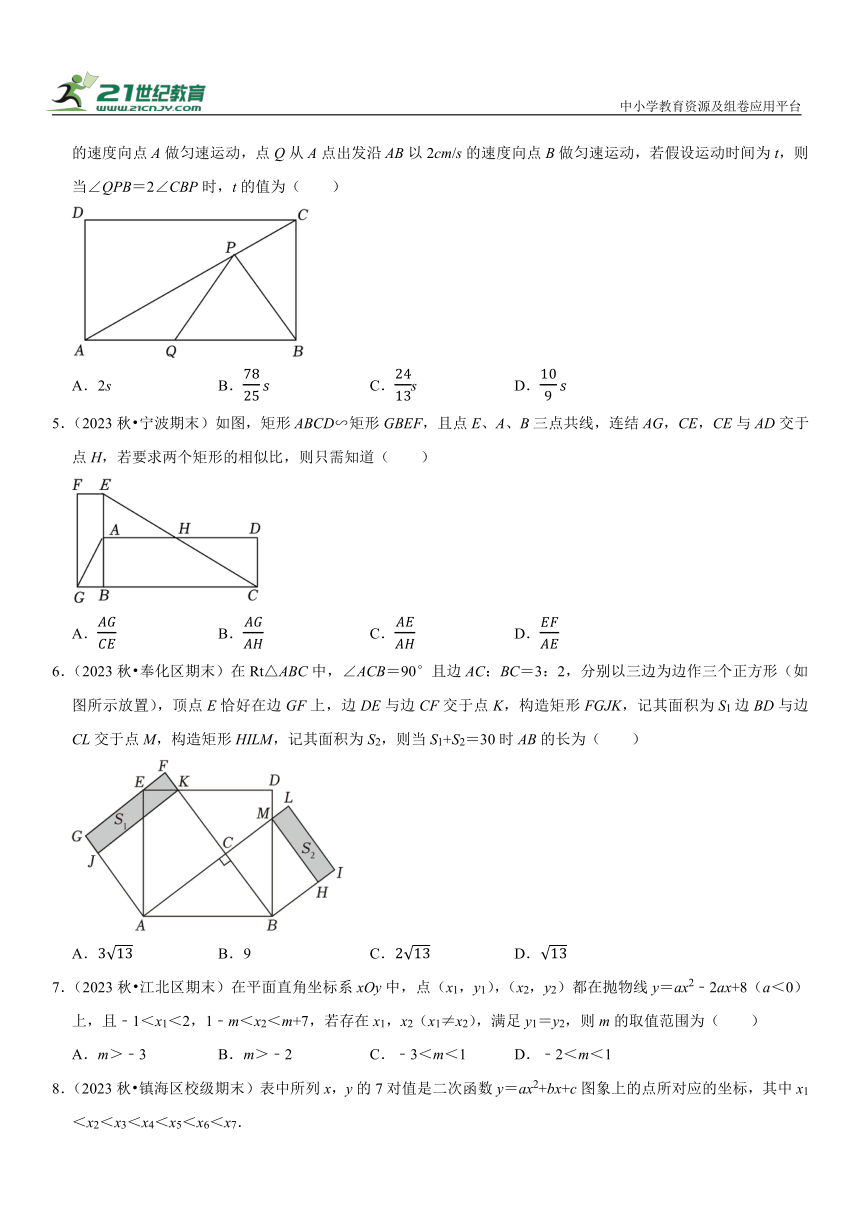
1.(2022秋 慈溪市期末)一个大矩形按如图方式分割成五个小矩形后仍是中心对称图形,且矩形ABCD∽矩形BEFG.设矩形ABCD与矩形AHIE的面积分别为m和n,则这个大矩形的面积一定可以表示为( )
A.4m B.2m+3n C.m+3n D.3m+n
2.(2022秋 宁波期末)如图,在平行四边形FBCE中,点J,G分别在边BC,EF上,JG∥BF,四边形ABCD∽四边形HGFA,相似比k=3,则下列一定能求出△BIJ面积的条件( )
A.四边形HDEG和四边形AHGF的面积之差
B.四边形ABCD和四边形HDEG的面积之差
C.四边形ABCD和四边形ADEF的面积之差
D.四边形JCDH和四边形HDEG的面积之差
3.(2023秋 鄞州区期末)如图,在等腰Rt△ABC中,D,E分别在边BC上,,AF⊥AD,FE⊥DE,若已知CD的长,则能求出下列哪个量( )
A.△DEF的周长 B.△DEF的面积
C.△ADF的周长 D.△ADF的面积
4.(2023秋 海曙区期末)如图,在矩形ABCD中,BC=5cm,AB=12cm,点P从C点出发沿对角线AC以1cm/s的速度向点A做匀速运动,点Q从A点出发沿AB以2cm/s的速度向点B做匀速运动,若假设运动时间为t,则当∠QPB=2∠CBP时,t的值为( )
A.2s B. C.s D.
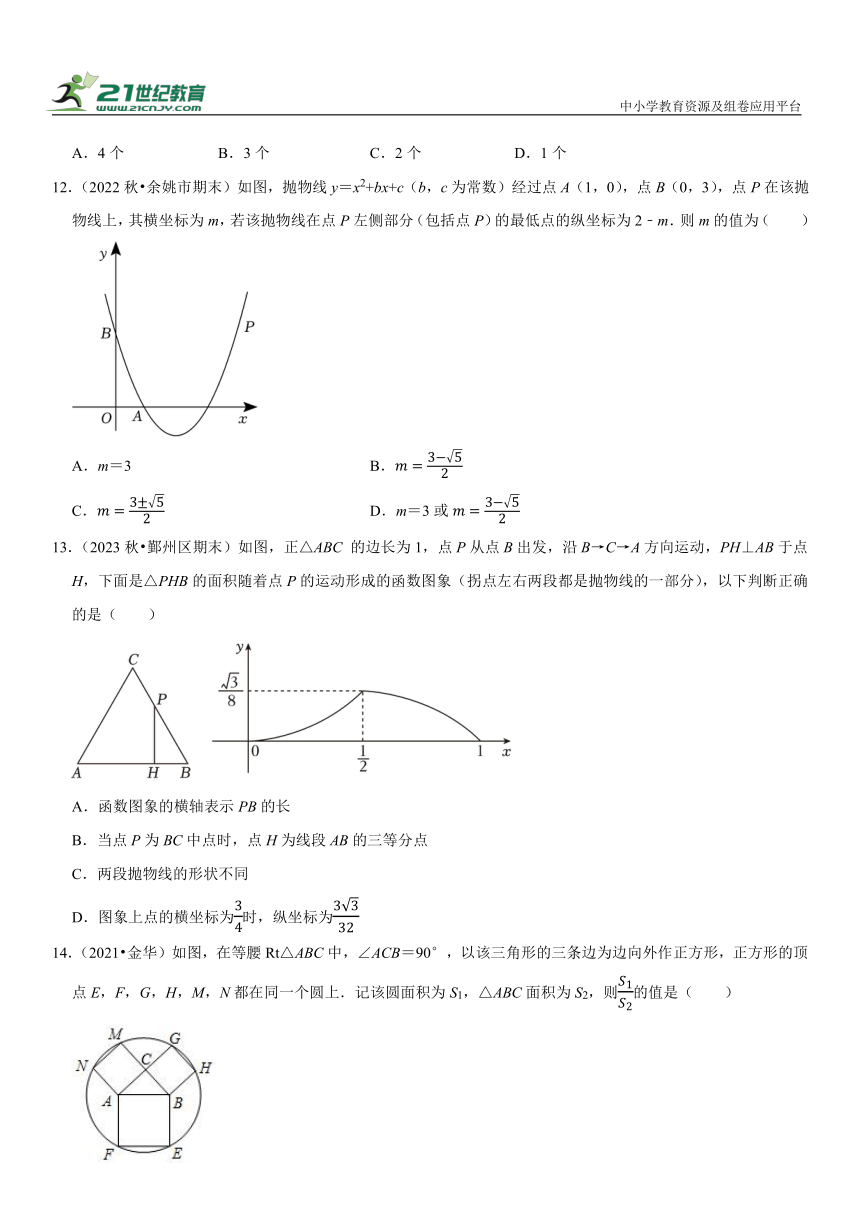
5.(2023秋 宁波期末)如图,矩形ABCD∽矩形GBEF,且点E、A、B三点共线,连结AG,CE,CE与AD交于点H,若要求两个矩形的相似比,则只需知道( )
A. B. C. D.
6.(2023秋 奉化区期末)在Rt△ABC中,∠ACB=90°且边AC:BC=3:2,分别以三边为边作三个正方形(如图所示放置),顶点E恰好在边GF上,边DE与边CF交于点K,构造矩形FGJK,记其面积为S1边BD与边CL交于点M,构造矩形HILM,记其面积为S2,则当S1+S2=30时AB的长为( )
A. B.9 C. D.
7.(2023秋 江北区期末)在平面直角坐标系xOy中,点(x1,y1),(x2,y2)都在抛物线y=ax2﹣2ax+8(a<0)上,且﹣1<x1<2,1﹣m<x2<m+7,若存在x1,x2(x1≠x2),满足y1=y2,则m的取值范围为( )
A.m>﹣3 B.m>﹣2 C.﹣3<m<1 D.﹣2<m<1
8.(2023秋 镇海区校级期末)表中所列x,y的7对值是二次函数y=ax2+bx+c图象上的点所对应的坐标,其中x1<x2<x3<x4<x5<x6<x7.
x … x1 x2 x3 x4 x5 x6 x7 …
y … 7 m 14 k 14 m 7 …
根据表中提供的信息,有以下四个判断:
①a<0;②7<m<14;③当时,y的值是k;④b2≥4a(c﹣k);其中判断正确的有( )个.
A.1 B.2 C.3 D.4
9.(2023秋 余姚市期末)如图,在△ABC中,点D是AB上一点(不与点A,B重合),过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC于点F,点G是线段AE上一点,AG=GE,点H是线段DF上一点,DH=HF,若已知△BGH的面积,则一定能求出( )
A.△ADE的面积 B.△BDF的面积
C.△ABG的面积 D.△CEF的面积
10.(2023秋 北仑区期末)如图,点D是△ABC的边BC上一点,将△ADC沿AD翻折,点C落在点E处,AE与BC相交于点F,若EF=3,CF=17,AF=AD,则FD的长是( )
A.8 B.8.5 C. D.
11.(2022秋 余姚市期末)如图,已知直线l1∥l2∥l3,直线AB分别交三条平行线于点A、E、B,直线CD分别交三条平行线于点C、F、D,直线AB、CD相交于点O,若AE:EO:OB=4:2:7,则下列式子①;②;③;④中,正确的个数有( )
A.4个 B.3个 C.2个 D.1个
12.(2022秋 余姚市期末)如图,抛物线y=x2+bx+c(b,c为常数)经过点A(1,0),点B(0,3),点P在该抛物线上,其横坐标为m,若该抛物线在点P左侧部分(包括点P)的最低点的纵坐标为2﹣m.则m的值为( )
A.m=3 B.
C. D.m=3或
13.(2023秋 鄞州区期末)如图,正△ABC 的边长为1,点P从点B出发,沿B→C→A方向运动,PH⊥AB于点H,下面是△PHB的面积随着点P的运动形成的函数图象(拐点左右两段都是抛物线的一部分),以下判断正确的是( )
A.函数图象的横轴表示PB的长
B.当点P为BC中点时,点H为线段AB的三等分点
C.两段抛物线的形状不同
D.图象上点的横坐标为时,纵坐标为
14.(2021 金华)如图,在等腰Rt△ABC中,∠ACB=90°,以该三角形的三条边为边向外作正方形,正方形的顶点E,F,G,H,M,N都在同一个圆上.记该圆面积为S1,△ABC面积为S2,则的值是( )
A. B.3π C.5π D.
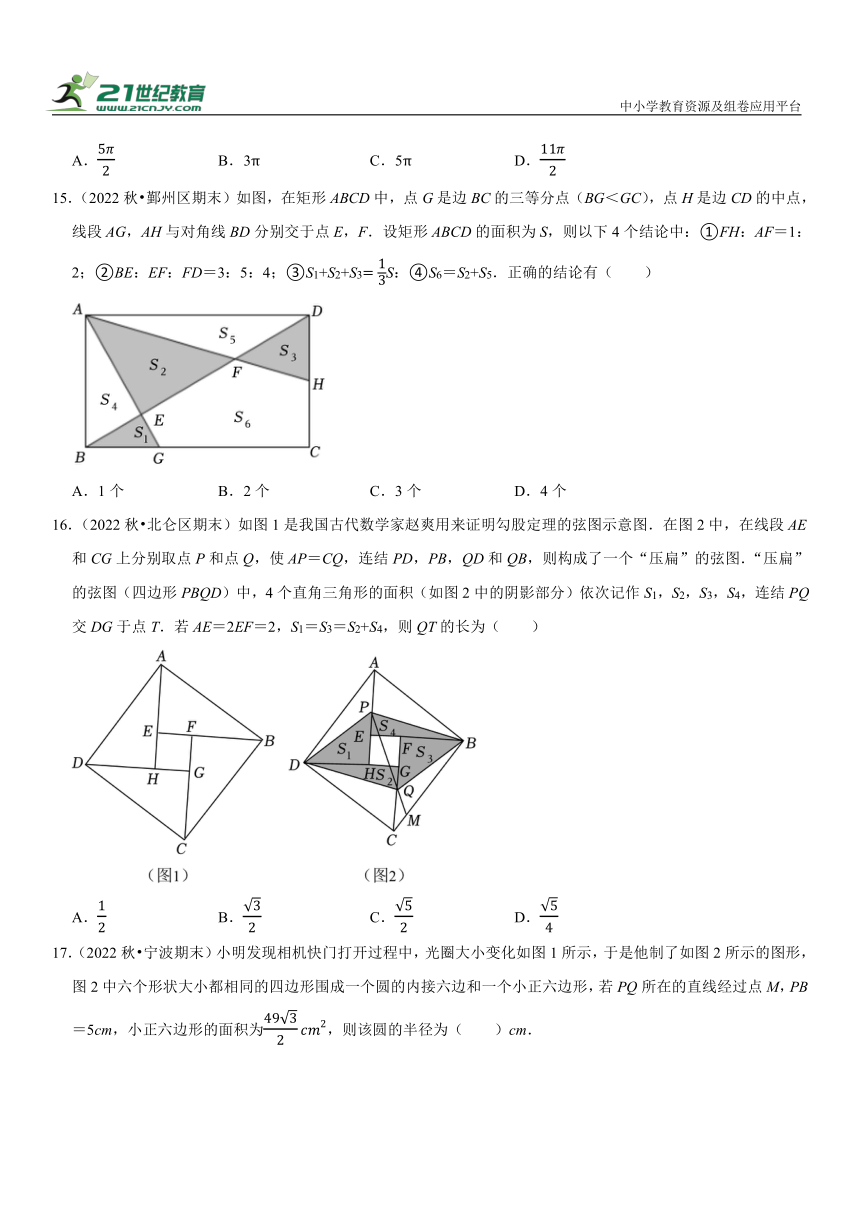
15.(2022秋 鄞州区期末)如图,在矩形ABCD中,点G是边BC的三等分点(BG<GC),点H是边CD的中点,线段AG,AH与对角线BD分别交于点E,F.设矩形ABCD的面积为S,则以下4个结论中:①FH:AF=1:2;②BE:EF:FD=3:5:4;③S1+S2+S3S:④S6=S2+S5.正确的结论有( )
A.1个 B.2个 C.3个 D.4个
16.(2022秋 北仑区期末)如图1是我国古代数学家赵爽用来证明勾股定理的弦图示意图.在图2中,在线段AE和CG上分别取点P和点Q,使AP=CQ,连结PD,PB,QD和QB,则构成了一个“压扁”的弦图.“压扁”的弦图(四边形PBQD)中,4个直角三角形的面积(如图2中的阴影部分)依次记作S1,S2,S3,S4,连结PQ交DG于点T.若AE=2EF=2,S1=S3=S2+S4,则QT的长为( )
A. B. C. D.
17.(2022秋 宁波期末)小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他制了如图2所示的图形,图2中六个形状大小都相同的四边形围成一个圆的内接六边和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为,则该圆的半径为( )cm.
A. B. C.7 D.8
18.(2023秋 慈溪市期末)在一次课题学习中,某学习小组受赵爽弦图的启发,将正方形改编成矩形,如图所示,由两对全等的直角三角形(△AHD≌△CFB,△ABE≌△CDG)和矩形EFGH拼成大矩形ABCD.连结CH,设∠CHG=α,∠CDG=β.若BC=2AB,tanβ=tan2α,则矩形EFGH与矩形ABCD的面积比为( )
A. B. C. D.
二.填空题
19.(2022秋 宁波期末)如图,在正方形ABCD中,点E在AB上,AE=3BE,连接CE,取CE中点F,过F作GF⊥CF且使得GF=CF,连接AG并延长,将△CFG绕点C旋转到△CF'G',当A,G,G'三点共线且AG=3时,KG'= .
20.(2023秋 奉化区期末)如图,点C是上一点,且半径为2,AC=BC,∠ACB=120°,点D在BC上运动,连接AD交BC于点E,则AB的值为 ;当DE:AE的值最大时,CE= .
21.(2022秋 慈溪市期末)如图,△ABC内接于⊙O,BC>AC,AC=4,连接CO并延长至点E,使∠EAC=∠ABC=60°.
(1)⊙O的半径为 .
(2)若BC=2,则BE的长为 .
22.(2022秋 余姚市期末)如图,抛物线y=ax2﹣2ax+3(a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M,P为抛物线的顶点,若直线OP交直线AM于点B,且M为线段AB的中点,则线段PB的长为 .
23.(2023秋 鄞州区期末)如图,Rt△ABC中,∠ACB=90°,AC=8,BC=6,CE是斜边AB上的中线,在直线AB上方作△DEF∽△ABC,DE,FE分别与AC边交于点M,N,当△EMN与△BEC相似时,线段CN长度为 .
24.(2023秋 鄞州区期末)如图,在△ABC中,∠C=90°,AC=8,BC=7,过BC上的动点D作半径为4的⊙A的切线,切点为E、F,若G为EF的中点,则BG的最小值为 .
25.(2023秋 慈溪市期末)如图,△ABC内接于⊙O,高AD,CE相交于点F,若AF=AO,CF=5,BC,则⊙O的半径为 ,AB的长为 .
26.(2022秋 北仑区期末)在△ABC中,若点O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=6,EF=4,点M在以半径为2的⊙D上运动,则MF2+MG2的最大值为 .
27.(2023秋 江北区期末)如图,一组抛物线满足二次函数表达式y=x2﹣2mx+m2+3,它们与一个半径为的圆的重叠部分面积为,则该圆圆心的纵坐标为 .
28.(2023秋 镇海区校级期末)设实数a1,a2, ,a100满足以下三个条件:(1)a1≥a2≥…≥a100≥0,(2)a1+a2≤100,(3)a3+a4+…+a100≤100,则的最大值为 .
29.(2023秋 海曙区期末)如图,AB为⊙O的直径,C为圆上一点,且AC=2,tan∠ABC,D在上一点,过点D作AB的垂线交BC于点E,连接AD交BC于点F,若△DEF是以EF为腰的等腰三角形,则BF的长为 .
30.(2023秋 余姚市期末)如图,在四边形ABCD中,AD∥BC,点E是AB上一点,连结AC,CE,ED,∠BEC=∠ADC,AB=AC=10,BC=12,将△ACD沿CD翻折得到△A'CD,若点A'恰好落在ED的延长线上,则CE= ,BE= .
31.(2023秋 宁波期末)如图,在⊙O中,AB=AC,点F为直径AD上一点,连结CF并延长交AB于点G,交⊙O于点E,若AG=AF,BG=4,GF=6,则AB的长为 .
32.(2022秋 镇海区期末)如图,在矩形ABCD中,AB=8,AD=6,点E是对角线AC上一动点,连接DE,过E作EF⊥DE,交AB边于点F,以DE、EF为邻边作矩形DEFG.
(1)当CE=4时,则EF的长为 .
(2)点H在DC上,且HD=1,连接HG,则HG长的最小值是 .
33.(2022秋 余姚市期末)定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为6的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .
34.(2022秋 鄞州区校级期末)抛物线y=ax2+bx+c(a,b,c是常数,a<0)经过A(0,3),B(4,3).
下列四个结论:
①4a+b=0;
②点P1(x1,y1),P2(x2,y2)在抛物线上,当|x1﹣2|﹣|x2﹣2|>0时,y1>y2;
③若抛物线与x轴交于不同两点C,D,且CD≤6,则a;
④若3≤x≤4,对应的y的整数值有3个,则﹣1<a.
其中正确的结论是 (填写序号).
35.(2022秋 鄞州区期末)如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知AB⊥BC,MN⊥BC,AB=6.5,BP=4,PD=8.
(1)ED的长为 .
(2)将木条BC绕点B按顺时针方向旋转一定角度得到BC′(如图2),点P的对应点为P′,BC′与MN的交点为D′,从A点发出的光束经平面镜P′反射后,在MN上的光点为E′.若DD′=5,则EE′的长为 .
36.(2021 慈溪市校级四模)如图,在以AB为直径的半圆O中,C是半圆的三等分点,点P是弧BC上一动点,连接CP,AP,作OM垂直CP交AP于N,连接BN,若AB=12,则NB的最小值是 .
三.解答题
37.(2022秋 慈溪市期末)如图,⊙O的两条弦AB,CD互相垂直,垂足为E,直径CF交线段BE于点G,且.
(1)求证:.
(2)若⊙O的半径为4,AB=6,求AG的长.
(3)设.
①若点E为AG中点,求x.
②若,求y与x的函数表达式.
38.(2023秋 慈溪市期末)已知二次函数y=x2﹣2tx+t2﹣t.
(1)求该二次函数图象的顶点坐标(用含t的代数式表示).
(2)点P(m,n)在该二次函数图象上,其中t﹣2≤m≤t+1.
①当t=2时,求n的取值范围.
②请探究n的最大值与最小值之差是否会随着t的变化而变化.若不变,请求出这个差;若变化,请用含t的代数式表示这个差.
39.(2023秋 慈溪市期末)如图1,以Rt△ABC的直角边AB为直径画⊙O,过A作斜边AC的垂线交⊙O于点D,连结CD,交⊙O于点E,交AB于点F,连结BE.
(1)求证:∠ACD=∠EBC.
(2)如图2,当△ABC是等腰直角三角形时.
①求∠BCD的正切值;
②求的值.
(3)若AB=1,设CD=x,y,求y关于x的函数表达式.
40.(2022秋 北仑区期末)我们知道,对角线互相垂直的圆内接四边形有许多特殊的结论成立,如对边的平方和相等,等等.如图1,四边形ABCD内接于⊙O,AC⊥BD,AC,BD交于点E.
(1)若AC=BD=4,则∠BDC= 度,四边形ABCD的面积为 .
(2)如图2,在AD上找一点M,连结BM,OM,使BM⊥OM,求证:BM2=AM DM.
(3)如图1,已知BD=4,且.
①当时,求AC的长.
②如图3,在四边形ABCD内取一点P,连结AP,BP,CP,DP,使∠APB=∠CPD=90°,当AB取最小值时,直接写出tan∠ABP的值.
41.(2023秋 海曙区期末)如图,抛物线y=ax2+bx﹣3与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,点D为直线BC下方抛物线上一动点.
(1)求抛物线的解析式;
(2)过点D作y轴的平行线,交BC于点P,小明认为当点D为抛物线顶点时,此时DP最大,试判断小明的说法是否正确,并说明理由.
42.(2023秋 余姚市期末)平面直角坐标系中,点(1,m),(2,n)在函数y=x2+bx+c(b,c是常数)的图象上.
(1)若m=2,n=1,求该函数的表达式;
(2)若m=2n,求证:该函数的图象经过点(3,2);
(3)已知点(3,0),(﹣2,y1),(5,y2)在该函数图象上,若m>0,n<0,试比较y1,y2的大小,并说明理由.
43.(2023秋 北仑区期末)已知二次函数y=ax2+(a+2)x﹣2a﹣2(a为常数且a≠0).
(1)当函数图象经过点(0,﹣6)时,求函数的表达式并写出函数图象的顶点坐标;
(2)求证:当时,函数图象与x轴必有两个不同的交点;
(3)若函数图象经过A(x1,y1),B(x2,y2)两点,其中x1+x2=3,且当x1<x2时,总有y1>y2,求a的取值范围.
44.(2022秋 镇海区期末)如图1,在锐角△ABC中,AB=AC,圆O为△ABC的外接圆.
(1)求证:OA平分∠BAC.
(2)如图2,点E在弧AB上,CE分别与OA,BA交于点F,G,且CF=BE.
①求证:BG⊥EF;
②若EF=2,CF=3,求圆O的半径.
③如图3,连结BO并延长交AC于D,交CE于H,若DH=OH,求cos∠BAC的值.
45.(2022秋 北仑区期末)在平面直角坐标系中,我们定义直线y=2ax﹣b为抛物线y=ax2+bx+c(a,b,c为常数且a≠0)的“倍系直线”.已知抛物线与x轴交于点A(﹣2,0),与y轴交于点B,与其“倍系直线”交于A、C两点.
(1)填空:b= ,该抛物线的“倍系直线”的函数表达式为 ,点C的坐标为 .
(2)过点B作BD∥x轴,交抛物线于点D,连结AD,过点D作DM∥y轴,交AC于点M,求点M的坐标,并求证:AO平分∠CAD.
(3)设“倍系直线”AC交y轴于点E,点F为线段EM上一点,使FE=2FM,连结DF并延长,交y轴于点G,求△GEF与△CDF的面积之比.
46.(2023秋 江北区期末)如图1,四边形ABCD内接于⊙O,连接BD,AC交于点G,点E是AB上一点,连接CE,交BD于点F,且满足∠ACD=∠ACF.
(1)求证:∠ACE=∠ABD.
(2)若点C是的中点,
①求证:CE=CD;
②若,时,求的值.
(3)如图2,当点F是BG的中点时,若AB=2,AC=3,求CG的值.
47.(2023秋 海曙区期末)如图,AB是⊙O的直径,C为AB下方半圆上一动点,OD∥AC交于点D.
(1)求证:;
(2)已知⊙O半径为r,设BD=x,AC=y,求x与y的关系式;
(3)点P为AB上方圆外一点,且∠PAB=2∠APO,连结PA、PB、PO,PA交上半圆于点E,已知当时y=9,,求sin∠PAB的值.
48.(2023秋 宁波期末)如图1,四边形ABCD内接于⊙O,AC为直径,∠BDC=45°,AC,BD交于点E,AB=2,过点O作GH⊥CD,垂足为G,交BD于点H.
(1)求⊙O的半径;
(2)当DE=EH时,求OH:OG的值;
(3)延长GH交CB的延长线于点Q,当HG=3OG时,求BQ的长.
49.(2022秋 宁波期末)(1)如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,判断线段DG与BE的数量关系并说明理由;
(2)如图2,四边形ABCD是矩形,AB=3,BC=6,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE又有怎样的数量关系,并说明理由;
(3)如图3,在(2)的条件下,连接BG,求2BG+BE的最小值.
50.(2023秋 鄞州区期末)如图1,△ABC 内接于⊙O,直径AB=12,弦,作弦CD与AB相交于点E.
(1)如图1,若AE=AC,求∠ACD的度数;
(2)如图2,若AE=4,求CD的长;
(3)如图3,过点A作CD的平行线交⊙O于点M,连结BD,MC,若,求△BCD的面积.
51.(2023秋 江北区期末)【基础巩固】(1)如图1,在△ABC中,AB=AC,D为BC上一点,AD=AE,∠BAD=∠CAE.求证:△ABC∽△ADE;
【尝试应用】(2)如图2,在(1)的条件下,DE交AC于点F,若∠B=45°,,求的值;
【拓展延伸】(3)如图3,在(1)的条件下,若,M,N分别是BC,DE的中点,请直接写出△AMN周长的值.
52.(2023秋 余姚市期末)如图,△ABC内接于⊙O,BC是⊙O的直径,tan∠ACB=2,过点A作AD⊥BC,交⊙O于点E,点F是上一点,连结EF交BC于点G,连结CF交AD于点H.
(1)求证:△AFC∽△HFE;
(2)若BC=10,CF=8,求EF的长;
(3)设,,求y关于x的函数表达式.
53.(2023秋 北仑区期末)如图,AB,AC,AD是⊙O中的三条弦,且AD平分∠BAC.
(1)如图1,若∠BAC=120°,测量AB,AC,AD的长度,猜想它们之间的数量关系为: ;
(2)如图2,若∠BAC=90°,求证:;
(3)如图3,若∠BAC=2θ(0°<θ<90°),直接写出AB,AC,AD与θ角三角函数之间的数量关系.
54.(2022秋 宁波期末)如图1,△ABC为圆O的内接三角形,△ABC的三条角平分线交于点I,延长AI交圆O于点D,连接DC.
(1)求证:DI=DC.
(2)如图2,连接BD,设BC与AD交于点P,若OI⊥AD,AB=8,求BP的长.
(3)如图3,四边形ABCD内接于圆O,连接对角线AC,BD交于点E,且AC平分∠BAD,过B作BF∥CD交AC于点F,BG平分∠ABD交AC于点G,若,AD=6,求FG的最大值,并求此时圆O的半径.
55.(2023秋 鄞州区期末)如图1,四边形ABCD内接于⊙O,对角线AC与BD交于点E,AC>BD,点F在AC上,∠ADF+∠ABC=90°.
(1)求∠CDF的度数.
(2)如图2,作DG⊥AB于点G,DG与AC交于点H,BG=CD,E为BD中点,求证:CF=2DE.
(3)在(2)的条件下,BD=2.
①若△BDG的面积是△DEH面积的3倍,求AC的长.
②如图3,当圆心O在高DG上时,求⊙O的半径.
56.(2023秋 镇海区校级期末)如图1,⊙O是△ABC的外接圆,点D是上一动点(不与点A、C重合),且∠ADB=∠BAC=45°.
(1)求证:AC是⊙O的直径;
(2)当点D在运动到使AD+CD=5时,则线段BD的长为 ;(直接写出结果)
(3)如图2,把△DBC沿直线BC翻折得到△EBC,连接AE,当点D在运动时,探究线段AE、BD、CD之间的数量关系,并说明理由.
57.(2022秋 宁波期末)已知二次函数y=ax2+bx+c的图象经过三点A(﹣1,0),B(4,0),C(0,3).
(1)求二次函数的表达式.
(2)二次函数的图象上若有两点(,y1),(m,y2)且y1<y2,根据图象直接写出m的取值范围.
(3)点D是第一象限内二次函数的图象上的一动点,作DE∥y轴交BC于点E,作DF⊥BC于点F.当D点运动时,求△DEF面积的最大值.
58.(2022秋 镇海区期末)【基础巩固】
(1)如图1,在△ABC中,E是AB上一点,过点E作BC的平行线交AC于点F,点D是BC上任意一点,连结AD交EF于点G,求证:;
【尝试应用】
(2)如图2,在(1)的条件下,连结BF,DF,若∠C=30°,FE、FB恰好将∠AFD三等分,求的值;
【拓展延伸】
(3)如图3,在等边△ABC中,BD=4DC,连结AD,点E在AD上,若∠BEC=120°,求的值.
59.(2022秋 余姚市期末)[基础巩固]
(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证:AC2=AD AB.
[尝试应用]
(2)如图②,在矩形ABCD中,AD=2,点F在AB上,FB=2AF,DF⊥AC于点E,求AE的长.
[拓展提高]
(3)如图③,在矩形ABCD中,点E在边BC上,△DCE与△DFE关于直线DE对称,点C的对称点F在边AB上,G为AD中点,连结GC交DF于点M,GC∥FE,若AD=2,求GM的长.
60.如图,在矩形ABCD中,AB=6cm,BC=8cm,如果点E由点B出发沿BC方向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为每秒2cm和1cm,FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t秒(0<t<4).
(1)连接EF,若运动时间t= 时,EF⊥AC;
(2)连接EP,设△EPC的面积为S cm2,求S与t的关系式,并求S的最大值;
(3)若△EPQ与△ADC相似,求t的值.
参考答案
一.选择题
1.【分析】设BC=a,CD=b,AE=c,IE=d,根据题意得到ab=m,cd=n,由矩形ABCD~矩形BEFG可得,代入整理可得ac+bd=2ab,最后表示出大长方形的周长,代入化简即可求得.
【解答】解:设BC=a,CD=b,AE=c,IE=d,
则ab=m,cd=n,
依题意得:BG=a﹣d,BE=c﹣b,
矩形ABCD~矩形BEFG,
∴,
∴,
整理得ac+bd=2ab,
这个大矩形的面积为:
(a+d)(b+c)
=ab+cd+ac+bd
=ab+cd+(ac+bd)
=ab+cd+2ab
=3ab+cd
=3m+n.
故选:D.
2.【分析】分别过点A,D作BC的平行线,根据相似比,找出对应相似图形的面积关系,然后找出符合的选项即可.
【解答】解:如图,分别过点A,D作BC的平行线交CE于点M,交BF于点N,
∵四边形ABCD~四边形HGFA,相似比k=3,
∴CD=3AF=3ME,BC=3FG=3BJ,△BCD∽△BJI,相似比k=3,
则S平行四边形BCDN=3S平行四边形MEFA=2S△BCD,9S△BJI=S△BCD,
∵S△ADN=S△ADM,
∴S四边形ABCD﹣S四边形ADEF=S BCDN﹣S MEFAS△BCD=12S△BIJ,选项C符合题意,
故选:C.
3.【分析】设AC,EF交于H,设CD=a,BD=CE=b,则DE=a﹣b,BC=a+b,由勾股定理得AB=AC(a+b),HCb,则AH=AC﹣HC(a﹣b),再证△AFH和△ABD相似得FH,则EF=EH+FH,再由勾股定理求出DF,据此可求出△DEF的周长=2a,而△DEF的面积,△ADF的周长和面积都不能求出,据此即可得出答案.
【解答】解:设AC,EF交于H,如图所示:
在等腰△ABC中,∠BAC=90°,AB=AC,
∵∠B=∠C=45°,
设CD=a,BD=CE=b,
∴DE=CD﹣CE=a﹣b,BC=CD+BD=a+b,
在Rt△ABC中,AB=AC,BC=a+b,
由勾股定理得:AB2+AC2=BC2,
∴AB=AC(a+b),
∵FE⊥DE,
∴∠CHE=∠AHF=∠C=45°,
∴HE=CE=b,
由勾股定理得:HCb,
∴AH=AC﹣HC(a+b)﹣√2b(a﹣b),
∵AF⊥AD,∠BAC=90°,
∴∠DAC+∠HAF=90°,∠BAD+∠DAC=90°,
∴∠HAF=∠BAD,
又∵∠AHF=∠B=45°,
∴△AFH∽△ABD,
∴FH:BD=AH:AB,
即FH:b(a﹣b):(a+b),
∴FH,
∴EF=EH+FH=b,
在Rt△EDF中,EF,DE=a﹣b,
由勾股定理得:DF,
∴△DEF的周长为DE+EF+DF=a﹣b2a,
∴已知CD的长可以求出△DEF的周长,
故选项A符合题意;
∵DE=a﹣b,EF,
∴S△DEFDE EF (a﹣b) ,
∵b的大小不是已知的,
∴不能求出△DEF的面积;
故选项B不符合题意;
根据已知条件不能用a,b的代数式表示出AD和AF,
∴不能求出△ADF的周长和面积,
∴选项C,D不符合题意.
故选:A.
4.【分析】先根据勾股定理求出AC,过点P作PM⊥AB于点M,证明△PQM≌△PBM,推出QM=BM,分别表示AM和AP的长,根据△APM∽△ACB,进而,求出t的值,进而作答即可.
【解答】解:∵矩形ABCD,
∴AB∥CD,∠ABC=90°,
在Rt△ABC中,
AC13cm,
过点P作PM⊥AB于点M,如图,
∴PM∥BC,
∴∠CBP=∠BPM,
∵∠QPB=2∠CBP,
∴∠CBP=∠BPM=∠QPM,
在△QPM与△BPM中,
,
∴△QPM≌△BPM(ASA),
∴QM=BM,
BQ=12﹣2t,QM=BM,
∴AM=6+t,AP=13﹣t,
∵∠BAC=∠BAC,∠PMA=∠CBA=90°,
∴△APM∽△ACB,
∴,
即,
∴t,
故选:B.
5.【分析】由矩形GBEF∽矩形ABCD,得到矩形GBEF与矩形ABCD的相似比是,由△EBC∽△EAH,推出,即可得到答案.
【解答】解:∵矩形GBEF∽矩形ABCD,
∴矩形GBEF与矩形ABCD的相似比是,
∵四边形ABCD是矩形,
∴AH∥BC,
∴△EBC∽△EAH,
∴,
∴要求两个矩形的相似比,只需知道.
故选:C.
6.【分析】根据AC:BC=3:2可设AC=3a,BC=2a,则ABa,设∠BAC=α,则tanα,证∠GAE=∠BAC=α,在Rt△AGE中可求出GE=2a,则EF=a,再证∠FEK=∠GAE=α,在Rt△FEK中可求出FKa,进而得S1=2a2,然后证∠CBM=∠BAC=α,在Rt△BCM中可求出CMa,则MLa,进而得S2a2,最后再根据S1+S2=30求出a=3,由此可得AB的长.
【解答】解:∵AC:BC=3:2,
∴设AC=3a,BC=2a,
在Rt△ABC中,由勾股定理得:ABa,
∵四边形ACFG,四边形BCLI,四边形ABDE均为正方形,
∴AG=AC=GF=3a,BC=LI=CL=2a,∠G=∠CAG=∠AED=∠ABD=∠CBI=∠F=90°,
设∠BAC=α,
在Rt△ABC中,BC=2a,AC=3a,
∴tanα,
∵∠GAE+∠EAC=90°,∠EAC+∠BAC=90°,
∴∠GAE=∠BAC=α,
在Rt△AGE中,tan∠GAE,
∴GE=AG tan∠GAE=3a tanα=3a 2a,
∴EF=GF﹣GE=3a﹣2a=a,
∵∠GAE+∠GEA=90°,∠FEK+∠GEA=90°,
∴∠FEK=∠GAE=α,
在Rt△FEK中,tan∠FEK,
∴FK=EF tan∠FEK=a tanαa,
∴S1=GF FK=3a a=2a2,
∵∠BAC+∠ABC=90°,∠ABC+∠CBM=90°,
∴∠CBM=∠BAC=α,
在Rt△BCM中,tan∠CBM,
∴CM=BC tan∠CBM=2a tanαa,
∴ML=CL﹣CM=2aaa,
∴S2=ML LIa 2aa2,
∵S1+S2=30,
∴2a2a2=30,
即a2=9,
∴a=3,(舍去负值),
∴AB.
故选:A.
7.【分析】根据抛物线y=ax2﹣2ax+8(a<0)可知的对称轴为直线x=1,开口向下;由1﹣m<m+7,得m>﹣3,根据存在x1,x2,满足y1=y2,﹣1<x1<2,知1﹣m<3,m>﹣2,即可得m的取值范围是m>﹣2.
【解答】解:∵y=ax2﹣2ax+8(a<0),
∴抛物线开口向下,对称轴为直线x1,
∵存在x1,x2(x1≠x2),满足y1=y2,
∴点(x1,y1),(x2,y2)关于x=1对称,
∴x1+x2=2,
∵﹣1<x1<2,
∴0<x2<3,
∵1﹣m<x2<m+7,
∴1﹣m<m+7,
∴m>﹣3,
∴1﹣m<3,
∴m>﹣2,
综上所述,m的取值范围是m>﹣2.
故选:B.
8.【分析】依据题意,首先根据x1<x2<x3<x4<x5<x6<x7,其对应的函数值是先增大后减小,可得抛物线开口向下,所以a<0;然后根据函数值是先增大后减小,可得7<m<14<k;最后根据a<0,可得二次函数有最大值,而且二次函数的最小值,所以b2≥4a(c﹣k),据此判断即可.
【解答】解:∵x1<x2<x3<x4<x5<x6<x7,其对应的函数值是先增大后减小,
∴抛物线开口向下,
∴a<0,①符合题意;
∴7<m<14<k,
∴7<m<14,②符合题意;
根据图表中的数据知,只有当x是抛物线的对称轴,抛物线的顶点坐标纵坐标不一定是k,故③不符合题意;
∵k,a<0,
∴4ac﹣b2≤4ak,
∴b2≥4a(c﹣k),④符合题意.
综上,可得判断正确的是:①②④.
故选:C.
9.【分析】连接DG,利用平行线的性质和相似三角形的判定定理得到△ADE∽△DBF,利用线段中点的定义得到AG=GEAE,DH=HFDF,进而得到,利用相似三角形的判定得到△GDE∽△HBF,再利用利用三边对应成比例的三角形相似得到△ADG∽△DBH,则∠ADG=∠DBH,利用平行线的判定定理得到DG∥BH,利用平行线间的距离相等,同底等高的三角形的面积相等的性质得到△BGH的面积=△BDH的面积,由于△BHF的面积=△BDH的面积,则△BDF的面积=2×△BDH的面积=2×△BGH的面积.
【解答】解:连接DG,如图,
∵DE∥BC,
∴∠AED=∠C,∠ADE=∠ABC,
∵DF∥AC,
∴∠C=∠DFB,
∴∠AED=∠DFB,
∴△ADE∽△DBF,
∴,
∴.
∵AG=GE,DH=HF,
∴AG=GEAE,DH=HFDF,
∴,
∵∠AED=∠DFB,
∴△GDE∽△HBF,
∴,
∵△ADE∽△DBF,
∴,
∴,
∴△ADG∽△DBH,
∴∠ADG=∠DBH,
∴DG∥BH,
∴△BGH的面积=△BDH的面积,
∵DH=HF,
∴△BHF的面积=△BDH的面积,
∴△BDF的面积=2×△BDH的面积=2×△BGH的面积.
∴若已知△BGH的面积,则一定能求出△BDF的面积.
故选:B.
10.【分析】由AF=AD,得∠AFD=∠ADF,由翻折得∠C=∠E,∠CAD=∠EAD,则∠ADF=∠C+∠CAD=∠E+∠EAD,而∠AFD=∠E+∠EDF,即可推导出∠EDF=∠EAD,进而证明△EDF∽△EAD,得,因为EF=3,CF=17,所以(17﹣FD)2=3(3+AF),3AF=FD(17﹣FD),于是得(17﹣FD)2=9+FD(17﹣FD),求得FD=8,于是得到问题的答案.
【解答】解:∵AF=AD,
∴∠AFD=∠ADF,
由翻折得∠C=∠E,∠CAD=∠EAD,
∴∠ADF=∠C+∠CAD=∠E+∠EAD,
∵∠AFD=∠E+∠EDF,
∴∠E+∠EDF=∠E+∠EAD,
∴∠EDF=∠EAD,
∵∠E=∠E,
∴△EDF∽△EAD,
∴,
∴ED2=EF EA,EF AD=FD ED,
∵EF=3,CF=17,
∴ED=CD=17﹣FD,EA=3+AF,
∴(17﹣FD)2=3(3+AF),3AF=FD(17﹣FD),
∴(17﹣FD)2=9+FD(17﹣FD),
整理得2FD2﹣51FD+280=0,
解得FD=8或FD(不符合题意,舍去),
∴FD的长是8,
故选:A.
11.【分析】根据平行线分线段成比例定理,相似三角形的判定和性质逐项判断便可.
【解答】解:∵l1∥l2,
∴CF:OF=AE:EO=4:2,
∴,故①正确;
∵AE:EO:OB=4:2:7,
∴AE:BE=4:9,
∵l1∥l2∥l3,
∴,故②正确;
∵l2∥l3,
∴△OEF∽△OBD,
∴,故③正确;
∵l1∥l2,
∴△OEF∽△OAC,
∴,故④错误;
∴正确的说法有3个.
故选:B.
12.【分析】首先通过待定系数法求该抛物线的解析式及顶点坐标,再分类讨论点P在抛物线对称轴右侧及左侧两种情况,分别求出顶点为最低点和点P为最低点时m的值即可.
【解答】解:将(1,0),(0,3)分别代入y=x2+bx+c得,
解得,
∴y=x2﹣4x+3,
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线顶点坐标为(2,﹣1),对称轴为直线x=2,
当m>2时,抛物线顶点为最低点,
∴﹣1=2﹣m,
解得m=3,
当m≤2时,点P为最低点,
将x=m代入y=x2﹣4x+3得y=m2﹣4m+3,
∴m2﹣4m+3=2﹣m,
解得(舍),,
∴m=3或.
故选:D.
13.【分析】第二个图形中点(,)在两段函数中,是关键点.结合第一个图形,可得此时点P移动到点C,H在AB的中点,那么BH,△PHB的面积为.所以横轴表示BH的长,故A错误;当P为BC的中点时,作CD⊥AB于点D,可得BDAB,根据平行线分线段成比例定理可得BHDB,那么BHAB,H为AB的四等分点,那么B错误;根据P在BC和AC上,分别计算出△PHB的面积,得到相应函数解析式,看二次项的比例系数的绝对值是否相等,若相等,则形状相同;把x代入点P在AC上的函数解析式中可求得面积的值,判断出D是否正确.
【解答】解:∵点(,)在两段函数中,
∴点P点C重合.
∵正△ABC 的边长为1,PH⊥AB,
∴BC=1,BH.
∴CH.
∴S△PHB.
∵符合所给点(,).
∴横轴表示BH的长,故A错误;
作CD⊥AB于点D.
又∵△ABC是等边三角形,
∴BDAB.
∵PH⊥AB,
∴PH∥CD.
∵P为BC中点,
∴BPBC.
∴BHBD.
∴BHAB.
∴点H为AB的四等分点,故B错误;
当P在BC上时,BH为x,则PHx,
∴y=S△PHB x xx2.
当P在BC上时,BH为x,则AH=1﹣x,
∴PH(1﹣x)
∴y=S△PHB x (1﹣x).
∵两个二次函数的比例系数的绝对值相等,
∴形状相同,故C错误;
当x时,点P在AC上,∴y=S△PHB,故D正确.
故选D.
14.【分析】先设Rt△ABC的三边长为a,b,c,其中c为斜边,设⊙O的半径为r,根据图形找出a,b,c,r的关系,用含c的式子表示S1和S2,即可求出比值.
【解答】解:如图,取AB的中点为O,AC的中点为D,连接OE,OG,OD,OC,
设AB=c,AC=b,BC=a,
则a2+b2=c2,①
取AB的中点为O,
∵△ABC是直角三角形,
∴OA=OB=OC,
∵圆心在MN和HG的垂直平分线上,
∴O为圆心,
由勾股定理得:
,②
由①②得a=b,
∴,
∴,,
∴,
故选:C.
15.【分析】设AB=CD=m,DA=BC=n,则S=mn,S△ABD=S△CDBmnS,BGn,HDm,由△HDF∽△ABF,,可判断①正确;
由△GBE∽△ADE,得,则BEBD,而FDBD,所以EFBD,可求得BE:EF:FD=3:5:4,可判断②正确;
由GEAG,AEAG,得S1S△ABGS,S4S△ABGS,由HFAH,AFAH,得S3S△ADHS,S5S△ADHS,则S2S,S6S,所以S1+S2+S3S,可判③正确;
因为S2+S5SSS,所以S6=S2+S5,可判断④正确,于是得到问题的答案.
【解答】解:∵四边形ABCD为矩形,
∴AB=CD,DA=BC,AB∥CD,DA∥BC,
设AB=CD=m,DA=BC=n,则S=mn,S△ABD=S△CDBmnS,
∵点G是边BC的三等分点(BG<GC),点H是边CD的中点,
∴BGn,HDm,
∴S△ABGmnmnS,S△ADHnmmnS,
∵HD∥AB,
∴△HDF∽△ABF,
∴,
故①正确;
∵BG∥DA,
∴△GBE∽△ADE,
∴,
∴BEBD,
∵FDBD,
∴EF=BDBDBDBD,
∴BE:EF:FDBD:BDBD=3:5:4,
故②正确;
∵GEAG,AEAG,
∴S1S△ABGSS,S4S△ABGSS,
∵HFAH,AFAH,
∴S3S△ADHSS,S5S△ADHSS,
∴S2SSSS,S6SSSS,
∴S1+S2+S3SSSS,
故③正确;
∴S2+S5SSS,
∴S6=S2+S5,
故④正确,
故选:D.
16.【分析】根据题意得AE=CG=BF=DH,BE=DG,四边形EFG是正方形,∠AEB=∠DGC=90°.先证明△BPE≌△DQG,得到GQ,再根据△TGQ∽△KFQ,求出TG,再根据勾股定理求解.
【解答】解:根据题意:AE=CG=BF=DH,BE=DG.
∵四边形EFG是正方形,∠AEB=∠DGC=90°.
∵AE=2EF=2.
∴CG=AE=DH=2,EF=FG=EH=1,EH∥FG.
∵AP=CQ.
∴PE=GQ.
∴
∴△BPE≌△DQG(SAS).
∴S△BPE=S△DQG,
即S4=S2.
∵S1=S3=S2+S4.
∴S1=S3=2S4.
∴DH (PE+EH)=2PE (BF+EF).
即.
∴PE=GQ.
∴CQ=CG﹣GQ.
∵EH∥FG.
∴∠PET=∠GQT.
∵∠PQK=∠TGQ=90°,PE=GQ.
∴.
∴△PEK≌△QGT.
∴EK=TG
设TG=EK=a,则FT=1﹣a,
∵HG∥EF.
∴△TGQ∽△KFQ.
∴,即.
解得:a.
即TG.
在△QGT中,根据勾股定理知:
QT.
故选:D.
17.【分析】设两个正六边形的中心为O,连接OP,OB,过O作OG⊥PM,OH⊥AB,由正六边形的性质及邻补角性质得到三角形PMN为等边三角形,由小正六边形的面积求出边长,确定出PM的长,进而求出三角形PMN的面积,利用垂径定理求出PG的长,在直角三角形OPG中,利用勾股定理求出OP的长,设OB=x cm,根据勾股定理列出关于x的方程,求出方程的解即可得到结果.
【解答】解:设两个正六边形的中心为O,连接OP,OB,过O作OG⊥PM,OH⊥AB,
由题意得:∠MNP=∠NMP=∠MPN=60°,
∵小正六边形的面积为cm2,
∴小正六边形的边长为cm,即PM=7cm,
∴S△MPNcm2,
∵OG⊥PM,且O为正六边形的中心,
∴PGPMcm,OGPMcm,
在Rt△OPG中,根据勾股定理得:OP7cm,
设OB=x cm,
∵OH⊥AB,且O为正六边形的中心,
∴BHx,OHx,
∴PH=(5x)cm,
在Rt△PHO中,根据勾股定理得:OP2=(x)2+(5x)2=49,
解得:x=8(负值舍去),
则该圆的半径为8cm.
故选:D.
18.【分析】设CG=x,HG=y,证△ADH∽△DCG,用含x、y的式子表示DG、AH、EH,再根据tanβ=tan2α,推出x与的关系,最后利用勾股定理求出DC、EH和AD的长,代入矩形面积计算即可.
【解答】解:∵四边形ABCD是矩形,BC=2AB,
∴AB=CD,AD=BC,
∴AD=2CD,
设CG=x,HG=y,
∵△AHD≌△CFB,△ABE≌△CDG,且这四个三角形均为直角三角形,
∴∠AHD=∠DGC=90°,
∴∠DAH+∠ADH=∠ADH+∠CDG=90°,
∴∠CDG=∠DAH,
∴△ADH∽△DCG,
∴2,
∴DH=2x,
∴DG=2x+y,AH=4x+2y,EH=3x+2y,
∵∠CHG=α,∠CDG=β,tanβ=tan2α,
∴,即2x2+xy=y2,
∴y2﹣xy﹣2x2=0,
∴(y﹣2x)(y+x)=0,
∵y+x≠0,
∴y=2x,
∴DG=4x,DCx,EH=3x+2y=7x,
∴AD=2x,
∴,
故选:B.
二.填空题
19.【分析】如图,过G作GT⊥BC于T交CE于R,过G作GQ⊥AB于Q,交DC于N,连接EG,证明GE=GC,EF=FC=GF,设BE=a,求解,求解,,,证明AQ=QE,,过C作CS⊥GG'于S,求解,,,可得,过K作KV⊥CG'于V,可得KV:VG':KG'=8:15:17,再解直角三角形可得答案.
【解答】解:如图,过G作GT⊥BC于T交CE于R,过G作GQ⊥AB于Q,交DC于N,连接EG,
∵CE中点为F,GF⊥CF,GF=CF,
∴GE=GC,EF=FC=GF,
设BE=a,
∵正方形ABCD中,AE=3BE,
∴AE=3a,AB=BC=CD=AD=4a,
∴,tan∠BCE,
∴,,
∵∠GFR=∠CTR=90°,∠GRF=∠CRT,
∴∠FGR=∠RCT,
∴,
∴,
∴,
∴,
∴,,
∴,
∴,,,
∴AQ=QE,
∴,
∵GT⊥BC于T交CE于R,过G作GQ⊥AB于Q,交DC于N,
∴∠GNC=∠NCT=∠CFG=90°,
∴四边形GTCN为矩形,
∴,,
∴,
∴,,
∴,
过C作CS⊥GG'于S,
同理可得:,,
∴,
∵CG=CG',
∴,
∵CG=CG',
∴∠CGG'=∠CG'G,
∴,
过K作KV⊥CG'于V,
由旋转可得:∠F'CG=∠FCG=45°,
∴设KV=CV=n,
∴,
∴,
∴KV:VG':KG'=8:15:17,
∴,
∴,
∵,
∴.
故答案为:.
20.【分析】作出圆心O,连接OB,OC,OC与AB交于点F,根据垂径定理和等腰三角形的性质与判定证明出△BOC是等边三角形,即可得出半径长;过点D作DM∥AC,DN⊥BC,得出△AEC∽△DEM,从而得到,再根据平行的性质和锐角三角函数得到DM,从而得到当DN最大时,最大,求出此时的DN即可得解.
【解答】解:作出圆心O,连接OB,OC,OC与AB交于点F,过点D作DM∥AC,DN⊥BC于点N,连接BD,
∵AC=BC,
∴,
∴OC⊥AB,AF=BF,
∴∠ACF=∠BCFACB=60°,
∵OB=OC,
∴△BOC是等边三角形,
∴BC=OC=OB=2=AC,
∴BFOB,
∴AB=2,
∵DM∥AC,
∴△AEC∽△DEM,
∴,
∵DM∥AC,
∴∠DME=∠ACB=120°,
∴∠DMN=60°,
∴DM,
∴当DN最大时,DE:AE最大,
由题意知D为中点时,DN最大,
此时DN的长等于半径减去△BOC的高,
∴DN=2,CN:BN=1,
∴DM,
∴MN1,
∴CM=CN﹣MN=2,
∴,
∵DM∥AC,
∴,
∴,
∴CE1,
故答案为:2,1.
21.【分析】(1)连接OA,过点O作OM⊥AC,根据圆周角定理、垂径定理及等腰三角形的性质得出∠OAC=∠OCA=30°,,再由余弦函数求解即可;
(2)连接OB,过点O作OD⊥BC,过点E作EF⊥BD,利用角的等量代换得出∠AEC=90°,再由正弦函数确定OE=2,根据相似三角形的判定和性质及勾股定理求解即可.
【解答】解:(1)连接OA,过点O作OM⊥AC,
∵∠ABC=60°,
∴∠AOC=120°,
∵OA=OC,OM⊥AC,
∴∠OAC=∠OCA=30°,,
∵,
∴,
∴⊙O的半径为4;
故答案为:4;
(2)连接OB,过点O作OD⊥BC,过点E作EF⊥BD,如图所示:
∵∠EAC=60°,∠OAC=30°,
∴∠EAO=30°,
∵∠EAC=60°,∠OCA=30°,
∴∠AEC=90°,
∵,
∴OE=OA sin∠EAO=2,
∴CE=CO+OE=6,
∵OD⊥BC,
∴,
∴,
∵∠ODC=∠EFC=90°,∠DCO=∠FCE,
∴△DCO∽△FCE,
∴即,
∴,,
∴,
∴,
故答案为:.
22.【分析】先根据抛物线解析式求出点A坐标和其对称轴,再根据对称性求出点M坐标,利用点M为线段AB中点,得出点B的坐标;再将点B的坐标代入直线OP的解析式,用含a的式子表示出点P坐标,即可求解出a的值,据此即可解答.
【解答】解:∵抛物线y=ax2﹣2ax+3(a>0)与y轴交于点A,
∴A(0,3),抛物线的对称轴为直线x=1,
∴顶点P坐标为(1,3﹣a),点M坐标为(2,3)
∵点M为线段AB的中点,
∴点B坐标为(4,3),
设直线OP解析式为y=kx(k为常数,且k≠0),
将点B(4,3)代入得4k=3,
解得,
∴直线OP解析式为,
将点P(1,3﹣a)代入得,
得,
解得,
∴点,
∴
故答案为:.
23.【分析】分两种情形:如图1中,当EF⊥AB时,如图2中,当ME⊥EC时,分别证明两个三角形相似,构建方程求解.
【解答】解:∵∠ACB=90°,CE是中线,
∴EC=EA=EB,
∴∠B=∠ECB,
∵△DEF∽△ABC,
∴∠DEF=∠B,
如图1中,当EF⊥AB时,∵∠A+∠ANE=90°,∠A+∠B=90°,
∴∠ANE=∠B,
∴∠MEN=∠MNE=∠B=∠ECB,
∴△EMN∽△BCE,
∵AC=8,BC=6,
∴AB10,
∵∠A=∠A,∠AEN=∠ACB=90°,
∴△AEN∽△ACB,
∴,
∴,
∴AN,
∴CN=AC﹣AN=8;
如图2中,当ME⊥EC时,同法可证∠EMN=∠MEN=∠B=∠ECB,
∴△EMN∽△BCE,NM=NE,
∵∠EMN+∠MCE=90°,∠MEN+∠CEN=90°,
∴∠ECM=∠NEC,
∴NE=CN=MN,
∵∠ACE=∠A,∠CEM=∠ACB=90°,
∴△CEM∽△ACB,
∴,
∴,
∴CM,
∴CNCM.
故答案为:或.
24.【分析】连接AE、AG、DG,设AC与EF交于点K,由∠AGE=90°可得点G在以AK为直径的圆上,进而可得当O、G、B三点共线时,BG有最小值,BG最小=OB﹣OG,证明△AEG∽△ADE与△AKG∽△ADC可求AK=2,再求出OB即可.
【解答】解:连接AE、AG、DG,设AC与EF交于点K,如图,
∵AE=AF,G为EF的中点,
∴AG⊥EF,
∵DE、DF是⊙A的切线,
∴DE=DF,
∵G为EF的中点,
∴DG⊥EF,
∴A、G、D三点共线,
∵∠AGE=90°,
∴点G在以AK为直径的圆上,
∴当O、G、B三点共线时,BG有最小值,BG最小=OB﹣OG,
∵∠AGE=∠AED=90°,∠EAG=∠DAE,
∴△AEG∽△ADE,
∴,
∴AE2=AD AG,
∵∠AGK=∠ACD=90°,∠KAG=∠DAC,
∴△AKG∽△ADC,
∴,
即AK AC=AD AG,
∴AE2=AK AC,
∴AK2,
∴OA=OG=1,
∴OC=AC=OA=7,
∵∠ACB=90°,BC=7,
∴OB=7,
∴BG的最小值为:71,
故答案为:71.
25.【分析】作直径BK,连接AK,CK,由圆周角定理推出∠BCK=∠BAK=90°,而AD⊥BC,判定AF∥KC,同理:AK∥CF,推出四边形AFCK是平行四边形,得到AK=CF=5,CK=AF=AO,由sin∠CBK,得到∠CBK=30°,求出CKBC,得到⊙O的半径是,由勾股定理求出AB3.
【解答】解:作直径BK,连接AK,CK,
∵BK是圆的直径,
∴∠BCK=∠BAK=90°,
∴KC⊥BC,
∵AD⊥BC,
∴AF∥KC,
同理:AK∥CF,
∴四边形AFCK是平行四边形,
∴AK=CF=5,CK=AF=AO,
∴CK:BK=1:2,
∵∠BCK=90°,
∴sin∠CBK,
∴∠CBK=30°,
∴CKBC,
∴AO,
∴⊙O的半径是,
∵∠BAK=90°,AK=5,BK=2AO=2,
∴AB3.
故答案为:,3.
26.【分析】取GF的中点O,连接OM,OD,DM.,由题意,MG2+MF2=2GO2+2OM2,因为OG=OF=3,所以OM的值最大时,MG2+MF2的值最大.
【解答】解答:设点O是GF的中点,连接OM,OD,DM.
在矩形DEFG中,已知DE=6,EF=4,
∴∠DGO=90°,DG=EF=4,FG=DE=6,
∵MG2+MF2=2GO2+2OM2,
∵OG=OF=3,
∴OM的值最大时,MG2+MF2 的值最大,
∵DM=2,,
∴OM≤OD+DM=5+2=7,
∴OM的最大值为7,
∴MG2+MF2 的最大值=2×32+2×72=116.
故答案为:116.
27.【分析】把二次配方成顶点式,确定顶点坐标为(m,3),进而确定抛物线扫过的面积为 y=3 上方,再利用重叠部分面积为列出关于α的等式求出α,再确定点A的纵坐标即可.
【解答】解:二次函数表达式y=x2﹣2mx+m2+3,化为顶点式:y=(x﹣m)2+3,
∴抛物线的顶点为(m,3),
∴抛物线的顶点在直线 y=3上,且开口向上,
∴抛物线扫过的面积为 y=3 上方,如图所示,
∵抛物线与圆重合面积为 ,
即α,
即 ,
解得 α=60°
∴A到BC的距离,
∴A点纵坐标为:.
28.【分析】将要求的代数式进行变形,再对其进行讨论即可解决问题.
【解答】解:因为a1+a2≤100,
所以a1≤100﹣a2,
又因为a1≥a2≥…≥a100≥0,
记S,
则S≤(100﹣a2)2
=1002﹣200a2.
因为a1+a2≤100,a3+a4+…+a100≤100,
所以a1+a2+a3+…+a100≤200,
即﹣200≤﹣(a1+a2+a3+…+a100),
所以S≤1002
=1002﹣a1a2﹣a3a2﹣a4a2﹣…﹣a100a2
=1002﹣a2(a1﹣a2)﹣a3(a2﹣a3)﹣a4(a2﹣a4)﹣…﹣a100(a2﹣a100)
≤1002
=10000,
当a1=100,ai=0(i>1)或者a1=a2=a3=a4=50,aj=0(j>4)时,等号成立.
故答案为:10000.
29.【分析】利用勾股定理,直角三角形的边角关系定理求得BC.AB.利用分类讨论的思想方法分两种情况讨论解答:①当EF=DF时,过点F作FH⊥DE于点H,利用等腰三角形的性质,平行线的判定与性质得到FB=FA,设FB=x,则FA=x,FC=BC﹣FB=4﹣x,利用勾股定理列出方程,解方程即可得出结论;②当EF=DE时,连接BD,过点F作FG⊥AB于点G,利用圆周角定理,等腰三角形的性质,垂径定理得到∠CAD=∠BAD,利用全等三角形的判定与性质求得AG,则BG可得,利用直角三角形的边角关系定理求得FG,则FC可求,所以BF=BC﹣FC.
【解答】解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵AC=2,tan∠ABC,
∴,
∴BC=4,
∴2.
①当EF=DF时,过点F作FH⊥DE于点H,如图,
∵EF=DF,FH⊥DE,
∴∠DFH=∠EFH.
∵FH⊥DE,ED⊥AB,
∴FH∥AB,
∴∠DAB=∠DFH,∠B=∠EFH,
∴∠DAB=∠B,
∴FB=FA.
设FB=x,则FA=x,FC=BC﹣FB=4﹣x.
∵AC2+FC2=AF2,
∴,
∴x=3,
∴BF=3;
②当EF=DE时,连接BD,过点F作FG⊥AB于点G,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵EF=DE,
∴∠EFD=∠EDF,
∵∠EFD+∠EBD=90°,∠EDF+∠BDE=90°,
∴∠BDE=∠EDB,
∵∠CAD=∠DBE,
∴∠CAD=∠BDE.
∵AB⊥DK,AB为直径,
∴,
∴∠DAB=∠EDB,
∴∠CAD=∠BAD.
在△ACF和△AGF中,
,
∴△ACF≌△AGF(AAS),
∴AC=AG=2,FC=FG.
∴BG=AB﹣AG=22,
∵tan∠ABC,
∴,
∴FG(22)=22,
∴FC=22,
∴BF=BC﹣FC=4﹣(22)=6﹣2.
综上,若△DEF是以EF为腰的等腰三角形,则BF的长为3或6﹣2.
故答案为:3或6﹣2.
30.【分析】由AD∥BC,得∠CAD=∠ACB,由AB=AC,得∠B=∠ACB,则∠B=∠CAD,而∠BEC=∠ADC,可证明△BEC∽△ADC,得∠BCE=∠ACD,,则,∠ACB=∠DCE,所以△ABC∽△DEC,则∠B=∠CED=∠CAD,∠ACB=∠DCE,所以∠DCE=∠CED,由翻折得∠CAD=∠A′,A′C=AC=10,则∠B=∠ACB=∠CED=∠DCE=∠A′,CE=A′C=AC=10,再证明△ABC∽△CEA′,得1,则A′E=BC=12,再证明△DEC∽△CEA′,得,求得DE,则AD=A′D,所以BE,于是得到问题的答案.
【解答】解:∵AD∥BC,
∴∠CAD=∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠CAD,
∵∠BEC=∠ADC,
∴△BEC∽△ADC,
∴∠BCE=∠ACD,,
∴∠BCE+∠ACE=∠ACD+∠ACE,,
∴∠ACB=∠DCE,
∴△ABC∽△DEC,
∴∠B=∠CED=∠CAD,∠ACB=∠DCE,
∴∠DCE=∠CED,
由翻折得∠CAD=∠A′,A′C=AC=10,
∴∠B=∠ACB=∠CED=∠DCE=∠A′,
∴CE=A′C=AC=10,
∵∠B=∠CED,∠ACB=∠A′,
∴△ABC∽△CEA′,
∴1,
∴A′E=BC=12,
∴∠DCE=∠A′,∠DEC=∠CEA′,
∴△DEC∽△CEA′,
∴,
∴DE,
∴AD=A′D=A′E﹣DE=12,
∴BE,
故答案为:10,.
31.【分析】设AG=AF=x,则AB=x+4,连接BF,根据已知条件得到∠BAD=CAD,根据全等三角形的判定和性质得到∠AFB=∠AFC,根据等腰三角形的性质得到∠AGF=∠AFG,根据相似三角形的性质即可得到结论.
【解答】解:设AG=AF=x,则AB=x+4,
连接BF,∵AD是⊙O的直径,AB=AC,
∴,,
∴,
∴∠BAD=CAD,
在△ABF与△ACF中,
,
∴△ABF≌△ACF(SAS)
∴∠AFB=∠AFC,
∵AG=AF,
∴∠AGF=∠AFG,
∴∠BGF=∠AFC,
∴∠BGF=∠AFB,
∵∠ABF=∠FBG,
∴△ABF∽△FBG,
∴,
∴,
解得x=12,
∴AB=12+4=16.
故答案为:16.
32.【分析】(1)过E作EM⊥DC于M,延长ME交AB于N,证明△CEM∽△CAD和△DME∽△ENF,根据相似三角形的性质可求解;
(2)连结AG并延长交CD的延长线与L,分别证明△ANE∽△ABC和△CDE∽△ADG,根据相似三角形的性质可求解.
【解答】解:(1)过E作EM⊥DC于M,延长ME交AB于N,
则△CEM∽△CAD,
∴,
∴ME,CM,
∴DM,EN,
在Rt△DME中,DE,
∵∠DME+∠EDM=90°,∠DEM+∠FEN=90°,
∴∠EDM=∠FEN,
又∠DEM=∠FNE,
∴△DME∽△ENF,
∴,
∴EF,
故答案为:;
(2)连结AG并延长交CD的延长线与L,
∵△DME∽△ENF,
∴,
∵△ANE∽△ABC,
∴,
∴,
∴,
∵∠CDE=∠ADG,
∴△CDE∽△ADG,
∴∠DCA=∠DAL,
∴tan∠DCA=tan∠DAL,
∴当HG⊥AL时,HG最小,S△ALHAD HLGH AL,
∵AD=6,DL,LH,AL,
∴HG,
故答案为:4.4.
33.【分析】根据题意画出相应的图形,利用圆周角定理、直角三角形的边角关系以及三角形的面积公式进行计算即可.
【解答】解:如图所示:
∵圆与三角形的三条边都有两个交点,截得的三条弦相等,
∴圆心O就是三角形的内心,
∴当⊙O过C时,且在等腰直角三角形ABC的三边上截得的弦相等,即CG=CF=DE,此时⊙O最大,
过点O分别作弦CG、CF、DE的垂线,垂足分别为P、N、M,连接OC、OA、OB,
∵CG=CF=DE,
∴OP=OM=ON,
∵∠C=90°,AB=6,AC=BC,
∴,
∵S△AOC+S△BOC+S△AOB=S△ABC,
∴,
设OM=x,则OP=ON=x,
∴,
解得:,
即,
在Rt△CON中,,
故答案为:.
34.【分析】把AB两点的坐标代入函数解析式即可判断①正确;由平行于坐标轴直线上两点之间的距离的几何意义即可判断②;由于C、D是抛物线与x轴的交点,有根与系数的关系和CD≤6,可以判断③;x=4时,y=3,3≤x≤4,对应的y的整数值有3个,y对应得整数值为:3,4,5,结合图象,可以判断④.
【解答】解:①将A、B两点坐标代入抛物线y=ax2+bx+c中,
则:,
解得:,
故①正确;
②∵|x1﹣2|﹣|x2﹣2|>0,即|x1﹣2|>|x2﹣2|,
∴x1距离x=2比x2距离x=2更远,
如图:
从图中可以看出x距离x=2越远对应的函数值越小,
故y1<y2,
故②错误;
③∵a<0,
设C(x3,0)、D(x4,0),
则由根与系数的关系得:x3+x4=4,x3 x4,
∴|x3﹣x4|6,
解得:a,
故③正确;
④由题意知:x=4时,y=3,
∵3≤x≤4,对应的y的整数值有3个,
∴y对应得整数值为:3,4,5,
则x=3时对应的函数值y的取值范围为:5≤9a﹣12a+3<6,
解得:﹣1<a,
故④正确.
故答案为:①③④.
35.【分析】(1)由题意可得,△ABP∽△EDP,则,进而可得出DE的长;
(2)过点E′作∠E′FG=∠E′D′F,过点E′作E′G⊥BC′于点G,易得△ABP′∽△E′FP′,由此可得,在Rt△BDD′中,由勾股定理可求出BD′的长,可求出∠BD′D的正切值,设P′F的长,分别表示E′F和E′D′及FG和GD′的长,再根据BD′=13,可建立等式,可得结论.
【解答】解:(1)如图,由题意可得,∠APB=∠EPD,∠B=∠EDP=90°,
∴△ABP∽△EDP,
∴,
∵AB=6.5,BP=4,PD=8,
∴,
∴DE=13;
故答案为:13.
(2)如图2,过点E′作∠E′FD′=∠E′D′F,过点E′作E′G⊥BC′于点G,
∴E′F=E′D′,FG=GD′,
∵AB∥MN,
∴∠ABD′+∠E′D′B=180°,
∴∠ABD′+∠E′FG=180°,
∵∠E′FB+∠E′FG=180°,
∴∠ABP′=∠E′FP′,
又∠AP′B=∠E′P′F,
∴△ABP′∽△E′FP′,
∴即,,
设P′F=4a,则E′F=6.5a,
∴E′D′=6.5a,
在Rt△BDD′中,∠BDD′=90°,DD′=5,BD=BP+PD=12,
由勾股定理可得,BD′=13,
∴cos∠BD′D,
在Rt△E′GD′中,cos∠BD′D,
∴GD′=2.5a,
∴FG=GD′=2.5a,
∵BP′+P′F+FG+GD′=13,
∴4+4a+2.5a+2.5a=13,解得a=1,
∴E′D′=6.5,
∴EE′=DE+DD′﹣D′E′=13+5﹣6.5=11.5.
故答案为:11.5.
36.【分析】如图,连接AC,OC.证明点N在⊙T上,运动轨迹是,过点T作TH⊥AB于H.求出BT,TN,可得结论.
【解答】解:如图,连接AC,OC.
∵C是半圆的三等分点,
∴∠AOC=60°,
∵OA=OC,
∴△AOC是等边三角形,
作△AOC的外接圆⊙T,连接TA=TC,TN,TB.
∵OM⊥PC,
∴CM=PM,
∴NC=NP,
∴∠NPC=∠NCP∠AOC=30°,
∴∠CNM=60°,
∴∠CNO=120°,
∵CNO+∠OAC=180°,
∴点N在⊙T上,运动轨迹是,
过点T作TH⊥AB于H.
在Rt△ATH中,AH=OH=3,∠TAH=30°,
∴TH=AH tan30°,
∴AT=TN=2HN=2,
在Rt△BHT中,BT2,
∵BN≥BT﹣TN,
∴BN≥22,
∴BN的最小值为22.
故答案为:22.
三.解答题
37.【分析】(1)连接DF,AF,根据直径所对的圆周角是直角,得出∠CDF=90°,再根据平行线的判定,得出AB∥DF,再根据平行线的性质,得出∠BAF=∠AFD,再根据同圆或等圆中,同弧或等弧所对的圆周角相等,即可得出结论;
(2)连接BF,AC,根据直径所对的圆周角是直角,得出∠CAF=90°,再根据,得出,再根据等边对等角,得出∠CFA=∠ACF=45°,再根据同弧或等弧所对的圆周角相等,得出∠B=∠ACF=45°,再根据等量代换,得出∠B=∠AFC,再根据相似三角形的判定,得出△ABF∽△AFG,再根据相似三角形的性质,得出AF2=AG AB,然后计算即可得出答案;
(3)①连接AD,根据等腰三角形的判定,得出CA=CG,再根据等边对等角,对顶角相等以及同弧或等弧所对的圆周角相等,得出∠CAG=∠CGA=∠BGF=∠BFG,再根据等角对等边,得出BG=BF,再根据弧与弦的关系,得出AD=BF,进而得出BG=BF=AD,再根据题意,得出,进而得出CD=AB,再根据对称性,得出AE=ED,再根据等腰直角三角形的性质,得出,进而得出,然后变形,即可得出答案;
②连接AO交CE于P,设AE=1,则BG=x,设EG=t根据全等三角形的判定,得出△CPO≌△AGO,再根据全等三角形的性质,得出CP=AG=t+1,再根据线段之间的数量关系,得出CE=EB=t+x,进而得出PE=x﹣1,再根据相似三角形的性质,得出,进而得出,解得,再根据平行线分线段成比例定理,得出,然后代入计算,即可得出答案.
【解答】(1)证明:连接DF,AF,
∵CF是⊙O的直径,
∴∠CDF=90°,
∵AB⊥CD,
∴AB∥DF,
∴∠BAF=∠AFD,
∴;
(2)解:连接BF,AC,
∵CF是⊙O的直径,
∴∠CAF=90°,
∵,
∴,
∴∠CFA=∠ACF=45°,
∴∠B=∠ACF=45°,
∴∠B=∠AFC,
∵∠BAF=∠FAG,
∴△ABF∽△AFG,
∴AF2=AG AB,
∴;
(3)解:①连接AD,
∵点E为AG中点,AB与CD互相垂直,
∴CA=CG,
∴∠CAG=∠CGA=∠BGF=∠BFG,
∴BG=BF,
∵,
∴AD=BF,
∴BG=BF=AD,
又∵,,
∴,
∴CD=AB,
由对称性知,AE=ED,
∴,
∴,
∴,
∴;
②连接AO交CE于P,设AE=1,则BG=x,设EG=t,
∵,
∴AO⊥CF,
∴∠COP=∠AOG=90°,
∴∠OCP+∠OPC=90°,
∵∠APE+∠PAE=90°,
又∵∠OPC=∠APE,
∴∠OCP=∠PAE,即∠OCP=∠OAG,
在△CPO与△AGO中,
,
∴△CPO≌△AGO(AAS),
∴CP=AG=t+1,
由①知CE=EB=t+x,
∴PE=x﹣1,
∵△APE∽△CGE,
∴,
即,
解得,
∵AB∥DF,
∴,
即.
38.【分析】(1)把解析式化成顶点时,即可求出二次函数图象的顶点坐标;
(2)①当t=2时,则二次函数y=x2﹣4x+2,0≤m≤3,即可求得n的取值范围是﹣2≤n≤2;
②由题意可知n的最小值为﹣t,最大值为x=t﹣2时的值,即n的最大值为(t﹣2)2﹣2t(t﹣2)+t2﹣t=4﹣t,可得n的最大值与最小值之差=4﹣t+t=4.
【解答】解:(1)∵y=x2﹣2tx+t2﹣t=(x﹣t)2﹣t,
∴该二次函数图象的顶点坐标为(t,﹣t);
(2)①当t=2时,则二次函数y=x2﹣4x+2,0≤m≤3.
∵y=x2﹣4x+2=(x﹣2)2﹣2,
∴抛物线开口向上,x=2时有最小值﹣2,
当x=0时,y=2,
∴n的取值范围是﹣2≤n≤2;
②二次函数y=x2﹣2tx+t2﹣t的图象开口向上,对称轴为直线x=t,顶点坐标为(t,﹣t),
∵点P(m,n)在该二次函数图象上,其中t﹣2≤m≤t+1.
∴n的最小值为t,最大值为x=t﹣2时的值,即n的最大值为(t﹣2)2﹣2t(t﹣2)+t2﹣t=4﹣t,
∴n的最大值与最小值之差=4﹣t+t=4,
∴n的最大值与最小值之差不会随着t的变化而变化,n的最大值与最小值之差是4.
39.【分析】(1)利用同弧所对的圆周角相等,通过等量代换证明即可;
(2)①过点D作DG⊥BC交延长线于点G,连接OD,设圆的半径为r,证明四边形BODG是正方形,再求解即可;
②设圆的半径为r,则ADr,AC=2r,过E点作EH⊥BC交于H点,则tan∠EBC=tan∠ACD,结合tan∠BCD,推导出HC=3EH,CEEH,即可得到;
(3)连接AE,证明△ABE∽△CDA和△FAE∽△FCA,推导y与x的关系即可.
【解答】(1)证明:∵,
∴∠D=∠ABE,
∵∠ABC=90°,AD⊥AC,
∴∠D+∠ACD=∠ABE+∠CBE=90°,
∴∠ACD=∠EBC;
(2)解:①过点D作DG⊥BC交延长线于点G,连接OD,
设圆的半径为r,
∵△ABC是等腰直角三角形,∠DAC=90°,
∴△AOD是等腰直角三角形,
∴四边形BODG是正方形,
∴DG=BG=r,BC=2r,
∴tan∠BCD;
②设圆的半径为r,则ADr,AC=2r,
过E点作EH⊥BC交于H点,
∴tan∠EBC=tan∠ACD,
∴BH=2EH,BEEH,
∵tan∠BCD,
∴HC=3EH,CEEH,
∴;
(3)连接AE,
∵AB是圆的直径,
∴∠AEB=90°=∠DAC,
∵∠ADC=∠ABE,
∴△ABE∽△CDA,
∴x,
∵∠FAE=∠FCA,∠AFE=∠CFA,
∴△FAE∽△FCA,
∴x,
∴x2,
∴yx2﹣1.
40.【分析】(1)根据弦,圆周角直角的关系得出∠ADC=∠BCD,即可得出∠ECD=∠EDC=45°,再利用对角线互相垂直的四边形的面积等于对角线乘积的一半即可求面积;
(2)延长BM交⊙O于点E,连结DE,证明△AMB∽△EMD,根据对应边成比例即可解答;
(3)①先证明△ABE∽△DCE.设AE=x,利用对应边成比例表示出DE,BE,根据勾股定理列出方程,解出x即可解答;
②设AB的长度为a,AE=x,根据相似三角形的性质表示出DE,BE,利用勾股定理求出a的最小值,进而求出x,再证明△APC∽△BPD,得出解答.
【解答】(1)解:∵AC⊥BD,
∴∠CED=90°,
∵AC=BD,
∴∠ADC=∠BCD,
∵∠ADB=∠ACB,
∴∠ECD=∠EDC=45°,
∴四边形ABCD的面积为AC BD=8,
故答案为:45°,8;
(2)证明:延长BM交⊙O于点E,连结DE,
∵∠A=∠E,∠AMB=∠EMD,
∴△AMB∽△EMD,
∴,
∴BM EM=AM DM,
∵OM⊥BM,
∴BM=EM,
∴BM2=AM DM;
(3)解:①设AE=x,
∵∠AEB=∠DEC=90°,∠BAC=∠BDC,
∴△ABE∽△DCE.
∴,
∴,
∵BD=4,
∴.
∴,解得:.
∵当 时, (舍去),
∴x,
∴.
∴,
∴;
②设AB的长度为a,AE=x,
∵△ABE∽△DCE.
∴,
∴,
∴,
∴,
∵,
∴a2≥4.
∵a>0,
∴a≥2,
∴a有最小值2.即AB的长度最小值为2.
∴,解得:,
∴DE=3∴BE=1,
∴,
∴.
∵∠APB=∠CPD=90°,
∴∠APC=∠BPD,
∵∠APB=∠AEB=90°,
∴∠PAC=∠PBD,
∴△APC∽△BPD,
∴,
∴tan∠ABP.
41.【分析】(1)设交点式y=a(x﹣3)(x+1),即y=ax2﹣2ax﹣3a,所以﹣3a=﹣3,然后求出a得到抛物线解析式;
(2)先抛物线的顶点坐标为(1,﹣4),再利用待定系数法求出直线BC的解析式为y=x﹣3,设D(t,t2﹣2t﹣3)(0<t<3),则P(t,t﹣3),所以DP=﹣(t)2,则当t,DP最大,由于抛物线的顶点坐标为(1,﹣4),于是可判断小明的说法不正确.
【解答】解:(1)∵抛物线y=ax2+bx﹣3(a≠0)的图象与x轴交于A(﹣1,0)、B(3,0)两点,
∴抛物线解析式可设为y=a(x﹣3)(x+1),
即y=ax2﹣2ax﹣3a,
∴﹣3a=﹣3,
解得a=1,
∴抛物线解析式为y=x2﹣2x﹣3;
(2)小明的说法不正确.
理由如下:
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的顶点坐标为(1,﹣4),
当x=0时,y=x2﹣2x﹣3=﹣3,则C(0,﹣3),
设直线BC的解析式为y=mx+n,
把B(3,0),C(0,﹣3)分别代入得,
解得,
∴直线BC的解析式为y=x﹣3,
设D(t,t2﹣2t﹣3)(0<t<3),则P(t,t﹣3),
∴DP=t﹣3﹣(t2﹣2t﹣3)=﹣t2+3t=﹣(t)2,
∴当t,DP最大,
而抛物线的顶点坐标为(1,﹣4),
∴小明的说法不正确.
42.【分析】(1)用待定系数法即可解决问题.
(2)用b去表示c,再将点(3,2)坐标代入即可.
(3)根据m>0,n<0及抛物线经过点(3,0)可判断出抛物线对称轴所处位置的范围,再根据抛物线开口方向及(﹣2,y1)和(5,y2)离对称轴的远近即可解决问题.
【解答】解:(1)将(1,2)和(2,1)代入函数解析式得,
,
解得.
所以该函数的表达式为y=x2﹣4x+5.
证明:(2)将(1,m)和(2,n)代入函数解析式得,
,
又因为m=2n,
则2×②﹣①得,
c=﹣3b﹣7,
所以二次函数的解析式为y=x2+bx﹣3b﹣7,
将x=3代入函数解析式得,
y=9+3b﹣3b﹣7=2,
所以该函数的图象经过点(3,2).
(3)y1>y2.
因为m>0,n<0,
所以x=1时,y>0;x=2时,y<0,
则抛物线与x轴的一个交点在(1,0)和(2,0)之间.
又因为抛物线经过点(3,0),
所以抛物线的对称轴在直线x=2的右侧,在直线x=2.5的左侧.
因为点(﹣2,y1)到对称轴的距离在4到4.5之间,
点(5,y2)到对称轴的距离在2.5到3时间,
显然点(﹣2,y1)到对称轴的距离大于点(5,y2)到对称轴的距离,
又因为抛物线的开口向上,
所以y1>y2.
43.【分析】(1)将(0,﹣6)代入函数表达式,求出a的值即可解决问题.
(2)证明b2﹣4ac>0即可解决问题.
(3)用含a的代数式表示出y1和y2,再利用作差法即可解决问题.
【解答】(1)解:将点(0,﹣6)代入函数解析式得,
﹣2a﹣2=﹣6,
解得a=2,
所以函数的表达式为y=2x2+4x﹣6.
则,
将x=﹣1代入函数解析式得,
y=2﹣4﹣6=﹣8.
所以函数图象的顶点坐标为(﹣1,﹣8).
(2)证明:因为Δ=(a+2)2﹣4a(﹣2a﹣2)=9a2+12a+4=9()2,
又因为a,
所以Δ>0,
所以二次函数的图象与x轴必有两个不同的交点.
(3)解:将A,B两点坐标代入函数解析式得,
,
,
两式相减得,
,
又因为x1+x2=3,
所以y1﹣y2=2(2a+1)(x1﹣x2).
又因为当x1<x2时,总有y1>y2,
所以2a+1<0,
解得.
所以a的取值范围是:a.
44.【分析】(1)证明△AOB≌△AOC,即可得出OA平分∠BAC;
(2)①连结BF,证明△ABF≌△ACF,推出∠ABE=∠ABF,即可求证;②连结BO并延长交⊙O于M,连结CM,根据,即可求出半径的长;③延长BD交⊙O于M,连结CM,利用相似三角形的性质和判定即可求解.
【解答】(1)证明:连结OB、OC,
∵OA=OA,OB=OC,AB=AC,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO;
(2)①连结BF,
∵AF=AF,∠BAF=∠CAF,AB=AC,
∴△ABF≌△ACF(SAS),
∴∠ACF=∠ABF,BF=CF,
又∵∠ACF=∠ABE,BE=CF,
∴∠ABE=∠ABF,BE=BF,
∴BG⊥EF,且EG=FG;
②连结BO并延长交⊙O于M,连结CM,
则∠BCM=90°,
由EF=2,CF=3知EG=FG=1,BF=CF=3,
∴,,
∴,
∴,即半径为;
③延长BD交⊙O于M,连结CM,
∵∠DAO=∠OAB=∠ABO,∠ADO=∠BDA,
∴△ADO∽△BDA,
∴,
即AD2=DO DB,
∵∠DBC=90°﹣∠M=90°﹣∠BAC=∠DCH∠CDH=∠BDC,
∴△DCH∽△DBC,
∴,即CD2=DH DB,
又∵DH=HO,
∴,
∴,
∵AO⊥BC,CM⊥BC,
∴AO∥CM,
∴△DCM∽△DAO,
∴,即,
∴,,
∴.
45.【分析】(1)根据“倍系直线”的定义得直线为yx﹣b,将点A(﹣2,0)代入yx2+bx﹣3可得b=﹣1,联立抛物线yx2﹣x﹣3与直线yx+1可得点C的坐标;
(2)求出点D的坐标为(4,﹣3),点M的坐标为(4,3),则AO是DM的垂直平分线,AM=AD,根据等腰三角形的性质即可得并AO平分∠CAD;
(3)由点E、M、C的坐标可得M是CE的中点,由FE=2FM得FMMC,可得,证明△GEF∽△DMF,可得,即可得△GEF与△CDF的面积之比.
【解答】(1)解:∵直线y=2ax﹣b为抛物线y=ax2+bx+c(a,b,c为常数且a≠0)的“倍系直线”.
∴yx2+bx﹣3的“倍系直线”为yx﹣b,
将点A(﹣2,0)代入yx2+bx﹣3得1﹣2b﹣3=0,
解得b=﹣1,
∴该抛物线的“倍系直线”的函数表达式为yx+1,抛物线为yx2﹣x﹣3,
联立抛物线yx2﹣x﹣3与直线yx+1得,
解得或,
∴点C的坐标为(8,5).
故答案为:﹣1,yx+1,(8,5);
(2)证明:∵抛物线yx2﹣x﹣3与y轴交于点B,
∴B(0,﹣3),
∵BD∥x轴,交抛物线yx2﹣x﹣3于点D,
∴点D的坐标为(4,﹣3),
∵DM∥y轴,交AC于点M,直线AC为yx+1,
∴点M的坐标为(4,3),
∴AO是DM的垂直平分线,
∴AM=AD,
∴AO平分∠CAD;
(3)解:∵AC交y轴于点E,直线AC为yx+1,
∴E(0,1),
∵点M的坐标为(4,3),点C的坐标为(8,5).
∴M是CE的中点,
∴CM=EM,
∵FE=2FM,
∴FMEMMC,
∴FMCF,
∴,
∴S△CDF=4S△DFM,
∵DM∥y轴,
∴△GEF∽△DMF,
∴,
∴S△GEF=4S△DMF,
∴△GEF与△CDF的面积之比为1:1.
46.【分析】(1)通过等量代换求证即可;
(2)①通过证明∠BEC=∠ABC,利用等角对等边可得BC=EC,即可证明EC=DC;
②延长CE交⊙O于点P,易得△CBF∽△CPB,设CF=3k,DC=CE=4k,则EF=k,由BC2=CF CP,可得,,,cos∠∠DBC=cos∠BAC,,设DF=y,再由△FBP∽△FCD,得到,,则或;
(3)过点F作FH∥AB,交AC于点H,设AH=HG=a,由FH2=HG HC,求出 (舍)或,即可得.
【解答】(1)证明:∵∠ACD=∠ACE,
又∵∠ABD=∠ACD,
∴∠ACE=∠ABD;
(2)①证明:∵C是BD中点,
∴∠BAC=∠DAC,BC=DC,
∴∠BAC=∠DAC=∠DBC,
∴∠BEC=∠BAC+∠ACE,∠ABC=∠ABD+∠DBC,
∴∠BEC=∠ABC,
∴BC=EC,
∴EC=DC;
②解:延长CE交⊙O于点P,连接PB,
∵∠BDC=∠P,
∴△CBF∽△CPB,
设CF=3k,DC=CE=BC=4k,则EF=k,由BC2=CF CP,
∴,则有 ,
过点C作CH⊥BD交于H点,
∵tan∠BDC,
∴,
∴DHk,
∴BDk,
∵△FBP∽△FCD,
∴,
设DF=y,
∴,
解得 ,
∴或;
(3)解:过点F作FH∥AB,交AC于点H,设AH=HG=a,
∴FH2=HG HC,
∴1=a(3﹣a),
解得 (舍)或,
∴.
47.【分析】(1)通过条件证明∠BOD=∠COD,即可得到结论;
(2)连OC、BC、BD,BC与OD交于点Q,证明△BOQ∽△BAC,用含y的式子表示OQ和QD,在Rt△COQ和Rt△BDQ中运用勾股定理即可得到x与y的关系式;
(3)利用(2)的关系式求出r,连接OE,BE,证明三角形POE是等腰三角形,得到PE的长,在Rt△BPE中,运用勾股定理求出BE,在Rt△ABE中运用正弦函数的定义即可得到sin∠PAB的值.
【解答】(1)证明:连接OC,
∵OD∥AC,
∴∠BAC=∠BOD,∠OCA=∠COD,
∵OA=OC,
∴∠BAC=∠OCA,
∴∠BOD=∠COD,
∴;
(2)解:连OC、BC、BD,BC与OD交于点Q,
∵OD∥AC,
∴△BOQ∽△BAC,
∴,
∵AB=2OB,
∴,BQ=CQ,
∵OD=r,
∴QD=OD﹣OD,
∵OD是半径,BQ=CQ,
∴OD⊥BC,
在Rt△COQ和Rt△BDQ中,
由勾股定理得CQ2=OC2﹣OQ2,BQ2=BD2﹣QD2,
∵BQ=CQ,
∴OC2﹣OQ2=BD2﹣QD2,即,
整理得x2+ry﹣2r2=0;
(3)解:连接OE,BE,
把,y=9代入x2+ry﹣2r2=0,
得5+9r﹣2r2=0,
解得(不合题意,舍去),r=5,
∵OA=OE,
∴∠PAB=∠AEO=2∠APO,
∵∠AEO是△POE的外角,
∴∠AEO=∠APO+∠POE,
∴∠APO=∠POE,
∴OE=PE=5,
∵AB是直径,
∴∠AEB=∠BEP=90°,
在Rt△BPE中,
∵PE=5,PB,
∴BE,
在Rt△ABE中,
∵BE=6,AB=2r=10,
∴sin∠PAB.
48.【分析】(1)利用圆周角定理,等腰直角三角形的判定与性质解答即可;
(2)利用垂径定理,三角形的中位线定理,等腰直角三角形的判定与性质,全等三角形的判定与性质解答即可;
(3)设OG=k,则HG=3k,利用垂径定理和勾股定理求得k值;连接EG,CH,利用(2)的结论,三角形的中位线定理和等腰直角三角形的性质和相似三角形的判定与性质解答即可得出结论.
【解答】解:(1)∵AC为直径,
∴∠ABC=∠ADC=90°,
∵∠BAC=∠BDC=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=2,
∴ACAB=2.
∴⊙O的半径AC;
(2)∵过点O作GH⊥CD,
∴GD=GC,
∵OA=OC,
∴OG为△CAD的中位线,
∴OGAD.
∵OG⊥DC,AD⊥DC,
∴OG∥AD,
∴∠ADE=∠OHE.
在△ADE和△OHE中,
,
∴△ADE≌△OHE(ASA),
∴AD=OH.
∴OGOH,
∴OH:OG=2;
(3)∵HG=3OG,
设OG=k,则HG=3k,
∴AD=OH=2k,DG=GC=3k,
∴CD=6k.
∵AD2+CD2=AC2,
∴,
解得:k=±(负数不合题意,舍去).
∴OH=AD=2k.
连接EG,CH,如图,
∵HG=3OG,
∴OH:OG=2,
由(2)知:E为DH的中点,
∵G为CD的中点,
∴EG为△DCH的中位线,
∴EG∥CH,
∵EG⊥BD,
∴CH⊥BD,
∴∠CHB=∠ADC=90°,
∵∠DBC=∠DAC,
∴△BHC∽△ADC,
∴,
∴,
∴BH.
∵∠BDC=45°,HG⊥CD,CH⊥BD,
∴∠DHG=∠GHC=45°,
∴∠BHQ=∠DHG=45°,
∴∠BHQ=∠GHC.
∵∠QBH=∠QBA+∠ABD=90°+∠ABD,∠HOC=∠OGC+∠ACD=90°+∠ACD,∠ACD=∠ABD,
∴∠QBH=∠HOC,
∴△QBH∽△COH,
∴,
∴,
∴BQ=1.
49.【分析】(1)通过证明△DCG和△BCE(SAS)全等,得到DG=BE.
(2)通过证明△DCG∽△BCE得到,所以DGBE.∠BEC=∠DGC.延长BE、GD相交于点H.因为矩形ECGF,所以∠FEC=∠FGC=90°,所以∠HEF
+∠BEC=180°﹣∠FEC=90°,∠FGH+∠DGC=90°,所以∠H=∠F=90°,所以DG⊥BE.
(3)作EN⊥BC于N,GM⊥BC交BC的延长线于M.首先证明点G的运动轨迹是线段GM,将2BG+BE的最小值转化为求2(BG+DG)的最小值.
【解答】解:(1)DG=BE.
理由:
∵正方形ABCD,
∴CD=CB∠BCD=90°,
∵正方形ECGF,
∴CG=CE∠ECG=90°,
∴∠ECG=∠BCD=90°,
∴∠DCG=∠BCE,
在△DCG和△BCE中,
,
∴△DCG≌△BCE(SAS),
∴DG=BE.
(2)DGBE.
理由如下:延长BE、GD相交于点H.
∵矩形ECGF、矩形ABCD,
∴∠ECG=∠BCD=90°,
∴∠DCG=∠BCE,
∵CD:CB=3:6=1:2,CG:CE=1:2,
∴CD:CB=CG:CE,
∵∠DCG=∠BCE,
∴△DCG∽△BCE,
∴,∠BEC=∠DGC,
∴DGBE.
(3)作EN⊥BC于N,GM⊥BC交BC的延长线于M,
∴∠ENC=∠CMG=90°.
∵∠ECN+∠CEN=90°,∠ECN+∠GCM=90°,
∴∠CEN=∠GCM.
∴△ECN∽△CGM,
∴2,
∵EN=AB=3,
∴CM=1.5,
∴点G的运动轨迹是直线MG,
作点D关于直线GM的对称点G′,连接BG′交GM于G,此时BG+GD的值最小,最小值=BG′.
由(2)知,DGBE,
∴BE=2DG,
∴2BG+BE=2BG+2DG=2(BG+DG),
∴2BG+BE的最小值就是2(BG+DG)的最小值.
∵BG′3,
∴2BG+BE的最小值为6.
50.【分析】(1)求AC的长度,证明△ABC是等腰直角三角形,得到∠A的度数,根据等腰三角形的性质求出角度;
(2)证明△COE是直角三角形,求出CE的长度,证明△ACE∽△DCA,从而求出CD的长度;
(3)根据题意分当E在线段OB上和当点E在线段OA上两种情况,分别画出对应的图,求出CE和BE的长度,根据相似三角形的性质求出△BCD的面积.
【解答】解:(1)∵△ABC 内接于⊙O,
∴∠ACB=90°,
在Rt△ABC中,
∵AB=12,BC,
∴,
∴△ABC是等腰直角三角形,
∴∠A=45°,
∵AE=AC,
∴∠ACD;
(2)连接OC,AD,
∵直径AB=12,
∴OA=OB=OC=6,
∴OE=OA﹣AE=2,
∵∠CAB=45°,OA=OC,
∴∠AOC=90°,
在Rt△COE中,
∵OE=2,OC=6,
∴,
∵,
∴∠ADC=∠ABC=∠BAC=45°,
∵∠ACE=∠DCA,
∴△ACE∽△DCA,
∴,
∴CD;
(3)①当E在线段OB上时,连接OC,连接BM交CD于点N,
∵CD∥AM,
∴∠BNE=∠BMA=∠BOC=90°,
∵∠BEN=∠CEO,
∴∠ECO=∠ABM=∠ACM,
∴tan∠ECO=tan∠ACM,
∵OC=6,
∴OE=OC tan∠ECO=2,
∴EC,BE=6﹣2=4,
∴,
由(2)得△BCD∽△ECB,
∴,
∴;
②当点E在线段OA上时,
同理tan∠ECO=tan∠ACM,
∴OE=OC tan∠ECO=2,
∴CE,BE=6+2=8,
∴,
∵△BCD∽△ECB,
∴,
∴.
综上所述,△BCD的面积的面积为.
51.【分析】(1)利用相似三角形的判定定理解答即可;
(2)连接CE,利用全等三角形的判定与性质得到∠ECD=90°,过F作FM⊥CD于点M,过F作FN⊥CE于点N,设FN=t,则CM=FM=t,利用正方形的判定与性质,直角三角形的边角关系定理解答即可;
(3)在BC上截取CH=CE交BC于点H,利用直角三角形的边角关系定理,等腰三角形的性质和三角形的中位线定理解答即可.
【解答】解:(1)∵AB=AC,AD=AE,
∴,
∵∠BAD=∠CAE,
∴∠BAC=∠DAE,
∴△ABC∽△ADE;
(2)连接CE,如图,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE=45°,
∵AB=AC,
∴∠B=∠ACB=45°,
∴∠ACE=∠ACB=45°,
∴∠ECD=90°,
过F作FM⊥CD于点M,过F作FN⊥CE于点N,
∴FM=FN,FM=CM,CN=FN,
∴四边形FMCN是正方形,
设FN=t,则CM=FM=t,
∵,tan∠EDC,
∴,
∴MD=2t,
∴DC=3t.
∵FN∥CD,
∴△ENF∽△ECD.
∴,
∴;
(3)在BC上截取CH=CE交BC于点H,如图,
∵AB=AC,M为BC的中点,
∴AM⊥BC,BMBC=3,
∵AB=2,
∴cosB,
∴∠B=30°.
由(2)知:△ABD≌△ACE,
∴∠B=∠ACB=∠ACE=30°,BD=EC,
∴∠ECH=60°,EH⊥AC,
∴△CEH是等边三角形,
∴EH=CH=CE=BD,
∵M是BC中点,
∴BM=CM,
∴BM﹣BD=CM﹣CH,
即DM=MH,
∴M是DH中点,
∵N是DE中点,
∴MN是△DHE的中位线,
∴MNEH,
∴,
∴CE=2,
∴EH=2,
∴MN=1,
∵DM=BM﹣BD=1,AMAB,
∴AD2,
∵AD=AE,N为DE的中点,
∴AN⊥DE,
∵∠ADE=∠ABC=30°,
∴ANAD=1,
∴△AMN的周长为AM+AN+MN.
52.【分析】(1)根据垂径定理和同弧所对的圆周角相等,能够推导出∠AFC=∠CFE,∠ACF=∠FEA,即可证明三角形相似;
(2)连接BF,由题意可得AB=2AC,在Rt△ABC中,利用勾股定理求出AC=2,再由tan∠ACB=2,得到AD=2CD,在Rt△ACD中,利用勾股定理求出CD=2,AD=4,则ED=AD=4,证明△BFC∽△HDC,求得HD,则HE=ED+HD,再由△AFC∽△HFE,求出EF;
(3)设OC=r,则BC=2r,CDr,ADr,分两种情况讨论:①当点G在线段OD上时,x,则OG=xr,CG=(1﹣x)r,BG=(1+x)r,过点G作GM⊥CF交于点M,推导出FM=2GM,再由GM∥BE,推导出,,从而求出DH,AH=AD﹣HDr,即可求y;②当点G在线段OB上时,同理可得y.
【解答】(1)证明:∵BC是⊙O的直径,AD⊥BC,
∴,
∴∠AFC=∠CFE,
∵,
∴∠ACF=∠FEA,
∴△AFC∽△HFE;
(2)解:连接BF,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵tan∠ACB=2,
∴AB=2AC,
在Rt△ABC中,BC=10,
∴AC=2,
∵AD⊥BC,
∴∠ADC=90°,
∵tan∠ACB=2,
∴AD=2CD,
在Rt△ACD中,AD2+CD2=AC2,则CD=2,AD=4,
∴ED=AD=4,
∵BC是⊙O的直径,
∴∠BFC=90°,
∵BC=10,CF=8,
∴BF=6,
∵∠BFC=∠HDC=90°,∠FCB=∠DCH,
∴△BFC∽△HDC,
∴,
∴HD,
∴HE=ED+HD,
∵△AFC∽△HFE,
∴,
∴EF;
(3)解:设OC=r,则BC=2r,
∵tan∠ACB=2,
∴AD=2CD,BD=2AD,
∴CDr,ADr,
①当点G在线段OD上时,
∵x,
∴OG=xr,CG=(1﹣x)r,BG=(1+x)r,
过点G作GM⊥CF交于点M,
∴∠GMF=90°,
∵∠ADC=90°,∠CAE=∠CFE,
∴∠FGM=∠ACB,
∴tan∠FGM=tan∠ACB=2,
∴FM=2GM,
∵∠GMC=∠BFC=90°,
∴GM∥BE,
∴,
∴,即,
∵,
∴,
∴DH,
∴AH=AD﹣HDr,
∴,
∴y;
②当点G在线段OB上时,同理可得y;
综上所述:当点G在线段OD上时,y;当点G在线段OB上时,y.
53.【分析】(1)如图1,延长AC至点E,使得CE=AB,连接BD,CD,DE,根据圆内接四边形的性质得到∠B=∠DCE,得到BD=CD,根据全等三角形的性质得到∠E=∠BAD=60°,推出△ADE是等边三角形,于是得到AD=AB+AC;
(2)如图2,延长AC至点E,使得CE=AB,连接BD,CD,DE,根据圆内接四边形的性质得到∠B=∠DCE,得到BD=CD,根据全等三角形的性质得到∠E=∠BAD=45°,推出△ADE是等腰直角三角形,于是得到AD=AB+AC;
(3)如图3,延长AC至点E,使得CE=AB,连接BD,CD,DE,根据圆内接四边形的性质得到∠B=∠DCE,得到BD=CD,根据全等三角形的性质得到∠E=∠BAD=θ,推出△ADE是等腰三角形,过D作DH⊥AE于H,根据三角函数的定义得到结论.
【解答】(1)解:AD=AB+AC;
证明:如图1,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=120°,AD平分∠BAC,
∴∠BAD=∠DAC=60°,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=60°,
∴∠E=∠BAD=∠ADE=60°,
∴△ADE是等边三角形,
∴AE=AD,
即AD=AB+AC;
故答案为:AD=AB+AC;
(2)证明:如图2,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=90°,AD平分∠BAC,
∴∠BAD=∠DAC=45°,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=45°,
∴∠E=∠BAD=∠ADE=45°,
∴△ADE是等腰直角三角形,
∴AEAD,
即AB+ACAE;
(3)解:如图3,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=2θ,AD平分∠BAC,
∴∠BAD=∠DAC=θ,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=θ,
∴∠E=∠BAD=∠ADE=θ,
∴AD=DE,AE=AB+AC,
过D作DH⊥AE于H,
∴AH=EHAE(AB+AC),
∴cosθ.
54.【分析】(1)根据角平分线的定义,通过外角性质及圆周角定理,即可证明∠DCI=∠DIC,从而证得结论;
(2)首先由垂径定理,可得,根据圆周角定理及(1)可得DI=DC=BD,,再根据角平分线的定义及圆周角定理,即可证得△BDP∽△ADB,根据相似三角形的性质即可求解;
(3)过C作CH⊥BD于点H,延长BF交⊙O于点M,作直径CP,连接BP,CH,MD,设CH=m,则CB=CD=CG=3m,,再根据平行线的性质及圆周角定理,可证得∠BFC=∠ABD,∠BCF=∠ADB,可证得:△BCF∽△ADB,根据相似三角形的性质可得,FG=|CG﹣CF|=|3m﹣2m2|,再证得MD=BC=3m,求得:m≤2,再运用二次函数的图象和性质即可求得答案.
【解答】(1)证明:∵△ABC的三条角平分线交于点I,
∴∠BAD=∠CAD,∠ACI=∠BCI,
∴∠BCD+∠BCI=∠CAD+∠ACI,即∠DCI=∠DIC,
∴DC=DI;
(2)解:∵OI⊥AD,
∴AI=DIAD,
由(1)知DC=DI,
∴DI=DC=BD,
∴.
∵△ABC的三条角平分线交于点I,
∴∠BAD=∠CAD,
又∵∠BDP=∠ADB,
∴△BDP∽△ADB,
∴,
∴;
(3)解:如图:过C作CH⊥BD于点H,延长BF交⊙O于点M,作直径CP,连接BP,CH,MD,
∵AC平分∠BAD,BG平分∠ABD,
∴∠BAC=∠DAC=∠CBD=∠CDB,
同(1)可证得BC=DC=CG,
∴,
设CH=m,则CB=CD=CG=3m,,
∴,
∵BF∥CD,
∴∠BFC=∠ACD=∠ABD,
又∵∠BCF=∠ADB,
∴△BCF∽△ADB,
∴,
∴,
∴,
∴FG=|CG﹣CF|=|3m﹣2m2|,
又∵点F在线段AC上,
∴点M一定在上,
∵BF∥CD,
∴MD=BC=3m,
∴MD≤AD,即3m≤6,
解得:m≤2,
∵直径PC3BC=9m≥AD,
∴m,
即m≤2,
如图,作出FG=|3m﹣2m2|的图象,
∴由图象知:
当m时,FG=2;当m=2时,FG=86;
∵86>2,
∴FG最大值=86,此时圆O的半径为PCm=9.
55.【分析】(1)根据圆的内接四边形性质得:∠ADC+∠ABC=180°,结合已知∠ADF+∠ABC=90°,进而得出结果;
(2)可证明△BDG≌△CFD,从而CF=BD,进一步得出结论;
(3)①根据S△BDG=3S△DEH得出S△CFD=3S△DEG,从而EHCF,可证得△DEH∽△FED,从而DE2=EH EF,从而得出EF的值,可证得△ABE∽△CED,从而得出BE DE=CE AE,进一步得出结果;
②作DW⊥AC于W,作直径CV,连接DV,可得出AD=BD=2,△ABE∽△CED,从而,进而得出CE,AE=2,设EW=x,则AW=2﹣x,根据勾股定理得出DW2=DE2﹣EW2=AD2﹣AW2,,从而12﹣x2=22﹣(2﹣x)2,从而得出x的值,进而计算出CD的长,根据sinV=sin∠ACD得出,进一步得出结果.
【解答】(1)解:∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠CDF+∠ADF+∠ABC=180°,
∵∠ADF+∠ABC=90°,
∴∠CDF=90°;
(2)证明:∵DG⊥AB,
∴∠BGD=90°,
∵∠CDF=90°,
∴∠BGD=∠CDF,
∵,
∴∠ABD=∠ACD,
∵BG=CD,
∴△BDG≌△CFD(ASA),
∴CF=BD,
∵点E是BD的中点,
∴BD=2DE,
∴CF=2DE;
(3)①解:由(2)知:△BDG≌△CFD,CF=BD=2,∠BDG=∠CFD,
∵S△BDG=3S△DEH,
∴S△CFD=3S△DEG,
∴EHCF,
∵∠DEH=∠FED,
∴△DEH∽△FED,
∴DE2=EH EF,
∴12EF,
∴EF,
∴CE=CF﹣EF,
∵∠ABD=∠ACD,∠AEB=∠CED,
∴△ABE∽△CED,
∴BE DE=CE AE,
∴1×1AE,
∴AE=2,
∴AC=CE+AE;
②解:如图,
作DW⊥AC于W,作直径CV,连接DV,
∵DO⊥AB,
∴BG=AG,
∴AD=BD=2,
由①知:△ABE∽△CED,
∴,
∴AB=2BC,BC=CD,
∴
∴CE,AE=2,
设EW=x,则AW=2﹣x,
∵DW2=DE2﹣EW2=AD2﹣AW2,
∴12﹣x2=22﹣(2﹣x)2,
∴x,
∴EW,DW,
∴CW=EW+CE,
∴CD,
∵sinV=sin∠ACD,
∴,
∴,
∴CV,
∴⊙O的半径为:.
56.【分析】(1)证明∠ADC=90°即可解决问题.
(2)如图1中,作BM⊥DA交DA的延长线于M,BN⊥CD于N.利用全等三角形的性质证明四边形DMBN是正方形,证明AM=CN,推出DA+DC=2DM,求出DM即可解决问题.
(3)结论:AE2=2DB2+CD2.如图2中,作BM⊥BE,使得BM=BE,连接EM,CM.利用全等三角形的性质证明AE=CM,再利用勾股定理即可得出结论.
【解答】(1)证明:如图1中,
∵∠BAC=∠BDC=45°,∠ADB=45°,
∴∠ADC=∠ADB+∠BDC=90°,
∴AC是⊙O的直径.
(2)解:如图1中,作BM⊥DA交DA的延长线于M,BN⊥CD于N.
∵∠BDA=∠BDC=45°,BM⊥DM,BN⊥DC,
∴BM=BN,
∵AC是直径,
∴∠ABC=90°,
∴∠BAC=∠BCA=45°,
∴BA=BC,
∵∠M=∠BNC=∠BND,BD=BD,
∴Rt△BDM≌Rt△BDN(HL),Rt△BMA≌Rt△BNC(HL),
∴DM=DN,AM=CN,
∵∠M=∠BND=∠MDN=90°,
∴四边形BMDN是矩形,
∵BM=BN,
∴四边形BMDN是正方形,
∴BM=DM,
∴DA+DC=DM﹣AM+DN+CN=2DM=5,
∴DM=BM,
∴BDDM=5.
故答案为5.
(3)解:结论:AE2=2DB2+CD2.
如图2中,作BM⊥BE,使得BM=BE,连接EM,CM.
∵∠ABC=∠EBM=90°,
∴∠ABE=∠CBM,
∵BA=BC,BE=BM,
∴△ABE≌△CBM(SAS),
∴AE=CM,
∵∠BEC=∠BDC=∠BEM=45°,
∴∠CEM=90°,
∴CM2=EM2+EC2,
∴EM2=2BE2=2BD2,EC=CD,
∴AE2=2DB2+CD2.
57.【分析】(1)根据题意设二次函数表达式为y=a(x+1)(x﹣4),将C(0,3)代入二次函数得:a×1×(﹣4)=3,求出a的值,即可得到答案;
(2)直接根据二次函数的图象观察即可得到答案;
(3)用待定系数法求出直线BC的解析式,设,则点,则,当当m=2时,DEmax=3,易证△DFE∽△BOC,从而得到,因此计算即可得到答案.
【解答】解:(1)由交点式设二次函数表达式为y=a(x+1)(x﹣4),
把C(0,3)代入二次函数得:a×1×(﹣4)=3,
解得:,
∴二次函数表达式为;
(2)由(1)得,二次函数解析式为:,
∴对称轴为,
∴对应的点关于对称的点为,
∵二次函数的图象上若有两点,(m,y2)且y1<y2,
∴由图象可得m的取值范围为;
(3)设直线BC的解析式为:y=kx+b,
将B(4,0),C(0,3)代入得:,
解得:,
∴直线BC的解析式为,
设,则点,
则,
∴当m=2时,DEmax=3,
∵DE∥y轴,
∴∠DEF=∠OCB,
∵DF⊥BC,
∴∠DFE=∠BOC=90°,
∴△DFE∽△BOC,
∴,
∵OB=4,OC=3,
∴,
∴,
∴,
∴,
当DE最大时,S△DEF最大,即当m=2时,DEmax=3,
此时:.
58.【分析】(1)根据EG∥BD,可得△AEG∽△ABD,从而得到,同理,进而得到,即可;
(2)根据EF∥BC,可得∠C=∠AFE=30°,∠
2024年浙江省宁波市近2年九年级期末精选考试压轴真题集训
一.选择题
1.(2022秋 慈溪市期末)一个大矩形按如图方式分割成五个小矩形后仍是中心对称图形,且矩形ABCD∽矩形BEFG.设矩形ABCD与矩形AHIE的面积分别为m和n,则这个大矩形的面积一定可以表示为( )
A.4m B.2m+3n C.m+3n D.3m+n
2.(2022秋 宁波期末)如图,在平行四边形FBCE中,点J,G分别在边BC,EF上,JG∥BF,四边形ABCD∽四边形HGFA,相似比k=3,则下列一定能求出△BIJ面积的条件( )
A.四边形HDEG和四边形AHGF的面积之差
B.四边形ABCD和四边形HDEG的面积之差
C.四边形ABCD和四边形ADEF的面积之差
D.四边形JCDH和四边形HDEG的面积之差
3.(2023秋 鄞州区期末)如图,在等腰Rt△ABC中,D,E分别在边BC上,,AF⊥AD,FE⊥DE,若已知CD的长,则能求出下列哪个量( )
A.△DEF的周长 B.△DEF的面积
C.△ADF的周长 D.△ADF的面积
4.(2023秋 海曙区期末)如图,在矩形ABCD中,BC=5cm,AB=12cm,点P从C点出发沿对角线AC以1cm/s的速度向点A做匀速运动,点Q从A点出发沿AB以2cm/s的速度向点B做匀速运动,若假设运动时间为t,则当∠QPB=2∠CBP时,t的值为( )
A.2s B. C.s D.
5.(2023秋 宁波期末)如图,矩形ABCD∽矩形GBEF,且点E、A、B三点共线,连结AG,CE,CE与AD交于点H,若要求两个矩形的相似比,则只需知道( )
A. B. C. D.
6.(2023秋 奉化区期末)在Rt△ABC中,∠ACB=90°且边AC:BC=3:2,分别以三边为边作三个正方形(如图所示放置),顶点E恰好在边GF上,边DE与边CF交于点K,构造矩形FGJK,记其面积为S1边BD与边CL交于点M,构造矩形HILM,记其面积为S2,则当S1+S2=30时AB的长为( )
A. B.9 C. D.
7.(2023秋 江北区期末)在平面直角坐标系xOy中,点(x1,y1),(x2,y2)都在抛物线y=ax2﹣2ax+8(a<0)上,且﹣1<x1<2,1﹣m<x2<m+7,若存在x1,x2(x1≠x2),满足y1=y2,则m的取值范围为( )
A.m>﹣3 B.m>﹣2 C.﹣3<m<1 D.﹣2<m<1
8.(2023秋 镇海区校级期末)表中所列x,y的7对值是二次函数y=ax2+bx+c图象上的点所对应的坐标,其中x1<x2<x3<x4<x5<x6<x7.
x … x1 x2 x3 x4 x5 x6 x7 …
y … 7 m 14 k 14 m 7 …
根据表中提供的信息,有以下四个判断:
①a<0;②7<m<14;③当时,y的值是k;④b2≥4a(c﹣k);其中判断正确的有( )个.
A.1 B.2 C.3 D.4
9.(2023秋 余姚市期末)如图,在△ABC中,点D是AB上一点(不与点A,B重合),过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC于点F,点G是线段AE上一点,AG=GE,点H是线段DF上一点,DH=HF,若已知△BGH的面积,则一定能求出( )
A.△ADE的面积 B.△BDF的面积
C.△ABG的面积 D.△CEF的面积
10.(2023秋 北仑区期末)如图,点D是△ABC的边BC上一点,将△ADC沿AD翻折,点C落在点E处,AE与BC相交于点F,若EF=3,CF=17,AF=AD,则FD的长是( )
A.8 B.8.5 C. D.
11.(2022秋 余姚市期末)如图,已知直线l1∥l2∥l3,直线AB分别交三条平行线于点A、E、B,直线CD分别交三条平行线于点C、F、D,直线AB、CD相交于点O,若AE:EO:OB=4:2:7,则下列式子①;②;③;④中,正确的个数有( )
A.4个 B.3个 C.2个 D.1个
12.(2022秋 余姚市期末)如图,抛物线y=x2+bx+c(b,c为常数)经过点A(1,0),点B(0,3),点P在该抛物线上,其横坐标为m,若该抛物线在点P左侧部分(包括点P)的最低点的纵坐标为2﹣m.则m的值为( )
A.m=3 B.
C. D.m=3或
13.(2023秋 鄞州区期末)如图,正△ABC 的边长为1,点P从点B出发,沿B→C→A方向运动,PH⊥AB于点H,下面是△PHB的面积随着点P的运动形成的函数图象(拐点左右两段都是抛物线的一部分),以下判断正确的是( )
A.函数图象的横轴表示PB的长
B.当点P为BC中点时,点H为线段AB的三等分点
C.两段抛物线的形状不同
D.图象上点的横坐标为时,纵坐标为
14.(2021 金华)如图,在等腰Rt△ABC中,∠ACB=90°,以该三角形的三条边为边向外作正方形,正方形的顶点E,F,G,H,M,N都在同一个圆上.记该圆面积为S1,△ABC面积为S2,则的值是( )
A. B.3π C.5π D.
15.(2022秋 鄞州区期末)如图,在矩形ABCD中,点G是边BC的三等分点(BG<GC),点H是边CD的中点,线段AG,AH与对角线BD分别交于点E,F.设矩形ABCD的面积为S,则以下4个结论中:①FH:AF=1:2;②BE:EF:FD=3:5:4;③S1+S2+S3S:④S6=S2+S5.正确的结论有( )
A.1个 B.2个 C.3个 D.4个
16.(2022秋 北仑区期末)如图1是我国古代数学家赵爽用来证明勾股定理的弦图示意图.在图2中,在线段AE和CG上分别取点P和点Q,使AP=CQ,连结PD,PB,QD和QB,则构成了一个“压扁”的弦图.“压扁”的弦图(四边形PBQD)中,4个直角三角形的面积(如图2中的阴影部分)依次记作S1,S2,S3,S4,连结PQ交DG于点T.若AE=2EF=2,S1=S3=S2+S4,则QT的长为( )
A. B. C. D.
17.(2022秋 宁波期末)小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他制了如图2所示的图形,图2中六个形状大小都相同的四边形围成一个圆的内接六边和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为,则该圆的半径为( )cm.
A. B. C.7 D.8
18.(2023秋 慈溪市期末)在一次课题学习中,某学习小组受赵爽弦图的启发,将正方形改编成矩形,如图所示,由两对全等的直角三角形(△AHD≌△CFB,△ABE≌△CDG)和矩形EFGH拼成大矩形ABCD.连结CH,设∠CHG=α,∠CDG=β.若BC=2AB,tanβ=tan2α,则矩形EFGH与矩形ABCD的面积比为( )
A. B. C. D.
二.填空题
19.(2022秋 宁波期末)如图,在正方形ABCD中,点E在AB上,AE=3BE,连接CE,取CE中点F,过F作GF⊥CF且使得GF=CF,连接AG并延长,将△CFG绕点C旋转到△CF'G',当A,G,G'三点共线且AG=3时,KG'= .
20.(2023秋 奉化区期末)如图,点C是上一点,且半径为2,AC=BC,∠ACB=120°,点D在BC上运动,连接AD交BC于点E,则AB的值为 ;当DE:AE的值最大时,CE= .
21.(2022秋 慈溪市期末)如图,△ABC内接于⊙O,BC>AC,AC=4,连接CO并延长至点E,使∠EAC=∠ABC=60°.
(1)⊙O的半径为 .
(2)若BC=2,则BE的长为 .
22.(2022秋 余姚市期末)如图,抛物线y=ax2﹣2ax+3(a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M,P为抛物线的顶点,若直线OP交直线AM于点B,且M为线段AB的中点,则线段PB的长为 .
23.(2023秋 鄞州区期末)如图,Rt△ABC中,∠ACB=90°,AC=8,BC=6,CE是斜边AB上的中线,在直线AB上方作△DEF∽△ABC,DE,FE分别与AC边交于点M,N,当△EMN与△BEC相似时,线段CN长度为 .
24.(2023秋 鄞州区期末)如图,在△ABC中,∠C=90°,AC=8,BC=7,过BC上的动点D作半径为4的⊙A的切线,切点为E、F,若G为EF的中点,则BG的最小值为 .
25.(2023秋 慈溪市期末)如图,△ABC内接于⊙O,高AD,CE相交于点F,若AF=AO,CF=5,BC,则⊙O的半径为 ,AB的长为 .
26.(2022秋 北仑区期末)在△ABC中,若点O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=6,EF=4,点M在以半径为2的⊙D上运动,则MF2+MG2的最大值为 .
27.(2023秋 江北区期末)如图,一组抛物线满足二次函数表达式y=x2﹣2mx+m2+3,它们与一个半径为的圆的重叠部分面积为,则该圆圆心的纵坐标为 .
28.(2023秋 镇海区校级期末)设实数a1,a2, ,a100满足以下三个条件:(1)a1≥a2≥…≥a100≥0,(2)a1+a2≤100,(3)a3+a4+…+a100≤100,则的最大值为 .
29.(2023秋 海曙区期末)如图,AB为⊙O的直径,C为圆上一点,且AC=2,tan∠ABC,D在上一点,过点D作AB的垂线交BC于点E,连接AD交BC于点F,若△DEF是以EF为腰的等腰三角形,则BF的长为 .
30.(2023秋 余姚市期末)如图,在四边形ABCD中,AD∥BC,点E是AB上一点,连结AC,CE,ED,∠BEC=∠ADC,AB=AC=10,BC=12,将△ACD沿CD翻折得到△A'CD,若点A'恰好落在ED的延长线上,则CE= ,BE= .
31.(2023秋 宁波期末)如图,在⊙O中,AB=AC,点F为直径AD上一点,连结CF并延长交AB于点G,交⊙O于点E,若AG=AF,BG=4,GF=6,则AB的长为 .
32.(2022秋 镇海区期末)如图,在矩形ABCD中,AB=8,AD=6,点E是对角线AC上一动点,连接DE,过E作EF⊥DE,交AB边于点F,以DE、EF为邻边作矩形DEFG.
(1)当CE=4时,则EF的长为 .
(2)点H在DC上,且HD=1,连接HG,则HG长的最小值是 .
33.(2022秋 余姚市期末)定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为6的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .
34.(2022秋 鄞州区校级期末)抛物线y=ax2+bx+c(a,b,c是常数,a<0)经过A(0,3),B(4,3).
下列四个结论:
①4a+b=0;
②点P1(x1,y1),P2(x2,y2)在抛物线上,当|x1﹣2|﹣|x2﹣2|>0时,y1>y2;
③若抛物线与x轴交于不同两点C,D,且CD≤6,则a;
④若3≤x≤4,对应的y的整数值有3个,则﹣1<a.
其中正确的结论是 (填写序号).
35.(2022秋 鄞州区期末)如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知AB⊥BC,MN⊥BC,AB=6.5,BP=4,PD=8.
(1)ED的长为 .
(2)将木条BC绕点B按顺时针方向旋转一定角度得到BC′(如图2),点P的对应点为P′,BC′与MN的交点为D′,从A点发出的光束经平面镜P′反射后,在MN上的光点为E′.若DD′=5,则EE′的长为 .
36.(2021 慈溪市校级四模)如图,在以AB为直径的半圆O中,C是半圆的三等分点,点P是弧BC上一动点,连接CP,AP,作OM垂直CP交AP于N,连接BN,若AB=12,则NB的最小值是 .
三.解答题
37.(2022秋 慈溪市期末)如图,⊙O的两条弦AB,CD互相垂直,垂足为E,直径CF交线段BE于点G,且.
(1)求证:.
(2)若⊙O的半径为4,AB=6,求AG的长.
(3)设.
①若点E为AG中点,求x.
②若,求y与x的函数表达式.
38.(2023秋 慈溪市期末)已知二次函数y=x2﹣2tx+t2﹣t.
(1)求该二次函数图象的顶点坐标(用含t的代数式表示).
(2)点P(m,n)在该二次函数图象上,其中t﹣2≤m≤t+1.
①当t=2时,求n的取值范围.
②请探究n的最大值与最小值之差是否会随着t的变化而变化.若不变,请求出这个差;若变化,请用含t的代数式表示这个差.
39.(2023秋 慈溪市期末)如图1,以Rt△ABC的直角边AB为直径画⊙O,过A作斜边AC的垂线交⊙O于点D,连结CD,交⊙O于点E,交AB于点F,连结BE.
(1)求证:∠ACD=∠EBC.
(2)如图2,当△ABC是等腰直角三角形时.
①求∠BCD的正切值;
②求的值.
(3)若AB=1,设CD=x,y,求y关于x的函数表达式.
40.(2022秋 北仑区期末)我们知道,对角线互相垂直的圆内接四边形有许多特殊的结论成立,如对边的平方和相等,等等.如图1,四边形ABCD内接于⊙O,AC⊥BD,AC,BD交于点E.
(1)若AC=BD=4,则∠BDC= 度,四边形ABCD的面积为 .
(2)如图2,在AD上找一点M,连结BM,OM,使BM⊥OM,求证:BM2=AM DM.
(3)如图1,已知BD=4,且.
①当时,求AC的长.
②如图3,在四边形ABCD内取一点P,连结AP,BP,CP,DP,使∠APB=∠CPD=90°,当AB取最小值时,直接写出tan∠ABP的值.
41.(2023秋 海曙区期末)如图,抛物线y=ax2+bx﹣3与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,点D为直线BC下方抛物线上一动点.
(1)求抛物线的解析式;
(2)过点D作y轴的平行线,交BC于点P,小明认为当点D为抛物线顶点时,此时DP最大,试判断小明的说法是否正确,并说明理由.
42.(2023秋 余姚市期末)平面直角坐标系中,点(1,m),(2,n)在函数y=x2+bx+c(b,c是常数)的图象上.
(1)若m=2,n=1,求该函数的表达式;
(2)若m=2n,求证:该函数的图象经过点(3,2);
(3)已知点(3,0),(﹣2,y1),(5,y2)在该函数图象上,若m>0,n<0,试比较y1,y2的大小,并说明理由.
43.(2023秋 北仑区期末)已知二次函数y=ax2+(a+2)x﹣2a﹣2(a为常数且a≠0).
(1)当函数图象经过点(0,﹣6)时,求函数的表达式并写出函数图象的顶点坐标;
(2)求证:当时,函数图象与x轴必有两个不同的交点;
(3)若函数图象经过A(x1,y1),B(x2,y2)两点,其中x1+x2=3,且当x1<x2时,总有y1>y2,求a的取值范围.
44.(2022秋 镇海区期末)如图1,在锐角△ABC中,AB=AC,圆O为△ABC的外接圆.
(1)求证:OA平分∠BAC.
(2)如图2,点E在弧AB上,CE分别与OA,BA交于点F,G,且CF=BE.
①求证:BG⊥EF;
②若EF=2,CF=3,求圆O的半径.
③如图3,连结BO并延长交AC于D,交CE于H,若DH=OH,求cos∠BAC的值.
45.(2022秋 北仑区期末)在平面直角坐标系中,我们定义直线y=2ax﹣b为抛物线y=ax2+bx+c(a,b,c为常数且a≠0)的“倍系直线”.已知抛物线与x轴交于点A(﹣2,0),与y轴交于点B,与其“倍系直线”交于A、C两点.
(1)填空:b= ,该抛物线的“倍系直线”的函数表达式为 ,点C的坐标为 .
(2)过点B作BD∥x轴,交抛物线于点D,连结AD,过点D作DM∥y轴,交AC于点M,求点M的坐标,并求证:AO平分∠CAD.
(3)设“倍系直线”AC交y轴于点E,点F为线段EM上一点,使FE=2FM,连结DF并延长,交y轴于点G,求△GEF与△CDF的面积之比.
46.(2023秋 江北区期末)如图1,四边形ABCD内接于⊙O,连接BD,AC交于点G,点E是AB上一点,连接CE,交BD于点F,且满足∠ACD=∠ACF.
(1)求证:∠ACE=∠ABD.
(2)若点C是的中点,
①求证:CE=CD;
②若,时,求的值.
(3)如图2,当点F是BG的中点时,若AB=2,AC=3,求CG的值.
47.(2023秋 海曙区期末)如图,AB是⊙O的直径,C为AB下方半圆上一动点,OD∥AC交于点D.
(1)求证:;
(2)已知⊙O半径为r,设BD=x,AC=y,求x与y的关系式;
(3)点P为AB上方圆外一点,且∠PAB=2∠APO,连结PA、PB、PO,PA交上半圆于点E,已知当时y=9,,求sin∠PAB的值.
48.(2023秋 宁波期末)如图1,四边形ABCD内接于⊙O,AC为直径,∠BDC=45°,AC,BD交于点E,AB=2,过点O作GH⊥CD,垂足为G,交BD于点H.
(1)求⊙O的半径;
(2)当DE=EH时,求OH:OG的值;
(3)延长GH交CB的延长线于点Q,当HG=3OG时,求BQ的长.
49.(2022秋 宁波期末)(1)如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,判断线段DG与BE的数量关系并说明理由;
(2)如图2,四边形ABCD是矩形,AB=3,BC=6,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE又有怎样的数量关系,并说明理由;
(3)如图3,在(2)的条件下,连接BG,求2BG+BE的最小值.
50.(2023秋 鄞州区期末)如图1,△ABC 内接于⊙O,直径AB=12,弦,作弦CD与AB相交于点E.
(1)如图1,若AE=AC,求∠ACD的度数;
(2)如图2,若AE=4,求CD的长;
(3)如图3,过点A作CD的平行线交⊙O于点M,连结BD,MC,若,求△BCD的面积.
51.(2023秋 江北区期末)【基础巩固】(1)如图1,在△ABC中,AB=AC,D为BC上一点,AD=AE,∠BAD=∠CAE.求证:△ABC∽△ADE;
【尝试应用】(2)如图2,在(1)的条件下,DE交AC于点F,若∠B=45°,,求的值;
【拓展延伸】(3)如图3,在(1)的条件下,若,M,N分别是BC,DE的中点,请直接写出△AMN周长的值.
52.(2023秋 余姚市期末)如图,△ABC内接于⊙O,BC是⊙O的直径,tan∠ACB=2,过点A作AD⊥BC,交⊙O于点E,点F是上一点,连结EF交BC于点G,连结CF交AD于点H.
(1)求证:△AFC∽△HFE;
(2)若BC=10,CF=8,求EF的长;
(3)设,,求y关于x的函数表达式.
53.(2023秋 北仑区期末)如图,AB,AC,AD是⊙O中的三条弦,且AD平分∠BAC.
(1)如图1,若∠BAC=120°,测量AB,AC,AD的长度,猜想它们之间的数量关系为: ;
(2)如图2,若∠BAC=90°,求证:;
(3)如图3,若∠BAC=2θ(0°<θ<90°),直接写出AB,AC,AD与θ角三角函数之间的数量关系.
54.(2022秋 宁波期末)如图1,△ABC为圆O的内接三角形,△ABC的三条角平分线交于点I,延长AI交圆O于点D,连接DC.
(1)求证:DI=DC.
(2)如图2,连接BD,设BC与AD交于点P,若OI⊥AD,AB=8,求BP的长.
(3)如图3,四边形ABCD内接于圆O,连接对角线AC,BD交于点E,且AC平分∠BAD,过B作BF∥CD交AC于点F,BG平分∠ABD交AC于点G,若,AD=6,求FG的最大值,并求此时圆O的半径.
55.(2023秋 鄞州区期末)如图1,四边形ABCD内接于⊙O,对角线AC与BD交于点E,AC>BD,点F在AC上,∠ADF+∠ABC=90°.
(1)求∠CDF的度数.
(2)如图2,作DG⊥AB于点G,DG与AC交于点H,BG=CD,E为BD中点,求证:CF=2DE.
(3)在(2)的条件下,BD=2.
①若△BDG的面积是△DEH面积的3倍,求AC的长.
②如图3,当圆心O在高DG上时,求⊙O的半径.
56.(2023秋 镇海区校级期末)如图1,⊙O是△ABC的外接圆,点D是上一动点(不与点A、C重合),且∠ADB=∠BAC=45°.
(1)求证:AC是⊙O的直径;
(2)当点D在运动到使AD+CD=5时,则线段BD的长为 ;(直接写出结果)
(3)如图2,把△DBC沿直线BC翻折得到△EBC,连接AE,当点D在运动时,探究线段AE、BD、CD之间的数量关系,并说明理由.
57.(2022秋 宁波期末)已知二次函数y=ax2+bx+c的图象经过三点A(﹣1,0),B(4,0),C(0,3).
(1)求二次函数的表达式.
(2)二次函数的图象上若有两点(,y1),(m,y2)且y1<y2,根据图象直接写出m的取值范围.
(3)点D是第一象限内二次函数的图象上的一动点,作DE∥y轴交BC于点E,作DF⊥BC于点F.当D点运动时,求△DEF面积的最大值.
58.(2022秋 镇海区期末)【基础巩固】
(1)如图1,在△ABC中,E是AB上一点,过点E作BC的平行线交AC于点F,点D是BC上任意一点,连结AD交EF于点G,求证:;
【尝试应用】
(2)如图2,在(1)的条件下,连结BF,DF,若∠C=30°,FE、FB恰好将∠AFD三等分,求的值;
【拓展延伸】
(3)如图3,在等边△ABC中,BD=4DC,连结AD,点E在AD上,若∠BEC=120°,求的值.
59.(2022秋 余姚市期末)[基础巩固]
(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证:AC2=AD AB.
[尝试应用]
(2)如图②,在矩形ABCD中,AD=2,点F在AB上,FB=2AF,DF⊥AC于点E,求AE的长.
[拓展提高]
(3)如图③,在矩形ABCD中,点E在边BC上,△DCE与△DFE关于直线DE对称,点C的对称点F在边AB上,G为AD中点,连结GC交DF于点M,GC∥FE,若AD=2,求GM的长.
60.如图,在矩形ABCD中,AB=6cm,BC=8cm,如果点E由点B出发沿BC方向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为每秒2cm和1cm,FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t秒(0<t<4).
(1)连接EF,若运动时间t= 时,EF⊥AC;
(2)连接EP,设△EPC的面积为S cm2,求S与t的关系式,并求S的最大值;
(3)若△EPQ与△ADC相似,求t的值.
参考答案
一.选择题
1.【分析】设BC=a,CD=b,AE=c,IE=d,根据题意得到ab=m,cd=n,由矩形ABCD~矩形BEFG可得,代入整理可得ac+bd=2ab,最后表示出大长方形的周长,代入化简即可求得.
【解答】解:设BC=a,CD=b,AE=c,IE=d,
则ab=m,cd=n,
依题意得:BG=a﹣d,BE=c﹣b,
矩形ABCD~矩形BEFG,
∴,
∴,
整理得ac+bd=2ab,
这个大矩形的面积为:
(a+d)(b+c)
=ab+cd+ac+bd
=ab+cd+(ac+bd)
=ab+cd+2ab
=3ab+cd
=3m+n.
故选:D.
2.【分析】分别过点A,D作BC的平行线,根据相似比,找出对应相似图形的面积关系,然后找出符合的选项即可.
【解答】解:如图,分别过点A,D作BC的平行线交CE于点M,交BF于点N,
∵四边形ABCD~四边形HGFA,相似比k=3,
∴CD=3AF=3ME,BC=3FG=3BJ,△BCD∽△BJI,相似比k=3,
则S平行四边形BCDN=3S平行四边形MEFA=2S△BCD,9S△BJI=S△BCD,
∵S△ADN=S△ADM,
∴S四边形ABCD﹣S四边形ADEF=S BCDN﹣S MEFAS△BCD=12S△BIJ,选项C符合题意,
故选:C.
3.【分析】设AC,EF交于H,设CD=a,BD=CE=b,则DE=a﹣b,BC=a+b,由勾股定理得AB=AC(a+b),HCb,则AH=AC﹣HC(a﹣b),再证△AFH和△ABD相似得FH,则EF=EH+FH,再由勾股定理求出DF,据此可求出△DEF的周长=2a,而△DEF的面积,△ADF的周长和面积都不能求出,据此即可得出答案.
【解答】解:设AC,EF交于H,如图所示:
在等腰△ABC中,∠BAC=90°,AB=AC,
∵∠B=∠C=45°,
设CD=a,BD=CE=b,
∴DE=CD﹣CE=a﹣b,BC=CD+BD=a+b,
在Rt△ABC中,AB=AC,BC=a+b,
由勾股定理得:AB2+AC2=BC2,
∴AB=AC(a+b),
∵FE⊥DE,
∴∠CHE=∠AHF=∠C=45°,
∴HE=CE=b,
由勾股定理得:HCb,
∴AH=AC﹣HC(a+b)﹣√2b(a﹣b),
∵AF⊥AD,∠BAC=90°,
∴∠DAC+∠HAF=90°,∠BAD+∠DAC=90°,
∴∠HAF=∠BAD,
又∵∠AHF=∠B=45°,
∴△AFH∽△ABD,
∴FH:BD=AH:AB,
即FH:b(a﹣b):(a+b),
∴FH,
∴EF=EH+FH=b,
在Rt△EDF中,EF,DE=a﹣b,
由勾股定理得:DF,
∴△DEF的周长为DE+EF+DF=a﹣b2a,
∴已知CD的长可以求出△DEF的周长,
故选项A符合题意;
∵DE=a﹣b,EF,
∴S△DEFDE EF (a﹣b) ,
∵b的大小不是已知的,
∴不能求出△DEF的面积;
故选项B不符合题意;
根据已知条件不能用a,b的代数式表示出AD和AF,
∴不能求出△ADF的周长和面积,
∴选项C,D不符合题意.
故选:A.
4.【分析】先根据勾股定理求出AC,过点P作PM⊥AB于点M,证明△PQM≌△PBM,推出QM=BM,分别表示AM和AP的长,根据△APM∽△ACB,进而,求出t的值,进而作答即可.
【解答】解:∵矩形ABCD,
∴AB∥CD,∠ABC=90°,
在Rt△ABC中,
AC13cm,
过点P作PM⊥AB于点M,如图,
∴PM∥BC,
∴∠CBP=∠BPM,
∵∠QPB=2∠CBP,
∴∠CBP=∠BPM=∠QPM,
在△QPM与△BPM中,
,
∴△QPM≌△BPM(ASA),
∴QM=BM,
BQ=12﹣2t,QM=BM,
∴AM=6+t,AP=13﹣t,
∵∠BAC=∠BAC,∠PMA=∠CBA=90°,
∴△APM∽△ACB,
∴,
即,
∴t,
故选:B.
5.【分析】由矩形GBEF∽矩形ABCD,得到矩形GBEF与矩形ABCD的相似比是,由△EBC∽△EAH,推出,即可得到答案.
【解答】解:∵矩形GBEF∽矩形ABCD,
∴矩形GBEF与矩形ABCD的相似比是,
∵四边形ABCD是矩形,
∴AH∥BC,
∴△EBC∽△EAH,
∴,
∴要求两个矩形的相似比,只需知道.
故选:C.
6.【分析】根据AC:BC=3:2可设AC=3a,BC=2a,则ABa,设∠BAC=α,则tanα,证∠GAE=∠BAC=α,在Rt△AGE中可求出GE=2a,则EF=a,再证∠FEK=∠GAE=α,在Rt△FEK中可求出FKa,进而得S1=2a2,然后证∠CBM=∠BAC=α,在Rt△BCM中可求出CMa,则MLa,进而得S2a2,最后再根据S1+S2=30求出a=3,由此可得AB的长.
【解答】解:∵AC:BC=3:2,
∴设AC=3a,BC=2a,
在Rt△ABC中,由勾股定理得:ABa,
∵四边形ACFG,四边形BCLI,四边形ABDE均为正方形,
∴AG=AC=GF=3a,BC=LI=CL=2a,∠G=∠CAG=∠AED=∠ABD=∠CBI=∠F=90°,
设∠BAC=α,
在Rt△ABC中,BC=2a,AC=3a,
∴tanα,
∵∠GAE+∠EAC=90°,∠EAC+∠BAC=90°,
∴∠GAE=∠BAC=α,
在Rt△AGE中,tan∠GAE,
∴GE=AG tan∠GAE=3a tanα=3a 2a,
∴EF=GF﹣GE=3a﹣2a=a,
∵∠GAE+∠GEA=90°,∠FEK+∠GEA=90°,
∴∠FEK=∠GAE=α,
在Rt△FEK中,tan∠FEK,
∴FK=EF tan∠FEK=a tanαa,
∴S1=GF FK=3a a=2a2,
∵∠BAC+∠ABC=90°,∠ABC+∠CBM=90°,
∴∠CBM=∠BAC=α,
在Rt△BCM中,tan∠CBM,
∴CM=BC tan∠CBM=2a tanαa,
∴ML=CL﹣CM=2aaa,
∴S2=ML LIa 2aa2,
∵S1+S2=30,
∴2a2a2=30,
即a2=9,
∴a=3,(舍去负值),
∴AB.
故选:A.
7.【分析】根据抛物线y=ax2﹣2ax+8(a<0)可知的对称轴为直线x=1,开口向下;由1﹣m<m+7,得m>﹣3,根据存在x1,x2,满足y1=y2,﹣1<x1<2,知1﹣m<3,m>﹣2,即可得m的取值范围是m>﹣2.
【解答】解:∵y=ax2﹣2ax+8(a<0),
∴抛物线开口向下,对称轴为直线x1,
∵存在x1,x2(x1≠x2),满足y1=y2,
∴点(x1,y1),(x2,y2)关于x=1对称,
∴x1+x2=2,
∵﹣1<x1<2,
∴0<x2<3,
∵1﹣m<x2<m+7,
∴1﹣m<m+7,
∴m>﹣3,
∴1﹣m<3,
∴m>﹣2,
综上所述,m的取值范围是m>﹣2.
故选:B.
8.【分析】依据题意,首先根据x1<x2<x3<x4<x5<x6<x7,其对应的函数值是先增大后减小,可得抛物线开口向下,所以a<0;然后根据函数值是先增大后减小,可得7<m<14<k;最后根据a<0,可得二次函数有最大值,而且二次函数的最小值,所以b2≥4a(c﹣k),据此判断即可.
【解答】解:∵x1<x2<x3<x4<x5<x6<x7,其对应的函数值是先增大后减小,
∴抛物线开口向下,
∴a<0,①符合题意;
∴7<m<14<k,
∴7<m<14,②符合题意;
根据图表中的数据知,只有当x是抛物线的对称轴,抛物线的顶点坐标纵坐标不一定是k,故③不符合题意;
∵k,a<0,
∴4ac﹣b2≤4ak,
∴b2≥4a(c﹣k),④符合题意.
综上,可得判断正确的是:①②④.
故选:C.
9.【分析】连接DG,利用平行线的性质和相似三角形的判定定理得到△ADE∽△DBF,利用线段中点的定义得到AG=GEAE,DH=HFDF,进而得到,利用相似三角形的判定得到△GDE∽△HBF,再利用利用三边对应成比例的三角形相似得到△ADG∽△DBH,则∠ADG=∠DBH,利用平行线的判定定理得到DG∥BH,利用平行线间的距离相等,同底等高的三角形的面积相等的性质得到△BGH的面积=△BDH的面积,由于△BHF的面积=△BDH的面积,则△BDF的面积=2×△BDH的面积=2×△BGH的面积.
【解答】解:连接DG,如图,
∵DE∥BC,
∴∠AED=∠C,∠ADE=∠ABC,
∵DF∥AC,
∴∠C=∠DFB,
∴∠AED=∠DFB,
∴△ADE∽△DBF,
∴,
∴.
∵AG=GE,DH=HF,
∴AG=GEAE,DH=HFDF,
∴,
∵∠AED=∠DFB,
∴△GDE∽△HBF,
∴,
∵△ADE∽△DBF,
∴,
∴,
∴△ADG∽△DBH,
∴∠ADG=∠DBH,
∴DG∥BH,
∴△BGH的面积=△BDH的面积,
∵DH=HF,
∴△BHF的面积=△BDH的面积,
∴△BDF的面积=2×△BDH的面积=2×△BGH的面积.
∴若已知△BGH的面积,则一定能求出△BDF的面积.
故选:B.
10.【分析】由AF=AD,得∠AFD=∠ADF,由翻折得∠C=∠E,∠CAD=∠EAD,则∠ADF=∠C+∠CAD=∠E+∠EAD,而∠AFD=∠E+∠EDF,即可推导出∠EDF=∠EAD,进而证明△EDF∽△EAD,得,因为EF=3,CF=17,所以(17﹣FD)2=3(3+AF),3AF=FD(17﹣FD),于是得(17﹣FD)2=9+FD(17﹣FD),求得FD=8,于是得到问题的答案.
【解答】解:∵AF=AD,
∴∠AFD=∠ADF,
由翻折得∠C=∠E,∠CAD=∠EAD,
∴∠ADF=∠C+∠CAD=∠E+∠EAD,
∵∠AFD=∠E+∠EDF,
∴∠E+∠EDF=∠E+∠EAD,
∴∠EDF=∠EAD,
∵∠E=∠E,
∴△EDF∽△EAD,
∴,
∴ED2=EF EA,EF AD=FD ED,
∵EF=3,CF=17,
∴ED=CD=17﹣FD,EA=3+AF,
∴(17﹣FD)2=3(3+AF),3AF=FD(17﹣FD),
∴(17﹣FD)2=9+FD(17﹣FD),
整理得2FD2﹣51FD+280=0,
解得FD=8或FD(不符合题意,舍去),
∴FD的长是8,
故选:A.
11.【分析】根据平行线分线段成比例定理,相似三角形的判定和性质逐项判断便可.
【解答】解:∵l1∥l2,
∴CF:OF=AE:EO=4:2,
∴,故①正确;
∵AE:EO:OB=4:2:7,
∴AE:BE=4:9,
∵l1∥l2∥l3,
∴,故②正确;
∵l2∥l3,
∴△OEF∽△OBD,
∴,故③正确;
∵l1∥l2,
∴△OEF∽△OAC,
∴,故④错误;
∴正确的说法有3个.
故选:B.
12.【分析】首先通过待定系数法求该抛物线的解析式及顶点坐标,再分类讨论点P在抛物线对称轴右侧及左侧两种情况,分别求出顶点为最低点和点P为最低点时m的值即可.
【解答】解:将(1,0),(0,3)分别代入y=x2+bx+c得,
解得,
∴y=x2﹣4x+3,
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线顶点坐标为(2,﹣1),对称轴为直线x=2,
当m>2时,抛物线顶点为最低点,
∴﹣1=2﹣m,
解得m=3,
当m≤2时,点P为最低点,
将x=m代入y=x2﹣4x+3得y=m2﹣4m+3,
∴m2﹣4m+3=2﹣m,
解得(舍),,
∴m=3或.
故选:D.
13.【分析】第二个图形中点(,)在两段函数中,是关键点.结合第一个图形,可得此时点P移动到点C,H在AB的中点,那么BH,△PHB的面积为.所以横轴表示BH的长,故A错误;当P为BC的中点时,作CD⊥AB于点D,可得BDAB,根据平行线分线段成比例定理可得BHDB,那么BHAB,H为AB的四等分点,那么B错误;根据P在BC和AC上,分别计算出△PHB的面积,得到相应函数解析式,看二次项的比例系数的绝对值是否相等,若相等,则形状相同;把x代入点P在AC上的函数解析式中可求得面积的值,判断出D是否正确.
【解答】解:∵点(,)在两段函数中,
∴点P点C重合.
∵正△ABC 的边长为1,PH⊥AB,
∴BC=1,BH.
∴CH.
∴S△PHB.
∵符合所给点(,).
∴横轴表示BH的长,故A错误;
作CD⊥AB于点D.
又∵△ABC是等边三角形,
∴BDAB.
∵PH⊥AB,
∴PH∥CD.
∵P为BC中点,
∴BPBC.
∴BHBD.
∴BHAB.
∴点H为AB的四等分点,故B错误;
当P在BC上时,BH为x,则PHx,
∴y=S△PHB x xx2.
当P在BC上时,BH为x,则AH=1﹣x,
∴PH(1﹣x)
∴y=S△PHB x (1﹣x).
∵两个二次函数的比例系数的绝对值相等,
∴形状相同,故C错误;
当x时,点P在AC上,∴y=S△PHB,故D正确.
故选D.
14.【分析】先设Rt△ABC的三边长为a,b,c,其中c为斜边,设⊙O的半径为r,根据图形找出a,b,c,r的关系,用含c的式子表示S1和S2,即可求出比值.
【解答】解:如图,取AB的中点为O,AC的中点为D,连接OE,OG,OD,OC,
设AB=c,AC=b,BC=a,
则a2+b2=c2,①
取AB的中点为O,
∵△ABC是直角三角形,
∴OA=OB=OC,
∵圆心在MN和HG的垂直平分线上,
∴O为圆心,
由勾股定理得:
,②
由①②得a=b,
∴,
∴,,
∴,
故选:C.
15.【分析】设AB=CD=m,DA=BC=n,则S=mn,S△ABD=S△CDBmnS,BGn,HDm,由△HDF∽△ABF,,可判断①正确;
由△GBE∽△ADE,得,则BEBD,而FDBD,所以EFBD,可求得BE:EF:FD=3:5:4,可判断②正确;
由GEAG,AEAG,得S1S△ABGS,S4S△ABGS,由HFAH,AFAH,得S3S△ADHS,S5S△ADHS,则S2S,S6S,所以S1+S2+S3S,可判③正确;
因为S2+S5SSS,所以S6=S2+S5,可判断④正确,于是得到问题的答案.
【解答】解:∵四边形ABCD为矩形,
∴AB=CD,DA=BC,AB∥CD,DA∥BC,
设AB=CD=m,DA=BC=n,则S=mn,S△ABD=S△CDBmnS,
∵点G是边BC的三等分点(BG<GC),点H是边CD的中点,
∴BGn,HDm,
∴S△ABGmnmnS,S△ADHnmmnS,
∵HD∥AB,
∴△HDF∽△ABF,
∴,
故①正确;
∵BG∥DA,
∴△GBE∽△ADE,
∴,
∴BEBD,
∵FDBD,
∴EF=BDBDBDBD,
∴BE:EF:FDBD:BDBD=3:5:4,
故②正确;
∵GEAG,AEAG,
∴S1S△ABGSS,S4S△ABGSS,
∵HFAH,AFAH,
∴S3S△ADHSS,S5S△ADHSS,
∴S2SSSS,S6SSSS,
∴S1+S2+S3SSSS,
故③正确;
∴S2+S5SSS,
∴S6=S2+S5,
故④正确,
故选:D.
16.【分析】根据题意得AE=CG=BF=DH,BE=DG,四边形EFG是正方形,∠AEB=∠DGC=90°.先证明△BPE≌△DQG,得到GQ,再根据△TGQ∽△KFQ,求出TG,再根据勾股定理求解.
【解答】解:根据题意:AE=CG=BF=DH,BE=DG.
∵四边形EFG是正方形,∠AEB=∠DGC=90°.
∵AE=2EF=2.
∴CG=AE=DH=2,EF=FG=EH=1,EH∥FG.
∵AP=CQ.
∴PE=GQ.
∴
∴△BPE≌△DQG(SAS).
∴S△BPE=S△DQG,
即S4=S2.
∵S1=S3=S2+S4.
∴S1=S3=2S4.
∴DH (PE+EH)=2PE (BF+EF).
即.
∴PE=GQ.
∴CQ=CG﹣GQ.
∵EH∥FG.
∴∠PET=∠GQT.
∵∠PQK=∠TGQ=90°,PE=GQ.
∴.
∴△PEK≌△QGT.
∴EK=TG
设TG=EK=a,则FT=1﹣a,
∵HG∥EF.
∴△TGQ∽△KFQ.
∴,即.
解得:a.
即TG.
在△QGT中,根据勾股定理知:
QT.
故选:D.
17.【分析】设两个正六边形的中心为O,连接OP,OB,过O作OG⊥PM,OH⊥AB,由正六边形的性质及邻补角性质得到三角形PMN为等边三角形,由小正六边形的面积求出边长,确定出PM的长,进而求出三角形PMN的面积,利用垂径定理求出PG的长,在直角三角形OPG中,利用勾股定理求出OP的长,设OB=x cm,根据勾股定理列出关于x的方程,求出方程的解即可得到结果.
【解答】解:设两个正六边形的中心为O,连接OP,OB,过O作OG⊥PM,OH⊥AB,
由题意得:∠MNP=∠NMP=∠MPN=60°,
∵小正六边形的面积为cm2,
∴小正六边形的边长为cm,即PM=7cm,
∴S△MPNcm2,
∵OG⊥PM,且O为正六边形的中心,
∴PGPMcm,OGPMcm,
在Rt△OPG中,根据勾股定理得:OP7cm,
设OB=x cm,
∵OH⊥AB,且O为正六边形的中心,
∴BHx,OHx,
∴PH=(5x)cm,
在Rt△PHO中,根据勾股定理得:OP2=(x)2+(5x)2=49,
解得:x=8(负值舍去),
则该圆的半径为8cm.
故选:D.
18.【分析】设CG=x,HG=y,证△ADH∽△DCG,用含x、y的式子表示DG、AH、EH,再根据tanβ=tan2α,推出x与的关系,最后利用勾股定理求出DC、EH和AD的长,代入矩形面积计算即可.
【解答】解:∵四边形ABCD是矩形,BC=2AB,
∴AB=CD,AD=BC,
∴AD=2CD,
设CG=x,HG=y,
∵△AHD≌△CFB,△ABE≌△CDG,且这四个三角形均为直角三角形,
∴∠AHD=∠DGC=90°,
∴∠DAH+∠ADH=∠ADH+∠CDG=90°,
∴∠CDG=∠DAH,
∴△ADH∽△DCG,
∴2,
∴DH=2x,
∴DG=2x+y,AH=4x+2y,EH=3x+2y,
∵∠CHG=α,∠CDG=β,tanβ=tan2α,
∴,即2x2+xy=y2,
∴y2﹣xy﹣2x2=0,
∴(y﹣2x)(y+x)=0,
∵y+x≠0,
∴y=2x,
∴DG=4x,DCx,EH=3x+2y=7x,
∴AD=2x,
∴,
故选:B.
二.填空题
19.【分析】如图,过G作GT⊥BC于T交CE于R,过G作GQ⊥AB于Q,交DC于N,连接EG,证明GE=GC,EF=FC=GF,设BE=a,求解,求解,,,证明AQ=QE,,过C作CS⊥GG'于S,求解,,,可得,过K作KV⊥CG'于V,可得KV:VG':KG'=8:15:17,再解直角三角形可得答案.
【解答】解:如图,过G作GT⊥BC于T交CE于R,过G作GQ⊥AB于Q,交DC于N,连接EG,
∵CE中点为F,GF⊥CF,GF=CF,
∴GE=GC,EF=FC=GF,
设BE=a,
∵正方形ABCD中,AE=3BE,
∴AE=3a,AB=BC=CD=AD=4a,
∴,tan∠BCE,
∴,,
∵∠GFR=∠CTR=90°,∠GRF=∠CRT,
∴∠FGR=∠RCT,
∴,
∴,
∴,
∴,
∴,,
∴,
∴,,,
∴AQ=QE,
∴,
∵GT⊥BC于T交CE于R,过G作GQ⊥AB于Q,交DC于N,
∴∠GNC=∠NCT=∠CFG=90°,
∴四边形GTCN为矩形,
∴,,
∴,
∴,,
∴,
过C作CS⊥GG'于S,
同理可得:,,
∴,
∵CG=CG',
∴,
∵CG=CG',
∴∠CGG'=∠CG'G,
∴,
过K作KV⊥CG'于V,
由旋转可得:∠F'CG=∠FCG=45°,
∴设KV=CV=n,
∴,
∴,
∴KV:VG':KG'=8:15:17,
∴,
∴,
∵,
∴.
故答案为:.
20.【分析】作出圆心O,连接OB,OC,OC与AB交于点F,根据垂径定理和等腰三角形的性质与判定证明出△BOC是等边三角形,即可得出半径长;过点D作DM∥AC,DN⊥BC,得出△AEC∽△DEM,从而得到,再根据平行的性质和锐角三角函数得到DM,从而得到当DN最大时,最大,求出此时的DN即可得解.
【解答】解:作出圆心O,连接OB,OC,OC与AB交于点F,过点D作DM∥AC,DN⊥BC于点N,连接BD,
∵AC=BC,
∴,
∴OC⊥AB,AF=BF,
∴∠ACF=∠BCFACB=60°,
∵OB=OC,
∴△BOC是等边三角形,
∴BC=OC=OB=2=AC,
∴BFOB,
∴AB=2,
∵DM∥AC,
∴△AEC∽△DEM,
∴,
∵DM∥AC,
∴∠DME=∠ACB=120°,
∴∠DMN=60°,
∴DM,
∴当DN最大时,DE:AE最大,
由题意知D为中点时,DN最大,
此时DN的长等于半径减去△BOC的高,
∴DN=2,CN:BN=1,
∴DM,
∴MN1,
∴CM=CN﹣MN=2,
∴,
∵DM∥AC,
∴,
∴,
∴CE1,
故答案为:2,1.
21.【分析】(1)连接OA,过点O作OM⊥AC,根据圆周角定理、垂径定理及等腰三角形的性质得出∠OAC=∠OCA=30°,,再由余弦函数求解即可;
(2)连接OB,过点O作OD⊥BC,过点E作EF⊥BD,利用角的等量代换得出∠AEC=90°,再由正弦函数确定OE=2,根据相似三角形的判定和性质及勾股定理求解即可.
【解答】解:(1)连接OA,过点O作OM⊥AC,
∵∠ABC=60°,
∴∠AOC=120°,
∵OA=OC,OM⊥AC,
∴∠OAC=∠OCA=30°,,
∵,
∴,
∴⊙O的半径为4;
故答案为:4;
(2)连接OB,过点O作OD⊥BC,过点E作EF⊥BD,如图所示:
∵∠EAC=60°,∠OAC=30°,
∴∠EAO=30°,
∵∠EAC=60°,∠OCA=30°,
∴∠AEC=90°,
∵,
∴OE=OA sin∠EAO=2,
∴CE=CO+OE=6,
∵OD⊥BC,
∴,
∴,
∵∠ODC=∠EFC=90°,∠DCO=∠FCE,
∴△DCO∽△FCE,
∴即,
∴,,
∴,
∴,
故答案为:.
22.【分析】先根据抛物线解析式求出点A坐标和其对称轴,再根据对称性求出点M坐标,利用点M为线段AB中点,得出点B的坐标;再将点B的坐标代入直线OP的解析式,用含a的式子表示出点P坐标,即可求解出a的值,据此即可解答.
【解答】解:∵抛物线y=ax2﹣2ax+3(a>0)与y轴交于点A,
∴A(0,3),抛物线的对称轴为直线x=1,
∴顶点P坐标为(1,3﹣a),点M坐标为(2,3)
∵点M为线段AB的中点,
∴点B坐标为(4,3),
设直线OP解析式为y=kx(k为常数,且k≠0),
将点B(4,3)代入得4k=3,
解得,
∴直线OP解析式为,
将点P(1,3﹣a)代入得,
得,
解得,
∴点,
∴
故答案为:.
23.【分析】分两种情形:如图1中,当EF⊥AB时,如图2中,当ME⊥EC时,分别证明两个三角形相似,构建方程求解.
【解答】解:∵∠ACB=90°,CE是中线,
∴EC=EA=EB,
∴∠B=∠ECB,
∵△DEF∽△ABC,
∴∠DEF=∠B,
如图1中,当EF⊥AB时,∵∠A+∠ANE=90°,∠A+∠B=90°,
∴∠ANE=∠B,
∴∠MEN=∠MNE=∠B=∠ECB,
∴△EMN∽△BCE,
∵AC=8,BC=6,
∴AB10,
∵∠A=∠A,∠AEN=∠ACB=90°,
∴△AEN∽△ACB,
∴,
∴,
∴AN,
∴CN=AC﹣AN=8;
如图2中,当ME⊥EC时,同法可证∠EMN=∠MEN=∠B=∠ECB,
∴△EMN∽△BCE,NM=NE,
∵∠EMN+∠MCE=90°,∠MEN+∠CEN=90°,
∴∠ECM=∠NEC,
∴NE=CN=MN,
∵∠ACE=∠A,∠CEM=∠ACB=90°,
∴△CEM∽△ACB,
∴,
∴,
∴CM,
∴CNCM.
故答案为:或.
24.【分析】连接AE、AG、DG,设AC与EF交于点K,由∠AGE=90°可得点G在以AK为直径的圆上,进而可得当O、G、B三点共线时,BG有最小值,BG最小=OB﹣OG,证明△AEG∽△ADE与△AKG∽△ADC可求AK=2,再求出OB即可.
【解答】解:连接AE、AG、DG,设AC与EF交于点K,如图,
∵AE=AF,G为EF的中点,
∴AG⊥EF,
∵DE、DF是⊙A的切线,
∴DE=DF,
∵G为EF的中点,
∴DG⊥EF,
∴A、G、D三点共线,
∵∠AGE=90°,
∴点G在以AK为直径的圆上,
∴当O、G、B三点共线时,BG有最小值,BG最小=OB﹣OG,
∵∠AGE=∠AED=90°,∠EAG=∠DAE,
∴△AEG∽△ADE,
∴,
∴AE2=AD AG,
∵∠AGK=∠ACD=90°,∠KAG=∠DAC,
∴△AKG∽△ADC,
∴,
即AK AC=AD AG,
∴AE2=AK AC,
∴AK2,
∴OA=OG=1,
∴OC=AC=OA=7,
∵∠ACB=90°,BC=7,
∴OB=7,
∴BG的最小值为:71,
故答案为:71.
25.【分析】作直径BK,连接AK,CK,由圆周角定理推出∠BCK=∠BAK=90°,而AD⊥BC,判定AF∥KC,同理:AK∥CF,推出四边形AFCK是平行四边形,得到AK=CF=5,CK=AF=AO,由sin∠CBK,得到∠CBK=30°,求出CKBC,得到⊙O的半径是,由勾股定理求出AB3.
【解答】解:作直径BK,连接AK,CK,
∵BK是圆的直径,
∴∠BCK=∠BAK=90°,
∴KC⊥BC,
∵AD⊥BC,
∴AF∥KC,
同理:AK∥CF,
∴四边形AFCK是平行四边形,
∴AK=CF=5,CK=AF=AO,
∴CK:BK=1:2,
∵∠BCK=90°,
∴sin∠CBK,
∴∠CBK=30°,
∴CKBC,
∴AO,
∴⊙O的半径是,
∵∠BAK=90°,AK=5,BK=2AO=2,
∴AB3.
故答案为:,3.
26.【分析】取GF的中点O,连接OM,OD,DM.,由题意,MG2+MF2=2GO2+2OM2,因为OG=OF=3,所以OM的值最大时,MG2+MF2的值最大.
【解答】解答:设点O是GF的中点,连接OM,OD,DM.
在矩形DEFG中,已知DE=6,EF=4,
∴∠DGO=90°,DG=EF=4,FG=DE=6,
∵MG2+MF2=2GO2+2OM2,
∵OG=OF=3,
∴OM的值最大时,MG2+MF2 的值最大,
∵DM=2,,
∴OM≤OD+DM=5+2=7,
∴OM的最大值为7,
∴MG2+MF2 的最大值=2×32+2×72=116.
故答案为:116.
27.【分析】把二次配方成顶点式,确定顶点坐标为(m,3),进而确定抛物线扫过的面积为 y=3 上方,再利用重叠部分面积为列出关于α的等式求出α,再确定点A的纵坐标即可.
【解答】解:二次函数表达式y=x2﹣2mx+m2+3,化为顶点式:y=(x﹣m)2+3,
∴抛物线的顶点为(m,3),
∴抛物线的顶点在直线 y=3上,且开口向上,
∴抛物线扫过的面积为 y=3 上方,如图所示,
∵抛物线与圆重合面积为 ,
即α,
即 ,
解得 α=60°
∴A到BC的距离,
∴A点纵坐标为:.
28.【分析】将要求的代数式进行变形,再对其进行讨论即可解决问题.
【解答】解:因为a1+a2≤100,
所以a1≤100﹣a2,
又因为a1≥a2≥…≥a100≥0,
记S,
则S≤(100﹣a2)2
=1002﹣200a2.
因为a1+a2≤100,a3+a4+…+a100≤100,
所以a1+a2+a3+…+a100≤200,
即﹣200≤﹣(a1+a2+a3+…+a100),
所以S≤1002
=1002﹣a1a2﹣a3a2﹣a4a2﹣…﹣a100a2
=1002﹣a2(a1﹣a2)﹣a3(a2﹣a3)﹣a4(a2﹣a4)﹣…﹣a100(a2﹣a100)
≤1002
=10000,
当a1=100,ai=0(i>1)或者a1=a2=a3=a4=50,aj=0(j>4)时,等号成立.
故答案为:10000.
29.【分析】利用勾股定理,直角三角形的边角关系定理求得BC.AB.利用分类讨论的思想方法分两种情况讨论解答:①当EF=DF时,过点F作FH⊥DE于点H,利用等腰三角形的性质,平行线的判定与性质得到FB=FA,设FB=x,则FA=x,FC=BC﹣FB=4﹣x,利用勾股定理列出方程,解方程即可得出结论;②当EF=DE时,连接BD,过点F作FG⊥AB于点G,利用圆周角定理,等腰三角形的性质,垂径定理得到∠CAD=∠BAD,利用全等三角形的判定与性质求得AG,则BG可得,利用直角三角形的边角关系定理求得FG,则FC可求,所以BF=BC﹣FC.
【解答】解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵AC=2,tan∠ABC,
∴,
∴BC=4,
∴2.
①当EF=DF时,过点F作FH⊥DE于点H,如图,
∵EF=DF,FH⊥DE,
∴∠DFH=∠EFH.
∵FH⊥DE,ED⊥AB,
∴FH∥AB,
∴∠DAB=∠DFH,∠B=∠EFH,
∴∠DAB=∠B,
∴FB=FA.
设FB=x,则FA=x,FC=BC﹣FB=4﹣x.
∵AC2+FC2=AF2,
∴,
∴x=3,
∴BF=3;
②当EF=DE时,连接BD,过点F作FG⊥AB于点G,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵EF=DE,
∴∠EFD=∠EDF,
∵∠EFD+∠EBD=90°,∠EDF+∠BDE=90°,
∴∠BDE=∠EDB,
∵∠CAD=∠DBE,
∴∠CAD=∠BDE.
∵AB⊥DK,AB为直径,
∴,
∴∠DAB=∠EDB,
∴∠CAD=∠BAD.
在△ACF和△AGF中,
,
∴△ACF≌△AGF(AAS),
∴AC=AG=2,FC=FG.
∴BG=AB﹣AG=22,
∵tan∠ABC,
∴,
∴FG(22)=22,
∴FC=22,
∴BF=BC﹣FC=4﹣(22)=6﹣2.
综上,若△DEF是以EF为腰的等腰三角形,则BF的长为3或6﹣2.
故答案为:3或6﹣2.
30.【分析】由AD∥BC,得∠CAD=∠ACB,由AB=AC,得∠B=∠ACB,则∠B=∠CAD,而∠BEC=∠ADC,可证明△BEC∽△ADC,得∠BCE=∠ACD,,则,∠ACB=∠DCE,所以△ABC∽△DEC,则∠B=∠CED=∠CAD,∠ACB=∠DCE,所以∠DCE=∠CED,由翻折得∠CAD=∠A′,A′C=AC=10,则∠B=∠ACB=∠CED=∠DCE=∠A′,CE=A′C=AC=10,再证明△ABC∽△CEA′,得1,则A′E=BC=12,再证明△DEC∽△CEA′,得,求得DE,则AD=A′D,所以BE,于是得到问题的答案.
【解答】解:∵AD∥BC,
∴∠CAD=∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠CAD,
∵∠BEC=∠ADC,
∴△BEC∽△ADC,
∴∠BCE=∠ACD,,
∴∠BCE+∠ACE=∠ACD+∠ACE,,
∴∠ACB=∠DCE,
∴△ABC∽△DEC,
∴∠B=∠CED=∠CAD,∠ACB=∠DCE,
∴∠DCE=∠CED,
由翻折得∠CAD=∠A′,A′C=AC=10,
∴∠B=∠ACB=∠CED=∠DCE=∠A′,
∴CE=A′C=AC=10,
∵∠B=∠CED,∠ACB=∠A′,
∴△ABC∽△CEA′,
∴1,
∴A′E=BC=12,
∴∠DCE=∠A′,∠DEC=∠CEA′,
∴△DEC∽△CEA′,
∴,
∴DE,
∴AD=A′D=A′E﹣DE=12,
∴BE,
故答案为:10,.
31.【分析】设AG=AF=x,则AB=x+4,连接BF,根据已知条件得到∠BAD=CAD,根据全等三角形的判定和性质得到∠AFB=∠AFC,根据等腰三角形的性质得到∠AGF=∠AFG,根据相似三角形的性质即可得到结论.
【解答】解:设AG=AF=x,则AB=x+4,
连接BF,∵AD是⊙O的直径,AB=AC,
∴,,
∴,
∴∠BAD=CAD,
在△ABF与△ACF中,
,
∴△ABF≌△ACF(SAS)
∴∠AFB=∠AFC,
∵AG=AF,
∴∠AGF=∠AFG,
∴∠BGF=∠AFC,
∴∠BGF=∠AFB,
∵∠ABF=∠FBG,
∴△ABF∽△FBG,
∴,
∴,
解得x=12,
∴AB=12+4=16.
故答案为:16.
32.【分析】(1)过E作EM⊥DC于M,延长ME交AB于N,证明△CEM∽△CAD和△DME∽△ENF,根据相似三角形的性质可求解;
(2)连结AG并延长交CD的延长线与L,分别证明△ANE∽△ABC和△CDE∽△ADG,根据相似三角形的性质可求解.
【解答】解:(1)过E作EM⊥DC于M,延长ME交AB于N,
则△CEM∽△CAD,
∴,
∴ME,CM,
∴DM,EN,
在Rt△DME中,DE,
∵∠DME+∠EDM=90°,∠DEM+∠FEN=90°,
∴∠EDM=∠FEN,
又∠DEM=∠FNE,
∴△DME∽△ENF,
∴,
∴EF,
故答案为:;
(2)连结AG并延长交CD的延长线与L,
∵△DME∽△ENF,
∴,
∵△ANE∽△ABC,
∴,
∴,
∴,
∵∠CDE=∠ADG,
∴△CDE∽△ADG,
∴∠DCA=∠DAL,
∴tan∠DCA=tan∠DAL,
∴当HG⊥AL时,HG最小,S△ALHAD HLGH AL,
∵AD=6,DL,LH,AL,
∴HG,
故答案为:4.4.
33.【分析】根据题意画出相应的图形,利用圆周角定理、直角三角形的边角关系以及三角形的面积公式进行计算即可.
【解答】解:如图所示:
∵圆与三角形的三条边都有两个交点,截得的三条弦相等,
∴圆心O就是三角形的内心,
∴当⊙O过C时,且在等腰直角三角形ABC的三边上截得的弦相等,即CG=CF=DE,此时⊙O最大,
过点O分别作弦CG、CF、DE的垂线,垂足分别为P、N、M,连接OC、OA、OB,
∵CG=CF=DE,
∴OP=OM=ON,
∵∠C=90°,AB=6,AC=BC,
∴,
∵S△AOC+S△BOC+S△AOB=S△ABC,
∴,
设OM=x,则OP=ON=x,
∴,
解得:,
即,
在Rt△CON中,,
故答案为:.
34.【分析】把AB两点的坐标代入函数解析式即可判断①正确;由平行于坐标轴直线上两点之间的距离的几何意义即可判断②;由于C、D是抛物线与x轴的交点,有根与系数的关系和CD≤6,可以判断③;x=4时,y=3,3≤x≤4,对应的y的整数值有3个,y对应得整数值为:3,4,5,结合图象,可以判断④.
【解答】解:①将A、B两点坐标代入抛物线y=ax2+bx+c中,
则:,
解得:,
故①正确;
②∵|x1﹣2|﹣|x2﹣2|>0,即|x1﹣2|>|x2﹣2|,
∴x1距离x=2比x2距离x=2更远,
如图:
从图中可以看出x距离x=2越远对应的函数值越小,
故y1<y2,
故②错误;
③∵a<0,
设C(x3,0)、D(x4,0),
则由根与系数的关系得:x3+x4=4,x3 x4,
∴|x3﹣x4|6,
解得:a,
故③正确;
④由题意知:x=4时,y=3,
∵3≤x≤4,对应的y的整数值有3个,
∴y对应得整数值为:3,4,5,
则x=3时对应的函数值y的取值范围为:5≤9a﹣12a+3<6,
解得:﹣1<a,
故④正确.
故答案为:①③④.
35.【分析】(1)由题意可得,△ABP∽△EDP,则,进而可得出DE的长;
(2)过点E′作∠E′FG=∠E′D′F,过点E′作E′G⊥BC′于点G,易得△ABP′∽△E′FP′,由此可得,在Rt△BDD′中,由勾股定理可求出BD′的长,可求出∠BD′D的正切值,设P′F的长,分别表示E′F和E′D′及FG和GD′的长,再根据BD′=13,可建立等式,可得结论.
【解答】解:(1)如图,由题意可得,∠APB=∠EPD,∠B=∠EDP=90°,
∴△ABP∽△EDP,
∴,
∵AB=6.5,BP=4,PD=8,
∴,
∴DE=13;
故答案为:13.
(2)如图2,过点E′作∠E′FD′=∠E′D′F,过点E′作E′G⊥BC′于点G,
∴E′F=E′D′,FG=GD′,
∵AB∥MN,
∴∠ABD′+∠E′D′B=180°,
∴∠ABD′+∠E′FG=180°,
∵∠E′FB+∠E′FG=180°,
∴∠ABP′=∠E′FP′,
又∠AP′B=∠E′P′F,
∴△ABP′∽△E′FP′,
∴即,,
设P′F=4a,则E′F=6.5a,
∴E′D′=6.5a,
在Rt△BDD′中,∠BDD′=90°,DD′=5,BD=BP+PD=12,
由勾股定理可得,BD′=13,
∴cos∠BD′D,
在Rt△E′GD′中,cos∠BD′D,
∴GD′=2.5a,
∴FG=GD′=2.5a,
∵BP′+P′F+FG+GD′=13,
∴4+4a+2.5a+2.5a=13,解得a=1,
∴E′D′=6.5,
∴EE′=DE+DD′﹣D′E′=13+5﹣6.5=11.5.
故答案为:11.5.
36.【分析】如图,连接AC,OC.证明点N在⊙T上,运动轨迹是,过点T作TH⊥AB于H.求出BT,TN,可得结论.
【解答】解:如图,连接AC,OC.
∵C是半圆的三等分点,
∴∠AOC=60°,
∵OA=OC,
∴△AOC是等边三角形,
作△AOC的外接圆⊙T,连接TA=TC,TN,TB.
∵OM⊥PC,
∴CM=PM,
∴NC=NP,
∴∠NPC=∠NCP∠AOC=30°,
∴∠CNM=60°,
∴∠CNO=120°,
∵CNO+∠OAC=180°,
∴点N在⊙T上,运动轨迹是,
过点T作TH⊥AB于H.
在Rt△ATH中,AH=OH=3,∠TAH=30°,
∴TH=AH tan30°,
∴AT=TN=2HN=2,
在Rt△BHT中,BT2,
∵BN≥BT﹣TN,
∴BN≥22,
∴BN的最小值为22.
故答案为:22.
三.解答题
37.【分析】(1)连接DF,AF,根据直径所对的圆周角是直角,得出∠CDF=90°,再根据平行线的判定,得出AB∥DF,再根据平行线的性质,得出∠BAF=∠AFD,再根据同圆或等圆中,同弧或等弧所对的圆周角相等,即可得出结论;
(2)连接BF,AC,根据直径所对的圆周角是直角,得出∠CAF=90°,再根据,得出,再根据等边对等角,得出∠CFA=∠ACF=45°,再根据同弧或等弧所对的圆周角相等,得出∠B=∠ACF=45°,再根据等量代换,得出∠B=∠AFC,再根据相似三角形的判定,得出△ABF∽△AFG,再根据相似三角形的性质,得出AF2=AG AB,然后计算即可得出答案;
(3)①连接AD,根据等腰三角形的判定,得出CA=CG,再根据等边对等角,对顶角相等以及同弧或等弧所对的圆周角相等,得出∠CAG=∠CGA=∠BGF=∠BFG,再根据等角对等边,得出BG=BF,再根据弧与弦的关系,得出AD=BF,进而得出BG=BF=AD,再根据题意,得出,进而得出CD=AB,再根据对称性,得出AE=ED,再根据等腰直角三角形的性质,得出,进而得出,然后变形,即可得出答案;
②连接AO交CE于P,设AE=1,则BG=x,设EG=t根据全等三角形的判定,得出△CPO≌△AGO,再根据全等三角形的性质,得出CP=AG=t+1,再根据线段之间的数量关系,得出CE=EB=t+x,进而得出PE=x﹣1,再根据相似三角形的性质,得出,进而得出,解得,再根据平行线分线段成比例定理,得出,然后代入计算,即可得出答案.
【解答】(1)证明:连接DF,AF,
∵CF是⊙O的直径,
∴∠CDF=90°,
∵AB⊥CD,
∴AB∥DF,
∴∠BAF=∠AFD,
∴;
(2)解:连接BF,AC,
∵CF是⊙O的直径,
∴∠CAF=90°,
∵,
∴,
∴∠CFA=∠ACF=45°,
∴∠B=∠ACF=45°,
∴∠B=∠AFC,
∵∠BAF=∠FAG,
∴△ABF∽△AFG,
∴AF2=AG AB,
∴;
(3)解:①连接AD,
∵点E为AG中点,AB与CD互相垂直,
∴CA=CG,
∴∠CAG=∠CGA=∠BGF=∠BFG,
∴BG=BF,
∵,
∴AD=BF,
∴BG=BF=AD,
又∵,,
∴,
∴CD=AB,
由对称性知,AE=ED,
∴,
∴,
∴,
∴;
②连接AO交CE于P,设AE=1,则BG=x,设EG=t,
∵,
∴AO⊥CF,
∴∠COP=∠AOG=90°,
∴∠OCP+∠OPC=90°,
∵∠APE+∠PAE=90°,
又∵∠OPC=∠APE,
∴∠OCP=∠PAE,即∠OCP=∠OAG,
在△CPO与△AGO中,
,
∴△CPO≌△AGO(AAS),
∴CP=AG=t+1,
由①知CE=EB=t+x,
∴PE=x﹣1,
∵△APE∽△CGE,
∴,
即,
解得,
∵AB∥DF,
∴,
即.
38.【分析】(1)把解析式化成顶点时,即可求出二次函数图象的顶点坐标;
(2)①当t=2时,则二次函数y=x2﹣4x+2,0≤m≤3,即可求得n的取值范围是﹣2≤n≤2;
②由题意可知n的最小值为﹣t,最大值为x=t﹣2时的值,即n的最大值为(t﹣2)2﹣2t(t﹣2)+t2﹣t=4﹣t,可得n的最大值与最小值之差=4﹣t+t=4.
【解答】解:(1)∵y=x2﹣2tx+t2﹣t=(x﹣t)2﹣t,
∴该二次函数图象的顶点坐标为(t,﹣t);
(2)①当t=2时,则二次函数y=x2﹣4x+2,0≤m≤3.
∵y=x2﹣4x+2=(x﹣2)2﹣2,
∴抛物线开口向上,x=2时有最小值﹣2,
当x=0时,y=2,
∴n的取值范围是﹣2≤n≤2;
②二次函数y=x2﹣2tx+t2﹣t的图象开口向上,对称轴为直线x=t,顶点坐标为(t,﹣t),
∵点P(m,n)在该二次函数图象上,其中t﹣2≤m≤t+1.
∴n的最小值为t,最大值为x=t﹣2时的值,即n的最大值为(t﹣2)2﹣2t(t﹣2)+t2﹣t=4﹣t,
∴n的最大值与最小值之差=4﹣t+t=4,
∴n的最大值与最小值之差不会随着t的变化而变化,n的最大值与最小值之差是4.
39.【分析】(1)利用同弧所对的圆周角相等,通过等量代换证明即可;
(2)①过点D作DG⊥BC交延长线于点G,连接OD,设圆的半径为r,证明四边形BODG是正方形,再求解即可;
②设圆的半径为r,则ADr,AC=2r,过E点作EH⊥BC交于H点,则tan∠EBC=tan∠ACD,结合tan∠BCD,推导出HC=3EH,CEEH,即可得到;
(3)连接AE,证明△ABE∽△CDA和△FAE∽△FCA,推导y与x的关系即可.
【解答】(1)证明:∵,
∴∠D=∠ABE,
∵∠ABC=90°,AD⊥AC,
∴∠D+∠ACD=∠ABE+∠CBE=90°,
∴∠ACD=∠EBC;
(2)解:①过点D作DG⊥BC交延长线于点G,连接OD,
设圆的半径为r,
∵△ABC是等腰直角三角形,∠DAC=90°,
∴△AOD是等腰直角三角形,
∴四边形BODG是正方形,
∴DG=BG=r,BC=2r,
∴tan∠BCD;
②设圆的半径为r,则ADr,AC=2r,
过E点作EH⊥BC交于H点,
∴tan∠EBC=tan∠ACD,
∴BH=2EH,BEEH,
∵tan∠BCD,
∴HC=3EH,CEEH,
∴;
(3)连接AE,
∵AB是圆的直径,
∴∠AEB=90°=∠DAC,
∵∠ADC=∠ABE,
∴△ABE∽△CDA,
∴x,
∵∠FAE=∠FCA,∠AFE=∠CFA,
∴△FAE∽△FCA,
∴x,
∴x2,
∴yx2﹣1.
40.【分析】(1)根据弦,圆周角直角的关系得出∠ADC=∠BCD,即可得出∠ECD=∠EDC=45°,再利用对角线互相垂直的四边形的面积等于对角线乘积的一半即可求面积;
(2)延长BM交⊙O于点E,连结DE,证明△AMB∽△EMD,根据对应边成比例即可解答;
(3)①先证明△ABE∽△DCE.设AE=x,利用对应边成比例表示出DE,BE,根据勾股定理列出方程,解出x即可解答;
②设AB的长度为a,AE=x,根据相似三角形的性质表示出DE,BE,利用勾股定理求出a的最小值,进而求出x,再证明△APC∽△BPD,得出解答.
【解答】(1)解:∵AC⊥BD,
∴∠CED=90°,
∵AC=BD,
∴∠ADC=∠BCD,
∵∠ADB=∠ACB,
∴∠ECD=∠EDC=45°,
∴四边形ABCD的面积为AC BD=8,
故答案为:45°,8;
(2)证明:延长BM交⊙O于点E,连结DE,
∵∠A=∠E,∠AMB=∠EMD,
∴△AMB∽△EMD,
∴,
∴BM EM=AM DM,
∵OM⊥BM,
∴BM=EM,
∴BM2=AM DM;
(3)解:①设AE=x,
∵∠AEB=∠DEC=90°,∠BAC=∠BDC,
∴△ABE∽△DCE.
∴,
∴,
∵BD=4,
∴.
∴,解得:.
∵当 时, (舍去),
∴x,
∴.
∴,
∴;
②设AB的长度为a,AE=x,
∵△ABE∽△DCE.
∴,
∴,
∴,
∴,
∵,
∴a2≥4.
∵a>0,
∴a≥2,
∴a有最小值2.即AB的长度最小值为2.
∴,解得:,
∴DE=3∴BE=1,
∴,
∴.
∵∠APB=∠CPD=90°,
∴∠APC=∠BPD,
∵∠APB=∠AEB=90°,
∴∠PAC=∠PBD,
∴△APC∽△BPD,
∴,
∴tan∠ABP.
41.【分析】(1)设交点式y=a(x﹣3)(x+1),即y=ax2﹣2ax﹣3a,所以﹣3a=﹣3,然后求出a得到抛物线解析式;
(2)先抛物线的顶点坐标为(1,﹣4),再利用待定系数法求出直线BC的解析式为y=x﹣3,设D(t,t2﹣2t﹣3)(0<t<3),则P(t,t﹣3),所以DP=﹣(t)2,则当t,DP最大,由于抛物线的顶点坐标为(1,﹣4),于是可判断小明的说法不正确.
【解答】解:(1)∵抛物线y=ax2+bx﹣3(a≠0)的图象与x轴交于A(﹣1,0)、B(3,0)两点,
∴抛物线解析式可设为y=a(x﹣3)(x+1),
即y=ax2﹣2ax﹣3a,
∴﹣3a=﹣3,
解得a=1,
∴抛物线解析式为y=x2﹣2x﹣3;
(2)小明的说法不正确.
理由如下:
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的顶点坐标为(1,﹣4),
当x=0时,y=x2﹣2x﹣3=﹣3,则C(0,﹣3),
设直线BC的解析式为y=mx+n,
把B(3,0),C(0,﹣3)分别代入得,
解得,
∴直线BC的解析式为y=x﹣3,
设D(t,t2﹣2t﹣3)(0<t<3),则P(t,t﹣3),
∴DP=t﹣3﹣(t2﹣2t﹣3)=﹣t2+3t=﹣(t)2,
∴当t,DP最大,
而抛物线的顶点坐标为(1,﹣4),
∴小明的说法不正确.
42.【分析】(1)用待定系数法即可解决问题.
(2)用b去表示c,再将点(3,2)坐标代入即可.
(3)根据m>0,n<0及抛物线经过点(3,0)可判断出抛物线对称轴所处位置的范围,再根据抛物线开口方向及(﹣2,y1)和(5,y2)离对称轴的远近即可解决问题.
【解答】解:(1)将(1,2)和(2,1)代入函数解析式得,
,
解得.
所以该函数的表达式为y=x2﹣4x+5.
证明:(2)将(1,m)和(2,n)代入函数解析式得,
,
又因为m=2n,
则2×②﹣①得,
c=﹣3b﹣7,
所以二次函数的解析式为y=x2+bx﹣3b﹣7,
将x=3代入函数解析式得,
y=9+3b﹣3b﹣7=2,
所以该函数的图象经过点(3,2).
(3)y1>y2.
因为m>0,n<0,
所以x=1时,y>0;x=2时,y<0,
则抛物线与x轴的一个交点在(1,0)和(2,0)之间.
又因为抛物线经过点(3,0),
所以抛物线的对称轴在直线x=2的右侧,在直线x=2.5的左侧.
因为点(﹣2,y1)到对称轴的距离在4到4.5之间,
点(5,y2)到对称轴的距离在2.5到3时间,
显然点(﹣2,y1)到对称轴的距离大于点(5,y2)到对称轴的距离,
又因为抛物线的开口向上,
所以y1>y2.
43.【分析】(1)将(0,﹣6)代入函数表达式,求出a的值即可解决问题.
(2)证明b2﹣4ac>0即可解决问题.
(3)用含a的代数式表示出y1和y2,再利用作差法即可解决问题.
【解答】(1)解:将点(0,﹣6)代入函数解析式得,
﹣2a﹣2=﹣6,
解得a=2,
所以函数的表达式为y=2x2+4x﹣6.
则,
将x=﹣1代入函数解析式得,
y=2﹣4﹣6=﹣8.
所以函数图象的顶点坐标为(﹣1,﹣8).
(2)证明:因为Δ=(a+2)2﹣4a(﹣2a﹣2)=9a2+12a+4=9()2,
又因为a,
所以Δ>0,
所以二次函数的图象与x轴必有两个不同的交点.
(3)解:将A,B两点坐标代入函数解析式得,
,
,
两式相减得,
,
又因为x1+x2=3,
所以y1﹣y2=2(2a+1)(x1﹣x2).
又因为当x1<x2时,总有y1>y2,
所以2a+1<0,
解得.
所以a的取值范围是:a.
44.【分析】(1)证明△AOB≌△AOC,即可得出OA平分∠BAC;
(2)①连结BF,证明△ABF≌△ACF,推出∠ABE=∠ABF,即可求证;②连结BO并延长交⊙O于M,连结CM,根据,即可求出半径的长;③延长BD交⊙O于M,连结CM,利用相似三角形的性质和判定即可求解.
【解答】(1)证明:连结OB、OC,
∵OA=OA,OB=OC,AB=AC,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO;
(2)①连结BF,
∵AF=AF,∠BAF=∠CAF,AB=AC,
∴△ABF≌△ACF(SAS),
∴∠ACF=∠ABF,BF=CF,
又∵∠ACF=∠ABE,BE=CF,
∴∠ABE=∠ABF,BE=BF,
∴BG⊥EF,且EG=FG;
②连结BO并延长交⊙O于M,连结CM,
则∠BCM=90°,
由EF=2,CF=3知EG=FG=1,BF=CF=3,
∴,,
∴,
∴,即半径为;
③延长BD交⊙O于M,连结CM,
∵∠DAO=∠OAB=∠ABO,∠ADO=∠BDA,
∴△ADO∽△BDA,
∴,
即AD2=DO DB,
∵∠DBC=90°﹣∠M=90°﹣∠BAC=∠DCH∠CDH=∠BDC,
∴△DCH∽△DBC,
∴,即CD2=DH DB,
又∵DH=HO,
∴,
∴,
∵AO⊥BC,CM⊥BC,
∴AO∥CM,
∴△DCM∽△DAO,
∴,即,
∴,,
∴.
45.【分析】(1)根据“倍系直线”的定义得直线为yx﹣b,将点A(﹣2,0)代入yx2+bx﹣3可得b=﹣1,联立抛物线yx2﹣x﹣3与直线yx+1可得点C的坐标;
(2)求出点D的坐标为(4,﹣3),点M的坐标为(4,3),则AO是DM的垂直平分线,AM=AD,根据等腰三角形的性质即可得并AO平分∠CAD;
(3)由点E、M、C的坐标可得M是CE的中点,由FE=2FM得FMMC,可得,证明△GEF∽△DMF,可得,即可得△GEF与△CDF的面积之比.
【解答】(1)解:∵直线y=2ax﹣b为抛物线y=ax2+bx+c(a,b,c为常数且a≠0)的“倍系直线”.
∴yx2+bx﹣3的“倍系直线”为yx﹣b,
将点A(﹣2,0)代入yx2+bx﹣3得1﹣2b﹣3=0,
解得b=﹣1,
∴该抛物线的“倍系直线”的函数表达式为yx+1,抛物线为yx2﹣x﹣3,
联立抛物线yx2﹣x﹣3与直线yx+1得,
解得或,
∴点C的坐标为(8,5).
故答案为:﹣1,yx+1,(8,5);
(2)证明:∵抛物线yx2﹣x﹣3与y轴交于点B,
∴B(0,﹣3),
∵BD∥x轴,交抛物线yx2﹣x﹣3于点D,
∴点D的坐标为(4,﹣3),
∵DM∥y轴,交AC于点M,直线AC为yx+1,
∴点M的坐标为(4,3),
∴AO是DM的垂直平分线,
∴AM=AD,
∴AO平分∠CAD;
(3)解:∵AC交y轴于点E,直线AC为yx+1,
∴E(0,1),
∵点M的坐标为(4,3),点C的坐标为(8,5).
∴M是CE的中点,
∴CM=EM,
∵FE=2FM,
∴FMEMMC,
∴FMCF,
∴,
∴S△CDF=4S△DFM,
∵DM∥y轴,
∴△GEF∽△DMF,
∴,
∴S△GEF=4S△DMF,
∴△GEF与△CDF的面积之比为1:1.
46.【分析】(1)通过等量代换求证即可;
(2)①通过证明∠BEC=∠ABC,利用等角对等边可得BC=EC,即可证明EC=DC;
②延长CE交⊙O于点P,易得△CBF∽△CPB,设CF=3k,DC=CE=4k,则EF=k,由BC2=CF CP,可得,,,cos∠∠DBC=cos∠BAC,,设DF=y,再由△FBP∽△FCD,得到,,则或;
(3)过点F作FH∥AB,交AC于点H,设AH=HG=a,由FH2=HG HC,求出 (舍)或,即可得.
【解答】(1)证明:∵∠ACD=∠ACE,
又∵∠ABD=∠ACD,
∴∠ACE=∠ABD;
(2)①证明:∵C是BD中点,
∴∠BAC=∠DAC,BC=DC,
∴∠BAC=∠DAC=∠DBC,
∴∠BEC=∠BAC+∠ACE,∠ABC=∠ABD+∠DBC,
∴∠BEC=∠ABC,
∴BC=EC,
∴EC=DC;
②解:延长CE交⊙O于点P,连接PB,
∵∠BDC=∠P,
∴△CBF∽△CPB,
设CF=3k,DC=CE=BC=4k,则EF=k,由BC2=CF CP,
∴,则有 ,
过点C作CH⊥BD交于H点,
∵tan∠BDC,
∴,
∴DHk,
∴BDk,
∵△FBP∽△FCD,
∴,
设DF=y,
∴,
解得 ,
∴或;
(3)解:过点F作FH∥AB,交AC于点H,设AH=HG=a,
∴FH2=HG HC,
∴1=a(3﹣a),
解得 (舍)或,
∴.
47.【分析】(1)通过条件证明∠BOD=∠COD,即可得到结论;
(2)连OC、BC、BD,BC与OD交于点Q,证明△BOQ∽△BAC,用含y的式子表示OQ和QD,在Rt△COQ和Rt△BDQ中运用勾股定理即可得到x与y的关系式;
(3)利用(2)的关系式求出r,连接OE,BE,证明三角形POE是等腰三角形,得到PE的长,在Rt△BPE中,运用勾股定理求出BE,在Rt△ABE中运用正弦函数的定义即可得到sin∠PAB的值.
【解答】(1)证明:连接OC,
∵OD∥AC,
∴∠BAC=∠BOD,∠OCA=∠COD,
∵OA=OC,
∴∠BAC=∠OCA,
∴∠BOD=∠COD,
∴;
(2)解:连OC、BC、BD,BC与OD交于点Q,
∵OD∥AC,
∴△BOQ∽△BAC,
∴,
∵AB=2OB,
∴,BQ=CQ,
∵OD=r,
∴QD=OD﹣OD,
∵OD是半径,BQ=CQ,
∴OD⊥BC,
在Rt△COQ和Rt△BDQ中,
由勾股定理得CQ2=OC2﹣OQ2,BQ2=BD2﹣QD2,
∵BQ=CQ,
∴OC2﹣OQ2=BD2﹣QD2,即,
整理得x2+ry﹣2r2=0;
(3)解:连接OE,BE,
把,y=9代入x2+ry﹣2r2=0,
得5+9r﹣2r2=0,
解得(不合题意,舍去),r=5,
∵OA=OE,
∴∠PAB=∠AEO=2∠APO,
∵∠AEO是△POE的外角,
∴∠AEO=∠APO+∠POE,
∴∠APO=∠POE,
∴OE=PE=5,
∵AB是直径,
∴∠AEB=∠BEP=90°,
在Rt△BPE中,
∵PE=5,PB,
∴BE,
在Rt△ABE中,
∵BE=6,AB=2r=10,
∴sin∠PAB.
48.【分析】(1)利用圆周角定理,等腰直角三角形的判定与性质解答即可;
(2)利用垂径定理,三角形的中位线定理,等腰直角三角形的判定与性质,全等三角形的判定与性质解答即可;
(3)设OG=k,则HG=3k,利用垂径定理和勾股定理求得k值;连接EG,CH,利用(2)的结论,三角形的中位线定理和等腰直角三角形的性质和相似三角形的判定与性质解答即可得出结论.
【解答】解:(1)∵AC为直径,
∴∠ABC=∠ADC=90°,
∵∠BAC=∠BDC=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=2,
∴ACAB=2.
∴⊙O的半径AC;
(2)∵过点O作GH⊥CD,
∴GD=GC,
∵OA=OC,
∴OG为△CAD的中位线,
∴OGAD.
∵OG⊥DC,AD⊥DC,
∴OG∥AD,
∴∠ADE=∠OHE.
在△ADE和△OHE中,
,
∴△ADE≌△OHE(ASA),
∴AD=OH.
∴OGOH,
∴OH:OG=2;
(3)∵HG=3OG,
设OG=k,则HG=3k,
∴AD=OH=2k,DG=GC=3k,
∴CD=6k.
∵AD2+CD2=AC2,
∴,
解得:k=±(负数不合题意,舍去).
∴OH=AD=2k.
连接EG,CH,如图,
∵HG=3OG,
∴OH:OG=2,
由(2)知:E为DH的中点,
∵G为CD的中点,
∴EG为△DCH的中位线,
∴EG∥CH,
∵EG⊥BD,
∴CH⊥BD,
∴∠CHB=∠ADC=90°,
∵∠DBC=∠DAC,
∴△BHC∽△ADC,
∴,
∴,
∴BH.
∵∠BDC=45°,HG⊥CD,CH⊥BD,
∴∠DHG=∠GHC=45°,
∴∠BHQ=∠DHG=45°,
∴∠BHQ=∠GHC.
∵∠QBH=∠QBA+∠ABD=90°+∠ABD,∠HOC=∠OGC+∠ACD=90°+∠ACD,∠ACD=∠ABD,
∴∠QBH=∠HOC,
∴△QBH∽△COH,
∴,
∴,
∴BQ=1.
49.【分析】(1)通过证明△DCG和△BCE(SAS)全等,得到DG=BE.
(2)通过证明△DCG∽△BCE得到,所以DGBE.∠BEC=∠DGC.延长BE、GD相交于点H.因为矩形ECGF,所以∠FEC=∠FGC=90°,所以∠HEF
+∠BEC=180°﹣∠FEC=90°,∠FGH+∠DGC=90°,所以∠H=∠F=90°,所以DG⊥BE.
(3)作EN⊥BC于N,GM⊥BC交BC的延长线于M.首先证明点G的运动轨迹是线段GM,将2BG+BE的最小值转化为求2(BG+DG)的最小值.
【解答】解:(1)DG=BE.
理由:
∵正方形ABCD,
∴CD=CB∠BCD=90°,
∵正方形ECGF,
∴CG=CE∠ECG=90°,
∴∠ECG=∠BCD=90°,
∴∠DCG=∠BCE,
在△DCG和△BCE中,
,
∴△DCG≌△BCE(SAS),
∴DG=BE.
(2)DGBE.
理由如下:延长BE、GD相交于点H.
∵矩形ECGF、矩形ABCD,
∴∠ECG=∠BCD=90°,
∴∠DCG=∠BCE,
∵CD:CB=3:6=1:2,CG:CE=1:2,
∴CD:CB=CG:CE,
∵∠DCG=∠BCE,
∴△DCG∽△BCE,
∴,∠BEC=∠DGC,
∴DGBE.
(3)作EN⊥BC于N,GM⊥BC交BC的延长线于M,
∴∠ENC=∠CMG=90°.
∵∠ECN+∠CEN=90°,∠ECN+∠GCM=90°,
∴∠CEN=∠GCM.
∴△ECN∽△CGM,
∴2,
∵EN=AB=3,
∴CM=1.5,
∴点G的运动轨迹是直线MG,
作点D关于直线GM的对称点G′,连接BG′交GM于G,此时BG+GD的值最小,最小值=BG′.
由(2)知,DGBE,
∴BE=2DG,
∴2BG+BE=2BG+2DG=2(BG+DG),
∴2BG+BE的最小值就是2(BG+DG)的最小值.
∵BG′3,
∴2BG+BE的最小值为6.
50.【分析】(1)求AC的长度,证明△ABC是等腰直角三角形,得到∠A的度数,根据等腰三角形的性质求出角度;
(2)证明△COE是直角三角形,求出CE的长度,证明△ACE∽△DCA,从而求出CD的长度;
(3)根据题意分当E在线段OB上和当点E在线段OA上两种情况,分别画出对应的图,求出CE和BE的长度,根据相似三角形的性质求出△BCD的面积.
【解答】解:(1)∵△ABC 内接于⊙O,
∴∠ACB=90°,
在Rt△ABC中,
∵AB=12,BC,
∴,
∴△ABC是等腰直角三角形,
∴∠A=45°,
∵AE=AC,
∴∠ACD;
(2)连接OC,AD,
∵直径AB=12,
∴OA=OB=OC=6,
∴OE=OA﹣AE=2,
∵∠CAB=45°,OA=OC,
∴∠AOC=90°,
在Rt△COE中,
∵OE=2,OC=6,
∴,
∵,
∴∠ADC=∠ABC=∠BAC=45°,
∵∠ACE=∠DCA,
∴△ACE∽△DCA,
∴,
∴CD;
(3)①当E在线段OB上时,连接OC,连接BM交CD于点N,
∵CD∥AM,
∴∠BNE=∠BMA=∠BOC=90°,
∵∠BEN=∠CEO,
∴∠ECO=∠ABM=∠ACM,
∴tan∠ECO=tan∠ACM,
∵OC=6,
∴OE=OC tan∠ECO=2,
∴EC,BE=6﹣2=4,
∴,
由(2)得△BCD∽△ECB,
∴,
∴;
②当点E在线段OA上时,
同理tan∠ECO=tan∠ACM,
∴OE=OC tan∠ECO=2,
∴CE,BE=6+2=8,
∴,
∵△BCD∽△ECB,
∴,
∴.
综上所述,△BCD的面积的面积为.
51.【分析】(1)利用相似三角形的判定定理解答即可;
(2)连接CE,利用全等三角形的判定与性质得到∠ECD=90°,过F作FM⊥CD于点M,过F作FN⊥CE于点N,设FN=t,则CM=FM=t,利用正方形的判定与性质,直角三角形的边角关系定理解答即可;
(3)在BC上截取CH=CE交BC于点H,利用直角三角形的边角关系定理,等腰三角形的性质和三角形的中位线定理解答即可.
【解答】解:(1)∵AB=AC,AD=AE,
∴,
∵∠BAD=∠CAE,
∴∠BAC=∠DAE,
∴△ABC∽△ADE;
(2)连接CE,如图,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE=45°,
∵AB=AC,
∴∠B=∠ACB=45°,
∴∠ACE=∠ACB=45°,
∴∠ECD=90°,
过F作FM⊥CD于点M,过F作FN⊥CE于点N,
∴FM=FN,FM=CM,CN=FN,
∴四边形FMCN是正方形,
设FN=t,则CM=FM=t,
∵,tan∠EDC,
∴,
∴MD=2t,
∴DC=3t.
∵FN∥CD,
∴△ENF∽△ECD.
∴,
∴;
(3)在BC上截取CH=CE交BC于点H,如图,
∵AB=AC,M为BC的中点,
∴AM⊥BC,BMBC=3,
∵AB=2,
∴cosB,
∴∠B=30°.
由(2)知:△ABD≌△ACE,
∴∠B=∠ACB=∠ACE=30°,BD=EC,
∴∠ECH=60°,EH⊥AC,
∴△CEH是等边三角形,
∴EH=CH=CE=BD,
∵M是BC中点,
∴BM=CM,
∴BM﹣BD=CM﹣CH,
即DM=MH,
∴M是DH中点,
∵N是DE中点,
∴MN是△DHE的中位线,
∴MNEH,
∴,
∴CE=2,
∴EH=2,
∴MN=1,
∵DM=BM﹣BD=1,AMAB,
∴AD2,
∵AD=AE,N为DE的中点,
∴AN⊥DE,
∵∠ADE=∠ABC=30°,
∴ANAD=1,
∴△AMN的周长为AM+AN+MN.
52.【分析】(1)根据垂径定理和同弧所对的圆周角相等,能够推导出∠AFC=∠CFE,∠ACF=∠FEA,即可证明三角形相似;
(2)连接BF,由题意可得AB=2AC,在Rt△ABC中,利用勾股定理求出AC=2,再由tan∠ACB=2,得到AD=2CD,在Rt△ACD中,利用勾股定理求出CD=2,AD=4,则ED=AD=4,证明△BFC∽△HDC,求得HD,则HE=ED+HD,再由△AFC∽△HFE,求出EF;
(3)设OC=r,则BC=2r,CDr,ADr,分两种情况讨论:①当点G在线段OD上时,x,则OG=xr,CG=(1﹣x)r,BG=(1+x)r,过点G作GM⊥CF交于点M,推导出FM=2GM,再由GM∥BE,推导出,,从而求出DH,AH=AD﹣HDr,即可求y;②当点G在线段OB上时,同理可得y.
【解答】(1)证明:∵BC是⊙O的直径,AD⊥BC,
∴,
∴∠AFC=∠CFE,
∵,
∴∠ACF=∠FEA,
∴△AFC∽△HFE;
(2)解:连接BF,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵tan∠ACB=2,
∴AB=2AC,
在Rt△ABC中,BC=10,
∴AC=2,
∵AD⊥BC,
∴∠ADC=90°,
∵tan∠ACB=2,
∴AD=2CD,
在Rt△ACD中,AD2+CD2=AC2,则CD=2,AD=4,
∴ED=AD=4,
∵BC是⊙O的直径,
∴∠BFC=90°,
∵BC=10,CF=8,
∴BF=6,
∵∠BFC=∠HDC=90°,∠FCB=∠DCH,
∴△BFC∽△HDC,
∴,
∴HD,
∴HE=ED+HD,
∵△AFC∽△HFE,
∴,
∴EF;
(3)解:设OC=r,则BC=2r,
∵tan∠ACB=2,
∴AD=2CD,BD=2AD,
∴CDr,ADr,
①当点G在线段OD上时,
∵x,
∴OG=xr,CG=(1﹣x)r,BG=(1+x)r,
过点G作GM⊥CF交于点M,
∴∠GMF=90°,
∵∠ADC=90°,∠CAE=∠CFE,
∴∠FGM=∠ACB,
∴tan∠FGM=tan∠ACB=2,
∴FM=2GM,
∵∠GMC=∠BFC=90°,
∴GM∥BE,
∴,
∴,即,
∵,
∴,
∴DH,
∴AH=AD﹣HDr,
∴,
∴y;
②当点G在线段OB上时,同理可得y;
综上所述:当点G在线段OD上时,y;当点G在线段OB上时,y.
53.【分析】(1)如图1,延长AC至点E,使得CE=AB,连接BD,CD,DE,根据圆内接四边形的性质得到∠B=∠DCE,得到BD=CD,根据全等三角形的性质得到∠E=∠BAD=60°,推出△ADE是等边三角形,于是得到AD=AB+AC;
(2)如图2,延长AC至点E,使得CE=AB,连接BD,CD,DE,根据圆内接四边形的性质得到∠B=∠DCE,得到BD=CD,根据全等三角形的性质得到∠E=∠BAD=45°,推出△ADE是等腰直角三角形,于是得到AD=AB+AC;
(3)如图3,延长AC至点E,使得CE=AB,连接BD,CD,DE,根据圆内接四边形的性质得到∠B=∠DCE,得到BD=CD,根据全等三角形的性质得到∠E=∠BAD=θ,推出△ADE是等腰三角形,过D作DH⊥AE于H,根据三角函数的定义得到结论.
【解答】(1)解:AD=AB+AC;
证明:如图1,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=120°,AD平分∠BAC,
∴∠BAD=∠DAC=60°,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=60°,
∴∠E=∠BAD=∠ADE=60°,
∴△ADE是等边三角形,
∴AE=AD,
即AD=AB+AC;
故答案为:AD=AB+AC;
(2)证明:如图2,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=90°,AD平分∠BAC,
∴∠BAD=∠DAC=45°,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=45°,
∴∠E=∠BAD=∠ADE=45°,
∴△ADE是等腰直角三角形,
∴AEAD,
即AB+ACAE;
(3)解:如图3,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=2θ,AD平分∠BAC,
∴∠BAD=∠DAC=θ,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=θ,
∴∠E=∠BAD=∠ADE=θ,
∴AD=DE,AE=AB+AC,
过D作DH⊥AE于H,
∴AH=EHAE(AB+AC),
∴cosθ.
54.【分析】(1)根据角平分线的定义,通过外角性质及圆周角定理,即可证明∠DCI=∠DIC,从而证得结论;
(2)首先由垂径定理,可得,根据圆周角定理及(1)可得DI=DC=BD,,再根据角平分线的定义及圆周角定理,即可证得△BDP∽△ADB,根据相似三角形的性质即可求解;
(3)过C作CH⊥BD于点H,延长BF交⊙O于点M,作直径CP,连接BP,CH,MD,设CH=m,则CB=CD=CG=3m,,再根据平行线的性质及圆周角定理,可证得∠BFC=∠ABD,∠BCF=∠ADB,可证得:△BCF∽△ADB,根据相似三角形的性质可得,FG=|CG﹣CF|=|3m﹣2m2|,再证得MD=BC=3m,求得:m≤2,再运用二次函数的图象和性质即可求得答案.
【解答】(1)证明:∵△ABC的三条角平分线交于点I,
∴∠BAD=∠CAD,∠ACI=∠BCI,
∴∠BCD+∠BCI=∠CAD+∠ACI,即∠DCI=∠DIC,
∴DC=DI;
(2)解:∵OI⊥AD,
∴AI=DIAD,
由(1)知DC=DI,
∴DI=DC=BD,
∴.
∵△ABC的三条角平分线交于点I,
∴∠BAD=∠CAD,
又∵∠BDP=∠ADB,
∴△BDP∽△ADB,
∴,
∴;
(3)解:如图:过C作CH⊥BD于点H,延长BF交⊙O于点M,作直径CP,连接BP,CH,MD,
∵AC平分∠BAD,BG平分∠ABD,
∴∠BAC=∠DAC=∠CBD=∠CDB,
同(1)可证得BC=DC=CG,
∴,
设CH=m,则CB=CD=CG=3m,,
∴,
∵BF∥CD,
∴∠BFC=∠ACD=∠ABD,
又∵∠BCF=∠ADB,
∴△BCF∽△ADB,
∴,
∴,
∴,
∴FG=|CG﹣CF|=|3m﹣2m2|,
又∵点F在线段AC上,
∴点M一定在上,
∵BF∥CD,
∴MD=BC=3m,
∴MD≤AD,即3m≤6,
解得:m≤2,
∵直径PC3BC=9m≥AD,
∴m,
即m≤2,
如图,作出FG=|3m﹣2m2|的图象,
∴由图象知:
当m时,FG=2;当m=2时,FG=86;
∵86>2,
∴FG最大值=86,此时圆O的半径为PCm=9.
55.【分析】(1)根据圆的内接四边形性质得:∠ADC+∠ABC=180°,结合已知∠ADF+∠ABC=90°,进而得出结果;
(2)可证明△BDG≌△CFD,从而CF=BD,进一步得出结论;
(3)①根据S△BDG=3S△DEH得出S△CFD=3S△DEG,从而EHCF,可证得△DEH∽△FED,从而DE2=EH EF,从而得出EF的值,可证得△ABE∽△CED,从而得出BE DE=CE AE,进一步得出结果;
②作DW⊥AC于W,作直径CV,连接DV,可得出AD=BD=2,△ABE∽△CED,从而,进而得出CE,AE=2,设EW=x,则AW=2﹣x,根据勾股定理得出DW2=DE2﹣EW2=AD2﹣AW2,,从而12﹣x2=22﹣(2﹣x)2,从而得出x的值,进而计算出CD的长,根据sinV=sin∠ACD得出,进一步得出结果.
【解答】(1)解:∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠CDF+∠ADF+∠ABC=180°,
∵∠ADF+∠ABC=90°,
∴∠CDF=90°;
(2)证明:∵DG⊥AB,
∴∠BGD=90°,
∵∠CDF=90°,
∴∠BGD=∠CDF,
∵,
∴∠ABD=∠ACD,
∵BG=CD,
∴△BDG≌△CFD(ASA),
∴CF=BD,
∵点E是BD的中点,
∴BD=2DE,
∴CF=2DE;
(3)①解:由(2)知:△BDG≌△CFD,CF=BD=2,∠BDG=∠CFD,
∵S△BDG=3S△DEH,
∴S△CFD=3S△DEG,
∴EHCF,
∵∠DEH=∠FED,
∴△DEH∽△FED,
∴DE2=EH EF,
∴12EF,
∴EF,
∴CE=CF﹣EF,
∵∠ABD=∠ACD,∠AEB=∠CED,
∴△ABE∽△CED,
∴BE DE=CE AE,
∴1×1AE,
∴AE=2,
∴AC=CE+AE;
②解:如图,
作DW⊥AC于W,作直径CV,连接DV,
∵DO⊥AB,
∴BG=AG,
∴AD=BD=2,
由①知:△ABE∽△CED,
∴,
∴AB=2BC,BC=CD,
∴
∴CE,AE=2,
设EW=x,则AW=2﹣x,
∵DW2=DE2﹣EW2=AD2﹣AW2,
∴12﹣x2=22﹣(2﹣x)2,
∴x,
∴EW,DW,
∴CW=EW+CE,
∴CD,
∵sinV=sin∠ACD,
∴,
∴,
∴CV,
∴⊙O的半径为:.
56.【分析】(1)证明∠ADC=90°即可解决问题.
(2)如图1中,作BM⊥DA交DA的延长线于M,BN⊥CD于N.利用全等三角形的性质证明四边形DMBN是正方形,证明AM=CN,推出DA+DC=2DM,求出DM即可解决问题.
(3)结论:AE2=2DB2+CD2.如图2中,作BM⊥BE,使得BM=BE,连接EM,CM.利用全等三角形的性质证明AE=CM,再利用勾股定理即可得出结论.
【解答】(1)证明:如图1中,
∵∠BAC=∠BDC=45°,∠ADB=45°,
∴∠ADC=∠ADB+∠BDC=90°,
∴AC是⊙O的直径.
(2)解:如图1中,作BM⊥DA交DA的延长线于M,BN⊥CD于N.
∵∠BDA=∠BDC=45°,BM⊥DM,BN⊥DC,
∴BM=BN,
∵AC是直径,
∴∠ABC=90°,
∴∠BAC=∠BCA=45°,
∴BA=BC,
∵∠M=∠BNC=∠BND,BD=BD,
∴Rt△BDM≌Rt△BDN(HL),Rt△BMA≌Rt△BNC(HL),
∴DM=DN,AM=CN,
∵∠M=∠BND=∠MDN=90°,
∴四边形BMDN是矩形,
∵BM=BN,
∴四边形BMDN是正方形,
∴BM=DM,
∴DA+DC=DM﹣AM+DN+CN=2DM=5,
∴DM=BM,
∴BDDM=5.
故答案为5.
(3)解:结论:AE2=2DB2+CD2.
如图2中,作BM⊥BE,使得BM=BE,连接EM,CM.
∵∠ABC=∠EBM=90°,
∴∠ABE=∠CBM,
∵BA=BC,BE=BM,
∴△ABE≌△CBM(SAS),
∴AE=CM,
∵∠BEC=∠BDC=∠BEM=45°,
∴∠CEM=90°,
∴CM2=EM2+EC2,
∴EM2=2BE2=2BD2,EC=CD,
∴AE2=2DB2+CD2.
57.【分析】(1)根据题意设二次函数表达式为y=a(x+1)(x﹣4),将C(0,3)代入二次函数得:a×1×(﹣4)=3,求出a的值,即可得到答案;
(2)直接根据二次函数的图象观察即可得到答案;
(3)用待定系数法求出直线BC的解析式,设,则点,则,当当m=2时,DEmax=3,易证△DFE∽△BOC,从而得到,因此计算即可得到答案.
【解答】解:(1)由交点式设二次函数表达式为y=a(x+1)(x﹣4),
把C(0,3)代入二次函数得:a×1×(﹣4)=3,
解得:,
∴二次函数表达式为;
(2)由(1)得,二次函数解析式为:,
∴对称轴为,
∴对应的点关于对称的点为,
∵二次函数的图象上若有两点,(m,y2)且y1<y2,
∴由图象可得m的取值范围为;
(3)设直线BC的解析式为:y=kx+b,
将B(4,0),C(0,3)代入得:,
解得:,
∴直线BC的解析式为,
设,则点,
则,
∴当m=2时,DEmax=3,
∵DE∥y轴,
∴∠DEF=∠OCB,
∵DF⊥BC,
∴∠DFE=∠BOC=90°,
∴△DFE∽△BOC,
∴,
∵OB=4,OC=3,
∴,
∴,
∴,
∴,
当DE最大时,S△DEF最大,即当m=2时,DEmax=3,
此时:.
58.【分析】(1)根据EG∥BD,可得△AEG∽△ABD,从而得到,同理,进而得到,即可;
(2)根据EF∥BC,可得∠C=∠AFE=30°,∠
同课章节目录
