2.4一元一次不等式 第1课时 一元一次不等式的解法 课件(共19张PPT)
文档属性
| 名称 | 2.4一元一次不等式 第1课时 一元一次不等式的解法 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 22:23:09 | ||
图片预览






文档简介
(共19张PPT)
2.4 一元一次不等式
第1课时 一元一次不等式的解法
1. 知道什么是一元一次不等式,会解简单的一元一次不等式并把解集表示在数轴上;(重点)
2. 通过观察一元一次不等式的解法,对比解一元一次方程的步骤,归纳出解一元一次不等式的基本步骤.(难点)
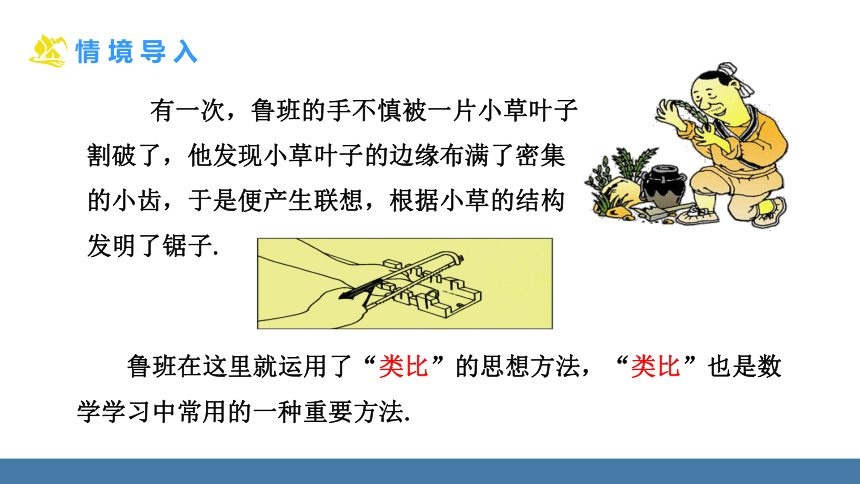
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法,“类比”也是数学学习中常用的一种重要方法.
1.不等式的三条基本性质是什么?
不等式的基本性质1 不等式的两边加(或减)同一个整式,不等号的方向不变.
不等式的基本性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3 不等式的两边乘(或除以)同一个负数,不等号的方向改变.
只含有一个未知数、未知数的最高次数为1且两边都为整式的等式.
解一元一次方程的步骤:
①去分母;
②去括号;
③移项;
④合并同类项;
⑤系数化为1.
2.什么叫一元一次方程?解一元一次方程的步骤是什么?
观察下列不等式:
6+3x>30, x+17<5x, x>5 ,
这些不等式有哪些共同特点
一元一次不等式
1.只有一个未知数
2.未知数的指数是一次
3.不等号的两边都是整式
(1)含有几个未知数?
(2)未知数的最高次数是多少?
{
不等式的左右两边都是整式,只含有一个未知数,且未知数的最高次数是1,像这样的不等式称为一元一次不等式.
判别条件:
(1)两边都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知数的系数不为0.
例1 解不等式3-x<2x+6,并把它的解集表示在数轴上.
解:两边都加 -2x,得
3-x-2x<2x +6-2x.
合并同类项,得 3-3x<6.
两边都加-3,得 3-3x-3<6-3.
合并同类项,得 -3x<3.
两边都除以-3,得 x>-1.
0
1
2
-1
-2
这个不等式的解集在数轴上的表示为:
例2 解不等式 ,并把它的解集表示在数轴上.
解:去分母,得 3(x-2)≥2(7-x).
去括号,得 3x-6≥14-2x.
移项、合并同类项,得 5x≥20.
两边都除以5,得 x≥4.
这个不等式的解集在数轴上的表示为:
5
6
7
4
3
2
1
0
1.解一元一次不等式大致要分五个步骤进行:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1.?
2.在数轴上表示不等式的解集时,要注意不等号以及端点的情况.
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
2.解不等式 ≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
D
1.判断下列式子是否是一元一次不等式.
(1)
解:(1)不是;(2)不是;(3)不是;(4)是.
解:
去分母,得
3(x-1)-2(4x-5)<6
去括号,得 3x-3-8x+10<6
移项,得 3x-8x<6+3-10
合并同类项,得 -5x<-1
两边同除以-5,得 x>
注意:一定不要漏乘以及记得“遇负则变”哦!
3.解不等式:
1.解不等式 的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.① B.② C.③ D.④
D
2. 求不等式 4(x + 1) ≤ 24的正整数解.
解: 去括号,得 4x + 4 ≤ 24.
移项、合并同类项,得 4x ≤ 20.
两边都除以4,得 x ≤ 5.
这个不等式的解集在数轴上的表示为:
所以原不等式的正整数解为 1,2,3,4,5.
-3 -2 -1 0 1 2 3 4 5 6 7 8
去分母,得 3(1+x)≥-2(2x-5)
去括号,得 3+3x≥-4x+10
移项,得 3x+4x≥10-3
合并同类项,得 7x≥7
两边同除以7,得 x≥1
这个不等式的解集在数轴上的表示为:
3.解不等式:
-3 -2 -1 0 1 2 3 4 5 6 7 8
4.下面是某同学解不等式 的过程:
解:去分母,得2×8+3(y+l)<3-2(y-1),
去括号,得16+3y+3<3-2y-2,
移项,合并同类项,得5y<-18,
系数化为1,得
他的过程有错误吗?如果有错误,请你改过来.
解:有错误.
去分母,得2×8+3(y+l)<3×8-2(y-1),
去括号,得16+3y+3<24-2y+2,
移项,合并同类项,得5y<7,
系数化为1,得y<.
定义
一元一次不等式
不等式的左右两边都是整式,只含有一个未知数,且未知数的最高次数是1.
(1)去分母;(2)去括号;(3)移项;
(4)合并同类项;(5)把系数化为1.
解一元一次不等式步骤
2.4 一元一次不等式
第1课时 一元一次不等式的解法
1. 知道什么是一元一次不等式,会解简单的一元一次不等式并把解集表示在数轴上;(重点)
2. 通过观察一元一次不等式的解法,对比解一元一次方程的步骤,归纳出解一元一次不等式的基本步骤.(难点)
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法,“类比”也是数学学习中常用的一种重要方法.
1.不等式的三条基本性质是什么?
不等式的基本性质1 不等式的两边加(或减)同一个整式,不等号的方向不变.
不等式的基本性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3 不等式的两边乘(或除以)同一个负数,不等号的方向改变.
只含有一个未知数、未知数的最高次数为1且两边都为整式的等式.
解一元一次方程的步骤:
①去分母;
②去括号;
③移项;
④合并同类项;
⑤系数化为1.
2.什么叫一元一次方程?解一元一次方程的步骤是什么?
观察下列不等式:
6+3x>30, x+17<5x, x>5 ,
这些不等式有哪些共同特点
一元一次不等式
1.只有一个未知数
2.未知数的指数是一次
3.不等号的两边都是整式
(1)含有几个未知数?
(2)未知数的最高次数是多少?
{
不等式的左右两边都是整式,只含有一个未知数,且未知数的最高次数是1,像这样的不等式称为一元一次不等式.
判别条件:
(1)两边都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知数的系数不为0.
例1 解不等式3-x<2x+6,并把它的解集表示在数轴上.
解:两边都加 -2x,得
3-x-2x<2x +6-2x.
合并同类项,得 3-3x<6.
两边都加-3,得 3-3x-3<6-3.
合并同类项,得 -3x<3.
两边都除以-3,得 x>-1.
0
1
2
-1
-2
这个不等式的解集在数轴上的表示为:
例2 解不等式 ,并把它的解集表示在数轴上.
解:去分母,得 3(x-2)≥2(7-x).
去括号,得 3x-6≥14-2x.
移项、合并同类项,得 5x≥20.
两边都除以5,得 x≥4.
这个不等式的解集在数轴上的表示为:
5
6
7
4
3
2
1
0
1.解一元一次不等式大致要分五个步骤进行:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1.?
2.在数轴上表示不等式的解集时,要注意不等号以及端点的情况.
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
2.解不等式 ≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
D
1.判断下列式子是否是一元一次不等式.
(1)
解:(1)不是;(2)不是;(3)不是;(4)是.
解:
去分母,得
3(x-1)-2(4x-5)<6
去括号,得 3x-3-8x+10<6
移项,得 3x-8x<6+3-10
合并同类项,得 -5x<-1
两边同除以-5,得 x>
注意:一定不要漏乘以及记得“遇负则变”哦!
3.解不等式:
1.解不等式 的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.① B.② C.③ D.④
D
2. 求不等式 4(x + 1) ≤ 24的正整数解.
解: 去括号,得 4x + 4 ≤ 24.
移项、合并同类项,得 4x ≤ 20.
两边都除以4,得 x ≤ 5.
这个不等式的解集在数轴上的表示为:
所以原不等式的正整数解为 1,2,3,4,5.
-3 -2 -1 0 1 2 3 4 5 6 7 8
去分母,得 3(1+x)≥-2(2x-5)
去括号,得 3+3x≥-4x+10
移项,得 3x+4x≥10-3
合并同类项,得 7x≥7
两边同除以7,得 x≥1
这个不等式的解集在数轴上的表示为:
3.解不等式:
-3 -2 -1 0 1 2 3 4 5 6 7 8
4.下面是某同学解不等式 的过程:
解:去分母,得2×8+3(y+l)<3-2(y-1),
去括号,得16+3y+3<3-2y-2,
移项,合并同类项,得5y<-18,
系数化为1,得
他的过程有错误吗?如果有错误,请你改过来.
解:有错误.
去分母,得2×8+3(y+l)<3×8-2(y-1),
去括号,得16+3y+3<24-2y+2,
移项,合并同类项,得5y<7,
系数化为1,得y<.
定义
一元一次不等式
不等式的左右两边都是整式,只含有一个未知数,且未知数的最高次数是1.
(1)去分母;(2)去括号;(3)移项;
(4)合并同类项;(5)把系数化为1.
解一元一次不等式步骤
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
