2.6一元一次不等式组 第1课时 一元一次不等式组的解法(1) 课件(共24张PPT)
文档属性
| 名称 | 2.6一元一次不等式组 第1课时 一元一次不等式组的解法(1) 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 22:30:09 | ||
图片预览








文档简介
(共24张PPT)
2.6 一元一次不等式组
第1课时 一元一次不等式组的解法(1)
1. 理解一元一次不等式组的概念;(重点)
2. 会解一元一次不等式组.(难点)
1.什么是一元一次不等式?
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
2.如何在数轴上表示不等式的解集?
(1)大于向右,小于向左;
(2)有等号是用实心圆点,无等号时用空心圆圈.
a
b
同学们,你能根据上图对话片断估计出这头大象的体重范围吗 请说说你的理由!
若设大象的体重为 x 吨,请用不等式的知识分别表示上面两位同学所谈话的内容:
x ≥3 ①
x<5 ②
看,这头大象好大呀,体重肯定不少于 3 吨!
嗨,我听说管理员说,这头大象的体重不足 5 吨呢!
某校今年冬季烧煤取暖时间为4个月. 如果每月比计划多烧5t煤,那么取暖用煤量将超过100t;如果每月比计划少烧5t 煤,那么取暖用煤总量不足68t.若该校计划每月烧煤 xt,则 x 满足怎样的关系式?
4(x + 5) > 100,
4(x - 5) < 68.
根据题意,得 4(x + 5) > 100, ① 且4(x - 5) < 68. ②
未知数x同时满足①②两个条件.把①②两个不等式合在一起,就组成一个一元一次不等式组,记作
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
注意:1.几个指两个或两个以上;
2.只有一个未知数;
3.由一元一次不等式组成.
一元一次不等式组的概念:
1.下列各不等式组,其中是一元一次不等式组的有________.(填序号)
③④⑤
确定一个不等式组是一元一次不等式组需要满足三点:
(1)不等式组中只有一个未知数;
(2)未知数的最高次数是1;
(3)组成不等式的代数式都是整式.
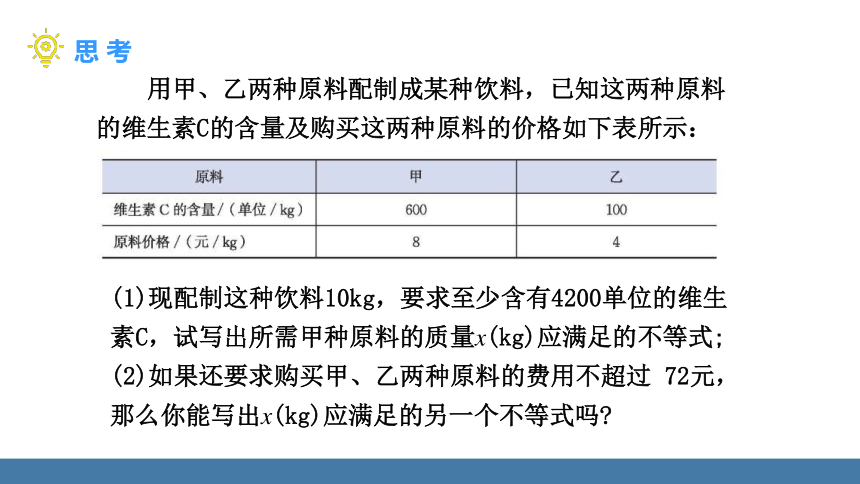
用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C的含量及购买这两种原料的价格如下表所示:
(1)现配制这种饮料10kg,要求至少含有4200单位的维生素C,试写出所需甲种原料的质量x(kg)应满足的不等式;
(2)如果还要求购买甲、乙两种原料的费用不超过 72元,那么你能写出x(kg)应满足的另一个不等式吗
解:(1)600x+100(10-x)≥4200
(2)8x+4(10-x)≤72
如果要配制的饮料同时满足两个小题的条件那么你能列出一个不等式组吗
你能尝试找出符合上面一元一次不等式组(*)的未知数的值吗 与同伴交流.
解不等式组
解:解不等式①,得
解不等式②,得
x≥6.4.
x≤8.
600x+100(10-x)≥4200 , ①
8x+4(10-x)≤72 . ②
不等式组
的解集就是 x≥6.4与x≤8的公共部分.
我们在同一数轴上把 x≥6.4与x≤8表示出来,如图所示
0
6.4
8
由图容易发现它们的公共部分是6.4≤x≤8,这就是由不等式①、②组成的不等式组 的解集.
600x+100(10-x)≥4200 ,①
8x+4(10-x)≤72 . ②
600x+100(10-x)≥4200 ,
8x+4(10-x)≤72 .
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集.
求不等式组的解集的过程,叫做解不等式组.
小tip:确定几个不等式的解集的公共部分的方法是先将几个不等式的解集在同一条数轴上表示出来,然后找出它们重叠的部分.
0
-3
3
x
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
所以这个不等式组的解集为 -3<x≤3.
试一试:借助数轴表示出不等式组 的解集.
x>-3. ②
x≤3, ①
公共部分
①
②
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
a b
a b
a b
a b
同大取大
同小取小
大小、小大中间找
大大小小无处找
x>b
x<a
a<x<b
无解
x
x
x
x
填表:
不等式组
不等式组的解集
x>-3
-5<x≤-3
x< -3
无解
解不等式②,得
x<6.
例1 解不等式组:
解: 解不等式①,得
在同一条数轴上表示不等式①②的解集,如图:
3
0
6
因此,原不等式组的解集为
①
②
解一元一次不等式组的一般步骤:
1.求出这个不等式组中各个不等式的解集;
2.利用数轴找寻这些不等式的解集的公共部分,即求出了这个不等式组的解集;若这些不等式的解集没有公共部分,则这个不等式组无解;
3.表示这个不等式组的解集.
解不等式②,得
x >4.
1. 解不等式组:
解: 解不等式①,得
x >2.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
2
0
4
所以这个不等式组的解集是 x> 4.
x
1.若关于 x 的不等式组的解表示在数轴上如图所示,则这个不等式组的解集为( )
A. x ≤ 2 B. x > 1
C. 1 < x < 2 D. 1< x ≤ 2
D
2.不等式组 的解集在数轴上表示正确的是( )
D
3.解不等式组:
5x–2>3(x+1), ①
x-1≥7-x. ②
解:解不等式①,得 x> .
解不等式②,得 x≥4 .
在同一条数轴上表示不等式①②的解集,如图
0
1
2
3
4
5
所以原不等式组的解集为 x≥4 .
A
4.若关于x的不等式组 有且只有3个整数解则满足条
件的所有整数a的和是( )
A.-3 B. -2 C. -5 D. -6
概念
一元一次不等式组的解法
关于同一未知数的几个一元一次不等式合在一起
(1)求各个不等式的解集;
(2)在数轴上表示各个不等式的解集;
(3)找出各个不等式解集的公共部分.
解集
步骤
一元一次不等式组中各个不等式的解集的公共部分
2.6 一元一次不等式组
第1课时 一元一次不等式组的解法(1)
1. 理解一元一次不等式组的概念;(重点)
2. 会解一元一次不等式组.(难点)
1.什么是一元一次不等式?
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
2.如何在数轴上表示不等式的解集?
(1)大于向右,小于向左;
(2)有等号是用实心圆点,无等号时用空心圆圈.
a
b
同学们,你能根据上图对话片断估计出这头大象的体重范围吗 请说说你的理由!
若设大象的体重为 x 吨,请用不等式的知识分别表示上面两位同学所谈话的内容:
x ≥3 ①
x<5 ②
看,这头大象好大呀,体重肯定不少于 3 吨!
嗨,我听说管理员说,这头大象的体重不足 5 吨呢!
某校今年冬季烧煤取暖时间为4个月. 如果每月比计划多烧5t煤,那么取暖用煤量将超过100t;如果每月比计划少烧5t 煤,那么取暖用煤总量不足68t.若该校计划每月烧煤 xt,则 x 满足怎样的关系式?
4(x + 5) > 100,
4(x - 5) < 68.
根据题意,得 4(x + 5) > 100, ① 且4(x - 5) < 68. ②
未知数x同时满足①②两个条件.把①②两个不等式合在一起,就组成一个一元一次不等式组,记作
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
注意:1.几个指两个或两个以上;
2.只有一个未知数;
3.由一元一次不等式组成.
一元一次不等式组的概念:
1.下列各不等式组,其中是一元一次不等式组的有________.(填序号)
③④⑤
确定一个不等式组是一元一次不等式组需要满足三点:
(1)不等式组中只有一个未知数;
(2)未知数的最高次数是1;
(3)组成不等式的代数式都是整式.
用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C的含量及购买这两种原料的价格如下表所示:
(1)现配制这种饮料10kg,要求至少含有4200单位的维生素C,试写出所需甲种原料的质量x(kg)应满足的不等式;
(2)如果还要求购买甲、乙两种原料的费用不超过 72元,那么你能写出x(kg)应满足的另一个不等式吗
解:(1)600x+100(10-x)≥4200
(2)8x+4(10-x)≤72
如果要配制的饮料同时满足两个小题的条件那么你能列出一个不等式组吗
你能尝试找出符合上面一元一次不等式组(*)的未知数的值吗 与同伴交流.
解不等式组
解:解不等式①,得
解不等式②,得
x≥6.4.
x≤8.
600x+100(10-x)≥4200 , ①
8x+4(10-x)≤72 . ②
不等式组
的解集就是 x≥6.4与x≤8的公共部分.
我们在同一数轴上把 x≥6.4与x≤8表示出来,如图所示
0
6.4
8
由图容易发现它们的公共部分是6.4≤x≤8,这就是由不等式①、②组成的不等式组 的解集.
600x+100(10-x)≥4200 ,①
8x+4(10-x)≤72 . ②
600x+100(10-x)≥4200 ,
8x+4(10-x)≤72 .
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集.
求不等式组的解集的过程,叫做解不等式组.
小tip:确定几个不等式的解集的公共部分的方法是先将几个不等式的解集在同一条数轴上表示出来,然后找出它们重叠的部分.
0
-3
3
x
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
所以这个不等式组的解集为 -3<x≤3.
试一试:借助数轴表示出不等式组 的解集.
x>-3. ②
x≤3, ①
公共部分
①
②
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
a b
a b
a b
a b
同大取大
同小取小
大小、小大中间找
大大小小无处找
x>b
x<a
a<x<b
无解
x
x
x
x
填表:
不等式组
不等式组的解集
x>-3
-5<x≤-3
x< -3
无解
解不等式②,得
x<6.
例1 解不等式组:
解: 解不等式①,得
在同一条数轴上表示不等式①②的解集,如图:
3
0
6
因此,原不等式组的解集为
①
②
解一元一次不等式组的一般步骤:
1.求出这个不等式组中各个不等式的解集;
2.利用数轴找寻这些不等式的解集的公共部分,即求出了这个不等式组的解集;若这些不等式的解集没有公共部分,则这个不等式组无解;
3.表示这个不等式组的解集.
解不等式②,得
x >4.
1. 解不等式组:
解: 解不等式①,得
x >2.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
2
0
4
所以这个不等式组的解集是 x> 4.
x
1.若关于 x 的不等式组的解表示在数轴上如图所示,则这个不等式组的解集为( )
A. x ≤ 2 B. x > 1
C. 1 < x < 2 D. 1< x ≤ 2
D
2.不等式组 的解集在数轴上表示正确的是( )
D
3.解不等式组:
5x–2>3(x+1), ①
x-1≥7-x. ②
解:解不等式①,得 x> .
解不等式②,得 x≥4 .
在同一条数轴上表示不等式①②的解集,如图
0
1
2
3
4
5
所以原不等式组的解集为 x≥4 .
A
4.若关于x的不等式组 有且只有3个整数解则满足条
件的所有整数a的和是( )
A.-3 B. -2 C. -5 D. -6
概念
一元一次不等式组的解法
关于同一未知数的几个一元一次不等式合在一起
(1)求各个不等式的解集;
(2)在数轴上表示各个不等式的解集;
(3)找出各个不等式解集的公共部分.
解集
步骤
一元一次不等式组中各个不等式的解集的公共部分
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
