3.1图形的平移 第1课时 平移的概念与性质 课件(共28张PPT)
文档属性
| 名称 | 3.1图形的平移 第1课时 平移的概念与性质 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 06:30:02 | ||
图片预览







文档简介
(共28张PPT)
第三章 图形的平移与旋转
游乐园的一些娱乐项目曾经让你流连忘返,但不知你是否观察过,旋转的木马、荡起的秋千、开动的小火车……这些物体的运动有什么特点 传送带上物体随传送带一起运动、电梯里人们乘电梯上上下下、钟表上指针随时间的流逝周而复始、风扇中叶片飞速地转动……这些现象中蕴含着怎样的运动和变化形式
本章将在小学学习的基础上进一步认识平面图形的平移和旋转,探索平移、旋转的性质,认识并欣赏平移、中心对称在自然界和现实生活中的应用.
3.1 图形的平移
第1课时 平移的概念与性质
1. 理解平移的概念及会找出平移前后图形中对应点、对应角和对应线段;(重点)
2. 掌握平移的性质及运用.(难点)
情 境 导 入
上面图片反映的是日常生活中物体运动的一些场景,你还能举出一些类似的例子吗 这些运动现象有什么共同的特点
它们都在___________________移动.
沿着某一个方向
平 移
你还能举出一些平移的例子吗?
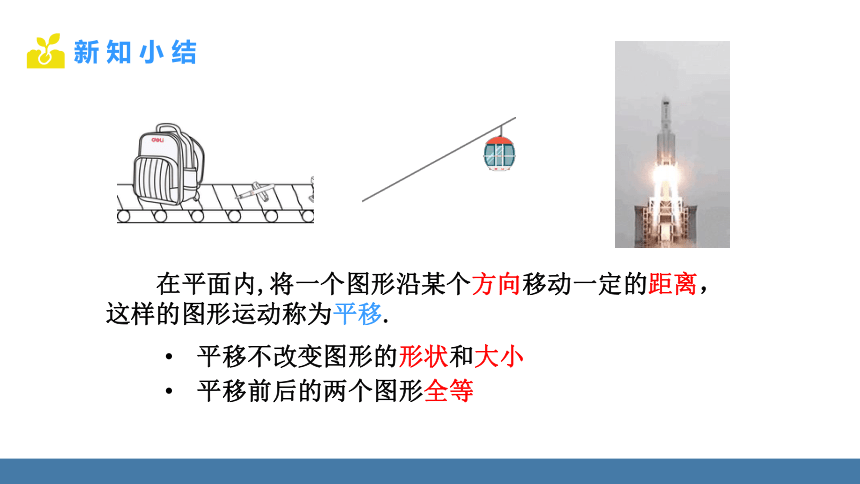
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移不改变图形的形状和大小
平移前后的两个图形全等
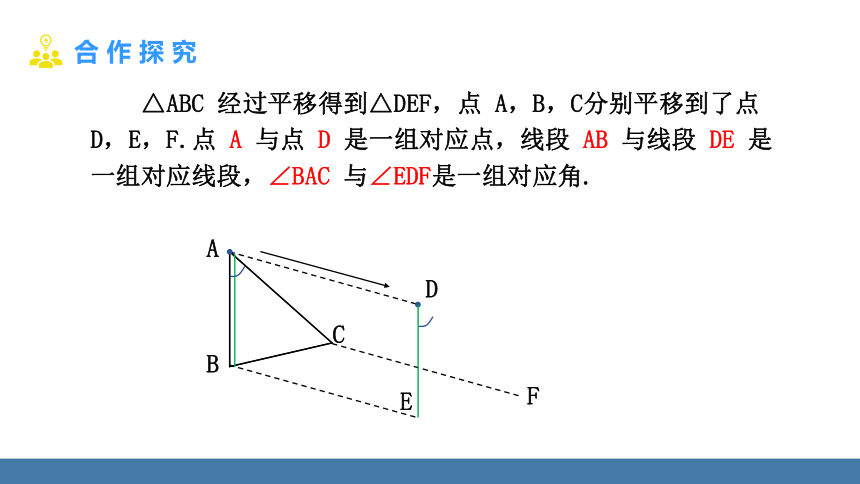
△ABC 经过平移得到△DEF,点 A,B,C分别平移到了点 D,E,F.点 A 与点 D 是一组对应点,线段 AB 与线段 DE 是一组对应线段,∠BAC 与∠EDF是一组对应角.
A
B
C
D
E
F
A
B
C
D
E
F
你还能从图中找出其他的对应点、对应线段和对应角吗?
对应点:B 和 E,C 和 F.
对应线段:BC 和 EF,AC 和 DF.
对应角:∠ABC 和∠DEF,
∠ACB 和∠DFE.
例1 如图,下列各组图形中,可以经过平移由一个图形得到另一个图形的是( )
A
1.下列各组图形中,可以通过平移得到的是___________.
③④⑤
2.如图,△ABC经过平移得到△A′B′C′,则图中平行线段共有( )
A.3对 B.4对
C.5对 D.6对
D
将如图所示的四边形硬纸片按某一方向平移一定距离.画出了平移前的四边形 ABCD 和平移后的四边形 EFGH.
D
A
B
C
E
F
G
H
(1)在图中任意选一组对应线段,这两条线段之间有怎样的位置和数量关系
(2)在图中任意选一组对应角,这两个角之间有怎样的关系
(3)连接对应点的线段AE, BF, CG, DH之间有怎样位置和数量的关系
D
A
B
C
E
F
G
H
(1)在图中任意选一组对应线段,这两条线段之间有怎样的位置和数量关系
解:(1)平行且相等.
(2)在图中任意选一组对应角,这两个角之间有怎样的关系
(2)相等.
(3)连接对应点的线段AE, BF, CG, DH之间有怎样位置和数量的关系
(3)平行且相等.
平移性质归纳
平移的性质 数量关系 位置关系
①
②
③
相等
相等
相等
平行(或在同一条直线上)
平行(或在同一条直线上)
对应线段
对应角
对应点的连线
例2 如图,经过平移,△ABC 的顶点 A移到了点 D.
(1)指出平移的方向和平移的距离;
(2)画出平移后的三角形.
A
B
C
D
解:(1)如图,连接AD,平移的方向是点 A到点 D 的方向,平移的距离是线段 AD 的长度.
(2)如图,分别过点B,C按射线AD的方向作线段BE,CF,使得它们与线段AD平行且相等,连接 DE,DF,EF,△DEF就是△ABC平移后的图形.
A
B
C
D
E
F
1.确定图形的特殊点;
3.在平行线上截取特殊点移动的距离,确定特殊点平移后的位置;
2.过特殊点沿平移的方向作平行线;
平移作图步骤:
4.按原图方式连接平移后的各点.
作图依据 平移前后对应点所连的线段平行且相等.
3.已知△ABD沿BD平移到了△FCE的位置,CE=10,CD=4,则平移的方向是____________________,平移的距离是 _____.
6
点B到点C的方向
请在图中找出平行且相等的线段,以及相等的角
相等的角:
AB和DE ;
BC和DF ;
AC和EF;
AE和BD ;
BD和CF ;
AE和CF.
∠BAC和∠DEF ;
∠ABC和∠EDF ;
∠ACB和∠DFE.
平行且相等的线段:
A
B
C
D
E
F
你还有其他画△DEF的方法吗?
作法:
1、过点D分别作线段AB、AC的平行线DM、DN
2、在DM、DN上截取DE=AB,DF=AC
3、连接D,E,F所以, △DEF即为所求作的三角形
M
N
E
确定一个图形平移后的位置,需要哪些条件?
原图形的位置
平移的方向
平移的距离
1. 以下现象:
①打开教室的门,门的移动;②打气筒打气时,活塞的运动;
③钟摆的摆动; ④直传送带上,瓶装饮料的移动.
属于平移的是 .
②④
2.如图,将周长为9 cm的△ABC沿边BC向右平移3 cm,得到△DEF,连接AD,则四边形ABFD的周长为( B )
A.17 cm B.15 cm C.13 cm D.12 cm
第2题图
B
3.如图,在△ABC中,∠C=90°,AC=BC=5.现将△ABC沿着CB的方向平移到△A'B'C'的位置.若平移的距离为2,则图中阴影部分的面积为 8 .
第3题图
8
3.如图,平移四边形ABCD,使点A移动到点A′,画出平移后的四边形A′B′C′D′,并指出平移的方向和平移的距离.
解:如图,平移的方向为AA′所在射线方向,平移的距离为线段AA′的长.
(1)解:∵在Rt△ABC中,
∠ACB=90°,∠A=33°,
∴∠CBA=180°-90°-33°=57°.
由平移得,BC∥EF,
∴∠E=∠CBA=57°.
4.如图,在Rt△ABC中,∠ACB=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.
(1)试求出∠E的度数;
4.如图,在Rt△ABC中,∠ACB=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.
(2)若AE=13 cm,DB=2 cm,请求出CF的长度.
(2)解:由平移得,AD=BE=CF.
∵AE=13 cm,DB=2 cm,
∴AD=BE=×(13-2)=5.5(cm),
∴CF=5.5 cm.
定义
图形的平移
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
①平移前后的图形是全等形②对应点及对应线段所连的线段平行(或在条直线上)且相等;对应角相等.
性质
第三章 图形的平移与旋转
游乐园的一些娱乐项目曾经让你流连忘返,但不知你是否观察过,旋转的木马、荡起的秋千、开动的小火车……这些物体的运动有什么特点 传送带上物体随传送带一起运动、电梯里人们乘电梯上上下下、钟表上指针随时间的流逝周而复始、风扇中叶片飞速地转动……这些现象中蕴含着怎样的运动和变化形式
本章将在小学学习的基础上进一步认识平面图形的平移和旋转,探索平移、旋转的性质,认识并欣赏平移、中心对称在自然界和现实生活中的应用.
3.1 图形的平移
第1课时 平移的概念与性质
1. 理解平移的概念及会找出平移前后图形中对应点、对应角和对应线段;(重点)
2. 掌握平移的性质及运用.(难点)
情 境 导 入
上面图片反映的是日常生活中物体运动的一些场景,你还能举出一些类似的例子吗 这些运动现象有什么共同的特点
它们都在___________________移动.
沿着某一个方向
平 移
你还能举出一些平移的例子吗?
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移不改变图形的形状和大小
平移前后的两个图形全等
△ABC 经过平移得到△DEF,点 A,B,C分别平移到了点 D,E,F.点 A 与点 D 是一组对应点,线段 AB 与线段 DE 是一组对应线段,∠BAC 与∠EDF是一组对应角.
A
B
C
D
E
F
A
B
C
D
E
F
你还能从图中找出其他的对应点、对应线段和对应角吗?
对应点:B 和 E,C 和 F.
对应线段:BC 和 EF,AC 和 DF.
对应角:∠ABC 和∠DEF,
∠ACB 和∠DFE.
例1 如图,下列各组图形中,可以经过平移由一个图形得到另一个图形的是( )
A
1.下列各组图形中,可以通过平移得到的是___________.
③④⑤
2.如图,△ABC经过平移得到△A′B′C′,则图中平行线段共有( )
A.3对 B.4对
C.5对 D.6对
D
将如图所示的四边形硬纸片按某一方向平移一定距离.画出了平移前的四边形 ABCD 和平移后的四边形 EFGH.
D
A
B
C
E
F
G
H
(1)在图中任意选一组对应线段,这两条线段之间有怎样的位置和数量关系
(2)在图中任意选一组对应角,这两个角之间有怎样的关系
(3)连接对应点的线段AE, BF, CG, DH之间有怎样位置和数量的关系
D
A
B
C
E
F
G
H
(1)在图中任意选一组对应线段,这两条线段之间有怎样的位置和数量关系
解:(1)平行且相等.
(2)在图中任意选一组对应角,这两个角之间有怎样的关系
(2)相等.
(3)连接对应点的线段AE, BF, CG, DH之间有怎样位置和数量的关系
(3)平行且相等.
平移性质归纳
平移的性质 数量关系 位置关系
①
②
③
相等
相等
相等
平行(或在同一条直线上)
平行(或在同一条直线上)
对应线段
对应角
对应点的连线
例2 如图,经过平移,△ABC 的顶点 A移到了点 D.
(1)指出平移的方向和平移的距离;
(2)画出平移后的三角形.
A
B
C
D
解:(1)如图,连接AD,平移的方向是点 A到点 D 的方向,平移的距离是线段 AD 的长度.
(2)如图,分别过点B,C按射线AD的方向作线段BE,CF,使得它们与线段AD平行且相等,连接 DE,DF,EF,△DEF就是△ABC平移后的图形.
A
B
C
D
E
F
1.确定图形的特殊点;
3.在平行线上截取特殊点移动的距离,确定特殊点平移后的位置;
2.过特殊点沿平移的方向作平行线;
平移作图步骤:
4.按原图方式连接平移后的各点.
作图依据 平移前后对应点所连的线段平行且相等.
3.已知△ABD沿BD平移到了△FCE的位置,CE=10,CD=4,则平移的方向是____________________,平移的距离是 _____.
6
点B到点C的方向
请在图中找出平行且相等的线段,以及相等的角
相等的角:
AB和DE ;
BC和DF ;
AC和EF;
AE和BD ;
BD和CF ;
AE和CF.
∠BAC和∠DEF ;
∠ABC和∠EDF ;
∠ACB和∠DFE.
平行且相等的线段:
A
B
C
D
E
F
你还有其他画△DEF的方法吗?
作法:
1、过点D分别作线段AB、AC的平行线DM、DN
2、在DM、DN上截取DE=AB,DF=AC
3、连接D,E,F所以, △DEF即为所求作的三角形
M
N
E
确定一个图形平移后的位置,需要哪些条件?
原图形的位置
平移的方向
平移的距离
1. 以下现象:
①打开教室的门,门的移动;②打气筒打气时,活塞的运动;
③钟摆的摆动; ④直传送带上,瓶装饮料的移动.
属于平移的是 .
②④
2.如图,将周长为9 cm的△ABC沿边BC向右平移3 cm,得到△DEF,连接AD,则四边形ABFD的周长为( B )
A.17 cm B.15 cm C.13 cm D.12 cm
第2题图
B
3.如图,在△ABC中,∠C=90°,AC=BC=5.现将△ABC沿着CB的方向平移到△A'B'C'的位置.若平移的距离为2,则图中阴影部分的面积为 8 .
第3题图
8
3.如图,平移四边形ABCD,使点A移动到点A′,画出平移后的四边形A′B′C′D′,并指出平移的方向和平移的距离.
解:如图,平移的方向为AA′所在射线方向,平移的距离为线段AA′的长.
(1)解:∵在Rt△ABC中,
∠ACB=90°,∠A=33°,
∴∠CBA=180°-90°-33°=57°.
由平移得,BC∥EF,
∴∠E=∠CBA=57°.
4.如图,在Rt△ABC中,∠ACB=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.
(1)试求出∠E的度数;
4.如图,在Rt△ABC中,∠ACB=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.
(2)若AE=13 cm,DB=2 cm,请求出CF的长度.
(2)解:由平移得,AD=BE=CF.
∵AE=13 cm,DB=2 cm,
∴AD=BE=×(13-2)=5.5(cm),
∴CF=5.5 cm.
定义
图形的平移
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
①平移前后的图形是全等形②对应点及对应线段所连的线段平行(或在条直线上)且相等;对应角相等.
性质
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
