6.2平行四边形的判定 第1课时 利用边判定平行四边形 课件(共19张PPT)
文档属性
| 名称 | 6.2平行四边形的判定 第1课时 利用边判定平行四边形 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 06:35:55 | ||
图片预览



文档简介
(共19张PPT)
6.2 平行四边形的判定
第1课时 利用边判定平行四边形
1. 探究平行四边形的判定方法;(重点)
2. 理解平行四边形的判定方法并会灵活应用.(难点)
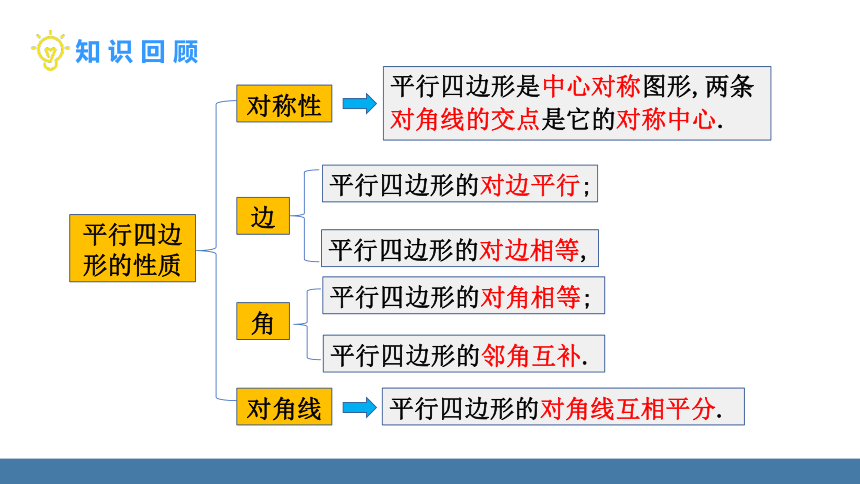
平行四边形的对边平行;
平行四边形的对边相等,
平行四边形的对角相等;
平行四边形的邻角互补.
平行四边形的对角线互相平分.
平行四边形的性质
边
角
对角线
对称性
平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
除了定义法判定平行四边形,还有没有其他方法呢?下面我们一起来探究!
问题:如何判定一个四边形是平行四边形呢?
B C
A D
根据定义就可以判定一个四边形是否为平行四边形:
如果一个四边形的两组对边分别平行,那么这个四边形就是平行四边形.
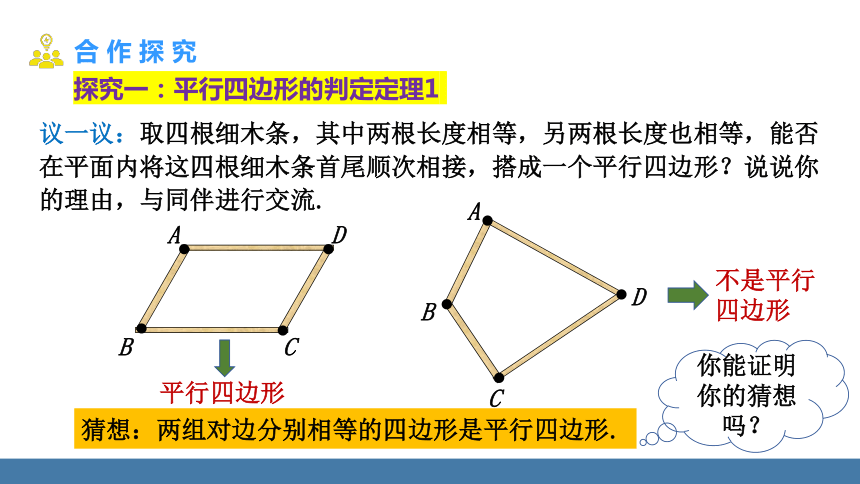
探究一:平行四边形的判定定理1
议一议:取四根细木条,其中两根长度相等,另两根长度也相等,能否在平面内将这四根细木条首尾顺次相接,搭成一个平行四边形?说说你的理由,与同伴进行交流.
猜想:两组对边分别相等的四边形是平行四边形.
A D
B C
B
A
C
D
不是平行四边形
平行四边形
你能证明你的猜想吗?
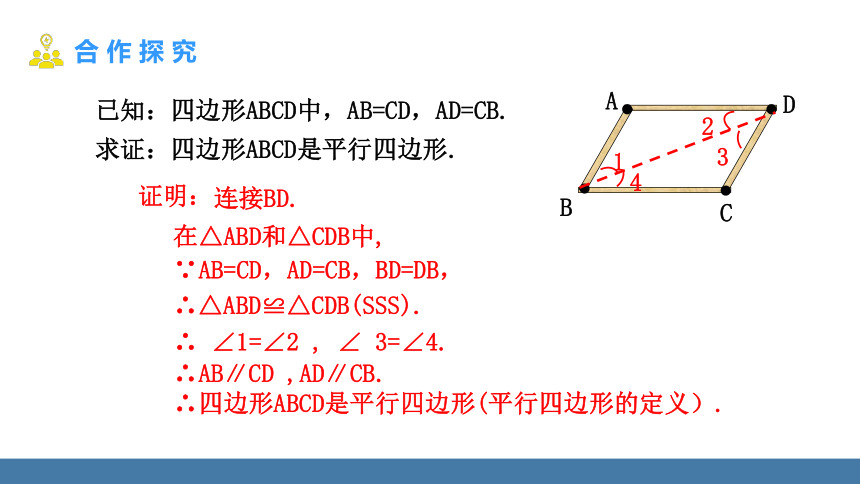
已知:四边形ABCD中,AB=CD,AD=CB.
求证:四边形ABCD是平行四边形.
A
B
C
D
连接BD.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB(SSS).
∴ ∠1=∠2 , ∠ 3=∠4.
∴AB∥CD ,AD∥CB.
∴四边形ABCD是平行四边形(平行四边形的定义).
证明:
1
4
2
3
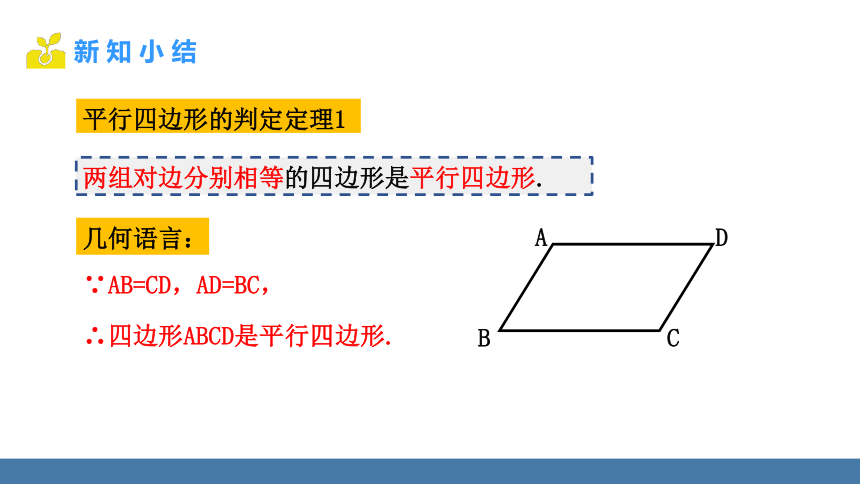
两组对边分别相等的四边形是平行四边形.
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形的判定定理1
B
D
C
A
例1 如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且AF=CE.
求证:四边形AECF为平行四边形.
B
A
C
D
F
E
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
∵AF=CE,
∴AD-AF=BC-CE,即DF=BE.
∴△ABE≌△CDF(SAS).
∴AE=CF.
又∵AF=CE,
∴四边形AECF是平行四边形(两组对边分别相等的四边形是平行四边形).
1.如图所示,在四边形ABCD中,AB=CD,BC=AD.若∠B=110°,则∠A的度数为( )
A.110° B.80°
C.70° D.90°
C
2.如图所示,在四边形ABCD中,AB=5,BC=8,当CD= ,AD= 时,四边形ABCD是平行四边形.
5
8
议一议:(1)取两根长度相等的细木条AD、BC,你能将它们摆放在一张纸上,使得这两根细木条的四个端恰好是一个平行四边形的四个顶点吗?
猜想:一组对边平行且相等的四边形是平行四边形.
探究二:平行四边形的判定定理2
将细木条AD、BC平行摆放
四边形ABCD是平行四边形
证明你的猜想.
A D
B C
D
A
B
C
已知:如图,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD是平行四边形.
∵AB//CD,
∴∠BAC=∠DCA.
又∵AB=CD,AC=CA,
∴△ABC≌△CDA(SAS).
∴BC=DA.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
证明:连接AC.
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形的判定定理2
B
D
C
A
例2 已知:如图,在 ABCD中,E,F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
D
A
B
C
E
F
证明:∵四边形ABCD是平行四边形,
∴AD=BC(平行四边形的对边相等),
AD∥BC(平行四边形的定义).
∵E,F分别是AD,CB的中点,
∴ED=AD,FB= CB.
∴ED=FB,ED∥FB.
∴四边形BFDE是平行四边形
(一组对边平行且相等的四边形是平行四边形).
D
A
B
C
E
F
例3 如图,AC=BD,AB=CD=EF,CE=DF.图中有哪些互相平行的线段?为什么?
解:∵AC=BD, AB=CD,
∴四边形ABDC是平行四边形,
∴AB∥CD,AC∥BD,
∵CD=EF,CE=DF,
∴四边形CDFE是平行四边形,
∴CD∥EF,CE∥DF,
∵CD∥EF,AB∥CD,
∴EF∥AB.
5.如图所示,在四边形ABCD中,对角线BD⊥AD,BD⊥BC,AD=11-x,BC=x-5,则当x= 时,四边形ABCD是平行四边形.
4.如图所示,D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,CB,则四边形ABCD是 ,理由是_______________________________________.
平行四边形
两组对边分别相等的四边形是平行四边形
8
3.下列条件中,不能使四边形ABCD是平行四边形的是( )
A.AB∥CD,AB=CD B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD D.AB=CD,BC=AD
C
1.能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD=BC B.AB=CD,AD=BC
C.∠A=∠B,∠C=∠D D.AB=AD,CB=CD
B
2.下列叙述正确的的有( )
①对角线互相垂直的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③一组对边平行,另一组对边相等的四边形是平行四边形.
A.3个 B.2个 C.1个 D.0个
C
3.在四边形ABCD中:①AB∥CD;②AD∥BC;③AB=CD;④AD=BC.从以上条件中选择两个条件,使四边形ABCD为平行四边形的选法共有( )
A.3种 B.4种 C.5种 D.6种
B
6.已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1).若以O,A,B,C为顶点的四边形是平行四边形,则x= .
4.在四边形ABCD中,AD=8cm,AB=4cm.当BC=___cm,CD=_____cm 时,四边形ABCD为平行四边形.
5.在四边形ABCD中,AD=BC,BD为对角线,∠ADB=∠CBD,则AB和CD的关系为_________.
8
4
相等
4或-2
7.如图所示,BD是△ABC的角平分线,DE∥BC交AB于点E,EF∥AC交BC于点F,猜想BE与CF之间的数量关系,并加以证明.
证明:BE=CF.
∵DE∥BC,
∴∠DBC=∠BDE.
∵BD是△ABC的角平分线,
∴∠DBC=∠ABD.
∴∠ABD=∠BDE.
∴DE=BE.
∵DE∥BC,EF∥AC,
∴四边形DEFC是平行四边形.
∴DE=CF.
∴BE=CF.
平行四边形的判定(1)
判定定理1
判定定理2
定义法
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
6.2 平行四边形的判定
第1课时 利用边判定平行四边形
1. 探究平行四边形的判定方法;(重点)
2. 理解平行四边形的判定方法并会灵活应用.(难点)
平行四边形的对边平行;
平行四边形的对边相等,
平行四边形的对角相等;
平行四边形的邻角互补.
平行四边形的对角线互相平分.
平行四边形的性质
边
角
对角线
对称性
平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
除了定义法判定平行四边形,还有没有其他方法呢?下面我们一起来探究!
问题:如何判定一个四边形是平行四边形呢?
B C
A D
根据定义就可以判定一个四边形是否为平行四边形:
如果一个四边形的两组对边分别平行,那么这个四边形就是平行四边形.
探究一:平行四边形的判定定理1
议一议:取四根细木条,其中两根长度相等,另两根长度也相等,能否在平面内将这四根细木条首尾顺次相接,搭成一个平行四边形?说说你的理由,与同伴进行交流.
猜想:两组对边分别相等的四边形是平行四边形.
A D
B C
B
A
C
D
不是平行四边形
平行四边形
你能证明你的猜想吗?
已知:四边形ABCD中,AB=CD,AD=CB.
求证:四边形ABCD是平行四边形.
A
B
C
D
连接BD.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB(SSS).
∴ ∠1=∠2 , ∠ 3=∠4.
∴AB∥CD ,AD∥CB.
∴四边形ABCD是平行四边形(平行四边形的定义).
证明:
1
4
2
3
两组对边分别相等的四边形是平行四边形.
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形的判定定理1
B
D
C
A
例1 如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且AF=CE.
求证:四边形AECF为平行四边形.
B
A
C
D
F
E
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
∵AF=CE,
∴AD-AF=BC-CE,即DF=BE.
∴△ABE≌△CDF(SAS).
∴AE=CF.
又∵AF=CE,
∴四边形AECF是平行四边形(两组对边分别相等的四边形是平行四边形).
1.如图所示,在四边形ABCD中,AB=CD,BC=AD.若∠B=110°,则∠A的度数为( )
A.110° B.80°
C.70° D.90°
C
2.如图所示,在四边形ABCD中,AB=5,BC=8,当CD= ,AD= 时,四边形ABCD是平行四边形.
5
8
议一议:(1)取两根长度相等的细木条AD、BC,你能将它们摆放在一张纸上,使得这两根细木条的四个端恰好是一个平行四边形的四个顶点吗?
猜想:一组对边平行且相等的四边形是平行四边形.
探究二:平行四边形的判定定理2
将细木条AD、BC平行摆放
四边形ABCD是平行四边形
证明你的猜想.
A D
B C
D
A
B
C
已知:如图,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD是平行四边形.
∵AB//CD,
∴∠BAC=∠DCA.
又∵AB=CD,AC=CA,
∴△ABC≌△CDA(SAS).
∴BC=DA.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
证明:连接AC.
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形的判定定理2
B
D
C
A
例2 已知:如图,在 ABCD中,E,F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
D
A
B
C
E
F
证明:∵四边形ABCD是平行四边形,
∴AD=BC(平行四边形的对边相等),
AD∥BC(平行四边形的定义).
∵E,F分别是AD,CB的中点,
∴ED=AD,FB= CB.
∴ED=FB,ED∥FB.
∴四边形BFDE是平行四边形
(一组对边平行且相等的四边形是平行四边形).
D
A
B
C
E
F
例3 如图,AC=BD,AB=CD=EF,CE=DF.图中有哪些互相平行的线段?为什么?
解:∵AC=BD, AB=CD,
∴四边形ABDC是平行四边形,
∴AB∥CD,AC∥BD,
∵CD=EF,CE=DF,
∴四边形CDFE是平行四边形,
∴CD∥EF,CE∥DF,
∵CD∥EF,AB∥CD,
∴EF∥AB.
5.如图所示,在四边形ABCD中,对角线BD⊥AD,BD⊥BC,AD=11-x,BC=x-5,则当x= 时,四边形ABCD是平行四边形.
4.如图所示,D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,CB,则四边形ABCD是 ,理由是_______________________________________.
平行四边形
两组对边分别相等的四边形是平行四边形
8
3.下列条件中,不能使四边形ABCD是平行四边形的是( )
A.AB∥CD,AB=CD B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD D.AB=CD,BC=AD
C
1.能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD=BC B.AB=CD,AD=BC
C.∠A=∠B,∠C=∠D D.AB=AD,CB=CD
B
2.下列叙述正确的的有( )
①对角线互相垂直的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③一组对边平行,另一组对边相等的四边形是平行四边形.
A.3个 B.2个 C.1个 D.0个
C
3.在四边形ABCD中:①AB∥CD;②AD∥BC;③AB=CD;④AD=BC.从以上条件中选择两个条件,使四边形ABCD为平行四边形的选法共有( )
A.3种 B.4种 C.5种 D.6种
B
6.已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1).若以O,A,B,C为顶点的四边形是平行四边形,则x= .
4.在四边形ABCD中,AD=8cm,AB=4cm.当BC=___cm,CD=_____cm 时,四边形ABCD为平行四边形.
5.在四边形ABCD中,AD=BC,BD为对角线,∠ADB=∠CBD,则AB和CD的关系为_________.
8
4
相等
4或-2
7.如图所示,BD是△ABC的角平分线,DE∥BC交AB于点E,EF∥AC交BC于点F,猜想BE与CF之间的数量关系,并加以证明.
证明:BE=CF.
∵DE∥BC,
∴∠DBC=∠BDE.
∵BD是△ABC的角平分线,
∴∠DBC=∠ABD.
∴∠ABD=∠BDE.
∴DE=BE.
∵DE∥BC,EF∥AC,
∴四边形DEFC是平行四边形.
∴DE=CF.
∴BE=CF.
平行四边形的判定(1)
判定定理1
判定定理2
定义法
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
