6.2平行四边形的判定 第3课时 平行四边形的性质与判定的综合应用 课件(共21张PPT)
文档属性
| 名称 | 6.2平行四边形的判定 第3课时 平行四边形的性质与判定的综合应用 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 06:45:23 | ||
图片预览








文档简介
(共21张PPT)
6.2 平行四边形的判定
第3课时 平行四边形的性质与判定
的综合应用
1. 掌握平行线间的距离的概念及性质,会运用平行四边形的性质计算和证明;(重点)
2. 能够综合运用平行四边形的判定定理和性质.(难点)
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
两组对角分别相等的四边形是平行四边形(拓展)
对角线互相平分的四边形是平行四边形(判定定理3)
平行四边形的判定
这是小明家的楼梯,扶手是用实木制作的,这些竖直的实木
长度相等吗?
在笔直的铁轨上,夹在两根铁轨之间的平行枕木是否一样长 你能说明理由吗?与同伴交流.
探究一:平行线之间的距离
做一做:如图,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺度量出平行线之间的垂线段的长度.
经过度量,我们可以发现这些垂线段的长度都相等.
猜想:平行线间距离处处相等.
你能证明猜想的正确性吗?试一试.
a
b
A
B
C
D
1
2
例1 已知:如图,直线 a∥b,A,B 是直线 a 上任意两点,AC⊥b,BD⊥b,垂足分别为 C,D.
求证:AC = BD.
证明:∵AC⊥CD,BD⊥CD,
∴∠1=∠2=90°.
∴AC∥BD.
∵AB∥CD,
∴四边形ACDB是平行四边形(平行四边形的定义).
∴AC=BD(平行四边形的对边相等).
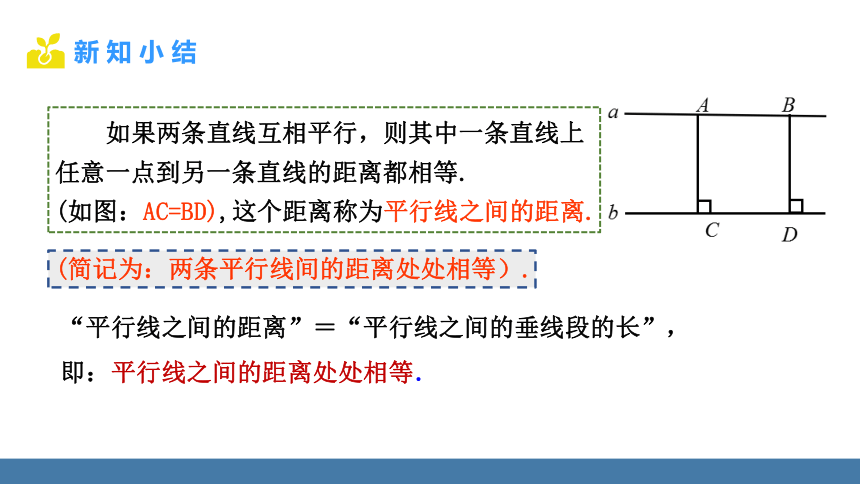
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等.
(如图:AC=BD),这个距离称为平行线之间的距离.
(简记为:两条平行线间的距离处处相等).
“平行线之间的距离”=“平行线之间的垂线段的长”,
即:平行线之间的距离处处相等.
例2 平行线之间的距离是指两条平行线中( )
A.从一条直线上一点到另一条直线的垂线段
B.从一条直线上一点到另一条直线的垂线段的长度
C.从一条直线上一点到另一条直线的垂线的长度
D.从一条直线上一点到另一条直线上的一点间线段的长度
B
2.在四边形ABCD中,AB∥CD,再添加下列其中一个条件后,四边形ABCD不一定是平行四边形的是( )
A.AB=CD B.AD=BC
C.AD∥BC D.∠A=∠C
1.如图所示,a∥b,AB∥CD,CE⊥b,FG⊥b,垂足分别为E,G,则下列说法中错误的是( )
A.AB=CD
B.CE=FG
C.A,B两点间的距离就是线段AB的长
D.直线a,b间的距离就是线段CD的长
D
B
3.如图,设点P是 ABCD的边AB上任意一点,设△APD的面积为S1,△BPC的面积为S2,△CDP的面积为S3,则 ( )
A.S3=S1+S2
B.S3>S1+S2
C.S3<S1+S2
D.S3=(S1+S2)
A
若垂线段改为夹在两条线段间的平行线段呢?它们是否相等呢?
由“两组对边分别平行的四边形是平行四边形”易知其围成的封闭图形为平行四边形,再由平行四边形性质易知夹在两条平行线间的平行线段相等.
解:
做一做 如图,以方格纸的格点为顶点画出几个平行四边形,并说明的画的方法和其中的道理.
C
B
F
E
A
D
由平行四边形的性质得AB=CD=EF.
四边形ABDC,DCEF均为平行四边形.
结论:夹在两条平行线间的平行线段一定相等.
道理: 一组对边平行且相等的四边形
是平行四边形.
画法:在方格纸分别取AC=BD,CE=DF,
再连接另一组对边即可.
证明:∵ 四边形ABCD是平行四边形,
∴ AD∥BC(平行四边形的定义).
∴ ∠MDF=∠NBE.
∵ DM=BN,DF=BE,
∴ △MDF≌△NBE(SAS).
∴ MF=NE,∠MFD=∠NEB.
∴ ∠MFE=∠NEF.
∴ MF∥NE.
∴ 四边形MENF是平行四边形(一组对边平行且相等的四边形是平行四边形).
例3 已知:如图,在□ABCD中,点M,N分别在AD和BC上,点E,F在BD上,且DM=BN,DF=BE.
求证:四边形MENF是平行四边形.
M
C
B
N
D
F
E
A
探究二:平行四边形判定方法的综合运用
4.如图所示,在 ABCD中,点E,F分别在BC,AD上,AC与EF相交于点O,且AO=CO.
(1)求证:△AOF≌△COE;
证明: (1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠OAF=∠OCE.
在△AOF和△COE中,
∵∠OAF=∠OCE,AO=CO,∠AOF=∠COE,
∴△AOF≌△COE(ASA).
(2)连接AE,CF,则四边形AECF (填“是”或“不是”)平行四边形,请说明理由,并指出最后一步推理的依据.
(2)理由如下:
由(1)得△AOF≌△COE,
∴FO=EO.
又∵AO=CO,
∴四边形AECF是平行四边形.
最后一步推理的依据是对角线互相平分的四边形是平行四边形.
(证明方法不同,最后一步推理的依据也可能不同)
是
2.如图所示,直线a∥b,点A,B分别在直线a,b上,∠1=45°,直线a和b之间的距离为3,则线段AB 的长度为 ( )
A. B.
C.3 D.6
1.如图所示,AD∥BC,AB⊥BC,DC⊥BC,AB=1,AD=2,
那么AD,BC 间的距离为 ( )
A.1 B.2 C.3 D.4
A
A
4.小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带来了两块碎玻璃,其编号应该是 .
3.已知直线m∥n,点A在直线m上,点B,C,D在直线n上,且AB=4 cm,AC=5 cm,AD=6 cm,则直线m与n之间的距离 ( )
A.等于5 cm B.等于6 cm
C.等于4 cm D.小于或等于4 cm
D
②③
5.如图所示,点B,F,C,E在同一条直线上,AB∥DE,AC∥DF,BF=CE,AD交BE于点O.
求证:AD与BE互相平分.
证明: 连接BD,AE.
∵AB∥DE,
∴∠ABC=∠DEF.
∵AC∥DF,
∴∠ACB=∠DFE.
∵BF=CE,
∴BC=EF.
在△ACB和△DFE中,
∵∠ABC=∠DEF,BC=EF, ∠ACB=∠DFE,
∴△ACB≌△DFE,
∴AB=DE.
又∵AB∥DE,
∴四边形ABDE是平行四边形,
∴AD与BE互相平分.
(2)若A,B,C为三个定点,点D在直线a上移动,那么无论点D移动到何处,总有 与△ABC的面积相等.这两个三角形底边AB上的高相等的理由是 .
6.如图,直线a∥b,A,B为直线b上两点,C,D为直线a上两点,AD与BC交于点E.
(1)请写出图中所有面积相等的三角形: ;
△ABD
平行线之间的距离处处相等
S△ABC=S△ABD,S△ACE=S△BDE,S△ACD=S△BCD
平行四边形的判定(3)
判定的综合应用
平行线之间的距离
五种判定方法.
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等,这个距离称为平行线之间的距离(简记为:两条平行线间的距离处处相等).
补充:夹在两条平行线间的平行线段相等.
6.2 平行四边形的判定
第3课时 平行四边形的性质与判定
的综合应用
1. 掌握平行线间的距离的概念及性质,会运用平行四边形的性质计算和证明;(重点)
2. 能够综合运用平行四边形的判定定理和性质.(难点)
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
两组对角分别相等的四边形是平行四边形(拓展)
对角线互相平分的四边形是平行四边形(判定定理3)
平行四边形的判定
这是小明家的楼梯,扶手是用实木制作的,这些竖直的实木
长度相等吗?
在笔直的铁轨上,夹在两根铁轨之间的平行枕木是否一样长 你能说明理由吗?与同伴交流.
探究一:平行线之间的距离
做一做:如图,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺度量出平行线之间的垂线段的长度.
经过度量,我们可以发现这些垂线段的长度都相等.
猜想:平行线间距离处处相等.
你能证明猜想的正确性吗?试一试.
a
b
A
B
C
D
1
2
例1 已知:如图,直线 a∥b,A,B 是直线 a 上任意两点,AC⊥b,BD⊥b,垂足分别为 C,D.
求证:AC = BD.
证明:∵AC⊥CD,BD⊥CD,
∴∠1=∠2=90°.
∴AC∥BD.
∵AB∥CD,
∴四边形ACDB是平行四边形(平行四边形的定义).
∴AC=BD(平行四边形的对边相等).
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等.
(如图:AC=BD),这个距离称为平行线之间的距离.
(简记为:两条平行线间的距离处处相等).
“平行线之间的距离”=“平行线之间的垂线段的长”,
即:平行线之间的距离处处相等.
例2 平行线之间的距离是指两条平行线中( )
A.从一条直线上一点到另一条直线的垂线段
B.从一条直线上一点到另一条直线的垂线段的长度
C.从一条直线上一点到另一条直线的垂线的长度
D.从一条直线上一点到另一条直线上的一点间线段的长度
B
2.在四边形ABCD中,AB∥CD,再添加下列其中一个条件后,四边形ABCD不一定是平行四边形的是( )
A.AB=CD B.AD=BC
C.AD∥BC D.∠A=∠C
1.如图所示,a∥b,AB∥CD,CE⊥b,FG⊥b,垂足分别为E,G,则下列说法中错误的是( )
A.AB=CD
B.CE=FG
C.A,B两点间的距离就是线段AB的长
D.直线a,b间的距离就是线段CD的长
D
B
3.如图,设点P是 ABCD的边AB上任意一点,设△APD的面积为S1,△BPC的面积为S2,△CDP的面积为S3,则 ( )
A.S3=S1+S2
B.S3>S1+S2
C.S3<S1+S2
D.S3=(S1+S2)
A
若垂线段改为夹在两条线段间的平行线段呢?它们是否相等呢?
由“两组对边分别平行的四边形是平行四边形”易知其围成的封闭图形为平行四边形,再由平行四边形性质易知夹在两条平行线间的平行线段相等.
解:
做一做 如图,以方格纸的格点为顶点画出几个平行四边形,并说明的画的方法和其中的道理.
C
B
F
E
A
D
由平行四边形的性质得AB=CD=EF.
四边形ABDC,DCEF均为平行四边形.
结论:夹在两条平行线间的平行线段一定相等.
道理: 一组对边平行且相等的四边形
是平行四边形.
画法:在方格纸分别取AC=BD,CE=DF,
再连接另一组对边即可.
证明:∵ 四边形ABCD是平行四边形,
∴ AD∥BC(平行四边形的定义).
∴ ∠MDF=∠NBE.
∵ DM=BN,DF=BE,
∴ △MDF≌△NBE(SAS).
∴ MF=NE,∠MFD=∠NEB.
∴ ∠MFE=∠NEF.
∴ MF∥NE.
∴ 四边形MENF是平行四边形(一组对边平行且相等的四边形是平行四边形).
例3 已知:如图,在□ABCD中,点M,N分别在AD和BC上,点E,F在BD上,且DM=BN,DF=BE.
求证:四边形MENF是平行四边形.
M
C
B
N
D
F
E
A
探究二:平行四边形判定方法的综合运用
4.如图所示,在 ABCD中,点E,F分别在BC,AD上,AC与EF相交于点O,且AO=CO.
(1)求证:△AOF≌△COE;
证明: (1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠OAF=∠OCE.
在△AOF和△COE中,
∵∠OAF=∠OCE,AO=CO,∠AOF=∠COE,
∴△AOF≌△COE(ASA).
(2)连接AE,CF,则四边形AECF (填“是”或“不是”)平行四边形,请说明理由,并指出最后一步推理的依据.
(2)理由如下:
由(1)得△AOF≌△COE,
∴FO=EO.
又∵AO=CO,
∴四边形AECF是平行四边形.
最后一步推理的依据是对角线互相平分的四边形是平行四边形.
(证明方法不同,最后一步推理的依据也可能不同)
是
2.如图所示,直线a∥b,点A,B分别在直线a,b上,∠1=45°,直线a和b之间的距离为3,则线段AB 的长度为 ( )
A. B.
C.3 D.6
1.如图所示,AD∥BC,AB⊥BC,DC⊥BC,AB=1,AD=2,
那么AD,BC 间的距离为 ( )
A.1 B.2 C.3 D.4
A
A
4.小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带来了两块碎玻璃,其编号应该是 .
3.已知直线m∥n,点A在直线m上,点B,C,D在直线n上,且AB=4 cm,AC=5 cm,AD=6 cm,则直线m与n之间的距离 ( )
A.等于5 cm B.等于6 cm
C.等于4 cm D.小于或等于4 cm
D
②③
5.如图所示,点B,F,C,E在同一条直线上,AB∥DE,AC∥DF,BF=CE,AD交BE于点O.
求证:AD与BE互相平分.
证明: 连接BD,AE.
∵AB∥DE,
∴∠ABC=∠DEF.
∵AC∥DF,
∴∠ACB=∠DFE.
∵BF=CE,
∴BC=EF.
在△ACB和△DFE中,
∵∠ABC=∠DEF,BC=EF, ∠ACB=∠DFE,
∴△ACB≌△DFE,
∴AB=DE.
又∵AB∥DE,
∴四边形ABDE是平行四边形,
∴AD与BE互相平分.
(2)若A,B,C为三个定点,点D在直线a上移动,那么无论点D移动到何处,总有 与△ABC的面积相等.这两个三角形底边AB上的高相等的理由是 .
6.如图,直线a∥b,A,B为直线b上两点,C,D为直线a上两点,AD与BC交于点E.
(1)请写出图中所有面积相等的三角形: ;
△ABD
平行线之间的距离处处相等
S△ABC=S△ABD,S△ACE=S△BDE,S△ACD=S△BCD
平行四边形的判定(3)
判定的综合应用
平行线之间的距离
五种判定方法.
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等,这个距离称为平行线之间的距离(简记为:两条平行线间的距离处处相等).
补充:夹在两条平行线间的平行线段相等.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
