6.1平行四边形的性质 第1课时 平行四边形边、角的性质 课件(共24张PPT)
文档属性
| 名称 | 6.1平行四边形的性质 第1课时 平行四边形边、角的性质 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 06:44:23 | ||
图片预览








文档简介
(共24张PPT)
第六章 平行四边形
生活中有哪些物体的形状是平行四边形 平行四边形有哪些性质 你能证明它们吗 取四根细木条,其中两根长度相等,另两根长度也相等,你能用这四根细木条搭出一个平行四边形吗 任意画一个四边形,依次连接它的各边中点,你能得到一个怎样的四边形呢
本章将研究平行四边形的性质与判定,以及三角形中位线的性质,还将探索多边形的内角和、外角和的规律;经历操作、实验等几何发现之旅,享受几何证明之完美.
6.1 平行四边形的性质
第1课时 平行四边形边、角的性质
1. 经历探索平行四边形有关概念和性质的过程,在活动中发展探究意识和合作交流的习惯;(重点)
2. 探索并掌握平行四边形的性质,并能简单应用.(难点)
平行四边形是生活中常见的图形,你能举出一些实例吗?
思考:满足什么样的条件才是平行四边形呢?平行四边形有什么特殊的性质呢?下面我们一起来探究!
探究一:平行四边形的相关概念
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
议一议:观察下列四边形,说说它们有什么特征?
梯形
平行四边形
你能给出平行四边形的定义吗?
A
B
C
D
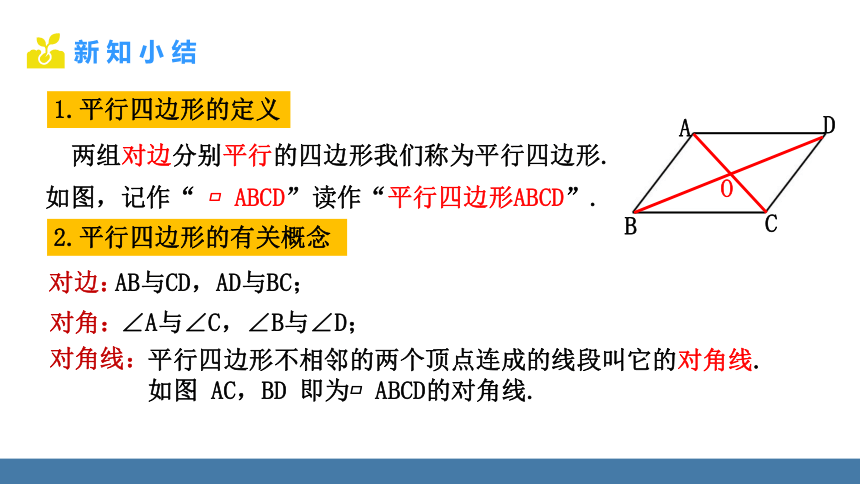
两组对边分别平行的四边形我们称为平行四边形.
读作“平行四边形ABCD”.
如图,记作“ ABCD”
AB与CD,AD与BC;
∠A与∠C,∠B与∠D;
平行四边形不相邻的两个顶点连成的线段叫它的对角线.
如图 AC,BD 即为 ABCD的对角线.
对角:
对角线:
1.平行四边形的定义
对边:
2.平行四边形的有关概念
O
∥
∥
例1 在四边形ABCD中,若AB CD,BC AD,则四边形ABCD为平行四边形.
[解析] 依据平行四边形的定义解答即可.
A
B
C
D
2.如图所示,已知 ABCD的面积为24,EF过AC,BD的交点O,则图中阴影部分的面积为 .
1.如图所示,点D,E,F分别在△ABC的边AB,BC,AC上,且DE∥AC,DF∥BC,EF∥AB,则图中有 个平行四边形.
3
12
做一做:动手操作,将两张完全相同的平行四边形纸片叠合在一起,下面的纸片看成原图形,旋转上面的纸片,你发现了什么
探究二:平行四边形的性质
□ABCD绕它的中心O旋转180°后与自身重合,这时我们说□ABCD是中心对称图形,两条对角线的交点O是它的对称中心.
平行四边形是什么图形?
平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
平行四边形的对称性
A
B
C
D
O
我们还发现:平行四边形的对边相等、对角相等.
议一议:小组合作,继续对平行四边形纸片进行研究,你还能发现哪些平行四边形的性质呢?发散你的思维,有不同的方法吗?
提示:可采取度量、平移、旋转、折叠、拼图、等方法探究平行四边形的边和角的数量关系.
尝试证明这些结论.
已知:四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
证明:连接AC
∵ 四边形ABCD是平行四边形
∴ AB∥CD,BC∥DA(平行四边形的定义)
∴ ∠1=∠2 ,∠3=∠4
∵ AC=CA
∴ △ABC ≌△CDA(ASA)
∴ AB=CD,BC=DA .
由上述证明过程你能得到平行四边形的对角相等吗?
∵△ABC≌ △CDA
∴∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3即∠BAD=∠DCB.
已知:四边形ABCD是平行四边形.
求证:∠A=∠C,∠B=∠D.
A
B
C
D
证明:∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠A+∠B=180 °
∠A+∠D=180 °
∴ ∠B=∠D
同理可得:∠A=∠C.
思考:不添加辅助线,你能否直接运用平行四边形的定义,证明
其对角相等?
平行四边形的性质定理
①平行四边形的对边 ; ②平行四边形的对角 .
相等
相等
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF(SAS).
∴ AB=CD,AB ∥ CD
又∵AE=CF,
∴BE=DF.
例2 已知:如图,在平行四边形ABCD中,E,F是对角线AC上的两点,且AE=CF.
求证:BE = DF.
A
D
B
C
E
F
4.如图所示,在 ABCD中,AD=3 cm,AB=2 cm,则 ABCD的周长等于( )
A.10 cm B.6 cm
C.5 cm D.4 cm
3.平行四边形ABCD的四个内角度数的比∠A∶∠B∶∠C∶∠D可以是( )
A.2∶3∶3∶2 B.2∶3∶2∶3
C.1∶2∶3∶4 D.2∶2∶1∶1
B
B
5.已知:如图所示,E是 ABCD的边BC延长线上的一点,且CE=BC.
求证:△ABC≌△DCE.
证明: ∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠DCE.
在△ABC和△DCE中,
∵AB=DC,∠B=∠DCE,BC=CE,
∴△ABC≌△DCE(SAS).
1.如图所示,将 ABCD沿对角线BD折叠,使点A落在点E处,DE与BC交于点F.若∠ABD=48°,∠CFD=40°,则∠E为( )
A.102° B.112° C.122° D.92°
2.如图所示,在平行四边形ABCD中,E是AB边上一点,连接DE,CE.若DE,CE分别是∠ADC,∠BCD的平分线,且AB=4,则平行四边形ABCD的周长为( )
A.10 B.8 C.5 D.12
D
B
4.在□ABCD中,∠A=150°,AB=8cm,BC=10cm,则S□ABCD= .
3.如图,在 ABCD中,∠ADC=125°,∠CAD=21°,求∠ABC= °,∠CAB= °.
125
34
40cm2
6.如图所示,平行四边形ABCO的顶点O,A,C的坐标分别为(0,0),(2,3),(5,0),则顶点B的坐标为 .
5.如图所示,在 ABCD中,过点C作CE⊥AB,垂足为E,若∠EAD=40°,则∠BCE的度数为 .
50°
(7,3)
7.如图所示,在 ABCD中,DE=CE,连接AE并延长,交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.
解: (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠ECF.
在△ADE和△FCE中,
∵∠D=∠ECF,DE=CE,∠AED=∠FEC,
∴△ADE≌△FCE.
(2)∵△ADE≌△FCE,
∴AD=FC.
∵四边形ABCD是平行四边形,
∴AD=BC,∴BC=FC.
又∵AB=2BC,
∴AB=FB,
∴∠BAF=∠F=36°,
∴∠B=180°-2×36°=108°.
两组对边分别平行的四边形是平行四边形.
平行四边形不相邻的两个顶点连成的线段叫它的对角线.
平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
平行四边形的对边相等,
平行四边形的对角相等.
平行四边形的性质(1)
平行四边形的定义
平行四边形的性质
对称性
性质定理
第六章 平行四边形
生活中有哪些物体的形状是平行四边形 平行四边形有哪些性质 你能证明它们吗 取四根细木条,其中两根长度相等,另两根长度也相等,你能用这四根细木条搭出一个平行四边形吗 任意画一个四边形,依次连接它的各边中点,你能得到一个怎样的四边形呢
本章将研究平行四边形的性质与判定,以及三角形中位线的性质,还将探索多边形的内角和、外角和的规律;经历操作、实验等几何发现之旅,享受几何证明之完美.
6.1 平行四边形的性质
第1课时 平行四边形边、角的性质
1. 经历探索平行四边形有关概念和性质的过程,在活动中发展探究意识和合作交流的习惯;(重点)
2. 探索并掌握平行四边形的性质,并能简单应用.(难点)
平行四边形是生活中常见的图形,你能举出一些实例吗?
思考:满足什么样的条件才是平行四边形呢?平行四边形有什么特殊的性质呢?下面我们一起来探究!
探究一:平行四边形的相关概念
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
议一议:观察下列四边形,说说它们有什么特征?
梯形
平行四边形
你能给出平行四边形的定义吗?
A
B
C
D
两组对边分别平行的四边形我们称为平行四边形.
读作“平行四边形ABCD”.
如图,记作“ ABCD”
AB与CD,AD与BC;
∠A与∠C,∠B与∠D;
平行四边形不相邻的两个顶点连成的线段叫它的对角线.
如图 AC,BD 即为 ABCD的对角线.
对角:
对角线:
1.平行四边形的定义
对边:
2.平行四边形的有关概念
O
∥
∥
例1 在四边形ABCD中,若AB CD,BC AD,则四边形ABCD为平行四边形.
[解析] 依据平行四边形的定义解答即可.
A
B
C
D
2.如图所示,已知 ABCD的面积为24,EF过AC,BD的交点O,则图中阴影部分的面积为 .
1.如图所示,点D,E,F分别在△ABC的边AB,BC,AC上,且DE∥AC,DF∥BC,EF∥AB,则图中有 个平行四边形.
3
12
做一做:动手操作,将两张完全相同的平行四边形纸片叠合在一起,下面的纸片看成原图形,旋转上面的纸片,你发现了什么
探究二:平行四边形的性质
□ABCD绕它的中心O旋转180°后与自身重合,这时我们说□ABCD是中心对称图形,两条对角线的交点O是它的对称中心.
平行四边形是什么图形?
平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
平行四边形的对称性
A
B
C
D
O
我们还发现:平行四边形的对边相等、对角相等.
议一议:小组合作,继续对平行四边形纸片进行研究,你还能发现哪些平行四边形的性质呢?发散你的思维,有不同的方法吗?
提示:可采取度量、平移、旋转、折叠、拼图、等方法探究平行四边形的边和角的数量关系.
尝试证明这些结论.
已知:四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
证明:连接AC
∵ 四边形ABCD是平行四边形
∴ AB∥CD,BC∥DA(平行四边形的定义)
∴ ∠1=∠2 ,∠3=∠4
∵ AC=CA
∴ △ABC ≌△CDA(ASA)
∴ AB=CD,BC=DA .
由上述证明过程你能得到平行四边形的对角相等吗?
∵△ABC≌ △CDA
∴∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3即∠BAD=∠DCB.
已知:四边形ABCD是平行四边形.
求证:∠A=∠C,∠B=∠D.
A
B
C
D
证明:∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠A+∠B=180 °
∠A+∠D=180 °
∴ ∠B=∠D
同理可得:∠A=∠C.
思考:不添加辅助线,你能否直接运用平行四边形的定义,证明
其对角相等?
平行四边形的性质定理
①平行四边形的对边 ; ②平行四边形的对角 .
相等
相等
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF(SAS).
∴ AB=CD,AB ∥ CD
又∵AE=CF,
∴BE=DF.
例2 已知:如图,在平行四边形ABCD中,E,F是对角线AC上的两点,且AE=CF.
求证:BE = DF.
A
D
B
C
E
F
4.如图所示,在 ABCD中,AD=3 cm,AB=2 cm,则 ABCD的周长等于( )
A.10 cm B.6 cm
C.5 cm D.4 cm
3.平行四边形ABCD的四个内角度数的比∠A∶∠B∶∠C∶∠D可以是( )
A.2∶3∶3∶2 B.2∶3∶2∶3
C.1∶2∶3∶4 D.2∶2∶1∶1
B
B
5.已知:如图所示,E是 ABCD的边BC延长线上的一点,且CE=BC.
求证:△ABC≌△DCE.
证明: ∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠DCE.
在△ABC和△DCE中,
∵AB=DC,∠B=∠DCE,BC=CE,
∴△ABC≌△DCE(SAS).
1.如图所示,将 ABCD沿对角线BD折叠,使点A落在点E处,DE与BC交于点F.若∠ABD=48°,∠CFD=40°,则∠E为( )
A.102° B.112° C.122° D.92°
2.如图所示,在平行四边形ABCD中,E是AB边上一点,连接DE,CE.若DE,CE分别是∠ADC,∠BCD的平分线,且AB=4,则平行四边形ABCD的周长为( )
A.10 B.8 C.5 D.12
D
B
4.在□ABCD中,∠A=150°,AB=8cm,BC=10cm,则S□ABCD= .
3.如图,在 ABCD中,∠ADC=125°,∠CAD=21°,求∠ABC= °,∠CAB= °.
125
34
40cm2
6.如图所示,平行四边形ABCO的顶点O,A,C的坐标分别为(0,0),(2,3),(5,0),则顶点B的坐标为 .
5.如图所示,在 ABCD中,过点C作CE⊥AB,垂足为E,若∠EAD=40°,则∠BCE的度数为 .
50°
(7,3)
7.如图所示,在 ABCD中,DE=CE,连接AE并延长,交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.
解: (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠ECF.
在△ADE和△FCE中,
∵∠D=∠ECF,DE=CE,∠AED=∠FEC,
∴△ADE≌△FCE.
(2)∵△ADE≌△FCE,
∴AD=FC.
∵四边形ABCD是平行四边形,
∴AD=BC,∴BC=FC.
又∵AB=2BC,
∴AB=FB,
∴∠BAF=∠F=36°,
∴∠B=180°-2×36°=108°.
两组对边分别平行的四边形是平行四边形.
平行四边形不相邻的两个顶点连成的线段叫它的对角线.
平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
平行四边形的对边相等,
平行四边形的对角相等.
平行四边形的性质(1)
平行四边形的定义
平行四边形的性质
对称性
性质定理
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
