6.3三角形的中位线 课件(共22张PPT)
文档属性
| 名称 | 6.3三角形的中位线 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 06:43:37 | ||
图片预览







文档简介
(共22张PPT)
6.3 三角形的中位线
1. 理解中位线的概念和性质;(重点)
2. 能够利用中位线解决相关问题.(难点)
平行四边形的性质与判定
性质 判定
边
角
对角线
推论 两组对边分别平行,两组对边分别相等.
对角相等,邻角互补.
对角线互相平分.
夹在两条平行线间的平行线段相等.
两组对边分别平行的四边形;
两组对边分别相等的四边形;
一组对边平行且相等的四边形.
对角线互相平分的四边形.
(拓展)两组对角分别相等的四边形;
如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状和大小都相同,请设计合理的解决方案.
A
B
C
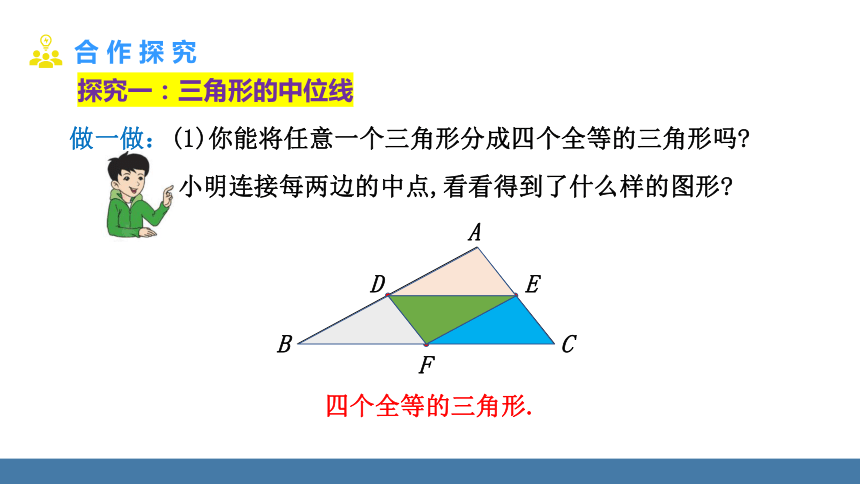
探究一:三角形的中位线
做一做:(1)你能将任意一个三角形分成四个全等的三角形吗
小明连接每两边的中点,看看得到了什么样的图形
四个全等的三角形.
D
F
E
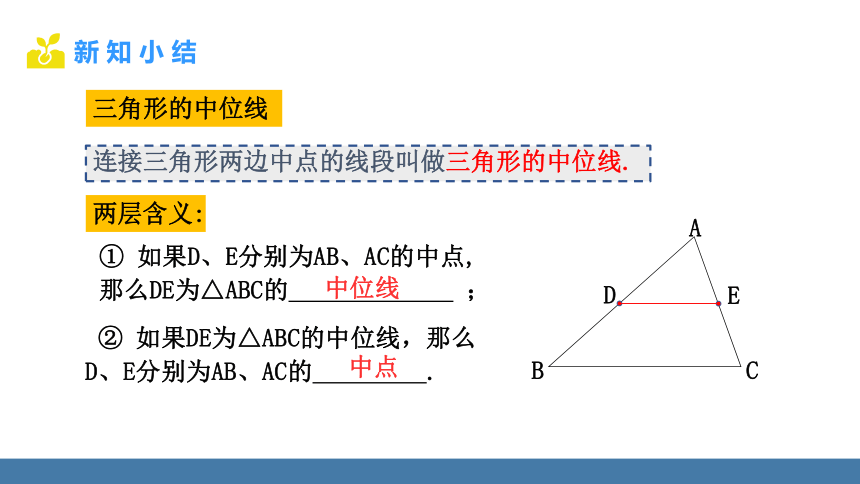
两层含义:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 .
① 如果D、E分别为AB、AC的中点,那么DE为△ABC的 ;
A
B
C
D
E
连接三角形两边中点的线段叫做三角形的中位线.
中位线
中点
三角形的中位线
(2)你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?
小明的做法:将△ADE绕点E按顺时针方向旋转180°到△CFE的位置(如图),这样就得到了一个与△ABC面积相等的平行四边形DBCF.
A
D
E
F
C
B
数量关系:
位置关系:
平行
DE是BC的一半
能说出理由吗
DE和边BC的关系
想一想:三角形两边中点的连线与第三边有怎样的关系 能证明你的猜想吗
A
D
E
F
C
B
已知:如图,在△ABC中,DE是△ABC的中位线.
求证:DE∥BC,DE=BC.
E
A
B
C
D
证明:如图,延长DE至F,使EF=DE,连接CF.
∵ AE=CE, ∠AED=∠CEF,
∴△ADE≌△CFE(SAS),
∴AD=CF,∠A=∠ECF.
∴CF∥AB.
∵AD=BD,
∴四边形DBCF是平行四边形.
∴BD=CF.
∴DF∥BC,DF=BC.
F
∴DE∥BC,DE=DF=BC.
三角形中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
用符号语言表示:
D
A
B
C
E
∵DE是△ABC的中位线,
∴DE∥BC,DE=BC.
利用三角形中位线定理就可以将任意一个三角形分成四个全等的三角形.
例1 如图所示,在△ABC中,D,E分别是边AB,BC的中点.若△DBE的周长是7,则△ABC的周长是( )
A.8 B.10
C.12 D.14
D
2.在△ABC中,D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED的度数为( )
A.22° B.68°
C.96° D.112°
1.如图所示,已知DE是△ABC的中位线,若AC=8,则DE的长为( )
A.2 B.4 C.6 D.8
B
B
议一议:任意画一个四边形,以四边形的中点为顶点组成一个新四边形,这个新四边形的形状有什么特征?请证明你的结论,并与同伴交流.
A
B
C
E
D
H
G
F
探究二:中点四边形
这个新四边形是平行四边形.
已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.
求证:四边形EFGH是平行四边形.
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴四边形EFGH是平行四边形.
∴EF∥AC,
HG∥AC,
你还有其他证明方法吗?
中点四边形:
依次连接任意四边形各边中点所得的四边形称为中点四边形.
A
B
C
E
D
H
G
F
中点四边形一定是平行四边形.
例2 如图所示,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是 .
14
想一想:如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,有通过学习方法估测出了A,B两地之间的距离:先在AB外选一点C,然后步测出AC,BC的中点M,N,并测出MN的长,由此他就知道了A,B间的距离.你能说出其中的道理吗
C
M
B
A
N
探究三:三角形的中位线定理的应用
利用三角形中位线定理可以测量两点之间不能到达的距离.
其中的道理是:连结A、B,
∵MN是△ABC的的中位线,
∴AB=2MN.
3.如图所示,在△ABC中,D,E,F分别为边AB,BC,CA的中点.
(1)求证:四边形DECF是平行四边形;
证明:
(1)∵D,F分别是边AB,AC的中点,
∴DF∥BC.
同理DE∥AC.
∴四边形DECF是平行四边形
3.如图所示,在△ABC中,D,E,F分别为边AB,BC,CA的中点.
(2)若边AC=BC=8,求四边形DECF的周长.
(2)∵AC=BC=8,E,F分别是边BC,AC的中点,
∴EC=BC=4,FC=AC=4.
∵四边形DECF是平行四边形,
∴ DECF的周长=2(EC+FC)=2×(4+4)=16.
1.如图所示,吴伯伯家有一块等边三角形的空地ABC,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )
A.15米 B.20米
C.25米 D.30米
2.如图所示,在△ABC中,AD,AE分别是其角平分线和中线,AB=4,AC=3,过点C作CG⊥AD于点F,交AB于点G,连接EF,则线段EF的长为( )
A. B.1
C. D.7
C
A
4.如图所示, ABCD的对角线AC,BD相交于点O,E是AD的中点,连接OE,若OA=1,△AOE的周长等于5,则 ABCD的周长等于 .
3. 如所示,在△ABC中,M,N分别是AB和AC的中点,连接MN,E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为 .
2
16
5.如图所示,△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点.求证:EF∥DG,且EF=DG.
证明: 如图, 连接DE,FG.
∵BD,CE是△ABC的中线,
∴E,D分别是AB,AC的中点,则DE是△ABC的中位线,
∴DE∥BC,DE=BC.
同理FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,且EF=DG.
三角形的中位线
定义:连结三角形两边中点的线段叫做三角形的中位线.
中点四边形
性质:三角形的中位线平行于第三边,并且等于第三边的一半.
三角形的中位线
应用
定义:依次连接任意四边形各边中点所得的四边形称为中点四边形.
性质:中点四边形一定是平行四边形.
测量两点之间不能到达的距离.
6.3 三角形的中位线
1. 理解中位线的概念和性质;(重点)
2. 能够利用中位线解决相关问题.(难点)
平行四边形的性质与判定
性质 判定
边
角
对角线
推论 两组对边分别平行,两组对边分别相等.
对角相等,邻角互补.
对角线互相平分.
夹在两条平行线间的平行线段相等.
两组对边分别平行的四边形;
两组对边分别相等的四边形;
一组对边平行且相等的四边形.
对角线互相平分的四边形.
(拓展)两组对角分别相等的四边形;
如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状和大小都相同,请设计合理的解决方案.
A
B
C
探究一:三角形的中位线
做一做:(1)你能将任意一个三角形分成四个全等的三角形吗
小明连接每两边的中点,看看得到了什么样的图形
四个全等的三角形.
D
F
E
两层含义:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 .
① 如果D、E分别为AB、AC的中点,那么DE为△ABC的 ;
A
B
C
D
E
连接三角形两边中点的线段叫做三角形的中位线.
中位线
中点
三角形的中位线
(2)你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?
小明的做法:将△ADE绕点E按顺时针方向旋转180°到△CFE的位置(如图),这样就得到了一个与△ABC面积相等的平行四边形DBCF.
A
D
E
F
C
B
数量关系:
位置关系:
平行
DE是BC的一半
能说出理由吗
DE和边BC的关系
想一想:三角形两边中点的连线与第三边有怎样的关系 能证明你的猜想吗
A
D
E
F
C
B
已知:如图,在△ABC中,DE是△ABC的中位线.
求证:DE∥BC,DE=BC.
E
A
B
C
D
证明:如图,延长DE至F,使EF=DE,连接CF.
∵ AE=CE, ∠AED=∠CEF,
∴△ADE≌△CFE(SAS),
∴AD=CF,∠A=∠ECF.
∴CF∥AB.
∵AD=BD,
∴四边形DBCF是平行四边形.
∴BD=CF.
∴DF∥BC,DF=BC.
F
∴DE∥BC,DE=DF=BC.
三角形中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
用符号语言表示:
D
A
B
C
E
∵DE是△ABC的中位线,
∴DE∥BC,DE=BC.
利用三角形中位线定理就可以将任意一个三角形分成四个全等的三角形.
例1 如图所示,在△ABC中,D,E分别是边AB,BC的中点.若△DBE的周长是7,则△ABC的周长是( )
A.8 B.10
C.12 D.14
D
2.在△ABC中,D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED的度数为( )
A.22° B.68°
C.96° D.112°
1.如图所示,已知DE是△ABC的中位线,若AC=8,则DE的长为( )
A.2 B.4 C.6 D.8
B
B
议一议:任意画一个四边形,以四边形的中点为顶点组成一个新四边形,这个新四边形的形状有什么特征?请证明你的结论,并与同伴交流.
A
B
C
E
D
H
G
F
探究二:中点四边形
这个新四边形是平行四边形.
已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.
求证:四边形EFGH是平行四边形.
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴四边形EFGH是平行四边形.
∴EF∥AC,
HG∥AC,
你还有其他证明方法吗?
中点四边形:
依次连接任意四边形各边中点所得的四边形称为中点四边形.
A
B
C
E
D
H
G
F
中点四边形一定是平行四边形.
例2 如图所示,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是 .
14
想一想:如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,有通过学习方法估测出了A,B两地之间的距离:先在AB外选一点C,然后步测出AC,BC的中点M,N,并测出MN的长,由此他就知道了A,B间的距离.你能说出其中的道理吗
C
M
B
A
N
探究三:三角形的中位线定理的应用
利用三角形中位线定理可以测量两点之间不能到达的距离.
其中的道理是:连结A、B,
∵MN是△ABC的的中位线,
∴AB=2MN.
3.如图所示,在△ABC中,D,E,F分别为边AB,BC,CA的中点.
(1)求证:四边形DECF是平行四边形;
证明:
(1)∵D,F分别是边AB,AC的中点,
∴DF∥BC.
同理DE∥AC.
∴四边形DECF是平行四边形
3.如图所示,在△ABC中,D,E,F分别为边AB,BC,CA的中点.
(2)若边AC=BC=8,求四边形DECF的周长.
(2)∵AC=BC=8,E,F分别是边BC,AC的中点,
∴EC=BC=4,FC=AC=4.
∵四边形DECF是平行四边形,
∴ DECF的周长=2(EC+FC)=2×(4+4)=16.
1.如图所示,吴伯伯家有一块等边三角形的空地ABC,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )
A.15米 B.20米
C.25米 D.30米
2.如图所示,在△ABC中,AD,AE分别是其角平分线和中线,AB=4,AC=3,过点C作CG⊥AD于点F,交AB于点G,连接EF,则线段EF的长为( )
A. B.1
C. D.7
C
A
4.如图所示, ABCD的对角线AC,BD相交于点O,E是AD的中点,连接OE,若OA=1,△AOE的周长等于5,则 ABCD的周长等于 .
3. 如所示,在△ABC中,M,N分别是AB和AC的中点,连接MN,E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为 .
2
16
5.如图所示,△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点.求证:EF∥DG,且EF=DG.
证明: 如图, 连接DE,FG.
∵BD,CE是△ABC的中线,
∴E,D分别是AB,AC的中点,则DE是△ABC的中位线,
∴DE∥BC,DE=BC.
同理FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,且EF=DG.
三角形的中位线
定义:连结三角形两边中点的线段叫做三角形的中位线.
中点四边形
性质:三角形的中位线平行于第三边,并且等于第三边的一半.
三角形的中位线
应用
定义:依次连接任意四边形各边中点所得的四边形称为中点四边形.
性质:中点四边形一定是平行四边形.
测量两点之间不能到达的距离.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
