浙教版2024学年八年级上册期末数学提高卷1(含答案)
文档属性
| 名称 | 浙教版2024学年八年级上册期末数学提高卷1(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 06:52:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024学年八年级上册期末数学提高卷1(附答案)
选择题(本题共10小题,每小题3分,共30分)
用三根木棒首尾相接围成△ABC,若AC=5cm,BC=8cm,设AB=cm,则的取值范围是( )
B. C. D.
已知,则下列式子成立的是( )
B. C. D.
下列命题中属于真命题的个数是( )
①三角形的一个外角大于三角形的每一个内角;②等腰三角形的高、中线、角平分线互相重合;
③有两边及其中一条边的对角对应相等的两个三角形全等;
④如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
1个 B. 2个 C. 3个 D. 4个
若点在第二象限,则的取值范围是( )
B. C. 或 D.
点关于直线的对称点的坐标为( )
B. C. D.
已知不等式的解是,则一次函数的图象可能是( )
某种蜡烛燃烧的长度与燃烧的时间成正比例关系.若点燃6分钟后,高度下降2.4cm,则长24cm的此种蜡烛点燃15分钟后,剩余蜡烛的长度为( )
17cm B. 18cm C. 19cm D. 21cm
如图,在Rt△ABC中,∠ACB=,分别以A、B为圆心,大于AB长为半径画弧,两弧交于点M、N,作直线MN分别交AB、AC于点D、E,连接CD、BE.若∠CBE=,则∠BDC的度数为( )
B. C. D.
如图,在锐角△ABC中,AB=5,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD、AB上的动点,则BM+MN的最小值是( )
B. C. D.
如图,正方形EGMP和正方形FNHP的顶点E、F、G、M、N在长方形ABCD的边上.已知DM=DN=20,BE+CF=EF,则长方形ABCD的面积为( )
A. 320 B. 480 C. 640 D. 800
填空题(本题共6小题,每小题3分,共18分)
在函数中,若函数值为0,则自变量的值是 .
已知关于的不等式组恰有4个整数解,则的取值范围是 .
把一次函数的图象向右平移m个单位,得到的图象与的交点坐标为,则m= .
如图,AD是Rt△ABC的角平分线.若BD=4,AC=10,△ABC的面积为32,则AB的长为 .
将一块三角形纸板ABC剪成如图1所示的①②③三块,在拼成不重叠,无缝隙的正方形GHPQ(如图2).若BC=24,AC=CD+4,AB= .
如图,在△ABC中,AD=AB=37,AC=58,D在线段BC上,若BD和DC的长均为整数,则BC= .
解答题:(本题共7小题,共52分)
17(本题6分).解不等式组,并求出它的所有非正整数解的和.
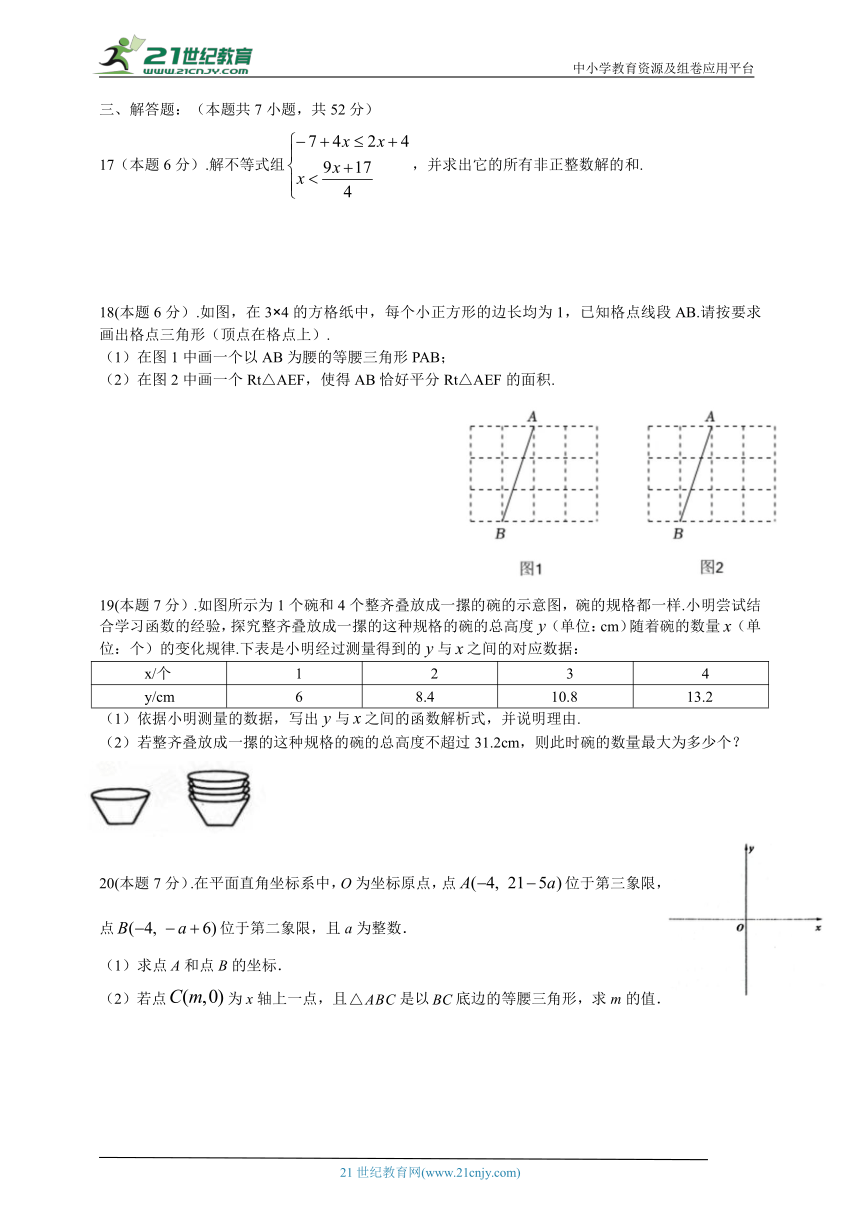
18(本题6分).如图,在3×4的方格纸中,每个小正方形的边长均为1,已知格点线段AB.请按要求画出格点三角形(顶点在格点上).
在图1中画一个以AB为腰的等腰三角形PAB;
在图2中画一个Rt△AEF,使得AB恰好平分Rt△AEF的面积.
19(本题7分).如图所示为1个碗和4个整齐叠放成一摞的碗的示意图,碗的规格都一样.小明尝试结合学习函数的经验,探究整齐叠放成一摞的这种规格的碗的总高度(单位:cm)随着碗的数量(单位:个)的变化规律.下表是小明经过测量得到的与之间的对应数据:
x/个 1 2 3 4
y/cm 6 8.4 10.8 13.2
依据小明测量的数据,写出与之间的函数解析式,并说明理由.
若整齐叠放成一摞的这种规格的碗的总高度不超过31.2cm,则此时碗的数量最大为多少个?
20(本题7分).在平面直角坐标系中,O为坐标原点,点位于第三象限,点位于第二象限,且a为整数.
(1)求点A和点B的坐标.
(2)若点为x轴上一点,且是以底边的等腰三角形,求m的值.
21(本题8分).如图,在等腰Rt△ABC中,CA=CB,点D是CB上的点,点M是CA延长线上的点,连接DM交AB于N点,已知N恰好是DM的中点;过D点向BA作垂线交BA于H.
(1)求证∶BD=AM;
(2)当AB =16时,求HN的长.
22(本题8分).深圳文博会期间,某展商展出了、两种商品,已知用120元可购得的种商品比种商品多2件,种商品的单价是种商品的1.5倍.
(1)求、两种商品的单价各是多少元?
(2)小亮用不超过330元购买、两种商品共13件,并且种商品的数量不超过种商品数量的2倍,那么他有哪几种购买方案?要使购买这两种商品所需费用尽可能少,应选用哪种方案?
23(本题10分).如图1,在中,,是直线上的一点,将线段绕点逆时针旋转至,连接,求证:;
【尝试应用】如图2,在图1的条件下,延长、交于点,交于点,猜想FG与AE的数量关系,并给以证明;
【拓展创新】如图3,是内一点,,,BD=,直接写出的面积为 .
参考答案:
选择题:1. C 2. D 3. A 4. D 5. B 6. D 7. B. 提示:设蜡烛燃烧的长度为y,燃烧的时间为x.由题意可设y=kx(k≠0),则2.4=6k,∴k=0.4,∴y=0.4x.当x=15时,y=0.4×15=6,.∴剩余蜡烛的长度为:24-6=18cm.故选B. 8.D 提示:由∠ACB=,∠CBE=得
∠CEB=.由画图可知直线EF为AB的中垂线,∴EA=EB.∴∠A=∠EBA=∠CEB=.
由∠ACB=,D为AB的中点,得CD=AD.∴∠ACD=∠A=.∴∠BDC=∠A+∠ACD=.故选D.
A. 提示:作BT⊥AC于T,在AC上截取AF=AN,连接FM.易得△AMN≌△AMF.∴MF=MN.∴BM+MN=BM+MF≥BT.∴当B、M、F三点共线且BF⊥AC(即F与T重合)时,BM+MN=BT==为最小值.故选A.
C. 提示:过点P作AB的平行线分别交AD、BC于点Q、T.易证△AGM≌△BEG≌△TPE≌△QMP,△TPF≌△CFN.则MQ=AG=BE=PT=CF=(设为),AM=BG=ET=PQ=(设为),CN=TF=(设为).由DM=20得 ①.由,即DN=16,得 ②. 由BE+CF=EF得 ③.由 ①、②、③解得.∴BC=,AB=.∴长方形ABCD的面积=BC×AB=32×20=640.故选C.
填空题:11.-3 12.. 提示:解不等式组得.∵原不等式组恰有4个整数解,∴.∴.
. 提示:把一次函数的图象向右平移m个单位,得到的一次函数解析式为,即.把点(0, 5)代入得,解得.
6.提示:作DM⊥AC于M.∵AD平分∠BAC,又∠ABD=,∴DM=BD=4.∴.∴.
∴.∴.∴
. 提示:易知AF=CF=GM=(设为),AC=.又BE=BD+DE=NP+HN=HP=GQ=CE=(设为),BC=BE+CE,..由AC=CD+4得CD+4.∴CD=.而AD=GH=GQ=CE=,
又AD⊥BC,∴..解得.∴AC=.∴CD=AC-4=20-4=16.∴BD=BC-CD=24-16=8.∴.
. 提示:作AN⊥BC于N,由AD=AB得BN=DN.设BN=DN=,CD=y,
....,
..
.
解答题:17.解:解不等式,得,.
解不等式,得,∴.∴原不等式组的解为.
∴非正整数解为-3、-2、-1、0. ∵-3+(-2)+(-1)+0=-6,∴所有非正整数解的和为-6.
18.(1)答案不唯一,如图1,图2,图3.
答案不唯一,如图4,图5,图6,图7.
19.解:(1).理由:由表中的数据,的增量不变,y的增量也不变,∴y是的一次函数.设,由题意得,解得.∴y与的函数解析式为.
设碗的数量有个,由题意得.解得.∴的最大整数解为11.
答:碗的数量最多为11个.
解:(1)由题意得,解得.∵为整数,∴.∴A(-4,-4),B(-4,1).
设AB交轴于G,则AG=4,AC=AB=5,CG=. 由勾股定理得.∴.解得或.
∴的值为-1或-7.
(1)证明:作DE//AC交AB于E,则∠DEN=∠MAN.∵N是DM的中点,∴DN=MN.又∠DNE=∠MNA,∴△DEN≌MAN.∴DE=AM.∵△ABC是等腰Rt△∴∠BAC=∠B=.由DE//AC,得∠BED=∠BAC=.
∴∠B=∠BED.∴BD=DE.又DE=AM,∴BD=AM.
(2)解:∵DH⊥BE,又由(1)知BD=DE,∴HE=.由(1)知△DEN≌MAN,∴NE=NA.∴NE=AE.
∴HN=HE+NE=BE+AE=AB=×16=8.
解:(1)设A种商品的单价为元,则B种商品的单价为1.5元.由题意得:.
解得.经检验是原方程的解.∴.
∴A种商品的单价为20元,B种商品的单价为30元.
设购买A种商品y件,则购买B种商品(13-y)件.由题意得:.
解得.∴整数y=6,7,8.∴共有三种方案.
方案一:购买A种商品6件,B种商品7件,所需费用为20×6+30×7=330元;
方案二:购买A种商品7件,B种商品6件,所需费用为20×7+30×6=320元;
方案三:购买A种商品8件,B种商品5件,所需费用为20×8+30×5=310元;
答:共有三种购买方案.其中方案三所需费用最少,所以应选用方案三.
(1)证明:由题意可知AD=AE,∠DAE=∠BAC=.∴∠BAD=∠CAE.又AB=AC,∴△ABD≌△ACE.
(2)FG=AE.理由:作 DK⊥DC交FB的延长线于K.∵AB=AC,∠BAC=,∴∠ABC=∠ACB=.由(1)知△ABD≌△ACE,可得∠ACE=∠ABD=.∵BF⊥AB,BA⊥AC,∴BF//AC.∴∠G=∠DFK.又∠DBK=∠CBF=.∴∠K==∠ECG=∠DBK.
∴DK=BD=CE.∴△ECG≌△DKF.∴DF=EG.∴DE=FG.由等腰直角三角形ADE得DE=AE. FG=AE.
作AE⊥AD交BD于E,连接CE,则△ADE、△ABC都是等腰直角三角形.由(1)知△ABD≌△ACE,
∴CE=BD=,∠AEC=∠ADB=.又∠AED=,∴∠CED=.
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版2024学年八年级上册期末数学提高卷1(附答案)
选择题(本题共10小题,每小题3分,共30分)
用三根木棒首尾相接围成△ABC,若AC=5cm,BC=8cm,设AB=cm,则的取值范围是( )
B. C. D.
已知,则下列式子成立的是( )
B. C. D.
下列命题中属于真命题的个数是( )
①三角形的一个外角大于三角形的每一个内角;②等腰三角形的高、中线、角平分线互相重合;
③有两边及其中一条边的对角对应相等的两个三角形全等;
④如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
1个 B. 2个 C. 3个 D. 4个
若点在第二象限,则的取值范围是( )
B. C. 或 D.
点关于直线的对称点的坐标为( )
B. C. D.
已知不等式的解是,则一次函数的图象可能是( )
某种蜡烛燃烧的长度与燃烧的时间成正比例关系.若点燃6分钟后,高度下降2.4cm,则长24cm的此种蜡烛点燃15分钟后,剩余蜡烛的长度为( )
17cm B. 18cm C. 19cm D. 21cm
如图,在Rt△ABC中,∠ACB=,分别以A、B为圆心,大于AB长为半径画弧,两弧交于点M、N,作直线MN分别交AB、AC于点D、E,连接CD、BE.若∠CBE=,则∠BDC的度数为( )
B. C. D.
如图,在锐角△ABC中,AB=5,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD、AB上的动点,则BM+MN的最小值是( )
B. C. D.
如图,正方形EGMP和正方形FNHP的顶点E、F、G、M、N在长方形ABCD的边上.已知DM=DN=20,BE+CF=EF,则长方形ABCD的面积为( )
A. 320 B. 480 C. 640 D. 800
填空题(本题共6小题,每小题3分,共18分)
在函数中,若函数值为0,则自变量的值是 .
已知关于的不等式组恰有4个整数解,则的取值范围是 .
把一次函数的图象向右平移m个单位,得到的图象与的交点坐标为,则m= .
如图,AD是Rt△ABC的角平分线.若BD=4,AC=10,△ABC的面积为32,则AB的长为 .
将一块三角形纸板ABC剪成如图1所示的①②③三块,在拼成不重叠,无缝隙的正方形GHPQ(如图2).若BC=24,AC=CD+4,AB= .
如图,在△ABC中,AD=AB=37,AC=58,D在线段BC上,若BD和DC的长均为整数,则BC= .
解答题:(本题共7小题,共52分)
17(本题6分).解不等式组,并求出它的所有非正整数解的和.
18(本题6分).如图,在3×4的方格纸中,每个小正方形的边长均为1,已知格点线段AB.请按要求画出格点三角形(顶点在格点上).
在图1中画一个以AB为腰的等腰三角形PAB;
在图2中画一个Rt△AEF,使得AB恰好平分Rt△AEF的面积.
19(本题7分).如图所示为1个碗和4个整齐叠放成一摞的碗的示意图,碗的规格都一样.小明尝试结合学习函数的经验,探究整齐叠放成一摞的这种规格的碗的总高度(单位:cm)随着碗的数量(单位:个)的变化规律.下表是小明经过测量得到的与之间的对应数据:
x/个 1 2 3 4
y/cm 6 8.4 10.8 13.2
依据小明测量的数据,写出与之间的函数解析式,并说明理由.
若整齐叠放成一摞的这种规格的碗的总高度不超过31.2cm,则此时碗的数量最大为多少个?
20(本题7分).在平面直角坐标系中,O为坐标原点,点位于第三象限,点位于第二象限,且a为整数.
(1)求点A和点B的坐标.
(2)若点为x轴上一点,且是以底边的等腰三角形,求m的值.
21(本题8分).如图,在等腰Rt△ABC中,CA=CB,点D是CB上的点,点M是CA延长线上的点,连接DM交AB于N点,已知N恰好是DM的中点;过D点向BA作垂线交BA于H.
(1)求证∶BD=AM;
(2)当AB =16时,求HN的长.
22(本题8分).深圳文博会期间,某展商展出了、两种商品,已知用120元可购得的种商品比种商品多2件,种商品的单价是种商品的1.5倍.
(1)求、两种商品的单价各是多少元?
(2)小亮用不超过330元购买、两种商品共13件,并且种商品的数量不超过种商品数量的2倍,那么他有哪几种购买方案?要使购买这两种商品所需费用尽可能少,应选用哪种方案?
23(本题10分).如图1,在中,,是直线上的一点,将线段绕点逆时针旋转至,连接,求证:;
【尝试应用】如图2,在图1的条件下,延长、交于点,交于点,猜想FG与AE的数量关系,并给以证明;
【拓展创新】如图3,是内一点,,,BD=,直接写出的面积为 .
参考答案:
选择题:1. C 2. D 3. A 4. D 5. B 6. D 7. B. 提示:设蜡烛燃烧的长度为y,燃烧的时间为x.由题意可设y=kx(k≠0),则2.4=6k,∴k=0.4,∴y=0.4x.当x=15时,y=0.4×15=6,.∴剩余蜡烛的长度为:24-6=18cm.故选B. 8.D 提示:由∠ACB=,∠CBE=得
∠CEB=.由画图可知直线EF为AB的中垂线,∴EA=EB.∴∠A=∠EBA=∠CEB=.
由∠ACB=,D为AB的中点,得CD=AD.∴∠ACD=∠A=.∴∠BDC=∠A+∠ACD=.故选D.
A. 提示:作BT⊥AC于T,在AC上截取AF=AN,连接FM.易得△AMN≌△AMF.∴MF=MN.∴BM+MN=BM+MF≥BT.∴当B、M、F三点共线且BF⊥AC(即F与T重合)时,BM+MN=BT==为最小值.故选A.
C. 提示:过点P作AB的平行线分别交AD、BC于点Q、T.易证△AGM≌△BEG≌△TPE≌△QMP,△TPF≌△CFN.则MQ=AG=BE=PT=CF=(设为),AM=BG=ET=PQ=(设为),CN=TF=(设为).由DM=20得 ①.由,即DN=16,得 ②. 由BE+CF=EF得 ③.由 ①、②、③解得.∴BC=,AB=.∴长方形ABCD的面积=BC×AB=32×20=640.故选C.
填空题:11.-3 12.. 提示:解不等式组得.∵原不等式组恰有4个整数解,∴.∴.
. 提示:把一次函数的图象向右平移m个单位,得到的一次函数解析式为,即.把点(0, 5)代入得,解得.
6.提示:作DM⊥AC于M.∵AD平分∠BAC,又∠ABD=,∴DM=BD=4.∴.∴.
∴.∴.∴
. 提示:易知AF=CF=GM=(设为),AC=.又BE=BD+DE=NP+HN=HP=GQ=CE=(设为),BC=BE+CE,..由AC=CD+4得CD+4.∴CD=.而AD=GH=GQ=CE=,
又AD⊥BC,∴..解得.∴AC=.∴CD=AC-4=20-4=16.∴BD=BC-CD=24-16=8.∴.
. 提示:作AN⊥BC于N,由AD=AB得BN=DN.设BN=DN=,CD=y,
....,
..
.
解答题:17.解:解不等式,得,.
解不等式,得,∴.∴原不等式组的解为.
∴非正整数解为-3、-2、-1、0. ∵-3+(-2)+(-1)+0=-6,∴所有非正整数解的和为-6.
18.(1)答案不唯一,如图1,图2,图3.
答案不唯一,如图4,图5,图6,图7.
19.解:(1).理由:由表中的数据,的增量不变,y的增量也不变,∴y是的一次函数.设,由题意得,解得.∴y与的函数解析式为.
设碗的数量有个,由题意得.解得.∴的最大整数解为11.
答:碗的数量最多为11个.
解:(1)由题意得,解得.∵为整数,∴.∴A(-4,-4),B(-4,1).
设AB交轴于G,则AG=4,AC=AB=5,CG=. 由勾股定理得.∴.解得或.
∴的值为-1或-7.
(1)证明:作DE//AC交AB于E,则∠DEN=∠MAN.∵N是DM的中点,∴DN=MN.又∠DNE=∠MNA,∴△DEN≌MAN.∴DE=AM.∵△ABC是等腰Rt△∴∠BAC=∠B=.由DE//AC,得∠BED=∠BAC=.
∴∠B=∠BED.∴BD=DE.又DE=AM,∴BD=AM.
(2)解:∵DH⊥BE,又由(1)知BD=DE,∴HE=.由(1)知△DEN≌MAN,∴NE=NA.∴NE=AE.
∴HN=HE+NE=BE+AE=AB=×16=8.
解:(1)设A种商品的单价为元,则B种商品的单价为1.5元.由题意得:.
解得.经检验是原方程的解.∴.
∴A种商品的单价为20元,B种商品的单价为30元.
设购买A种商品y件,则购买B种商品(13-y)件.由题意得:.
解得.∴整数y=6,7,8.∴共有三种方案.
方案一:购买A种商品6件,B种商品7件,所需费用为20×6+30×7=330元;
方案二:购买A种商品7件,B种商品6件,所需费用为20×7+30×6=320元;
方案三:购买A种商品8件,B种商品5件,所需费用为20×8+30×5=310元;
答:共有三种购买方案.其中方案三所需费用最少,所以应选用方案三.
(1)证明:由题意可知AD=AE,∠DAE=∠BAC=.∴∠BAD=∠CAE.又AB=AC,∴△ABD≌△ACE.
(2)FG=AE.理由:作 DK⊥DC交FB的延长线于K.∵AB=AC,∠BAC=,∴∠ABC=∠ACB=.由(1)知△ABD≌△ACE,可得∠ACE=∠ABD=.∵BF⊥AB,BA⊥AC,∴BF//AC.∴∠G=∠DFK.又∠DBK=∠CBF=.∴∠K==∠ECG=∠DBK.
∴DK=BD=CE.∴△ECG≌△DKF.∴DF=EG.∴DE=FG.由等腰直角三角形ADE得DE=AE. FG=AE.
作AE⊥AD交BD于E,连接CE,则△ADE、△ABC都是等腰直角三角形.由(1)知△ABD≌△ACE,
∴CE=BD=,∠AEC=∠ADB=.又∠AED=,∴∠CED=.
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
