期末常考易错检测卷(含答案)-2024-2025学年数学六年级上册苏教版
文档属性
| 名称 | 期末常考易错检测卷(含答案)-2024-2025学年数学六年级上册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 568.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 10:20:37 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末常考易错检测卷-2024-2025学年数学六年级上册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.为了践行“绿水青山就是金山银山”的理念,“环保卫士”小分队28人参加植树活动。女生每人栽2棵树,男生每人栽3棵树,小分队一共栽了71棵树,其中男生一共栽了( )棵。
A.13 B.15 C.26 D.45
2.两根同样长的绳子,第一根截去,第二根截去米。经过比较,发现第一根截去的长一些。那么原来两根绳子( )。
A.都比1米长 B.都等于1米 C.都比1米短 D.无法判断
3.一杯糖水,糖与水的质量比是1∶6,喝掉一半后,糖与水的质量比是( )。
A.1∶3 B.1∶6 C.1∶12 D.无法确定
4.大圆直径是小圆直径的4倍,则小圆面积是大圆面积的( )。
A. B. C. D.
5.一项工程,甲队单独做15天完成,乙队单独做12天完成。甲队做3天,乙队做5天共完成了这项工程的几分之几?正确的答案是( )。
A. B. C. D.
6.一个书包原价80元,儿童节期间打八折,打完折后买这个书包,节约了( )元。
A.64 B.20 C.16 D.12
7.把一个土豆浸没在盛有水的量杯中,水没有溢出,但水上升了0.6厘米,量杯的底面积是0.8平方分米,土豆的体积是( )。
A.480立方厘米 B.0.48立方分米 C.48立方厘米 D.48立方分米
8.一个长方体从它的顶点处取走一个小长方体,如图,下列说法正确的是( )。
A.表面积减少,体积减少 B.表面积增加,体积减少
C.表面积不变,体积减少 D.表面积不变,体积不变
二、填空题
9.把一根长3米的长方体木料,平均锯成三段,表面积增加了平方米,原来这根木料的体积是( )立方米。
10.将长8分米的长方体木料沿与横截面平行的方向平均截成若干段,一共截了4次,每段长占全长的( ),每段长( )分米;如果表面积增加120平方厘米,原来长方体木料的体积是( )立方厘米。
11.( )的是,( )千克是千克的。
12.学校体育室购进6个篮球和8个足球共用去1320元,每个足球的价钱是篮球的2倍,每个篮球( )元,每个足球( )元。
13.一根彩带长20米第一次用去它的,第二次用去剩下的,第二次用去( )米,还剩下( )米。
14.修一条公路,已经完成,还有( )没有完成。已经完成的和没有完成的工程量的比是( )(填最简单的整数比)。
15.一个长方体木箱,从里面量得长6分米,宽4分米,高5分米。如果在木箱里放棱长2分米的正方体木块,最多放( )块。
16.王叔叔因一项科技发明,获得了5000元奖金。按规定应缴纳20%的个人所得税,王叔叔实际获得奖金( )元;他把实得奖金存入银行,定期三年,年利率是2.75%,到期他应得到本金和利息一共( )元。
三、判断题
17.求做一个抽屉用多少木板,是求这个抽屉5个面的面积之和。( )
18.。( )
19.甲、乙、丙三人分水果,按2∶4∶3分配或按1∶4∶5分配,乙所得相同。( )
20.一个长方形的长增加,要使它的面积不变,宽应该减少。( )
21.36%去掉百分号后,这个数就扩大到原来的100倍。( )
四、计算题
22.直接写得数。
1.2+0.26= 0.03÷0.4= 1÷150%= 25×4÷25×4=
23.计算下面各题,能简便计算的用简便方法计算。
24.解方程。
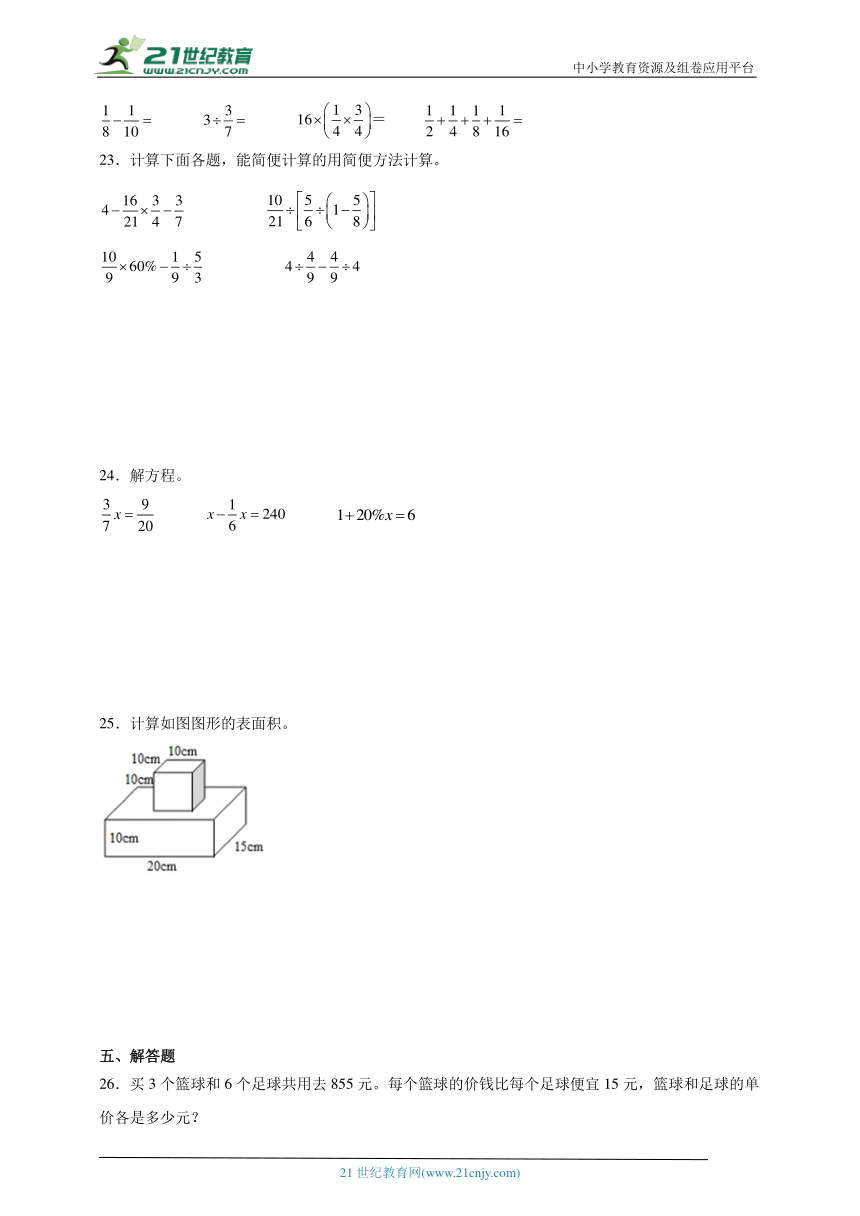
25.计算如图图形的表面积。
五、解答题
26.买3个篮球和6个足球共用去855元。每个篮球的价钱比每个足球便宜15元,篮球和足球的单价各是多少元?
27.用一根18米长的丝带编织手链,第一天用去全长的,第二天用去全长的。第二天比第一天多用去多少米?
28.国庆期间,明明一家三口驾车从徐州到济南,行到全程的时,他们到服务区休息,再行23千米就能到达中点,徐州到济南两地相距多少千米?
29.两列火车同时从两地对开。甲车每小时行62千米,乙车每小时行70千米 ,经过小时两车相遇。两地间的铁路长多少千米?
30.振兴纺织厂共有职工480人。厂工会在做人员统计时发现,男职工人数的50%只相当于女职工人数的,振兴纺织厂的男、女职工分别是多少人?
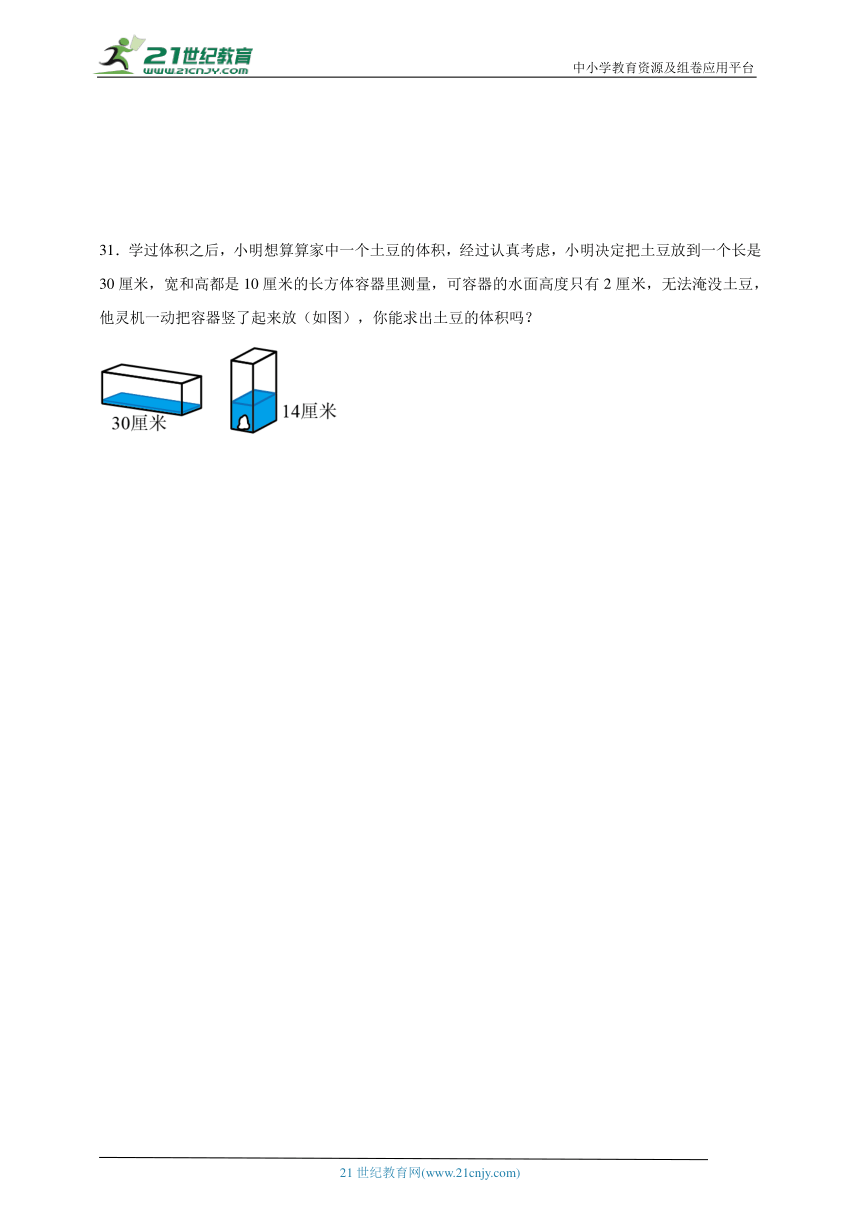
31.学过体积之后,小明想算算家中一个土豆的体积,经过认真考虑,小明决定把土豆放到一个长是30厘米,宽和高都是10厘米的长方体容器里测量,可容器的水面高度只有2厘米,无法淹没土豆,他灵机一动把容器竖了起来放(如图),你能求出土豆的体积吗?
参考答案:
题号 1 2 3 4 5 6 7 8
答案 D A B D D C C C
1.D
【分析】假设全是男生,那么栽了28×3=84(棵)树。比实际栽的树多84-71=13(棵)。每名男生比女生多栽3-2=1(棵)树,则女生有13÷1=13(人),男生就有28-13=15(人)。再用男生人数乘每名男生栽树棵数,求出男生栽树总棵数。
【详解】假设全是男生,则女生有:
(28×3-71)÷(3-2)
=(84-71)÷1
=13÷1
=13(人)
男生有:28-13=15(人)
15×3=45(棵)
其中男生一共栽了45棵。
故答案为:D
【点睛】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论。
2.A
【分析】可以分三种情况来讨论:①这两根绳子的长度都是1米;②两根绳子的长度都小于1米;③两根绳子的长度都大于1米;找出哪一种情况可以满足第一根截去的长一些即可。
【详解】①假设这两根绳子长度都是1米时
第一根截去:1×=(米);第二根截去米
因为米=米,所以当两根绳子长度都是1米时,两根绳子截去的长度相等,不符合题意。
②假设这两根绳子长度都是米时
第一根截去:×=(米),第二根截去米
=
因为米<米,所以当两根绳子长度都小于1米时,第一根绳子截去的长度小于第二根绳子截去的长度,不符合题意。
③假设这两根绳子长度都是2米时
第一根截去:(米),第二根截去米
因为米>米,所以当两根绳子长度都大于1米时,第一根绳子截去的长度大于第二根绳子截去的长度,符合题意。
因此原来两根绳子都比1米大。
故答案为:A
3.B
【分析】一杯糖水,糖和水的比是1∶6,喝了一半后,糖水的浓度不变,剩下的糖水中糖和水的比不变。
【详解】喝了一半后,糖水的浓度不变,剩下的糖水中糖和水的比不变,还是1∶6。
故答案为:B
【点睛】本题关键是理解溶质均匀的液体,倒出一部分液体后,剩下的不会随着体积的减少浓度变化的,只有再加入溶质或溶液时,浓度才会变化。
4.D
【分析】由大圆直径是小圆直径的4倍,设大圆与小圆的直径分别为4a、a,则它们的半径分别是:(4a÷2)、(a÷2),它们的面积分别是:π(4a÷2)2、π(a÷2)2,然后用小圆的面积除以大圆的面积即可得到答案。
【详解】设大圆与小圆的直径分别为4a、a,则它们的半径分别是:(4a÷2)、(a÷2),
小圆面积是:π(a÷2)2= ,
大圆面积是:π×(4a÷2)2=4πa2,
小圆面积是大圆面积的÷4πa2=
故答案为:D
【点睛】本题主要利用圆的面积公式进行计算即可。
5.D
【分析】工作效率=工作总量÷工作时间,将工程总量看作单位“1”,算出甲、乙两队单独的工作效率;然后根据“工作量=工作效率×时间”分别求出甲队做3天,乙队做5天的工作量,再相加。据此解答。
【详解】甲:1÷15=
乙:1÷12=
3×+5×
=+
=
故答案为:D
6.C
【分析】打八折是现价是原价的80%,求一个数的百分之几用乘法,节约的钱=原价-现价。
【详解】80-80×80%
=80-64
=16(元)
则节约了16元。
故答案为:C
7.C
【分析】根据题意,把一个土豆浸没在盛有水的量杯中,水上升了0.6厘米,那么水上升部分的体积等于土豆的体积;根据圆柱的体积公式V=Sh,代入数据计算,求出土豆的体积。注意单位的换算:1平方分米=100平方厘米,1立方分米=1000立方厘米。
【详解】0.8平方分米=80平方厘米
80×0.6=48(立方厘米)
48立方厘米=0.048立方分米
所以,土豆的体积是48立方厘米或0.048立方分米。
故答案为:C
8.C
【分析】长方体从它的顶点处取走一个小长方体,体积减少了一个小长方体的体积;由于取走了一个小长方体,表面积凹进去的顶点处与原面积相等,即表面积不变。据此可得出答案。
【详解】一个长方体从它的顶点处取走一个小长方体,它的表面积不变,体积减少。
故答案为:C
9.1.8
【分析】把一根长3米的长方体木料,平均锯成三段,需要锯3-1=2(次),表面积增加了2×2=4(个)横截面的面积,用增加的表面积除以4,求出横截面的面积;然后根据这根木料的体积=横截面的面积×长,求出这根木料的体积是多少即可。
【详解】=2.4
3-1=2(次)
[2.4÷(2×2)]×3
=[2.4÷4]×3
=0.6×3
=1.8(立方米)
所以这根木料的体积是1.8立方米。
10. 1200
【分析】截4次,截成4+1=5段,每段是全长的1÷5=;求每段的长度,根据分数乘法的意义,用8×计算即可;截4次增加4×2=8个横截面面积,是120平方厘米。由此求出长方体木料横截面面积是120÷8=15平方厘米,带入长方体体积公式:V=Sh计算即可。
【详解】每段是全长的:1÷(4+1)
=1÷5
=
每段长度:8×=(分米)
120÷(4×2)
=120÷8
=15(平方厘米)
8分米=80厘米
15×80=1200(立方厘米)
【点睛】本题主要考查植树问题、长方体体积公式、立体图形的切拼,解题的关键是求出长方体的底面积。
11.
【分析】( )的是,根据已知一个数的几分之几是多少,求这个数,用除法计算,用计算即可求第一个空;
( )千克是千克的,求一个数的几分之几是多少,用乘法计算,用×计算即可求第二个空。
【详解】=;×=(千克)
所以的是;千克是千克的。
12. 60 120
【分析】根据题意,设篮球的价钱是x元,则足球的价钱是2x元;6个篮球是6x元,8个足球是8×2x元,6个篮球和8个足球共用去1320元,列方程:6x+8×2x=1320,解方程,即可解答。
【详解】解:设篮球的价钱是x元,则足球的价钱是2x元
6x+8×2x=1320
6x+16x=1320
22x=1320
x=1320÷22
x=60
足球:60×2=120(元)
【点睛】本题考查方程的实际应用,设篮球为未知数,根据足球是篮球的2倍,找出相关的量,列方程,解方程。
13. 5 5
【分析】把这根彩带长度看作单位“1”,第一次用去它的,还剩(1-),用彩带的长度×(1-),求出彩带剩下的长度,再用剩下的长度×,求出第二次用去的长度,再用第一次剩下的长度-第二次用去的长度,即可求出第二次用去后,剩下的长度。
【详解】20×(1-)×
=20××
=10×
=5(米)
20×(1-)-5
=20×-5
=10-5
=5(米)
一根彩带长20米第一次用去它的,第二次用去剩下的,第二次用去5米,还剩下5米。
【点睛】解答本题的关键是单位“1”的确定,注意第一次和第二次的单位“1”不同。
14. 35 13∶7
【分析】把这条公路的长度看作单位“1”,已经完成65%,还有(1-65)没有完成;根据比的意义可写出已经完成的和没有完成的工程量的比,再化成最简整数比。
【详解】
还有()没有完成;已经完成的和没有完成的工程量的比是()。
15.12
【分析】由题意可知,用长方体的长、宽和高分别除以正方体木块的棱长,据此求出每条棱长上最多能放的块数,再用长放的块数乘宽放的块数,最后再乘高放的块数即可。
【详解】6÷2=3(块)
4÷2=2(块)
5÷2=2(块)……1(分米)
3×2×2
=6×2
=12(块)
最多放12块。
16. 4000 4330
【分析】将5000元奖金看成单位“1”,应缴纳20%的个人所得税,则实际得到1-20%=80%,根据分数乘法的意义,用5000×80%求出实际获得的奖金;利息=本金×利率×时间,代入数据求出利息,最后加上本金即可。
【详解】5000×(1-20%)
=5000×0.8
=4000(元)
4000×2.75%×3+4000
=110×3+4000
=330+4000
=4330(元)
即王叔叔实际获得奖金4000元,把实得奖金存入银行,定期三年,年利率是2.75%,到期他应得到本金和利息一共4330元。
【点睛】本题考查税率、利率问题,理解税率及利息结算方法是解题的关键。
17.√
【分析】结合生活实际可知,抽屉是一个无盖的长方体,所以求做一个抽屉用多少木板,就是求长方体的上下面、左右面和后面共5个面的面积之和,据此判断。
【详解】求做一个抽屉用多少木板,是求这个抽屉5个面的面积之和。
原题说法正确。
故答案为:√
18.√
【分析】把23看成24-1,然后按照乘法分配律进行判断即可解答。
【详解】
=
=
故答案为:√
19.×
【分析】根据比的意义,按2∶4∶3分配表示把水果总量平均分为份,乙分得4份;按1∶4∶5分配表示把水果总量平均分为份,乙分得4份。因为水果总量平均分的份数不同,每份的多少也不同,所以乙得到的4份也不相同。据此解答。
【详解】据分析可知,甲、乙、丙三人分水果,按2∶4∶3分配或按1∶4∶5分配,乙所得不相同。原题说法错误。
故答案为:×
20.×
【分析】假设长方形原来的长为a,宽为b,根据长方形的面积=长×宽,先计算长方形的长增加后此时长方形的面积,再和原来的面积对比,即可判断宽的变化情况。
【详解】假设原来长方形的长为a,宽为b,原来的面积:a×b=ab;
现在的面积:(1+)×a×现在的宽=a×现在的宽;
要使面积不变,现在的宽应为原来宽的,
1-=,所以宽应该减少,因此原题干的说法是错误的。
故答案为:×
【点睛】解答本题的关键是抓住面积不变,结合长方形的面积计算公式来求解。
21.√
【分析】百分数化小数,去掉百分号,小数点向左移动两位,据此将36%化成小数,再与去掉百分号后的数求商即可。
【详解】36%=0.36、36÷0.36=100
36%去掉百分号后,这个数就扩大到原来的100倍,说法正确。
故答案为:√
22.1.46;0.075;;16;
;7;3;
【详解】略
23.3;
;
【分析】(1)先算乘法,再运用减法的性质进行计算即可;
(2)先算小括号里面的减法,再算中括号里面的除法,最后算括号外面的除法即可;
(3)把原式化为,再运用乘法分配律进行计算即可;
(4)先算除法,再算减法即可。
【详解】
=
=
=
=3
=
=
=
=
=
=
=
=
=
=
=
=
24.;;
【分析】根据等式的性质解方程。
(1)方程两边同时除以,求出方程的解;
(2)先把方程化简成,然后方程两边同时除以,求出方程的解;
(3)先把20%改写成0.2,然后方程两边先同时减去1,再同时除以0.2,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
25.1700平方厘米
【分析】组合图形的表面积=正方体的四个侧面面积+长方体的表面积。其中长方体的表面积=(长×宽+长×高+宽×高)×2,正方体的四个侧面积之和=棱长×棱长×4,据此代入数据计算即可。
【详解】10×10×4+(20×15+20×10+15×10)×2
=400+(300+200+150)×2
=400+1300
=1700(平方厘米)
26.篮球85元,足球100元
【分析】设篮球的单价为x元,则足球的单价为(x+15)元,根据3个篮球的价钱+6个足球的价钱=855,列方程解答求出篮球的单价,继而求出足球的单价。
【详解】解:设篮球的单价为x元,则足球的单价为(x+15)元。
3x+6(x+15)=855
9x+90=855
9x=765
x=85
足球:85+15=100(元)
答:篮球的单价为85元,篮球的单价为100元。
【点睛】本题用方程解答比较简便。列方程时,找出题目的等量关系式是解题的关键。
27.0.8米
【分析】第一天用去全长的,这里单位“1”是全长,单位“1”已知用乘法,即18×,第二天用去了全长的,这里单位“1”是全长,单位“1”已知用乘法,即18×,用第二天用的量减去第一天用的量即可求出第二天比第一天多用多少米。
【详解】18×-18×
=8-7.2
=0.8(米)
答:第二天比第一天多用去0.8米。
【点睛】本题主要考查分数乘法的应用,一个数的几分之几是多少,用这个数乘几分之几。
28.322千米
【分析】将徐州到济南两地距离看作单位“1”,明明一家已行驶了,到达中点是占了,则到达中点的剩余距离是总长度的,已知剩余23千米,已知部分求整体,运用分数除法得出答案。
【详解】徐州到济南两地相距:
(千米)
答:徐州到济南两地相距322千米。
29.88千米
【分析】根据路程=速度和×相遇时间,代入数据计算即可。
【详解】(62+70)×
=132×
=88(千米)
答:两地间的铁路长88千米。
【点睛】此题考查了相遇问题,也可根据路程=速度×时间,分别求出两车行驶的路程,再相加。
30.男职工:120人;女职工:360人
【分析】把女职工人数看成单位“1”,男职工人数50%相当于女职工人数的,找出等量关系式:男职工人数×50%=女职工人数×,设女职工有x人,则男职工就有(480-x)人,列方程:(480-x)×50%=x,解方程,即可即可。
【详解】解:设女职工有x人,则男职工有(480-x)人。
(480-x)×50%=x
480×50%-50%x=x
x+x=240
x=240
x=240÷
x=240×
x=360
男职工:480-360=120(人)
答:男职工有120人,女职工有360人。
【点睛】根据方程的实际应用,找出男女职工之间的关系,设出未知数,列方程,解方程。
31.800立方厘米
【分析】根据题意可知:平放和竖放容器内的水的体积没变,只是水在容器内体积的形状改变了;先根据长方体的体积公式:V=abh,求出容器内水的体积,然后用竖着的体积(含土豆的体积)减去横着时水的体积,列式解答即可。
【详解】10×10×14-30×10×2
=1400-600
=800(立方厘米)
答:土豆的体积是800立方厘米。
【点睛】此题主要考查长方体的体积计算方法,以及已知体积和底面积求高,注意无论平放,还是竖放容器内水的体积不变。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末常考易错检测卷-2024-2025学年数学六年级上册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.为了践行“绿水青山就是金山银山”的理念,“环保卫士”小分队28人参加植树活动。女生每人栽2棵树,男生每人栽3棵树,小分队一共栽了71棵树,其中男生一共栽了( )棵。
A.13 B.15 C.26 D.45
2.两根同样长的绳子,第一根截去,第二根截去米。经过比较,发现第一根截去的长一些。那么原来两根绳子( )。
A.都比1米长 B.都等于1米 C.都比1米短 D.无法判断
3.一杯糖水,糖与水的质量比是1∶6,喝掉一半后,糖与水的质量比是( )。
A.1∶3 B.1∶6 C.1∶12 D.无法确定
4.大圆直径是小圆直径的4倍,则小圆面积是大圆面积的( )。
A. B. C. D.
5.一项工程,甲队单独做15天完成,乙队单独做12天完成。甲队做3天,乙队做5天共完成了这项工程的几分之几?正确的答案是( )。
A. B. C. D.
6.一个书包原价80元,儿童节期间打八折,打完折后买这个书包,节约了( )元。
A.64 B.20 C.16 D.12
7.把一个土豆浸没在盛有水的量杯中,水没有溢出,但水上升了0.6厘米,量杯的底面积是0.8平方分米,土豆的体积是( )。
A.480立方厘米 B.0.48立方分米 C.48立方厘米 D.48立方分米
8.一个长方体从它的顶点处取走一个小长方体,如图,下列说法正确的是( )。
A.表面积减少,体积减少 B.表面积增加,体积减少
C.表面积不变,体积减少 D.表面积不变,体积不变
二、填空题
9.把一根长3米的长方体木料,平均锯成三段,表面积增加了平方米,原来这根木料的体积是( )立方米。
10.将长8分米的长方体木料沿与横截面平行的方向平均截成若干段,一共截了4次,每段长占全长的( ),每段长( )分米;如果表面积增加120平方厘米,原来长方体木料的体积是( )立方厘米。
11.( )的是,( )千克是千克的。
12.学校体育室购进6个篮球和8个足球共用去1320元,每个足球的价钱是篮球的2倍,每个篮球( )元,每个足球( )元。
13.一根彩带长20米第一次用去它的,第二次用去剩下的,第二次用去( )米,还剩下( )米。
14.修一条公路,已经完成,还有( )没有完成。已经完成的和没有完成的工程量的比是( )(填最简单的整数比)。
15.一个长方体木箱,从里面量得长6分米,宽4分米,高5分米。如果在木箱里放棱长2分米的正方体木块,最多放( )块。
16.王叔叔因一项科技发明,获得了5000元奖金。按规定应缴纳20%的个人所得税,王叔叔实际获得奖金( )元;他把实得奖金存入银行,定期三年,年利率是2.75%,到期他应得到本金和利息一共( )元。
三、判断题
17.求做一个抽屉用多少木板,是求这个抽屉5个面的面积之和。( )
18.。( )
19.甲、乙、丙三人分水果,按2∶4∶3分配或按1∶4∶5分配,乙所得相同。( )
20.一个长方形的长增加,要使它的面积不变,宽应该减少。( )
21.36%去掉百分号后,这个数就扩大到原来的100倍。( )
四、计算题
22.直接写得数。
1.2+0.26= 0.03÷0.4= 1÷150%= 25×4÷25×4=
23.计算下面各题,能简便计算的用简便方法计算。
24.解方程。
25.计算如图图形的表面积。
五、解答题
26.买3个篮球和6个足球共用去855元。每个篮球的价钱比每个足球便宜15元,篮球和足球的单价各是多少元?
27.用一根18米长的丝带编织手链,第一天用去全长的,第二天用去全长的。第二天比第一天多用去多少米?
28.国庆期间,明明一家三口驾车从徐州到济南,行到全程的时,他们到服务区休息,再行23千米就能到达中点,徐州到济南两地相距多少千米?
29.两列火车同时从两地对开。甲车每小时行62千米,乙车每小时行70千米 ,经过小时两车相遇。两地间的铁路长多少千米?
30.振兴纺织厂共有职工480人。厂工会在做人员统计时发现,男职工人数的50%只相当于女职工人数的,振兴纺织厂的男、女职工分别是多少人?
31.学过体积之后,小明想算算家中一个土豆的体积,经过认真考虑,小明决定把土豆放到一个长是30厘米,宽和高都是10厘米的长方体容器里测量,可容器的水面高度只有2厘米,无法淹没土豆,他灵机一动把容器竖了起来放(如图),你能求出土豆的体积吗?
参考答案:
题号 1 2 3 4 5 6 7 8
答案 D A B D D C C C
1.D
【分析】假设全是男生,那么栽了28×3=84(棵)树。比实际栽的树多84-71=13(棵)。每名男生比女生多栽3-2=1(棵)树,则女生有13÷1=13(人),男生就有28-13=15(人)。再用男生人数乘每名男生栽树棵数,求出男生栽树总棵数。
【详解】假设全是男生,则女生有:
(28×3-71)÷(3-2)
=(84-71)÷1
=13÷1
=13(人)
男生有:28-13=15(人)
15×3=45(棵)
其中男生一共栽了45棵。
故答案为:D
【点睛】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论。
2.A
【分析】可以分三种情况来讨论:①这两根绳子的长度都是1米;②两根绳子的长度都小于1米;③两根绳子的长度都大于1米;找出哪一种情况可以满足第一根截去的长一些即可。
【详解】①假设这两根绳子长度都是1米时
第一根截去:1×=(米);第二根截去米
因为米=米,所以当两根绳子长度都是1米时,两根绳子截去的长度相等,不符合题意。
②假设这两根绳子长度都是米时
第一根截去:×=(米),第二根截去米
=
因为米<米,所以当两根绳子长度都小于1米时,第一根绳子截去的长度小于第二根绳子截去的长度,不符合题意。
③假设这两根绳子长度都是2米时
第一根截去:(米),第二根截去米
因为米>米,所以当两根绳子长度都大于1米时,第一根绳子截去的长度大于第二根绳子截去的长度,符合题意。
因此原来两根绳子都比1米大。
故答案为:A
3.B
【分析】一杯糖水,糖和水的比是1∶6,喝了一半后,糖水的浓度不变,剩下的糖水中糖和水的比不变。
【详解】喝了一半后,糖水的浓度不变,剩下的糖水中糖和水的比不变,还是1∶6。
故答案为:B
【点睛】本题关键是理解溶质均匀的液体,倒出一部分液体后,剩下的不会随着体积的减少浓度变化的,只有再加入溶质或溶液时,浓度才会变化。
4.D
【分析】由大圆直径是小圆直径的4倍,设大圆与小圆的直径分别为4a、a,则它们的半径分别是:(4a÷2)、(a÷2),它们的面积分别是:π(4a÷2)2、π(a÷2)2,然后用小圆的面积除以大圆的面积即可得到答案。
【详解】设大圆与小圆的直径分别为4a、a,则它们的半径分别是:(4a÷2)、(a÷2),
小圆面积是:π(a÷2)2= ,
大圆面积是:π×(4a÷2)2=4πa2,
小圆面积是大圆面积的÷4πa2=
故答案为:D
【点睛】本题主要利用圆的面积公式进行计算即可。
5.D
【分析】工作效率=工作总量÷工作时间,将工程总量看作单位“1”,算出甲、乙两队单独的工作效率;然后根据“工作量=工作效率×时间”分别求出甲队做3天,乙队做5天的工作量,再相加。据此解答。
【详解】甲:1÷15=
乙:1÷12=
3×+5×
=+
=
故答案为:D
6.C
【分析】打八折是现价是原价的80%,求一个数的百分之几用乘法,节约的钱=原价-现价。
【详解】80-80×80%
=80-64
=16(元)
则节约了16元。
故答案为:C
7.C
【分析】根据题意,把一个土豆浸没在盛有水的量杯中,水上升了0.6厘米,那么水上升部分的体积等于土豆的体积;根据圆柱的体积公式V=Sh,代入数据计算,求出土豆的体积。注意单位的换算:1平方分米=100平方厘米,1立方分米=1000立方厘米。
【详解】0.8平方分米=80平方厘米
80×0.6=48(立方厘米)
48立方厘米=0.048立方分米
所以,土豆的体积是48立方厘米或0.048立方分米。
故答案为:C
8.C
【分析】长方体从它的顶点处取走一个小长方体,体积减少了一个小长方体的体积;由于取走了一个小长方体,表面积凹进去的顶点处与原面积相等,即表面积不变。据此可得出答案。
【详解】一个长方体从它的顶点处取走一个小长方体,它的表面积不变,体积减少。
故答案为:C
9.1.8
【分析】把一根长3米的长方体木料,平均锯成三段,需要锯3-1=2(次),表面积增加了2×2=4(个)横截面的面积,用增加的表面积除以4,求出横截面的面积;然后根据这根木料的体积=横截面的面积×长,求出这根木料的体积是多少即可。
【详解】=2.4
3-1=2(次)
[2.4÷(2×2)]×3
=[2.4÷4]×3
=0.6×3
=1.8(立方米)
所以这根木料的体积是1.8立方米。
10. 1200
【分析】截4次,截成4+1=5段,每段是全长的1÷5=;求每段的长度,根据分数乘法的意义,用8×计算即可;截4次增加4×2=8个横截面面积,是120平方厘米。由此求出长方体木料横截面面积是120÷8=15平方厘米,带入长方体体积公式:V=Sh计算即可。
【详解】每段是全长的:1÷(4+1)
=1÷5
=
每段长度:8×=(分米)
120÷(4×2)
=120÷8
=15(平方厘米)
8分米=80厘米
15×80=1200(立方厘米)
【点睛】本题主要考查植树问题、长方体体积公式、立体图形的切拼,解题的关键是求出长方体的底面积。
11.
【分析】( )的是,根据已知一个数的几分之几是多少,求这个数,用除法计算,用计算即可求第一个空;
( )千克是千克的,求一个数的几分之几是多少,用乘法计算,用×计算即可求第二个空。
【详解】=;×=(千克)
所以的是;千克是千克的。
12. 60 120
【分析】根据题意,设篮球的价钱是x元,则足球的价钱是2x元;6个篮球是6x元,8个足球是8×2x元,6个篮球和8个足球共用去1320元,列方程:6x+8×2x=1320,解方程,即可解答。
【详解】解:设篮球的价钱是x元,则足球的价钱是2x元
6x+8×2x=1320
6x+16x=1320
22x=1320
x=1320÷22
x=60
足球:60×2=120(元)
【点睛】本题考查方程的实际应用,设篮球为未知数,根据足球是篮球的2倍,找出相关的量,列方程,解方程。
13. 5 5
【分析】把这根彩带长度看作单位“1”,第一次用去它的,还剩(1-),用彩带的长度×(1-),求出彩带剩下的长度,再用剩下的长度×,求出第二次用去的长度,再用第一次剩下的长度-第二次用去的长度,即可求出第二次用去后,剩下的长度。
【详解】20×(1-)×
=20××
=10×
=5(米)
20×(1-)-5
=20×-5
=10-5
=5(米)
一根彩带长20米第一次用去它的,第二次用去剩下的,第二次用去5米,还剩下5米。
【点睛】解答本题的关键是单位“1”的确定,注意第一次和第二次的单位“1”不同。
14. 35 13∶7
【分析】把这条公路的长度看作单位“1”,已经完成65%,还有(1-65)没有完成;根据比的意义可写出已经完成的和没有完成的工程量的比,再化成最简整数比。
【详解】
还有()没有完成;已经完成的和没有完成的工程量的比是()。
15.12
【分析】由题意可知,用长方体的长、宽和高分别除以正方体木块的棱长,据此求出每条棱长上最多能放的块数,再用长放的块数乘宽放的块数,最后再乘高放的块数即可。
【详解】6÷2=3(块)
4÷2=2(块)
5÷2=2(块)……1(分米)
3×2×2
=6×2
=12(块)
最多放12块。
16. 4000 4330
【分析】将5000元奖金看成单位“1”,应缴纳20%的个人所得税,则实际得到1-20%=80%,根据分数乘法的意义,用5000×80%求出实际获得的奖金;利息=本金×利率×时间,代入数据求出利息,最后加上本金即可。
【详解】5000×(1-20%)
=5000×0.8
=4000(元)
4000×2.75%×3+4000
=110×3+4000
=330+4000
=4330(元)
即王叔叔实际获得奖金4000元,把实得奖金存入银行,定期三年,年利率是2.75%,到期他应得到本金和利息一共4330元。
【点睛】本题考查税率、利率问题,理解税率及利息结算方法是解题的关键。
17.√
【分析】结合生活实际可知,抽屉是一个无盖的长方体,所以求做一个抽屉用多少木板,就是求长方体的上下面、左右面和后面共5个面的面积之和,据此判断。
【详解】求做一个抽屉用多少木板,是求这个抽屉5个面的面积之和。
原题说法正确。
故答案为:√
18.√
【分析】把23看成24-1,然后按照乘法分配律进行判断即可解答。
【详解】
=
=
故答案为:√
19.×
【分析】根据比的意义,按2∶4∶3分配表示把水果总量平均分为份,乙分得4份;按1∶4∶5分配表示把水果总量平均分为份,乙分得4份。因为水果总量平均分的份数不同,每份的多少也不同,所以乙得到的4份也不相同。据此解答。
【详解】据分析可知,甲、乙、丙三人分水果,按2∶4∶3分配或按1∶4∶5分配,乙所得不相同。原题说法错误。
故答案为:×
20.×
【分析】假设长方形原来的长为a,宽为b,根据长方形的面积=长×宽,先计算长方形的长增加后此时长方形的面积,再和原来的面积对比,即可判断宽的变化情况。
【详解】假设原来长方形的长为a,宽为b,原来的面积:a×b=ab;
现在的面积:(1+)×a×现在的宽=a×现在的宽;
要使面积不变,现在的宽应为原来宽的,
1-=,所以宽应该减少,因此原题干的说法是错误的。
故答案为:×
【点睛】解答本题的关键是抓住面积不变,结合长方形的面积计算公式来求解。
21.√
【分析】百分数化小数,去掉百分号,小数点向左移动两位,据此将36%化成小数,再与去掉百分号后的数求商即可。
【详解】36%=0.36、36÷0.36=100
36%去掉百分号后,这个数就扩大到原来的100倍,说法正确。
故答案为:√
22.1.46;0.075;;16;
;7;3;
【详解】略
23.3;
;
【分析】(1)先算乘法,再运用减法的性质进行计算即可;
(2)先算小括号里面的减法,再算中括号里面的除法,最后算括号外面的除法即可;
(3)把原式化为,再运用乘法分配律进行计算即可;
(4)先算除法,再算减法即可。
【详解】
=
=
=
=3
=
=
=
=
=
=
=
=
=
=
=
=
24.;;
【分析】根据等式的性质解方程。
(1)方程两边同时除以,求出方程的解;
(2)先把方程化简成,然后方程两边同时除以,求出方程的解;
(3)先把20%改写成0.2,然后方程两边先同时减去1,再同时除以0.2,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
25.1700平方厘米
【分析】组合图形的表面积=正方体的四个侧面面积+长方体的表面积。其中长方体的表面积=(长×宽+长×高+宽×高)×2,正方体的四个侧面积之和=棱长×棱长×4,据此代入数据计算即可。
【详解】10×10×4+(20×15+20×10+15×10)×2
=400+(300+200+150)×2
=400+1300
=1700(平方厘米)
26.篮球85元,足球100元
【分析】设篮球的单价为x元,则足球的单价为(x+15)元,根据3个篮球的价钱+6个足球的价钱=855,列方程解答求出篮球的单价,继而求出足球的单价。
【详解】解:设篮球的单价为x元,则足球的单价为(x+15)元。
3x+6(x+15)=855
9x+90=855
9x=765
x=85
足球:85+15=100(元)
答:篮球的单价为85元,篮球的单价为100元。
【点睛】本题用方程解答比较简便。列方程时,找出题目的等量关系式是解题的关键。
27.0.8米
【分析】第一天用去全长的,这里单位“1”是全长,单位“1”已知用乘法,即18×,第二天用去了全长的,这里单位“1”是全长,单位“1”已知用乘法,即18×,用第二天用的量减去第一天用的量即可求出第二天比第一天多用多少米。
【详解】18×-18×
=8-7.2
=0.8(米)
答:第二天比第一天多用去0.8米。
【点睛】本题主要考查分数乘法的应用,一个数的几分之几是多少,用这个数乘几分之几。
28.322千米
【分析】将徐州到济南两地距离看作单位“1”,明明一家已行驶了,到达中点是占了,则到达中点的剩余距离是总长度的,已知剩余23千米,已知部分求整体,运用分数除法得出答案。
【详解】徐州到济南两地相距:
(千米)
答:徐州到济南两地相距322千米。
29.88千米
【分析】根据路程=速度和×相遇时间,代入数据计算即可。
【详解】(62+70)×
=132×
=88(千米)
答:两地间的铁路长88千米。
【点睛】此题考查了相遇问题,也可根据路程=速度×时间,分别求出两车行驶的路程,再相加。
30.男职工:120人;女职工:360人
【分析】把女职工人数看成单位“1”,男职工人数50%相当于女职工人数的,找出等量关系式:男职工人数×50%=女职工人数×,设女职工有x人,则男职工就有(480-x)人,列方程:(480-x)×50%=x,解方程,即可即可。
【详解】解:设女职工有x人,则男职工有(480-x)人。
(480-x)×50%=x
480×50%-50%x=x
x+x=240
x=240
x=240÷
x=240×
x=360
男职工:480-360=120(人)
答:男职工有120人,女职工有360人。
【点睛】根据方程的实际应用,找出男女职工之间的关系,设出未知数,列方程,解方程。
31.800立方厘米
【分析】根据题意可知:平放和竖放容器内的水的体积没变,只是水在容器内体积的形状改变了;先根据长方体的体积公式:V=abh,求出容器内水的体积,然后用竖着的体积(含土豆的体积)减去横着时水的体积,列式解答即可。
【详解】10×10×14-30×10×2
=1400-600
=800(立方厘米)
答:土豆的体积是800立方厘米。
【点睛】此题主要考查长方体的体积计算方法,以及已知体积和底面积求高,注意无论平放,还是竖放容器内水的体积不变。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
