1.3 带电粒子在匀强磁场中的运动 课件(共39张PPT) 2024-2025学年人教版(2019)高中物理选择性必修第二册
文档属性
| 名称 | 1.3 带电粒子在匀强磁场中的运动 课件(共39张PPT) 2024-2025学年人教版(2019)高中物理选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-19 00:00:00 | ||
图片预览









文档简介
(共39张PPT)
1.3 带电粒子在匀强磁场中的运动
人教版(2019)物理(选择性必修第二册)
第一章 安培力与洛伦兹力
目录
素养目标
01
课程导入
02
新课讲解
03
总结归纳
04
课堂练习
05
素养目标
1.理解洛伦兹力对粒子不做功,带电粒子初速度方向与磁感应强度方向垂直时,粒子在匀强磁场中做匀速圆周运动
2.会推导带电粒子在匀强磁场中做匀速圆周运动的半径、周期公式,知道它们和哪些因素有关
3.能够解答带电粒子在匀强磁场中运动相关问题
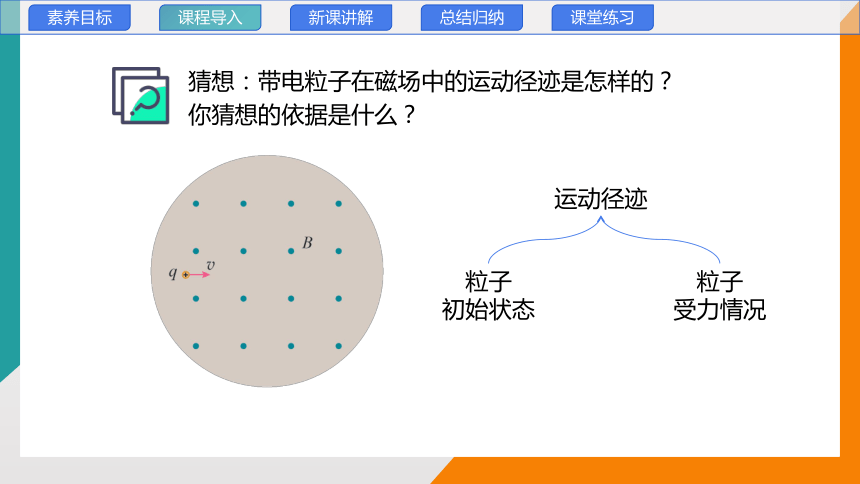
猜想:带电粒子在磁场中的运动径迹是怎样的?
你猜想的依据是什么?
运动径迹
粒子
初始状态
粒子
受力情况
新课讲解
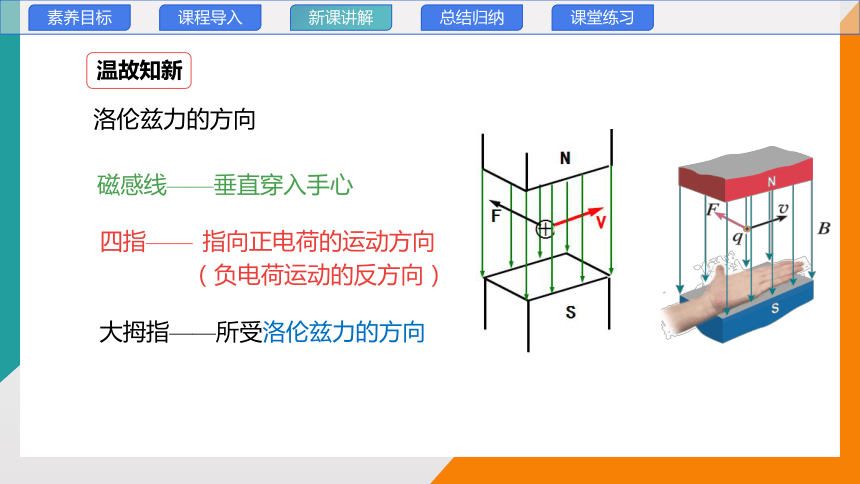
磁感线——垂直穿入手心
四指——
大拇指——所受洛伦兹力的方向
指向正电荷的运动方向
(负电荷运动的反方向)
洛伦兹力的方向
温故知新
洛伦兹力只会改变粒子速度的 ,
不改变速度的 ,
故粒子将做
方向
大小
匀速圆周运动
-
v
v
F
F
-
思考2:洛伦兹力的方向总与速度方向?
思考1:由于是匀强磁场,洛伦兹力大小?
不变
垂直
洛伦兹力对电荷做功吗?
不做功
一、带电粒子在匀强磁场中的运动
v ⊥ B,洛伦兹力总是与粒子的运动方向垂直,只改变粒子速度的方向,不改变粒子速度的大小,
由于洛伦兹力提供向心力,
所以带电粒子做匀速圆周运动。
F
F
1.带电粒子平行射入匀强磁场
v//B,F洛=0,粒子做匀速直线运动
2.带电粒子的速度垂直于磁场的方向进入磁场
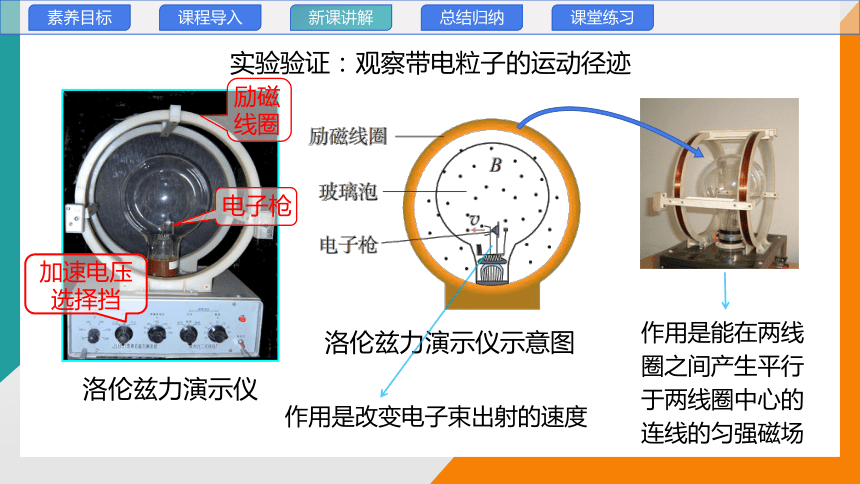
实验验证:观察带电粒子的运动径迹
励磁线圈
电子枪
加速电压选择挡
洛伦兹力演示仪
洛伦兹力演示仪示意图
作用是改变电子束出射的速度
作用是能在两线圈之间产生平行于两线圈中心的连线的匀强磁场
实验验证:观察带电粒子的运动径迹
不加磁场
加磁场
实验现象:在没有磁场作用时,电子的轨迹是直线;在管外加上垂直初速度方向的匀强磁场,电子的轨迹变弯曲成圆形
垂直射入磁场的带电粒子在匀强磁场中做匀速圆周运动,圆周的半径可能与哪些因素有关?周期可能与哪些因素有关?
假设一个电荷量为q的粒子,在磁感应强度为B的匀强磁场中以速度v运动,那么带电粒子所受的洛伦兹力为
思考
圆周运动的向心力公式
洛伦兹力提供向心力
二、带电粒子在匀强磁场中做圆周运动的半径和周期
B
F
v
电荷做匀速圆周运动的向心力由洛伦兹力提供
则:
得:
B
r
v
r
从这个结果看出,带电粒子在匀强磁场中做匀速圆周运动的半径与它的质量、速度成正比,与电荷量、磁感应强度成反比。
你能根据以前所学的知识,推导一下带电粒子在匀强磁场做圆周运动的周期规律吗?
方法一:
根据匀速圆周运动规律:
又由
得
方法二:
根据向心力与周期关系:
又由
得
①圆心的确定
情景一:如图,若已知入射点P、出射点M及其两点的速度方向,如何确定带电粒子运动轨迹圆心?
v0
M
O
【思路点拨】作入射速度出射速度的垂线,两垂线交点就是圆弧轨道的圆心。
三、带电粒子在匀强磁场中做匀速圆周运动的情况分析
基本思路
一找圆心
二求半径
三求周期或时间
P
情景二:如图,若已知入射点P及速度方向、出射点M的位置,如何确定带电粒子运动轨迹圆心?
v0
P
M
O
【思路点拨】做入射速度垂线,再连接PM,并做PM的中垂线,两条线的交点就是圆弧轨道的圆心。
①圆心的确定
②运动半径的确定
情景一:如图,若已知入射点P、出射点M及其两点的速度方向,且已知粒子到M点后速度偏转角为θ,磁场宽度为L,则带电粒子在磁场中运动轨迹半径为多少?
v0
P
M
O
θ
θ
由几何关系可以知道:
根据直角三角形的三边关系可以知道:
即:
L
【思路点拨】
情景二:如图,若粒子在P点垂直于磁场左边界入射,且从M点飞出,若已知M点距P点粒子入射线方向上的Q点距离为H,磁场宽度为L,则带电粒子在磁场中运动轨迹半径为多少?
由几何关系可以知道:
根据直角三角形的三边关系可以知道:
即:
v0
P
M
O
L
H
Q
【思路点拨】
②运动半径的确定
③运动时间的确定
粒子在磁场中运动一周的时间为T,当粒子运动的圆弧所对应的圆心角为α时,其运动时间为多少?
α单位是弧度
α单位是角度
利用圆心角与弦切角的关系,或者是四边形内角和等计算出圆心角的大小,由公式可求出运动时间。
【思路点拨】
画轨迹
找联系
用规律
画出轨迹,并确定圆心,利用几何方法求半径
轨道半径与磁感应强度、运动速度相联系,偏转角度与圆心角、运动时间相联系,在磁场中运动的时间与周期相联系
牛顿第二定律和圆周运动的规律,特别是周期用规律公式,半径公式。
①直线边界:进出磁场具有对称性v
②平行边界:存在临界条件
带电粒子在有界磁场中的运动轨迹特点
1.“月球勘探者号”空间探测器运用高科技手段对月球进行了近距离勘探,在月球重力分布、磁场分布及元素测定方面取得了新的成果。月球上的磁场极其微弱,通过探测器拍摄电子在月球磁场中的运动轨迹,可分析月球磁场的强弱分布情况,如图所示是探测器通过月球表面①、②、③、④四个位置时,拍摄到的电子运动轨迹照片(尺寸比例相同),设电子速率相同,且与磁场方向垂直,则可知磁场从强到弱的位置排列正确的是( )
A.①②③④ B.①④②③ C.④③②① D.③④②①
经典例题
A
答案:A
解析:电子在月球磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得 ,解得 ,由图可知带电粒子做圆周运动的半径 ,可得 ,
故选A。
2.如图所示,在直角坐标系第一象限存在方向垂直纸面向外、磁感应强度大小为B的匀强磁场,一个质量为m、电荷量为q的粒子从x轴上的P点射入磁场中,入射方向与x轴成 ,射入后恰好能垂直于y轴射出磁场,不计粒子重力,已知 。则( )
A.粒子带正电荷
B.射出点与O点距离为2a
C.若只改变θ,粒子射出点与O点最远的距离为4a
D.若只改变θ,粒子在磁场中运动时间最长为
D
答案:D
解析:A.粒子受洛伦兹力做匀速圆周运动垂直于y轴射出磁场,即水平向左
离开,由左手定则可知粒子带负电,故A错误;
B.粒子的运动轨迹如图所示
由几何关系可得 可得圆周的半径为
则射出点与O点距离为 故B错误;
答案:D
解析:C.若只改变θ,出射点与入射点为直径时,购成的直角
三角形使得粒子射出点与O点最远,如图所示
则 故C错误;
D.若只改变θ,粒子在磁场中运动时间由圆心角决定,圆心角最大时时间最长,则当 时,即粒子的速度水平向右进入磁场时运动时间最大,如图所示
有 解得
则最长运动时间为
故D正确。
带电粒子在匀强磁场中的运动
带电粒子在匀强磁场中的运动
带电粒子在磁场中做圆周运动的半径和周期
带电粒子在磁场中运动情况研究
1.如图所示,虚线框MNPQ内存在匀强磁场,磁场方向垂直纸面向里。a、b、c是三个质量和电荷量都相等的带电粒子,它们从PQ边上的中点沿垂直于磁场的方向射入磁场,图中画出了它们在磁场中的运动轨迹。若不计粒子所受重力,则( )
A.粒子a带负电,粒子b、c带正电
B.粒子c在磁场中的速度最大
C.粒子c在磁场中的加速度最大
D.粒子c在磁场中运动的时间最长
D
答案:D
解析:A.根据左手定则可知,粒子a带正电,粒子b、c带负电,故A错误;
BC.带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律有 得
粒子c的轨迹半径最小,速度最小,所以粒子c的加速度最小,故BC错误;
D.带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律有 且 解得 三个带电粒子的质量和电荷量都相等,故三个粒子在同一磁场中运动的周期相等,粒子c的轨迹对应的圆心角最大,所以粒子c在磁场中运动的时间最长,故D正确。
2.如图所示,两个速度大小不同的同种带电粒子1、2,沿水平方向从同一点垂直射入匀强磁场中,磁场方向垂直纸面向里。当它们从磁场下边界飞出时相对入射方向的偏转角分别为90°、60°,则它们在磁场中运动的( )
A.轨迹半径之比为2:1
B.速度之比为1:2
C.时间之比为2:3
D.周期之比为1:2
B
答案:B
解析:CD.由牛顿第二定律可得
化简可得 ,又 ,联立可得 ,故两粒子的周期相同,速度的偏转角即圆心角,故粒子1的运动时间
粒子2的运动时间
故时间之比为3:2,CD错误;
答案:B
解析:AB.粒子1和粒子2的圆心和如图所示
设粒子1的半径 ,对于粒子2,
由几何关系可得
解得 ,故轨迹半径之比为1:2,由半径公式 可知,速度之比为1:2,A错误,B正确。
3.如图所示,半径为R的圆形区域内有垂直于纸面向里的匀强磁场.重力不计、电荷量一定的带电粒子以速度v正对着圆心O射入磁场,若粒子射入、射出磁场点间的距离为R,则粒子在磁场中的运动时间为( )
A. B.
C. D.
A
答案:A
解析:粒子在磁场中做匀速圆周运动,画出轨迹,如图所示:
由几何关系得,轨道半径:
根据牛顿第二定律,有:
解得:
联立解得:
故在磁场中的运动时间:
故A正确;
4.如图所示,在理想的虚线边界内有范围足够大的匀强磁场,ab、cd段水平,bc、de段竖直,且 .在纸面内大量质子从a点垂直于ab以不同速率射入磁场,不计质子间的相互作用力和重力,则从边界de垂直射出的质子与在磁场中运动时间最长的质子的速率之比为( )
A.3:2
B.36:13
C.9:4
D.36:17
B
答案:B
解析:画出质子的运动轨迹如图所示,设bc长度为2L,则 ,从边界de垂直射出的质子,运动轨迹如图中1所示,圆心为O1,由几何关系可知 ,由几何知识知,当质子过c点时,质子运动轨迹对应的圆心角最大,在磁场中的运动时间最长,运动轨迹如图中2所示,圆心为O2,设半径为R2,则有 ,
可得 ,由 ,可得 ,所以
从边界de垂直射出的质子与在磁场中运动时间最长的
质子的速率之比为 ,故选B.
5.如图,光滑绝缘水平桌面xOy的第一象限存在匀强磁场B,方向垂直桌面向内.从P点垂直Ox轴滚入一个带电小球甲,随后沿着轨迹b离开磁场,在磁场中经历的时间为t。现在Q点放置一个不带电的同种小球乙,再次从P点垂直Ox轴滚入一个带电小球甲,二者发生碰撞后结合在一起,则( )
A.二者将继续沿着轨迹b离开磁场,经历的时间同样为t
B.二者将继续沿着轨迹b离开磁场,经历的时间大于t
C.二者将沿着轨迹a离开磁场,经历的时间大于t
D.二者将沿着轨迹c离开磁场,经历的时间小于t
B
答案:
解析:二者结合在一起,总动量不变,故轨迹半径 ,
大小不变,轨迹依旧沿着b,周期 ,
变大,故经历的时间增加。故选B。
B
1.3 带电粒子在匀强磁场中的运动
人教版(2019)物理(选择性必修第二册)
第一章 安培力与洛伦兹力
目录
素养目标
01
课程导入
02
新课讲解
03
总结归纳
04
课堂练习
05
素养目标
1.理解洛伦兹力对粒子不做功,带电粒子初速度方向与磁感应强度方向垂直时,粒子在匀强磁场中做匀速圆周运动
2.会推导带电粒子在匀强磁场中做匀速圆周运动的半径、周期公式,知道它们和哪些因素有关
3.能够解答带电粒子在匀强磁场中运动相关问题
猜想:带电粒子在磁场中的运动径迹是怎样的?
你猜想的依据是什么?
运动径迹
粒子
初始状态
粒子
受力情况
新课讲解
磁感线——垂直穿入手心
四指——
大拇指——所受洛伦兹力的方向
指向正电荷的运动方向
(负电荷运动的反方向)
洛伦兹力的方向
温故知新
洛伦兹力只会改变粒子速度的 ,
不改变速度的 ,
故粒子将做
方向
大小
匀速圆周运动
-
v
v
F
F
-
思考2:洛伦兹力的方向总与速度方向?
思考1:由于是匀强磁场,洛伦兹力大小?
不变
垂直
洛伦兹力对电荷做功吗?
不做功
一、带电粒子在匀强磁场中的运动
v ⊥ B,洛伦兹力总是与粒子的运动方向垂直,只改变粒子速度的方向,不改变粒子速度的大小,
由于洛伦兹力提供向心力,
所以带电粒子做匀速圆周运动。
F
F
1.带电粒子平行射入匀强磁场
v//B,F洛=0,粒子做匀速直线运动
2.带电粒子的速度垂直于磁场的方向进入磁场
实验验证:观察带电粒子的运动径迹
励磁线圈
电子枪
加速电压选择挡
洛伦兹力演示仪
洛伦兹力演示仪示意图
作用是改变电子束出射的速度
作用是能在两线圈之间产生平行于两线圈中心的连线的匀强磁场
实验验证:观察带电粒子的运动径迹
不加磁场
加磁场
实验现象:在没有磁场作用时,电子的轨迹是直线;在管外加上垂直初速度方向的匀强磁场,电子的轨迹变弯曲成圆形
垂直射入磁场的带电粒子在匀强磁场中做匀速圆周运动,圆周的半径可能与哪些因素有关?周期可能与哪些因素有关?
假设一个电荷量为q的粒子,在磁感应强度为B的匀强磁场中以速度v运动,那么带电粒子所受的洛伦兹力为
思考
圆周运动的向心力公式
洛伦兹力提供向心力
二、带电粒子在匀强磁场中做圆周运动的半径和周期
B
F
v
电荷做匀速圆周运动的向心力由洛伦兹力提供
则:
得:
B
r
v
r
从这个结果看出,带电粒子在匀强磁场中做匀速圆周运动的半径与它的质量、速度成正比,与电荷量、磁感应强度成反比。
你能根据以前所学的知识,推导一下带电粒子在匀强磁场做圆周运动的周期规律吗?
方法一:
根据匀速圆周运动规律:
又由
得
方法二:
根据向心力与周期关系:
又由
得
①圆心的确定
情景一:如图,若已知入射点P、出射点M及其两点的速度方向,如何确定带电粒子运动轨迹圆心?
v0
M
O
【思路点拨】作入射速度出射速度的垂线,两垂线交点就是圆弧轨道的圆心。
三、带电粒子在匀强磁场中做匀速圆周运动的情况分析
基本思路
一找圆心
二求半径
三求周期或时间
P
情景二:如图,若已知入射点P及速度方向、出射点M的位置,如何确定带电粒子运动轨迹圆心?
v0
P
M
O
【思路点拨】做入射速度垂线,再连接PM,并做PM的中垂线,两条线的交点就是圆弧轨道的圆心。
①圆心的确定
②运动半径的确定
情景一:如图,若已知入射点P、出射点M及其两点的速度方向,且已知粒子到M点后速度偏转角为θ,磁场宽度为L,则带电粒子在磁场中运动轨迹半径为多少?
v0
P
M
O
θ
θ
由几何关系可以知道:
根据直角三角形的三边关系可以知道:
即:
L
【思路点拨】
情景二:如图,若粒子在P点垂直于磁场左边界入射,且从M点飞出,若已知M点距P点粒子入射线方向上的Q点距离为H,磁场宽度为L,则带电粒子在磁场中运动轨迹半径为多少?
由几何关系可以知道:
根据直角三角形的三边关系可以知道:
即:
v0
P
M
O
L
H
Q
【思路点拨】
②运动半径的确定
③运动时间的确定
粒子在磁场中运动一周的时间为T,当粒子运动的圆弧所对应的圆心角为α时,其运动时间为多少?
α单位是弧度
α单位是角度
利用圆心角与弦切角的关系,或者是四边形内角和等计算出圆心角的大小,由公式可求出运动时间。
【思路点拨】
画轨迹
找联系
用规律
画出轨迹,并确定圆心,利用几何方法求半径
轨道半径与磁感应强度、运动速度相联系,偏转角度与圆心角、运动时间相联系,在磁场中运动的时间与周期相联系
牛顿第二定律和圆周运动的规律,特别是周期用规律公式,半径公式。
①直线边界:进出磁场具有对称性v
②平行边界:存在临界条件
带电粒子在有界磁场中的运动轨迹特点
1.“月球勘探者号”空间探测器运用高科技手段对月球进行了近距离勘探,在月球重力分布、磁场分布及元素测定方面取得了新的成果。月球上的磁场极其微弱,通过探测器拍摄电子在月球磁场中的运动轨迹,可分析月球磁场的强弱分布情况,如图所示是探测器通过月球表面①、②、③、④四个位置时,拍摄到的电子运动轨迹照片(尺寸比例相同),设电子速率相同,且与磁场方向垂直,则可知磁场从强到弱的位置排列正确的是( )
A.①②③④ B.①④②③ C.④③②① D.③④②①
经典例题
A
答案:A
解析:电子在月球磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得 ,解得 ,由图可知带电粒子做圆周运动的半径 ,可得 ,
故选A。
2.如图所示,在直角坐标系第一象限存在方向垂直纸面向外、磁感应强度大小为B的匀强磁场,一个质量为m、电荷量为q的粒子从x轴上的P点射入磁场中,入射方向与x轴成 ,射入后恰好能垂直于y轴射出磁场,不计粒子重力,已知 。则( )
A.粒子带正电荷
B.射出点与O点距离为2a
C.若只改变θ,粒子射出点与O点最远的距离为4a
D.若只改变θ,粒子在磁场中运动时间最长为
D
答案:D
解析:A.粒子受洛伦兹力做匀速圆周运动垂直于y轴射出磁场,即水平向左
离开,由左手定则可知粒子带负电,故A错误;
B.粒子的运动轨迹如图所示
由几何关系可得 可得圆周的半径为
则射出点与O点距离为 故B错误;
答案:D
解析:C.若只改变θ,出射点与入射点为直径时,购成的直角
三角形使得粒子射出点与O点最远,如图所示
则 故C错误;
D.若只改变θ,粒子在磁场中运动时间由圆心角决定,圆心角最大时时间最长,则当 时,即粒子的速度水平向右进入磁场时运动时间最大,如图所示
有 解得
则最长运动时间为
故D正确。
带电粒子在匀强磁场中的运动
带电粒子在匀强磁场中的运动
带电粒子在磁场中做圆周运动的半径和周期
带电粒子在磁场中运动情况研究
1.如图所示,虚线框MNPQ内存在匀强磁场,磁场方向垂直纸面向里。a、b、c是三个质量和电荷量都相等的带电粒子,它们从PQ边上的中点沿垂直于磁场的方向射入磁场,图中画出了它们在磁场中的运动轨迹。若不计粒子所受重力,则( )
A.粒子a带负电,粒子b、c带正电
B.粒子c在磁场中的速度最大
C.粒子c在磁场中的加速度最大
D.粒子c在磁场中运动的时间最长
D
答案:D
解析:A.根据左手定则可知,粒子a带正电,粒子b、c带负电,故A错误;
BC.带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律有 得
粒子c的轨迹半径最小,速度最小,所以粒子c的加速度最小,故BC错误;
D.带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律有 且 解得 三个带电粒子的质量和电荷量都相等,故三个粒子在同一磁场中运动的周期相等,粒子c的轨迹对应的圆心角最大,所以粒子c在磁场中运动的时间最长,故D正确。
2.如图所示,两个速度大小不同的同种带电粒子1、2,沿水平方向从同一点垂直射入匀强磁场中,磁场方向垂直纸面向里。当它们从磁场下边界飞出时相对入射方向的偏转角分别为90°、60°,则它们在磁场中运动的( )
A.轨迹半径之比为2:1
B.速度之比为1:2
C.时间之比为2:3
D.周期之比为1:2
B
答案:B
解析:CD.由牛顿第二定律可得
化简可得 ,又 ,联立可得 ,故两粒子的周期相同,速度的偏转角即圆心角,故粒子1的运动时间
粒子2的运动时间
故时间之比为3:2,CD错误;
答案:B
解析:AB.粒子1和粒子2的圆心和如图所示
设粒子1的半径 ,对于粒子2,
由几何关系可得
解得 ,故轨迹半径之比为1:2,由半径公式 可知,速度之比为1:2,A错误,B正确。
3.如图所示,半径为R的圆形区域内有垂直于纸面向里的匀强磁场.重力不计、电荷量一定的带电粒子以速度v正对着圆心O射入磁场,若粒子射入、射出磁场点间的距离为R,则粒子在磁场中的运动时间为( )
A. B.
C. D.
A
答案:A
解析:粒子在磁场中做匀速圆周运动,画出轨迹,如图所示:
由几何关系得,轨道半径:
根据牛顿第二定律,有:
解得:
联立解得:
故在磁场中的运动时间:
故A正确;
4.如图所示,在理想的虚线边界内有范围足够大的匀强磁场,ab、cd段水平,bc、de段竖直,且 .在纸面内大量质子从a点垂直于ab以不同速率射入磁场,不计质子间的相互作用力和重力,则从边界de垂直射出的质子与在磁场中运动时间最长的质子的速率之比为( )
A.3:2
B.36:13
C.9:4
D.36:17
B
答案:B
解析:画出质子的运动轨迹如图所示,设bc长度为2L,则 ,从边界de垂直射出的质子,运动轨迹如图中1所示,圆心为O1,由几何关系可知 ,由几何知识知,当质子过c点时,质子运动轨迹对应的圆心角最大,在磁场中的运动时间最长,运动轨迹如图中2所示,圆心为O2,设半径为R2,则有 ,
可得 ,由 ,可得 ,所以
从边界de垂直射出的质子与在磁场中运动时间最长的
质子的速率之比为 ,故选B.
5.如图,光滑绝缘水平桌面xOy的第一象限存在匀强磁场B,方向垂直桌面向内.从P点垂直Ox轴滚入一个带电小球甲,随后沿着轨迹b离开磁场,在磁场中经历的时间为t。现在Q点放置一个不带电的同种小球乙,再次从P点垂直Ox轴滚入一个带电小球甲,二者发生碰撞后结合在一起,则( )
A.二者将继续沿着轨迹b离开磁场,经历的时间同样为t
B.二者将继续沿着轨迹b离开磁场,经历的时间大于t
C.二者将沿着轨迹a离开磁场,经历的时间大于t
D.二者将沿着轨迹c离开磁场,经历的时间小于t
B
答案:
解析:二者结合在一起,总动量不变,故轨迹半径 ,
大小不变,轨迹依旧沿着b,周期 ,
变大,故经历的时间增加。故选B。
B
