【新情境·新趋势】北师大版初中数学九年级上册期末情境模拟卷1(A3版含解析)
文档属性
| 名称 | 【新情境·新趋势】北师大版初中数学九年级上册期末情境模拟卷1(A3版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 14:16:08 | ||
图片预览




文档简介
/ 让教学更有效
初三数学上册期末考试复习卷
(考试时间:120分钟,分值:120分)
一、选择题(本大题共8小题,每小题3分,共24分)
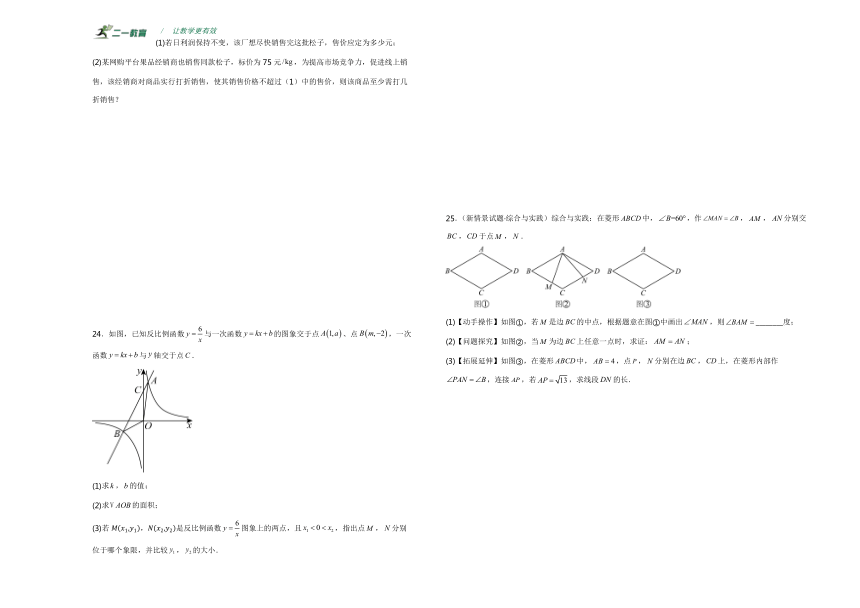
1.如图所示的几何体,其俯视图是( )
A. B.
C. D.
2.已知一元二次方程的两根分别是,则的值是( )
A. B. C. D.
3.如图,随机闭合开关中的两个,则灯泡发光的概率为( )
A. B. C. D.
4.如图所示,电线杆上的路灯距离地面6m,身高 1.2m的小丽(AB)站在距离电线杆的底部(点O)20m的A处,则小丽的影子AM长约为( )
A.4 m B.5 m C.6 m D.8 m
5.如图,四边形是菱形,于点H,则的长是( )
A.4 B.5 C. D.
6.如图,矩形的对角线,交与点O,于E,点F为中点,连接,若,则的度数为( )
A. B. C. D.
7.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:).是体积(单位:)的反比例函数,其图象如图,当时,气体的密度是( )
A. B. C. D.
8.宾馆有60间房供游客居住,当每间房每天定价为170元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房,如果有游客居住,宾馆需对居住的每间房每天支出15元的费用,当房价定为多少元时,宾馆当天的利润为10890元?设房价定为元.则有( )
A. B.
C. D.
二、填空题:(本大题共5小题,每小题3分,共15分)
9.(新情景试题·游戏活动型)袋中装有个黑球和若干个白球,每个球除颜色外都相同.现进行摸球试验,每次摸出一个记下颜色后放回,经过大量的试验,发现摸到黑球的频率稳定在附近,则袋中随机摸出一个球是黑球的概率为 .
10.如图,在平面直角坐标系中,点A是x轴上任意一点,点B,C分别为反比例函数的图象上的点,且轴,已知的面积为3,则k的值为 .
11.某超市销售某种礼盒,该礼盒的原价为元.因销量持续攀升,商家在月份提价,后发现销量锐减,于是经过核算决定在月份售价的基础上,,月份按照相同的降价率连续降价.已知月份礼盒的售价为元,则 .
12.如图,在中,,点D,E分别为,上一个动点,沿折叠得到、点C的对应点为F,若点F落在上,且与相似,则的长为 .
13.如图,为正方形内一点,,,,将绕点按顺时针方向旋转,得到.延长交于点,连接,的长为 .
三、解答题(本题共13小题,共81分。其中:14-20每题5分,21题每题6分,22-23题每题7分,24-25题每题8分,26题10分)。
14.解方程:
(1);
(2).
15.如图,在平面直角坐标系中,给出了格点(顶点是网格线的交点),已知点的坐标为.
(1)画出绕原点顺时针旋转得到的,并写出的坐标;
(2)在给定的网格中,以点为位似中心,将作位似变换且放大到原来的两倍,得到,画出并写出的坐标;
(3)的长度为__________.
16.(1)用配方法解方程:;
(2)①一木杆按如图1所示的方式直立在地面上,请在图中画出它在阳光下的影子;(用线段表示)
②图2是两根标杆及它们在灯光下的影子,请在图中画出光源的位置(用点P表示),并在图中画出人在此光源下的影子(用线段表示).
17.(新情景试题·生活应用型)太原市某校为了落实“五育”并举,提升学生的综合素养,在课外活动中开设了四个兴趣小组:A.跳长绳;B.篮球;C.书法;D.绘画.该校学生会围绕“你最喜欢的项目是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项).根据调查统计结果,绘制了如下两种不完整的统计图,请结合图中信息回答下列问题.
(1)本次共调查了________名学生,并将条形统计图补充完整.
(2)求篮球小组所对应扇形的圆心角度数.
(3)跳长绳小组的4名学生由3名男生和1名女生构成.从中随机抽取2名学生参加比赛.请用列表或画树状图的方法,求恰好抽到1名男生与1名女生的概率.
18.(新情景试题·生活应用型)为预防疾病传播,某小区业主对自己的家庭进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量与时间成正比例;燃烧完,y与x成反比例(如图).现测得药物燃烧完,此时教室内每立方米空气含药量为,根据以上信息解答下列问题:
(1)直接写出药物燃烧阶段y关于x的正比例函数表达式和药物燃烧完y关于x的反比例函数表达式.(需要写出各函数的自变量取值范围)
(2)当每立方米空气中的含药量低于时,对人体方才无毒害作用,那么从消毒开始,经多长时间业主才可以回家?
19.(新情景试题·数学传统文化)《周髀算经》中记载了“平矩以正绳,偃矩以望高,覆矩以测深,卧矩以知远,环矩以为圆,合矩以为方”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).小南利用“矩”可测量大树的高度.如图,通过不断调整自己的姿势和“矩”的摆放位置,使斜边保持水平,并且边与点B在同一直线上,已知“矩”的两边长分别为,,小南的眼睛到地面的距离为,测得,求树高.
20.如图,和相交于点,点在上,,.
(1)求的长;
(2)已知,求的面积.
21.如图,中,,平分,,.
(1)求证:四边形是矩形;
(2)作于F,若,,求的长.
22.(新情景试题·生活应用型)据统计,云梦县博物馆开馆第一个月进馆人次,近日,跟随习近平总书记的考察足迹,云梦县博物馆受到广泛关注,进馆人数逐月增加,第三个月进馆人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,该博物馆月接纳能力不能超过人次,在进馆人次的月平均增长率不变的条件下,该博物馆能否接纳第四个月的进馆人次?并说明理由.
23.(新情景试题·生活应用型)金秋时节,辽北农村山货迎来丰收季,某乡村坚果加工厂购进一批成本价为50元的松子,经加工后对外批量销售,如果按70元销售,每天可卖出.通过市场调查发现,松子售价每降低2元,日销售量就增加.
(1)若日利润保持不变,该厂想尽快销售完这批松子,售价应定为多少元;
(2)某网购平台果品经销商也销售同款松子,标价为75元,为提高市场竞争力,促进线上销售,该经销商对商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?
24.如图,已知反比例函数与一次函数的图象交于点、点,一次函数与轴交于点.
(1)求,的值;
(2)求的面积;
(3)若,是反比例函数图象上的两点,且,指出点,分别位于哪个象限,并比较,的大小.
25.(新情景试题·综合与实践)综合与实践:在菱形中,,作,,分别交,于点,.
(1)【动手操作】如图①,若是边的中点,根据题意在图①中画出,则________度;
(2)【问题探究】如图②,当为边上任意一点时,求证:;
(3)【拓展延伸】如图③,在菱形中,,点,分别在边,上,在菱形内部作,连接,若,求线段的长.
26.(新情景试题·综合与实践)【综合实践】
如图所示,是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境(杠杆原理:阻力阻力臂动力×动力臂,如图1,即),受桔槔的启发,小杰组装了如图所示的装置.其中,杠杆可绕支点在竖直平面内转动,支点距左端,距右端,在杠杆左端悬挂重力为80N的物体.
10 20 30 40 50 …
… 8 2 …
(1)若在杠杆右端挂重物,杠杆在水平位置平衡时,重物所受拉力为____________;
(2)为了让装置有更多的使用空间,小杰准备调整装置,当重物的质量变化时,的长度随之变化.设重物的质量为,的长度为.则:
①关于的函数解析式是________________.
②完成表格:______________;________________.
③在图2的直角坐标系中画出该函数的图象.
(3)在(2)的条件下,若点的坐标为,点的坐标为,在(2)中所求函数的图象上存在点,使得,请直接写出所有满足条件的点的坐标.
答案解析部分
1.D
【分析】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.找到从上面看所得到的图形即可.
【详解】解:从上面可看,可得如下图形:
.
故选:D.
2.D
【分析】本题主要考查了一元二次方程根与系数的关系,掌握一元二次方程根与系数的关系:,是解本题的关键.
根据一元二次方程根与系数的关系可得,,然后利用完全平方公式把变形求解即可.
【详解】解:∵一元二次方程的两个根分别是,
∴,,
∴.
故选D.
3.B
【分析】本题考查了利用列举法求概率,熟练掌握列举法是解题关键.先画出树状图,从而可得随机闭合开关中的两个的所有等可能的结果,再找出灯泡发光的结果,利用概率公式求解即可得.
【详解】解:由题意,画出树状图如下:
由图可知,随机闭合开关中的两个共有6种等可能的结果,其中,灯泡发光的结果有4种,
则灯泡发光的概率为,
故选:B.
4.B
【分析】本题考查了相似三角形的应用,利用相似三角形对应边成比例列出比例式是解题的关键.
根据相似三角形对应边成比例列式计算即可得解.
【详解】解:如图,设路灯底部为点,则,
∵,
∴,
∴,
即,
解得:( m) .
故选:B.
5.D
【分析】本题考查了菱形的性质,菱形的面积,又由菱形的对角线互相平分且垂直,可根据勾股定理得的长,根据菱形的面积的求解方法:底乘以高或对角线积的一半,即可得菱形的高.
【详解】解:如图,设与的交点为O,
∵四边形是菱形,,,
∴,,,
∴,
∵,
∴,
故选:D.
6.B
【分析】根据矩形的性质,,利用等腰三角形的性质,直角三角形的性质,三角形内角和定理解答即可.
【详解】解:∵ 矩形的对角线,交与点O,
∴,
∴,
∵,
∴,
∴,
∵,点F为中点,
∴,,
∴,
故选:B.
【点睛】本题考查了矩形的性质,等腰三角形的性质,直角三角形的性质,三角形内角和定理,熟练掌握性质和定理是解题的关键.
7.B
【分析】本题考查了反比例函数的应用,先利用待定系数法求出密度与体积的函数关系式,再把代入即可求出答案,正确求出反比例函数的关系式是解题的关键.
【详解】解:∵密度是体积的反比例函数,
∴设,
由题意可得:点在反比例函数图象上,
∴,即,
∴,
∴当时,气体的密度;
故选:B.
8.A
【分析】本题主要考查了由实际问题抽象出一元二次方程,根据利润=房价的净利润×入住的房间数即可得解,解题的关键是理解题意找到题目蕴含的相等关系.
【详解】∵房价定为x元,宾馆需对居住的每间房每天支出15元的费用,
∴每间房的利润为元,
∵当每间房每天的定价每增加10元时,就会空闲一间房,
∴可住间房,
∵宾馆当天的利润为10890元,
∴.
故选:A.
9.
【分析】本题考查了频率估计概率,根据经过大量重复的试验得到的频率可以当作概率,即可求解.
【详解】解:经过大量的试验,发现摸到黑球的频率稳定在附近,
随机摸出一个球是黑球的概率为,
故答案为:.
10.
【分析】本题考查反比例函数图象上点的坐标,的几何意义,解题的关键是根据题意作出辅助线.连结,,由轴,可得,由反比例函数性质可得,则,则,从而求得结论.
【详解】解:如解图,连结,,
轴,
,而,
,
,
解得,
,
.
故答案为:.
11.
【分析】本题考查的是一元二次方程的应用.4月份价格从元开始降价,如果两个月平均降价率为r,根据“5月份的售价为元”作为相等关系得到方程求解即可.
【详解】解:根据题意得,
解得,(不合理舍去).
所以4,5月份两个月平均降价率为.即.
故答案为:.
12.或5
【分析】本题考查相似三角形的判定与性质,勾股定理;先求出,再分和两种情况,分别画出图形利用相似三角形的判定与性质求解即可.
【详解】解:∵在中,,
∴,
当时,如图,连接,
∴,,
∴,
∵沿折叠得到、点C的对应点为F,若点F落在上,
∴垂直平分,
∴,
∵,
∴,
∴;
当时,如图,过作于,过作于,则,
∵,
∴,即,
∴设,则,
∴,,
∵,
∴,
∴,即,
∴,,
同理可得,,
∴,
∵沿折叠得到、点C的对应点为F,若点F落在上,
∴,,,
∴,
∴,
∴,即,
解得,,
∴,
故答案为:或.
13.
【分析】本题考查旋转的性质、勾股定理、正方形的判定与性质,熟练掌握旋转的性质、勾股定理、正方形的判定与性质是解答本题的关键.由旋转得,,可得出四边形为正方形,可得5.在中,由勾股定理得,,则.在中,由勾股定理得,,进而可得答案.
【详解】解:由旋转得,
四边形为矩形,
四边形为正方形,
在中,由勾股定理得,,
在中,由勾股定理得,.
故答案为:.
14.(1),;
(2)此方程无解.
【分析】本题主要考查了解一元二次方程,
对于(1),先求出,再根据求根公式求解即可;
对于(2),求出,判断即可.
【详解】(1)解:由,
得,
∴,
即,;
(2)原方程可化为:,
由,
得,
∴此方程无解.
15.(1)作图见解析;
(2)作图见解析;
(3)
【分析】本题考查了作图一位似变换,旋转变换,坐标系中借助勾股定理求线段长,熟练掌握旋转和位似的性质是解题的关键.
(1)按要求作图即可;
(2)按要求作图即可;
(3)利用勾股定理计算即可.
【详解】(1)解:如图所示,.
(2)解:如图所示,.
(3)解:由图可知,.
16.(1)(2)①图见解析②图见解析
【分析】本题考查解一元二次方程,平行投影和中心投影:
(1)利用一除,二移,三配,四变形的方法,进行配方,再进行求解即可;
(2)①根据平行投影,过木杆的顶点,画太阳光的平行线,即可得到线段;
②先确定光源的位置,再画出人在此光源下的影子即可.
【详解】解:(1)
,
,
,
∴,
∴,
∴;
(2)①如图,即为所求;
②如图,点,线段即为所求.
17.(1)40,补全条形统计图如下:
(2)
(3)
【分析】本题考查了条形统计图和扇形统计图,及用列表法或树状图法求概率,准确理解题意,熟练掌握知识点是解题的关键.
(1)由A组人数及其所占百分比可得总人数,总人数减去A、B、D人数求出C组人数即可补全图形;
(2)用360度乘以篮球组人数所占比例即可;
(3)画树状图,共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果有6种,再由概率公式求解即可.
【详解】(1)解:本次调查总人数为(名),
C组人数为(名),
补全图形如下:
故答案为:40;
(2)解:,
故答案为:72;
(3)解:画树状图如下:
共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果共有6种,
∴刚好抽到1名男生与1名女生的概率为.
18.(1);
(2)从消毒开始,经过业主才可以回家
【分析】本题主要考查了一次函数与反比例函数的实际应用,正确求出对应的函数解析式是解题的关键.
(1)利用待定系数法求解即可;
(2)求出药物燃烧后,时,x的值即可得到答案.
【详解】(1)解:设药物燃烧时y关于x的函数表达式为,
∴,
∴,
∴药物燃烧时y关于x的函数表达式为;
设药物燃烧后y关于x的函数表达式为,
∴,
∴,
∴药物燃烧后y关于x的函数表达式为;
(2)解:对于,当时,,
∴从消毒开始,经过业主才可以回家.
19.树高为
【分析】本题主要考查了相似三角形的应用举例,据题意可得,,即可得出,由相似三角形的性质可得出,即可得出,再根据即可得出答案.
【详解】解:据题意可得,,
,
.
,,,
,
,
.
答:树高为.
20.(1)
(2)4
【分析】本题考查相似三角形的判定与性质,利用面积比得对应线段比证明线段平行,掌握相似三角形的判定和性质是解题关键.
(1)过作于,由,可证,可得,由,可得,可证,可得,可证,可得即可;
(2)由,可得即可.
【详解】(1)解:过作于,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
解得:.
(2)解:,
,
,
.
21.(1)见解析;
(2).
【分析】本题主要考查了矩形的性质和判定,等腰三角形的性质,勾股定理,
(1),根据等腰三角形的性质得,再根据平行线的性质得,然后根据,可得,即可得出结论;
(2),根据等腰三角形的性质求出,再根据勾股定理得,然后根据矩形的性质得,,最后根据三角形的面积相等得出答案.
【详解】(1)证明:∵,平分,
∴,
∴.
∵,
∴.
∵,
∴,
∴四边形是矩形;
(2)解:∵,平分,
∴.
∵,
∴.
∵四边形是矩形,
∴,.
∵,
∴.
22.(1)进馆人次的月平均增长率为;
(2)不能,理由见详解;
【分析】本题考查了一元二次方程的增长率的应用,正确掌握相关性质内容是解题的关键:
(1)设进馆人次的月平均增长率为x根据第三个月进馆人次列方程进行计算即可得到答案;
(2)根据(1)的月平均增长率算出第四个月的进馆人次为与人次比较即可得到答案;
【详解】(1)解:设进馆人次的月平均增长率为x,由题意可得,
,
解得:,(不符合题意舍去),
答:进馆人次的月平均增长率为;
(2)解:不能,理由如下,
由(1)得,
四月的人数为:,
∴该博物馆不能接纳第四个月的进馆人次.
23.(1)60元;
(2)8折销售.
【分析】本题主要考查了一元二次方程的应用、不等式的应用等知识点,根据题意正确列出方程和不等式成为解题的关键.
(1)设售价应定为x元,则每的利润为元,根据等量关系利润不变列出一元二次方程求解即可;
(2)设该款松子需要打a折销售,再根据不等关系销售价格不超过60列不等式求解即可.
【详解】(1)解:设售价应定为x元,则每的利润为元,
依题意,得:,
整理得:,
解得:(不合题意,舍去).
答:若日利润保持不变,该厂为尽快销售完这批松子,售价应定为60元.
(2)解:设该款松子需要打a折销售,
由题意,得,,解得:.
答:该商品至少需打8折销售.
24.(1)
(2)
(3)点在第三象限,点在第一象限,
【分析】本题考查反比例函数和一次函数的图象与性质,待定系数法求函数解析式,解题的关键是灵活运用反比例函数和一次函数的图象与性质解决问题.
(1)先求出点,,再利用待定系数法即可求解;
(2)先求得,再利用铅锤法求面积即可;
(3)结合图象即可判断.
【详解】(1)解:把点代入,得:,
∴,
再把点代入,得:,
∴,
∴点,,
∵点,在的图象上,
∴,解得.
(2)解:由(1)可知:,,
∴一次函数解析式为:,
当时,,
∴点,
∴,
∴.
(3)解:由图像可知,点在第三象限,点在第一象限,.
25.(1)图见解析,
(2)见解析
(3)1或3
【分析】(1)根据题意作图,由菱形的性质可得是等边三角形,根据等腰三角形的性质可得,由直角三角形的性质即可求解;
(2)如解图,连接,由四边形是菱形,可得和都是等边三角形,再证即可求解;
(3)根据题意作图如解图,过点作于点,连接,可得是等边三角形,由勾股定理可得,在中,,,由勾股定理可得,同理可得,分类讨论:当点在点的左侧(的位置)时,;当点在点的右侧(的位置)时,;再由(2)知,可得线段的长为1或3,由此即可求解.
【详解】(1)解:作如解图,
∵四边形是菱形,
∴,
如图所示,连接,,
∴是等边三角形,
∴,
∵点是中点,
∴,即,
∴,
故答案为:;
(2)证明:如解图,连接,
四边形是菱形,且,
,,
和都是等边三角形,
,,
,
,
,
,
,
.
(3)解:根据题意作图如解图,过点作于点,连接,
四边形是菱形,且,,
,
是等边三角形,
,
,
在中,,,
,同理可得,
当点在点的左侧(的位置)时,;
当点在点的右侧(的位置)时,;
或3;
由(2)知,
,
,
线段的长为1或3.
【点睛】本题主要考查菱形的性质,等边三角形的判定和性质,全等三角形的判定和性质,勾股定理的综合运用,掌握菱形的性质,全等三角形的判定和性质,等边三角形的判定和性质,分类讨论思想是解题的关键.
26.(1)
(2)①;②,;③见解析
(3)或
【分析】本题考查反比例函数的应用,理解题意,求得函数的解析式是解答的关键.
(1)根据题意,直接根据求解即可;
(2)①由公式可得关于的函数解析式;②将和代入①中解析式中求解即可;③根据表格数据进行描点、连线即可画出图象;
(3)由题意,设,利用坐标与图形性质得,进而由解方程求解即可.
【详解】(1)解:∵,,,,
∴,
∴重物所受拉力为,
故答案为:;
(2)解:①由得,则,
∴关于的函数解析式为;
②当时,;
当时,;
③列表:
10 20 30 40 50 …
… 8 4 2 …
描点,连线,可得该函数的图象:
(3)解:如图,
由题意,设,
∵点的坐标为,点的坐标为,
∴,
由得,
解得,,
经检验,和是所列方程的解,
当时,,当时,,
∴点C的坐标为或.
初三数学上册期末考试复习卷
(考试时间:120分钟,分值:120分)
一、选择题(本大题共8小题,每小题3分,共24分)
1.如图所示的几何体,其俯视图是( )
A. B.
C. D.
2.已知一元二次方程的两根分别是,则的值是( )
A. B. C. D.
3.如图,随机闭合开关中的两个,则灯泡发光的概率为( )
A. B. C. D.
4.如图所示,电线杆上的路灯距离地面6m,身高 1.2m的小丽(AB)站在距离电线杆的底部(点O)20m的A处,则小丽的影子AM长约为( )
A.4 m B.5 m C.6 m D.8 m
5.如图,四边形是菱形,于点H,则的长是( )
A.4 B.5 C. D.
6.如图,矩形的对角线,交与点O,于E,点F为中点,连接,若,则的度数为( )
A. B. C. D.
7.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:).是体积(单位:)的反比例函数,其图象如图,当时,气体的密度是( )
A. B. C. D.
8.宾馆有60间房供游客居住,当每间房每天定价为170元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房,如果有游客居住,宾馆需对居住的每间房每天支出15元的费用,当房价定为多少元时,宾馆当天的利润为10890元?设房价定为元.则有( )
A. B.
C. D.
二、填空题:(本大题共5小题,每小题3分,共15分)
9.(新情景试题·游戏活动型)袋中装有个黑球和若干个白球,每个球除颜色外都相同.现进行摸球试验,每次摸出一个记下颜色后放回,经过大量的试验,发现摸到黑球的频率稳定在附近,则袋中随机摸出一个球是黑球的概率为 .
10.如图,在平面直角坐标系中,点A是x轴上任意一点,点B,C分别为反比例函数的图象上的点,且轴,已知的面积为3,则k的值为 .
11.某超市销售某种礼盒,该礼盒的原价为元.因销量持续攀升,商家在月份提价,后发现销量锐减,于是经过核算决定在月份售价的基础上,,月份按照相同的降价率连续降价.已知月份礼盒的售价为元,则 .
12.如图,在中,,点D,E分别为,上一个动点,沿折叠得到、点C的对应点为F,若点F落在上,且与相似,则的长为 .
13.如图,为正方形内一点,,,,将绕点按顺时针方向旋转,得到.延长交于点,连接,的长为 .
三、解答题(本题共13小题,共81分。其中:14-20每题5分,21题每题6分,22-23题每题7分,24-25题每题8分,26题10分)。
14.解方程:
(1);
(2).
15.如图,在平面直角坐标系中,给出了格点(顶点是网格线的交点),已知点的坐标为.
(1)画出绕原点顺时针旋转得到的,并写出的坐标;
(2)在给定的网格中,以点为位似中心,将作位似变换且放大到原来的两倍,得到,画出并写出的坐标;
(3)的长度为__________.
16.(1)用配方法解方程:;
(2)①一木杆按如图1所示的方式直立在地面上,请在图中画出它在阳光下的影子;(用线段表示)
②图2是两根标杆及它们在灯光下的影子,请在图中画出光源的位置(用点P表示),并在图中画出人在此光源下的影子(用线段表示).
17.(新情景试题·生活应用型)太原市某校为了落实“五育”并举,提升学生的综合素养,在课外活动中开设了四个兴趣小组:A.跳长绳;B.篮球;C.书法;D.绘画.该校学生会围绕“你最喜欢的项目是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项).根据调查统计结果,绘制了如下两种不完整的统计图,请结合图中信息回答下列问题.
(1)本次共调查了________名学生,并将条形统计图补充完整.
(2)求篮球小组所对应扇形的圆心角度数.
(3)跳长绳小组的4名学生由3名男生和1名女生构成.从中随机抽取2名学生参加比赛.请用列表或画树状图的方法,求恰好抽到1名男生与1名女生的概率.
18.(新情景试题·生活应用型)为预防疾病传播,某小区业主对自己的家庭进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量与时间成正比例;燃烧完,y与x成反比例(如图).现测得药物燃烧完,此时教室内每立方米空气含药量为,根据以上信息解答下列问题:
(1)直接写出药物燃烧阶段y关于x的正比例函数表达式和药物燃烧完y关于x的反比例函数表达式.(需要写出各函数的自变量取值范围)
(2)当每立方米空气中的含药量低于时,对人体方才无毒害作用,那么从消毒开始,经多长时间业主才可以回家?
19.(新情景试题·数学传统文化)《周髀算经》中记载了“平矩以正绳,偃矩以望高,覆矩以测深,卧矩以知远,环矩以为圆,合矩以为方”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).小南利用“矩”可测量大树的高度.如图,通过不断调整自己的姿势和“矩”的摆放位置,使斜边保持水平,并且边与点B在同一直线上,已知“矩”的两边长分别为,,小南的眼睛到地面的距离为,测得,求树高.
20.如图,和相交于点,点在上,,.
(1)求的长;
(2)已知,求的面积.
21.如图,中,,平分,,.
(1)求证:四边形是矩形;
(2)作于F,若,,求的长.
22.(新情景试题·生活应用型)据统计,云梦县博物馆开馆第一个月进馆人次,近日,跟随习近平总书记的考察足迹,云梦县博物馆受到广泛关注,进馆人数逐月增加,第三个月进馆人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,该博物馆月接纳能力不能超过人次,在进馆人次的月平均增长率不变的条件下,该博物馆能否接纳第四个月的进馆人次?并说明理由.
23.(新情景试题·生活应用型)金秋时节,辽北农村山货迎来丰收季,某乡村坚果加工厂购进一批成本价为50元的松子,经加工后对外批量销售,如果按70元销售,每天可卖出.通过市场调查发现,松子售价每降低2元,日销售量就增加.
(1)若日利润保持不变,该厂想尽快销售完这批松子,售价应定为多少元;
(2)某网购平台果品经销商也销售同款松子,标价为75元,为提高市场竞争力,促进线上销售,该经销商对商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?
24.如图,已知反比例函数与一次函数的图象交于点、点,一次函数与轴交于点.
(1)求,的值;
(2)求的面积;
(3)若,是反比例函数图象上的两点,且,指出点,分别位于哪个象限,并比较,的大小.
25.(新情景试题·综合与实践)综合与实践:在菱形中,,作,,分别交,于点,.
(1)【动手操作】如图①,若是边的中点,根据题意在图①中画出,则________度;
(2)【问题探究】如图②,当为边上任意一点时,求证:;
(3)【拓展延伸】如图③,在菱形中,,点,分别在边,上,在菱形内部作,连接,若,求线段的长.
26.(新情景试题·综合与实践)【综合实践】
如图所示,是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境(杠杆原理:阻力阻力臂动力×动力臂,如图1,即),受桔槔的启发,小杰组装了如图所示的装置.其中,杠杆可绕支点在竖直平面内转动,支点距左端,距右端,在杠杆左端悬挂重力为80N的物体.
10 20 30 40 50 …
… 8 2 …
(1)若在杠杆右端挂重物,杠杆在水平位置平衡时,重物所受拉力为____________;
(2)为了让装置有更多的使用空间,小杰准备调整装置,当重物的质量变化时,的长度随之变化.设重物的质量为,的长度为.则:
①关于的函数解析式是________________.
②完成表格:______________;________________.
③在图2的直角坐标系中画出该函数的图象.
(3)在(2)的条件下,若点的坐标为,点的坐标为,在(2)中所求函数的图象上存在点,使得,请直接写出所有满足条件的点的坐标.
答案解析部分
1.D
【分析】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.找到从上面看所得到的图形即可.
【详解】解:从上面可看,可得如下图形:
.
故选:D.
2.D
【分析】本题主要考查了一元二次方程根与系数的关系,掌握一元二次方程根与系数的关系:,是解本题的关键.
根据一元二次方程根与系数的关系可得,,然后利用完全平方公式把变形求解即可.
【详解】解:∵一元二次方程的两个根分别是,
∴,,
∴.
故选D.
3.B
【分析】本题考查了利用列举法求概率,熟练掌握列举法是解题关键.先画出树状图,从而可得随机闭合开关中的两个的所有等可能的结果,再找出灯泡发光的结果,利用概率公式求解即可得.
【详解】解:由题意,画出树状图如下:
由图可知,随机闭合开关中的两个共有6种等可能的结果,其中,灯泡发光的结果有4种,
则灯泡发光的概率为,
故选:B.
4.B
【分析】本题考查了相似三角形的应用,利用相似三角形对应边成比例列出比例式是解题的关键.
根据相似三角形对应边成比例列式计算即可得解.
【详解】解:如图,设路灯底部为点,则,
∵,
∴,
∴,
即,
解得:( m) .
故选:B.
5.D
【分析】本题考查了菱形的性质,菱形的面积,又由菱形的对角线互相平分且垂直,可根据勾股定理得的长,根据菱形的面积的求解方法:底乘以高或对角线积的一半,即可得菱形的高.
【详解】解:如图,设与的交点为O,
∵四边形是菱形,,,
∴,,,
∴,
∵,
∴,
故选:D.
6.B
【分析】根据矩形的性质,,利用等腰三角形的性质,直角三角形的性质,三角形内角和定理解答即可.
【详解】解:∵ 矩形的对角线,交与点O,
∴,
∴,
∵,
∴,
∴,
∵,点F为中点,
∴,,
∴,
故选:B.
【点睛】本题考查了矩形的性质,等腰三角形的性质,直角三角形的性质,三角形内角和定理,熟练掌握性质和定理是解题的关键.
7.B
【分析】本题考查了反比例函数的应用,先利用待定系数法求出密度与体积的函数关系式,再把代入即可求出答案,正确求出反比例函数的关系式是解题的关键.
【详解】解:∵密度是体积的反比例函数,
∴设,
由题意可得:点在反比例函数图象上,
∴,即,
∴,
∴当时,气体的密度;
故选:B.
8.A
【分析】本题主要考查了由实际问题抽象出一元二次方程,根据利润=房价的净利润×入住的房间数即可得解,解题的关键是理解题意找到题目蕴含的相等关系.
【详解】∵房价定为x元,宾馆需对居住的每间房每天支出15元的费用,
∴每间房的利润为元,
∵当每间房每天的定价每增加10元时,就会空闲一间房,
∴可住间房,
∵宾馆当天的利润为10890元,
∴.
故选:A.
9.
【分析】本题考查了频率估计概率,根据经过大量重复的试验得到的频率可以当作概率,即可求解.
【详解】解:经过大量的试验,发现摸到黑球的频率稳定在附近,
随机摸出一个球是黑球的概率为,
故答案为:.
10.
【分析】本题考查反比例函数图象上点的坐标,的几何意义,解题的关键是根据题意作出辅助线.连结,,由轴,可得,由反比例函数性质可得,则,则,从而求得结论.
【详解】解:如解图,连结,,
轴,
,而,
,
,
解得,
,
.
故答案为:.
11.
【分析】本题考查的是一元二次方程的应用.4月份价格从元开始降价,如果两个月平均降价率为r,根据“5月份的售价为元”作为相等关系得到方程求解即可.
【详解】解:根据题意得,
解得,(不合理舍去).
所以4,5月份两个月平均降价率为.即.
故答案为:.
12.或5
【分析】本题考查相似三角形的判定与性质,勾股定理;先求出,再分和两种情况,分别画出图形利用相似三角形的判定与性质求解即可.
【详解】解:∵在中,,
∴,
当时,如图,连接,
∴,,
∴,
∵沿折叠得到、点C的对应点为F,若点F落在上,
∴垂直平分,
∴,
∵,
∴,
∴;
当时,如图,过作于,过作于,则,
∵,
∴,即,
∴设,则,
∴,,
∵,
∴,
∴,即,
∴,,
同理可得,,
∴,
∵沿折叠得到、点C的对应点为F,若点F落在上,
∴,,,
∴,
∴,
∴,即,
解得,,
∴,
故答案为:或.
13.
【分析】本题考查旋转的性质、勾股定理、正方形的判定与性质,熟练掌握旋转的性质、勾股定理、正方形的判定与性质是解答本题的关键.由旋转得,,可得出四边形为正方形,可得5.在中,由勾股定理得,,则.在中,由勾股定理得,,进而可得答案.
【详解】解:由旋转得,
四边形为矩形,
四边形为正方形,
在中,由勾股定理得,,
在中,由勾股定理得,.
故答案为:.
14.(1),;
(2)此方程无解.
【分析】本题主要考查了解一元二次方程,
对于(1),先求出,再根据求根公式求解即可;
对于(2),求出,判断即可.
【详解】(1)解:由,
得,
∴,
即,;
(2)原方程可化为:,
由,
得,
∴此方程无解.
15.(1)作图见解析;
(2)作图见解析;
(3)
【分析】本题考查了作图一位似变换,旋转变换,坐标系中借助勾股定理求线段长,熟练掌握旋转和位似的性质是解题的关键.
(1)按要求作图即可;
(2)按要求作图即可;
(3)利用勾股定理计算即可.
【详解】(1)解:如图所示,.
(2)解:如图所示,.
(3)解:由图可知,.
16.(1)(2)①图见解析②图见解析
【分析】本题考查解一元二次方程,平行投影和中心投影:
(1)利用一除,二移,三配,四变形的方法,进行配方,再进行求解即可;
(2)①根据平行投影,过木杆的顶点,画太阳光的平行线,即可得到线段;
②先确定光源的位置,再画出人在此光源下的影子即可.
【详解】解:(1)
,
,
,
∴,
∴,
∴;
(2)①如图,即为所求;
②如图,点,线段即为所求.
17.(1)40,补全条形统计图如下:
(2)
(3)
【分析】本题考查了条形统计图和扇形统计图,及用列表法或树状图法求概率,准确理解题意,熟练掌握知识点是解题的关键.
(1)由A组人数及其所占百分比可得总人数,总人数减去A、B、D人数求出C组人数即可补全图形;
(2)用360度乘以篮球组人数所占比例即可;
(3)画树状图,共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果有6种,再由概率公式求解即可.
【详解】(1)解:本次调查总人数为(名),
C组人数为(名),
补全图形如下:
故答案为:40;
(2)解:,
故答案为:72;
(3)解:画树状图如下:
共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果共有6种,
∴刚好抽到1名男生与1名女生的概率为.
18.(1);
(2)从消毒开始,经过业主才可以回家
【分析】本题主要考查了一次函数与反比例函数的实际应用,正确求出对应的函数解析式是解题的关键.
(1)利用待定系数法求解即可;
(2)求出药物燃烧后,时,x的值即可得到答案.
【详解】(1)解:设药物燃烧时y关于x的函数表达式为,
∴,
∴,
∴药物燃烧时y关于x的函数表达式为;
设药物燃烧后y关于x的函数表达式为,
∴,
∴,
∴药物燃烧后y关于x的函数表达式为;
(2)解:对于,当时,,
∴从消毒开始,经过业主才可以回家.
19.树高为
【分析】本题主要考查了相似三角形的应用举例,据题意可得,,即可得出,由相似三角形的性质可得出,即可得出,再根据即可得出答案.
【详解】解:据题意可得,,
,
.
,,,
,
,
.
答:树高为.
20.(1)
(2)4
【分析】本题考查相似三角形的判定与性质,利用面积比得对应线段比证明线段平行,掌握相似三角形的判定和性质是解题关键.
(1)过作于,由,可证,可得,由,可得,可证,可得,可证,可得即可;
(2)由,可得即可.
【详解】(1)解:过作于,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
解得:.
(2)解:,
,
,
.
21.(1)见解析;
(2).
【分析】本题主要考查了矩形的性质和判定,等腰三角形的性质,勾股定理,
(1),根据等腰三角形的性质得,再根据平行线的性质得,然后根据,可得,即可得出结论;
(2),根据等腰三角形的性质求出,再根据勾股定理得,然后根据矩形的性质得,,最后根据三角形的面积相等得出答案.
【详解】(1)证明:∵,平分,
∴,
∴.
∵,
∴.
∵,
∴,
∴四边形是矩形;
(2)解:∵,平分,
∴.
∵,
∴.
∵四边形是矩形,
∴,.
∵,
∴.
22.(1)进馆人次的月平均增长率为;
(2)不能,理由见详解;
【分析】本题考查了一元二次方程的增长率的应用,正确掌握相关性质内容是解题的关键:
(1)设进馆人次的月平均增长率为x根据第三个月进馆人次列方程进行计算即可得到答案;
(2)根据(1)的月平均增长率算出第四个月的进馆人次为与人次比较即可得到答案;
【详解】(1)解:设进馆人次的月平均增长率为x,由题意可得,
,
解得:,(不符合题意舍去),
答:进馆人次的月平均增长率为;
(2)解:不能,理由如下,
由(1)得,
四月的人数为:,
∴该博物馆不能接纳第四个月的进馆人次.
23.(1)60元;
(2)8折销售.
【分析】本题主要考查了一元二次方程的应用、不等式的应用等知识点,根据题意正确列出方程和不等式成为解题的关键.
(1)设售价应定为x元,则每的利润为元,根据等量关系利润不变列出一元二次方程求解即可;
(2)设该款松子需要打a折销售,再根据不等关系销售价格不超过60列不等式求解即可.
【详解】(1)解:设售价应定为x元,则每的利润为元,
依题意,得:,
整理得:,
解得:(不合题意,舍去).
答:若日利润保持不变,该厂为尽快销售完这批松子,售价应定为60元.
(2)解:设该款松子需要打a折销售,
由题意,得,,解得:.
答:该商品至少需打8折销售.
24.(1)
(2)
(3)点在第三象限,点在第一象限,
【分析】本题考查反比例函数和一次函数的图象与性质,待定系数法求函数解析式,解题的关键是灵活运用反比例函数和一次函数的图象与性质解决问题.
(1)先求出点,,再利用待定系数法即可求解;
(2)先求得,再利用铅锤法求面积即可;
(3)结合图象即可判断.
【详解】(1)解:把点代入,得:,
∴,
再把点代入,得:,
∴,
∴点,,
∵点,在的图象上,
∴,解得.
(2)解:由(1)可知:,,
∴一次函数解析式为:,
当时,,
∴点,
∴,
∴.
(3)解:由图像可知,点在第三象限,点在第一象限,.
25.(1)图见解析,
(2)见解析
(3)1或3
【分析】(1)根据题意作图,由菱形的性质可得是等边三角形,根据等腰三角形的性质可得,由直角三角形的性质即可求解;
(2)如解图,连接,由四边形是菱形,可得和都是等边三角形,再证即可求解;
(3)根据题意作图如解图,过点作于点,连接,可得是等边三角形,由勾股定理可得,在中,,,由勾股定理可得,同理可得,分类讨论:当点在点的左侧(的位置)时,;当点在点的右侧(的位置)时,;再由(2)知,可得线段的长为1或3,由此即可求解.
【详解】(1)解:作如解图,
∵四边形是菱形,
∴,
如图所示,连接,,
∴是等边三角形,
∴,
∵点是中点,
∴,即,
∴,
故答案为:;
(2)证明:如解图,连接,
四边形是菱形,且,
,,
和都是等边三角形,
,,
,
,
,
,
,
.
(3)解:根据题意作图如解图,过点作于点,连接,
四边形是菱形,且,,
,
是等边三角形,
,
,
在中,,,
,同理可得,
当点在点的左侧(的位置)时,;
当点在点的右侧(的位置)时,;
或3;
由(2)知,
,
,
线段的长为1或3.
【点睛】本题主要考查菱形的性质,等边三角形的判定和性质,全等三角形的判定和性质,勾股定理的综合运用,掌握菱形的性质,全等三角形的判定和性质,等边三角形的判定和性质,分类讨论思想是解题的关键.
26.(1)
(2)①;②,;③见解析
(3)或
【分析】本题考查反比例函数的应用,理解题意,求得函数的解析式是解答的关键.
(1)根据题意,直接根据求解即可;
(2)①由公式可得关于的函数解析式;②将和代入①中解析式中求解即可;③根据表格数据进行描点、连线即可画出图象;
(3)由题意,设,利用坐标与图形性质得,进而由解方程求解即可.
【详解】(1)解:∵,,,,
∴,
∴重物所受拉力为,
故答案为:;
(2)解:①由得,则,
∴关于的函数解析式为;
②当时,;
当时,;
③列表:
10 20 30 40 50 …
… 8 4 2 …
描点,连线,可得该函数的图象:
(3)解:如图,
由题意,设,
∵点的坐标为,点的坐标为,
∴,
由得,
解得,,
经检验,和是所列方程的解,
当时,,当时,,
∴点C的坐标为或.
同课章节目录
