浙江省2024年九年级(上)期末压轴题精选分类训练:圆的综合题(含解析)
文档属性
| 名称 | 浙江省2024年九年级(上)期末压轴题精选分类训练:圆的综合题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 17:36:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省2024年九年级(上)期末压轴题精选分类训练
圆的综合题
1.如图,在⊙O中,弦AB是直径,点C,D是⊙O上的两点,连结AC,OD,且满足AC∥OD.
(1)若的度数为80°,求∠A的度数.
(2)求证:.
(3)连结BD,若AC=6,AB=10,求BD的长.
2.如图1,在直角坐标系中,以原点O为圆心,半径为10作圆,交x轴于点A,B(点A在点B的左边).点C为直径AB上一动点,过点C作弦DE⊥AB(点D在点E上方),连接AE,过点D作DF∥AE交圆O于另一点,记为点F.直线EF交x轴于点G,连接OE,BF,AD.
(1)若∠BOE=80°,求∠ADF的度数;
(2)求证:OE∥BF;
(3)若OG=2CG,请直接写出点C横坐标.
3.如图,圆O的弦AB=8,点E为圆外一点,连结BE,AE分别交圆O于点C,点D,∠E=30°,连结CD.
(1)如图1,若圆的半径5,∠ABC=90°,求CD的长;
(2)如图2,若,
①求的值;
②求圆O的半径.
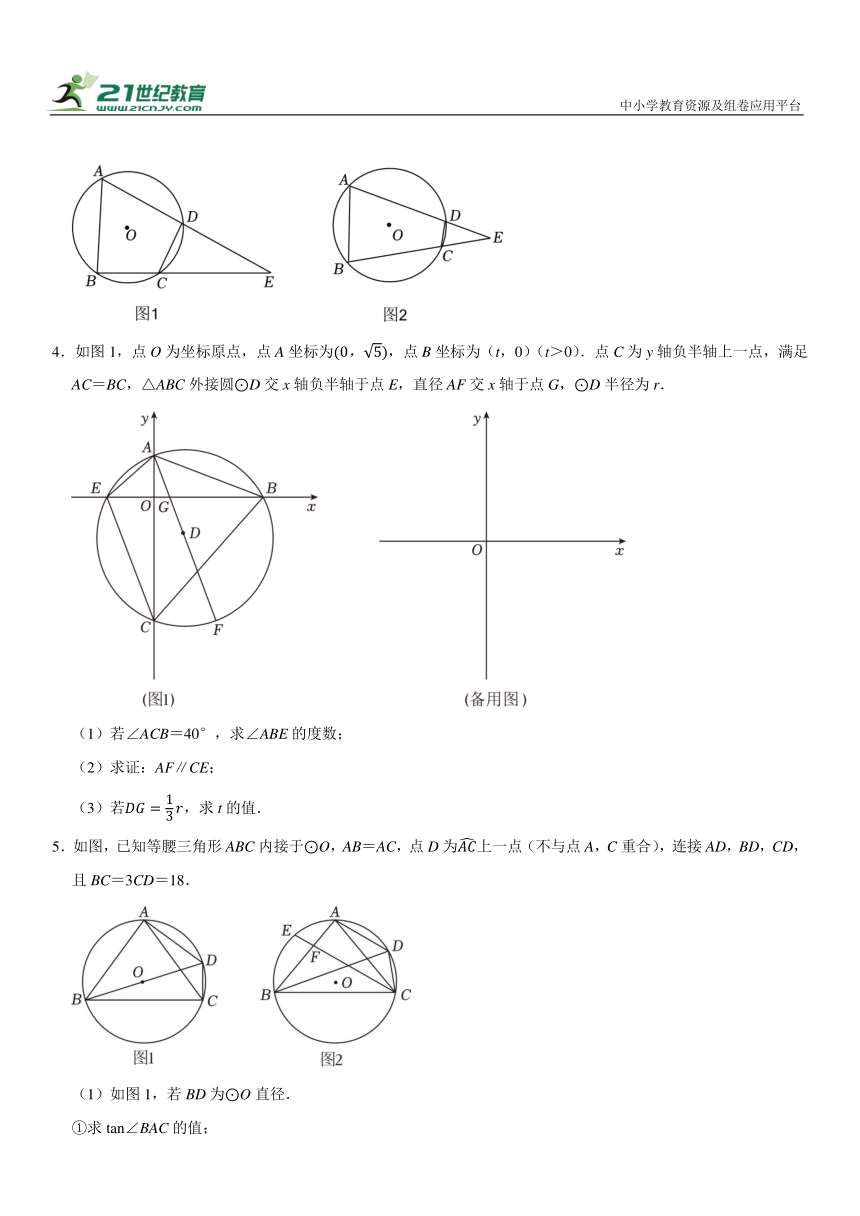
4.如图1,点O为坐标原点,点A坐标为,点B坐标为(t,0)(t>0).点C为y轴负半轴上一点,满足AC=BC,△ABC外接圆⊙D交x轴负半轴于点E,直径AF交x轴于点G,⊙D半径为r.
(1)若∠ACB=40°,求∠ABE的度数;
(2)求证:AF∥CE;
(3)若,求t的值.
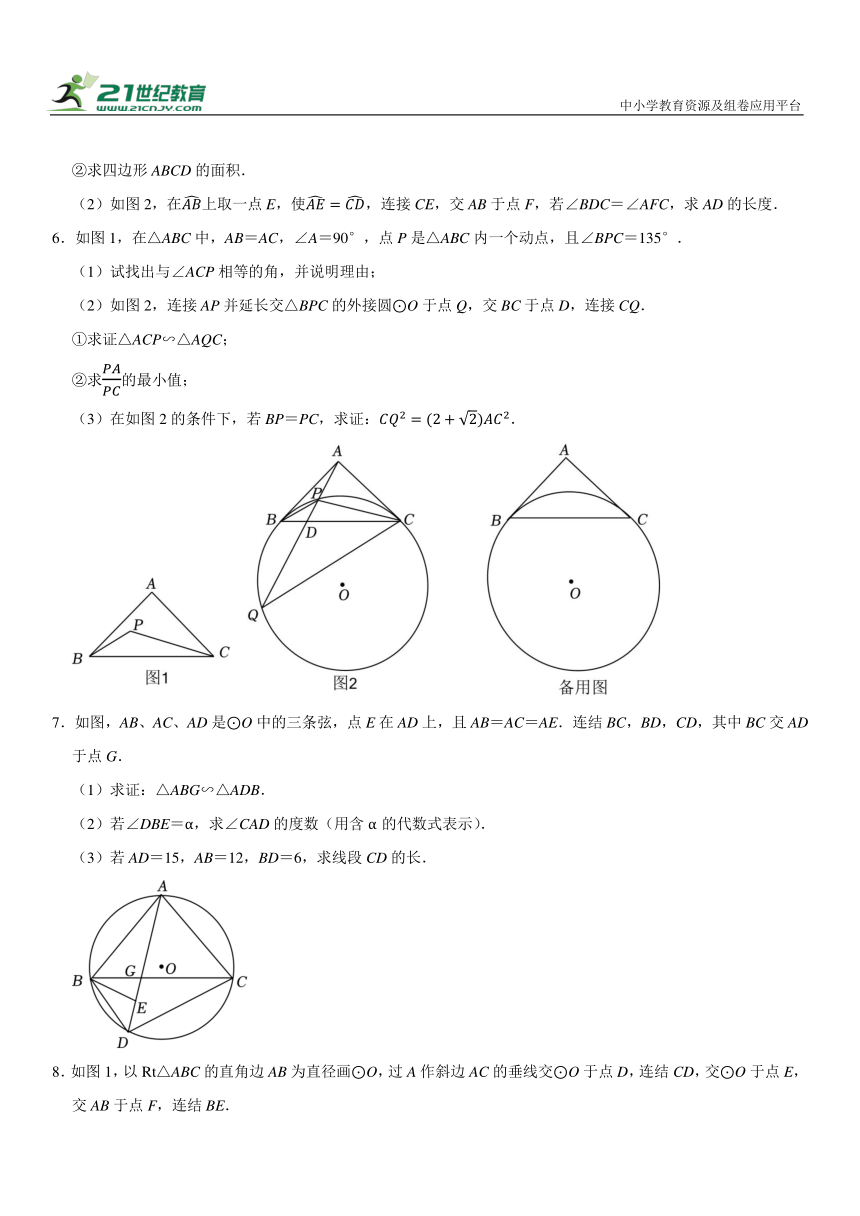
5.如图,已知等腰三角形ABC内接于⊙O,AB=AC,点D为上一点(不与点A,C重合),连接AD,BD,CD,且BC=3CD=18.
(1)如图1,若BD为⊙O直径.
①求tan∠BAC的值;
②求四边形ABCD的面积.
(2)如图2,在上取一点E,使,连接CE,交AB于点F,若∠BDC=∠AFC,求AD的长度.
6.如图1,在△ABC中,AB=AC,∠A=90°,点P是△ABC内一个动点,且∠BPC=135°.
(1)试找出与∠ACP相等的角,并说明理由;
(2)如图2,连接AP并延长交△BPC的外接圆⊙O于点Q,交BC于点D,连接CQ.
①求证△ACP∽△AQC;
②求的最小值;
(3)在如图2的条件下,若BP=PC,求证:.
7.如图,AB、AC、AD是⊙O中的三条弦,点E在AD上,且AB=AC=AE.连结BC,BD,CD,其中BC交AD于点G.
(1)求证:△ABG∽△ADB.
(2)若∠DBE=α,求∠CAD的度数(用含α的代数式表示).
(3)若AD=15,AB=12,BD=6,求线段CD的长.
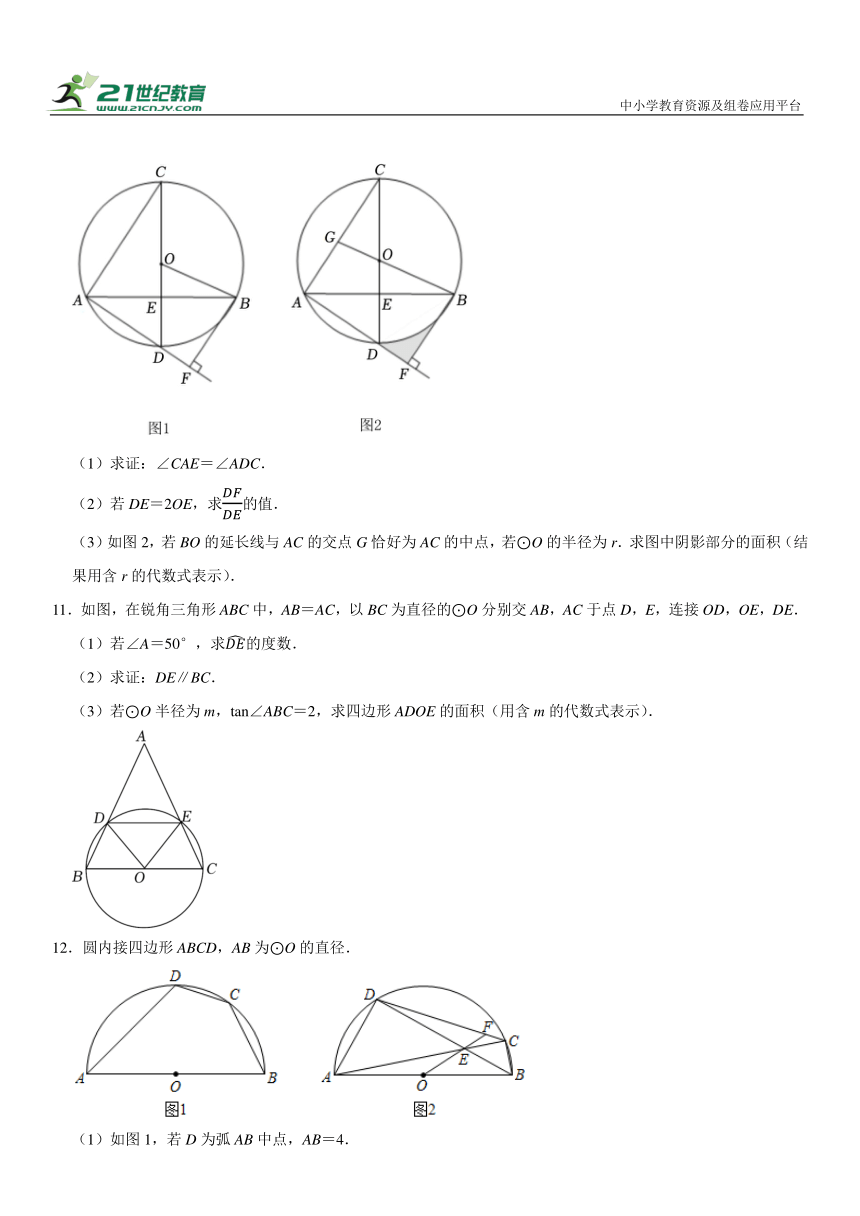
8.如图1,以Rt△ABC的直角边AB为直径画⊙O,过A作斜边AC的垂线交⊙O于点D,连结CD,交⊙O于点E,交AB于点F,连结BE.
(1)求证:∠ACD=∠EBC.
(2)如图2,当△ABC是等腰直角三角形时.
①求∠BCD的正切值;
②求的值.
(3)若AB=1,设CD=x,y,求y关于x的函数表达式.
9.如图,⊙O的半径为1,直径AB,CD的夹角∠AOD=60°,点P是上一点,连接PA,PC分别交CD,AB于点M,N.
(1)若PC⊥AB,求证:PA⊥CD.
(2)当点P在上运动时,
①猜想:线段AM与CN有怎样的数量关系,并给出证明.
②求证:PA+PC.
10.如图1,在⊙O中,AB为弦,CD为直径,且AB⊥CD于点E,过点B作BF⊥AD,交AD的延长线于点F.连接AC,BO.
(1)求证:∠CAE=∠ADC.
(2)若DE=2OE,求的值.
(3)如图2,若BO的延长线与AC的交点G恰好为AC的中点,若⊙O的半径为r.求图中阴影部分的面积(结果用含r的代数式表示).
11.如图,在锐角三角形ABC中,AB=AC,以BC为直径的⊙O分别交AB,AC于点D,E,连接OD,OE,DE.
(1)若∠A=50°,求的度数.
(2)求证:DE∥BC.
(3)若⊙O半径为m,tan∠ABC=2,求四边形ADOE的面积(用含m的代数式表示).
12.圆内接四边形ABCD,AB为⊙O的直径.
(1)如图1,若D为弧AB中点,AB=4.
①求∠DCB的度数;
②求四边形ABCD面积的最大值.
(2)如图2,对角线AC,BD交于点E,连结OE并延长交CD于点F,若OE=3EF=3,求AB的长.
13.如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC,设△DOE的面积为S1,四边形OCBD的面积为S2,若,用含n的代数式表示.
14.如图,△ABC内接于⊙O,∠ABC>90°,△ABC的外角∠EAC的平分线交⊙O于点D,连接DB,DC,DB交AC于点F.
(1)求证:△DBC是等腰三角形.
(2)若DA=DF.
①求证:BC2=DC BF.
②若⊙O的半径为5,BC=6,求的值.
15.如图,点A在y轴正半轴上,OA=1,点B是第一象限内的一点,以AB为直径的圆交x轴于D,C两点,D,C两点的横坐标是方程x2﹣4x+3=0的两个根,OC>OD,连接BC.
(1)如图(1),连接BD.
①求∠ABD的正切值;
②求点B的坐标.
(2)如图(2),若点E是的中点,作EF⊥BC于点F,连接EB,ED,EC,求证:2CF=BC+CD.
16.如图,AB是⊙O的直径,C为AB下方半圆上一动点,OD∥AC交于点D.
(1)求证:;
(2)已知⊙O半径为r,设BD=x,AC=y,求x与y的关系式;
(3)点P为AB上方圆外一点,且∠PAB=2∠APO,连结PA、PB、PO,PA交上半圆于点E,已知当时y=9,,求sin∠PAB的值.
17.如图1,AC是平行四边形ABCD的一条对角线,且AB=AC,△ABC的外接圆⊙O与CD边交于点E,连结AE.
(1)若tan∠ABC=3,△AEC的面积为,求⊙O的半径.
(2)如图2,过点E作EH⊥AB于H,直线EH与直线BC交于点F,若CEHE时,求的值.
18.如图,△ABC中,AB=AC,⊙O是△ABC的外接圆,BO的延长线交边AC于点D.
(1)求证:∠BAC=2∠ABD;
(2)当△BCD是等腰三角形时,求∠BCD的大小;
(3)当AD=2,CD=3时,求边BC的长.
19.如图,已知CE是圆O的直径,点B在圆O上由点E顺时针向点C运动(点B不与点E、C重合),弦BD交CE于点F,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.
(1)若圆O的半径为2,且点D为弧EC的中点时,求圆心O到弦CD的距离;
(2)在(1)的条件下,当DF DB=CD2时,求∠CBD的大小;
(3)若AB=2AE,且CD=12,求△BCD的面积.
20.已知,锐角三角形ABC内接于⊙O.
(1)如图1,当点A是的中点时,
①求证:AO⊥BC.
②若BC=8,AB=4,求⊙O的半径.
(2)如图2,当AB>AC时,连接BO并延长,交边AC于点D.若∠A=45°,,求.
21.如图1,△ABC 内接于⊙O,直径AB=12,弦,作弦CD与AB相交于点E.
(1)如图1,若AE=AC,求∠ACD的度数;
(2)如图2,若AE=4,求CD的长;
(3)如图3,过点A作CD的平行线交⊙O于点M,连结BD,MC,若,求△BCD的面积.
22.如图,△ABC内接于⊙O,BC是⊙O的直径,tan∠ACB=2,过点A作AD⊥BC,交⊙O于点E,点F是上一点,连结EF交BC于点G,连结CF交AD于点H.
(1)求证:△AFC∽△HFE;
(2)若BC=10,CF=8,求EF的长;
(3)设,,求y关于x的函数表达式.
23.如图,△ABC是直角三角形,∠ACB=90°,AC=2,BC=4,点P是边AB上的动点,⊙O是过C,P,B三点的圆,PQ是⊙O的直径,PQ与BC相交于点M.设AP=x.
(1)求证:△PQC∽△ABC.
(2)令△PQC的面积为S,求S关于x的函数关系式,并求当x为何值时,S的值最小.
(3)当时,求x的值.
24.正方形ABCD的四个顶点都在⊙O上,点P是劣弧上一点(点P与点C,D不重合),连结PA,PD.
(1)如图1,求∠APD的度数.
(2)如图2,连结PB.在线段PB上取点M,使得AM=AB,过点M作MN∥AB交PA于点N.记PA,PB与边CD交于点E,F.
①求证:△ADP≌△AMP.
②若MN=5,CF=12,求正方形ABCD的面积.
25.如图1,四边形ABCD内接于⊙O,对角线AC与BD交于点E,AC>BD,点F在AC上,∠ADF+∠ABC=90°.
(1)求∠CDF的度数.
(2)如图2,作DG⊥AB于点G,DG与AC交于点H,BG=CD,E为BD中点,求证:CF=2DE.
(3)在(2)的条件下,BD=2.
①若△BDG的面积是△DEH面积的3倍,求AC的长.
②如图3,当圆心O在高DG上时,求⊙O的半径.
参考答案
1.【分析】(1)连接OC,根据弧AC的度数求出∠AOC,利用三角形内角和求出∠A;
(2)利用平行线的性质求得∠BOD=∠A=50°,∠COD=∠OCA=50°,得出∠COD=∠BOD,进而得出弧相等;
(3)先根据勾股定理求出BC,然后利用勾股定理求出OE,再利用勾股定理求出BD即可.
【解答】(1)解:连接OC,
∵的度数为80°,
∴∠AOC=80°,
∵OA=OC,
∴∠A=∠OCA=50°;
(2)证明:∵AC∥OD,
∴∠BOD=∠A,∠COD=∠OCA,
∵OA=OC,
∴∠A=∠OCA,
∴∠COD=∠BOD,
∴;
(3)解:连接BC,交OD于点E,
∵弦AB是直径,
∴∠ACB=90°,
∵AC=6,AB=10,
∴BC8,
∵,
∴OD⊥BC,
∴CE=BE=4,
∴OE3,
∴DE=OD﹣OE=2,
∴BD2.
2.【分析】(1)由垂径定理得EB=DB,则得∠DAE=∠BOE=80°,再由平行线的性质即可求得结果;
(2)连接OF,由DF∥AE可得AD=EF,再由DE⊥AB得AD=AE,即有AE=EF,则可证明△AOE≌△FOE,得∠AEO=∠FEO,即有∠BOE=2∠AEO=∠AEF,即可得结论;
(3)由条件得OG的中点是C,有OE=GE,则∠OEC=∠GEC;设∠OEC=α,由(2)知∠GFB=∠OEG=∠EAB=2α;由∠EAB=∠OEA得∠EOC=4α,在Rt△OEC中,由两锐角互余得α的度数;连接OF,证明△OFG∽△EFO,则可求得FG,得OG的长,即可求得C点横坐标.
【解答】(1)解:∵AB是直径,DE⊥AB,
∴EB=DB,
∴;
∵,
∴∠DAE=∠BOE=80°;
∵DF∥AE,
∴∠ADF+∠DAE=180°,
∴∠ADF=180°﹣∠DAE=100°;
(2)证明:如图,连接OF,
∵DF∥AE,
∴∠FDE=∠AED,
∴AD=EF,
∵DE⊥AB,AB为直径,
∴AD=AE,
∴AE=EF;
∵OE=OE,OA=OF,
∴△AOE≌△FOE(SSS),
∴∠AEO=∠FEO,
∵OA=OE,
∴∠OAE=∠AEO,
∴∠BOE=∠OAE+∠AEO=2∠AEO=∠AEF;
∵∠FBA=∠AEF,
∴∠FBA=∠BOE,
∴BF∥OE;
(3)解:①∵OG=2CG,
∴OG的中点是C,
∵DE⊥AB,
∴GE=OE=10,
∴∠OEC=∠GEC;
设∠OEC=α,则∠OEC=∠GEC=α,
由(2)知BF∥OE,
∴∠GFB=∠OEG=∠EAB=2α;
∵∠EAB=∠OEA=2α,
∴∠EOC=4α,
在Rt△OEC中,∠OEC+∠EOC=90°,
即α+4α=90°,
∴α=18°;
连接OF,如图,
则∠BOE=∠OBF=75°,∠GFB=∠OEG=2α=36°;
∵OB=OF,
∴∠OFB=∠OBF=72°,∠OFG=∠OFB﹣∠GFB=36°=∠FOB;
∵OF=OE,∠OEG=36°,
∴∠OEG=∠OFG=36°,
∴△OFG∽△EFO,
∴,即OF2=EF FG,
设FG=x,则EF=EG+FG=10+x,
∴x(10+x)=100,
解得:(舍去),
∴;
∵∠OFG=∠FOB,
∴,
∴,
即点C的横坐标为.
②如图:∵OG=2CG,
∴OG的中点是C,
∵DE⊥AB,
∴GE=OE=10,
设∠AEC=α,
∵AE∥DF,
则∠D=∠AEC=α,
∴∠EOF=2α,
由(2)知BF∥OE,
∴∠EOF=∠OFB=2α;
∵OF=OB,
∵∠OFB=∠B=∠EOG=2α,
∴∠FOG=4α,
∵OE=EG,
∴∠EGO=∠EOG=2α,
∴∠OEF=4α,
∵OE=OF,
∴∠OFE=∠OEF=4α,
∵∠G=∠EOF=2α,∠GFO=∠OFE,
∴△OFG∽△EFO,
∴,即OF2=EF FG,
设FG=x,则EF=FG﹣10=x﹣10,
∴x(x﹣10)=100,
解得:x1=5+5,x2=5﹣5
∵∠OFG=∠FOB,
∴OG=FG=5+5或OG=FG=5﹣5,
∴OCOG(舍去)或,
综上所述:点C的横坐标为或.
3.【分析】(1)连结AC,由圆周角定理得出AC是直径,由勾股定理可得出答案;
(2)①证明△ECD∽△EAB,由相似三角形的性质得出;
②过C作CF∥AE交圆O于点F,连结AF,BF,OB,OF,AC,OA,OD,OC,求出,过点F作FH⊥AB,由勾股定理可得出答案.
【解答】解:(1)连结AC,
∵∠ABC=90°,
∴AC为直径10,AB=8,
∴BC6,∠ADC=90°,
∵∠E=30°,
∴AE=2AB=16,
∴BE8,
∴CE=BE﹣BC=86,
在Rt△CDE中,;
(2)①∵四边形ABCD内接于圆O,
∴∠B+∠ADC=180°,
∵∠CDE+∠ADC=180°,
∴∠CDE=∠B,
∵∠E=∠E,
∴△ECD∽△EAB,
∴;
②过C作CF∥AE交圆O于点F,连结AF,BF,OB,OF,AC,OA,OD,OC,
∴∠FAB=∠FCB=∠E=30°,
∴∠BOF=60°,
∵OF=OB,
∴△OBF为等边三角形,
∵CF∥AE,
∴∠ACF=∠CAE,
∴∠AOF=∠COD,
∴,
∴,
过点F作FH⊥AB,
∴,AH=3,
∴BH=AB﹣AH=5,
∴,
∴,
故圆O的半径为.
4.【分析】(1)由AC=BC,∠ACB=40°,可求得∠CAB=70°,由同弧所对的圆周角相等可知∠ACB=∠AEB=40°,进而可求得∠OAE=50°,再根据三角形内角和定理可求得∠ABE的度数.
(2)由AC=BC,等边对等角可得∠CAB=∠CBA,根据同弧所对的圆周角相等可知∠CAB=∠CEB,∠CBA=∠CFA,等量代换得∠CEB=∠CFA,再由直径所对的圆周角是直角,进而可求得两锐角互余,易证得∠ACE=∠CAF,即可证得AF∥CE.
(3)作DN⊥AC于点N,可得AC=CNAC,根据OG∥DN,可得线段成比例,可求得ON的长,进而求得OC和BC的长,最后根据勾股定理可求得OB的长即可求出t的值.
【解答】解:(1)∵AC=BC,∠ACB=40°.
∴∠CAB=70°.
∵∠ACB=∠AEB=40°,AO⊥EB.
∴∠OAE=90°﹣40°=50°.
∴∠EAB=50°+70°=120°.
∴在△AEB中,∠ABE=180°﹣120°﹣40°=20°.
(2)连接CF,如图所示:
∵AC=BC.
∴∠CAB=∠CBA.
∵∠CAB=∠CEB.
∠CBA=∠CFA.
∴∠CEB=∠CFA.
∵AO⊥EB,AF是⊙D的直径.
∴∠EOC=∠ACF=90°.
∴∠CEB+∠ACE=90°.
∠CFA+∠CAF=90°.
∴∠ACE=∠CAF.
∴AF∥CE.
(3)作DN⊥AC于点N,如图所示:
∵点A坐标为(0,).
∴AO.
∵DGr,AD=r.
∴AG=AD﹣DG=rrr.
∵在⊙D中,DN⊥AC.
∴AC=CNAC.
又∵OB⊥AC.
∴OG∥DN.
∴.
即.
解得ON.
∴AN.
∴AC=3.
∴BC=AC=3.
OC=AC﹣AO=2.
∵∠BOC=90°.
∴BC2=OB2+OC2.
∴OB5.
∵点B坐标为(t,0).
∴t=5.
5.【分析】(1)①根据圆周角定理得出∠BAC=∠BDC,根据BD为⊙O直径,得出∠BCD=90°,根据BC=3CD=18,得出;
②过点A作AE⊥BC于点E,连接CO,根据勾股定理得出,求出,根据BO=DO,得出,,证明AE垂直平分BC,根据BO=CO,得出点O在AE上,证明△AMO∽△CMD,得出,求出,得出,求出,最后求出四边形的面积即可;
(2)证明△BCF≌△DBA,得出BF=AD,∠BFC=∠BAD,BD=BC=18,求出FM∥AD,得出,证明△ACF∽△BCD,得出,求出,得出,设AD=x,则,,求出,证明△ACD∽△BCM,得出,即,求出x的值即可.
【解答】解:(1)①∵,
∴∠BAC=∠BDC,
∵BD为⊙O直径,
∴∠BCD=90°,
∵BC=3CD=18,
∴;
②过点A作AE⊥BC于点E,连接CO,如图所示:
∵∠BCD=90°,BC=3CD=18,
∴,
,
∵BO=DO,
∴,,
∴,
∵AB=AC,
∴CE=BE,
∴AE垂直平分BC,
∵BO=CO,
∴点O在AE上,
∵∠AEB=∠BCD=90°,
∴AE∥CD,
∴∠MAO=∠MCD,∠MOA=∠MDC,
∴△AMO∽△CMD,
∴,
∵,
∴,
即,
∴,
即,
∴,
∴.
(2)∵AB=AC,
∴,∠ABC=∠ACB,
∵,
∴∠BDC=∠BAC,
∵∠BDC=∠AFC,
∴∠BAC=∠AFC,
∴AC=CF,
∴AB=CF,
∵,
∴∠ADB=∠ACB,
∴∠FBC=∠ADB,
∵,,
∴,
∴∠BCF=∠ABD,
∴△BCF≌△DBA,
∴BF=AD,∠BFC=∠BAD,BD=BC=18,
∴FM∥AD,
∴,
∵,
∴∠CBD=∠ACF,
∵∠BDC=∠BAC,
∴△ACF∽△BCD,
∴,
∴,
∴,
∴,
设AD=x,则,,
∴,
∵,
∴∠BCE=∠ACD,
∵,
∴∠CBM=∠CAD,
∴△ACD∽△BCM,
∴,
即,
解得:,负值舍去,
即.
6.【分析】(1)根据∠ACB=∠ACP+∠BCP=45°,∠PBC+∠PCB=45°,等量代换即可得到∠ACP=∠PBC;
(2)①根据同弧所对的圆周角相等,结合(1)能得到∠Q=∠APC,即可证明;
②连接OB、CO,由△ACP∽△AQC,得到,当CQ经过圆心O时,的值最小,过点O作OM⊥BC交于M点,则M是BC的中点,连接AM,则A、O、M三点共线,则AO是BC的垂直平分线,再由CO=AC,得到CQ=2AC,即可求的最小值为;
(3)由题意可知P点AM上,则∠PBC=∠PCB=∠ACP,过点P作PH⊥AC交于H点,设PM=x,则PH=x,分别求出APx,AM=(1)x,AC(1)x,PC2=(4+2)x2,再由,即可证明.
【解答】(1)解:∵∠BPC=135°,
∴∠PBC+∠PCB=45°,
∵AB=AC,∠A=90°,
∴∠ACB=∠ACP+∠BCP=45°,
∴∠ACP=∠PBC;
(2)①证明:∵,
∴∠Q=∠PBC,
∵∠ACP=∠PBC,
∴∠Q=∠APC,
∴△ACP∽△AQC;
②连接OB、CO,
∵∠BPC=135°,
∴∠BOC=90°,
∵△ACP∽△AQC,
∴,
∴,
当CQ经过圆心O时,的值最小,
过点O作OM⊥BC交于M点,则M是BC的中点,连接AM,则A、O、M三点共线,
∴AO是BC的垂直平分线,
∵AM=BM=OM,
∴CO=AC,
∴CQ=2AC,
∴的最小值为;
(3)证明:∵BP=PC,
∴P点AM上,
∴∠PBC=∠PCB=∠ACP,
过点P作PH⊥AC交于H点,
∴PH=PM,
设PM=x,则PH=x,
∵∠PAH=45°,
∴APx,
∴AM=(1)x,AC(1)x,PC2=(4+2)x2,
∵,
∴()2,
∴CQ2=(2)AC2.
7.【分析】(1)由等弦所对弧相等,再由等弧所对圆周角相等得出∠ABC=∠ADB,又∠BAG=∠DAB,即可得出结论;
(2)由等边对等角的性质与圆周角性质得出∠DBE=∠CBE=α,即可由∠CAD=∠CBD=∠DBE+∠CBE求解;
(3)由△ABG∽△ADB,得,从而可求出,,从而求出,再证△BDG∽△ADC,得,代入即可求解.
【解答】(1)证明:∵AB=AC,
∴,
∴∠ABC=∠ADB,
又∵∠BAG=∠DAB,
∴△ABG∽△ADB;
(2)解:∵AB=AE,
∴∠AEB=∠ABE,
∴∠DBE+∠ADB=∠ABC+∠CBE,
∵AB=AC,,
∴∠ABC=∠ACB=∠ADB,
∴∠DBE=∠CBE=α,
∵,
∴∠CAD=∠CBD=∠DBE+∠CBE=2α;
(3)解:∵△ABG∽△ADB,
∴,
∵AD=15,AB=12,BD=6,
∴,
∴,,
∴,
∵∠CAD=∠CBD=2α,∠ADC=∠GDB,
∴△BDG∽△ADC,
∴,即,
∴.
8.【分析】(1)利用同弧所对的圆周角相等,通过等量代换证明即可;
(2)①过点D作DG⊥BC交延长线于点G,连接OD,设圆的半径为r,证明四边形BODG是正方形,再求解即可;
②设圆的半径为r,则ADr,AC=2r,过E点作EH⊥BC交于H点,则tan∠EBC=tan∠ACD,结合tan∠BCD,推导出HC=3EH,CEEH,即可得到;
(3)连接AE,证明△ABE∽△CDA和△FAE∽△FCA,推导y与x的关系即可.
【解答】(1)证明:∵,
∴∠D=∠ABE,
∵∠ABC=90°,AD⊥AC,
∴∠D+∠ACD=∠ABE+∠CBE=90°,
∴∠ACD=∠EBC;
(2)解:①过点D作DG⊥BC交延长线于点G,连接OD,
设圆的半径为r,
∵△ABC是等腰直角三角形,∠DAC=90°,
∴△AOD是等腰直角三角形,
∴四边形BODG是正方形,
∴DG=BG=r,BC=2r,
∴tan∠BCD;
②设圆的半径为r,则ADr,AC=2r,
过E点作EH⊥BC交于H点,
∴tan∠EBC=tan∠ACD,
∴BH=2EH,BEEH,
∵tan∠BCD,
∴HC=3EH,CEEH,
∴;
(3)连接AE,
∵AB是圆的直径,
∴∠AEB=90°=∠DAC,
∵∠ADC=∠ABE,
∴△ABE∽△CDA,
∴x,
∵∠FAE=∠FCA,∠AFE=∠CFA,
∴△FAE∽△FCA,
∴x,
∴x2,
∴yx2﹣1.
9.【分析】(1)由圆周角定理得出∠BAP=30°,由三角形内角和定理可求出∠AMO=90°,则可得出结论;
(2)①连接AD,证出∠D=60°,OA=AD=OD,证明△ADM≌△CON(ASA),由全等三角形的性质得出AM=CN;
②证明△AOM∽△APN,由相似三角形的性质得出,证明△CON∽△CPM,由相似三角形的性质得出,由全等三角形的性质得出AM=CN,DM=ON,代入PA+PC并化简整理可得出答案.
【解答】(1)证明:∵∠AOD=∠BOC=60°,PC⊥AB,
∴60°,
∴∠BAP=30°,
∴∠AMO=180°﹣∠MAO﹣∠AOM=180°﹣30°﹣60°=90°,
∴PA⊥CD;
(2)解:①AM=CN.
证明:连接AD,
∵OA=OD,∠AOD=60°,
∴△OAD是等边三角形,
∴∠D=60°,OA=AD=OD,
∵OC=OD,∠BOC=∠AOD=60°,
∴AD=OC,∠D=∠BOC=60°,
又∵∠DAP=∠DCP,
∴△ADM≌△CON(ASA),
∴AM=CN;
②证明:∵⊙O的半径为1,
∴OA=OB=OC=OD=1,
∵∠P=∠D=60°,∠AOD=60°,
∴∠P=∠AOD,
又∵∠BAP=∠BAP,
∴△AOM∽△APN,
∴,
∴,即PA,
∵∠BOC=∠CPM=60°,∠C=∠C,
∴△CON∽△CPM,
∴,
∴PC,
∵△ADM≌△CON,
∴AM=CN,DM=ON,
又∵DM+OM=OD=1,
∴PA+PC.
10.【分析】(1)由圆周角定理可得∠CAD=∠CAE+∠DAE=90°,再根据AB⊥CD,易得∠ADC+∠DAE=90°,即可证明∠CAE=∠ADC;
(2)连接BD,设OE=a,则DE=2a,OB=OD=3a,由勾股定理可得,,再证明△BOE∽△BDF,由相似三角形的性质可得,代入数值可求得,即可获得答案;
(3)连接BD,首先证明△OBE≌△DAE,结合全等三角形的性质进一步证明△OBD为等边三角形,即有∠BOD=60°;利用勾股定理、等边三角形的性质以及含30度角的直角三角形的性质依次求得OE、BE、AB、BF、AF等的值,然后由S阴影=S△ABF﹣S△DAE﹣(S扇形OBD﹣S△OBE)即可获得答案.
【解答】解:(1)∵CD为⊙O直径,
∴∠CAD=90°,即∠CAE+∠DAE=90°,
又∵AB⊥CD,
∴∠ADC+∠DAE=90°,
∴∠CAE=∠ADC;
(2)如图,连接BD,
∵AB⊥CD,DE=2OE,
∴OD=DE+OE=3OE,
设OE=a,则DE=2a,OB=OD=3a,
∴在Rt△OBE中,,
∴在Rt△DBE中,,
∵CD为⊙O直径,且AB⊥CD,
∴BE=AE,
∴AD=BD,
∴∠DAB=∠DBA,
∴∠BDF=∠DAB+∠DBA=2∠DAB,
又∵,
∴∠DOB=2∠DAB=∠BDF,
∵∠OEB=∠DFB=90°,
∴△BOE∽△BDF,
∴,即,
解得,
∴;
(3)如图,连接BD,
∵BO的延长线与AC的交点G恰好为AC的中点,
∴OG⊥AC,即∠OGC=∠CAD=90°,
∴BG∥AD,
∴∠OBE=∠DAE,
又∵BE=AE,∠OEB=∠DEA,
∴△OBE≌△DAE(ASA),
∴OB=DA,
∵CD为⊙O直径,AB⊥CD,
∴,
∴DA=DB,
∴OD=OB=DB,即△OBD为等边三角形,∠BOD=60°,
∵⊙O的半径为r,
∴OB=r,,
∴,
∴,
∵,
∴,
∴,
∴,
∵△OBE≌△DAE,
∴S△OBE=S△DAE,
∴S阴影=S△ABF﹣S△DAE﹣(S扇形OBD﹣S△OBE)
=S△ABF﹣S扇形OBD
.
11.【分析】(1)连接BE,求出∠ABE,可得结论;
(2)通过计算求出∠BED,∠CBE可得结论;
(3)证明AO⊥DE,求出AO,DE,可得结论.
【解答】(1)解:如图,连接BE.
∵BC是直径,
∴∠BEC=90°,
∴∠AEB=90°,
∵∠BAC=50°,
∴∠ABE=90°﹣50°=40°,
∴∠DOE=2∠DBE=80°,
∴的度数为80°;
(2)证明:设BAC=2α.
∵AB=AC,
∴∠ABC=∠ACB=90°﹣α,
∵∠ABE=90°﹣2α,
∴∠CBE=∠ABC﹣∠ABE=α,
∵OB=OD,
∴∠OBD=∠ODB=90°﹣α,
∴∠BOD=180°﹣2×(90°﹣α)=2α,
∴∠BED∠BOD=α,
∴∠CBE=∠BED,
∴DE∥BC;
(3)解:∵AB=AC,BO=OC,
∴AO⊥BC,
∴tan∠ABC2,
∵OB=m,
∴OA=2m,
∵tan∠C2,
∴ECm,
∵AB=ACm,
∴AE=AC﹣ECmmm,
∵DE∥CB,
∴,
∴,
∴DEm,
∵AO⊥BC,DE∥BC,
∴AO⊥DE,
∴S四边形ADOE AO DE2mmm2.
12.【分析】(1)①根据圆周角定理知∠A=45°,再利用圆内接四边形的性质可得答案;
②连接BD,OC交于点E,则△BCD面积最大时,四边形ABCD面积最大,当OC⊥BD时,CE最大,从而求出答案.
(2)直线OF交⊙O于点M,N,过F作PQ∥AB交直线BD,AC于点P,Q,根据△PFD∽△CFQ,得PF FQ=FD FC,再由△MFD∽△CFN,得MF FN=FD FC,从而得出PF FQ=MF FN,再利用平行线分线段成比例证明FP=FQ,设半径为r,则(r﹣4)(r+4),从而解决问题.
【解答】解:(1)①∵AB为直径,D为的中点,
∴∠A=45°,
∴∠DCB=180°﹣∠A=180°﹣45°=135°,
②连接BD,AC交于点E,
当四边形ABCD面积最大时,即△BCD面积最大,
当OC⊥BD时,CE最大,
∵AB=4,
∴BD=AD=2,
∴OE,
∴S,
∴S四边形ABCD的最大值为:S;
(2)直线OF交⊙O于点M,N,过F作PQ∥AB交直线BD,AC于点P,Q,
∵∠Q=∠A=∠CDE,
∴△PFD∽△CFQ,
∴PF FQ=FD FC,
∵∠N=∠MDF,∠MFD=∠CFN,
∴△MFD∽△CFN,
∴MF FN=FD FC,
∴PF FQ=MF FN,
∵PQ∥AB,
∴,
∴FP=FQ,
设半径为r,
∴(r﹣4)(r+4),
∵r>0,
∴r=3,
∴AB=6.
13.【分析】(1)根据圆周角定理和垂直求出∠DEO=∠ACB,根据平行得出∠DOE=∠ABC,根据相似三角形的判定得△DOE∽△ABC,根据圆周角定理得出∠A=∠BDC,推出∠ODE=∠BDC即可;
(2)根据圆周角定理和垂直求出∠DEO=∠ACB,根据平行得出∠DOE=∠ABC,根据相似三角形的判定得出结论;
(3)根据△DOE∽△ABC,求出S△ABC=4S△DOE=4S1,进而求解.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
∴∠ODE=∠A,
∵∠A和∠BDC是所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE;
(3)解:∵△DOE∽△ABC,
∴()2,
即S△ABC=4S△DOE=4S1,
∵OA=OB,
∴S△BOCS△ABC,即S△BOC=2S1,
∵,S2=S△BOC+S△DOE+S△DBE=2S1+S1+S△DBE,
∴S△DBES1,
∴BE=()OE,
即OEOBDO,
∴sinA=sin∠ODE.
14.【分析】(1)由题意易得∠BCD+∠BAD=180°,则有∠EAD=∠BCD,进而可得∠EAD=∠DAC,则∠BCD=∠CBD,然后问题可求证;
(2)①由题意易证△DAF∽△DBC,则有∠ADF=∠BDC,进而可得∠DFA=∠DCB,再由相似三角形的判定得出△FBC∽△BCD,利用其性质即可证明;
②连接DO交BC于G,由题意易得D、O都在中垂线上,即D、O、G共线,进而可得DO⊥BC且BG=GC=3,则有DG=4+OD=9,由①得,根据相似三角形的性质得出,再由相似三角形的判定得出△AFD∽△BFC,利用其性质即可求解.
【解答】(1)证明:∵四边形ABCD内接于⊙O,
∴∠BCD+∠BAD=180°,
∵∠DAB+∠EAD=180°,
∴∠EAD=∠BCD,
∴∠CAD=∠CBD,
∵AD平分∠EAC,
∴∠EAD=∠DAC,
∴∠BCD=∠CBD,
∴DB=DC,
∴△DBC是等腰三角形;
(2)①证明:∵DA=DF,
∴∠DAF=∠DFA,
∴∠DAF=∠DFA=∠CBD=∠BCD,
∴△DAF∽△DBC,
∴∠ADF=∠BDC,
∴∠DFA=∠DCB,
∵∠DBC=∠FBC,
∴△FBC∽△BCD,
∴,
∴BC2=BD BF,
∵DB=DC,
∴BC2=DC BF;
②解:连接DO交BC于G,
∵BD=DC,OB=OC,
∴D、O都在中垂线上,即D、O、G共线,
∴DO⊥BC且BG=GC=3,
∵OB=5,
∴在Rt△BOG中,OG=4,
∴DG=4+OD=9,
∴在Rt△BDG中,,
∵△FBC∽△BCD,
∴,
∴,
解得:,
∴,
∴,
∵∠DAC=∠DBC,∠DFA=∠BFC,
∴△AFD∽△BFC,
∴,
∴.
15.【分析】(1)①过点P作PH⊥DC于H,作AF⊥PH于F,连接PD、AD,利用因式分解法解出一元二次方程,求出OD、OC,根据垂径定理求出DH,根据勾股定理计算求出半径,根据圆周角定理得到∠ADB=90°,根据正切的定义计算即可;
②过点B作BE⊥x轴于点E,作AG⊥BE于G,根据平行线分线段成比例定理定理分别求出OE、BE,得到点B的坐标;
(2)过点E作EH⊥x轴于H,证明△EHD≌△EFB,得到EH=EF,DH=BF,再证明Rt△EHC≌Rt△EFC,得到CH=CF,结合图形计算,证明结论.
【解答】(1)解:①方法一、以AB为直径的圆的圆心为P,
过点P作PH⊥DC于H,作AF⊥PH于F,连接PD、AD,
则DH=HCDC,四边形AOHF为矩形,
∴AF=OH,FH=OA=1,
解方程x2﹣4x+3=0,得x1=1,x2=3,
∵OC>OD,
∴OD=1,OC=3,
∴DC=2,
∴DH=1,
∴AF=OH=2,
设圆的半径为r,则PH,
∴PF=PH﹣FH1,
在Rt△APF中,AP2=AF2+PF2,即r2=22+(1)2,
解得:r,
∵∠AOD=90°,OA=OD=1,
∴AD,
∵AB为直径,
∴∠ADB=90°,
∴BD3,
∴tan∠ABD;
方法二、连接AC,
根据圆周角定理得到:∠ABD=∠ACD,
求出tan∠ACD,得出tan∠ABD;
②过点B作BE⊥x轴于点E,作AG⊥BE于G,
则OA∥PH∥BE,
∵P为AB的中点,
∴OE=2OH=4,BG=2PF=2,
∴BE=BG+GE=3,
∴点B的坐标为(4,3);
(2)证明:过点E作EH⊥x轴于H,
∵点E是的中点,
∴,
∴ED=EB,
∵四边形EDCB为圆P的内接四边形,
∴∠EDH=∠EBF,
在△EHD和△EFB中,
,
∴△EHD≌△EFB(AAS),
∴EH=EF,DH=BF,
在Rt△EHC和Rt△EFC中,
,
∴Rt△EHC≌Rt△EFC(HL),
∴CH=CF,
∴2CF=CH+CF=CD+DH+BC﹣BF=BC+CD.
16.【分析】(1)通过条件证明∠BOD=∠COD,即可得到结论;
(2)连OC、BC、BD,BC与OD交于点Q,证明△BOQ∽△BAC,用含y的式子表示OQ和QD,在Rt△COQ和Rt△BDQ中运用勾股定理即可得到x与y的关系式;
(3)利用(2)的关系式求出r,连接OE,BE,证明三角形POE是等腰三角形,得到PE的长,在Rt△BPE中,运用勾股定理求出BE,在Rt△ABE中运用正弦函数的定义即可得到sin∠PAB的值.
【解答】(1)证明:连接OC,
∵OD∥AC,
∴∠BAC=∠BOD,∠OCA=∠COD,
∵OA=OC,
∴∠BAC=∠OCA,
∴∠BOD=∠COD,
∴;
(2)解:连OC、BC、BD,BC与OD交于点Q,
∵OD∥AC,
∴△BOQ∽△BAC,
∴,
∵AB=2OB,
∴,BQ=CQ,
∵OD=r,
∴QD=OD﹣OD,
∵OD是半径,BQ=CQ,
∴OD⊥BC,
在Rt△COQ和Rt△BDQ中,
由勾股定理得CQ2=OC2﹣OQ2,BQ2=BD2﹣QD2,
∵BQ=CQ,
∴OC2﹣OQ2=BD2﹣QD2,即,
整理得x2+ry﹣2r2=0;
(3)解:连接OE,BE,
把,y=9代入x2+ry﹣2r2=0,
得5+9r﹣2r2=0,
解得(不合题意,舍去),r=5,
∵OA=OE,
∴∠PAB=∠AEO=2∠APO,
∵∠AEO是△POE的外角,
∴∠AEO=∠APO+∠POE,
∴∠APO=∠POE,
∴OE=PE=5,
∵AB是直径,
∴∠AEB=∠BEP=90°,
在Rt△BPE中,
∵PE=5,PB,
∴BE,
在Rt△ABE中,
∵BE=6,AB=2r=10,
∴sin∠PAB.
17.【分析】(1)连接AO并延长交BC于点M,连接OB,OC,过点A作AG⊥DE,垂足为G,设BM=x,根据题意易得AM是BC的垂直平分线,从而可得BC=2BM=2x,进而在Rt△ABM中,利用锐角三角函数的定义求出AM=3x,从而利用勾股定理求出ABx,再利用等腰三角形和平行四边形的性质可得∠ABC=∠ACB,BC=AD=2x,AB=CDx,∠ABC=∠D,然后根据圆内接四边形对角互补以及平角定义可得∠AED=∠ABC,从而可得∠ABC=∠ACB=∠D=∠AED,再证明△ABC∽△ADE,从而利用相似三角形的性质可求出DE,AG的长,进而求出CE的长,再根据△AEC的面积为,列出关于x的方程,进行计算可求出BM,AM的长,最后设⊙O的半径为r,在Rt△BOM中,利用勾股定理进行计算即可解答;
(2)连接AO并延长交BC于点M,连接OB,OC,过点A作AG⊥DE,垂足为G,过点C作CL⊥AB,垂足为L,设CE=a,BL=b,则EH=2a,利用平行四边形的性质可得AD∥BC,AB∥CD,AD=BC,从而可得CL=EH=2a,进而可得AD=BC,再利用AAS证明△BLC≌△DGA,从而可得BL=DG=b,进而可得DE=2DG=2b,CD=2b+a,然后证明△DAE∽△DCA,从而利用相似三角形的性质进而计算可得ba,再证明△ABM∽△FCE,从而利用相似三角形的性质,进行计算即可解答.
【解答】解:(1)连接AO并延长交BC于点M,连接OB,OC,过点A作AG⊥DE,垂足为G,
设BM=x,
∵AB=AC,OB=OC,
∴AM是BC的垂直平分线,
∴BC=2BM=2x,
在Rt△ABM中,tan∠ABM=3,
∴AM=BM tan∠ABM=3x,
∴ABx,
∵AB=AC,
∴∠ABC=∠ACB,
∵四边形ABCD是平行四边形,
∴BC=AD=2x,AB=CDx,∠ABC=∠D,
∵四边形ABCE是⊙O的内接四边形,
∴∠ABC+∠AEC=180°,
∵∠AEC+∠AED=180°,
∴∠AED=∠ABC,
∴∠D=∠AED,
∴AE=AD,
∵∠ABC=∠ACB=∠D=∠AED,
∴△ABC∽△ADE,
∴
∴,
∴DEx,AGx,
∴CE=CD﹣DEx,
∵△AEC的面积为,
∴CE AG,
∴ x x,
解得:x=3或x=﹣3(舍去),
∴BM=3,AM=3x=9,
设⊙O的半径为r,
在Rt△BOM中,OM2+BM2=BO2,
∴(9﹣r)2+32=r2,
解得:r=5,
∴⊙O的半径为5;
(2)连接AO并延长交BC于点M,连接OB,OC,过点A作AG⊥DE,垂足为G,过点C作CL⊥AB,垂足为L,
设CE=a,BL=b,
∵CEEH,
∴EH=2a,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∴CL=EH=2a,
∴BC,
∴AD=BC,
∵∠BLC=∠DGA=90°,∠ABC=∠D,BC=AD,
∴△BLC≌△DGA(AAS),
∴BL=DG=b,
∵AE=AD,AG⊥DE,
∴DE=2DG=2b,
∴CD=DE+CE=2b+a,
∵AD∥BC,
∴∠CAD=∠ACB,
∵∠ACB=∠AED,
∴∠CAD=∠AED,
∵∠D=∠D,
∴△DAE∽△DCA,
∴,
∴DA2=DC DE,
∴()2=(2b+a) 2b,
∴b2+4a2=4b2+2ab,
整理得:3b2+2ab﹣4a2=0,
解得:ba或ba(舍去),
∵AB∥CD,
∴∠ABC=∠ECF,∠FEC=∠FHB=90°,
∴∠AME=∠FEC=90°,
∴△ABM∽△FCE,
∴22,
∴的值为.
18.【分析】(1)连接OA.利用垂径定理以及等腰三角形的性质解决问题即可.
(2)分三种情形:①若BD=CB,则∠C=∠BDC=∠ABD+∠BAC=3∠ABD.②若CD=CB,则∠CBD=∠CDB=3∠ABD.③若DB=DC,则D与A重合,这种情形不存在.分别利用三角形内角和定理构建方程求解即可.
(3)如图3中,作AE∥BC交BD的延长线于E.则,推出,设OB=OA=4a,OH=3a,根据BH2=AB2﹣AH2=OB2﹣OH2,构建方程求出a即可解决问题.
【解答】(1)证明:连接OA.
∵AB=AC,
∴,
∴OA⊥BC,
∴∠BAO=∠CAO,
∵OA=OB,
∴∠ABD=∠BAO,
∴∠BAC=2∠ABD.
(2)解:如图2中,延长AO交BC于H.
①若BD=CB,则∠C=∠BDC=∠ABD+∠BAC=3∠ABD,
∵AB=AC,
∴∠ABC=∠C,
∴∠DBC=2∠ABD,
∵∠DBC+∠C+∠BDC=180°,
∴8∠ABD=180°,
∴∠C=3∠ABD=67.5°.
②若CD=CB,则∠CBD=∠CDB=3∠ABD,
∴∠C=4∠ABD,
∵∠DBC+∠C+∠CDB=180°,
∴10∠ABD=180°,
∴∠BCD=4∠ABD=72°.
③若DB=DC,则D与A重合,这种情形不存在.
综上所述,∠C的值为67.5°或72°.
(3)如图3中,作AE∥BC交BD的延长线于E.
则,
∴,设OB=OA=4a,OH=3a,
∵BH2=AB2﹣AH2=OB2﹣OH2,
∴25﹣49a2=16a2﹣9a2,
∴a2,
∴BH2=7a2,
∴BH
∴BC=2BH.
19.【分析】(1)过O作OH⊥CD于H,根据点D为弧EC的中点,可得∠OCH=45°,进而得出OH=CH,再根据圆O的半径为2,即可得到OH;
(2)先判定△CDF∽△BDC,可得∠DCF=∠DBC,再根据∠DCF=45°,即可得出∠DBC=45°;
(3)连接BE,BO,DO,并延长BO至H点,依据∠ABE=∠OBC=∠OCB,∠A=∠A,判定△ABE∽△ACB,即可得到AC,设AE=x,再根据△AOB∽△COH,可得,即,解得x=5,OH=4.5,OB=7.5,即可得到△BCD的面积12×12=72.
【解答】解:(1)如图,过O作OH⊥CD于H,
∵点D为弧EC的中点,
∴弧ED=弧CD,
∴∠OCH=45°,
∴OH=CH,
∵圆O的半径为2,即OC=2,
∴OH;
(2)∵当DF DB=CD2时,,
又∵∠CDF=∠BDC,
∴△CDF∽△BDC,
∴∠DCF=∠DBC,
由(1)可得∠DCF=45°,
∴∠DBC=45°;
注:也可以由点D为弧EC的中点,可得弧ED=弧CD,即可得出∠DCF=∠DBC=45°;
(3)如图,连接BE,BO,DO,并延长BO至H点,
∵BD=BC,OD=OC,
∴BH垂直平分CD,
又∵AB∥CD,
∴∠ABO=90°=∠EBC,
∴∠ABE=∠OBC=∠OCB,
又∵∠A=∠A,
∴△ABE∽△ACB,
∴,即AB2=AE×AC,
∴AC,
设AE=x,则AB=2x,
∴AC=4x,EC=3x,
∴OE=OB=OC,
∵CD=12,
∴CH=6,
∵AB∥CH,
∴△AOB∽△COH,
∴,即,
解得x=5,OH=4.5,OB=7.5,
∴BH=BO+OH=12,
∴△BCD的面积12×12=72.
20.【分析】(1)①由题意可得AB=AC,可证AO是BC的垂直平分线,可得结论;
②由等腰三角形的性质可得BP=CP=4,由勾股定理可求AP的长,BO的长,即可求解;
(2)设BO=3a=OC=OH,OD=2a,由勾股定理可求CD长,CH的长,通过证明△ACH∽△HCD,可求AD的长,即可求解.
【解答】(1)①证明:连接OB,OC,设AB与BC交于点P,
∵点A是的中点,
∴,
∴AB=AC,
又∵OB=OC,
∴AO是BC的垂直平分线,
∴AO⊥BC;
②∵AB=AC,AP⊥BC,
∴BP=CP=4,
∴AP8,
∵BO2=OP2+BP2,
∴BO2=(8﹣OB)2+16,
∴BO=5,
∴⊙O的半径为5;
(2)延长BD交⊙O于点H,连接CH,CO,AH,
∵,
∴设BO=3a=OC=OH,OD=2a,
∴DH=a,
∵∠BAC=45°,
∴∠BOC=2∠BAC=90°,
∴CDa,CH3a,
∵∠ACH=∠DCH,∠BAC=∠BHC=45°,
∴△ACH∽△HCD,
∴,
∴,
∴ACa,
∴AD=AC﹣CDaaa,
∴.
21.【分析】(1)求AC的长度,证明△ABC是等腰直角三角形,得到∠A的度数,根据等腰三角形的性质求出角度;
(2)证明△COE是直角三角形,求出CE的长度,证明△ACE∽△DCA,从而求出CD的长度;
(3)根据题意分当E在线段OB上和当点E在线段OA上两种情况,分别画出对应的图,求出CE和BE的长度,根据相似三角形的性质求出△BCD的面积.
【解答】解:(1)∵△ABC 内接于⊙O,
∴∠ACB=90°,
在Rt△ABC中,
∵AB=12,BC,
∴,
∴△ABC是等腰直角三角形,
∴∠A=45°,
∵AE=AC,
∴∠ACD;
(2)连接OC,AD,
∵直径AB=12,
∴OA=OB=OC=6,
∴OE=OA﹣AE=2,
∵∠CAB=45°,OA=OC,
∴∠AOC=90°,
在Rt△COE中,
∵OE=2,OC=6,
∴,
∵,
∴∠ADC=∠ABC=∠BAC=45°,
∵∠ACE=∠DCA,
∴△ACE∽△DCA,
∴,
∴CD;
(3)①当E在线段OB上时,连接OC,连接BM交CD于点N,
∵CD∥AM,
∴∠BNE=∠BMA=∠BOC=90°,
∵∠BEN=∠CEO,
∴∠ECO=∠ABM=∠ACM,
∴tan∠ECO=tan∠ACM,
∵OC=6,
∴OE=OC tan∠ECO=2,
∴EC,BE=6﹣2=4,
∴,
由(2)得△BCD∽△ECB,
∴,
∴;
②当点E在线段OA上时,
同理tan∠ECO=tan∠ACM,
∴OE=OC tan∠ECO=2,
∴CE,BE=6+2=8,
∴,
∵△BCD∽△ECB,
∴,
∴.
综上所述,△BCD的面积的面积为.
22.【分析】(1)根据垂径定理和同弧所对的圆周角相等,能够推导出∠AFC=∠CFE,∠ACF=∠FEA,即可证明三角形相似;
(2)连接BF,由题意可得AB=2AC,在Rt△ABC中,利用勾股定理求出AC=2,再由tan∠ACB=2,得到AD=2CD,在Rt△ACD中,利用勾股定理求出CD=2,AD=4,则ED=AD=4,证明△BFC∽△HDC,求得HD,则HE=ED+HD,再由△AFC∽△HFE,求出EF;
(3)设OC=r,则BC=2r,CDr,ADr,分两种情况讨论:①当点G在线段OD上时,x,则OG=xr,CG=(1﹣x)r,BG=(1+x)r,过点G作GM⊥CF交于点M,推导出FM=2GM,再由GM∥BE,推导出,,从而求出DH,AH=AD﹣HDr,即可求y;②当点G在线段OB上时,同理可得y.
【解答】(1)证明:∵BC是⊙O的直径,AD⊥BC,
∴,
∴∠AFC=∠CFE,
∵,
∴∠ACF=∠FEA,
∴△AFC∽△HFE;
(2)解:连接BF,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵tan∠ACB=2,
∴AB=2AC,
在Rt△ABC中,BC=10,
∴AC=2,
∵AD⊥BC,
∴∠ADC=90°,
∵tan∠ACB=2,
∴AD=2CD,
在Rt△ACD中,AD2+CD2=AC2,则CD=2,AD=4,
∴ED=AD=4,
∵BC是⊙O的直径,
∴∠BFC=90°,
∵BC=10,CF=8,
∴BF=6,
∵∠BFC=∠HDC=90°,∠FCB=∠DCH,
∴△BFC∽△HDC,
∴,
∴HD,
∴HE=ED+HD,
∵△AFC∽△HFE,
∴,
∴EF;
(3)解:设OC=r,则BC=2r,
∵tan∠ACB=2,
∴AD=2CD,BD=2AD,
∴CDr,ADr,
①当点G在线段OD上时,
∵x,
∴OG=xr,CG=(1﹣x)r,BG=(1+x)r,
过点G作GM⊥CF交于点M,
∴∠GMF=90°,
∵∠ADC=90°,∠CAE=∠CFE,
∴∠FGM=∠ACB,
∴tan∠FGM=tan∠ACB=2,
∴FM=2GM,
∵∠GMC=∠BFC=90°,
∴GM∥BE,
∴,
∴,即,
∵,
∴,
∴DH,
∴AH=AD﹣HDr,
∴,
∴y;
②当点G在线段OB上时,同理可得y;
综上所述:当点G在线段OD上时,y;当点G在线段OB上时,y.
23.【分析】(1)根据圆周角定理可得∠PCQ=∠ACB=90°,即可求证;
(2)连接BQ,根据圆内接四边形的性质可得∠BQC=∠APC,可证明△ACP∽△BCQ,从而得到QC=2PC,BQ=2x,在Rt△ACB中,根据勾股定理可得,从而得到,再由勾股定理可得,从而得到,再根据三角形的面积公式可得到S关于x的函数关系式,即可求解;
(3)过点P作PH⊥BC于点H,KQ⊥BC于点K,则PH∥KQ,证明△PMH∽△QMK,可得KQ=3PH,再证△BPH∽△BAC,可得,,然后根据△ABC∽△BQK,可得,即可求解.
【解答】(1)证明:∵PQ是⊙O的直径,
∴∠PCQ=∠ACB=90°,
∵∠B=∠Q,
∴△PQC∽△ABC;
(2)解:如图1,连接BQ,
∵四边形BPCQ是圆内接四边形,
∴∠BPC+∠CQB=180°,
∵∠BPC+∠APC=180°,
∴∠BQC=∠APC,
∵∠PCQ=∠ACB=90°,
∴∠ACP=∠BCQ,
∴△ACP∽△BCQ,
∴,
∴,
∴QC=2PC,BQ=2x,
在Rt△ACB中,,
∴,
∵PQ是⊙O的直径,
∴∠PCQ=∠PBQ=90°,
∴,
∴PC2=x2x+4,
∴SPC×QCPC×2PC=PC2=x2x+4=(x)2,
∴当时,S有最大值,最大值为;
(3)解:如图2,过点P作PH⊥BC于点H,KQ⊥BC于点K,则PH∥KQ,
∴△PMH∽△QMK,
∴,
∵,PO=OQ,
∴,
即KQ=3PH,
∵∠ACB=90°,即AC∥PH,
∴△BPH∽△BAC,
∴,即,
解得:,
∴,
∵∠A+∠ABC=∠CBQ+∠ABC=90°,
∴∠A=∠CBQ,
∵∠BKQ=∠ACB=90°,
∴△ABC∽△BQK,
∴,
∴,
解得:.
24.【分析】(1)可通过∠APD=∠ACD=45°求得结果;
(2)①可证明∠ADP=∠AMP,∠APD=∠APM,PA是公共边得出△ADP≌△AMP;
(3)连接EM并延长交BC于Q,连接AQ,AQ交BF于G,可证得△DAE≌△MAE,从而∠AME=∠ADE=90°,进而△ABQ≌△AMQ,进而△ABQ≌△BCF,设∠PAD=∠PAM=α,可证得∠MNE=∠MEN=90°﹣α,可得EM=MN=5,从而EQ=EM+MQ=5+12=17,进一步求得结果.
【解答】(1)解:如图1,
连接AC,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠ACD,
∵,
∴∠APD=∠ACD=45°;
(2)①证明:∵AM=AB,
∴∠ABP=∠AMB,
∵四边形ABPD内接于⊙O,
∴∠ABP+∠ADP=180°,
∵∠AMB+∠AMP=180°,
∴∠ADP=∠AMP,
∵四边形ABCD是正方形,
∴AB=AD,
∴,AD=AM,
∴∠APD=∠APB,
在△ADP和△AMP中,
,
∴△ADP≌△AMP(AAS);
(3)解:如图2,
连接EM并延长交BC于Q,连接AQ,AQ交BF于G,
由①知:△ADP≌△AMP,
∴∠DAP=∠MAP,
在△DAE和△MAE中,
,
∴△DAE≌△MAE(SAS),
∴∠AME=∠ADE=90°,
∵AM=AB,AQ=AQ,
∴△ABQ≌△AMQ(HL),
∴MQ=BQ,
∵AM=AB,
∴AQ⊥BF,
∴∠BGQ=90°,
∵∠C=90°,∠GBQ=∠CBF,
∴∠AQB=∠BFC,
∵BC=AB,∠ABCQ=∠C=90°,
∴△ABQ≌△BCF(AAS),
∴BQ=CF=12,
∴MQ=12,
设∠PAD=∠PAM=α,
∴∠BAM=90°﹣∠DAM=90°﹣2α,
∵MN∥AB,
∴∠AMN=∠BAM=90°﹣2α,
∴∠MNE=∠PAM+∠AMN=α+90°﹣2α=90°﹣α,
∵∠MEN=90°﹣∠MAE=90°﹣α,
∴∠MNE=∠MEN,
∴EM=MN=5,
∴EQ=EM+MQ=5+12=17,
设正方形的边长是a,
∴CD=BC=a,
∴CE=CD﹣EM=a﹣5,
CQ=BC﹣BQ=a﹣12,
在Rt△ECQ中,
CE2+CQ2=EQ2,
∴(a﹣5)2+(a﹣12)2=172,
∴a1=20,a2=﹣3(舍去),
∴S正方形ABCD=a2=202=400.
25.【分析】(1)根据圆的内接四边形性质得:∠ADC+∠ABC=180°,结合已知∠ADF+∠ABC=90°,进而得出结果;
(2)可证明△BDG≌△CFD,从而CF=BD,进一步得出结论;
(3)①根据S△BDG=3S△DEH得出S△CFD=3S△DEG,从而EHCF,可证得△DEH∽△FED,从而DE2=EH EF,从而得出EF的值,可证得△ABE∽△CED,从而得出BE DE=CE AE,进一步得出结果;
②作DW⊥AC于W,作直径CV,连接DV,可得出AD=BD=2,△ABE∽△CED,从而,进而得出CE,AE=2,设EW=x,则AW=2﹣x,根据勾股定理得出DW2=DE2﹣EW2=AD2﹣AW2,,从而12﹣x2=22﹣(2﹣x)2,从而得出x的值,进而计算出CD的长,根据sinV=sin∠ACD得出,进一步得出结果.
【解答】(1)解:∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠CDF+∠ADF+∠ABC=180°,
∵∠ADF+∠ABC=90°,
∴∠CDF=90°;
(2)证明:∵DG⊥AB,
∴∠BGD=90°,
∵∠CDF=90°,
∴∠BGD=∠CDF,
∵,
∴∠ABD=∠ACD,
∵BG=CD,
∴△BDG≌△CFD(ASA),
∴CF=BD,
∵点E是BD的中点,
∴BD=2DE,
∴CF=2DE;
(3)①解:由(2)知:△BDG≌△CFD,CF=BD=2,∠BDG=∠CFD,
∵S△BDG=3S△DEH,
∴S△CFD=3S△DEG,
∴EHCF,
∵∠DEH=∠FED,
∴△DEH∽△FED,
∴DE2=EH EF,
∴12EF,
∴EF,
∴CE=CF﹣EF,
∵∠ABD=∠ACD,∠AEB=∠CED,
∴△ABE∽△CED,
∴BE DE=CE AE,
∴1×1AE,
∴AE=2,
∴AC=CE+AE;
②解:如图,
作DW⊥AC于W,作直径CV,连接DV,
∵DO⊥AB,
∴BG=AG,
∴AD=BD=2,
由①知:△ABE∽△CED,
∴,
∴AB=2BC,BC=CD,
∴
∴CE,AE=2,
设EW=x,则AW=2﹣x,
∵DW2=DE2﹣EW2=AD2﹣AW2,
∴12﹣x2=22﹣(2﹣x)2,
∴x,
∴EW,DW,
∴CW=EW+CE,
∴CD,
∵sinV=sin∠ACD,
∴,
∴,
∴CV,
∴⊙O的半径为:.
浙江省2024年九年级(上)期末压轴题精选分类训练
圆的综合题
1.如图,在⊙O中,弦AB是直径,点C,D是⊙O上的两点,连结AC,OD,且满足AC∥OD.
(1)若的度数为80°,求∠A的度数.
(2)求证:.
(3)连结BD,若AC=6,AB=10,求BD的长.
2.如图1,在直角坐标系中,以原点O为圆心,半径为10作圆,交x轴于点A,B(点A在点B的左边).点C为直径AB上一动点,过点C作弦DE⊥AB(点D在点E上方),连接AE,过点D作DF∥AE交圆O于另一点,记为点F.直线EF交x轴于点G,连接OE,BF,AD.
(1)若∠BOE=80°,求∠ADF的度数;
(2)求证:OE∥BF;
(3)若OG=2CG,请直接写出点C横坐标.
3.如图,圆O的弦AB=8,点E为圆外一点,连结BE,AE分别交圆O于点C,点D,∠E=30°,连结CD.
(1)如图1,若圆的半径5,∠ABC=90°,求CD的长;
(2)如图2,若,
①求的值;
②求圆O的半径.
4.如图1,点O为坐标原点,点A坐标为,点B坐标为(t,0)(t>0).点C为y轴负半轴上一点,满足AC=BC,△ABC外接圆⊙D交x轴负半轴于点E,直径AF交x轴于点G,⊙D半径为r.
(1)若∠ACB=40°,求∠ABE的度数;
(2)求证:AF∥CE;
(3)若,求t的值.
5.如图,已知等腰三角形ABC内接于⊙O,AB=AC,点D为上一点(不与点A,C重合),连接AD,BD,CD,且BC=3CD=18.
(1)如图1,若BD为⊙O直径.
①求tan∠BAC的值;
②求四边形ABCD的面积.
(2)如图2,在上取一点E,使,连接CE,交AB于点F,若∠BDC=∠AFC,求AD的长度.
6.如图1,在△ABC中,AB=AC,∠A=90°,点P是△ABC内一个动点,且∠BPC=135°.
(1)试找出与∠ACP相等的角,并说明理由;
(2)如图2,连接AP并延长交△BPC的外接圆⊙O于点Q,交BC于点D,连接CQ.
①求证△ACP∽△AQC;
②求的最小值;
(3)在如图2的条件下,若BP=PC,求证:.
7.如图,AB、AC、AD是⊙O中的三条弦,点E在AD上,且AB=AC=AE.连结BC,BD,CD,其中BC交AD于点G.
(1)求证:△ABG∽△ADB.
(2)若∠DBE=α,求∠CAD的度数(用含α的代数式表示).
(3)若AD=15,AB=12,BD=6,求线段CD的长.
8.如图1,以Rt△ABC的直角边AB为直径画⊙O,过A作斜边AC的垂线交⊙O于点D,连结CD,交⊙O于点E,交AB于点F,连结BE.
(1)求证:∠ACD=∠EBC.
(2)如图2,当△ABC是等腰直角三角形时.
①求∠BCD的正切值;
②求的值.
(3)若AB=1,设CD=x,y,求y关于x的函数表达式.
9.如图,⊙O的半径为1,直径AB,CD的夹角∠AOD=60°,点P是上一点,连接PA,PC分别交CD,AB于点M,N.
(1)若PC⊥AB,求证:PA⊥CD.
(2)当点P在上运动时,
①猜想:线段AM与CN有怎样的数量关系,并给出证明.
②求证:PA+PC.
10.如图1,在⊙O中,AB为弦,CD为直径,且AB⊥CD于点E,过点B作BF⊥AD,交AD的延长线于点F.连接AC,BO.
(1)求证:∠CAE=∠ADC.
(2)若DE=2OE,求的值.
(3)如图2,若BO的延长线与AC的交点G恰好为AC的中点,若⊙O的半径为r.求图中阴影部分的面积(结果用含r的代数式表示).
11.如图,在锐角三角形ABC中,AB=AC,以BC为直径的⊙O分别交AB,AC于点D,E,连接OD,OE,DE.
(1)若∠A=50°,求的度数.
(2)求证:DE∥BC.
(3)若⊙O半径为m,tan∠ABC=2,求四边形ADOE的面积(用含m的代数式表示).
12.圆内接四边形ABCD,AB为⊙O的直径.
(1)如图1,若D为弧AB中点,AB=4.
①求∠DCB的度数;
②求四边形ABCD面积的最大值.
(2)如图2,对角线AC,BD交于点E,连结OE并延长交CD于点F,若OE=3EF=3,求AB的长.
13.如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC,设△DOE的面积为S1,四边形OCBD的面积为S2,若,用含n的代数式表示.
14.如图,△ABC内接于⊙O,∠ABC>90°,△ABC的外角∠EAC的平分线交⊙O于点D,连接DB,DC,DB交AC于点F.
(1)求证:△DBC是等腰三角形.
(2)若DA=DF.
①求证:BC2=DC BF.
②若⊙O的半径为5,BC=6,求的值.
15.如图,点A在y轴正半轴上,OA=1,点B是第一象限内的一点,以AB为直径的圆交x轴于D,C两点,D,C两点的横坐标是方程x2﹣4x+3=0的两个根,OC>OD,连接BC.
(1)如图(1),连接BD.
①求∠ABD的正切值;
②求点B的坐标.
(2)如图(2),若点E是的中点,作EF⊥BC于点F,连接EB,ED,EC,求证:2CF=BC+CD.
16.如图,AB是⊙O的直径,C为AB下方半圆上一动点,OD∥AC交于点D.
(1)求证:;
(2)已知⊙O半径为r,设BD=x,AC=y,求x与y的关系式;
(3)点P为AB上方圆外一点,且∠PAB=2∠APO,连结PA、PB、PO,PA交上半圆于点E,已知当时y=9,,求sin∠PAB的值.
17.如图1,AC是平行四边形ABCD的一条对角线,且AB=AC,△ABC的外接圆⊙O与CD边交于点E,连结AE.
(1)若tan∠ABC=3,△AEC的面积为,求⊙O的半径.
(2)如图2,过点E作EH⊥AB于H,直线EH与直线BC交于点F,若CEHE时,求的值.
18.如图,△ABC中,AB=AC,⊙O是△ABC的外接圆,BO的延长线交边AC于点D.
(1)求证:∠BAC=2∠ABD;
(2)当△BCD是等腰三角形时,求∠BCD的大小;
(3)当AD=2,CD=3时,求边BC的长.
19.如图,已知CE是圆O的直径,点B在圆O上由点E顺时针向点C运动(点B不与点E、C重合),弦BD交CE于点F,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.
(1)若圆O的半径为2,且点D为弧EC的中点时,求圆心O到弦CD的距离;
(2)在(1)的条件下,当DF DB=CD2时,求∠CBD的大小;
(3)若AB=2AE,且CD=12,求△BCD的面积.
20.已知,锐角三角形ABC内接于⊙O.
(1)如图1,当点A是的中点时,
①求证:AO⊥BC.
②若BC=8,AB=4,求⊙O的半径.
(2)如图2,当AB>AC时,连接BO并延长,交边AC于点D.若∠A=45°,,求.
21.如图1,△ABC 内接于⊙O,直径AB=12,弦,作弦CD与AB相交于点E.
(1)如图1,若AE=AC,求∠ACD的度数;
(2)如图2,若AE=4,求CD的长;
(3)如图3,过点A作CD的平行线交⊙O于点M,连结BD,MC,若,求△BCD的面积.
22.如图,△ABC内接于⊙O,BC是⊙O的直径,tan∠ACB=2,过点A作AD⊥BC,交⊙O于点E,点F是上一点,连结EF交BC于点G,连结CF交AD于点H.
(1)求证:△AFC∽△HFE;
(2)若BC=10,CF=8,求EF的长;
(3)设,,求y关于x的函数表达式.
23.如图,△ABC是直角三角形,∠ACB=90°,AC=2,BC=4,点P是边AB上的动点,⊙O是过C,P,B三点的圆,PQ是⊙O的直径,PQ与BC相交于点M.设AP=x.
(1)求证:△PQC∽△ABC.
(2)令△PQC的面积为S,求S关于x的函数关系式,并求当x为何值时,S的值最小.
(3)当时,求x的值.
24.正方形ABCD的四个顶点都在⊙O上,点P是劣弧上一点(点P与点C,D不重合),连结PA,PD.
(1)如图1,求∠APD的度数.
(2)如图2,连结PB.在线段PB上取点M,使得AM=AB,过点M作MN∥AB交PA于点N.记PA,PB与边CD交于点E,F.
①求证:△ADP≌△AMP.
②若MN=5,CF=12,求正方形ABCD的面积.
25.如图1,四边形ABCD内接于⊙O,对角线AC与BD交于点E,AC>BD,点F在AC上,∠ADF+∠ABC=90°.
(1)求∠CDF的度数.
(2)如图2,作DG⊥AB于点G,DG与AC交于点H,BG=CD,E为BD中点,求证:CF=2DE.
(3)在(2)的条件下,BD=2.
①若△BDG的面积是△DEH面积的3倍,求AC的长.
②如图3,当圆心O在高DG上时,求⊙O的半径.
参考答案
1.【分析】(1)连接OC,根据弧AC的度数求出∠AOC,利用三角形内角和求出∠A;
(2)利用平行线的性质求得∠BOD=∠A=50°,∠COD=∠OCA=50°,得出∠COD=∠BOD,进而得出弧相等;
(3)先根据勾股定理求出BC,然后利用勾股定理求出OE,再利用勾股定理求出BD即可.
【解答】(1)解:连接OC,
∵的度数为80°,
∴∠AOC=80°,
∵OA=OC,
∴∠A=∠OCA=50°;
(2)证明:∵AC∥OD,
∴∠BOD=∠A,∠COD=∠OCA,
∵OA=OC,
∴∠A=∠OCA,
∴∠COD=∠BOD,
∴;
(3)解:连接BC,交OD于点E,
∵弦AB是直径,
∴∠ACB=90°,
∵AC=6,AB=10,
∴BC8,
∵,
∴OD⊥BC,
∴CE=BE=4,
∴OE3,
∴DE=OD﹣OE=2,
∴BD2.
2.【分析】(1)由垂径定理得EB=DB,则得∠DAE=∠BOE=80°,再由平行线的性质即可求得结果;
(2)连接OF,由DF∥AE可得AD=EF,再由DE⊥AB得AD=AE,即有AE=EF,则可证明△AOE≌△FOE,得∠AEO=∠FEO,即有∠BOE=2∠AEO=∠AEF,即可得结论;
(3)由条件得OG的中点是C,有OE=GE,则∠OEC=∠GEC;设∠OEC=α,由(2)知∠GFB=∠OEG=∠EAB=2α;由∠EAB=∠OEA得∠EOC=4α,在Rt△OEC中,由两锐角互余得α的度数;连接OF,证明△OFG∽△EFO,则可求得FG,得OG的长,即可求得C点横坐标.
【解答】(1)解:∵AB是直径,DE⊥AB,
∴EB=DB,
∴;
∵,
∴∠DAE=∠BOE=80°;
∵DF∥AE,
∴∠ADF+∠DAE=180°,
∴∠ADF=180°﹣∠DAE=100°;
(2)证明:如图,连接OF,
∵DF∥AE,
∴∠FDE=∠AED,
∴AD=EF,
∵DE⊥AB,AB为直径,
∴AD=AE,
∴AE=EF;
∵OE=OE,OA=OF,
∴△AOE≌△FOE(SSS),
∴∠AEO=∠FEO,
∵OA=OE,
∴∠OAE=∠AEO,
∴∠BOE=∠OAE+∠AEO=2∠AEO=∠AEF;
∵∠FBA=∠AEF,
∴∠FBA=∠BOE,
∴BF∥OE;
(3)解:①∵OG=2CG,
∴OG的中点是C,
∵DE⊥AB,
∴GE=OE=10,
∴∠OEC=∠GEC;
设∠OEC=α,则∠OEC=∠GEC=α,
由(2)知BF∥OE,
∴∠GFB=∠OEG=∠EAB=2α;
∵∠EAB=∠OEA=2α,
∴∠EOC=4α,
在Rt△OEC中,∠OEC+∠EOC=90°,
即α+4α=90°,
∴α=18°;
连接OF,如图,
则∠BOE=∠OBF=75°,∠GFB=∠OEG=2α=36°;
∵OB=OF,
∴∠OFB=∠OBF=72°,∠OFG=∠OFB﹣∠GFB=36°=∠FOB;
∵OF=OE,∠OEG=36°,
∴∠OEG=∠OFG=36°,
∴△OFG∽△EFO,
∴,即OF2=EF FG,
设FG=x,则EF=EG+FG=10+x,
∴x(10+x)=100,
解得:(舍去),
∴;
∵∠OFG=∠FOB,
∴,
∴,
即点C的横坐标为.
②如图:∵OG=2CG,
∴OG的中点是C,
∵DE⊥AB,
∴GE=OE=10,
设∠AEC=α,
∵AE∥DF,
则∠D=∠AEC=α,
∴∠EOF=2α,
由(2)知BF∥OE,
∴∠EOF=∠OFB=2α;
∵OF=OB,
∵∠OFB=∠B=∠EOG=2α,
∴∠FOG=4α,
∵OE=EG,
∴∠EGO=∠EOG=2α,
∴∠OEF=4α,
∵OE=OF,
∴∠OFE=∠OEF=4α,
∵∠G=∠EOF=2α,∠GFO=∠OFE,
∴△OFG∽△EFO,
∴,即OF2=EF FG,
设FG=x,则EF=FG﹣10=x﹣10,
∴x(x﹣10)=100,
解得:x1=5+5,x2=5﹣5
∵∠OFG=∠FOB,
∴OG=FG=5+5或OG=FG=5﹣5,
∴OCOG(舍去)或,
综上所述:点C的横坐标为或.
3.【分析】(1)连结AC,由圆周角定理得出AC是直径,由勾股定理可得出答案;
(2)①证明△ECD∽△EAB,由相似三角形的性质得出;
②过C作CF∥AE交圆O于点F,连结AF,BF,OB,OF,AC,OA,OD,OC,求出,过点F作FH⊥AB,由勾股定理可得出答案.
【解答】解:(1)连结AC,
∵∠ABC=90°,
∴AC为直径10,AB=8,
∴BC6,∠ADC=90°,
∵∠E=30°,
∴AE=2AB=16,
∴BE8,
∴CE=BE﹣BC=86,
在Rt△CDE中,;
(2)①∵四边形ABCD内接于圆O,
∴∠B+∠ADC=180°,
∵∠CDE+∠ADC=180°,
∴∠CDE=∠B,
∵∠E=∠E,
∴△ECD∽△EAB,
∴;
②过C作CF∥AE交圆O于点F,连结AF,BF,OB,OF,AC,OA,OD,OC,
∴∠FAB=∠FCB=∠E=30°,
∴∠BOF=60°,
∵OF=OB,
∴△OBF为等边三角形,
∵CF∥AE,
∴∠ACF=∠CAE,
∴∠AOF=∠COD,
∴,
∴,
过点F作FH⊥AB,
∴,AH=3,
∴BH=AB﹣AH=5,
∴,
∴,
故圆O的半径为.
4.【分析】(1)由AC=BC,∠ACB=40°,可求得∠CAB=70°,由同弧所对的圆周角相等可知∠ACB=∠AEB=40°,进而可求得∠OAE=50°,再根据三角形内角和定理可求得∠ABE的度数.
(2)由AC=BC,等边对等角可得∠CAB=∠CBA,根据同弧所对的圆周角相等可知∠CAB=∠CEB,∠CBA=∠CFA,等量代换得∠CEB=∠CFA,再由直径所对的圆周角是直角,进而可求得两锐角互余,易证得∠ACE=∠CAF,即可证得AF∥CE.
(3)作DN⊥AC于点N,可得AC=CNAC,根据OG∥DN,可得线段成比例,可求得ON的长,进而求得OC和BC的长,最后根据勾股定理可求得OB的长即可求出t的值.
【解答】解:(1)∵AC=BC,∠ACB=40°.
∴∠CAB=70°.
∵∠ACB=∠AEB=40°,AO⊥EB.
∴∠OAE=90°﹣40°=50°.
∴∠EAB=50°+70°=120°.
∴在△AEB中,∠ABE=180°﹣120°﹣40°=20°.
(2)连接CF,如图所示:
∵AC=BC.
∴∠CAB=∠CBA.
∵∠CAB=∠CEB.
∠CBA=∠CFA.
∴∠CEB=∠CFA.
∵AO⊥EB,AF是⊙D的直径.
∴∠EOC=∠ACF=90°.
∴∠CEB+∠ACE=90°.
∠CFA+∠CAF=90°.
∴∠ACE=∠CAF.
∴AF∥CE.
(3)作DN⊥AC于点N,如图所示:
∵点A坐标为(0,).
∴AO.
∵DGr,AD=r.
∴AG=AD﹣DG=rrr.
∵在⊙D中,DN⊥AC.
∴AC=CNAC.
又∵OB⊥AC.
∴OG∥DN.
∴.
即.
解得ON.
∴AN.
∴AC=3.
∴BC=AC=3.
OC=AC﹣AO=2.
∵∠BOC=90°.
∴BC2=OB2+OC2.
∴OB5.
∵点B坐标为(t,0).
∴t=5.
5.【分析】(1)①根据圆周角定理得出∠BAC=∠BDC,根据BD为⊙O直径,得出∠BCD=90°,根据BC=3CD=18,得出;
②过点A作AE⊥BC于点E,连接CO,根据勾股定理得出,求出,根据BO=DO,得出,,证明AE垂直平分BC,根据BO=CO,得出点O在AE上,证明△AMO∽△CMD,得出,求出,得出,求出,最后求出四边形的面积即可;
(2)证明△BCF≌△DBA,得出BF=AD,∠BFC=∠BAD,BD=BC=18,求出FM∥AD,得出,证明△ACF∽△BCD,得出,求出,得出,设AD=x,则,,求出,证明△ACD∽△BCM,得出,即,求出x的值即可.
【解答】解:(1)①∵,
∴∠BAC=∠BDC,
∵BD为⊙O直径,
∴∠BCD=90°,
∵BC=3CD=18,
∴;
②过点A作AE⊥BC于点E,连接CO,如图所示:
∵∠BCD=90°,BC=3CD=18,
∴,
,
∵BO=DO,
∴,,
∴,
∵AB=AC,
∴CE=BE,
∴AE垂直平分BC,
∵BO=CO,
∴点O在AE上,
∵∠AEB=∠BCD=90°,
∴AE∥CD,
∴∠MAO=∠MCD,∠MOA=∠MDC,
∴△AMO∽△CMD,
∴,
∵,
∴,
即,
∴,
即,
∴,
∴.
(2)∵AB=AC,
∴,∠ABC=∠ACB,
∵,
∴∠BDC=∠BAC,
∵∠BDC=∠AFC,
∴∠BAC=∠AFC,
∴AC=CF,
∴AB=CF,
∵,
∴∠ADB=∠ACB,
∴∠FBC=∠ADB,
∵,,
∴,
∴∠BCF=∠ABD,
∴△BCF≌△DBA,
∴BF=AD,∠BFC=∠BAD,BD=BC=18,
∴FM∥AD,
∴,
∵,
∴∠CBD=∠ACF,
∵∠BDC=∠BAC,
∴△ACF∽△BCD,
∴,
∴,
∴,
∴,
设AD=x,则,,
∴,
∵,
∴∠BCE=∠ACD,
∵,
∴∠CBM=∠CAD,
∴△ACD∽△BCM,
∴,
即,
解得:,负值舍去,
即.
6.【分析】(1)根据∠ACB=∠ACP+∠BCP=45°,∠PBC+∠PCB=45°,等量代换即可得到∠ACP=∠PBC;
(2)①根据同弧所对的圆周角相等,结合(1)能得到∠Q=∠APC,即可证明;
②连接OB、CO,由△ACP∽△AQC,得到,当CQ经过圆心O时,的值最小,过点O作OM⊥BC交于M点,则M是BC的中点,连接AM,则A、O、M三点共线,则AO是BC的垂直平分线,再由CO=AC,得到CQ=2AC,即可求的最小值为;
(3)由题意可知P点AM上,则∠PBC=∠PCB=∠ACP,过点P作PH⊥AC交于H点,设PM=x,则PH=x,分别求出APx,AM=(1)x,AC(1)x,PC2=(4+2)x2,再由,即可证明.
【解答】(1)解:∵∠BPC=135°,
∴∠PBC+∠PCB=45°,
∵AB=AC,∠A=90°,
∴∠ACB=∠ACP+∠BCP=45°,
∴∠ACP=∠PBC;
(2)①证明:∵,
∴∠Q=∠PBC,
∵∠ACP=∠PBC,
∴∠Q=∠APC,
∴△ACP∽△AQC;
②连接OB、CO,
∵∠BPC=135°,
∴∠BOC=90°,
∵△ACP∽△AQC,
∴,
∴,
当CQ经过圆心O时,的值最小,
过点O作OM⊥BC交于M点,则M是BC的中点,连接AM,则A、O、M三点共线,
∴AO是BC的垂直平分线,
∵AM=BM=OM,
∴CO=AC,
∴CQ=2AC,
∴的最小值为;
(3)证明:∵BP=PC,
∴P点AM上,
∴∠PBC=∠PCB=∠ACP,
过点P作PH⊥AC交于H点,
∴PH=PM,
设PM=x,则PH=x,
∵∠PAH=45°,
∴APx,
∴AM=(1)x,AC(1)x,PC2=(4+2)x2,
∵,
∴()2,
∴CQ2=(2)AC2.
7.【分析】(1)由等弦所对弧相等,再由等弧所对圆周角相等得出∠ABC=∠ADB,又∠BAG=∠DAB,即可得出结论;
(2)由等边对等角的性质与圆周角性质得出∠DBE=∠CBE=α,即可由∠CAD=∠CBD=∠DBE+∠CBE求解;
(3)由△ABG∽△ADB,得,从而可求出,,从而求出,再证△BDG∽△ADC,得,代入即可求解.
【解答】(1)证明:∵AB=AC,
∴,
∴∠ABC=∠ADB,
又∵∠BAG=∠DAB,
∴△ABG∽△ADB;
(2)解:∵AB=AE,
∴∠AEB=∠ABE,
∴∠DBE+∠ADB=∠ABC+∠CBE,
∵AB=AC,,
∴∠ABC=∠ACB=∠ADB,
∴∠DBE=∠CBE=α,
∵,
∴∠CAD=∠CBD=∠DBE+∠CBE=2α;
(3)解:∵△ABG∽△ADB,
∴,
∵AD=15,AB=12,BD=6,
∴,
∴,,
∴,
∵∠CAD=∠CBD=2α,∠ADC=∠GDB,
∴△BDG∽△ADC,
∴,即,
∴.
8.【分析】(1)利用同弧所对的圆周角相等,通过等量代换证明即可;
(2)①过点D作DG⊥BC交延长线于点G,连接OD,设圆的半径为r,证明四边形BODG是正方形,再求解即可;
②设圆的半径为r,则ADr,AC=2r,过E点作EH⊥BC交于H点,则tan∠EBC=tan∠ACD,结合tan∠BCD,推导出HC=3EH,CEEH,即可得到;
(3)连接AE,证明△ABE∽△CDA和△FAE∽△FCA,推导y与x的关系即可.
【解答】(1)证明:∵,
∴∠D=∠ABE,
∵∠ABC=90°,AD⊥AC,
∴∠D+∠ACD=∠ABE+∠CBE=90°,
∴∠ACD=∠EBC;
(2)解:①过点D作DG⊥BC交延长线于点G,连接OD,
设圆的半径为r,
∵△ABC是等腰直角三角形,∠DAC=90°,
∴△AOD是等腰直角三角形,
∴四边形BODG是正方形,
∴DG=BG=r,BC=2r,
∴tan∠BCD;
②设圆的半径为r,则ADr,AC=2r,
过E点作EH⊥BC交于H点,
∴tan∠EBC=tan∠ACD,
∴BH=2EH,BEEH,
∵tan∠BCD,
∴HC=3EH,CEEH,
∴;
(3)连接AE,
∵AB是圆的直径,
∴∠AEB=90°=∠DAC,
∵∠ADC=∠ABE,
∴△ABE∽△CDA,
∴x,
∵∠FAE=∠FCA,∠AFE=∠CFA,
∴△FAE∽△FCA,
∴x,
∴x2,
∴yx2﹣1.
9.【分析】(1)由圆周角定理得出∠BAP=30°,由三角形内角和定理可求出∠AMO=90°,则可得出结论;
(2)①连接AD,证出∠D=60°,OA=AD=OD,证明△ADM≌△CON(ASA),由全等三角形的性质得出AM=CN;
②证明△AOM∽△APN,由相似三角形的性质得出,证明△CON∽△CPM,由相似三角形的性质得出,由全等三角形的性质得出AM=CN,DM=ON,代入PA+PC并化简整理可得出答案.
【解答】(1)证明:∵∠AOD=∠BOC=60°,PC⊥AB,
∴60°,
∴∠BAP=30°,
∴∠AMO=180°﹣∠MAO﹣∠AOM=180°﹣30°﹣60°=90°,
∴PA⊥CD;
(2)解:①AM=CN.
证明:连接AD,
∵OA=OD,∠AOD=60°,
∴△OAD是等边三角形,
∴∠D=60°,OA=AD=OD,
∵OC=OD,∠BOC=∠AOD=60°,
∴AD=OC,∠D=∠BOC=60°,
又∵∠DAP=∠DCP,
∴△ADM≌△CON(ASA),
∴AM=CN;
②证明:∵⊙O的半径为1,
∴OA=OB=OC=OD=1,
∵∠P=∠D=60°,∠AOD=60°,
∴∠P=∠AOD,
又∵∠BAP=∠BAP,
∴△AOM∽△APN,
∴,
∴,即PA,
∵∠BOC=∠CPM=60°,∠C=∠C,
∴△CON∽△CPM,
∴,
∴PC,
∵△ADM≌△CON,
∴AM=CN,DM=ON,
又∵DM+OM=OD=1,
∴PA+PC.
10.【分析】(1)由圆周角定理可得∠CAD=∠CAE+∠DAE=90°,再根据AB⊥CD,易得∠ADC+∠DAE=90°,即可证明∠CAE=∠ADC;
(2)连接BD,设OE=a,则DE=2a,OB=OD=3a,由勾股定理可得,,再证明△BOE∽△BDF,由相似三角形的性质可得,代入数值可求得,即可获得答案;
(3)连接BD,首先证明△OBE≌△DAE,结合全等三角形的性质进一步证明△OBD为等边三角形,即有∠BOD=60°;利用勾股定理、等边三角形的性质以及含30度角的直角三角形的性质依次求得OE、BE、AB、BF、AF等的值,然后由S阴影=S△ABF﹣S△DAE﹣(S扇形OBD﹣S△OBE)即可获得答案.
【解答】解:(1)∵CD为⊙O直径,
∴∠CAD=90°,即∠CAE+∠DAE=90°,
又∵AB⊥CD,
∴∠ADC+∠DAE=90°,
∴∠CAE=∠ADC;
(2)如图,连接BD,
∵AB⊥CD,DE=2OE,
∴OD=DE+OE=3OE,
设OE=a,则DE=2a,OB=OD=3a,
∴在Rt△OBE中,,
∴在Rt△DBE中,,
∵CD为⊙O直径,且AB⊥CD,
∴BE=AE,
∴AD=BD,
∴∠DAB=∠DBA,
∴∠BDF=∠DAB+∠DBA=2∠DAB,
又∵,
∴∠DOB=2∠DAB=∠BDF,
∵∠OEB=∠DFB=90°,
∴△BOE∽△BDF,
∴,即,
解得,
∴;
(3)如图,连接BD,
∵BO的延长线与AC的交点G恰好为AC的中点,
∴OG⊥AC,即∠OGC=∠CAD=90°,
∴BG∥AD,
∴∠OBE=∠DAE,
又∵BE=AE,∠OEB=∠DEA,
∴△OBE≌△DAE(ASA),
∴OB=DA,
∵CD为⊙O直径,AB⊥CD,
∴,
∴DA=DB,
∴OD=OB=DB,即△OBD为等边三角形,∠BOD=60°,
∵⊙O的半径为r,
∴OB=r,,
∴,
∴,
∵,
∴,
∴,
∴,
∵△OBE≌△DAE,
∴S△OBE=S△DAE,
∴S阴影=S△ABF﹣S△DAE﹣(S扇形OBD﹣S△OBE)
=S△ABF﹣S扇形OBD
.
11.【分析】(1)连接BE,求出∠ABE,可得结论;
(2)通过计算求出∠BED,∠CBE可得结论;
(3)证明AO⊥DE,求出AO,DE,可得结论.
【解答】(1)解:如图,连接BE.
∵BC是直径,
∴∠BEC=90°,
∴∠AEB=90°,
∵∠BAC=50°,
∴∠ABE=90°﹣50°=40°,
∴∠DOE=2∠DBE=80°,
∴的度数为80°;
(2)证明:设BAC=2α.
∵AB=AC,
∴∠ABC=∠ACB=90°﹣α,
∵∠ABE=90°﹣2α,
∴∠CBE=∠ABC﹣∠ABE=α,
∵OB=OD,
∴∠OBD=∠ODB=90°﹣α,
∴∠BOD=180°﹣2×(90°﹣α)=2α,
∴∠BED∠BOD=α,
∴∠CBE=∠BED,
∴DE∥BC;
(3)解:∵AB=AC,BO=OC,
∴AO⊥BC,
∴tan∠ABC2,
∵OB=m,
∴OA=2m,
∵tan∠C2,
∴ECm,
∵AB=ACm,
∴AE=AC﹣ECmmm,
∵DE∥CB,
∴,
∴,
∴DEm,
∵AO⊥BC,DE∥BC,
∴AO⊥DE,
∴S四边形ADOE AO DE2mmm2.
12.【分析】(1)①根据圆周角定理知∠A=45°,再利用圆内接四边形的性质可得答案;
②连接BD,OC交于点E,则△BCD面积最大时,四边形ABCD面积最大,当OC⊥BD时,CE最大,从而求出答案.
(2)直线OF交⊙O于点M,N,过F作PQ∥AB交直线BD,AC于点P,Q,根据△PFD∽△CFQ,得PF FQ=FD FC,再由△MFD∽△CFN,得MF FN=FD FC,从而得出PF FQ=MF FN,再利用平行线分线段成比例证明FP=FQ,设半径为r,则(r﹣4)(r+4),从而解决问题.
【解答】解:(1)①∵AB为直径,D为的中点,
∴∠A=45°,
∴∠DCB=180°﹣∠A=180°﹣45°=135°,
②连接BD,AC交于点E,
当四边形ABCD面积最大时,即△BCD面积最大,
当OC⊥BD时,CE最大,
∵AB=4,
∴BD=AD=2,
∴OE,
∴S,
∴S四边形ABCD的最大值为:S;
(2)直线OF交⊙O于点M,N,过F作PQ∥AB交直线BD,AC于点P,Q,
∵∠Q=∠A=∠CDE,
∴△PFD∽△CFQ,
∴PF FQ=FD FC,
∵∠N=∠MDF,∠MFD=∠CFN,
∴△MFD∽△CFN,
∴MF FN=FD FC,
∴PF FQ=MF FN,
∵PQ∥AB,
∴,
∴FP=FQ,
设半径为r,
∴(r﹣4)(r+4),
∵r>0,
∴r=3,
∴AB=6.
13.【分析】(1)根据圆周角定理和垂直求出∠DEO=∠ACB,根据平行得出∠DOE=∠ABC,根据相似三角形的判定得△DOE∽△ABC,根据圆周角定理得出∠A=∠BDC,推出∠ODE=∠BDC即可;
(2)根据圆周角定理和垂直求出∠DEO=∠ACB,根据平行得出∠DOE=∠ABC,根据相似三角形的判定得出结论;
(3)根据△DOE∽△ABC,求出S△ABC=4S△DOE=4S1,进而求解.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
∴∠ODE=∠A,
∵∠A和∠BDC是所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE;
(3)解:∵△DOE∽△ABC,
∴()2,
即S△ABC=4S△DOE=4S1,
∵OA=OB,
∴S△BOCS△ABC,即S△BOC=2S1,
∵,S2=S△BOC+S△DOE+S△DBE=2S1+S1+S△DBE,
∴S△DBES1,
∴BE=()OE,
即OEOBDO,
∴sinA=sin∠ODE.
14.【分析】(1)由题意易得∠BCD+∠BAD=180°,则有∠EAD=∠BCD,进而可得∠EAD=∠DAC,则∠BCD=∠CBD,然后问题可求证;
(2)①由题意易证△DAF∽△DBC,则有∠ADF=∠BDC,进而可得∠DFA=∠DCB,再由相似三角形的判定得出△FBC∽△BCD,利用其性质即可证明;
②连接DO交BC于G,由题意易得D、O都在中垂线上,即D、O、G共线,进而可得DO⊥BC且BG=GC=3,则有DG=4+OD=9,由①得,根据相似三角形的性质得出,再由相似三角形的判定得出△AFD∽△BFC,利用其性质即可求解.
【解答】(1)证明:∵四边形ABCD内接于⊙O,
∴∠BCD+∠BAD=180°,
∵∠DAB+∠EAD=180°,
∴∠EAD=∠BCD,
∴∠CAD=∠CBD,
∵AD平分∠EAC,
∴∠EAD=∠DAC,
∴∠BCD=∠CBD,
∴DB=DC,
∴△DBC是等腰三角形;
(2)①证明:∵DA=DF,
∴∠DAF=∠DFA,
∴∠DAF=∠DFA=∠CBD=∠BCD,
∴△DAF∽△DBC,
∴∠ADF=∠BDC,
∴∠DFA=∠DCB,
∵∠DBC=∠FBC,
∴△FBC∽△BCD,
∴,
∴BC2=BD BF,
∵DB=DC,
∴BC2=DC BF;
②解:连接DO交BC于G,
∵BD=DC,OB=OC,
∴D、O都在中垂线上,即D、O、G共线,
∴DO⊥BC且BG=GC=3,
∵OB=5,
∴在Rt△BOG中,OG=4,
∴DG=4+OD=9,
∴在Rt△BDG中,,
∵△FBC∽△BCD,
∴,
∴,
解得:,
∴,
∴,
∵∠DAC=∠DBC,∠DFA=∠BFC,
∴△AFD∽△BFC,
∴,
∴.
15.【分析】(1)①过点P作PH⊥DC于H,作AF⊥PH于F,连接PD、AD,利用因式分解法解出一元二次方程,求出OD、OC,根据垂径定理求出DH,根据勾股定理计算求出半径,根据圆周角定理得到∠ADB=90°,根据正切的定义计算即可;
②过点B作BE⊥x轴于点E,作AG⊥BE于G,根据平行线分线段成比例定理定理分别求出OE、BE,得到点B的坐标;
(2)过点E作EH⊥x轴于H,证明△EHD≌△EFB,得到EH=EF,DH=BF,再证明Rt△EHC≌Rt△EFC,得到CH=CF,结合图形计算,证明结论.
【解答】(1)解:①方法一、以AB为直径的圆的圆心为P,
过点P作PH⊥DC于H,作AF⊥PH于F,连接PD、AD,
则DH=HCDC,四边形AOHF为矩形,
∴AF=OH,FH=OA=1,
解方程x2﹣4x+3=0,得x1=1,x2=3,
∵OC>OD,
∴OD=1,OC=3,
∴DC=2,
∴DH=1,
∴AF=OH=2,
设圆的半径为r,则PH,
∴PF=PH﹣FH1,
在Rt△APF中,AP2=AF2+PF2,即r2=22+(1)2,
解得:r,
∵∠AOD=90°,OA=OD=1,
∴AD,
∵AB为直径,
∴∠ADB=90°,
∴BD3,
∴tan∠ABD;
方法二、连接AC,
根据圆周角定理得到:∠ABD=∠ACD,
求出tan∠ACD,得出tan∠ABD;
②过点B作BE⊥x轴于点E,作AG⊥BE于G,
则OA∥PH∥BE,
∵P为AB的中点,
∴OE=2OH=4,BG=2PF=2,
∴BE=BG+GE=3,
∴点B的坐标为(4,3);
(2)证明:过点E作EH⊥x轴于H,
∵点E是的中点,
∴,
∴ED=EB,
∵四边形EDCB为圆P的内接四边形,
∴∠EDH=∠EBF,
在△EHD和△EFB中,
,
∴△EHD≌△EFB(AAS),
∴EH=EF,DH=BF,
在Rt△EHC和Rt△EFC中,
,
∴Rt△EHC≌Rt△EFC(HL),
∴CH=CF,
∴2CF=CH+CF=CD+DH+BC﹣BF=BC+CD.
16.【分析】(1)通过条件证明∠BOD=∠COD,即可得到结论;
(2)连OC、BC、BD,BC与OD交于点Q,证明△BOQ∽△BAC,用含y的式子表示OQ和QD,在Rt△COQ和Rt△BDQ中运用勾股定理即可得到x与y的关系式;
(3)利用(2)的关系式求出r,连接OE,BE,证明三角形POE是等腰三角形,得到PE的长,在Rt△BPE中,运用勾股定理求出BE,在Rt△ABE中运用正弦函数的定义即可得到sin∠PAB的值.
【解答】(1)证明:连接OC,
∵OD∥AC,
∴∠BAC=∠BOD,∠OCA=∠COD,
∵OA=OC,
∴∠BAC=∠OCA,
∴∠BOD=∠COD,
∴;
(2)解:连OC、BC、BD,BC与OD交于点Q,
∵OD∥AC,
∴△BOQ∽△BAC,
∴,
∵AB=2OB,
∴,BQ=CQ,
∵OD=r,
∴QD=OD﹣OD,
∵OD是半径,BQ=CQ,
∴OD⊥BC,
在Rt△COQ和Rt△BDQ中,
由勾股定理得CQ2=OC2﹣OQ2,BQ2=BD2﹣QD2,
∵BQ=CQ,
∴OC2﹣OQ2=BD2﹣QD2,即,
整理得x2+ry﹣2r2=0;
(3)解:连接OE,BE,
把,y=9代入x2+ry﹣2r2=0,
得5+9r﹣2r2=0,
解得(不合题意,舍去),r=5,
∵OA=OE,
∴∠PAB=∠AEO=2∠APO,
∵∠AEO是△POE的外角,
∴∠AEO=∠APO+∠POE,
∴∠APO=∠POE,
∴OE=PE=5,
∵AB是直径,
∴∠AEB=∠BEP=90°,
在Rt△BPE中,
∵PE=5,PB,
∴BE,
在Rt△ABE中,
∵BE=6,AB=2r=10,
∴sin∠PAB.
17.【分析】(1)连接AO并延长交BC于点M,连接OB,OC,过点A作AG⊥DE,垂足为G,设BM=x,根据题意易得AM是BC的垂直平分线,从而可得BC=2BM=2x,进而在Rt△ABM中,利用锐角三角函数的定义求出AM=3x,从而利用勾股定理求出ABx,再利用等腰三角形和平行四边形的性质可得∠ABC=∠ACB,BC=AD=2x,AB=CDx,∠ABC=∠D,然后根据圆内接四边形对角互补以及平角定义可得∠AED=∠ABC,从而可得∠ABC=∠ACB=∠D=∠AED,再证明△ABC∽△ADE,从而利用相似三角形的性质可求出DE,AG的长,进而求出CE的长,再根据△AEC的面积为,列出关于x的方程,进行计算可求出BM,AM的长,最后设⊙O的半径为r,在Rt△BOM中,利用勾股定理进行计算即可解答;
(2)连接AO并延长交BC于点M,连接OB,OC,过点A作AG⊥DE,垂足为G,过点C作CL⊥AB,垂足为L,设CE=a,BL=b,则EH=2a,利用平行四边形的性质可得AD∥BC,AB∥CD,AD=BC,从而可得CL=EH=2a,进而可得AD=BC,再利用AAS证明△BLC≌△DGA,从而可得BL=DG=b,进而可得DE=2DG=2b,CD=2b+a,然后证明△DAE∽△DCA,从而利用相似三角形的性质进而计算可得ba,再证明△ABM∽△FCE,从而利用相似三角形的性质,进行计算即可解答.
【解答】解:(1)连接AO并延长交BC于点M,连接OB,OC,过点A作AG⊥DE,垂足为G,
设BM=x,
∵AB=AC,OB=OC,
∴AM是BC的垂直平分线,
∴BC=2BM=2x,
在Rt△ABM中,tan∠ABM=3,
∴AM=BM tan∠ABM=3x,
∴ABx,
∵AB=AC,
∴∠ABC=∠ACB,
∵四边形ABCD是平行四边形,
∴BC=AD=2x,AB=CDx,∠ABC=∠D,
∵四边形ABCE是⊙O的内接四边形,
∴∠ABC+∠AEC=180°,
∵∠AEC+∠AED=180°,
∴∠AED=∠ABC,
∴∠D=∠AED,
∴AE=AD,
∵∠ABC=∠ACB=∠D=∠AED,
∴△ABC∽△ADE,
∴
∴,
∴DEx,AGx,
∴CE=CD﹣DEx,
∵△AEC的面积为,
∴CE AG,
∴ x x,
解得:x=3或x=﹣3(舍去),
∴BM=3,AM=3x=9,
设⊙O的半径为r,
在Rt△BOM中,OM2+BM2=BO2,
∴(9﹣r)2+32=r2,
解得:r=5,
∴⊙O的半径为5;
(2)连接AO并延长交BC于点M,连接OB,OC,过点A作AG⊥DE,垂足为G,过点C作CL⊥AB,垂足为L,
设CE=a,BL=b,
∵CEEH,
∴EH=2a,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∴CL=EH=2a,
∴BC,
∴AD=BC,
∵∠BLC=∠DGA=90°,∠ABC=∠D,BC=AD,
∴△BLC≌△DGA(AAS),
∴BL=DG=b,
∵AE=AD,AG⊥DE,
∴DE=2DG=2b,
∴CD=DE+CE=2b+a,
∵AD∥BC,
∴∠CAD=∠ACB,
∵∠ACB=∠AED,
∴∠CAD=∠AED,
∵∠D=∠D,
∴△DAE∽△DCA,
∴,
∴DA2=DC DE,
∴()2=(2b+a) 2b,
∴b2+4a2=4b2+2ab,
整理得:3b2+2ab﹣4a2=0,
解得:ba或ba(舍去),
∵AB∥CD,
∴∠ABC=∠ECF,∠FEC=∠FHB=90°,
∴∠AME=∠FEC=90°,
∴△ABM∽△FCE,
∴22,
∴的值为.
18.【分析】(1)连接OA.利用垂径定理以及等腰三角形的性质解决问题即可.
(2)分三种情形:①若BD=CB,则∠C=∠BDC=∠ABD+∠BAC=3∠ABD.②若CD=CB,则∠CBD=∠CDB=3∠ABD.③若DB=DC,则D与A重合,这种情形不存在.分别利用三角形内角和定理构建方程求解即可.
(3)如图3中,作AE∥BC交BD的延长线于E.则,推出,设OB=OA=4a,OH=3a,根据BH2=AB2﹣AH2=OB2﹣OH2,构建方程求出a即可解决问题.
【解答】(1)证明:连接OA.
∵AB=AC,
∴,
∴OA⊥BC,
∴∠BAO=∠CAO,
∵OA=OB,
∴∠ABD=∠BAO,
∴∠BAC=2∠ABD.
(2)解:如图2中,延长AO交BC于H.
①若BD=CB,则∠C=∠BDC=∠ABD+∠BAC=3∠ABD,
∵AB=AC,
∴∠ABC=∠C,
∴∠DBC=2∠ABD,
∵∠DBC+∠C+∠BDC=180°,
∴8∠ABD=180°,
∴∠C=3∠ABD=67.5°.
②若CD=CB,则∠CBD=∠CDB=3∠ABD,
∴∠C=4∠ABD,
∵∠DBC+∠C+∠CDB=180°,
∴10∠ABD=180°,
∴∠BCD=4∠ABD=72°.
③若DB=DC,则D与A重合,这种情形不存在.
综上所述,∠C的值为67.5°或72°.
(3)如图3中,作AE∥BC交BD的延长线于E.
则,
∴,设OB=OA=4a,OH=3a,
∵BH2=AB2﹣AH2=OB2﹣OH2,
∴25﹣49a2=16a2﹣9a2,
∴a2,
∴BH2=7a2,
∴BH
∴BC=2BH.
19.【分析】(1)过O作OH⊥CD于H,根据点D为弧EC的中点,可得∠OCH=45°,进而得出OH=CH,再根据圆O的半径为2,即可得到OH;
(2)先判定△CDF∽△BDC,可得∠DCF=∠DBC,再根据∠DCF=45°,即可得出∠DBC=45°;
(3)连接BE,BO,DO,并延长BO至H点,依据∠ABE=∠OBC=∠OCB,∠A=∠A,判定△ABE∽△ACB,即可得到AC,设AE=x,再根据△AOB∽△COH,可得,即,解得x=5,OH=4.5,OB=7.5,即可得到△BCD的面积12×12=72.
【解答】解:(1)如图,过O作OH⊥CD于H,
∵点D为弧EC的中点,
∴弧ED=弧CD,
∴∠OCH=45°,
∴OH=CH,
∵圆O的半径为2,即OC=2,
∴OH;
(2)∵当DF DB=CD2时,,
又∵∠CDF=∠BDC,
∴△CDF∽△BDC,
∴∠DCF=∠DBC,
由(1)可得∠DCF=45°,
∴∠DBC=45°;
注:也可以由点D为弧EC的中点,可得弧ED=弧CD,即可得出∠DCF=∠DBC=45°;
(3)如图,连接BE,BO,DO,并延长BO至H点,
∵BD=BC,OD=OC,
∴BH垂直平分CD,
又∵AB∥CD,
∴∠ABO=90°=∠EBC,
∴∠ABE=∠OBC=∠OCB,
又∵∠A=∠A,
∴△ABE∽△ACB,
∴,即AB2=AE×AC,
∴AC,
设AE=x,则AB=2x,
∴AC=4x,EC=3x,
∴OE=OB=OC,
∵CD=12,
∴CH=6,
∵AB∥CH,
∴△AOB∽△COH,
∴,即,
解得x=5,OH=4.5,OB=7.5,
∴BH=BO+OH=12,
∴△BCD的面积12×12=72.
20.【分析】(1)①由题意可得AB=AC,可证AO是BC的垂直平分线,可得结论;
②由等腰三角形的性质可得BP=CP=4,由勾股定理可求AP的长,BO的长,即可求解;
(2)设BO=3a=OC=OH,OD=2a,由勾股定理可求CD长,CH的长,通过证明△ACH∽△HCD,可求AD的长,即可求解.
【解答】(1)①证明:连接OB,OC,设AB与BC交于点P,
∵点A是的中点,
∴,
∴AB=AC,
又∵OB=OC,
∴AO是BC的垂直平分线,
∴AO⊥BC;
②∵AB=AC,AP⊥BC,
∴BP=CP=4,
∴AP8,
∵BO2=OP2+BP2,
∴BO2=(8﹣OB)2+16,
∴BO=5,
∴⊙O的半径为5;
(2)延长BD交⊙O于点H,连接CH,CO,AH,
∵,
∴设BO=3a=OC=OH,OD=2a,
∴DH=a,
∵∠BAC=45°,
∴∠BOC=2∠BAC=90°,
∴CDa,CH3a,
∵∠ACH=∠DCH,∠BAC=∠BHC=45°,
∴△ACH∽△HCD,
∴,
∴,
∴ACa,
∴AD=AC﹣CDaaa,
∴.
21.【分析】(1)求AC的长度,证明△ABC是等腰直角三角形,得到∠A的度数,根据等腰三角形的性质求出角度;
(2)证明△COE是直角三角形,求出CE的长度,证明△ACE∽△DCA,从而求出CD的长度;
(3)根据题意分当E在线段OB上和当点E在线段OA上两种情况,分别画出对应的图,求出CE和BE的长度,根据相似三角形的性质求出△BCD的面积.
【解答】解:(1)∵△ABC 内接于⊙O,
∴∠ACB=90°,
在Rt△ABC中,
∵AB=12,BC,
∴,
∴△ABC是等腰直角三角形,
∴∠A=45°,
∵AE=AC,
∴∠ACD;
(2)连接OC,AD,
∵直径AB=12,
∴OA=OB=OC=6,
∴OE=OA﹣AE=2,
∵∠CAB=45°,OA=OC,
∴∠AOC=90°,
在Rt△COE中,
∵OE=2,OC=6,
∴,
∵,
∴∠ADC=∠ABC=∠BAC=45°,
∵∠ACE=∠DCA,
∴△ACE∽△DCA,
∴,
∴CD;
(3)①当E在线段OB上时,连接OC,连接BM交CD于点N,
∵CD∥AM,
∴∠BNE=∠BMA=∠BOC=90°,
∵∠BEN=∠CEO,
∴∠ECO=∠ABM=∠ACM,
∴tan∠ECO=tan∠ACM,
∵OC=6,
∴OE=OC tan∠ECO=2,
∴EC,BE=6﹣2=4,
∴,
由(2)得△BCD∽△ECB,
∴,
∴;
②当点E在线段OA上时,
同理tan∠ECO=tan∠ACM,
∴OE=OC tan∠ECO=2,
∴CE,BE=6+2=8,
∴,
∵△BCD∽△ECB,
∴,
∴.
综上所述,△BCD的面积的面积为.
22.【分析】(1)根据垂径定理和同弧所对的圆周角相等,能够推导出∠AFC=∠CFE,∠ACF=∠FEA,即可证明三角形相似;
(2)连接BF,由题意可得AB=2AC,在Rt△ABC中,利用勾股定理求出AC=2,再由tan∠ACB=2,得到AD=2CD,在Rt△ACD中,利用勾股定理求出CD=2,AD=4,则ED=AD=4,证明△BFC∽△HDC,求得HD,则HE=ED+HD,再由△AFC∽△HFE,求出EF;
(3)设OC=r,则BC=2r,CDr,ADr,分两种情况讨论:①当点G在线段OD上时,x,则OG=xr,CG=(1﹣x)r,BG=(1+x)r,过点G作GM⊥CF交于点M,推导出FM=2GM,再由GM∥BE,推导出,,从而求出DH,AH=AD﹣HDr,即可求y;②当点G在线段OB上时,同理可得y.
【解答】(1)证明:∵BC是⊙O的直径,AD⊥BC,
∴,
∴∠AFC=∠CFE,
∵,
∴∠ACF=∠FEA,
∴△AFC∽△HFE;
(2)解:连接BF,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵tan∠ACB=2,
∴AB=2AC,
在Rt△ABC中,BC=10,
∴AC=2,
∵AD⊥BC,
∴∠ADC=90°,
∵tan∠ACB=2,
∴AD=2CD,
在Rt△ACD中,AD2+CD2=AC2,则CD=2,AD=4,
∴ED=AD=4,
∵BC是⊙O的直径,
∴∠BFC=90°,
∵BC=10,CF=8,
∴BF=6,
∵∠BFC=∠HDC=90°,∠FCB=∠DCH,
∴△BFC∽△HDC,
∴,
∴HD,
∴HE=ED+HD,
∵△AFC∽△HFE,
∴,
∴EF;
(3)解:设OC=r,则BC=2r,
∵tan∠ACB=2,
∴AD=2CD,BD=2AD,
∴CDr,ADr,
①当点G在线段OD上时,
∵x,
∴OG=xr,CG=(1﹣x)r,BG=(1+x)r,
过点G作GM⊥CF交于点M,
∴∠GMF=90°,
∵∠ADC=90°,∠CAE=∠CFE,
∴∠FGM=∠ACB,
∴tan∠FGM=tan∠ACB=2,
∴FM=2GM,
∵∠GMC=∠BFC=90°,
∴GM∥BE,
∴,
∴,即,
∵,
∴,
∴DH,
∴AH=AD﹣HDr,
∴,
∴y;
②当点G在线段OB上时,同理可得y;
综上所述:当点G在线段OD上时,y;当点G在线段OB上时,y.
23.【分析】(1)根据圆周角定理可得∠PCQ=∠ACB=90°,即可求证;
(2)连接BQ,根据圆内接四边形的性质可得∠BQC=∠APC,可证明△ACP∽△BCQ,从而得到QC=2PC,BQ=2x,在Rt△ACB中,根据勾股定理可得,从而得到,再由勾股定理可得,从而得到,再根据三角形的面积公式可得到S关于x的函数关系式,即可求解;
(3)过点P作PH⊥BC于点H,KQ⊥BC于点K,则PH∥KQ,证明△PMH∽△QMK,可得KQ=3PH,再证△BPH∽△BAC,可得,,然后根据△ABC∽△BQK,可得,即可求解.
【解答】(1)证明:∵PQ是⊙O的直径,
∴∠PCQ=∠ACB=90°,
∵∠B=∠Q,
∴△PQC∽△ABC;
(2)解:如图1,连接BQ,
∵四边形BPCQ是圆内接四边形,
∴∠BPC+∠CQB=180°,
∵∠BPC+∠APC=180°,
∴∠BQC=∠APC,
∵∠PCQ=∠ACB=90°,
∴∠ACP=∠BCQ,
∴△ACP∽△BCQ,
∴,
∴,
∴QC=2PC,BQ=2x,
在Rt△ACB中,,
∴,
∵PQ是⊙O的直径,
∴∠PCQ=∠PBQ=90°,
∴,
∴PC2=x2x+4,
∴SPC×QCPC×2PC=PC2=x2x+4=(x)2,
∴当时,S有最大值,最大值为;
(3)解:如图2,过点P作PH⊥BC于点H,KQ⊥BC于点K,则PH∥KQ,
∴△PMH∽△QMK,
∴,
∵,PO=OQ,
∴,
即KQ=3PH,
∵∠ACB=90°,即AC∥PH,
∴△BPH∽△BAC,
∴,即,
解得:,
∴,
∵∠A+∠ABC=∠CBQ+∠ABC=90°,
∴∠A=∠CBQ,
∵∠BKQ=∠ACB=90°,
∴△ABC∽△BQK,
∴,
∴,
解得:.
24.【分析】(1)可通过∠APD=∠ACD=45°求得结果;
(2)①可证明∠ADP=∠AMP,∠APD=∠APM,PA是公共边得出△ADP≌△AMP;
(3)连接EM并延长交BC于Q,连接AQ,AQ交BF于G,可证得△DAE≌△MAE,从而∠AME=∠ADE=90°,进而△ABQ≌△AMQ,进而△ABQ≌△BCF,设∠PAD=∠PAM=α,可证得∠MNE=∠MEN=90°﹣α,可得EM=MN=5,从而EQ=EM+MQ=5+12=17,进一步求得结果.
【解答】(1)解:如图1,
连接AC,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠ACD,
∵,
∴∠APD=∠ACD=45°;
(2)①证明:∵AM=AB,
∴∠ABP=∠AMB,
∵四边形ABPD内接于⊙O,
∴∠ABP+∠ADP=180°,
∵∠AMB+∠AMP=180°,
∴∠ADP=∠AMP,
∵四边形ABCD是正方形,
∴AB=AD,
∴,AD=AM,
∴∠APD=∠APB,
在△ADP和△AMP中,
,
∴△ADP≌△AMP(AAS);
(3)解:如图2,
连接EM并延长交BC于Q,连接AQ,AQ交BF于G,
由①知:△ADP≌△AMP,
∴∠DAP=∠MAP,
在△DAE和△MAE中,
,
∴△DAE≌△MAE(SAS),
∴∠AME=∠ADE=90°,
∵AM=AB,AQ=AQ,
∴△ABQ≌△AMQ(HL),
∴MQ=BQ,
∵AM=AB,
∴AQ⊥BF,
∴∠BGQ=90°,
∵∠C=90°,∠GBQ=∠CBF,
∴∠AQB=∠BFC,
∵BC=AB,∠ABCQ=∠C=90°,
∴△ABQ≌△BCF(AAS),
∴BQ=CF=12,
∴MQ=12,
设∠PAD=∠PAM=α,
∴∠BAM=90°﹣∠DAM=90°﹣2α,
∵MN∥AB,
∴∠AMN=∠BAM=90°﹣2α,
∴∠MNE=∠PAM+∠AMN=α+90°﹣2α=90°﹣α,
∵∠MEN=90°﹣∠MAE=90°﹣α,
∴∠MNE=∠MEN,
∴EM=MN=5,
∴EQ=EM+MQ=5+12=17,
设正方形的边长是a,
∴CD=BC=a,
∴CE=CD﹣EM=a﹣5,
CQ=BC﹣BQ=a﹣12,
在Rt△ECQ中,
CE2+CQ2=EQ2,
∴(a﹣5)2+(a﹣12)2=172,
∴a1=20,a2=﹣3(舍去),
∴S正方形ABCD=a2=202=400.
25.【分析】(1)根据圆的内接四边形性质得:∠ADC+∠ABC=180°,结合已知∠ADF+∠ABC=90°,进而得出结果;
(2)可证明△BDG≌△CFD,从而CF=BD,进一步得出结论;
(3)①根据S△BDG=3S△DEH得出S△CFD=3S△DEG,从而EHCF,可证得△DEH∽△FED,从而DE2=EH EF,从而得出EF的值,可证得△ABE∽△CED,从而得出BE DE=CE AE,进一步得出结果;
②作DW⊥AC于W,作直径CV,连接DV,可得出AD=BD=2,△ABE∽△CED,从而,进而得出CE,AE=2,设EW=x,则AW=2﹣x,根据勾股定理得出DW2=DE2﹣EW2=AD2﹣AW2,,从而12﹣x2=22﹣(2﹣x)2,从而得出x的值,进而计算出CD的长,根据sinV=sin∠ACD得出,进一步得出结果.
【解答】(1)解:∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠CDF+∠ADF+∠ABC=180°,
∵∠ADF+∠ABC=90°,
∴∠CDF=90°;
(2)证明:∵DG⊥AB,
∴∠BGD=90°,
∵∠CDF=90°,
∴∠BGD=∠CDF,
∵,
∴∠ABD=∠ACD,
∵BG=CD,
∴△BDG≌△CFD(ASA),
∴CF=BD,
∵点E是BD的中点,
∴BD=2DE,
∴CF=2DE;
(3)①解:由(2)知:△BDG≌△CFD,CF=BD=2,∠BDG=∠CFD,
∵S△BDG=3S△DEH,
∴S△CFD=3S△DEG,
∴EHCF,
∵∠DEH=∠FED,
∴△DEH∽△FED,
∴DE2=EH EF,
∴12EF,
∴EF,
∴CE=CF﹣EF,
∵∠ABD=∠ACD,∠AEB=∠CED,
∴△ABE∽△CED,
∴BE DE=CE AE,
∴1×1AE,
∴AE=2,
∴AC=CE+AE;
②解:如图,
作DW⊥AC于W,作直径CV,连接DV,
∵DO⊥AB,
∴BG=AG,
∴AD=BD=2,
由①知:△ABE∽△CED,
∴,
∴AB=2BC,BC=CD,
∴
∴CE,AE=2,
设EW=x,则AW=2﹣x,
∵DW2=DE2﹣EW2=AD2﹣AW2,
∴12﹣x2=22﹣(2﹣x)2,
∴x,
∴EW,DW,
∴CW=EW+CE,
∴CD,
∵sinV=sin∠ACD,
∴,
∴,
∴CV,
∴⊙O的半径为:.
同课章节目录
