2025人教A版高中数学选择性必修第三册强化练习题(含解析)--8.2 一元线性回归模型及其应用
文档属性
| 名称 | 2025人教A版高中数学选择性必修第三册强化练习题(含解析)--8.2 一元线性回归模型及其应用 |

|
|
| 格式 | docx | ||
| 文件大小 | 388.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 10:04:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025人教A版高中数学选择性必修第三册
8.2 一元线性回归模型及其应用
基础过关练
题组一 线性回归分析
1.(2024辽宁部分高中期末)下列有关回归分析的说法正确的是( )
A.样本相关系数r越大,两变量的相关性就越强
B.经验回归直线就是散点图中经过样本数据点最多的那条直线
C.经验回归直线不一定过样本点的中心()
D.回归分析中,若样本相关系数r<0,则两变量是负相关
2.(2024江苏常州期末)用最小二乘法得到一组数据(xi,yi)(i=1,2,3,4,5,6)的经验回归方程为=2x+3,若xi=30,则yi=( )
A.11 B.13 C.63 D.78
3.(2024重庆南开中学期中)已知变量x和y的统计数据如表:
x 1 2 3 4 5
y 0.5 0.6 1 1.4 1.5
若由表中数据得到的经验回归方程为,则当x=5时,残差为( )
A.-0.06 B.-0.04 C.0.12 D.0.14
4.(多选题)(2024江西师大附中期末)已知某产品的销售额y(单位:万元)与广告费用x(单位:万元)之间的关系如表:
x/万元 0 1 2 3 4
y/万元 10 15 m 30 35
若根据表中的数据用最小二乘法求得y与x的经验回归方程为=6.5x+9,则下列说法正确的是( )
A.m的值是20
B.该经验回归直线过点(2,22)
C.该产品的销售额与广告费用正相关
D.当广告费用为10万元时,销售额一定为74万元
5.(2024江西名校联盟期末)“守得住经典,当得了网红”,这是时下人们对国货最高的评价,网络平台的发展让越来越多的消费者意识到国货品牌的优势,使得各大国货品牌都受到了高度关注,销售额迅速增长,已知某国货品牌2023年8月至12月在D网络平台的月销售额y(单位:百万元)与月份x具有线性相关关系,并根据这5个月的月销售额求得经验回归方程为=4.2x+3,则该国货品牌2023年8月至12月在D网络平台的总销售额约为 百万元.
6.(2022江西抚州期中)某学校为了解学生中男生的体重y(单位:kg)与身高x(单位:cm)是否存在线性相关关系,收集了7位男生的数据,得到如下表格:
序号 1 2 3 4 5 6 7
身高x/cm 166 173 174 178 180 183 185
体重y/kg 57 62 59 71 67 75 78
根据表中数据计算得到y关于x的经验回归方程为x-136.55.
(1)= ;
(2)已知决定系数R2=1-,当R2≥0.9时,模型的拟合效果非常好,当0.8参考数据:)2=52.36.
7.(2024广东深圳中学期中)已知某水果种植基地苹果的种植面积x(单位:公顷)与其产量y(单位:吨)呈线性相关关系,小王准备承包一块苹果种植地,为了解市场行情,在该基地调查了5家果农,统计得到了苹果种植面积与其产量的数据如表所示:
种植面积x/公顷 1 2 3 4 5
产量y/吨 20 38 64 78 100
(1)求y关于x的经验回归方程;
(2)若苹果的销量等于产量,且所种苹果的总利润P(单位:千元)满足P=+180x,苹果种植面积x∈{1,2,3,…,14,15},请根据(1)的结果预测要使得单位面积的苹果利润最大,小王应该种植多少公顷的苹果.
附:经验回归直线.
题组二 非线性回归分析
8.(2024河南南阳期中联考)已知变量x和y之间的关系可以用模型y=menx来拟合.设z=ln y,若根据样本数据计算可得=0.9,且z关于x的经验回归方程为,则m≈ .(参考数据:ln 0.3≈-1.2,ln 0.25≈-1.4)
9.(2024广东广州华南师大附中期中)某地政府为提高当地农民收入,指导农民种植药材,取得了较好的效果.下表是某农户近5年种植药材的年收入的统计数据:
年份 2019 2020 2021 2022 2023
年份代码x 1 2 3 4 5
年收入y/千元 59 61 64 68 73
(1)根据表中数据,现决定使用函数模型y=bx2+a拟合y与x之间的关系,请求出此模型的经验回归方程;(结果保留一位小数)
(2)统计学中常通过计算残差的平方和来判断模型的拟合效果,若残差的平方和小于0.5,则认为拟合效果符合要求.请判断(1)中的经验回归方程的拟合效果是否符合要求,并说明理由.
能力提升练
题组一 线性回归分析
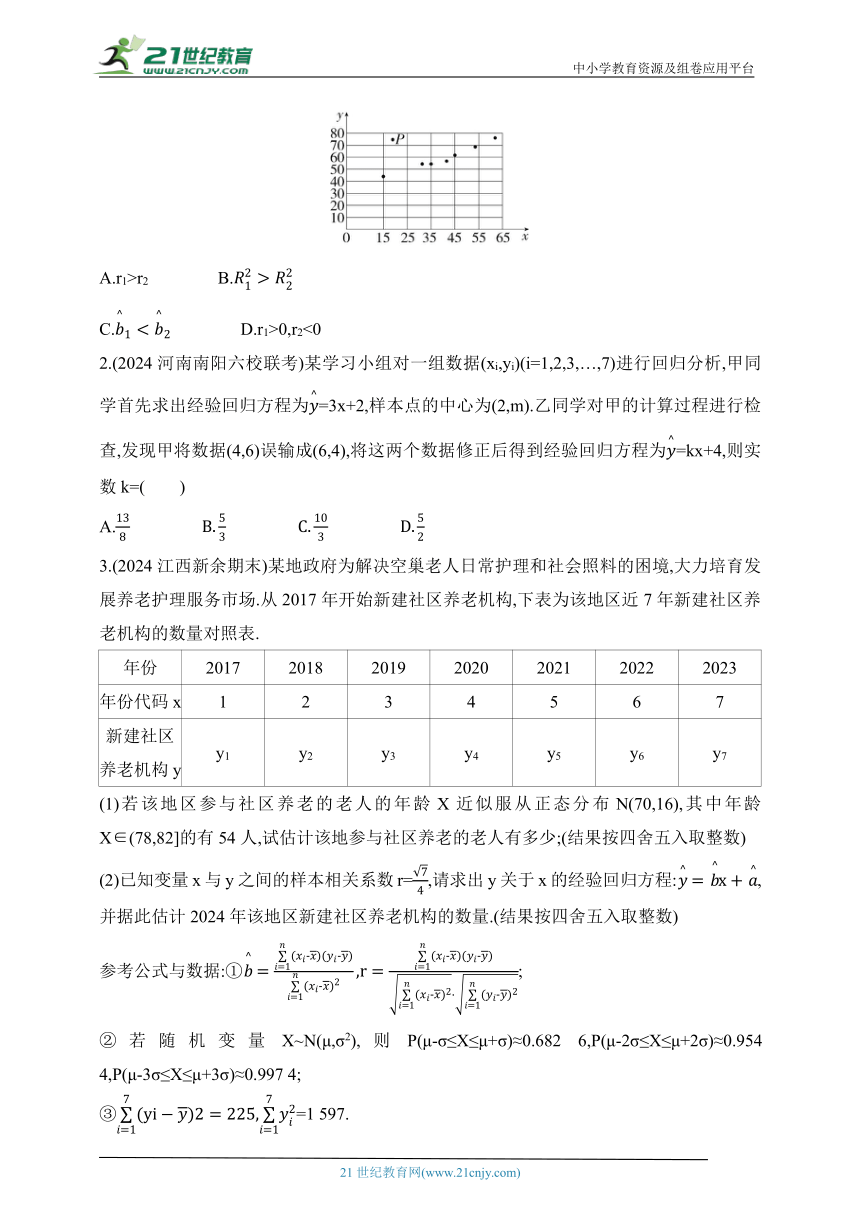
1.(2024浙江宁波期中)下图是某组数据的散点图,由最小二乘法计算得到经验回归直线l1的方程为,相关系数为r1,决定系数为,若经过残差分析后去掉点P,剩余的点重新计算得到经验回归直线l2的方程为,相关系数为r2,决定系数为,则下列结论一定正确的是( )
A.r1>r2 B.
C. D.r1>0,r2<0
2.(2024河南南阳六校联考)某学习小组对一组数据(xi,yi)(i=1,2,3,…,7)进行回归分析,甲同学首先求出经验回归方程为=3x+2,样本点的中心为(2,m).乙同学对甲的计算过程进行检查,发现甲将数据(4,6)误输成(6,4),将这两个数据修正后得到经验回归方程为=kx+4,则实数k=( )
A.
3.(2024江西新余期末)某地政府为解决空巢老人日常护理和社会照料的困境,大力培育发展养老护理服务市场.从2017年开始新建社区养老机构,下表为该地区近7年新建社区养老机构的数量对照表.
年份 2017 2018 2019 2020 2021 2022 2023
年份代码x 1 2 3 4 5 6 7
新建社区 养老机构y y1 y2 y3 y4 y5 y6 y7
(1)若该地区参与社区养老的老人的年龄X近似服从正态分布N(70,16),其中年龄X∈(78,82]的有54人,试估计该地参与社区养老的老人有多少;(结果按四舍五入取整数)
(2)已知变量x与y之间的样本相关系数r=,请求出y关于x的经验回归方程:,并据此估计2024年该地区新建社区养老机构的数量.(结果按四舍五入取整数)
参考公式与数据:①;
②若随机变量X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 6,P(μ-2σ≤X≤μ+2σ)≈0.954 4,P(μ-3σ≤X≤μ+3σ)≈0.997 4;
③=1 597.
4.大气污染物PM2.5(大气中直径小于或等于2.5 μm的颗粒物)的浓度超过一定的限度会影响人的身体健康.为了研究PM2.5的浓度受车流量影响的程度,某校数学建模社团选择了学校附近5个监测点,统计每个监测点24 h内的车流量x(单位:千辆),同时在低空相同的高度测定每个监测点该时间段内的PM2.5的平均浓度y(单位:μg/m3),得到的数据如表所示:
监测点编号 1 2 3 4 5
车流量x/千辆 1.3 1.2 1.6 1.0 0.9
PM2.5的平均 浓度y/(μg/m3) 66 72 113 34 35
(1)建立y关于x的一元线性回归模型,并用样本相关系数加以说明(一般地,样本相关系数的绝对值在0.75以上(含0.75),则认为线性相关性较强,否则认为线性相关性较弱);
(2)我国规定空气中PM2.5浓度的安全标准为24 h平均浓度75 μg/m3,该地为使24 h内PM2.5的平均浓度不超过68.6 μg/m3,拟对车流量作适当控制,请你根据本题数据估计车流量控制的最大值.
参考公式:在经验回归方程中,;样本相关系数r=.
题组二 非线性回归分析
5.红铃虫是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型:①y=ebx+a,②y=cx2+d分别进行拟合,由此得到相应的经验回归方程并进行残差分析,进一步得到图2所示的残差图.
根据收集到的数据,计算得到下表:
(xi -)2 (ti- )2 (zi- ) (yi- )
25 2.9 646 168 422 688 50.4 70 308
表中z=ln y;ti.
(1)根据残差图比较模型①和②的拟合效果,模型 比较合适;
(2)根据(1)中所选择的模型,求出y关于x的经验回归方程为 .
附:对于一组数据(ω1,v1),(ω2,v2),…,(ωn,vn),其经验回归直线ω的斜率和截距的最小二乘估计分别为.
6.(2024重庆第一中学校开学考试)当前,人工智能技术以前所未有的速度迅猛发展,并逐步影响我们的方方面面,人工智能被认为是推动未来社会发展和解决人类面临的全球性问题的重要手段.某公司在这个领域逐年加大投入,以下是近年来该公司对产品研发年投入额x(单位:百万元)与年销售量y(单位:千件)的数据统计表:
x 1 2 3 4 5 6
y 0.5 1 1.5 3 6 12
z=ln y -0.7 0 0.4 1.1 1.8 2.5
(1)公司拟分别用①y=bx+a和②y=enx+m两个函数模型作为年销售量y关于年投入额x的回归分析模型,请根据已知数据,确定模型①和②的经验回归方程;(a,b,m,n计算过程保留到小数点后两位,最后结果保留到小数点后一位)
(2)根据下表数据,用决定系数R2(只需比较出大小)比较哪个函数模型的拟合效果更好,并根据拟合精度更高的模型预测年投入额为7百万元时,产品的年销售量是多少.
函数模型 y=bx+a y=enx+m
残差平方和 )2 18.29 0.65
参考公式及数据:经验回归方程中,=0.85,e2.8≈16.4,e3≈20.1.
答案与分层梯度式解析
8.2 一元线性回归模型及其应用
基础过关练
1.D 2.D 3.A 4.ABC
1.D 两变量的相关性越强,样本相关系数r就越接近1或-1,故A不正确;经验回归直线是基于样本数据使残差平方和最小的拟合直线,故B不正确;经验回归直线一定过样本点的中心(),故C不正确;当相关系数r>0时,两个变量正相关,当r<0时,两个变量负相关,故D正确.
故选D.
2.D ∵×30=5,
∵经验回归直线=2x+3一定过点(),
∴+3=2×5+3=13,因此yi=6×13=78.故选D.
3.A 由题表中的数据得×(0.5+0.6+1+1.4+1.5)=1,
则样本点的中心为(3,1),代入,得=1-0.28×3=0.16,
∴经验回归方程为=0.28x+0.16,
令x=5,得=0.28×5+0.16=1.56.
∴当x=5时的残差为1.5-1.56=-0.06.故选A.
方法总结 经验回归直线不一定过样本点,但一定过样本点的中心(),常利用这一结论列方程求经验回归方程中的参数.
4.ABC 由题表中数据可得,
∵y与x的经验回归方程为=6.5×2+9,解得m=20,因此A正确;
∵=22,∴该经验回归直线过点(2,22),因此B正确;
∵=6.5>0,∴产品的销售额与广告费用正相关,因此C正确;
当x=10时,=6.5×10+9=74,故广告费用为10万元时,销售额约为74万元,因此D错误.故选ABC.
5.答案 225
解析 将x=8,9,10,11,12分别代入经验回归方程=4.2x+3,得=4.2×9+3=40.8,
=4.2×12+3=53.4,
因为36.6+40.8+45+49.2+53.4=225,
所以该国货品牌这五个月在D网络平台的总销售额约为225百万元.
6.答案 (1)1.15 (2)良好
解析 (1)由题表中数据可得,
=177,
=67,
所以67=×177-136.55,解得=1.15.
(2)由(1)知=67,故)2=(-10)2+(-5)2+(-8)2+42+02+82+112=390,
则有R2=1-≈0.87,因为0.8<0.87<0.9,
所以该经验回归方程对应模型的拟合效果良好.
7.解析 (1)由题可得=60,
则)=(-2)×(-40)+(-1)×(-22)+0×4+1×18+2×40=200,
)2=(-2)2+(-1)2+02+12+22=10,
所以=60-20×3=0,
故y关于x的经验回归方程为=20x.
(2)因为P=+180x,x∈{1,2,3,…,14,15},
所以单位面积的苹果利润(单位:千元)为+181,x∈{1,2,3,…,14,15}.
因此当,即x=10时,取得最大值,
故要使得单位面积的苹果利润最大,小王应该种植10公顷的苹果.
8.答案 0.3
解析 由题意知0.9=0.6×3.5+,解得=-1.2,所以=0.6x-1.2,
由z=ln y,得ln =0.6x-1.2,所以=e0.6x-1.2=e-1.2·e0.6x,则m=e-1.2≈0.3.
9.解析 (1)由题表数据可得×(59+61+64+68+73)=65,
设t=x2,则y关于t的经验回归方程为,易得)2=374.
则≈0.6,≈65-0.6×11=58.4,
所以y关于x的经验回归方程为=0.6x2+58.4.
(2)将x=1,2,3,4,5分别代入=0.6x2+58.4可得预测值分别为59,60.8,63.8,68,73.4,
则残差的平方和为(59-59)2+(61-60.8)2+(64-63.8)2+(68-68)2+(73-73.4)2=0.24,
因为0.24<0.5,所以经验回归方程=0.6x2+58.4拟合效果符合要求.
能力提升练
1.C 由题图可知共8个点,且离群点P的横坐标较小而纵坐标相对过大,去掉离群点后经验回归直线的斜率变大,因此C正确;去掉离群点后相关性更强,拟合效果也更好,且还是正相关,故02.D 由题意可得m=3×2+2=8,假设甲输入的(x1,y1)为(6,4),
则
改为正确数据后,有,
将点=kx+4,得k=.故选D.
3.解析 (1)由题意可知,μ=70,σ=4,则78=μ+2σ,82=μ+3σ,
所以P(78=[P(μ-3σ≤X≤μ+3σ)-P(μ-2σ≤X≤μ+2σ)]≈=0.021 5,
所以估计该地参与社区养老的老人人数为≈2 512.
(2)由题表中的数据可得=4,
所以)2=(1-4)2+(2-4)2+(3-4)2+(4-4)2+(5-4)2+(6-4)2+(7-4)2=28,
由已知条件可得r=,
所以,
又因为=1 597-7=225,所以=196,
显然≥0,所以=14,则,
所以y关于x的经验回归方程为,
当x=8时,=21.5≈22,
故2024年该地区新建社区养老机构的数量约为22个.
4.解析 (1)由题表得=1.2,
=64,
xiyi=1.3×66+1.2×72+1.6×113+1.0×34+0.9×35=418.5,
=1.32+1.22+1.62+1.02+0.92=7.5,
=662+722+1132+342+352=24 690,
所以=115,
=64-115×1.2=-74,
所以=115x-74.
样本相关系数r=
=≈0.97.
因为|0.97|>0.75,
所以y与x的线性相关性较强.
(2)令115x-74≤68.6,得x≤1.24,
故车流量控制的最大值约为1.24千辆.
5.答案 (1)① (2)=e0.3x-4.6
解析 (1)应该选择模型①.因为模型①残差点比较均匀地落在水平的带状区域中,且带状区域的宽度比模型②的窄,所以模型①的拟合精度更高,故选模型①比较合适.
(2)由z=ln y,得z=a+bx,
所以=0.3,
所以=2.9-0.3×25≈-4.6,
即z关于x的经验回归方程为=0.3x-4.6.
于是有ln =0.3x-4.6,
所以y关于x的经验回归方程为=e0.3x-4.6.
6.解析 (1)由题表数据得=4,
所以≈2.11,≈4-2.11×3.5≈-3.39,
因此=2.1x-3.4,
由y=enx+m,两边取以e为底的对数得ln y=nx+m,由z=ln y得z=nx+m,
≈0.63,≈0.85-0.63×3.5≈-1.36,
所以=0.6x-1.4,所以=e0.6x-1.4.
(2))2=(0.5-4)2+(1-4)2+(1.5-4)2+(3-4)2+(6-4)2+(12-4)2=96.5,
对于;
对于,
因为,所以②的拟合效果更好,当x=7时,=e0.6×7-1.4=e2.8≈16.4,故年投入额为7百万元时,年销售量约为16.4千件.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版高中数学选择性必修第三册
8.2 一元线性回归模型及其应用
基础过关练
题组一 线性回归分析
1.(2024辽宁部分高中期末)下列有关回归分析的说法正确的是( )
A.样本相关系数r越大,两变量的相关性就越强
B.经验回归直线就是散点图中经过样本数据点最多的那条直线
C.经验回归直线不一定过样本点的中心()
D.回归分析中,若样本相关系数r<0,则两变量是负相关
2.(2024江苏常州期末)用最小二乘法得到一组数据(xi,yi)(i=1,2,3,4,5,6)的经验回归方程为=2x+3,若xi=30,则yi=( )
A.11 B.13 C.63 D.78
3.(2024重庆南开中学期中)已知变量x和y的统计数据如表:
x 1 2 3 4 5
y 0.5 0.6 1 1.4 1.5
若由表中数据得到的经验回归方程为,则当x=5时,残差为( )
A.-0.06 B.-0.04 C.0.12 D.0.14
4.(多选题)(2024江西师大附中期末)已知某产品的销售额y(单位:万元)与广告费用x(单位:万元)之间的关系如表:
x/万元 0 1 2 3 4
y/万元 10 15 m 30 35
若根据表中的数据用最小二乘法求得y与x的经验回归方程为=6.5x+9,则下列说法正确的是( )
A.m的值是20
B.该经验回归直线过点(2,22)
C.该产品的销售额与广告费用正相关
D.当广告费用为10万元时,销售额一定为74万元
5.(2024江西名校联盟期末)“守得住经典,当得了网红”,这是时下人们对国货最高的评价,网络平台的发展让越来越多的消费者意识到国货品牌的优势,使得各大国货品牌都受到了高度关注,销售额迅速增长,已知某国货品牌2023年8月至12月在D网络平台的月销售额y(单位:百万元)与月份x具有线性相关关系,并根据这5个月的月销售额求得经验回归方程为=4.2x+3,则该国货品牌2023年8月至12月在D网络平台的总销售额约为 百万元.
6.(2022江西抚州期中)某学校为了解学生中男生的体重y(单位:kg)与身高x(单位:cm)是否存在线性相关关系,收集了7位男生的数据,得到如下表格:
序号 1 2 3 4 5 6 7
身高x/cm 166 173 174 178 180 183 185
体重y/kg 57 62 59 71 67 75 78
根据表中数据计算得到y关于x的经验回归方程为x-136.55.
(1)= ;
(2)已知决定系数R2=1-,当R2≥0.9时,模型的拟合效果非常好,当0.8
7.(2024广东深圳中学期中)已知某水果种植基地苹果的种植面积x(单位:公顷)与其产量y(单位:吨)呈线性相关关系,小王准备承包一块苹果种植地,为了解市场行情,在该基地调查了5家果农,统计得到了苹果种植面积与其产量的数据如表所示:
种植面积x/公顷 1 2 3 4 5
产量y/吨 20 38 64 78 100
(1)求y关于x的经验回归方程;
(2)若苹果的销量等于产量,且所种苹果的总利润P(单位:千元)满足P=+180x,苹果种植面积x∈{1,2,3,…,14,15},请根据(1)的结果预测要使得单位面积的苹果利润最大,小王应该种植多少公顷的苹果.
附:经验回归直线.
题组二 非线性回归分析
8.(2024河南南阳期中联考)已知变量x和y之间的关系可以用模型y=menx来拟合.设z=ln y,若根据样本数据计算可得=0.9,且z关于x的经验回归方程为,则m≈ .(参考数据:ln 0.3≈-1.2,ln 0.25≈-1.4)
9.(2024广东广州华南师大附中期中)某地政府为提高当地农民收入,指导农民种植药材,取得了较好的效果.下表是某农户近5年种植药材的年收入的统计数据:
年份 2019 2020 2021 2022 2023
年份代码x 1 2 3 4 5
年收入y/千元 59 61 64 68 73
(1)根据表中数据,现决定使用函数模型y=bx2+a拟合y与x之间的关系,请求出此模型的经验回归方程;(结果保留一位小数)
(2)统计学中常通过计算残差的平方和来判断模型的拟合效果,若残差的平方和小于0.5,则认为拟合效果符合要求.请判断(1)中的经验回归方程的拟合效果是否符合要求,并说明理由.
能力提升练
题组一 线性回归分析
1.(2024浙江宁波期中)下图是某组数据的散点图,由最小二乘法计算得到经验回归直线l1的方程为,相关系数为r1,决定系数为,若经过残差分析后去掉点P,剩余的点重新计算得到经验回归直线l2的方程为,相关系数为r2,决定系数为,则下列结论一定正确的是( )
A.r1>r2 B.
C. D.r1>0,r2<0
2.(2024河南南阳六校联考)某学习小组对一组数据(xi,yi)(i=1,2,3,…,7)进行回归分析,甲同学首先求出经验回归方程为=3x+2,样本点的中心为(2,m).乙同学对甲的计算过程进行检查,发现甲将数据(4,6)误输成(6,4),将这两个数据修正后得到经验回归方程为=kx+4,则实数k=( )
A.
3.(2024江西新余期末)某地政府为解决空巢老人日常护理和社会照料的困境,大力培育发展养老护理服务市场.从2017年开始新建社区养老机构,下表为该地区近7年新建社区养老机构的数量对照表.
年份 2017 2018 2019 2020 2021 2022 2023
年份代码x 1 2 3 4 5 6 7
新建社区 养老机构y y1 y2 y3 y4 y5 y6 y7
(1)若该地区参与社区养老的老人的年龄X近似服从正态分布N(70,16),其中年龄X∈(78,82]的有54人,试估计该地参与社区养老的老人有多少;(结果按四舍五入取整数)
(2)已知变量x与y之间的样本相关系数r=,请求出y关于x的经验回归方程:,并据此估计2024年该地区新建社区养老机构的数量.(结果按四舍五入取整数)
参考公式与数据:①;
②若随机变量X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 6,P(μ-2σ≤X≤μ+2σ)≈0.954 4,P(μ-3σ≤X≤μ+3σ)≈0.997 4;
③=1 597.
4.大气污染物PM2.5(大气中直径小于或等于2.5 μm的颗粒物)的浓度超过一定的限度会影响人的身体健康.为了研究PM2.5的浓度受车流量影响的程度,某校数学建模社团选择了学校附近5个监测点,统计每个监测点24 h内的车流量x(单位:千辆),同时在低空相同的高度测定每个监测点该时间段内的PM2.5的平均浓度y(单位:μg/m3),得到的数据如表所示:
监测点编号 1 2 3 4 5
车流量x/千辆 1.3 1.2 1.6 1.0 0.9
PM2.5的平均 浓度y/(μg/m3) 66 72 113 34 35
(1)建立y关于x的一元线性回归模型,并用样本相关系数加以说明(一般地,样本相关系数的绝对值在0.75以上(含0.75),则认为线性相关性较强,否则认为线性相关性较弱);
(2)我国规定空气中PM2.5浓度的安全标准为24 h平均浓度75 μg/m3,该地为使24 h内PM2.5的平均浓度不超过68.6 μg/m3,拟对车流量作适当控制,请你根据本题数据估计车流量控制的最大值.
参考公式:在经验回归方程中,;样本相关系数r=.
题组二 非线性回归分析
5.红铃虫是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型:①y=ebx+a,②y=cx2+d分别进行拟合,由此得到相应的经验回归方程并进行残差分析,进一步得到图2所示的残差图.
根据收集到的数据,计算得到下表:
(xi -)2 (ti- )2 (zi- ) (yi- )
25 2.9 646 168 422 688 50.4 70 308
表中z=ln y;ti.
(1)根据残差图比较模型①和②的拟合效果,模型 比较合适;
(2)根据(1)中所选择的模型,求出y关于x的经验回归方程为 .
附:对于一组数据(ω1,v1),(ω2,v2),…,(ωn,vn),其经验回归直线ω的斜率和截距的最小二乘估计分别为.
6.(2024重庆第一中学校开学考试)当前,人工智能技术以前所未有的速度迅猛发展,并逐步影响我们的方方面面,人工智能被认为是推动未来社会发展和解决人类面临的全球性问题的重要手段.某公司在这个领域逐年加大投入,以下是近年来该公司对产品研发年投入额x(单位:百万元)与年销售量y(单位:千件)的数据统计表:
x 1 2 3 4 5 6
y 0.5 1 1.5 3 6 12
z=ln y -0.7 0 0.4 1.1 1.8 2.5
(1)公司拟分别用①y=bx+a和②y=enx+m两个函数模型作为年销售量y关于年投入额x的回归分析模型,请根据已知数据,确定模型①和②的经验回归方程;(a,b,m,n计算过程保留到小数点后两位,最后结果保留到小数点后一位)
(2)根据下表数据,用决定系数R2(只需比较出大小)比较哪个函数模型的拟合效果更好,并根据拟合精度更高的模型预测年投入额为7百万元时,产品的年销售量是多少.
函数模型 y=bx+a y=enx+m
残差平方和 )2 18.29 0.65
参考公式及数据:经验回归方程中,=0.85,e2.8≈16.4,e3≈20.1.
答案与分层梯度式解析
8.2 一元线性回归模型及其应用
基础过关练
1.D 2.D 3.A 4.ABC
1.D 两变量的相关性越强,样本相关系数r就越接近1或-1,故A不正确;经验回归直线是基于样本数据使残差平方和最小的拟合直线,故B不正确;经验回归直线一定过样本点的中心(),故C不正确;当相关系数r>0时,两个变量正相关,当r<0时,两个变量负相关,故D正确.
故选D.
2.D ∵×30=5,
∵经验回归直线=2x+3一定过点(),
∴+3=2×5+3=13,因此yi=6×13=78.故选D.
3.A 由题表中的数据得×(0.5+0.6+1+1.4+1.5)=1,
则样本点的中心为(3,1),代入,得=1-0.28×3=0.16,
∴经验回归方程为=0.28x+0.16,
令x=5,得=0.28×5+0.16=1.56.
∴当x=5时的残差为1.5-1.56=-0.06.故选A.
方法总结 经验回归直线不一定过样本点,但一定过样本点的中心(),常利用这一结论列方程求经验回归方程中的参数.
4.ABC 由题表中数据可得,
∵y与x的经验回归方程为=6.5×2+9,解得m=20,因此A正确;
∵=22,∴该经验回归直线过点(2,22),因此B正确;
∵=6.5>0,∴产品的销售额与广告费用正相关,因此C正确;
当x=10时,=6.5×10+9=74,故广告费用为10万元时,销售额约为74万元,因此D错误.故选ABC.
5.答案 225
解析 将x=8,9,10,11,12分别代入经验回归方程=4.2x+3,得=4.2×9+3=40.8,
=4.2×12+3=53.4,
因为36.6+40.8+45+49.2+53.4=225,
所以该国货品牌这五个月在D网络平台的总销售额约为225百万元.
6.答案 (1)1.15 (2)良好
解析 (1)由题表中数据可得,
=177,
=67,
所以67=×177-136.55,解得=1.15.
(2)由(1)知=67,故)2=(-10)2+(-5)2+(-8)2+42+02+82+112=390,
则有R2=1-≈0.87,因为0.8<0.87<0.9,
所以该经验回归方程对应模型的拟合效果良好.
7.解析 (1)由题可得=60,
则)=(-2)×(-40)+(-1)×(-22)+0×4+1×18+2×40=200,
)2=(-2)2+(-1)2+02+12+22=10,
所以=60-20×3=0,
故y关于x的经验回归方程为=20x.
(2)因为P=+180x,x∈{1,2,3,…,14,15},
所以单位面积的苹果利润(单位:千元)为+181,x∈{1,2,3,…,14,15}.
因此当,即x=10时,取得最大值,
故要使得单位面积的苹果利润最大,小王应该种植10公顷的苹果.
8.答案 0.3
解析 由题意知0.9=0.6×3.5+,解得=-1.2,所以=0.6x-1.2,
由z=ln y,得ln =0.6x-1.2,所以=e0.6x-1.2=e-1.2·e0.6x,则m=e-1.2≈0.3.
9.解析 (1)由题表数据可得×(59+61+64+68+73)=65,
设t=x2,则y关于t的经验回归方程为,易得)2=374.
则≈0.6,≈65-0.6×11=58.4,
所以y关于x的经验回归方程为=0.6x2+58.4.
(2)将x=1,2,3,4,5分别代入=0.6x2+58.4可得预测值分别为59,60.8,63.8,68,73.4,
则残差的平方和为(59-59)2+(61-60.8)2+(64-63.8)2+(68-68)2+(73-73.4)2=0.24,
因为0.24<0.5,所以经验回归方程=0.6x2+58.4拟合效果符合要求.
能力提升练
1.C 由题图可知共8个点,且离群点P的横坐标较小而纵坐标相对过大,去掉离群点后经验回归直线的斜率变大,因此C正确;去掉离群点后相关性更强,拟合效果也更好,且还是正相关,故0
则
改为正确数据后,有,
将点=kx+4,得k=.故选D.
3.解析 (1)由题意可知,μ=70,σ=4,则78=μ+2σ,82=μ+3σ,
所以P(78
所以估计该地参与社区养老的老人人数为≈2 512.
(2)由题表中的数据可得=4,
所以)2=(1-4)2+(2-4)2+(3-4)2+(4-4)2+(5-4)2+(6-4)2+(7-4)2=28,
由已知条件可得r=,
所以,
又因为=1 597-7=225,所以=196,
显然≥0,所以=14,则,
所以y关于x的经验回归方程为,
当x=8时,=21.5≈22,
故2024年该地区新建社区养老机构的数量约为22个.
4.解析 (1)由题表得=1.2,
=64,
xiyi=1.3×66+1.2×72+1.6×113+1.0×34+0.9×35=418.5,
=1.32+1.22+1.62+1.02+0.92=7.5,
=662+722+1132+342+352=24 690,
所以=115,
=64-115×1.2=-74,
所以=115x-74.
样本相关系数r=
=≈0.97.
因为|0.97|>0.75,
所以y与x的线性相关性较强.
(2)令115x-74≤68.6,得x≤1.24,
故车流量控制的最大值约为1.24千辆.
5.答案 (1)① (2)=e0.3x-4.6
解析 (1)应该选择模型①.因为模型①残差点比较均匀地落在水平的带状区域中,且带状区域的宽度比模型②的窄,所以模型①的拟合精度更高,故选模型①比较合适.
(2)由z=ln y,得z=a+bx,
所以=0.3,
所以=2.9-0.3×25≈-4.6,
即z关于x的经验回归方程为=0.3x-4.6.
于是有ln =0.3x-4.6,
所以y关于x的经验回归方程为=e0.3x-4.6.
6.解析 (1)由题表数据得=4,
所以≈2.11,≈4-2.11×3.5≈-3.39,
因此=2.1x-3.4,
由y=enx+m,两边取以e为底的对数得ln y=nx+m,由z=ln y得z=nx+m,
≈0.63,≈0.85-0.63×3.5≈-1.36,
所以=0.6x-1.4,所以=e0.6x-1.4.
(2))2=(0.5-4)2+(1-4)2+(1.5-4)2+(3-4)2+(6-4)2+(12-4)2=96.5,
对于;
对于,
因为,所以②的拟合效果更好,当x=7时,=e0.6×7-1.4=e2.8≈16.4,故年投入额为7百万元时,年销售量约为16.4千件.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
