1.1 直角三角形的性质和判定(Ⅰ)-第2课时 含30°角的直角三角形的性质 同步分层练(含答案) 2024-2025学年数学湘教版八年级下册
文档属性
| 名称 | 1.1 直角三角形的性质和判定(Ⅰ)-第2课时 含30°角的直角三角形的性质 同步分层练(含答案) 2024-2025学年数学湘教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 86.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 00:00:00 | ||
图片预览

文档简介
第2课时 含30°角的直角三角形的性质
A组·基础达标 逐点击破
知识点 含30°角的直角三角形的性质
1.已知在直角三角形中 角所对的直角边为,则斜边的长为( )
A. B. C. D.
2.[2023贵州]5月26日,“2023中国国际大数据产业博览会”在贵阳市开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为 ,腰长为,则底边上的高是( )
A. B. C. D.
3.在中,,最短边,最长边的长是( )
A. B. C. D.
4.如图,某山坡的坡面,坡角 ,则该山坡的高为____.
第4题图
5.如图,在中, ,于点,,则________.
第5题图
6.[教材改编题]如图,小敏在河岸的点测得看对岸点的视线与其所在河岸的直线成 角,然后沿该直线行走到达点,此时测得看对岸点的视线与前进方向成 角,问河宽是多少米?
B组·能力提升 强化突破
7.[2024南充]如图,在中, , ,,平分交于点,点为边上一点,则线段长度的最小值为( )
A. B. C.2 D.3
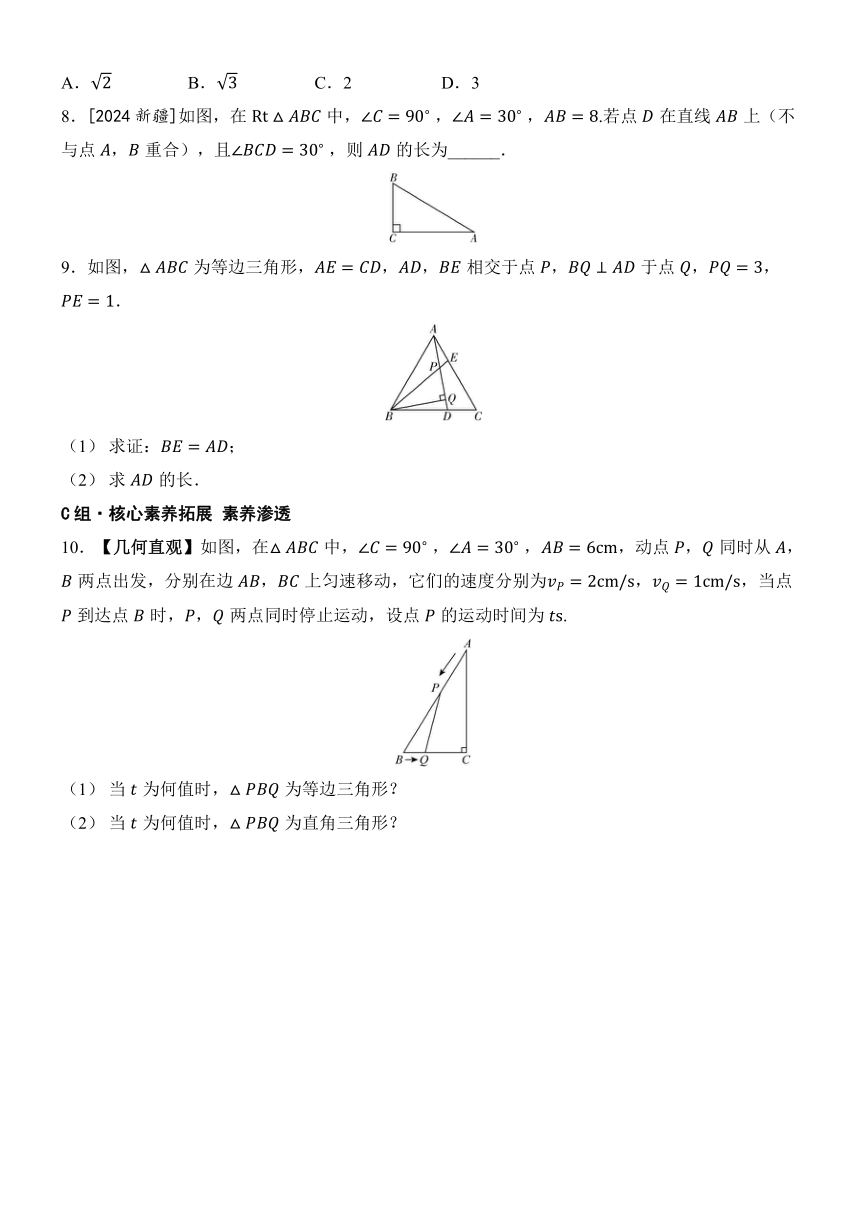
8.[2024新疆]如图,在中, , ,.若点在直线上(不与点,重合),且 ,则的长为______.
9.如图,为等边三角形,,,相交于点,于点,,.
(1) 求证:;
(2) 求的长.
C组·核心素养拓展 素养渗透
10.【几何直观】如图,在中, , ,,动点,同时从,两点出发,分别在边,上匀速移动,它们的速度分别为,,当点到达点时,,两点同时停止运动,设点的运动时间为.
(1) 当为何值时,为等边三角形?
(2) 当为何值时,为直角三角形?
第2课时 含30°角的直角三角形的性质
课堂导学
例题引路
【思路分析】过点作于点,过点作于点,则可得和的长,依据端点与之间的距离为,即可得到可以通过闸机的物体的最大宽度.
例 【规范解答】如答图,过点 作 于点,过点 作 于点.
例题答图
则在 中, ,同理可得.
又 点 与点 之间的距离为,
通过闸机的物体的最大宽度为.
答:当双翼收起时,可以通过闸机的物体的最大宽度为.
A组·基础达标 逐点击破
知识点 含30°角的直角三角形的性质
1.D 2.B 3.D
4.100
5.
6.解:如答图,过点作于点.
,
,
,,
在中,.
答:河宽是.
第6题答图
B组·能力提升 强化突破
7.C
[解析]在中, , .平分, ,,,即,平分,且, 点D到边的距离等于线段的长,即线段长度的最小值为2.
8.6或12
9.(1) 证明:是等边三角形,
, .
又,
.
.
(2) 解:由(1)知,
.
.
又,
.
.
.
.
C组·核心素养拓展 素养渗透
10.(1) 解:在中, , ,
.
,
,,.
当时,为等边三角形,
即,.
当时,为等边三角形.
(2) 若为直角三角形,
①当 时,,
即,
;
②当 时,,
即,
.
即当或时,为直角三角形.
A组·基础达标 逐点击破
知识点 含30°角的直角三角形的性质
1.已知在直角三角形中 角所对的直角边为,则斜边的长为( )
A. B. C. D.
2.[2023贵州]5月26日,“2023中国国际大数据产业博览会”在贵阳市开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为 ,腰长为,则底边上的高是( )
A. B. C. D.
3.在中,,最短边,最长边的长是( )
A. B. C. D.
4.如图,某山坡的坡面,坡角 ,则该山坡的高为____.
第4题图
5.如图,在中, ,于点,,则________.
第5题图
6.[教材改编题]如图,小敏在河岸的点测得看对岸点的视线与其所在河岸的直线成 角,然后沿该直线行走到达点,此时测得看对岸点的视线与前进方向成 角,问河宽是多少米?
B组·能力提升 强化突破
7.[2024南充]如图,在中, , ,,平分交于点,点为边上一点,则线段长度的最小值为( )
A. B. C.2 D.3
8.[2024新疆]如图,在中, , ,.若点在直线上(不与点,重合),且 ,则的长为______.
9.如图,为等边三角形,,,相交于点,于点,,.
(1) 求证:;
(2) 求的长.
C组·核心素养拓展 素养渗透
10.【几何直观】如图,在中, , ,,动点,同时从,两点出发,分别在边,上匀速移动,它们的速度分别为,,当点到达点时,,两点同时停止运动,设点的运动时间为.
(1) 当为何值时,为等边三角形?
(2) 当为何值时,为直角三角形?
第2课时 含30°角的直角三角形的性质
课堂导学
例题引路
【思路分析】过点作于点,过点作于点,则可得和的长,依据端点与之间的距离为,即可得到可以通过闸机的物体的最大宽度.
例 【规范解答】如答图,过点 作 于点,过点 作 于点.
例题答图
则在 中, ,同理可得.
又 点 与点 之间的距离为,
通过闸机的物体的最大宽度为.
答:当双翼收起时,可以通过闸机的物体的最大宽度为.
A组·基础达标 逐点击破
知识点 含30°角的直角三角形的性质
1.D 2.B 3.D
4.100
5.
6.解:如答图,过点作于点.
,
,
,,
在中,.
答:河宽是.
第6题答图
B组·能力提升 强化突破
7.C
[解析]在中, , .平分, ,,,即,平分,且, 点D到边的距离等于线段的长,即线段长度的最小值为2.
8.6或12
9.(1) 证明:是等边三角形,
, .
又,
.
.
(2) 解:由(1)知,
.
.
又,
.
.
.
.
C组·核心素养拓展 素养渗透
10.(1) 解:在中, , ,
.
,
,,.
当时,为等边三角形,
即,.
当时,为等边三角形.
(2) 若为直角三角形,
①当 时,,
即,
;
②当 时,,
即,
.
即当或时,为直角三角形.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
