1.2 直角三角形的性质和判定(Ⅱ)-第1课时 勾股定理 同步分层练(含答案) 2024-2025学年数学湘教版八年级下册
文档属性
| 名称 | 1.2 直角三角形的性质和判定(Ⅱ)-第1课时 勾股定理 同步分层练(含答案) 2024-2025学年数学湘教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 105.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 00:00:00 | ||
图片预览


文档简介
1.2 直角三角形的性质和判定(Ⅱ)
第1课时 勾股定理
A组·基础达标 逐点击破
知识点 勾股定理
1.已知,,分别为的三边,,,的对应角分别为,,.下列说法错误的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.总有
2.如图,在中, ,,,则( )
A.5 B.6 C.7 D.8
3.如图,在的三边上,向外作三个正方形,其中两个的面积为,,则另一个的面积为( )
A.50 B.30 C.25 D.100
4.如图,在中,,是的平分线.已知,,则的长为( )
A.5 B.6 C.8 D.10
5.如图①中,__;如图②中,__.
6.在中, ,且,,的对应边分别为,,.
(1) 已知,,求的长;
(2) 已知,,求的长;
(3) 已知,且,求,的长.
7.【数学文化】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示的“弦图”.在中, ,,,.求证:.
易错点 考虑不周全导致错误
8.若直角三角形的三边长分别为2,4,,则的值为( )
A.3 B. C. D.或
B组·能力提升 强化突破
9.如图,以的三边为直径分别向外作半圆,若斜边,则图中阴影部分的面积为( )
A. B. C. D.
10.[2024眉山]【数学文化】如图,图①是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图①中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图②,则图②中大正方形的面积为( )
A.24 B.36 C.40 D.44
11.[2024安徽]如图,在中,,点在的延长线上,且,则的长是( )
A. B. C. D.
12.[2024甘孜州]如图,在中, ,,,折叠,使点与点重合,折痕与交于点,与交于点,则的长为____.
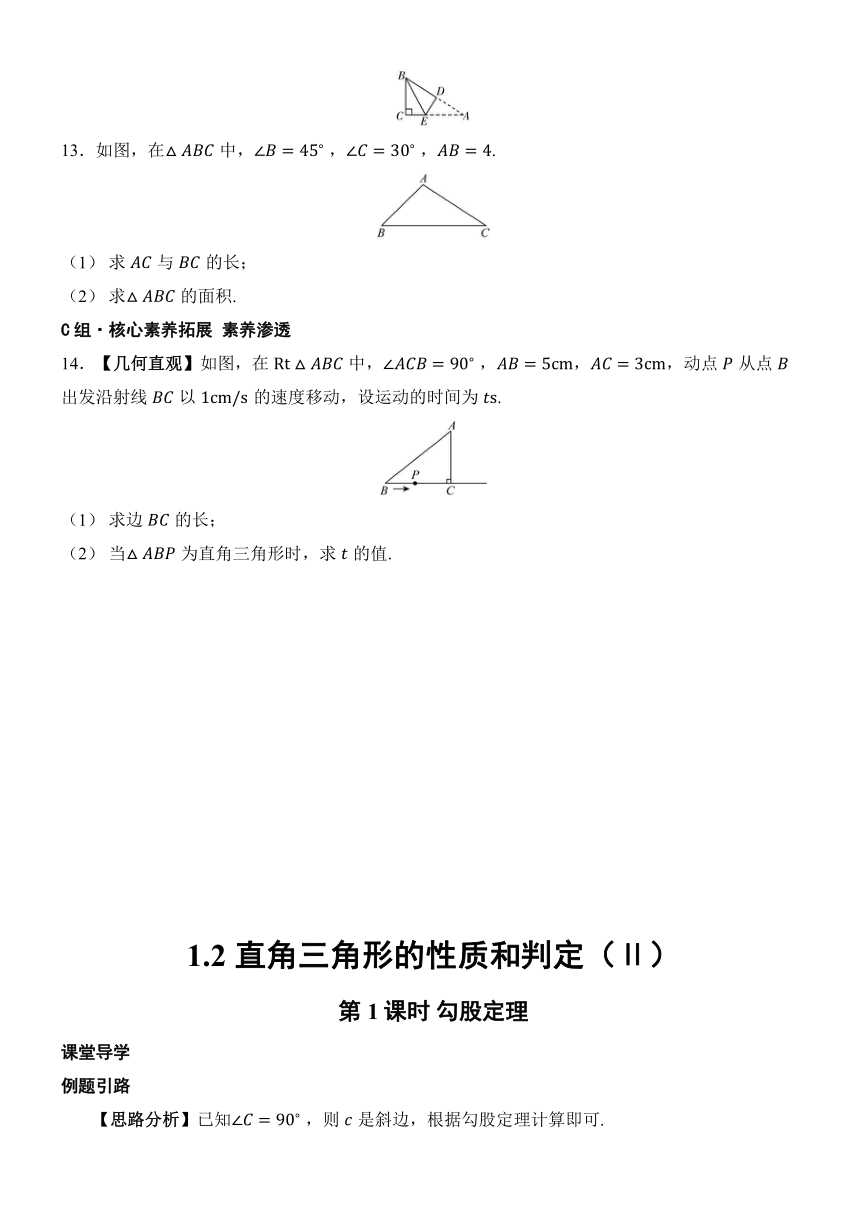
13.如图,在中, , ,.
(1) 求与的长;
(2) 求的面积.
C组·核心素养拓展 素养渗透
14.【几何直观】如图,在中, ,,,动点从点出发沿射线以的速度移动,设运动的时间为.
(1) 求边的长;
(2) 当为直角三角形时,求的值.
1.2 直角三角形的性质和判定(Ⅱ)
第1课时 勾股定理
课堂导学
例题引路
【思路分析】已知 ,则是斜边,根据勾股定理计算即可.
例1 (1) 【规范解答】 ,,,
.
(2) 【规范解答】 ,,,
.
(3) 【规范解答】,
设,则.
,,
,
即,
解得(负值已舍去).
,.
【思路分析】在直角三角形中,以两直角边为边的正方形的面积和等于以斜边为边的正方形的面积.
【规范解答】由勾股定理,得,
同理,,
.
例2 38
A组·基础达标 逐点击破
知识点 勾股定理
1.D 2.A 3.C 4.A
5.12; 30
6.(1) 解: ,,,
.
(2) ,,,
.
(3) , 设,则.
,,
,即.
解得(负值已舍去).
,.
7.证明: 大正方形的面积为,直角三角形的面积为,小正方形的面积为,
.
.
易错点 考虑不周全导致错误
8.D
B组·能力提升 强化突破
9.C
10.D
[解析]如答图,设直角三角形的两直角边为,,斜边为.
第10题答图
图①中大正方形的面积是24,
,
小正方形的面积是4,
,
,
图②中大正方形的面积为.
故选D.
11.B
[解析]如答图,过点C作于点.
第11题答图
, ,,
,
,
,
,
.
故选B.
12.3
[解析]由折叠的性质,得,设,则,由勾股定理,得,,解得的长为3.
13.(1) 解:如答图,过点作于点.
,
.
.
,,
.
.
,
.
.
.
.
第13题答图
(2) .
C组·核心素养拓展 素养渗透
14.(1) 解:在中,由勾股定理,得
.
(2) 由题意,得,分以下两种情况:
①当 时,如答图①所示.
第14题答图①
则点与点重合,
,
;
②当 时,如答图②所示.
第14题答图②
则, .
在中,由勾股定理,得
,
在中,由勾股定理,得
,
,
即,解得.
综上所述,当为直角三角形时,的值为4或.
第1课时 勾股定理
A组·基础达标 逐点击破
知识点 勾股定理
1.已知,,分别为的三边,,,的对应角分别为,,.下列说法错误的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.总有
2.如图,在中, ,,,则( )
A.5 B.6 C.7 D.8
3.如图,在的三边上,向外作三个正方形,其中两个的面积为,,则另一个的面积为( )
A.50 B.30 C.25 D.100
4.如图,在中,,是的平分线.已知,,则的长为( )
A.5 B.6 C.8 D.10
5.如图①中,__;如图②中,__.
6.在中, ,且,,的对应边分别为,,.
(1) 已知,,求的长;
(2) 已知,,求的长;
(3) 已知,且,求,的长.
7.【数学文化】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示的“弦图”.在中, ,,,.求证:.
易错点 考虑不周全导致错误
8.若直角三角形的三边长分别为2,4,,则的值为( )
A.3 B. C. D.或
B组·能力提升 强化突破
9.如图,以的三边为直径分别向外作半圆,若斜边,则图中阴影部分的面积为( )
A. B. C. D.
10.[2024眉山]【数学文化】如图,图①是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图①中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图②,则图②中大正方形的面积为( )
A.24 B.36 C.40 D.44
11.[2024安徽]如图,在中,,点在的延长线上,且,则的长是( )
A. B. C. D.
12.[2024甘孜州]如图,在中, ,,,折叠,使点与点重合,折痕与交于点,与交于点,则的长为____.
13.如图,在中, , ,.
(1) 求与的长;
(2) 求的面积.
C组·核心素养拓展 素养渗透
14.【几何直观】如图,在中, ,,,动点从点出发沿射线以的速度移动,设运动的时间为.
(1) 求边的长;
(2) 当为直角三角形时,求的值.
1.2 直角三角形的性质和判定(Ⅱ)
第1课时 勾股定理
课堂导学
例题引路
【思路分析】已知 ,则是斜边,根据勾股定理计算即可.
例1 (1) 【规范解答】 ,,,
.
(2) 【规范解答】 ,,,
.
(3) 【规范解答】,
设,则.
,,
,
即,
解得(负值已舍去).
,.
【思路分析】在直角三角形中,以两直角边为边的正方形的面积和等于以斜边为边的正方形的面积.
【规范解答】由勾股定理,得,
同理,,
.
例2 38
A组·基础达标 逐点击破
知识点 勾股定理
1.D 2.A 3.C 4.A
5.12; 30
6.(1) 解: ,,,
.
(2) ,,,
.
(3) , 设,则.
,,
,即.
解得(负值已舍去).
,.
7.证明: 大正方形的面积为,直角三角形的面积为,小正方形的面积为,
.
.
易错点 考虑不周全导致错误
8.D
B组·能力提升 强化突破
9.C
10.D
[解析]如答图,设直角三角形的两直角边为,,斜边为.
第10题答图
图①中大正方形的面积是24,
,
小正方形的面积是4,
,
,
图②中大正方形的面积为.
故选D.
11.B
[解析]如答图,过点C作于点.
第11题答图
, ,,
,
,
,
,
.
故选B.
12.3
[解析]由折叠的性质,得,设,则,由勾股定理,得,,解得的长为3.
13.(1) 解:如答图,过点作于点.
,
.
.
,,
.
.
,
.
.
.
.
第13题答图
(2) .
C组·核心素养拓展 素养渗透
14.(1) 解:在中,由勾股定理,得
.
(2) 由题意,得,分以下两种情况:
①当 时,如答图①所示.
第14题答图①
则点与点重合,
,
;
②当 时,如答图②所示.
第14题答图②
则, .
在中,由勾股定理,得
,
在中,由勾股定理,得
,
,
即,解得.
综上所述,当为直角三角形时,的值为4或.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
