1.3 直角三角形全等的判定 同步分层练(含答案)2024-2025学年数学湘教版八年级下册
文档属性
| 名称 | 1.3 直角三角形全等的判定 同步分层练(含答案)2024-2025学年数学湘教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 86.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 00:00:00 | ||
图片预览



文档简介
1.3 直角三角形全等的判定
A组·基础达标 逐点击破
知识点1 斜边、直角边定理
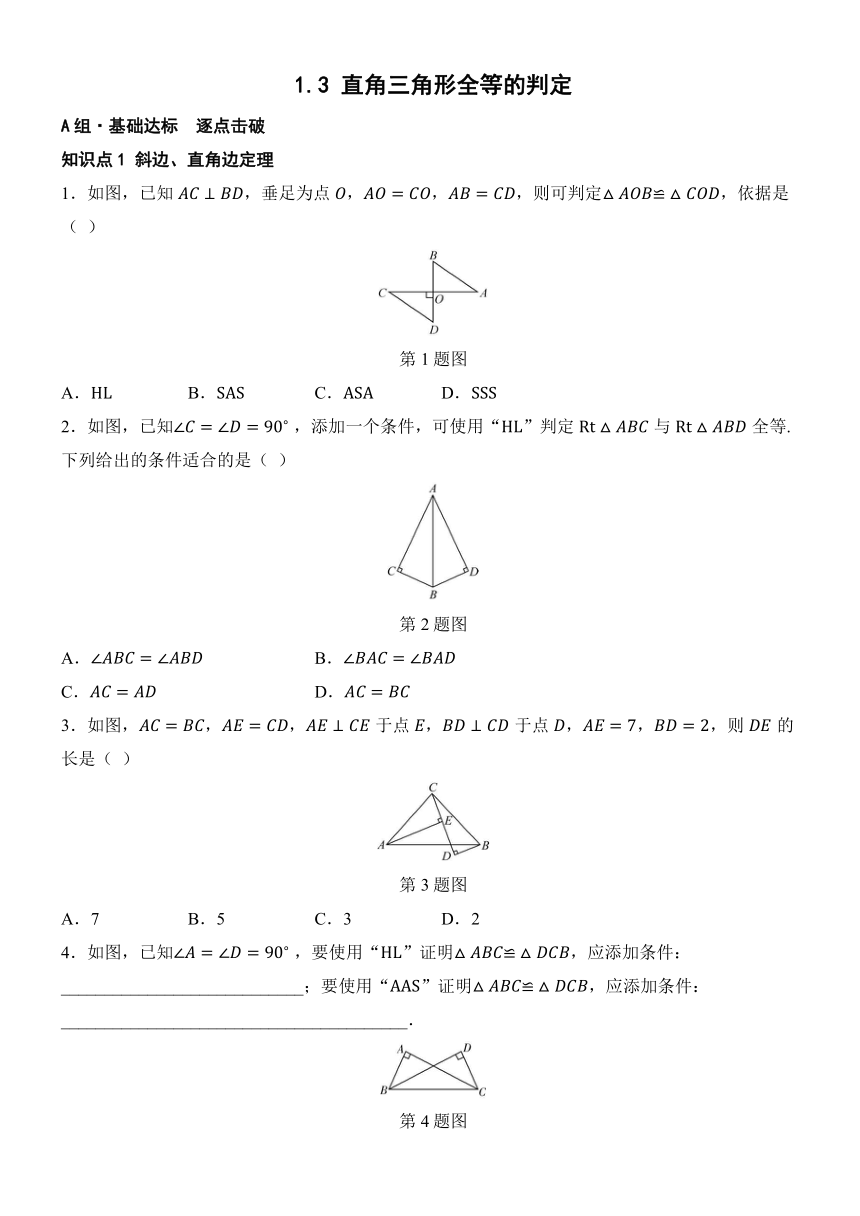
1.如图,已知,垂足为点,,,则可判定,依据是( )
第1题图
A. B. C. D.
2.如图,已知 ,添加一个条件,可使用“”判定与全等.下列给出的条件适合的是( )
第2题图
A. B.
C. D.
3.如图,,,于点,于点,,,则的长是( )
第3题图
A.7 B.5 C.3 D.2
4.如图,已知 ,要使用“”证明,应添加条件:____________________________;要使用“”证明,应添加条件:________________________________________.
第4题图
5.如图,,,点,,,分别在直线与上,点在上,,,,则____.
第5题图
6.如图,已知 ,,在线段上,与交于点,且,.求证:.
知识点2 作直角三角形
7.阅读下面材料:
已知线段,.
求作:,使得斜边,一条直角边.
作法:
(1)作射线,,且.
(2)以点为圆心,线段的长为半径作弧,交射线于点.
(3)以点为圆心,线段的长为半径作弧,交射线于点.
(4)连接.则就是所求作的三角形.
上述尺规作图过程中,用到的判定三角形全等的依据是( )
A. B. C. D.
B组·能力提升 强化突破
8.[2024镇江模拟]如图,在中,,于点,于点,于点,,则的长为( )
A. B.
C. D.以上答案都不对
9.如图,,是的高,且.
(1) 求证:是等腰三角形;
(2) 若 ,,求的高.
C组·核心素养拓展 素养渗透
10.【几何直观,推理能力】如图,在中,,是过点的直线,于点,于点,且.
(1) 如图①,若点,在直线的同侧,求证:.
(2) 如图②,若点,在直线的两侧,问与仍垂直吗?若是,请证明;若不是,请说明理由.
1.3 直角三角形全等的判定
课堂导学
知识梳理
一条直角边
例题引路
【思路分析】连接,由直角三角形全等的“”判定定理证得,根据全等三角形的性质得到,再由直角三角形全等的“”判定定理即可证得.
例 【规范解答】连接,如答图.
在和中,
,
.
于点,于点,
.
在和中,
.
例题答图
【点悟】“”是判定两个直角三角形全等的特有方法,对于一般三角形不适用,所以使用“”判定两个三角形全等的条件是这两个三角形是直角三角形.在书写证明时,两个三角形符号前要加上“”.
A组·基础达标 逐点击破
知识点1 斜边、直角边定理
1.A 2.C 3.B
4.(或); (或)
5.7
6.证明:,
,即.
,
与都为直角三角形,
在和中,
.
知识点2 作直角三角形
7.A
B组·能力提升 强化突破
8.A
9.(1) 证明:,是的高,
.
在和中,
,
,
,
是等腰三角形.
(2) 解: , ,
,
,
.
C组·核心素养拓展 素养渗透
10.(1) 证明:,,
.
在和中,
,
.
又 ,
,
,即.
(2) 解:.证明如下:
,,
.
在和中,
,
.
又 ,
,
即 ,
.
A组·基础达标 逐点击破
知识点1 斜边、直角边定理
1.如图,已知,垂足为点,,,则可判定,依据是( )
第1题图
A. B. C. D.
2.如图,已知 ,添加一个条件,可使用“”判定与全等.下列给出的条件适合的是( )
第2题图
A. B.
C. D.
3.如图,,,于点,于点,,,则的长是( )
第3题图
A.7 B.5 C.3 D.2
4.如图,已知 ,要使用“”证明,应添加条件:____________________________;要使用“”证明,应添加条件:________________________________________.
第4题图
5.如图,,,点,,,分别在直线与上,点在上,,,,则____.
第5题图
6.如图,已知 ,,在线段上,与交于点,且,.求证:.
知识点2 作直角三角形
7.阅读下面材料:
已知线段,.
求作:,使得斜边,一条直角边.
作法:
(1)作射线,,且.
(2)以点为圆心,线段的长为半径作弧,交射线于点.
(3)以点为圆心,线段的长为半径作弧,交射线于点.
(4)连接.则就是所求作的三角形.
上述尺规作图过程中,用到的判定三角形全等的依据是( )
A. B. C. D.
B组·能力提升 强化突破
8.[2024镇江模拟]如图,在中,,于点,于点,于点,,则的长为( )
A. B.
C. D.以上答案都不对
9.如图,,是的高,且.
(1) 求证:是等腰三角形;
(2) 若 ,,求的高.
C组·核心素养拓展 素养渗透
10.【几何直观,推理能力】如图,在中,,是过点的直线,于点,于点,且.
(1) 如图①,若点,在直线的同侧,求证:.
(2) 如图②,若点,在直线的两侧,问与仍垂直吗?若是,请证明;若不是,请说明理由.
1.3 直角三角形全等的判定
课堂导学
知识梳理
一条直角边
例题引路
【思路分析】连接,由直角三角形全等的“”判定定理证得,根据全等三角形的性质得到,再由直角三角形全等的“”判定定理即可证得.
例 【规范解答】连接,如答图.
在和中,
,
.
于点,于点,
.
在和中,
.
例题答图
【点悟】“”是判定两个直角三角形全等的特有方法,对于一般三角形不适用,所以使用“”判定两个三角形全等的条件是这两个三角形是直角三角形.在书写证明时,两个三角形符号前要加上“”.
A组·基础达标 逐点击破
知识点1 斜边、直角边定理
1.A 2.C 3.B
4.(或); (或)
5.7
6.证明:,
,即.
,
与都为直角三角形,
在和中,
.
知识点2 作直角三角形
7.A
B组·能力提升 强化突破
8.A
9.(1) 证明:,是的高,
.
在和中,
,
,
,
是等腰三角形.
(2) 解: , ,
,
,
.
C组·核心素养拓展 素养渗透
10.(1) 证明:,,
.
在和中,
,
.
又 ,
,
,即.
(2) 解:.证明如下:
,,
.
在和中,
,
.
又 ,
,
即 ,
.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
