鲁教版八年级上册期中综合测试卷(含答案)
文档属性
| 名称 | 鲁教版八年级上册期中综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-19 20:01:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期中综合测试卷
时间: 90分钟 满分: 120分
一、选择题(本题共12个小题,每小题3分,共36分,下列每小题均给出标号为A,B,C,D的四个备选答案,其中只有一个是正确的)
1.代数式 中,分式有 ( )
A.1个 B.2个 C.3个 D.4个
2.下列各式从左到右的变形属于因式分解的是 ( )
3.已知一组数据1,3,0,x,2,2,3有唯一的众数3,则这组数据的平均数、中位数分别是 ( )
A.2,3 B.3,2 C.2,2 D.3,3
4.下列因式分解中,错误的是 ( )
5.下列式子一定成立的是 ( )
6.计算 的值是 ( )
A.-2 B.2 C.2
7.若,则 的值是 ( )
A.-3 B.3
8.若分式 的值为0,则x的值为 ( )
A.0 B.1 C.-1 D.±1
9.如图是某市某周日最高气温的折线统计图,关于这7天的日最高气温的说法错误的是 ( )
A.最大值与最小值的差是10 B.中位数是24
C.众数是28 D.平均数是25.4
10.《四元玉鉴》是我国古代数学重要著作之一,为元代数学家朱世杰所著,该著作记载了“买椽多少”问题(椽一装于屋顶以支持屋顶材料的木杆).
设这批椽有x株,则符合题意的方程是 ( )
11.若关于x的分式方程 有增根,则m的值是 ( )
A.1 B.-1 C.2 D.-2
12.已知a,b,c是△ABC的三边,且 ,则△ABC一定是 ( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
二、填空题(本题共8个小题,每小题3分,共24分)
13.分式 的最简公分母是___________.
14.多项式 的公因式是___________.
15.计算 的结果是__________.
16.观察下列等式:1 ×则第 n个等式可表示为____________.
17.为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机取部分麦苗,获得苗高(单位;cm)的平均数与方差为: 则麦苗又高又整齐的是____________.
18.已知 且a+b≠0,则 的值为___________.
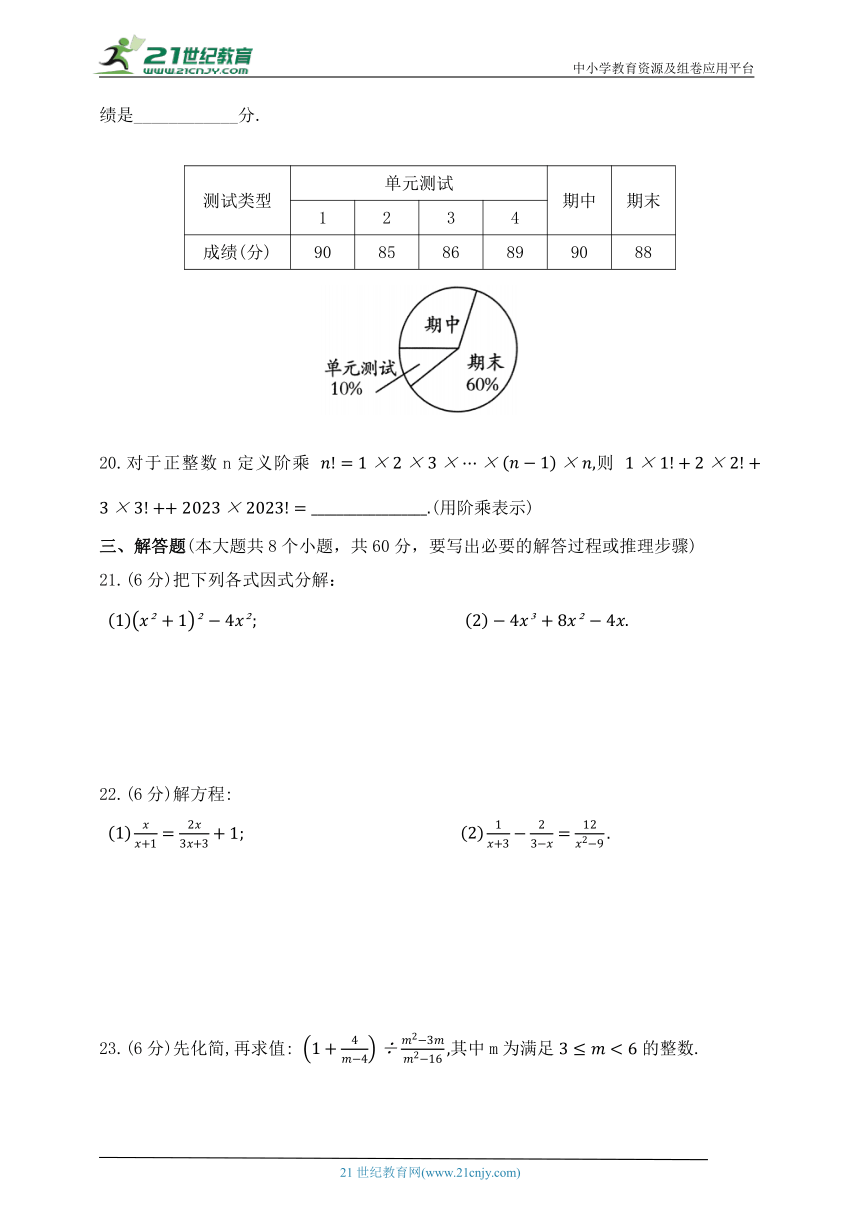
19.某同学在八年级下学期参加了四次单元测试,以及期中和期末考试,所有考试的数学成绩如表所示.若根据如图所示的权重计算本学期的总评成绩,则小明在下学期的总评成绩是____________分.
测试类型 单元测试 期中 期末
1 2 3 4
成绩(分) 90 85 86 89 90 88
20.对于正整数n定义阶乘 则 (用阶乘表示)
三、解答题(本大题共8个小题,共60分,要写出必要的解答过程或推理步骤)
21.(6分)把下列各式因式分解:
22.(6分)解方程:
23.(6分)先化简,再求值: 其中m为满足的整数.
24.(8分)已知关于x的分式方程 的解是非负数,求m的取值范围.
25.(8分)通过学习,我们知道常用的因式分解的方法有提公因式法和公式法,与此同时,某些多项式只用上述一种方法无法因式分解.下面是甲、乙两位同学对多项式进行因式分解的过程.
两位同学因式分解的方法叫做分组分解法,请你仔细观察并对以下多项式进行因式分解.
(1)试用上述方法因式分解:
(2)利用因式分解说明:因式 能被9 整除.
26.(8分)某超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11 000元资金购进该品种苹果,但这次的进货价比试销时每千克多了0.5元,购进苹果数量是试销时的2倍.
(1)试销时该品种苹果的进货价是每千克多少元
(2)如果超市将该品种苹果按每千克7元的定价出售,当大部分苹果售出后,余下的400千克按定价的七折(“七折”即定价的70%)售完,那么超市在这两次苹果销售中共盈利多少元
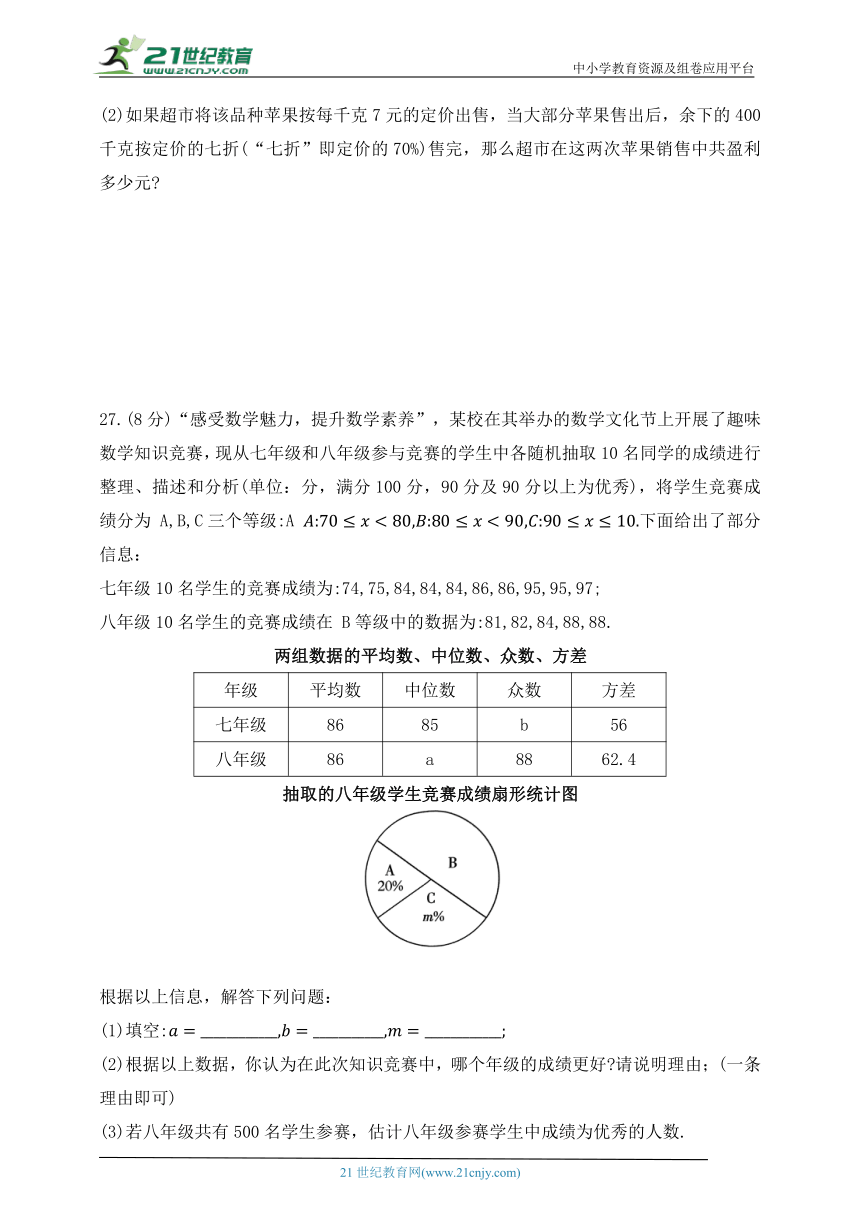
27.(8分)“感受数学魅力,提升数学素养”,某校在其举办的数学文化节上开展了趣味数学知识竞赛,现从七年级和八年级参与竞赛的学生中各随机抽取10名同学的成绩进行整理、描述和分析(单位:分,满分100分,90分及90分以上为优秀),将学生竞赛成绩分为 A,B,C三个等级:A 下面给出了部分信息:
七年级10名学生的竞赛成绩为:74,75,84,84,84,86,86,95,95,97;
八年级10名学生的竞赛成绩在 B等级中的数据为:81,82,84,88,88.
两组数据的平均数、中位数、众数、方差
年级 平均数 中位数 众数 方差
七年级 86 85 b 56
八年级 86 a 88 62.4
抽取的八年级学生竞赛成绩扇形统计图
根据以上信息,解答下列问题:
(1)填空:
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好 请说明理由;(一条理由即可)
(3)若八年级共有500名学生参赛,估计八年级参赛学生中成绩为优秀的人数.
28.(10分)用数学的眼光观察:
同学们,在学习中,你会发现 与 有着紧密的联系,请你认真观察等式:
用数学的思维思考并解决下列问题:
(1)填空:
(2)计算:①若 求 的值;
②若 求 的值;
③已知 求 的值.
参考答案
1. B 2. B 3. C 4. C 5. B 6. D 7. A 8. C 9. B 10. D
11. C 12. C
14. 17.丁
18. 1 19. 88.55
20.2024!-1 解析:∵1×1!=1×1=1,2×2!=2×1×2=4,
3×3!=3×1×2×3=18,4×4!=4×1×2×3×4=96,
∴1×1!=1=2!-1,
1×1!+2×2!=1+4=5=3!-1,
1×1!+2×2!+3×3!=1+4+18=23=4!-1,
1×1!+2×2!+3×3!+4×4!=1+4+18+96=119=5!-1,
…,
1×1!+2×2!+3×3!+…+n×n!=(n+1)!-1,
∴1×1!+2×2!+3×3!+…+2023×2023!=2024!-1.
21.解:
22.解:(1)方程两边同时乘3x+3,得3x=2x+3x+3,解得
检验:当 时,
∴原方程的解为
(2)方程两边同时乘(x+3)(x-3),得x-3+2(x+3)=12,解得x=3,
检验:当x=3时,(x+3)(x-3)=0,
∴x=3是原方程的增根,∴原方程无解.
23.解:
∵m为满足3≤m<6的整数,∴m=3或4或5,
且m-3≠0,且m≠0,∴m≠±4,且m≠3,且m≠0,
∴当m=5时,原式
24.解:方程两边同乘以x-1,得m-5=x-1, 解得x=m-4.
∵方程的解是非负数,∴m-4≥0,解得m≥4;
又∵x-1≠0,即x≠1,∴m≠5,
综上所述,m的取值范围为m≥4且m≠5.
25.解:
∴因式 能被9整除.
26.解:(1)设试销时这种苹果的进货价是每千克x元.
依题意,得 解得x=5,
经检验,x=5是原方程的解且符合题意.
答:试销时该品种苹果的进货价是每千克5元;
(2)试销时进苹果的数量为 1000(千克).
第二次进苹果的数量为2×1 000=2000(千克).
盈利为(3000-400)×7+400×7×0.7-5000-11000=4160(元).
答:商场在两次苹果销售中共盈利4 160元.
27.解:(1)七年级的成绩出现次数最多的是84,故众数
八年级A等级成绩的人数为 (人),
八年级 10名学生的竞赛成绩在 B等级中由小到大排序81,82,84,88,88,故排在第5、第
6的两个数分别为84,88,故中位数
故答案为:86,84,30;
(2)七年级的成绩更好,因为两个年级的平均数相同,而七年级的成绩的方差小于八年级,所以七年级的成绩更好;
(3)估计八年级参赛学生中成绩为优秀的人数为 (人).
28.解:
=4;
故答案为:4;
4=16,
②将 两边都除以a,得
③当 时,此时a>0,则 a=1,得
∵a>0,
当 时,此时,则 ,得
,故舍去.
综上所述, 的值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中综合测试卷
时间: 90分钟 满分: 120分
一、选择题(本题共12个小题,每小题3分,共36分,下列每小题均给出标号为A,B,C,D的四个备选答案,其中只有一个是正确的)
1.代数式 中,分式有 ( )
A.1个 B.2个 C.3个 D.4个
2.下列各式从左到右的变形属于因式分解的是 ( )
3.已知一组数据1,3,0,x,2,2,3有唯一的众数3,则这组数据的平均数、中位数分别是 ( )
A.2,3 B.3,2 C.2,2 D.3,3
4.下列因式分解中,错误的是 ( )
5.下列式子一定成立的是 ( )
6.计算 的值是 ( )
A.-2 B.2 C.2
7.若,则 的值是 ( )
A.-3 B.3
8.若分式 的值为0,则x的值为 ( )
A.0 B.1 C.-1 D.±1
9.如图是某市某周日最高气温的折线统计图,关于这7天的日最高气温的说法错误的是 ( )
A.最大值与最小值的差是10 B.中位数是24
C.众数是28 D.平均数是25.4
10.《四元玉鉴》是我国古代数学重要著作之一,为元代数学家朱世杰所著,该著作记载了“买椽多少”问题(椽一装于屋顶以支持屋顶材料的木杆).
设这批椽有x株,则符合题意的方程是 ( )
11.若关于x的分式方程 有增根,则m的值是 ( )
A.1 B.-1 C.2 D.-2
12.已知a,b,c是△ABC的三边,且 ,则△ABC一定是 ( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
二、填空题(本题共8个小题,每小题3分,共24分)
13.分式 的最简公分母是___________.
14.多项式 的公因式是___________.
15.计算 的结果是__________.
16.观察下列等式:1 ×则第 n个等式可表示为____________.
17.为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机取部分麦苗,获得苗高(单位;cm)的平均数与方差为: 则麦苗又高又整齐的是____________.
18.已知 且a+b≠0,则 的值为___________.
19.某同学在八年级下学期参加了四次单元测试,以及期中和期末考试,所有考试的数学成绩如表所示.若根据如图所示的权重计算本学期的总评成绩,则小明在下学期的总评成绩是____________分.
测试类型 单元测试 期中 期末
1 2 3 4
成绩(分) 90 85 86 89 90 88
20.对于正整数n定义阶乘 则 (用阶乘表示)
三、解答题(本大题共8个小题,共60分,要写出必要的解答过程或推理步骤)
21.(6分)把下列各式因式分解:
22.(6分)解方程:
23.(6分)先化简,再求值: 其中m为满足的整数.
24.(8分)已知关于x的分式方程 的解是非负数,求m的取值范围.
25.(8分)通过学习,我们知道常用的因式分解的方法有提公因式法和公式法,与此同时,某些多项式只用上述一种方法无法因式分解.下面是甲、乙两位同学对多项式进行因式分解的过程.
两位同学因式分解的方法叫做分组分解法,请你仔细观察并对以下多项式进行因式分解.
(1)试用上述方法因式分解:
(2)利用因式分解说明:因式 能被9 整除.
26.(8分)某超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11 000元资金购进该品种苹果,但这次的进货价比试销时每千克多了0.5元,购进苹果数量是试销时的2倍.
(1)试销时该品种苹果的进货价是每千克多少元
(2)如果超市将该品种苹果按每千克7元的定价出售,当大部分苹果售出后,余下的400千克按定价的七折(“七折”即定价的70%)售完,那么超市在这两次苹果销售中共盈利多少元
27.(8分)“感受数学魅力,提升数学素养”,某校在其举办的数学文化节上开展了趣味数学知识竞赛,现从七年级和八年级参与竞赛的学生中各随机抽取10名同学的成绩进行整理、描述和分析(单位:分,满分100分,90分及90分以上为优秀),将学生竞赛成绩分为 A,B,C三个等级:A 下面给出了部分信息:
七年级10名学生的竞赛成绩为:74,75,84,84,84,86,86,95,95,97;
八年级10名学生的竞赛成绩在 B等级中的数据为:81,82,84,88,88.
两组数据的平均数、中位数、众数、方差
年级 平均数 中位数 众数 方差
七年级 86 85 b 56
八年级 86 a 88 62.4
抽取的八年级学生竞赛成绩扇形统计图
根据以上信息,解答下列问题:
(1)填空:
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好 请说明理由;(一条理由即可)
(3)若八年级共有500名学生参赛,估计八年级参赛学生中成绩为优秀的人数.
28.(10分)用数学的眼光观察:
同学们,在学习中,你会发现 与 有着紧密的联系,请你认真观察等式:
用数学的思维思考并解决下列问题:
(1)填空:
(2)计算:①若 求 的值;
②若 求 的值;
③已知 求 的值.
参考答案
1. B 2. B 3. C 4. C 5. B 6. D 7. A 8. C 9. B 10. D
11. C 12. C
14. 17.丁
18. 1 19. 88.55
20.2024!-1 解析:∵1×1!=1×1=1,2×2!=2×1×2=4,
3×3!=3×1×2×3=18,4×4!=4×1×2×3×4=96,
∴1×1!=1=2!-1,
1×1!+2×2!=1+4=5=3!-1,
1×1!+2×2!+3×3!=1+4+18=23=4!-1,
1×1!+2×2!+3×3!+4×4!=1+4+18+96=119=5!-1,
…,
1×1!+2×2!+3×3!+…+n×n!=(n+1)!-1,
∴1×1!+2×2!+3×3!+…+2023×2023!=2024!-1.
21.解:
22.解:(1)方程两边同时乘3x+3,得3x=2x+3x+3,解得
检验:当 时,
∴原方程的解为
(2)方程两边同时乘(x+3)(x-3),得x-3+2(x+3)=12,解得x=3,
检验:当x=3时,(x+3)(x-3)=0,
∴x=3是原方程的增根,∴原方程无解.
23.解:
∵m为满足3≤m<6的整数,∴m=3或4或5,
且m-3≠0,且m≠0,∴m≠±4,且m≠3,且m≠0,
∴当m=5时,原式
24.解:方程两边同乘以x-1,得m-5=x-1, 解得x=m-4.
∵方程的解是非负数,∴m-4≥0,解得m≥4;
又∵x-1≠0,即x≠1,∴m≠5,
综上所述,m的取值范围为m≥4且m≠5.
25.解:
∴因式 能被9整除.
26.解:(1)设试销时这种苹果的进货价是每千克x元.
依题意,得 解得x=5,
经检验,x=5是原方程的解且符合题意.
答:试销时该品种苹果的进货价是每千克5元;
(2)试销时进苹果的数量为 1000(千克).
第二次进苹果的数量为2×1 000=2000(千克).
盈利为(3000-400)×7+400×7×0.7-5000-11000=4160(元).
答:商场在两次苹果销售中共盈利4 160元.
27.解:(1)七年级的成绩出现次数最多的是84,故众数
八年级A等级成绩的人数为 (人),
八年级 10名学生的竞赛成绩在 B等级中由小到大排序81,82,84,88,88,故排在第5、第
6的两个数分别为84,88,故中位数
故答案为:86,84,30;
(2)七年级的成绩更好,因为两个年级的平均数相同,而七年级的成绩的方差小于八年级,所以七年级的成绩更好;
(3)估计八年级参赛学生中成绩为优秀的人数为 (人).
28.解:
=4;
故答案为:4;
4=16,
②将 两边都除以a,得
③当 时,此时a>0,则 a=1,得
∵a>0,
当 时,此时,则 ,得
,故舍去.
综上所述, 的值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
