期末计算题专题练习--2024-2025学年浙教版八年级科学上册(含答案)
文档属性
| 名称 | 期末计算题专题练习--2024-2025学年浙教版八年级科学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2024-12-19 00:00:00 | ||
图片预览



文档简介
八年级上册科学期末计算题专题练习
一、浮力专题计算
1.如图所示,一边长为20cm的正方体木块漂浮在水面上,木块浸入水中的深度为12cm。(ρ水=1.0×103kg/m3,g取10N/kg)试求:
(1)木块受到的浮力F浮;
(2)木块下表面受到的水的压强p;
(3)木块的密度。
2.一边长为10cm,密度为0.6g/cm3的正方体木块,用细线置于容器的水中,如图所示,求:
(1)木块质量多大?
(2)将木块放置在水平桌面上,木块对桌面的压强多大?
(3)此时细线的拉力多大?
3.如图甲所示,将一长方体物块通过细线悬挂于弹簧测力计的挂钩上,手持弹簧测力计缓慢下降,让长方体物块从盛满水的溢水杯上方缓慢下降至水下一定深度。长方体物块下降过程中,弹簧测力计的示数F随下降高度h的变化关系如图乙所示,g取10N/kg。求:
(1)长方体物块受到的最大浮力为 N;
(2)长方体物块的密度;
(3)将长方体物块继续缓慢下降至容器的水平底部,当弹簧测力计示数为零时,长方体物块对容器底部的压强。
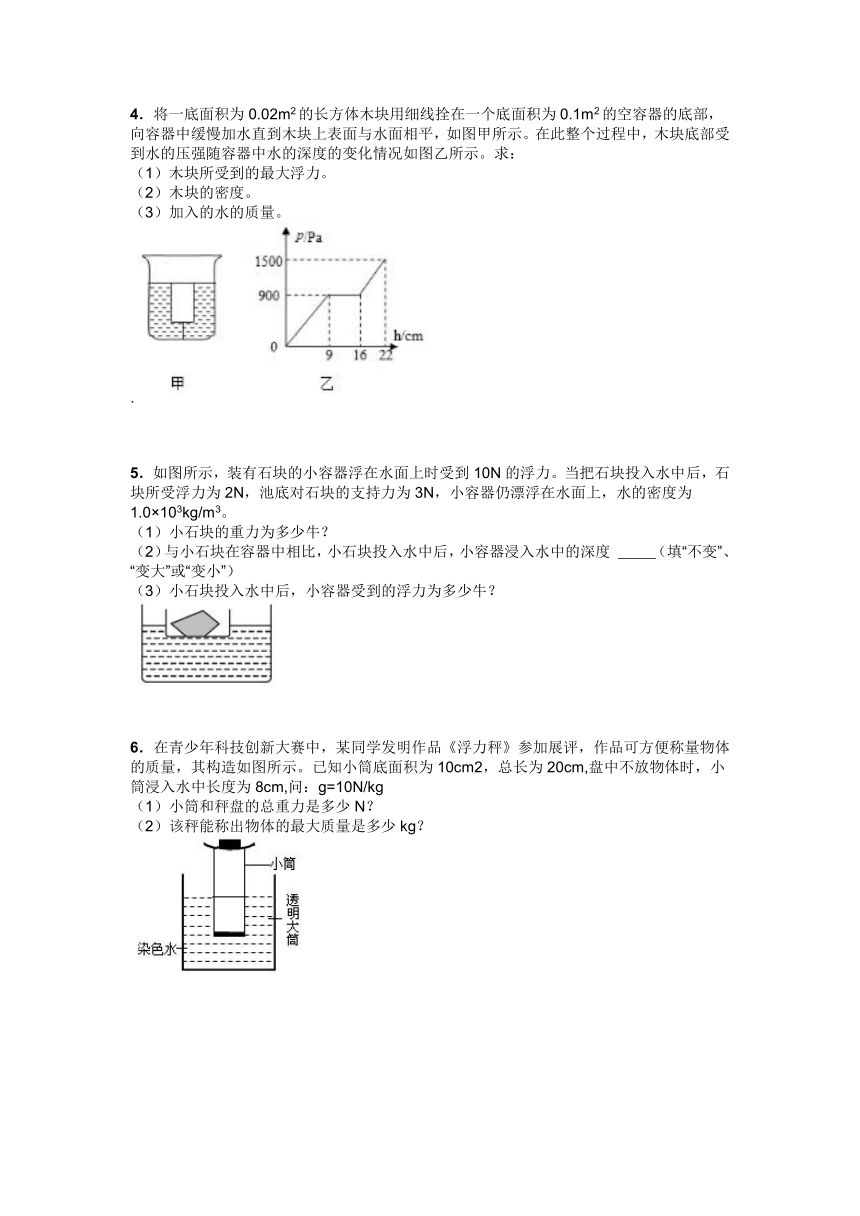
4.将一底面积为0.02m2的长方体木块用细线拴在一个底面积为0.1m2的空容器的底部,向容器中缓慢加水直到木块上表面与水面相平,如图甲所示。在此整个过程中,木块底部受到水的压强随容器中水的深度的变化情况如图乙所示。求:
(1)木块所受到的最大浮力。
(2)木块的密度。
(3)加入的水的质量。
·
5.如图所示,装有石块的小容器浮在水面上时受到10N的浮力。当把石块投入水中后,石块所受浮力为2N,池底对石块的支持力为3N,小容器仍漂浮在水面上,水的密度为1.0×103kg/m3。
(1)小石块的重力为多少牛?
(2)与小石块在容器中相比,小石块投入水中后,小容器浸入水中的深度 (填“不变”、“变大”或“变小”)
(3)小石块投入水中后,小容器受到的浮力为多少牛?
6.在青少年科技创新大赛中,某同学发明作品《浮力秤》参加展评,作品可方便称量物体的质量,其构造如图所示。已知小筒底面积为10cm2,总长为20cm,盘中不放物体时,小筒浸入水中长度为8cm,问:g=10N/kg
(1)小筒和秤盘的总重力是多少N?
(2)该秤能称出物体的最大质量是多少kg?
7.攻击核潜艇093是我国主力型号,总体积达到1.5×103m3,下潜深度可以超过400米。艇内两侧有水舱,潜水艇截面如图所示。(海水密度为1.03×103kg/m3,g取10N/kg)
(1)水舱未充海水时,潜水艇总重为8.24×106N,漂浮在海面上,潜水艇受到的浮力是多少?
(2)为使潜水艇完全潜入海水,至少应向水舱中充入海水的重力是多少?
(3)如图丙小之用一个潜水艇模型模拟该过程,在一个盛满水的水槽中放入潜水艇模型,水溢出且模型漂浮在水面,则放入模型后水槽对桌面的压强 (填“变大”“不变”或“变小”)
二、溶液专题计算
8.医生给病人输液时,常用葡萄糖注射液。如图为葡萄糖注射液的部分标签图,根据图回答下列问题:
(1)从该溶液中取出10mL,则取出溶液中溶质的质量分数为 。
(2)某病人一天共输入该葡萄糖注射液1500mL,此病人这一天共补充葡萄糖 g。
(3)某铅酸蓄电池使用的酸溶液是溶质质量分数为20%的稀硫酸。若用100g质量分数为98%的浓硫酸配制该稀硫酸时,需要蒸馏水多少克(精确到0.1)(写出计算过程)。
9.溶解是生活中常见的现象,不同物质在水中的溶解能力不同。表是硝酸钾、氯化钠在不同湿度下的溶解度(单位:g/100g水)
· 温度(℃) 0 20 40 60 80 100
硝酸钾 13.3 31.6 63.9 110 169 246
氯化钠 35.7 36.0 36.6 37.3 38.4 39.8
(1)40℃时,硝酸钾饱和溶液的溶质质量分数为多少?(写出计算过程)
(2)请写出一种将硝酸钾的不饱和溶液转化为饱和溶液的方法 。
(3)20℃时,将20g氯化钠放入50g水中,所得溶液的质量是 。
10.t℃时某氯化钠溶液310克,在温度不变的情况下,第一次蒸发20克水,析出晶体4克;第二次又蒸发20克水,析出晶体6克。则t℃时100克水最多可以溶解多少克氯化钠晶体?原310克氯化钠溶液中溶质质量多少?
11.读硫酸溶液和氨水的密度与其溶质的质量分数对照表(20℃),回答问题。
· 溶液中溶质的质量分数(%) 4 12 16 24 28
硫酸溶液的密度(克/厘米3) 1.02 1.08 1.11 1.17 1.20
氨水的密度(克/厘米3) 0.98 0.95 0.94 0.91 0.90
(1)20℃时,随着溶液中溶质的质量分数逐渐减小,硫酸溶液的密度逐渐 ,氨水的密度逐渐 。
(2)将50克16%的氨水稀释成4%的溶液,需要加水多少克?
(3)配制100克12%的硫酸溶液,需要24%的硫酸溶液多少毫升?(答案保留1位小数)
12.某兴趣小组用硝酸钾进行实验,如图甲是硝酸钾的溶解度与温度关系。
(1)10℃时,100g水中最多可溶解硝酸钾的质量为 g。
(2)20℃时,将15g硝酸钾加入50g水中,所得溶液的溶质质量分数为 (结果保留一位小数)。
(3)请写出一种能实现如图乙所示结果的操作方法,并写出计算过程(结果保留一位小数)。
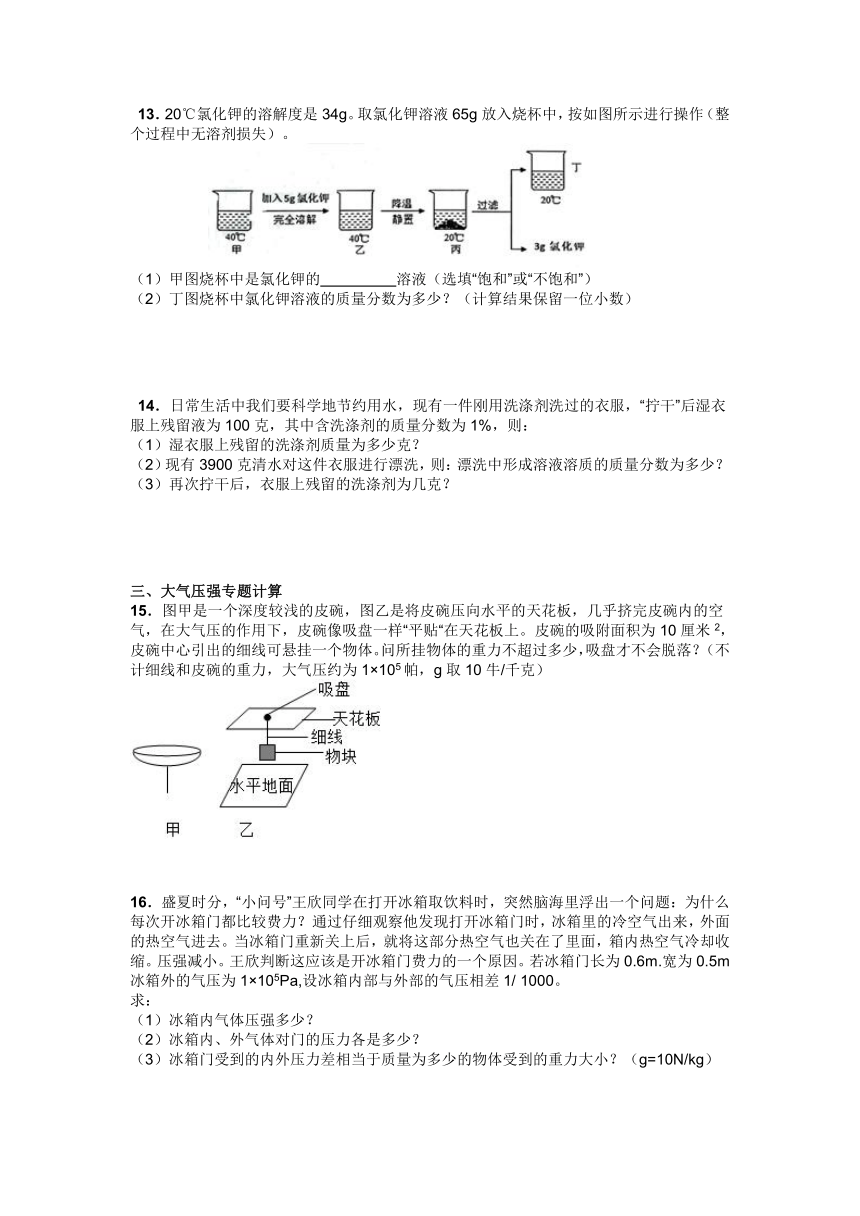
13.20℃氯化钾的溶解度是34g。取氯化钾溶液65g放入烧杯中,按如图所示进行操作(整个过程中无溶剂损失)。
(1)甲图烧杯中是氯化钾的 溶液(选填“饱和”或“不饱和”)
(2)丁图烧杯中氯化钾溶液的质量分数为多少?(计算结果保留一位小数)
14.日常生活中我们要科学地节约用水,现有一件刚用洗涤剂洗过的衣服,“拧干”后湿衣服上残留液为100克,其中含洗涤剂的质量分数为1%,则:
(1)湿衣服上残留的洗涤剂质量为多少克?
(2)现有3900克清水对这件衣服进行漂洗,则:漂洗中形成溶液溶质的质量分数为多少?
(3)再次拧干后,衣服上残留的洗涤剂为几克?
三、大气压强专题计算
15.图甲是一个深度较浅的皮碗,图乙是将皮碗压向水平的天花板,几乎挤完皮碗内的空气,在大气压的作用下,皮碗像吸盘一样“平贴“在天花板上。皮碗的吸附面积为10厘米2,皮碗中心引出的细线可悬挂一个物体。问所挂物体的重力不超过多少,吸盘才不会脱落?(不计细线和皮碗的重力,大气压约为1×105帕,g取10牛/千克)
16.盛夏时分,“小问号”王欣同学在打开冰箱取饮料时,突然脑海里浮出一个问题:为什么每次开冰箱门都比较费力?通过仔细观察他发现打开冰箱门时,冰箱里的冷空气出来,外面的热空气进去。当冰箱门重新关上后,就将这部分热空气也关在了里面,箱内热空气冷却收缩。压强减小。王欣判断这应该是开冰箱门费力的一个原因。若冰箱门长为0.6m.宽为0.5m冰箱外的气压为1×105Pa,设冰箱内部与外部的气压相差1/ 1000。
求:
(1)冰箱内气体压强多少?
(2)冰箱内、外气体对门的压力各是多少?
(3)冰箱门受到的内外压力差相当于质量为多少的物体受到的重力大小?(g=10N/kg)
17.一款新型家用电梯(如图所示)正走进我们的生活,它外形是长圆筒,升降过程不使用线缆,而是靠气压驱动。已知外界大气压为1×105Pa,电梯室质量为120kg,电梯室与圆筒壁之间的摩擦力为300N,底部和顶部面积均为1m2。
(1)请用所学知识分析说明该新型家用电梯是如何实现向上运动的。
(2)低压区的气压降到9.8×104Pa时,作用在电梯室上表面的大气压力是 牛。
(3)抽气机最多能把低压区的气压降到9.5×104Pa,,则该电梯匀速下降时能装载的物体的最大质量是 。
18.如图,高压锅是家庭厨房中常见的炊具,利用它可将食物加热到100℃以上,它省时高效,深受消费者欢迎。
(1)小明测得家中高压锅出气孔的横截面积S为12mm2,压在出气孔上的安全阀的质量为72g,g取10N/kg,计算安全阀自重对出气孔处气体所产生的压强。
(2)当高压锅内气压增大到某一值时,锅内气体就能自动顶开安全阀放气。在外界为标准大气压的环境下,该高压锅内的气体能达到的最大压强是多少?对照图所示水的沸点与气压的关系图线,利用这种高压锅烧煮食物时可以到达的最高温度大约是多少?(大气压值取1.0×105Pa)
19.如图是一种气压保温瓶的结构示意图。用手按下按压器时,气室上方的小孔被堵塞,使瓶内气体压强增大,水在气压作用下从出水管口流出.如果按压器面积是10cm2,瓶内水面低于水管口10cm,按压器的自重不计,大气压强p0=1.01×105Pa。求:
(1)要使水从出水管口流出,瓶内水面上方的气体压强至少要多大?
(2)如果在按下按压器的过程中,气室内弹簧产生的平均弹力是1.2N,为使水从出水管口流出,人手施加在按压器上的压力至少要多大?
20.美国东面是大西洋,西面是太平洋,每年都会受到龙卷风的袭击,造成人员伤亡和财产损失。假设某一次龙卷风发生时,室外的气压急剧下降到9×104Pa,当时门窗紧闭,室内气压约为1×105Pa。
(1)为什么龙卷风发生时,室外的气压会急剧下降?
(2)若水平屋顶的面积为100m2,试计算屋顶内外受到的大气压力差的大小。
四、电路专题计算
21.如图所示,电阻R1的阻值为20Ω,当开关闭合时,电流表A的示数为0.6A,电流表A1的示数为0.2A。求:
(1)电源电压;
(2)通过电阻R2的电流;
(3)电阻R2的阻值。
22.如图所示电路中定值电阻R1=20Ω,R2为滑动变阻器,电源电压保持不变。当滑片在a端时,电流表示数为0.6A,滑片在b端时电压表示数为8V。求:
(1)电源电压;
(2)滑动变阻器R2的最大阻值。
23.如图所示电路中,已知R1=40Ω,R2=60Ω,当开关S闭合后,通过电流表的示数为0.3安,求:
(1)电阻R1两端电压;
(2)通过电路的总电流。
24.如图甲是定值电阻R0和灯泡L的I-U图象,现将它们接入图乙所示的电路,其中电源电压不变,滑动变阻器R最大阻值为7.5欧。当只闭合开关S、S1,滑片P位于R最右端时,电流表示数0.2安,问:
(1)通过灯L的电流为0.2安时,灯L的电阻为多大?
(2)电源电压为几伏?
(3)通过控制开关和调节变阻器,电流表能达到的最大示数为多少?
25.如图1所示电路,电源电压保持不变,当闭合开关S,调节滑动变阻器阻值从最大变化到最小。两个电阻的“U-I”关系图象如图2所示。求:
(1)电源电压和定值电阻R1的阻值。
(2)滑动变阻器R2的阻值变化范围。
·
26.某兴趣小组利用热敏电阻设计了一只测量范围为0~100℃的水温表,其中热敏电阻随温度的变化情况如图乙所示,水温表的原理如图甲所示。已知电压表量程为0~3伏,定值电阻R0的阻值为100欧,电源电压保持不变。当水温达到100℃时,要求电压表的示数达到最大值。
(1)分析图乙可知,当温度为0℃时,热敏电阻的阻值为 欧;
(2)当电压表示数达到最大值时,通过热敏电阻的电流是多少?
(3)通过计算说明,改画的水温表刻度盘上的0℃应该与电压表刻度盘的什么位置对应?
27.参加全国青少年创新大赛,小强运用电学知识设计了一个电子身高测量仪,如图所示。其中定值电阻R0=5Ω,电源电压恒为4.5V,R是固定的、竖直放置的硬电阻棒,总电阻为15Ω,其接入电路的电阻与接入电路的棒长成正比,金属杆cd和MP(右端P是滑片)与电路接触良好,电阻不计。
(1)R0在电路中的作用是 。
(2)当被测身高增加时,电压表的示数 ,电流表的示数 。(选填“变大”、“变小”、“不变”)。
(3)身高为168cm小强用该测量仪测量时,电流表示数为0.5A,此时电阻棒R接入电路的电阻为多少Ω?
(4)若电压表量程为0~3V,电流表量程为0~0.6A,为保证电路各元件安全工作,则随着身高而变化大小的R能接入电路的最大阻值是多少Ω?
28.某科技小组设计了一个监测水位的装置。其原理如图甲,电路中电源电压保持不变,R0为定值电阻,AP与R组成滑动变阻器(最大阻值60Ω),浮子可带动金属滑杆AP在竖直方向上下移动。当水位上升时,浮子和金属滑杆AP一起向上滑动,当电压表的示数达到某一数值时提醒监测员水位达到警戒值。R接入电路的阻值随水位的变化关系如图乙,电路工作时电压表与电流表示数变化关系如图丙。求:
·
· (1)当滑片P置于最下端时,电流表示数为0.1A,则电压表示数为多少?
· (2)电源电压和R0的阻值。
· (3)当电压表的示数为3V时,报警装置发出警报,则警戒水位为多少米?
参考答案
1.解:(1)由阿基米德原理可得,木块受到的浮力:
F浮=ρ水gV排=ρ水gS木h浸=1.0×103kg/m3×10N/kg×0.2m×0.2m×0.12m=48N;
(2)木块下表面所受的压强:
p=ρ水gh=1.0×103kg/m3×10N/kg×0.12m=1200Pa;
(3)因为木块处于漂浮状态,
所以F浮=G木,
由阿基米德原理和重力公式可得:ρ水gV排=ρ木V木g,
即:ρ水gL2h浸=ρ木gL3,
则木块的密度:ρ木=0.6×103kg/m3。
答:(1)木块受到的浮力为48N。
(2)木块下表面受到的水的压强为1200Pa;
(3)木块的密度为0.6×103kg/m3。
2.解:(1)木块的体积V木=10cm×10cm×10cm=103cm3=10-3m3,
木块的质量:m木=ρ木V木=0.6×103kg/m3×10-3m3=0.6kg;
(2)==600Pa;
(3)因为木块浸没水中,所以木块排开水的体积:V排=V木=10-3 m3,
木块受到的浮力:F浮=ρ水gV排=103kg/m3×10N/kg×10-3m3=10N;
因为木块受到的重力G加上绳子的拉力F拉等于木块受到的浮力F浮,
所以细线对木块的拉力:F拉=F浮-G=10N-6N=4N。
答:(1)木块的质量为0.6kg;
(2)将木块放置在水平桌面上,木块对桌面的压强为600Pa;
(3)此时细线的拉力为4N。
3.解:(1)由图象知,G=20N,当物块完全浸没时,拉力F=10N,
则完全浸没时的浮力为F浮=G-F=20N-10N=10N,
此时物块完全浸没,所以浮力最大;
(2)由F浮=ρ液gV排得,物块的体积:
,
物块的质量:
则物块的密度:
(3)由图象可知,长方体物块的高度h=15cm-5cm=10cm=0.1m,
容器底面积
则将物块继续缓慢下降至容器的水平底部,当弹簧测力计示数为零时,物块对容器底部的压力等于其重力与浮力之差,即F=G-F浮=20N-10N=10N,
物块对容器底部的压强:
答:(1)10;(2)物块的密度2×103kg/m3;
(3)将物块继续缓慢下降至容器的水平底部,当弹簧测力计示数为零时,物块对容器底部的压强1000Pa。
4.解:(1)容器中的水和木块上表面恰好相平时,木块受到的浮力最大,
由图乙可知,此时木块底部受到水的压强p=1500Pa,
由p=可得,木块底部受到水的压力:F下=pS木=1500Pa×0.02m2=30N,
木块上表面受到水的压力:F上=0N,
则木块所受到的最大浮力:F浮=F下-F上=30N-0N=30N;
(2)因物体浸没时排开液体的体积和自身的体积相等,
所以,由F浮=ρ液gV排可得,木块的体积:
由图乙可知,9cm~16cm时木块漂浮,此时木块底部受到水的压强p′=900Pa,
木块底部受到水的压力:F下′=p′S木=900Pa×0.02m2=18N,
木块上表面受到水的压力:F上′=0N,
则木块所受到的浮力:F浮′=F下′-F上′=18N-0N=18N;
由木块漂浮时受到的浮力和自身的重力相等可知,木块的重力:G=F浮′=18N,
由G=mg可得,木块的质量:
木块的密度:
(3)由图乙可知,容器中的水和木块上表面恰好相平时,水的深度h=22cm=0.22m,
则木块和水的总体积:V总=S容h=0.1m2×0.22m=2.2×10-2m3,
容器内水的体积:V水=V总-V=2.2×10-2m3-0.3×10-2m3=1.9×10-2m3,
加入的水的质量:m水=ρ水V水=1.0×103kg/m3×1.9×10-2m3=19kg。
答:(1)木块所受到的最大浮力为30N。(2)木块的密度为0.6×103kg/m3。(3)加入的水的质量为19kg。
5.解:(1)把石块投入水中后,石块下沉至池底,
根据力的平衡条件可得,石块受到的重力为:G石=F浮+F支=2N+3N=5N;
(2)与小石块在容器中相比,小石块投入水中后,小容器的总重力减小,则由漂浮条件可知小容器受到的浮力变小,根据F浮=G排=ρ液gV排可知,小容器排开水的体积变小,所以小容器浸入水中的深度变小;
(3)石块在小容器中时小容器受到水的浮力:F浮1=G小容器+G石,
小容器的重力为:G小容器=F浮1-G石=10N-5N=5N,
小石块投入水中后,小容器在水中处于漂浮状态,
则此时小容器所受浮力为:F浮′=G小容器=5N。
答:(1)小石块的重力为5N;(2)变小;(3)小石块投入水中后,小容器受到的浮力为5N。
6.解:(1)小筒底面积为10cm2,小筒浸入水中的长度为8cm,故小筒排开水的体积为V排1=Sh1=10cm2×8cm=80cm3=8×10-5m3;
因小筒和秤盘是漂浮在水面上,故G筒=F浮=ρgV排1=1000kg/m3×10N/kg×8×10-5m3=0.8N;
(2)该秤测物体的最大质量时,就是V排=V筒=Sh=10cm2×20cm=200cm3=2×10-4m3;
此时物体和小筒秤盘的总重力G=F浮总=ρgV排=1000kg/m3×10N/kg×2×10-4m3=2N;
故此时物体的重力为G物=G-G筒=2N-0.8N=1.2N;
此时物体的质量为
答:(1)小筒和秤盘的总重力是0.8N;(2)能称出物体的最大质量是0.12kg;
7.解:(1)潜水艇漂浮在海面上时,由漂浮条件可知潜水艇受到的浮力:F浮=G=8.24×106N;
(2)此时潜水艇排开水的体积为:
当潜水艇完全潜入水中时,潜水艇排开海水体积的增大量:ΔV排=V-V排=1500m3-800m3=700m3;
为使潜水艇完全潜入海水,则向水舱中充入海水的重力至少应等于增大的浮力,
所以至少应向水舱中充入海水的重力为:G水=ΔF浮=ρ海水gΔV排=1.03×103kg/m3×10N/kg×700m3=7.21×106N;
(3)由图可知,在一个盛满水的水槽中放入潜水艇模型,水溢出且模型漂浮在水面,则放入模型后水槽中水的深度没有变化,由p=ρ液gh可知放入模型后水对水槽底部的压强没有变化;容器(空水槽)的压力不变,对桌面的压强也没有变化;故水槽对桌面的压强不变。
答:(1)潜水艇受到的浮力是8.24×106N;(2)至少应向水舱中充入海水的重力为7.21×106N;
(3)不变。
8.解:(1)溶液具有均一性,从该溶液中取出10mL,则取出溶液中溶质的质量分数仍为5%。
(2)500ml含葡萄糖25g,某病人一天共输入该葡萄糖注射液1500mL,此病人这一天共补充葡萄糖的质量为25g×=75g。
(3)设需要蒸馏水的质量为x,根据溶液稀释前后溶质的质量不变,
则100g×98%=(100g+x)×20% x=390.0g。
答:需要蒸馏水390.0g。
故答案为:(1)5%;(2)75;(3)390.0。
9.解:(1)40℃时,硝酸钾的溶解度为63.9g,则40℃时,硝酸钾饱和溶液的溶质质量分数为×100%≈39.0%。
答:40℃时,硝酸钾饱和溶液的溶质质量分数为39.0%。
(2)硝酸钾的溶解度随着温度的升高而增大,将硝酸钾的不饱和溶液转化为饱和溶液,可以采用加入硝酸钾、蒸发溶剂、降低温度等方法。
故答案为:加入硝酸钾等。
(3)20℃时,氯化钠的溶解度为36.0g,含义是20℃时,100g水中最多溶解36.0g氯化钠,溶液达到饱和状态,则20℃时,将20g氯化钠放入50g水中,最多能溶解18g,所得溶液的质量是18g+50g=68g。故答案为:68g。
10.解:t℃时某氯化钠溶液310克,在温度不变的情况下,第一次蒸发20克水,析出晶体4克,所得溶液为该温度下的饱和溶液;第二次又蒸发20克水,析出晶体6克,说明该温度下的饱和溶液,蒸发20g水,析出6g晶体,则t℃时100克水最多可以溶解6克×=30克氯化钠晶体。
t℃时某氯化钠溶液310克,在温度不变的情况下,第一次蒸发20克水,析出晶体4克,得到的是t℃时310克-20克-4克=286克氯化钠饱和溶液,含有氯化钠的质量为
30克×=66g。
原310克氯化钠溶液中溶质质量为66克+4克=70克。
答:t℃时100克水最多可以溶解30克氯化钠晶体;原310克氯化钠溶液中溶质质量70克。
11.解:(1)由硫酸溶液和氨水的密度与其溶质的质量分数对照表,20℃时,随着溶液中溶质的质量分数逐渐减小,硫酸溶液的密度逐渐减小,氨水的密度逐渐增大。
故答案为:减小;增大。
(2)设要加水的质量为x,根据溶液稀释前后溶质的质量不变,
则50g×16%=(50g+x)×4% x=150g。
(3)设配制100克12%的硫酸溶液,需要24%的硫酸溶液质量为y,则100g×12%=24%y,y=50g。
体积为50g÷1.17克/厘米3≈42.7厘米3(42.7毫升)。
答:(2)需要加水150g;(3)需要24%的硫酸溶液42.7毫升。
12.解:(1)根据图甲可知,10℃时硝酸钾的溶解度为20.9g,即100g水中最多可溶解硝酸钾的质量为20.9g;
(2)根据图甲可知,20℃时硝酸钾的溶解度为31.6g,即100g水中最多溶解硝酸钾31.6g,那么50g水中最多溶解硝酸钾15.8g;因为15g<15.8g,所以为不饱和溶液,那么溶质质量分数:;
(3)方法1:加硝酸钾溶质;在10%的硝酸钾溶液中加入硝酸钾质量为x,25%=,解得x=20g;
方法2:蒸发溶剂;对10%的硝酸钾溶液蒸发掉水的质量为y,
25%=,解得y=60g;
方法3:加入30%的硝酸钾溶液;在10%的硝酸钾溶液中加入 30%的硝酸钾溶液质量为z,
25%=,解得z=300g;
故答案为:
(1)20.9;(2)23.1%;(3)方法1:加硝酸钾溶质;20g;方法2:蒸发溶剂;60g;方法3:加入30%的硝酸钾溶液;300g。
13.解:(1)由流程图看出,甲图烧杯中加入5g氯化钾还能继续溶解,因此是不饱和溶液;故答案为:不饱和;
(2)由图看出,丁烧杯中为20℃氯化钾的溶解度是34g,20℃氯化钾的溶解度是34g,因此丁图烧杯中氯化钾溶液的质量分数为:×100%≈25.4%;故答案为:25.4%。
14.解:(1)湿衣服上残留的洗涤剂质量为100g×1%=1g,
答:湿衣服上残留的洗涤剂质量为1g。
(2)设漂洗中形成溶液溶质的质量分数为×100%=0.025%
答:漂洗中形成溶液溶质的质量分数为0.025%。
(3)再次拧干后,衣服上残留的洗涤剂为100g×0.025%=0.025g。
答:再次拧干后,衣服上残留的洗涤剂为0.025g。
15.解:由p=可得,吸盘所能承受物体的最大重力 G=F=pS=1×105Pa×10×10-4m2=100N。
答:所挂物体的重力不超过100N,吸盘才不会脱落。
16.解:(1)P内=1×105Pa×(1-1/1000)=9.99×104Pa。
答:冰箱内气体压强是9.99×104Pa。
(2)冰箱的面积是S=0.5m×0.6m=0.3m2,
F内=PS=9.99×104Pa×0.3m2=2.997×104N,
F外=PS=1×105Pa×0.3m2=3×104N。
答:冰箱内对门的压力是2.997×104N;冰箱外气体对门的压力是3×104N。
(3)冰箱门受到的内外压力差为
F外-F内=3×104N-2.997×104N=30N,
由G=mg得,m=G/g=3kg。
答:冰箱门受到的内外压力差相当于质量为3kg的物体受到的重力。
17.解:(1)抽气泵抽气,顶部气压减小,当顶部气压减小到一定程度,而底部气压不变,此时底部大气压大于顶部大气压,产生了一个向上的压强差、压力差,电梯室上升;
(2)根据p=F/S可知,作用在电梯室上表面的大气压力为:
F=pS=9.8×104Pa×1m2=9.8×104N;
(3)电梯的重力为:G电梯=mg=120kg×10N/kg=1200N;
此时高压区和低压区的压强差为:Δp=1×105Pa-9.5×104Pa=5×103Pa,
电梯室受到的压力差为:F'=ΔpS=5×103Pa×1m2=5×103N;
电梯匀速下降时,处于平衡状态,受到的合力为0,
则可装物体的重力为G=F'+f-G电梯=5×103N+300N-1200N=4100N;
故可装的物体质量为:m=G/g==410kg。
故答案为:(1)抽气泵抽气,顶部气压减小,当顶部气压减小到一定程度,而底部气压不变,此时底部大气压大于顶部大气压,产生了一个向上的压强差、压力差,电梯室上升;(2)9.8×104;(3)410kg。
18.解:(1)限压阀的重力:G=mg=0.072kg×10N/kg=0.72N,
气孔的面积:S=12mm2=1.2×10-5m2
限压阀对气孔处气体产生的压强:
p=F/S=G/S==6×104Pa;
(2)由题意知:锅内气压等于一标准大气压与限压阀对气体压强之和,则锅内气压是1.0×105Pa+6×104Pa=1.6×105Pa;
对照图象可知,当气压为1.6×105Pa时,所对应的温度大约是115℃。
答:(1)限压阀自重对出气孔处气体所产生的压强为6×104Pa;
(2)在外界为标准大气压的环境下,该高压锅内的气体能达到的最大压强是1.6×105Pa;利用这种高压锅烧煮食物时,可以达到的最高温度大约是115℃。
19.解:(1)由题意知,瓶内外气压以及水的压强存在以下平衡:
p内=p0+p水=p0+ρgh水=1.01×105Pa+1.0×103kg/m3×10N/kg×0.1m=1.02×105Pa;
(2)由题意知,手向下的压力为F,必须克服弹簧向上的弹力以及水面上方大气压强差所造成的向上的压力,
根据p=F/S可得,为使水从出水管口流出,人手施加在按压器上的压力至少为:
F=F弹+(p内-p0)S=1.2N+(1.02×105Pa-1.01×105Pa)×10×10-4m2=2.2N;
答:(1)要使水从出水管口流出,瓶内水面上方的气体压强至少要1.02×105Pa;
(2)为使水从出水管口流出,人手施加在按压器上的压力至少要2.2N。
20.解:(1)龙卷风刮过时,室外空气流速急剧增大,气压急剧下降。
(2)由于房屋外部靠近龙卷风的方向,空气流速大,压强小,房屋内空气流速小,压强大,屋顶在压强差的作用下,受到向上的压力差,巨大的压力可将屋顶掀飞;
屋顶内外受到的大气压差为:Δp=1.0×105Pa-9×104Pa=10000Pa;
屋内外的大气压力差ΔF=ΔpS=10000Pa×100m2=106N。
答:(1)龙卷风刮过时,室外空气流速急剧增大,气压急剧下降;(2)屋顶内外受到的大气压力差为106N。
21.解:由图可知,开关闭合时,两电阻并联,电流表A1测R1的电流,电流表A测总电流;
(1)由题意可知,干路电流为0.6A,通过R1的电流为0.2A,
因并联电路中各支路两端的电压相等,
则由欧姆定律可得电源电压:U=U1=I1R1=0.2A×20Ω=4V;
(2)因并联电路中干路电流等于各支路电流之和,
所以,通过R2的电流为:I2=I-I1=0.6A-0.2A=0.4A;
(3)由欧姆定律可得电阻R2的阻值:R2=U/I2==10Ω。
答:(1)电源电压为4V;(2)通过电阻R2的电流为0.4A;(3)电阻R2的阻值为10Ω。
22.解:(1)当滑片在a端时,只有电阻R1接入电路,由I=U/R可得电源电压:
U=U1=IR1=0.6A×20Ω=12V;
(2)滑片在b端时,两电阻串联,电压表测滑动变阻器两端电压,串联电路总电压等于各部分电压之和,所以电阻R1两端电压:
U1′=U-U2=12V-8V=4V,
电路电流I′===0.2A;
滑动变阻器R2的最大阻值:
答:(1)电源电压是12V;
(2)滑动变阻器R2的最大阻值是40Ω。
23.解:由电路图可知,电阻R1、R2并联,电流表测量通过R1的电流;
(1)由I=U/R知电阻R1两端的电压为:
U1=I1R1=0.3A×40Ω=12V;
(2)由于并联电路各支路两端的电压相等,所以U2=U1=12V,
通过电阻R2的电流为:
由于并联电路干路电流等于各支路电流的和,
所以电路中的总电流为:
I=I1+I2=0.3A+0.2A=0.5A。
答:(1)电阻R1两端电压为12V;(2)通过电路的总电流为0.5A。
24.解:(1)由图甲可得,通过灯泡L的电流为0.2安时,灯泡两端的电压UL=0.5V,
根据I=可得灯泡的电阻为:
(2)当只闭合开关S、S1,滑片P位于R最右端时,灯泡L与R最大值串联,电流表示数0.2安,
由图甲可得,通过灯泡L的电流为0.2安时,灯泡两端的电压UL=0.5V,
因串联电路中各处的电流相等,所以,滑动变阻器两端的电压:UR=IR=0.2A×7.5Ω=1.5V,
因串联电路中总电压等于各分电压之和,所以电源的电压:U=UL+UR=0.5V+1.5V=2V;
(3)当S、S1、S2闭合且滑片位于左端时,R0与L并联,电路的总电阻最小,电路的总电流最大,
此时R0与L两端的电压均等于电源电压,为2V,
由图甲可知,当U=2V时,通过灯泡L的电流为IL′=0.5A,通过R0的电流为I0=0.2A,
则电流表能达到的最大示数为:I=IL′+I0=0.5A+0.2A=0.7A。
答:(1)通过灯L的电流为0.2安时,灯L的电阻为2.5Ω;(2)电源电压为2V;(3)当S、S1、S2闭合且滑片位于左端时,电流表达到的最大示数为0.7A。
25.解:由电路图可知,R1与R2串联,电压表V1测R1两端的电压,电压表V2测R2两端的电压,电流表测电路中的电流。
(1)当滑动变阻器接入电路中的电阻为0时,电路中的电流最大,滑动变阻器两端的电压为0V,由图象可知,甲为滑动变阻器的U-I图象,则乙为定值电阻的U-I图象;
由图象可知,当电路中的电流I=0.2A,电阻R1两端的电压U1=2V,滑动变阻器两端的电压U2=4V,根据欧姆定律可知
因串联电路总电压等于各支路电压之和,
所以,电源的电压:
U=U1+U2=2V+4V=6V;
(2)滑动变阻器的最大阻值:
所以滑动变阻器R2的阻值变化范围为0~20Ω。
答:(1)电源电压和定值电阻R1的阻值分别为6V、10Ω。(2)滑动变阻器R2的阻值变化范围为0~20Ω。
26.解:(1)由图乙可知,当温度为0℃时,热敏电阻的阻值为500Ω;
(2)由图甲可知,热敏电阻与定值电阻R0串联,电压表测量R0两端的电压。
当电压表的示数达到最大值时,即R0两端的电压为U0=3V,
由于串联电路中各处电流相等,所以通过热敏电阻的电流为:
(3)当水温达到100℃时,由图乙可知,热敏电阻的阻值为:R热=100Ω,
因为串联电路的总电阻等于各串联电阻之和,所以电源电压为:
U=I热(R热+R0)=0.03A×(100Ω+100Ω)=6V,
当水温为0℃时,电路中的电流为:
此时R0两端的电压,即电压表的示数为:U0′=I′R0=0.01A×100Ω=1V,
即改画的水温表刻度盘上的0℃应该与电压表刻度盘的1V位置对应。
答:(1)500;(2)当电压表示数达到最大值时,通过热敏电阻的电流是0.03A;
(3)改画的水温表刻度盘上的0℃应该与电压表刻度盘的1V位置对应。
27.解:(1)由电路图可知,电阻R0在电路起保护电路的作用。
(2)由电路图可知,电压表测滑动变阻器两端电压,被测身高增加时,滑动变阻器电阻棒接入电路的长度增加,
滑动变阻器接入电路的阻值变大,滑动变阻器的分压变大,因此电压表示数变大。
根据欧姆定律可知,电路中电流变小,故电流表示数变小。
(3)由欧姆定律得,电路总电阻:
则滑动变阻器接入电路的阻值:
RPb1=R总1-R0=9Ω-5Ω=4Ω。
(4)当电压表的示数为3V,R0两端的电压:
U0=U-UR=4.5V-3V=1.5V,
电路中的电流:
此时身高测量仪测量的身高最大,电阻棒接入电路中的电阻最大,
最大阻值为:
故答案为:(1)保护电路;(2)变大;变小;(3)电阻棒R接入电路的电阻为4Ω;
(4)随着身高而变化大小的R能接入电路的最大阻值是10Ω。
28.解:(1)闭合开关,两电阻串联接入电路,电压表测滑动变阻器两端的电压,电流表测通过电路的电流,
当滑片P置于最下端时,滑动变阻器接入电路最大阻值,电流表示数为0.1A,则电压表示数为:UP=IRP=0.1A×60Ω=6V;
(2)当滑动变阻器接入电路的电阻为0时,电路为定值电阻的简单电路,根据欧姆定律可知此时通过电路的电流最大,由丙图可知通过电路的最大电流为0.3A,
根据欧姆定律可得电源电压:U=IR0=0.3A×R0------①,
因串联电路总电压等于各部分电压之和,通过电路的电流为0.1A时,根据欧姆定律可得电源电压:U=UP+I′R0=6V+0.1A×R0------②,
联立①②可得:R0=30Ω,U=9V;
(3)当电压表的示数为3V时,定值电阻两端的电压:U0=U-UP′=9V-3V=6V,
此时通过定值电阻的电流:
串联电路各处电流相等,此时滑动变阻器接入电路的阻值:
由乙图可知滑动变阻器的长度为195m-175m,滑片位于最下端时水位的高度为175m,
,浮子上升的距离:ΔL=×(195m-175m)=15m,则此时的警戒水位为175m+15m=190m。
答:(1)当滑片P置于最下端时,电流表示数为0.1A,电压表示数为6V;
(2)电源电压为9V,R0的阻值为30Ω;
(3)当电压表的示数为3V时,报警装置发出警报,警戒水位为190m。
一、浮力专题计算
1.如图所示,一边长为20cm的正方体木块漂浮在水面上,木块浸入水中的深度为12cm。(ρ水=1.0×103kg/m3,g取10N/kg)试求:
(1)木块受到的浮力F浮;
(2)木块下表面受到的水的压强p;
(3)木块的密度。
2.一边长为10cm,密度为0.6g/cm3的正方体木块,用细线置于容器的水中,如图所示,求:
(1)木块质量多大?
(2)将木块放置在水平桌面上,木块对桌面的压强多大?
(3)此时细线的拉力多大?
3.如图甲所示,将一长方体物块通过细线悬挂于弹簧测力计的挂钩上,手持弹簧测力计缓慢下降,让长方体物块从盛满水的溢水杯上方缓慢下降至水下一定深度。长方体物块下降过程中,弹簧测力计的示数F随下降高度h的变化关系如图乙所示,g取10N/kg。求:
(1)长方体物块受到的最大浮力为 N;
(2)长方体物块的密度;
(3)将长方体物块继续缓慢下降至容器的水平底部,当弹簧测力计示数为零时,长方体物块对容器底部的压强。
4.将一底面积为0.02m2的长方体木块用细线拴在一个底面积为0.1m2的空容器的底部,向容器中缓慢加水直到木块上表面与水面相平,如图甲所示。在此整个过程中,木块底部受到水的压强随容器中水的深度的变化情况如图乙所示。求:
(1)木块所受到的最大浮力。
(2)木块的密度。
(3)加入的水的质量。
·
5.如图所示,装有石块的小容器浮在水面上时受到10N的浮力。当把石块投入水中后,石块所受浮力为2N,池底对石块的支持力为3N,小容器仍漂浮在水面上,水的密度为1.0×103kg/m3。
(1)小石块的重力为多少牛?
(2)与小石块在容器中相比,小石块投入水中后,小容器浸入水中的深度 (填“不变”、“变大”或“变小”)
(3)小石块投入水中后,小容器受到的浮力为多少牛?
6.在青少年科技创新大赛中,某同学发明作品《浮力秤》参加展评,作品可方便称量物体的质量,其构造如图所示。已知小筒底面积为10cm2,总长为20cm,盘中不放物体时,小筒浸入水中长度为8cm,问:g=10N/kg
(1)小筒和秤盘的总重力是多少N?
(2)该秤能称出物体的最大质量是多少kg?
7.攻击核潜艇093是我国主力型号,总体积达到1.5×103m3,下潜深度可以超过400米。艇内两侧有水舱,潜水艇截面如图所示。(海水密度为1.03×103kg/m3,g取10N/kg)
(1)水舱未充海水时,潜水艇总重为8.24×106N,漂浮在海面上,潜水艇受到的浮力是多少?
(2)为使潜水艇完全潜入海水,至少应向水舱中充入海水的重力是多少?
(3)如图丙小之用一个潜水艇模型模拟该过程,在一个盛满水的水槽中放入潜水艇模型,水溢出且模型漂浮在水面,则放入模型后水槽对桌面的压强 (填“变大”“不变”或“变小”)
二、溶液专题计算
8.医生给病人输液时,常用葡萄糖注射液。如图为葡萄糖注射液的部分标签图,根据图回答下列问题:
(1)从该溶液中取出10mL,则取出溶液中溶质的质量分数为 。
(2)某病人一天共输入该葡萄糖注射液1500mL,此病人这一天共补充葡萄糖 g。
(3)某铅酸蓄电池使用的酸溶液是溶质质量分数为20%的稀硫酸。若用100g质量分数为98%的浓硫酸配制该稀硫酸时,需要蒸馏水多少克(精确到0.1)(写出计算过程)。
9.溶解是生活中常见的现象,不同物质在水中的溶解能力不同。表是硝酸钾、氯化钠在不同湿度下的溶解度(单位:g/100g水)
· 温度(℃) 0 20 40 60 80 100
硝酸钾 13.3 31.6 63.9 110 169 246
氯化钠 35.7 36.0 36.6 37.3 38.4 39.8
(1)40℃时,硝酸钾饱和溶液的溶质质量分数为多少?(写出计算过程)
(2)请写出一种将硝酸钾的不饱和溶液转化为饱和溶液的方法 。
(3)20℃时,将20g氯化钠放入50g水中,所得溶液的质量是 。
10.t℃时某氯化钠溶液310克,在温度不变的情况下,第一次蒸发20克水,析出晶体4克;第二次又蒸发20克水,析出晶体6克。则t℃时100克水最多可以溶解多少克氯化钠晶体?原310克氯化钠溶液中溶质质量多少?
11.读硫酸溶液和氨水的密度与其溶质的质量分数对照表(20℃),回答问题。
· 溶液中溶质的质量分数(%) 4 12 16 24 28
硫酸溶液的密度(克/厘米3) 1.02 1.08 1.11 1.17 1.20
氨水的密度(克/厘米3) 0.98 0.95 0.94 0.91 0.90
(1)20℃时,随着溶液中溶质的质量分数逐渐减小,硫酸溶液的密度逐渐 ,氨水的密度逐渐 。
(2)将50克16%的氨水稀释成4%的溶液,需要加水多少克?
(3)配制100克12%的硫酸溶液,需要24%的硫酸溶液多少毫升?(答案保留1位小数)
12.某兴趣小组用硝酸钾进行实验,如图甲是硝酸钾的溶解度与温度关系。
(1)10℃时,100g水中最多可溶解硝酸钾的质量为 g。
(2)20℃时,将15g硝酸钾加入50g水中,所得溶液的溶质质量分数为 (结果保留一位小数)。
(3)请写出一种能实现如图乙所示结果的操作方法,并写出计算过程(结果保留一位小数)。
13.20℃氯化钾的溶解度是34g。取氯化钾溶液65g放入烧杯中,按如图所示进行操作(整个过程中无溶剂损失)。
(1)甲图烧杯中是氯化钾的 溶液(选填“饱和”或“不饱和”)
(2)丁图烧杯中氯化钾溶液的质量分数为多少?(计算结果保留一位小数)
14.日常生活中我们要科学地节约用水,现有一件刚用洗涤剂洗过的衣服,“拧干”后湿衣服上残留液为100克,其中含洗涤剂的质量分数为1%,则:
(1)湿衣服上残留的洗涤剂质量为多少克?
(2)现有3900克清水对这件衣服进行漂洗,则:漂洗中形成溶液溶质的质量分数为多少?
(3)再次拧干后,衣服上残留的洗涤剂为几克?
三、大气压强专题计算
15.图甲是一个深度较浅的皮碗,图乙是将皮碗压向水平的天花板,几乎挤完皮碗内的空气,在大气压的作用下,皮碗像吸盘一样“平贴“在天花板上。皮碗的吸附面积为10厘米2,皮碗中心引出的细线可悬挂一个物体。问所挂物体的重力不超过多少,吸盘才不会脱落?(不计细线和皮碗的重力,大气压约为1×105帕,g取10牛/千克)
16.盛夏时分,“小问号”王欣同学在打开冰箱取饮料时,突然脑海里浮出一个问题:为什么每次开冰箱门都比较费力?通过仔细观察他发现打开冰箱门时,冰箱里的冷空气出来,外面的热空气进去。当冰箱门重新关上后,就将这部分热空气也关在了里面,箱内热空气冷却收缩。压强减小。王欣判断这应该是开冰箱门费力的一个原因。若冰箱门长为0.6m.宽为0.5m冰箱外的气压为1×105Pa,设冰箱内部与外部的气压相差1/ 1000。
求:
(1)冰箱内气体压强多少?
(2)冰箱内、外气体对门的压力各是多少?
(3)冰箱门受到的内外压力差相当于质量为多少的物体受到的重力大小?(g=10N/kg)
17.一款新型家用电梯(如图所示)正走进我们的生活,它外形是长圆筒,升降过程不使用线缆,而是靠气压驱动。已知外界大气压为1×105Pa,电梯室质量为120kg,电梯室与圆筒壁之间的摩擦力为300N,底部和顶部面积均为1m2。
(1)请用所学知识分析说明该新型家用电梯是如何实现向上运动的。
(2)低压区的气压降到9.8×104Pa时,作用在电梯室上表面的大气压力是 牛。
(3)抽气机最多能把低压区的气压降到9.5×104Pa,,则该电梯匀速下降时能装载的物体的最大质量是 。
18.如图,高压锅是家庭厨房中常见的炊具,利用它可将食物加热到100℃以上,它省时高效,深受消费者欢迎。
(1)小明测得家中高压锅出气孔的横截面积S为12mm2,压在出气孔上的安全阀的质量为72g,g取10N/kg,计算安全阀自重对出气孔处气体所产生的压强。
(2)当高压锅内气压增大到某一值时,锅内气体就能自动顶开安全阀放气。在外界为标准大气压的环境下,该高压锅内的气体能达到的最大压强是多少?对照图所示水的沸点与气压的关系图线,利用这种高压锅烧煮食物时可以到达的最高温度大约是多少?(大气压值取1.0×105Pa)
19.如图是一种气压保温瓶的结构示意图。用手按下按压器时,气室上方的小孔被堵塞,使瓶内气体压强增大,水在气压作用下从出水管口流出.如果按压器面积是10cm2,瓶内水面低于水管口10cm,按压器的自重不计,大气压强p0=1.01×105Pa。求:
(1)要使水从出水管口流出,瓶内水面上方的气体压强至少要多大?
(2)如果在按下按压器的过程中,气室内弹簧产生的平均弹力是1.2N,为使水从出水管口流出,人手施加在按压器上的压力至少要多大?
20.美国东面是大西洋,西面是太平洋,每年都会受到龙卷风的袭击,造成人员伤亡和财产损失。假设某一次龙卷风发生时,室外的气压急剧下降到9×104Pa,当时门窗紧闭,室内气压约为1×105Pa。
(1)为什么龙卷风发生时,室外的气压会急剧下降?
(2)若水平屋顶的面积为100m2,试计算屋顶内外受到的大气压力差的大小。
四、电路专题计算
21.如图所示,电阻R1的阻值为20Ω,当开关闭合时,电流表A的示数为0.6A,电流表A1的示数为0.2A。求:
(1)电源电压;
(2)通过电阻R2的电流;
(3)电阻R2的阻值。
22.如图所示电路中定值电阻R1=20Ω,R2为滑动变阻器,电源电压保持不变。当滑片在a端时,电流表示数为0.6A,滑片在b端时电压表示数为8V。求:
(1)电源电压;
(2)滑动变阻器R2的最大阻值。
23.如图所示电路中,已知R1=40Ω,R2=60Ω,当开关S闭合后,通过电流表的示数为0.3安,求:
(1)电阻R1两端电压;
(2)通过电路的总电流。
24.如图甲是定值电阻R0和灯泡L的I-U图象,现将它们接入图乙所示的电路,其中电源电压不变,滑动变阻器R最大阻值为7.5欧。当只闭合开关S、S1,滑片P位于R最右端时,电流表示数0.2安,问:
(1)通过灯L的电流为0.2安时,灯L的电阻为多大?
(2)电源电压为几伏?
(3)通过控制开关和调节变阻器,电流表能达到的最大示数为多少?
25.如图1所示电路,电源电压保持不变,当闭合开关S,调节滑动变阻器阻值从最大变化到最小。两个电阻的“U-I”关系图象如图2所示。求:
(1)电源电压和定值电阻R1的阻值。
(2)滑动变阻器R2的阻值变化范围。
·
26.某兴趣小组利用热敏电阻设计了一只测量范围为0~100℃的水温表,其中热敏电阻随温度的变化情况如图乙所示,水温表的原理如图甲所示。已知电压表量程为0~3伏,定值电阻R0的阻值为100欧,电源电压保持不变。当水温达到100℃时,要求电压表的示数达到最大值。
(1)分析图乙可知,当温度为0℃时,热敏电阻的阻值为 欧;
(2)当电压表示数达到最大值时,通过热敏电阻的电流是多少?
(3)通过计算说明,改画的水温表刻度盘上的0℃应该与电压表刻度盘的什么位置对应?
27.参加全国青少年创新大赛,小强运用电学知识设计了一个电子身高测量仪,如图所示。其中定值电阻R0=5Ω,电源电压恒为4.5V,R是固定的、竖直放置的硬电阻棒,总电阻为15Ω,其接入电路的电阻与接入电路的棒长成正比,金属杆cd和MP(右端P是滑片)与电路接触良好,电阻不计。
(1)R0在电路中的作用是 。
(2)当被测身高增加时,电压表的示数 ,电流表的示数 。(选填“变大”、“变小”、“不变”)。
(3)身高为168cm小强用该测量仪测量时,电流表示数为0.5A,此时电阻棒R接入电路的电阻为多少Ω?
(4)若电压表量程为0~3V,电流表量程为0~0.6A,为保证电路各元件安全工作,则随着身高而变化大小的R能接入电路的最大阻值是多少Ω?
28.某科技小组设计了一个监测水位的装置。其原理如图甲,电路中电源电压保持不变,R0为定值电阻,AP与R组成滑动变阻器(最大阻值60Ω),浮子可带动金属滑杆AP在竖直方向上下移动。当水位上升时,浮子和金属滑杆AP一起向上滑动,当电压表的示数达到某一数值时提醒监测员水位达到警戒值。R接入电路的阻值随水位的变化关系如图乙,电路工作时电压表与电流表示数变化关系如图丙。求:
·
· (1)当滑片P置于最下端时,电流表示数为0.1A,则电压表示数为多少?
· (2)电源电压和R0的阻值。
· (3)当电压表的示数为3V时,报警装置发出警报,则警戒水位为多少米?
参考答案
1.解:(1)由阿基米德原理可得,木块受到的浮力:
F浮=ρ水gV排=ρ水gS木h浸=1.0×103kg/m3×10N/kg×0.2m×0.2m×0.12m=48N;
(2)木块下表面所受的压强:
p=ρ水gh=1.0×103kg/m3×10N/kg×0.12m=1200Pa;
(3)因为木块处于漂浮状态,
所以F浮=G木,
由阿基米德原理和重力公式可得:ρ水gV排=ρ木V木g,
即:ρ水gL2h浸=ρ木gL3,
则木块的密度:ρ木=0.6×103kg/m3。
答:(1)木块受到的浮力为48N。
(2)木块下表面受到的水的压强为1200Pa;
(3)木块的密度为0.6×103kg/m3。
2.解:(1)木块的体积V木=10cm×10cm×10cm=103cm3=10-3m3,
木块的质量:m木=ρ木V木=0.6×103kg/m3×10-3m3=0.6kg;
(2)==600Pa;
(3)因为木块浸没水中,所以木块排开水的体积:V排=V木=10-3 m3,
木块受到的浮力:F浮=ρ水gV排=103kg/m3×10N/kg×10-3m3=10N;
因为木块受到的重力G加上绳子的拉力F拉等于木块受到的浮力F浮,
所以细线对木块的拉力:F拉=F浮-G=10N-6N=4N。
答:(1)木块的质量为0.6kg;
(2)将木块放置在水平桌面上,木块对桌面的压强为600Pa;
(3)此时细线的拉力为4N。
3.解:(1)由图象知,G=20N,当物块完全浸没时,拉力F=10N,
则完全浸没时的浮力为F浮=G-F=20N-10N=10N,
此时物块完全浸没,所以浮力最大;
(2)由F浮=ρ液gV排得,物块的体积:
,
物块的质量:
则物块的密度:
(3)由图象可知,长方体物块的高度h=15cm-5cm=10cm=0.1m,
容器底面积
则将物块继续缓慢下降至容器的水平底部,当弹簧测力计示数为零时,物块对容器底部的压力等于其重力与浮力之差,即F=G-F浮=20N-10N=10N,
物块对容器底部的压强:
答:(1)10;(2)物块的密度2×103kg/m3;
(3)将物块继续缓慢下降至容器的水平底部,当弹簧测力计示数为零时,物块对容器底部的压强1000Pa。
4.解:(1)容器中的水和木块上表面恰好相平时,木块受到的浮力最大,
由图乙可知,此时木块底部受到水的压强p=1500Pa,
由p=可得,木块底部受到水的压力:F下=pS木=1500Pa×0.02m2=30N,
木块上表面受到水的压力:F上=0N,
则木块所受到的最大浮力:F浮=F下-F上=30N-0N=30N;
(2)因物体浸没时排开液体的体积和自身的体积相等,
所以,由F浮=ρ液gV排可得,木块的体积:
由图乙可知,9cm~16cm时木块漂浮,此时木块底部受到水的压强p′=900Pa,
木块底部受到水的压力:F下′=p′S木=900Pa×0.02m2=18N,
木块上表面受到水的压力:F上′=0N,
则木块所受到的浮力:F浮′=F下′-F上′=18N-0N=18N;
由木块漂浮时受到的浮力和自身的重力相等可知,木块的重力:G=F浮′=18N,
由G=mg可得,木块的质量:
木块的密度:
(3)由图乙可知,容器中的水和木块上表面恰好相平时,水的深度h=22cm=0.22m,
则木块和水的总体积:V总=S容h=0.1m2×0.22m=2.2×10-2m3,
容器内水的体积:V水=V总-V=2.2×10-2m3-0.3×10-2m3=1.9×10-2m3,
加入的水的质量:m水=ρ水V水=1.0×103kg/m3×1.9×10-2m3=19kg。
答:(1)木块所受到的最大浮力为30N。(2)木块的密度为0.6×103kg/m3。(3)加入的水的质量为19kg。
5.解:(1)把石块投入水中后,石块下沉至池底,
根据力的平衡条件可得,石块受到的重力为:G石=F浮+F支=2N+3N=5N;
(2)与小石块在容器中相比,小石块投入水中后,小容器的总重力减小,则由漂浮条件可知小容器受到的浮力变小,根据F浮=G排=ρ液gV排可知,小容器排开水的体积变小,所以小容器浸入水中的深度变小;
(3)石块在小容器中时小容器受到水的浮力:F浮1=G小容器+G石,
小容器的重力为:G小容器=F浮1-G石=10N-5N=5N,
小石块投入水中后,小容器在水中处于漂浮状态,
则此时小容器所受浮力为:F浮′=G小容器=5N。
答:(1)小石块的重力为5N;(2)变小;(3)小石块投入水中后,小容器受到的浮力为5N。
6.解:(1)小筒底面积为10cm2,小筒浸入水中的长度为8cm,故小筒排开水的体积为V排1=Sh1=10cm2×8cm=80cm3=8×10-5m3;
因小筒和秤盘是漂浮在水面上,故G筒=F浮=ρgV排1=1000kg/m3×10N/kg×8×10-5m3=0.8N;
(2)该秤测物体的最大质量时,就是V排=V筒=Sh=10cm2×20cm=200cm3=2×10-4m3;
此时物体和小筒秤盘的总重力G=F浮总=ρgV排=1000kg/m3×10N/kg×2×10-4m3=2N;
故此时物体的重力为G物=G-G筒=2N-0.8N=1.2N;
此时物体的质量为
答:(1)小筒和秤盘的总重力是0.8N;(2)能称出物体的最大质量是0.12kg;
7.解:(1)潜水艇漂浮在海面上时,由漂浮条件可知潜水艇受到的浮力:F浮=G=8.24×106N;
(2)此时潜水艇排开水的体积为:
当潜水艇完全潜入水中时,潜水艇排开海水体积的增大量:ΔV排=V-V排=1500m3-800m3=700m3;
为使潜水艇完全潜入海水,则向水舱中充入海水的重力至少应等于增大的浮力,
所以至少应向水舱中充入海水的重力为:G水=ΔF浮=ρ海水gΔV排=1.03×103kg/m3×10N/kg×700m3=7.21×106N;
(3)由图可知,在一个盛满水的水槽中放入潜水艇模型,水溢出且模型漂浮在水面,则放入模型后水槽中水的深度没有变化,由p=ρ液gh可知放入模型后水对水槽底部的压强没有变化;容器(空水槽)的压力不变,对桌面的压强也没有变化;故水槽对桌面的压强不变。
答:(1)潜水艇受到的浮力是8.24×106N;(2)至少应向水舱中充入海水的重力为7.21×106N;
(3)不变。
8.解:(1)溶液具有均一性,从该溶液中取出10mL,则取出溶液中溶质的质量分数仍为5%。
(2)500ml含葡萄糖25g,某病人一天共输入该葡萄糖注射液1500mL,此病人这一天共补充葡萄糖的质量为25g×=75g。
(3)设需要蒸馏水的质量为x,根据溶液稀释前后溶质的质量不变,
则100g×98%=(100g+x)×20% x=390.0g。
答:需要蒸馏水390.0g。
故答案为:(1)5%;(2)75;(3)390.0。
9.解:(1)40℃时,硝酸钾的溶解度为63.9g,则40℃时,硝酸钾饱和溶液的溶质质量分数为×100%≈39.0%。
答:40℃时,硝酸钾饱和溶液的溶质质量分数为39.0%。
(2)硝酸钾的溶解度随着温度的升高而增大,将硝酸钾的不饱和溶液转化为饱和溶液,可以采用加入硝酸钾、蒸发溶剂、降低温度等方法。
故答案为:加入硝酸钾等。
(3)20℃时,氯化钠的溶解度为36.0g,含义是20℃时,100g水中最多溶解36.0g氯化钠,溶液达到饱和状态,则20℃时,将20g氯化钠放入50g水中,最多能溶解18g,所得溶液的质量是18g+50g=68g。故答案为:68g。
10.解:t℃时某氯化钠溶液310克,在温度不变的情况下,第一次蒸发20克水,析出晶体4克,所得溶液为该温度下的饱和溶液;第二次又蒸发20克水,析出晶体6克,说明该温度下的饱和溶液,蒸发20g水,析出6g晶体,则t℃时100克水最多可以溶解6克×=30克氯化钠晶体。
t℃时某氯化钠溶液310克,在温度不变的情况下,第一次蒸发20克水,析出晶体4克,得到的是t℃时310克-20克-4克=286克氯化钠饱和溶液,含有氯化钠的质量为
30克×=66g。
原310克氯化钠溶液中溶质质量为66克+4克=70克。
答:t℃时100克水最多可以溶解30克氯化钠晶体;原310克氯化钠溶液中溶质质量70克。
11.解:(1)由硫酸溶液和氨水的密度与其溶质的质量分数对照表,20℃时,随着溶液中溶质的质量分数逐渐减小,硫酸溶液的密度逐渐减小,氨水的密度逐渐增大。
故答案为:减小;增大。
(2)设要加水的质量为x,根据溶液稀释前后溶质的质量不变,
则50g×16%=(50g+x)×4% x=150g。
(3)设配制100克12%的硫酸溶液,需要24%的硫酸溶液质量为y,则100g×12%=24%y,y=50g。
体积为50g÷1.17克/厘米3≈42.7厘米3(42.7毫升)。
答:(2)需要加水150g;(3)需要24%的硫酸溶液42.7毫升。
12.解:(1)根据图甲可知,10℃时硝酸钾的溶解度为20.9g,即100g水中最多可溶解硝酸钾的质量为20.9g;
(2)根据图甲可知,20℃时硝酸钾的溶解度为31.6g,即100g水中最多溶解硝酸钾31.6g,那么50g水中最多溶解硝酸钾15.8g;因为15g<15.8g,所以为不饱和溶液,那么溶质质量分数:;
(3)方法1:加硝酸钾溶质;在10%的硝酸钾溶液中加入硝酸钾质量为x,25%=,解得x=20g;
方法2:蒸发溶剂;对10%的硝酸钾溶液蒸发掉水的质量为y,
25%=,解得y=60g;
方法3:加入30%的硝酸钾溶液;在10%的硝酸钾溶液中加入 30%的硝酸钾溶液质量为z,
25%=,解得z=300g;
故答案为:
(1)20.9;(2)23.1%;(3)方法1:加硝酸钾溶质;20g;方法2:蒸发溶剂;60g;方法3:加入30%的硝酸钾溶液;300g。
13.解:(1)由流程图看出,甲图烧杯中加入5g氯化钾还能继续溶解,因此是不饱和溶液;故答案为:不饱和;
(2)由图看出,丁烧杯中为20℃氯化钾的溶解度是34g,20℃氯化钾的溶解度是34g,因此丁图烧杯中氯化钾溶液的质量分数为:×100%≈25.4%;故答案为:25.4%。
14.解:(1)湿衣服上残留的洗涤剂质量为100g×1%=1g,
答:湿衣服上残留的洗涤剂质量为1g。
(2)设漂洗中形成溶液溶质的质量分数为×100%=0.025%
答:漂洗中形成溶液溶质的质量分数为0.025%。
(3)再次拧干后,衣服上残留的洗涤剂为100g×0.025%=0.025g。
答:再次拧干后,衣服上残留的洗涤剂为0.025g。
15.解:由p=可得,吸盘所能承受物体的最大重力 G=F=pS=1×105Pa×10×10-4m2=100N。
答:所挂物体的重力不超过100N,吸盘才不会脱落。
16.解:(1)P内=1×105Pa×(1-1/1000)=9.99×104Pa。
答:冰箱内气体压强是9.99×104Pa。
(2)冰箱的面积是S=0.5m×0.6m=0.3m2,
F内=PS=9.99×104Pa×0.3m2=2.997×104N,
F外=PS=1×105Pa×0.3m2=3×104N。
答:冰箱内对门的压力是2.997×104N;冰箱外气体对门的压力是3×104N。
(3)冰箱门受到的内外压力差为
F外-F内=3×104N-2.997×104N=30N,
由G=mg得,m=G/g=3kg。
答:冰箱门受到的内外压力差相当于质量为3kg的物体受到的重力。
17.解:(1)抽气泵抽气,顶部气压减小,当顶部气压减小到一定程度,而底部气压不变,此时底部大气压大于顶部大气压,产生了一个向上的压强差、压力差,电梯室上升;
(2)根据p=F/S可知,作用在电梯室上表面的大气压力为:
F=pS=9.8×104Pa×1m2=9.8×104N;
(3)电梯的重力为:G电梯=mg=120kg×10N/kg=1200N;
此时高压区和低压区的压强差为:Δp=1×105Pa-9.5×104Pa=5×103Pa,
电梯室受到的压力差为:F'=ΔpS=5×103Pa×1m2=5×103N;
电梯匀速下降时,处于平衡状态,受到的合力为0,
则可装物体的重力为G=F'+f-G电梯=5×103N+300N-1200N=4100N;
故可装的物体质量为:m=G/g==410kg。
故答案为:(1)抽气泵抽气,顶部气压减小,当顶部气压减小到一定程度,而底部气压不变,此时底部大气压大于顶部大气压,产生了一个向上的压强差、压力差,电梯室上升;(2)9.8×104;(3)410kg。
18.解:(1)限压阀的重力:G=mg=0.072kg×10N/kg=0.72N,
气孔的面积:S=12mm2=1.2×10-5m2
限压阀对气孔处气体产生的压强:
p=F/S=G/S==6×104Pa;
(2)由题意知:锅内气压等于一标准大气压与限压阀对气体压强之和,则锅内气压是1.0×105Pa+6×104Pa=1.6×105Pa;
对照图象可知,当气压为1.6×105Pa时,所对应的温度大约是115℃。
答:(1)限压阀自重对出气孔处气体所产生的压强为6×104Pa;
(2)在外界为标准大气压的环境下,该高压锅内的气体能达到的最大压强是1.6×105Pa;利用这种高压锅烧煮食物时,可以达到的最高温度大约是115℃。
19.解:(1)由题意知,瓶内外气压以及水的压强存在以下平衡:
p内=p0+p水=p0+ρgh水=1.01×105Pa+1.0×103kg/m3×10N/kg×0.1m=1.02×105Pa;
(2)由题意知,手向下的压力为F,必须克服弹簧向上的弹力以及水面上方大气压强差所造成的向上的压力,
根据p=F/S可得,为使水从出水管口流出,人手施加在按压器上的压力至少为:
F=F弹+(p内-p0)S=1.2N+(1.02×105Pa-1.01×105Pa)×10×10-4m2=2.2N;
答:(1)要使水从出水管口流出,瓶内水面上方的气体压强至少要1.02×105Pa;
(2)为使水从出水管口流出,人手施加在按压器上的压力至少要2.2N。
20.解:(1)龙卷风刮过时,室外空气流速急剧增大,气压急剧下降。
(2)由于房屋外部靠近龙卷风的方向,空气流速大,压强小,房屋内空气流速小,压强大,屋顶在压强差的作用下,受到向上的压力差,巨大的压力可将屋顶掀飞;
屋顶内外受到的大气压差为:Δp=1.0×105Pa-9×104Pa=10000Pa;
屋内外的大气压力差ΔF=ΔpS=10000Pa×100m2=106N。
答:(1)龙卷风刮过时,室外空气流速急剧增大,气压急剧下降;(2)屋顶内外受到的大气压力差为106N。
21.解:由图可知,开关闭合时,两电阻并联,电流表A1测R1的电流,电流表A测总电流;
(1)由题意可知,干路电流为0.6A,通过R1的电流为0.2A,
因并联电路中各支路两端的电压相等,
则由欧姆定律可得电源电压:U=U1=I1R1=0.2A×20Ω=4V;
(2)因并联电路中干路电流等于各支路电流之和,
所以,通过R2的电流为:I2=I-I1=0.6A-0.2A=0.4A;
(3)由欧姆定律可得电阻R2的阻值:R2=U/I2==10Ω。
答:(1)电源电压为4V;(2)通过电阻R2的电流为0.4A;(3)电阻R2的阻值为10Ω。
22.解:(1)当滑片在a端时,只有电阻R1接入电路,由I=U/R可得电源电压:
U=U1=IR1=0.6A×20Ω=12V;
(2)滑片在b端时,两电阻串联,电压表测滑动变阻器两端电压,串联电路总电压等于各部分电压之和,所以电阻R1两端电压:
U1′=U-U2=12V-8V=4V,
电路电流I′===0.2A;
滑动变阻器R2的最大阻值:
答:(1)电源电压是12V;
(2)滑动变阻器R2的最大阻值是40Ω。
23.解:由电路图可知,电阻R1、R2并联,电流表测量通过R1的电流;
(1)由I=U/R知电阻R1两端的电压为:
U1=I1R1=0.3A×40Ω=12V;
(2)由于并联电路各支路两端的电压相等,所以U2=U1=12V,
通过电阻R2的电流为:
由于并联电路干路电流等于各支路电流的和,
所以电路中的总电流为:
I=I1+I2=0.3A+0.2A=0.5A。
答:(1)电阻R1两端电压为12V;(2)通过电路的总电流为0.5A。
24.解:(1)由图甲可得,通过灯泡L的电流为0.2安时,灯泡两端的电压UL=0.5V,
根据I=可得灯泡的电阻为:
(2)当只闭合开关S、S1,滑片P位于R最右端时,灯泡L与R最大值串联,电流表示数0.2安,
由图甲可得,通过灯泡L的电流为0.2安时,灯泡两端的电压UL=0.5V,
因串联电路中各处的电流相等,所以,滑动变阻器两端的电压:UR=IR=0.2A×7.5Ω=1.5V,
因串联电路中总电压等于各分电压之和,所以电源的电压:U=UL+UR=0.5V+1.5V=2V;
(3)当S、S1、S2闭合且滑片位于左端时,R0与L并联,电路的总电阻最小,电路的总电流最大,
此时R0与L两端的电压均等于电源电压,为2V,
由图甲可知,当U=2V时,通过灯泡L的电流为IL′=0.5A,通过R0的电流为I0=0.2A,
则电流表能达到的最大示数为:I=IL′+I0=0.5A+0.2A=0.7A。
答:(1)通过灯L的电流为0.2安时,灯L的电阻为2.5Ω;(2)电源电压为2V;(3)当S、S1、S2闭合且滑片位于左端时,电流表达到的最大示数为0.7A。
25.解:由电路图可知,R1与R2串联,电压表V1测R1两端的电压,电压表V2测R2两端的电压,电流表测电路中的电流。
(1)当滑动变阻器接入电路中的电阻为0时,电路中的电流最大,滑动变阻器两端的电压为0V,由图象可知,甲为滑动变阻器的U-I图象,则乙为定值电阻的U-I图象;
由图象可知,当电路中的电流I=0.2A,电阻R1两端的电压U1=2V,滑动变阻器两端的电压U2=4V,根据欧姆定律可知
因串联电路总电压等于各支路电压之和,
所以,电源的电压:
U=U1+U2=2V+4V=6V;
(2)滑动变阻器的最大阻值:
所以滑动变阻器R2的阻值变化范围为0~20Ω。
答:(1)电源电压和定值电阻R1的阻值分别为6V、10Ω。(2)滑动变阻器R2的阻值变化范围为0~20Ω。
26.解:(1)由图乙可知,当温度为0℃时,热敏电阻的阻值为500Ω;
(2)由图甲可知,热敏电阻与定值电阻R0串联,电压表测量R0两端的电压。
当电压表的示数达到最大值时,即R0两端的电压为U0=3V,
由于串联电路中各处电流相等,所以通过热敏电阻的电流为:
(3)当水温达到100℃时,由图乙可知,热敏电阻的阻值为:R热=100Ω,
因为串联电路的总电阻等于各串联电阻之和,所以电源电压为:
U=I热(R热+R0)=0.03A×(100Ω+100Ω)=6V,
当水温为0℃时,电路中的电流为:
此时R0两端的电压,即电压表的示数为:U0′=I′R0=0.01A×100Ω=1V,
即改画的水温表刻度盘上的0℃应该与电压表刻度盘的1V位置对应。
答:(1)500;(2)当电压表示数达到最大值时,通过热敏电阻的电流是0.03A;
(3)改画的水温表刻度盘上的0℃应该与电压表刻度盘的1V位置对应。
27.解:(1)由电路图可知,电阻R0在电路起保护电路的作用。
(2)由电路图可知,电压表测滑动变阻器两端电压,被测身高增加时,滑动变阻器电阻棒接入电路的长度增加,
滑动变阻器接入电路的阻值变大,滑动变阻器的分压变大,因此电压表示数变大。
根据欧姆定律可知,电路中电流变小,故电流表示数变小。
(3)由欧姆定律得,电路总电阻:
则滑动变阻器接入电路的阻值:
RPb1=R总1-R0=9Ω-5Ω=4Ω。
(4)当电压表的示数为3V,R0两端的电压:
U0=U-UR=4.5V-3V=1.5V,
电路中的电流:
此时身高测量仪测量的身高最大,电阻棒接入电路中的电阻最大,
最大阻值为:
故答案为:(1)保护电路;(2)变大;变小;(3)电阻棒R接入电路的电阻为4Ω;
(4)随着身高而变化大小的R能接入电路的最大阻值是10Ω。
28.解:(1)闭合开关,两电阻串联接入电路,电压表测滑动变阻器两端的电压,电流表测通过电路的电流,
当滑片P置于最下端时,滑动变阻器接入电路最大阻值,电流表示数为0.1A,则电压表示数为:UP=IRP=0.1A×60Ω=6V;
(2)当滑动变阻器接入电路的电阻为0时,电路为定值电阻的简单电路,根据欧姆定律可知此时通过电路的电流最大,由丙图可知通过电路的最大电流为0.3A,
根据欧姆定律可得电源电压:U=IR0=0.3A×R0------①,
因串联电路总电压等于各部分电压之和,通过电路的电流为0.1A时,根据欧姆定律可得电源电压:U=UP+I′R0=6V+0.1A×R0------②,
联立①②可得:R0=30Ω,U=9V;
(3)当电压表的示数为3V时,定值电阻两端的电压:U0=U-UP′=9V-3V=6V,
此时通过定值电阻的电流:
串联电路各处电流相等,此时滑动变阻器接入电路的阻值:
由乙图可知滑动变阻器的长度为195m-175m,滑片位于最下端时水位的高度为175m,
,浮子上升的距离:ΔL=×(195m-175m)=15m,则此时的警戒水位为175m+15m=190m。
答:(1)当滑片P置于最下端时,电流表示数为0.1A,电压表示数为6V;
(2)电源电压为9V,R0的阻值为30Ω;
(3)当电压表的示数为3V时,报警装置发出警报,警戒水位为190m。
同课章节目录
