北师大版八年级数学上册7.5.2 三角形的内角和定理——三角形的外角学案(无答案)
文档属性
| 名称 | 北师大版八年级数学上册7.5.2 三角形的内角和定理——三角形的外角学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 360.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-21 00:00:00 | ||
图片预览

文档简介
年级 八年级 班级 学生姓名 科目 数学 制作人 编号
第七章 平行线的证明
7.5.2 三角形的内角和定理——三角形的外角
一、学习目标
1.了解并掌握三角形的外角的定义;
2.掌握三角形的外角的性质,能够利用三角形外角的性质进行简单的证明和计算.
二、导学指导与检测
导学指导 导学检测与课堂展示
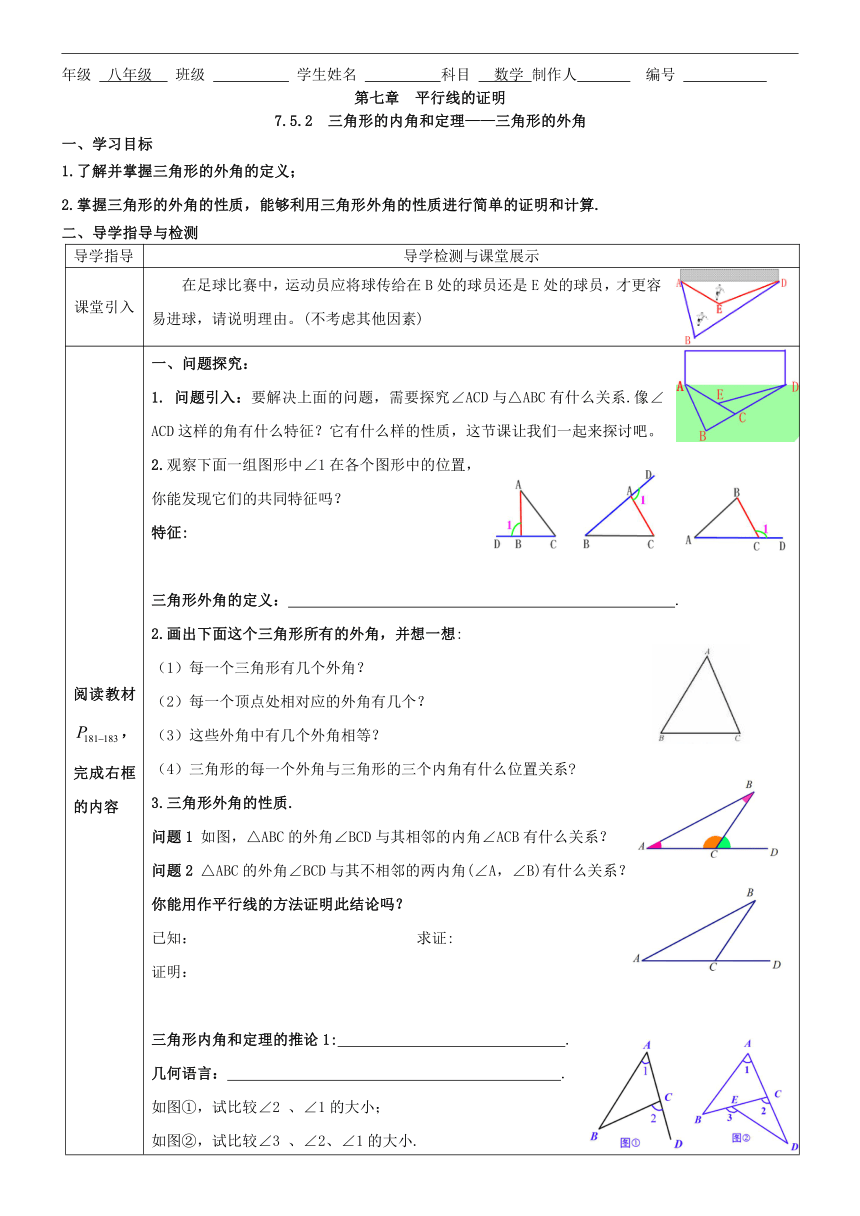
课堂引入 在足球比赛中,运动员应将球传给在B处的球员还是E处的球员,才更容易进球,请说明理由。(不考虑其他因素)
阅读教材,完成右框的内容 一、问题探究:1. 问题引入:要解决上面的问题,需要探究∠ACD与△ABC有什么关系.像∠ACD这样的角有什么特征?它有什么样的性质,这节课让我们一起来探讨吧。 2.观察下面一组图形中∠1在各个图形中的位置,你能发现它们的共同特征吗?特征:三角形外角的定义: .2.画出下面这个三角形所有的外角,并想一想:(1)每一个三角形有几个外角?(2)每一个顶点处相对应的外角有几个?(3)这些外角中有几个外角相等?(4)三角形的每一个外角与三角形的三个内角有什么位置关系 3.三角形外角的性质.问题1 如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?问题2 △ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?你能用作平行线的方法证明此结论吗?已知: 求证:证明:三角形内角和定理的推论1: .几何语言: .如图①,试比较∠2 、∠1的大小;如图②,试比较∠3 、∠2、∠1的大小.三角形内角和定理的推论2: .几何语言: .二、应用:1.如图,在△ABC中,AD平分外角∠EAC,∠B=∠C. 求证:AD∥BC.2.已知:如图,P是△ABC内一点,连接PB,PC.求证:∠BPC>∠A.3.如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
巩固诊断 A层 1.判断下列命题的对错.
(1)三角形的外角和是指三角形的所有外角的和.( )(2)三角形的外角和等于它的内角和的2倍.( )
(3)三角形的一个外角等于两个内角的和.( )(4)三角形的一个外角大于任何一个内角. ( )
(5)三角形的一个外角等于与它不相邻的两个内角的和.( )
(6)三角形的一个内角小于任何一个与它不相邻的外角.( )
2.如图, AB//CD, ∠A=37°, ∠C=63°, 那么∠F 等于( ).
A.26° B.63° C.37° D.60°
3.如图,试求出∠A+∠B+∠C+∠D+∠E+∠F= .
4.如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;(2)∠C的度数.
B层 5.如图,∠A=51°,∠B=20°,∠C=30°.(1)求∠BDC的度数.(2)∠BDC与∠A、∠B、∠C有何关系?
6.如图,求∠A+∠B+∠C+∠D+∠E的度数.
C层 6.如图,D是△ABC的BC边上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数
第七章 平行线的证明
7.5.2 三角形的内角和定理——三角形的外角
一、学习目标
1.了解并掌握三角形的外角的定义;
2.掌握三角形的外角的性质,能够利用三角形外角的性质进行简单的证明和计算.
二、导学指导与检测
导学指导 导学检测与课堂展示
课堂引入 在足球比赛中,运动员应将球传给在B处的球员还是E处的球员,才更容易进球,请说明理由。(不考虑其他因素)
阅读教材,完成右框的内容 一、问题探究:1. 问题引入:要解决上面的问题,需要探究∠ACD与△ABC有什么关系.像∠ACD这样的角有什么特征?它有什么样的性质,这节课让我们一起来探讨吧。 2.观察下面一组图形中∠1在各个图形中的位置,你能发现它们的共同特征吗?特征:三角形外角的定义: .2.画出下面这个三角形所有的外角,并想一想:(1)每一个三角形有几个外角?(2)每一个顶点处相对应的外角有几个?(3)这些外角中有几个外角相等?(4)三角形的每一个外角与三角形的三个内角有什么位置关系 3.三角形外角的性质.问题1 如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?问题2 △ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?你能用作平行线的方法证明此结论吗?已知: 求证:证明:三角形内角和定理的推论1: .几何语言: .如图①,试比较∠2 、∠1的大小;如图②,试比较∠3 、∠2、∠1的大小.三角形内角和定理的推论2: .几何语言: .二、应用:1.如图,在△ABC中,AD平分外角∠EAC,∠B=∠C. 求证:AD∥BC.2.已知:如图,P是△ABC内一点,连接PB,PC.求证:∠BPC>∠A.3.如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
巩固诊断 A层 1.判断下列命题的对错.
(1)三角形的外角和是指三角形的所有外角的和.( )(2)三角形的外角和等于它的内角和的2倍.( )
(3)三角形的一个外角等于两个内角的和.( )(4)三角形的一个外角大于任何一个内角. ( )
(5)三角形的一个外角等于与它不相邻的两个内角的和.( )
(6)三角形的一个内角小于任何一个与它不相邻的外角.( )
2.如图, AB//CD, ∠A=37°, ∠C=63°, 那么∠F 等于( ).
A.26° B.63° C.37° D.60°
3.如图,试求出∠A+∠B+∠C+∠D+∠E+∠F= .
4.如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;(2)∠C的度数.
B层 5.如图,∠A=51°,∠B=20°,∠C=30°.(1)求∠BDC的度数.(2)∠BDC与∠A、∠B、∠C有何关系?
6.如图,求∠A+∠B+∠C+∠D+∠E的度数.
C层 6.如图,D是△ABC的BC边上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
