【培优集训】2024年浙江省杭州市近2年八年级精选期末压轴真题集训40题(含解析)
文档属性
| 名称 | 【培优集训】2024年浙江省杭州市近2年八年级精选期末压轴真题集训40题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-20 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【培优集训】2024年浙江省杭州市近2年八年级精选期末压轴真题集训
一.选择题
1.如图,在△ABC中,AE⊥BC于点E,BD⊥AC于点D,点F是AB的中点,连接DF,EF,设∠ACB=x°,∠DFE=y°,则( )
A. B.y=x﹣30 C.y=90﹣x D.y=180﹣2x
2.如图,已知AB∥CD,∠ACD=70°,CE平分∠ACD交AB于点E,点P为线段CE上一点,∠CAP与∠EAP度数之比为k、若△ACP为直角三角形,且AP>PE,则k的值为( )
A.1 B. C.或1 D.1或
3.如图,在△ABC中,AB=BC=AC,AE=CD,AD与BE相交于点P,BQ⊥AD于Q.则BP与BQ的关系为( )
A.BP2=2BQ2 B.3BP2=4BQ2 C.4BP2=3BQ2 D.2BP2=3BQ2
4.如图,在△ABC中,AB=AC,点D是边AC的中点,点E在边BC上(不与点B,C重合),连接DE.( )
A.若AC>2DE,则BE>3EC B.若AC<2DE,则EC>3BE
C.若BE>3EC,则AC>2DE D.若BE<3EC,则AC<2DE
5.如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
①BF=CF;
②若BE⊥AC,则CF=DF;
③连结EF,若BE⊥AC,则∠DFE=2∠ABE;
④若BE平分∠ABC,则FG.
A.①②③ B.③④ C.①②④ D.①②③④
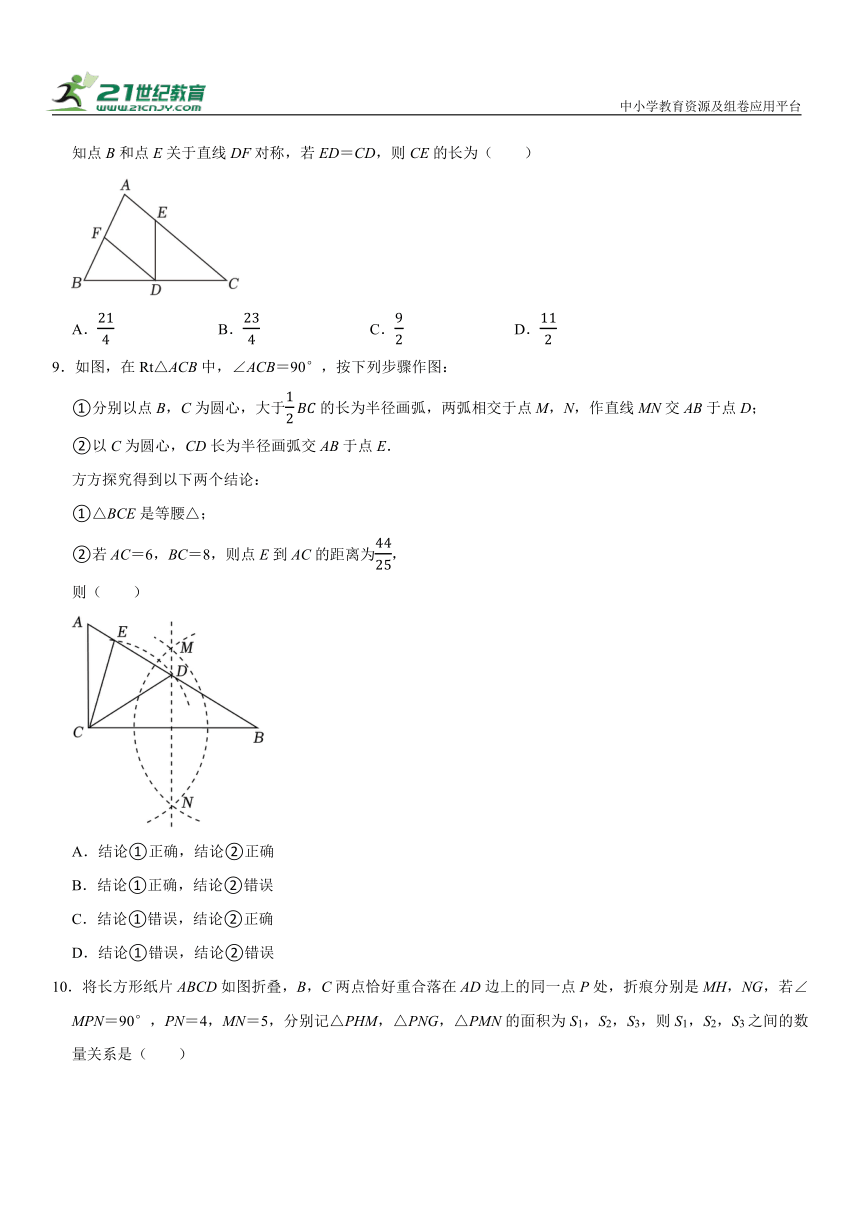
6.如图,在Rt△ABC中,∠ACB=90°,分别以Rt△ABC的三边为边在AB的同侧作三个正方形,顶点H恰为DE的中点,若阴影部分(四边形KNCM)的面积为9,则正方形ABHK的面积为( )
A.50 B.49 C.48 D.45
7.如图,在等腰直角△ABC中,点E,F将斜边AC三等分,且AC=12,点P在△ABC的边上,则满足PE+PF=9的点P的个数是( )
A.0个 B.2个 C.4个 D.6个
8.如图,在△ABC中,CA=CB=8,AB=6,∠C<90°,点D,E,F分别在边BC,AC,AB上,连接DF,DE.已知点B和点E关于直线DF对称,若ED=CD,则CE的长为( )
A. B. C. D.
9.如图,在Rt△ACB中,∠ACB=90°,按下列步骤作图:
①分别以点B,C为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点D;
②以C为圆心,CD长为半径画弧交AB于点E.
方方探究得到以下两个结论:
①△BCE是等腰△;
②若AC=6,BC=8,则点E到AC的距离为,
则( )
A.结论①正确,结论②正确
B.结论①正确,结论②错误
C.结论①错误,结论②正确
D.结论①错误,结论②错误
10.将长方形纸片ABCD如图折叠,B,C两点恰好重合落在AD边上的同一点P处,折痕分别是MH,NG,若∠MPN=90°,PN=4,MN=5,分别记△PHM,△PNG,△PMN的面积为S1,S2,S3,则S1,S2,S3之间的数量关系是( )
A.S3=S1+S2 B.3S3=2S1+2S2
C.2S3=3S2﹣S1 D.S3=5S2﹣5S1
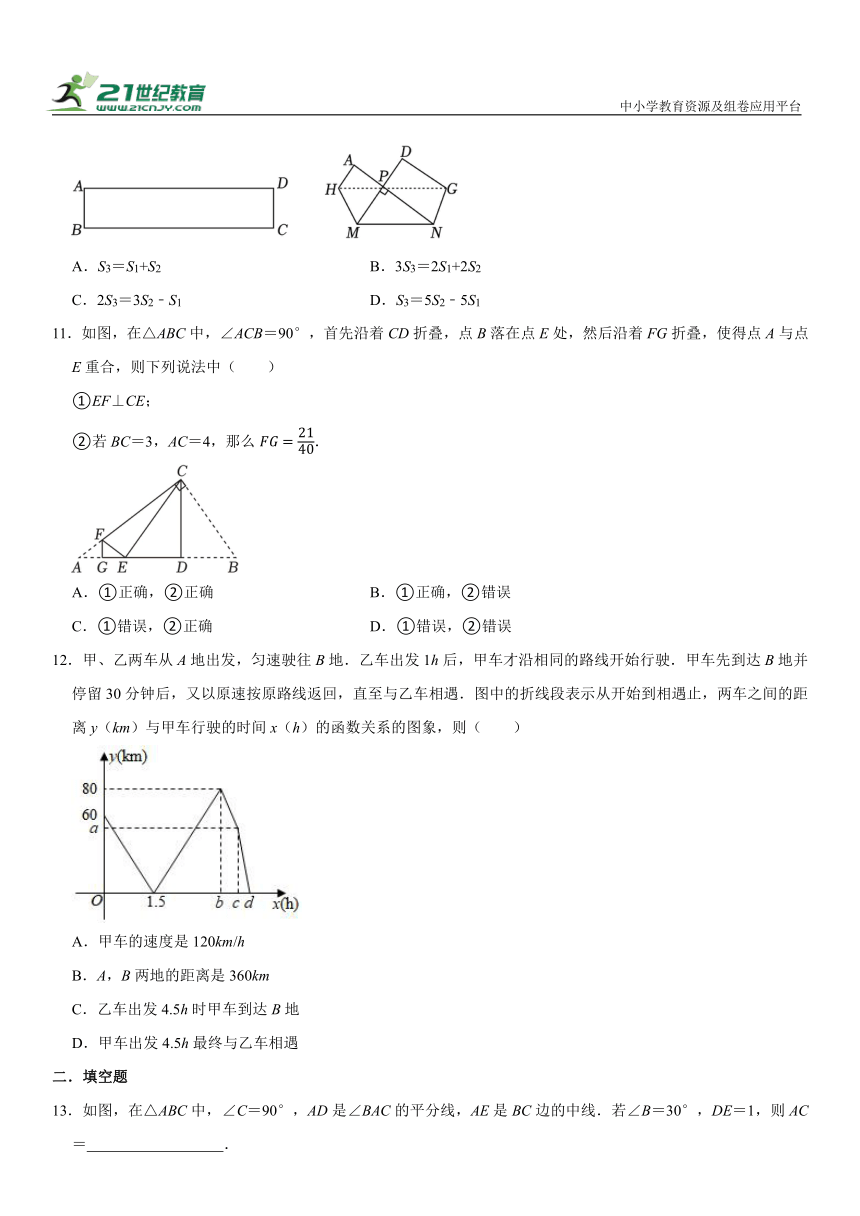
11.如图,在△ABC中,∠ACB=90°,首先沿着CD折叠,点B落在点E处,然后沿着FG折叠,使得点A与点E重合,则下列说法中( )
①EF⊥CE;
②若BC=3,AC=4,那么.
A.①正确,②正确 B.①正确,②错误
C.①错误,②正确 D.①错误,②错误
12.甲、乙两车从A地出发,匀速驶往B地.乙车出发1h后,甲车才沿相同的路线开始行驶.甲车先到达B地并停留30分钟后,又以原速按原路线返回,直至与乙车相遇.图中的折线段表示从开始到相遇止,两车之间的距离y(km)与甲车行驶的时间x(h)的函数关系的图象,则( )
A.甲车的速度是120km/h
B.A,B两地的距离是360km
C.乙车出发4.5h时甲车到达B地
D.甲车出发4.5h最终与乙车相遇
二.填空题
13.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,AE是BC边的中线.若∠B=30°,DE=1,则AC= .
14.若一次函数y=kx+b(k为常数且k≠0)的图象过点(2,﹣4),且经过第二、三、四象限.
(1)b= .(请用含k的代数式表示)
(2)若m=k+3b,则m的取值范围是 .
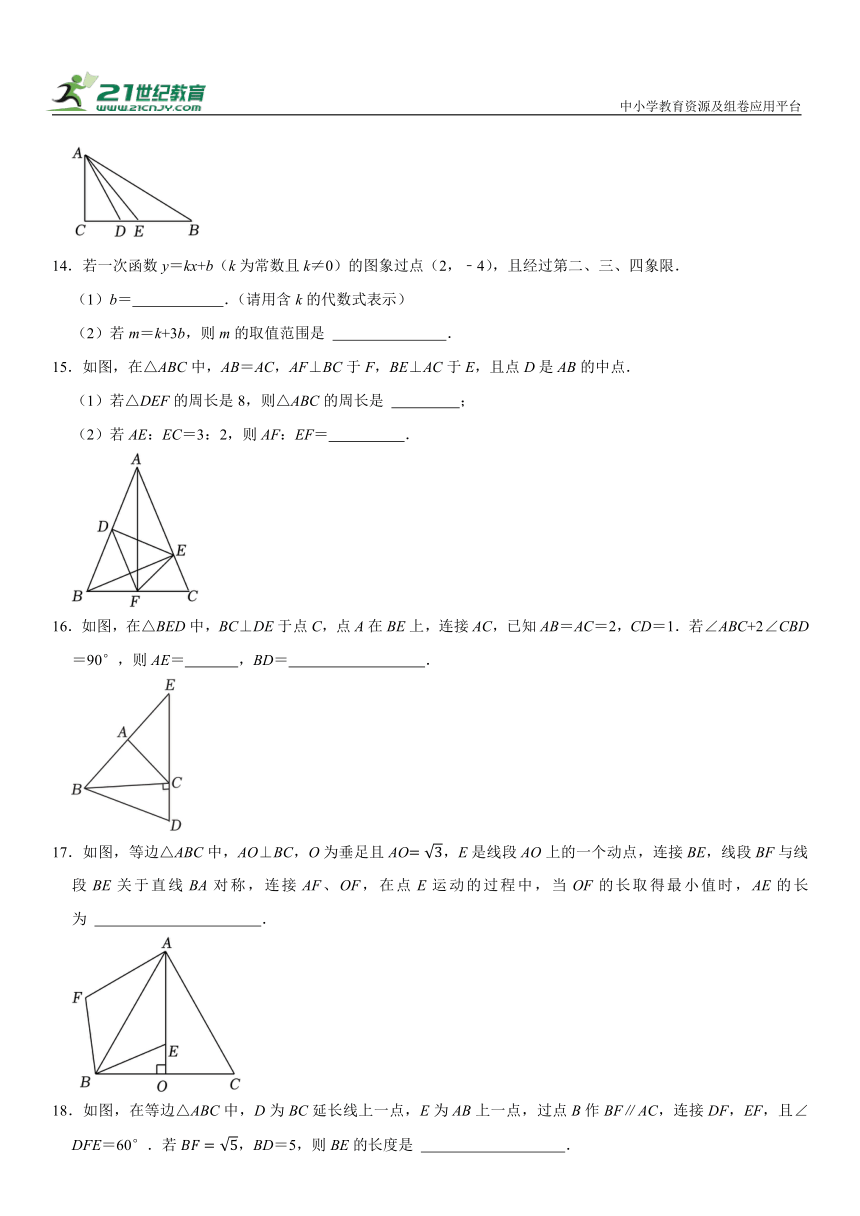
15.如图,在△ABC中,AB=AC,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点.
(1)若△DEF的周长是8,则△ABC的周长是 ;
(2)若AE:EC=3:2,则AF:EF= .
16.如图,在△BED中,BC⊥DE于点C,点A在BE上,连接AC,已知AB=AC=2,CD=1.若∠ABC+2∠CBD=90°,则AE= ,BD= .
17.如图,等边△ABC中,AO⊥BC,O为垂足且AO,E是线段AO上的一个动点,连接BE,线段BF与线段BE关于直线BA对称,连接AF、OF,在点E运动的过程中,当OF的长取得最小值时,AE的长为 .
18.如图,在等边△ABC中,D为BC延长线上一点,E为AB上一点,过点B作BF∥AC,连接DF,EF,且∠DFE=60°.若,BD=5,则BE的长度是 .
19.在一条笔直的公路上有A,B两地,甲骑自行车匀速从A地到B地,乙骑摩托车匀速从B地到A地,到达A地后立即按原路匀速返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象.若两人之间的距离不超过5km时,能够用无线电对讲机保持联系,甲、乙两人能够用无线电对讲机保持联系时.则x的取值范围是 .
20.清代数学家李锐在其著作《勾股算术细草》中利用三个正方形出入相补的方法证明了勾股定理.如图,在Rt△ABC中,∠ACB=90°,分别以AB,AC和BC为边,按如图所示的方式作正方形ABKH,ACIG和BCFD,KH与CI交于点J,AB与DF交于点E.若四边形BCFE和△HIJ的面积和为5,四边形ACJH和△BDE的面积和为12,则AC+BC的值为 .
21.如图,在矩形ABCD中,点E在边AD上,△CDE沿CE折叠得到△CFE,且点B,F,E三点共线,连接DF,若,DE=3,则AE= ,DF= .
22.如图,在长方形ABCD中,△AEF为等腰Rt△,且∠AEF=90°,点E在线段BC上,点F在线段CD上,若3(AB+BE)=2(AD+DF),则 .
23.如图,已知在Rt△ABC中,∠B=90°,AB=3,BC=4,点D,E分别在边BC,AC上,连接AD,DE.将△ABD沿AD翻折,将△DCE沿DE翻折,翻折后,点B,C分别落在点B′,C′处,且边DB′与DC′在同一直线上,连接AC′,当△ADC′是以AD为腰的等腰三角形时,则BD= .
24.如图,△ABC中,AB=AC,AD⊥BC于点D,DE平分∠ADC,交AC与点E,EF⊥AB于点F,且交AD于点G,若AG=2,BC=12,则AF= .
三.解答题
25.设两个不同的一次函数y1=kx+b,y2=bx+k(k,b是常数,且kb≠0).
(1)若函数y1的图象经过点(2,﹣1),函数y2的图象经过点(1,﹣3),求k,b的值.
(2)若函数y1的图象经过点(r,0),求证:函数y2的图象经过点;
(3)设y3=y1﹣y2,y4=y2﹣y1,当y3>y4时,求x的取值范围.
26.综合与实践:数学课上,老师让同学们根据下面情境提出问题并解答:
问题情境:如图1,在Rt△ABC中,AB=BC,∠ABC=90°,点P是斜边AC上动点,点E在直线BC上,满足PB=PE,过点E作EQ⊥AC,垂足为Q,设∠PBE=α.
圆圆同学提出的问题:探究PQ与AC之间的数量关系;
方方同学提出的问题:探究AP,PQ,QC之间的数量关系;
经过小组讨论,第一小组提出解决问题的思路:取AC中点D,连接BD,可以证明:△BDP≌△PQE,从而得到对应线段相等…
请你继续完成以下问题:
(1)特例探究:从特殊到一般是研究几何问题的常用方法,如图1,当α=60°时,请直接写出PQ与AC这两条线段长度之间的数量关系 ;
(2)数学思考:如图2,当45°≤α≤90°时,
①PQ与AC这两条线段长度之间的数量关系: ;
②探究AP,PQ,QC这三条线段长度之间的数量关系得: ;并写出探究过程;
(3)延伸拓展:如图3,当0°≤α<45°时,探究AP,PQ,QC这三条线段长度之间的数量关系得: ;并写出探究过程.
27.如图,在△ABC中,AB=AC,点D在边BC上(不与点B,C重合),且BD>CD,过点D作DP⊥BC,分别交BA的延长线和AC于点P和点Q.
(1)求证:AP=AQ.
(2)若点Q是线段DP的中点,探索AQ与QC的数量关系.
(3)若△ABC的形状和大小都确定,说说DP+DQ的值是否为定值,如果是定值,直接写出这个定值的几何意义;如果不是定值,说明理由.
28.综合与实践
问题情境:“综合与实践”课上,老师请同学们探索一次函数的图象与系数的关系.老师给出两个一次函数y1=ax﹣b,y2=bx﹣a(a,b均不为0,且a≠b),同学们利用图形计算器画出a,b不同取值下的两个一次函数的图象,并观察它们的交点位置.三个小组分别绘制了当a=1,b=2;a=2,b=﹣1;a=﹣1,b=﹣2时的函数图象,得到了不同情况下函数y和y2的图象的交点坐标.
数学思考:(Ⅰ)请从(1)当a=1,b=2时;(Ⅱ)当a=2,b=﹣1时;(Ⅲ)当a=﹣1,b=﹣2时,三组值中任选一组,求此时函数y1和y2的图象的交点坐标.
注:如果选择多组条件分别作答,按第一个解答计分.
深入探究:(2)老师请同学们经过思考,提出新的问题.
①“运河小组”提出问题:不论a,b如何取值,函数y1和y2的图象的交点的横坐标都是定值.请你证明结论,并求出这个定值.
②“武林小组”提出问题:若a>b,要比较y1和y2的大小,需要分类讨论.请你比较y1和y2的大小.
③不论a,b如何取值,当x等于某个正数时,函数y1和y2的值都存在某种确定的等量关系,请你直接写出结论.
29.如图,为了测量一条两岸平行的河流宽度,由于跨河测量困难,所以,三个数学研究小组设计了不同的方案,他们在河南岸的点B处,测得河北岸的一棵树底部A点恰好在点B的正北方向,测量方案如下表:
课题 测量河流宽度
工具 测量角度的仪器(仪器的高度忽略不计),标杆,皮尺等
小组 第一小组 第二小组 第三小组
测量方案 观测者从B点向正东走到C点,此时恰好测得:∠ACB=45° 观测者从B点向正东走到E点,O是BE的中点,继续从点E沿垂直于BE的EF方向走,直到点A,O,F在一条直线上.
测量示意图
(1)第一小组认为,河宽AB的长度就是线段 的长度.
(2)第二小组方案灵感来源于古希腊哲学家泰勒斯,他们认为只要测得EF的长就是所求河宽AB的长,你认为第二小组的方案可行吗?如果可行,请给出证明;如果不可行,请说明理由.
(3)请你代表第三小组,设计一个测量方案,把测量方案和测量示意图填入上表,然后指明你画的示意图中,只要测出哪条线段的长,就能推算出河宽AB长,并说明方案的可行性.
30.在△ABC中,AB=AC,点P为线段BC上任意一点(P与B,C不重合),连接AP.
(1)若BC=16,AB=10,
①求AP的最小值.
②当AP=7时,求BP的长.
(2)若AB=m,AP=n,请用含m,n的代数式表示BP PC,并说明理由.
31.综合与实践
【情境描述】
圆圆想把一些相同规格的塑料杯,尽可能多地放入高40cm的柜子里(如图1).她把杯子按如图这样整齐地叠放成一摞(如图2),但她不知道一摞最多能叠几个可以一次性放进柜子里.
【观察发现】
圆圆测量后发现,按这样叠放,这摞杯子的总高度随着杯子数量的变化而变化,记录的数据如下表所示:
杯子的数量x(只) 1 2 3 4 5 6 …
总高度h(cm) 10 11.4 12.8 14.2 15.6 17 …
【建立模型】
(1)请根据上表中的信息,在平面直角坐标系中描出对应点,观察这些点的分布规律,试求h关于x的函数表达式.
(2)当杯子的数量为12只时,求这摞杯子的总高度.
【解决问题】
请帮圆圆算一算,一摞最多能叠几个杯子,可以一次性放进柜子里?
32.综合与实践
生活中的数学:如何确定单肩包最佳背带长度
素材1 如图是一款单肩包,背带由双层部分、单层部分和调节扣构成.使用时可以通过调节扣加长或缩短单层部分的长度,使背带的总长度加长或缩短(总长度为单层部分与双层部分的长度和,其中调节扣的长度忽略不计).
素材2 对于该背包的背带长度进行测量,设双层的部分长度是x cm,单层部分的长度是y cm,得到如下数据: 双层部分长度x(cm)261014a单层部分长度y(cm)1161081009270
素材3 单肩包的最佳背带总长度与身高比例为2:3
素材4 小明爸爸准备购买此款背包.爸爸自然站立,将该背包的背带调节到最短提在手上,背带在背包的悬挂点离地面的高度为53.5cm;已知爸爸的臂展和身高一样,且肩宽为38cm,头顶到肩膀的垂直高度为总身高的.
任务1 在平面直角坐标系中,以所测得数据中的x为横坐标,以y为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量x、y是否满足一次函数关系.如果是,求出该函数的表达式,直接写出a值并确定x的取值范围.
任务2 设人身高为h,当单肩包背带长度调整为最佳背带总长度时,求此时人身高h与这款背包的背带双层部分的长度x之间的函数表达式.
任务3 当小明爸爸的单肩包背带长度调整为最佳背带总长度时.求此时双层部分的长度.
33.一次函数y1=kx+b(k≠0)恒过定点(3,2).
(1)若一次函数y1=kx+b还经过(0,5)点,求k的值;
(2)一次函数y1=kx+b不经过第四象限,求k的取值范围;
(3)另一函数y2=x﹣1,满足y1﹣y2=b+1,且k≠1,求x的值.
34.小王骑自行车从家出发沿公路匀速前往新华书店,小王妈妈骑电瓶车从新华书店出发沿同一条路回家,线段OA与折线B﹣C﹣D﹣E分别表示两人离家的距离y(km)与小王的行驶时间t(h)之间的函数关系的图象,请解决以下问题.
(1)求OA的函数表达式;
(2)求CD的函数表达式;
(3)求点K的坐标;
(4)设小王和妈妈两人之间的距离为S(km),当S≤3时,求t的取值范围.
35.如图,在△ABC中,AB=AC,点D在AC边上(不与A,C重合),连接BD,BD=AB.
(1)设∠C=α,∠ABD=β.
①当α=50°时,求β.
②请求出β与α的数量关系.
(2)若AB=5,BC=6,求AD的长.
36.如图,在Rt△ABC中,∠CAB=90°,点D是边BC的中点,以AD为底边向上作等腰△ADH,使得∠ADH=∠C,DH交AB于点K,
(1)若∠B=20°,求∠H度数;
(2)若HD=BC.
①求证:AD=2AC;
②设AC=a,求HK的长(用含a的代数式表示).
37.如图,在△ABC中,AB=AC,∠BAC=120°,延长BA至点D,使,连结CD,作∠BAC的平分线与∠BDC的平分线交于点E,连结EB,EC.
(1)求证:AD⊥CD;
(2)求∠DBE的度数;
(3)求的值.
38.如图1,已知△ABC和△DBE都是等边三角形,且点D在边AC上,AD>CD.
(1)求证:△ABD≌△CBE.
(2)求∠DCE的度数.
(3)如图2,过点B作BF⊥AC于点F,设△BCE的面积为S1,△BCD的面积为S2,求△BFD的面积(用含S1,S2的代数式表示).
39.【综合与实践】
问题情景:
在数学活动课上,老师展示一张直角三角形纸片,如图1,在Rt△ABC中,∠A=90°,AB=6,AC=4,点E,F分别在AB,AC上,将△AEF沿EF折叠得△DEF,使点A的对应点D落在线段CE上.各学习小组先解决老师提出的问题,然后又提出了新的数学问题,请你解决这些问题.
问题解决:
(1)老师提出问题:如图1,若∠ACE=30°,求AE:AF的值.
深入探究:
(2)如图2,勤学小组提出问题:若CE是AB边上的中线,求AE:AF的值.
拓展探究:
(3)如图3,奋进小组提出问题:将直角三角形纸片换成等边三角形纸片,即在等边△ABC中,若CE是AB边上的中线,求AE:AF的值.
40.【问题背景】如图①,在四边形ABCD中,∠A和∠C称为它的对角,若这个四边形满足:∠A+∠C=180°,则这个四边形叫作为“对角互补四边形”.
【问题解决】
(1)若四边形ABCD是“对角互补四边形”,且∠B=3∠D,求∠B的度数;
(2)如图②,∠MON=60°,OB平分∠MON,A是射线OM上一动点,C是射线OM上的动点,且四边形COAB是“对角互补四边形”.
①若△COB是等腰三角形,求∠BAN的度数;
②若OB=m,若S△BOC:S△BOA=n,求OC的长(用含m、n的代数式表示).
参考答案
一.选择题
1.【分析】由垂直的定义得到∠ADB=∠BEA=90°,根据直角三角形的性质得到AF=DF,BF=EF,根据等腰三角形的性质得到∠DAF=∠ADF,∠EFB=∠BEF,于是得到结论.
【解答】解:∵AE⊥BC于点E,BD⊥AC于点D,
∴∠ADB=∠BEA=90°,
∵点F是AB的中点,
∴AF=DF,BF=EF,
∴∠DAF=∠ADF,∠EBF=∠BEF,
∴∠AFD=180°﹣2∠CAB,∠BFE=180°﹣2∠ABC,
∴∠DFE=180°﹣∠AFD﹣∠BFE=2(∠CAB+∠CBA)﹣180°=2(180°﹣∠ACB)﹣180°=180°﹣2∠ACB,
∴y=180°﹣2x,
故选:D.
2.【分析】设∠EAP=x,则∠CAP=kx.根据角平分线定义及平行线的性质求出∠AEP=∠ECD=35°,根据题意求出x<35°,进而推出∠APC<70°,则∠CAP=kx=90°,据此求解即可.
【解答】解:设∠EAP=x,则∠CAP=kx.
∵CE平分∠ACD,∠ACD=70°,
∴∠ACE=∠ECD=35°,
∵AB∥CD,
∴∠AEP=∠ECD=35°,
∵AP>PE,
∴∠EAP<∠AEP,
即x<35°,
∴∠APC=∠EAP+∠AEP=x+35°<70°,
∵△ACP为直角三角形,
∴kx=90°,
∴∠ACP+∠APC=90°,
即35°+x+35°=90°,
解得x=20°,
∴,
故选:B.
3.【分析】由已知可得△ABC是等边三角形,从而得到∠BAC=∠C=60°,根据SAS即可判定△ADC≌△BEA,根据全等三角形的性质可得到∠ABE=∠CAD,再根据等角的性质即可求得∠BPQ=60°,再根据余角的性质得到∠PBQ=30°,根据在直角三角形中30°的角对的边是斜边的一半即可证得结果,由勾股定理可得出答案.
【解答】解:∵AB=BC=AC,
∴△ABC是等边三角形.
∴∠BAC=∠C=60°.
∵AB=AC,AE=CD,
∴△ADC≌△BEA(SAS),
∴∠ABE=∠CAD.
∵∠CAD+∠BAD=60°,
∴∠ABE+∠BAD=60°.
∴∠BPQ=60°.
∵BQ⊥AD,
∴∠PBQ=30°.
∴BP=2PQ,
∵∠BQP=90°,
∴BP2﹣PQ2=BQ2,
∴BQ2,
∴3BP2=4BQ2,
故选:B.
4.【分析】过点D作DF∥AB,过点D作DE′⊥BC于E′,可得DF是△ABC的中位线,可得AB=AC=2DF,则DF=DC,根据等腰三角形的性质得BC=2CF=4E′C,根据三角形角和边的关系即可求解.
【解答】解:过点D作DF∥AB,过点D作DE′⊥BC于E′,
∵点D是边AC的中点,
∴DF是△ABC的中位线,
∵AB=AC,
∴AB=AC=2DF,BF=CF,
∴DF=DC,
∵DE′⊥BC于E′,
∴CF=2E′C,DE′<DF,
∴BC=2CF=4E′C,
∴BE′=3E′C,
∵∠DFC=∠DEC+∠EDF,
∴DE>DF,
∴若AC>2DE,则BE>EC;若AC<2DE,则EC>BE,若BE>3EC,则AC>2DE;若BE<EC,则AC<2DE.
故选:C.
5.【分析】由“SAS”可证△BAE≌△CAD,可得∠ABE=∠ACD,可证∠GBC=∠GCB,可得BG=CG,则点G是BC的中垂线上,由线段垂直平分线的性质可得BF=CF,故①正确;
由全等三角形的性质可得∠ADC=∠AEB=90°,由直角三角形的性质可得CF=DF,故②正确;
由等腰三角形的性质和三角形内角和定理可得2∠DBF+2∠ECF﹣∠DFE=180°,由∠BAC+∠ABC+∠ACB=180°,可得∠DFE=2∠ABE,故③正确;
由角平分线的性质可证点G是角平分线的交点,可得点G到三边距离相等,由面积法可求FG,故④正确;即可求解.
【解答】解:在△BAE和△CAD中,
,
∴△BAE≌△CAD(SAS),
∴∠ABE=∠ACD,
∵AB=AC=5,
∴∠ABC=∠ACB,
∴∠GBC=∠GCB,
∴BG=CG,
∴点G是BC的中垂线上,
∵AB=AC,
∴点A在BC的中垂线上,
∴AG垂直平分BC,
∴BF=CF,故①正确;
若BE⊥AC,则∠AEB=90°,
∵△BAE≌△CAD,
∴∠ADC=∠AEB=90°,
∴∠BDC=90°,
又∵BF=CF,
∴CF=DF,故②正确;
如图,连接EF,
若BE⊥AC,则∠AEB=90°,
∵△BAE≌△CAD,
∴∠ADC=∠AEB=90°,
∴∠BDC=90°=∠BEC,
又∵BF=CF,
∴CF=DF=EF=BF,
∴∠DBF=∠BDF,∠FEC=∠FCE,
∴2∠DBF+∠DFB=180°,2∠ECF+∠EFC=180°,
又∵∠DFB+∠EFC+∠DFE=180°,
∴2∠DBF+2∠ECF﹣∠DFE=180°,
∵∠BAC+∠ABC+∠ACB=180°,
∴2∠BAC+2∠ABC+2∠ACB=360°,
∴2∠BAC+180°+∠DFE=360°,
∴2∠BAC+∠DFE=180°,
∵∠BAC+∠ABE=90°,
∴∠DFE=2∠ABE,故③正确,
若BE平分∠ABC,
∴∠ABE=∠CBE∠ABC,
∵∠ABE=∠ACD,∠GBC=∠GCB,
∴∠ACD=∠BCD,
∴点G是角平分线的交点,
∴点G到三边的距离为GF的长,
∵AB=AC=5,BC=6,BF=CF,
∴BF=CF=3,
∴AF4,
∵S△ABCBC AFAB GFAC GFCB GF,
∴FG,故④正确;
故选:D.
6.【分析】由正方形的性质推出AB=BH=AK,BC=BE=DE,∠ABH=∠BAK=90°,∠E=90°,由HL证明Rt△ABC≌Rt△HBE,得到AC=HE,由H是DE中点,得到BC=2AC,由余角的性质推出∠ABC=∠KAB,又AK=AB,∠K=∠BAK,即可证明△BAP≌△AKM(ASA),得到△BAP是的面积=△AKM的面积,因此△ABC的面积=阴影的面积=9,由三角形面积公式得到△ABC的面积AC BC=AC2=9,由勾股定理得到AB2=AC2+BC2=AC2+4AC2=5AC2=45,即可得到正方形ABHK的面积.
【解答】解:∵四边形ABHK,四边形BCDE是正方形,
∴AB=BH=AK,BC=BE=DE,∠ABH=∠BAK=90°,∠E=90°,
∴Rt△ABC≌Rt△HBE(HL),
∴AC=HE,
∵H是DE中点,
∴HEDE,
∴BC=2AC,
∵∠ACB=90°,∠BAK=90°,
∴∠ABC+∠BAC=∠MAK+∠BAC=90°,
∴∠ABC=∠KAB,
∵AK=AB,∠K=∠BAK,
∴△BAP≌△AKM(ASA),
∴△BAP是的面积=△AKM的面积,
∴△ABC的面积=阴影的面积=9,
∵△ABC的面积AC BC=AC2=9,
∴AB2=AC2+BC2=AC2+4AC2=5AC2=45,
∴正方形ABHK的面积=AB2=45.
故选:D.
7.【分析】作点F关于BC的对称点M,连接FM交BC于点N,连接EM交BC于点H,连接CM、BE、BF、FH,可得点H到点E和点F的距离之和最小,求出最小值即可解答.
【解答】解:如图,作点F关于BC的对称点M,连接FM交BC于点N,连接EM交BC于点H,连接CM、BE、BF、FH,
∵点E,F将对角线AC三等分,且AC=12,
∴EC=8,FC=4=AE,
∵点M与点F关于BC对称,
∴CF=CM=4,∠ACB=∠BCM=45°,
∴∠ACM=90°,
∴,
即EH+HM=EH+HF=4,
则在线段BC存在点H到点E和点F的距离之和最小为,
在点H右侧,当点P与点C重合时,则PE+PF=12,
∴点P在CH上时,,有一个点P使PE+PF=9,
在点H左侧,当点P与点B重合时,,
∵AB=BC,CF=AE,∠BAE=∠BCF,
∴△ABE≌△CBF(SAS),
∴,
∴BE+BF=4,
∴点P在BH上时,有一个点P使PE+PF=9,
∴在线段BC上的左右两边各有一个点P使PE+PF=9,
同理在线段AB、AC上也都存在两个点使PE+PF=9.
即共有6个点P满足PE+PF=9,
故选:D.
8.【分析】如图,连接EB,过点C作CJ⊥AB于点J.首先证明BE⊥AC,利用面积法求出BE,再利用勾股定理求出CE.
【解答】解:如图,连接EB,过点C作CJ⊥AB于点J.
∵B,E关于DF对称,
∴DB=DE,
∵ED=DC,
∴DB=DE=DC,
∴∠BEC=90°,
∴BE⊥AC,
∵CA=CB=8,CJ⊥AB,
∴AJ=JBAB=3,
∴CJ,
∴S△ABC AB CJ AC BE,
∴BE,
∴CE.
故选:B.
9.【分析】①错误,理由反证法判断即可;
②正确.求出AE,再利用平行线分线段成比例定理求解.
【解答】解:①错误.当∠B=30°时,E,A重合,△BCE明显不是等腰三角形;
②正确.
理由:过点C作CH⊥AB于点H,过点E作EG⊥AC于点G.
∵AC=6,BC=8,∠ACB=90°,
∴AB10,
∴CH,
∴AH,
由作图可知DA=DC=DB=5,
∵CE=CD=5,
∴EH,
∴AE=AH=EH,
∵S△ACE AC EG AE CH,
∴EG,故②正确.
故选:C.
10.【分析】根据折叠的性质和三角形的面积公式即可得到结论.
【解答】解:过P作PE⊥BC于E,如图:
∵∠MPN=90°,PN=4,MN=5,
∴PM3,
∵将长方形纸片ABCD如图折叠,B,C两点恰好重合落在AD边上的同一点P处,折痕分别是MH,NG,
∴B与P关于直线MH对称,C与P关于直线NG对称,
∴∠CNG=∠PNG,
∵AD∥BC,
∴∠CNG=∠PGN,
∴∠PNG=∠PGN,
∴PG=PN=4,
同理PH=PM,
∵HG∥MN,
∴PE⊥HG,
∴S1,
S2PG PE4.
S36,
∴A.S1+S2S3,故该选项不符合题意;
B.2S1+2S23S3,故该选项不符合题意;
C.3S2﹣S1S3,故该选项不符合题意;
D.5S2﹣5S1=24﹣18=6,故该选项符合题意;
故选:D.
11.【分析】由∠ACB=90°,得∠A+∠B=90°,由折叠得∠FEG=∠A,∠CED=∠B,则∠FEG+∠CED=∠A+∠B=90°,所以∠CEF=90°,则EF⊥CE,可判断①正确;由BC=3,AC=4,根据勾股定理求得AB=5,而∠BDC=∠EDC180°=90°,所以5CD3×4=S△ABC,求得CD,进而求得DE=DB,则AE=AB﹣2DE,所以AG=EG,由EF=AF,EC=BC=3,CF=4﹣AF,根据勾股定理得AF2+32=(4﹣AF)2,求得AF,而∠AGF=∠EGF180°=90°,所以FG,可判断②正确,于是得到问题的答案.
【解答】解:∵∠ACB=90°,
∴∠A+∠B=90°,
由折叠得∠FEG=∠A,∠CED=∠B,
∴∠FEG+∠CED=∠A+∠B=90°,
∴∠CEF=180°﹣(∠FEG+∠CED)=90°,
∴EF⊥CE,
故①正确;
∵BC=3,AC=4,
∴AB5,
∵∠BDC=∠EDC180°=90°,
∴CD⊥AB,
∴5CD3×4=S△ABC,
∴CD,
∴DE=DB,
∴AE=AB﹣2DE=5﹣2,
∴AG=EGAE,
∵EF2+EC2=CF2,EF=AF,EC=BC=3,CF=4﹣AF,
∴AF2+32=(4﹣AF)2,
解得AF,
∵∠AGF=∠EGF180°=90°,
∴FG,
故②正确,
故选:A.
12.【分析】由图象可知两车起始距离为60,从而得到乙车速度,根据图象变化规律和两车运动状态,得到相关未知量.
【解答】解:乙车先行1小时的路程是60千米,因此乙车的速度为60千米/小时,
甲车出发1.5小时就追上乙,因此速度差为60÷1.5=40千米/小时,
故甲车的速度为100千米/小时,故选项A不合题意;
甲车追上乙车后到两车距离为80千米需要时间为80÷40=2(小时),
甲车行全程需要2+1.5=3.5(小时),
全程为100×3.5=350千米,故选项B不合题意;
此时乙车出发3.5+1=4.5(小时),故选项C符合题意;
甲车休息小时准备返回时乙车行3.5+1+0.5=5(小时),
此时乙车距B地350﹣60×5=50(千米),
返回时相遇时间为50÷(100+60)小时,
此时甲车行驶的时间为3.5+0.5(h),故选项D不合题意.
故选:C.
二.填空题
13.【分析】先求出∠CAB=60°,则∠CAD=∠BAD=30°=∠B,根据含30°角的直角三角形的性质可得ACCD,AD=BD=2CD,则BC=3CD,由AE是BC边的中线得CEBCCD,根据DE=1即可求解.
【解答】解:∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD是∠BAC的平分线,
∴∠CAD=∠BAD=30°=∠B,
∴AD=BD,ACCD,AD=2CD,
∴AD=BD=2CD,
∴BC=3CD,
∵AE是BC边的中线,
∴CEBCCD,
∵DE=1,
∴CE﹣CDCD﹣CD=1,
∴CD=2,
∴ACCD=2,
故答案为:2.
14.【分析】(1)根据题意列方程即可得到结论;
(2)根据题意列不等式,解不等式即可得到结论.
【解答】解:(1)∵一次函数y=kx+b(k为常数且k≠0)的图象过点(2,﹣4),
∴﹣4=2k+b,
∴b=﹣2k﹣4,
故答案为:﹣2k﹣4;
(2)∵函数图形过第二、三、四象限,
∴k<0,b<0,
∴﹣2k﹣4<0,
解得﹣2<k<0,
∵m=k+3b,
∴m=﹣5k﹣12,
∴﹣12<﹣5k﹣12<﹣2,
即﹣12<m<﹣2,
故答案为:﹣12<m<﹣2.
15.【分析】(1)根据等腰三角形的性质和直角三角形斜边上的中线等于斜边的一半性质证明△ABC的周长是△DEF的周长的2倍解答即可;
(2)根据题意设AE=3x,EC=2x,利用勾股定理和直角三角形斜边上的中线等于斜边的一半的性质求得AF和EF的值,进而解答即可.
【解答】解:∵AB=AC,AF⊥BC,
∴BF=CF,
∵BE⊥AC,点F为BC的中点,
∴BC=2EF,
∵BE⊥AC,点D是AB的中点.
∴AB=2DE,
∵点F为BC的中点,点D是AB的中点,
∴DF为△ABC的中位线,
∴AC=2DF,
∴△ABC的周长是△DEF的周长的2倍,
∵△DEF的周长是8,
∴△ABC的周长是16,
故答案为:16;
(2)∵AE:EC=3:2,
∴设AE=3x,EC=2x,
则AC=AB=5x,
在Rt△ABE中,根据勾股定理可得:BE=4x,
在Rt△BCE中,
∵CE=2x,BE=4x,
∴BC=2x,
∵BC=2EF,
∴EFx,
∵BC×AF=AC×BE,
即:2x×AF=5x×4x,
解得:AF=2x,
∴AF:EF=2x:x=2:1,
故答案为:2:1,
16.【分析】根据直角三角形的性质、等腰三角形的性质得到∠E=∠ACE,得到AE=AC=2,设∠E=∠ACE=x,根据题意得到∠ABD=90°x=∠D,再根据勾股定理计算即可.
【解答】解:∵AB=AC,
∴∠ABC=∠ACB.
∵BC⊥DE,
∴∠BCE=90°.
∴∠E+∠EBC=90°,∠ACE+∠ACB=90°,
∴∠E=∠ACE,
∴AE=AC=AB=2,
设∠E=∠ACE=x,则∠ACB=∠ABC=90°﹣x.
∵∠ABC+2∠CBD=90°,
∴∠CBDx,
∴∠ABD=∠ABC+∠CBD=90°x=∠D,
∴DE=BE=AB+AE=4,
∴CE=DE﹣CD=3.
在Rt△BCE中,BC,
∴BD2,
故答案为:2,2.
17.【分析】过点O作OH⊥AF于H,连接OF.首先证明∠BAF=30°,推出点F的在射线AF上运动,根据垂线段最短可知,当点F与H重合时,OF的值最小,最小值=OH的长.
【解答】解:过点O作OH⊥AF于H,连接OF.
∵△ABC是等边三角形,AO⊥BC,
∴∠BAO=∠CAO∠BAC=30°
∵线段BF与线段BE关于直线BA对称,
∴∠BAF=∠BAE=30°,∠OAF=60°,
∴点F的在射线AF上运动,
根据垂线段最短可知,当点F与H重合时,OF的值最小,
在Rt△AHO中,
∵∠AOH=30°,
∴AHOA,
∴AE=AH.
故答案为:.
18.【分析】在AB的延长线上截取BG=BF,连接FG,证明△BFG为等边三角形,然后证明△DFB≌△EFG,即可解答.
【解答】解:如图,在AB的延长线上截取BG=BF,连接FG,
∵△ABC 是等边三角形,
∴∠A=∠ACB=60°,
∵BF∥AC,
∴∠DBF=∠ACB=60°,∠GBF=∠A=60°,
又∵BG=BF,
∴△BFG 为等边三角形,
∴∠GFB=∠G=60°=∠DBF,,
又∵∠DFE=60°=∠DBF,
∴∠DFB=∠EFG,
∴△DFB≌△EFG,
∴EG=DB=5,
∴.
故答案为:5.
19.【分析】利用待定系数法分别求出甲、乙两人离B地的距离y与行驶时间x之间的函数关系式;按照x不同的取值范围,根据二者y之差的绝对值不大于5,列绝对值不等式并求解即可.
【解答】解:设甲离B地的距离y与行驶时间x之间的函数关系式为y=k1x+b1(k1、b1为常数,且k1≠0).
将x=0,y=30和x=2,y=0代入y=k1x+b1,
得,解得,
∴y=﹣15x+30(0≤x≤2);
当0≤x<1时,设乙离B地的距离y与行驶时间x之间的函数关系式为y=k2x(k2为常数,且k2≠0).
将x=1,y=30代入y=k2x,得k2=30,
∴y=30x(0≤x<1);
当1≤x≤2时,设乙离B地的距离y与行驶时间x之间的函数关系式为y=k3x+b2(k3、b2为常数,且k3≠0).
将x=1,y=30和x=2,y=0代入y=k3x+b2,
得,解得,
∴y=﹣30x+60(1≤x≤2);
综上,乙离B地的距离y与行驶时间x之间的函数关系式为y.
①当0≤x<1时,若两人之间的距离不超过5km,则|﹣15x+30﹣30x|≤5,
经整理,得|9x﹣6|≤1,解得x;
②当1≤x≤2时,若两人之间的距离不超过5km,则|﹣15x+30﹣(﹣30x+60)|≤5,
经整理,得|3x﹣6|≤1,解得x,
∴x≤2;
综上,x的取值范围是x或x≤2,
故答案为:x或x≤2.
20.【分析】可证明△AEF与△HJI全等,进而得出△ABC的面积,再将所给的面积全部相加,得出正方形BCFD和梯形ACIH的面积之和,用AC和BC的长将其表示出来即可解决问题.
【解答】解:由题知,
令BC=a,AC=b,
∵四边形ABKH和四边形ACIG是正方形,
∴∠BAH=∠CAG=90°,AB=AH,AC=AG,
∴∠BAH﹣∠CAH=∠CAG﹣∠CAH,
即∠BAC=∠HAG.
在△BAC和△HAG中,
,
∴△BAC≌△HAG(SAS),
∴HG=BC=a.
又∵AF=b﹣a,IH=b﹣a,
∴AF=IH.
∵∠HAG+∠AHG=∠AHG+∠JHI=90°,
∴∠HAG=∠JHI,
∴∠BAC=∠JHI.
在△EAF和△JHI中,
,
∴△AEF≌△HJI(ASA),
∴S△AEF=S△HJI.
又∵四边形BCFE和△HIJ的面积和为5,
∴S四边形BCFE+S△AEF=5,
即S△ABC=5,
∴,
则ab=10.
又∵四边形BCFE和△HIJ的面积和为5,四边形ACJH和△BDE的面积和为12,
将四部分的面积相加得,
S正方形BDFC+S梯形ACIH=17,
∴a2+b2,
则a2+b2=22.
∴(a+b)2=a2+b2+2ab=22+2×10=42,
则a+b(舍负),
即AC+BC的值为.
故答案为:.
21.【分析】设CE交DF于H,AD=BC=x,AB=CD=y,在Rt△BFC中,()2+y2=x2①,在Rt△ABE中,y2+(x﹣3)2=()2②,①﹣②得:(x﹣3)2=x2,可解得AD,CD=y=4,故AE=AD﹣DE3;CE5,根据面积法有DHFH,故DF=DH+FH.
【解答】解:设CE交DF于H,如图:
设AD=BC=x,AB=CD=y,
∵△CDE沿CE折叠得到△CFE,
∴CF=CD=y,∠EDC=∠EFC=90°=∠BFC,EF=DE=3,
∵,
∴BF=BE﹣EF3,
在Rt△BFC中,BF2+CF2=BC2,
∴()2+y2=x2①,
在Rt△ABE中,AB2+AE2=BE2,
∴y2+(x﹣3)2=()2②,
①﹣②得:(x﹣3)2=x2,
解得x或x(舍去),
∴AD,CD=y4,
∴AE=AD﹣DE3;CE5,
∵△CDE沿CE折叠得到△CFE,
∴DF⊥CE,DH=FH,
∴2S△DCE=DE CD=CE DH,
∴DHFH,
∴DF=DH+FH;
故答案为:,.
22.【分析】利用矩形的性质和全等三角形的判定与性质得到△BAE≌△CEF,则AB=EC,BE=FC,代入运算得到AD=2DF,设DF=a,则AD=2a,设BA=x,则BE=BC﹣AB=2a﹣x,CF=x﹣a,利用BE=FC求得AB,利用三角形的面积公式和矩形的面积公式解答即可得出结论.
【解答】解:∵△AEF为等腰Rt△,且∠AEF=90°,
∴AE=EF,∠AEB+∠FEC=90°,
∵四边形ABCD为矩形,
∴∠B=∠C=90°,AD=BC,
∴∠BAE+∠BEA=90°,
∴∠BAE=∠CEF.
在△BAE和△CEF中,
,
∴△BAE≌△CEF(AAS),
∴AB=EC,BE=FC.
∵3(AB+BE)=2(AD+DF),
∴3(EC+BE)=2AD+2DF,
∴3AD=2AD+2DF,
∴AD=2DF,
设DF=a,则AD=2a,
设BA=x,则BE=BC﹣AB=2a﹣x,CF=x﹣a,
∴2a﹣x=x﹣a,
∴xa.
∵AFa,
∴AE=EFAFa.
∴.
故答案为:.
23.【分析】根据AD=DC'和AD=AC'两种情况展开讨论,当AD=DC',设BD=x可得DC=4﹣x,根据折叠的性质得AD=DC=4﹣x,再根据勾股定理建立方程,解方程即可得到答案;当AD=AC',可得B'是DC'的中点,设BD=x,DC=4﹣x,可得,根据折叠的性质得BD=DB',建立方程解方程即可得到答案.
【解答】解:当AD=DC'时,设BD=x,
得DC=4﹣x,
∵DC'=DC,
∴AD=DC=4﹣x,
在Rt△ABC中AB2+BD2=AD2,
∴9+x2=(4﹣x)2,
∴x;
当AD=AC'时,
∵AB'⊥DC',
∴B'是DC'的中点,
∵DC'=DC,
∴DB′=0.5DC,
设BD=x,则DC=4﹣x,
∴,
∵BD=DB',
∴,
∴x,
∴当BD或BD时,△ADC′是以AD为腰的等腰三角形.
故答案为:或.
24.【分析】连接BG,先证得△DGE≌△DCE(AAS),运用勾股定理可得AB=10,利用面积法可求得:GF,再运用勾股定理即可求得答案.
【解答】解:如图,连接BG,
∵DE平分∠ADC,
∴∠EDC=∠EDG,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,BD=CDBC=6,∠CAD+∠C=90°,
∵EF⊥AB,
∴∠BAD+∠AGF=90°,
又∵∠AGF=∠DGE,
∴∠DGE=∠C,
在△DGE和△DCE中,
,
∴△DGE≌△DCE(AAS),
∴DG=CD=6,
∴AD=AG+DG=2+6=8,
在Rt△ABD中,AB10,
∵S△ABGAB GFAG BD,
∴GF,
在Rt△AGF中,AF.
故答案为:.
三.解答题
25.【分析】(1)将点的坐标代入函数解析式,建立二元一次方程组即可解决问题.
(2)将点(r,0)代入y1,得出k,b,r的关系即可解决问题.
(3)先求出y3和y4,再用作差法即可解决问题.
【解答】(1)解:将点(2,﹣1)和(1,﹣3)分别代入y1和y2得,
,
解得,
所以k的值为2,b的值为﹣5.
(2)证明:因为函数y1的图象经过点(r,0),
所以kr+b=0.
将x代入y2得,
.
又因为kr+b=0,
所以k,
所以,
即y2=0,
所以函数y2的图象经过点().
(3)解:y3=y1﹣y2=kx+b﹣(bx+k)=(k﹣b)x+b﹣k,
y4=y2﹣y1=bx+k﹣(kx+b)=(b﹣k)x+k﹣b.
又因为y3>y4,
则y3﹣y4>0,
所以y3﹣y4=2(k﹣b)x+2(b﹣k)>0,
即(k﹣b)x>k﹣b.
所以当k>b时,x>1;
当k<b时,x<1;
当k=b时,不存在.
故k>b时,x>1;k<b时,x<1.
26.【分析】(1)取AC中点D,连接BD,先说明△PBE为等边三角形,再证明△BDP≌△PQE即可解答;
(2)①取AC的中点D,连接BD,证明△BDP≌△PQE即可解答;
②由①知AC=2PQ,结合AC=AP+PQ+QC,即可得到2PQ=AP+PQ+QC,进而得到答案;
(3)AP=QC+PQ,过B作BD⊥AC,证明△PDB≌△EQP得出BD=PQ,再根据线段直角的关系即可解答.
【解答】解:(1)取AC中点D,连接BD,
∵AB=BC,∠ABC=90°,D为中点,
∴∠ABD=∠CBD=∠BAC=∠BCA=45°,BD=AD=CDAC,∠BDA=∠CDB=90°,
当α=60°时,
∵PB=PE,
∴△PBE为等边三角形,
∴∠PBE=∠PEB=∠BPE=60°,
∴∠PBD=15°,
∴∠BPD=90°﹣15°=75°,
∴∠EPQ=75°﹣60°=15°=∠PBD,
∵∠PDB=∠PQE=90°,PB=PE,
∴△BDP≌△PQE(AAS),
∴BD=PQ,
∵BDAC,
∴PQAC;
故答案为:;
(2)①取AC的中点D,连接BD,
∵AB=BC,∠ABC=90°,D为中点,
∴∠ABD=∠CBD=∠BAC=∠BCA=45°,BD=AD=CDAC,∠BDA=∠CDB=90°,
∵PB=PE,
∴∠PBE=∠PEB,
∵∠PBE=∠DBC﹣∠DBP=45°﹣∠DBP,∠PEB=∠C﹣∠EPQ=45°﹣∠EPQ,
∴∠DBP=∠EPQ,
∵PB=PE,∠PDB=∠EQP,
∴△BDP≌△PQE(AAS),
∴BD=PQ,
∵BDAC,
∴PQAC;
故答案为:;
②AP+QC=PQ;
由①知AC=2PQ,
∵AC=AP+PQ+QC,
∴2PQ=AP+PQ+QC,
∴AP+QC=PQ;
故答案为:AP+QC=PQ;
(3)AP=QC+PQ,
过B作BD⊥AC,
∵∠DBP=45°﹣α,
在△PCE 中,∠QPE=45°﹣α,
∠DBP=∠QPE,
在△PDB与△EQP中,
,
∴△PDB≌△EQP(AAS),
∴QE=DP,PQ=BD=AD=CD,
在Rt△ABC中,AB=BC,∠ABC=90°,
∴BDAC,
∴PQAC,
∵PC=PQ﹣CQ,AP+PC=AC,
∴AP+PQ﹣CQ=AC=2PQ,
∴AP=QC+PQ.
27.【分析】(1)由等腰三角形的性质可得出结论;
(2)过点P作PE∥BC,交CA的延长线于点E,证明△EQP≌△CQD(AAS),由全等三角形的性质得出QE=QC,则可得出结论;
(3)方法一:过点A作AM⊥BC于点M,延长AM至E,使AM=ME,连接CE,延长QD交CE于点F,证明△AMB≌△EMC(SAS),得出∠B=∠ECM,证出PF=AE=2AM,DQ=DF,则可得出结论.
方法二:过A作PQ垂线,由等腰三角形的性质可得出结论.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵DP⊥BC,
∴∠B+∠P=∠C+∠CQD=90°,
∴∠AQP=∠CQD=∠P,
∴AP=AQ.
(2)解:QC=2AQ.
理由:过点P作PE∥BC,交CA的延长线于点E,
∴∠E=∠C,∠APE=∠B,
由题意,得∠E=∠APE,
∴AE=AP=AQ.
∴QE=2AQ.
∵点Q是线段DP的中点,
∴PQ=DQ,
∵∠EQP=∠DQC,
∴△EQP≌△CQD(AAS),
∴QE=QC,
∴QC=2AQ.
(3)解:DP+DQ的值是定值,这个定值是BC边上的高的2倍.
方法一:过点A作AM⊥BC于点M,延长AM至E,使AM=ME,连接CE,延长QD交CE于点F,
∵AB=AC,AM⊥BC,
∴BM=CM,
∵∠AMB=∠CME,AM=ME,
∴△AMB≌△EMC(SAS),
∴∠B=∠ECM,
∴AB∥CE,
∵AM⊥BC,PD⊥BC,
∴AM∥PD,
∴四边形AEFP是平行四边形,
∴PF=AE=2AM,
∵AM=ME,AM⊥CM,
∴AC=CE,
∴∠CAM=∠CEM,
∵AE∥QFD,
∴∠CAM=∠CQF,∠CEM=∠CFQ,
∴∠CQF=∠CFQ,
∴CQ=CF,
∴DQ=DF,
∴PD+DQ=PD+DF=PF=2AM.
即DP+DQ的值是定值,这个定值是BC边上的高的2倍.
方法二:过A作PQ垂线,由等腰三角形的性质可得出结论.
28.【分析】(1)数学思考:分别将三组数据代入解析式,联立方程组解答交点坐标即可;
(2)①联立解析式,求出x的值,根据a,b均不为0,且a≠b,得到x=﹣1为定值即可;
②令y1﹣y2≥0,则(a﹣b)x+a﹣b≥0,得x≥﹣1;令y1﹣y2<0,则(a﹣b)x+a﹣b<0得x<﹣1;
③两解析式相加得)=(a+b)(x﹣1),即x=1时,不论a,b如何取值,y1+y2=0.
【解答】解:(1)当a=1,b=2时;联立解析式,解得,交点坐标为(﹣1,﹣3);
当a=2,b=﹣1时;联立解析式,解得,交点坐标为(﹣1,﹣1);
当a=﹣1,b=﹣2时,联立解析式,解得,交点坐标为(﹣1,3).
(2)①联立解析式,
∴ax﹣b=bx﹣a,
∴(a﹣b)x=﹣(a﹣b),
∵a,b均不为0,且a≠b,
∴a﹣b≠0,
∴x1,
故y1和y2的图象的交点的横坐标都是定值﹣1.
②∵a>b,
∴a﹣b>0,
∴y1﹣y2=ax﹣b﹣(bx﹣a)=ax﹣b﹣bx+a=(a﹣b)x+a﹣b,
令y1﹣y2≥0,则(a﹣b)x+a﹣b≥0,
∴(a﹣b)x≥﹣(a﹣b),
∴x≥﹣1;
令y1﹣y2<0,则(a﹣b)x+a﹣b<0,
∴x<﹣1,
综上分析,当x≥﹣1时,y1≥y2;当x<﹣1时,y1<y2;
③y1+y2=ax﹣b+bx﹣a=(a+b)x﹣(a+b)=(a+b)(x﹣1),
∴当x﹣1=0时即x=1时,不论a,b如何取值,y1+y2=0.
29.【分析】(1)判定△ABC是等腰直角三角形,即可得到BC=AB,
(2)由ASA证明△ABO≌△FEO,推出EF=AB,
(3)由ASA证明△ABC≌△DBC,推出BD=AB.
【解答】解:(1)∵AB⊥BC,∠ACB=45°,
∴△ABC是等腰直角三角形,
∴BC=AB,
∴河宽AB的长度就是线段BC的长度.
故答案为:BC;
(2)第二小组的方案可行,理由如下:
∵O是BE中点,
∴OB=OE,
∵AB⊥BE,EF⊥BE,
∴∠ABO=∠FEO=90°,
在△ABO和△FEO中,
,
∴△ABO≌△FEO(ASA),
∴EF=AB,
∴河宽AB的长度就是线段EF的长度.
(3)见表格,
课题 测量河流宽度
工具 测量角度的仪器(仪器的高度忽略不计),标杆,皮尺等
小组 第一小组 第二小组 第三小组
测量方案 观测者从B点向正东走到C点,此时恰好测得:∠ACB=45° 观测者从B点向正东走到E点,O是BE的中点,继续从点E沿垂直于BE的EF方向走,直到点A,O,F在一条直线上. 观测者从B点向正西走到C点,使用测量角度的仪器测得∠BCD=∠ACB=65°,CD交AB延长线于D,
测量示意图
只要测出BD的长,就能推算出河宽AB长,理由如下:
∵AB⊥BC,
∴∠ABC=∠DBC=90°,
在△ABC和△DBC中,
,
∴△ABC≌△DBC(ASA),
∴BD=AB,
∴河宽AB的长等于线段BD的长.
30.【分析】(1)①过点A作AD⊥BC于点D,当点P与点D重合时,AP最小,由勾股定理可得出答案;
②由勾股定理求出PD,则可得出答案;
(2)过点A作AE⊥BC于点E,由勾股定理得出AB2=m2=AE2+BE2①,AP2=n2=AE2+PE2②,①﹣②可得出答案.
【解答】解:(1)①过点A作AD⊥BC于点D,
∵AB=AC,BC=16,
∴BD=CD=8,
∵AB=10,
∴6,
当点P与点D重合时,AP最小,
∴AP的最小值为6;
②∵PA=7,AD=6,
∴PD,
∴BP=BD﹣DP=8或BP=BD+DP=8;
(2)过点A作AE⊥BC于点E,由(1)可知BE=CE,
在Rt△ABE中,AB2=m2=AE2+BE2①,
在Rt△APE中,AP2=n2=AE2+PE2②,
①﹣②得,
m2﹣n2=BE2﹣PE2=(BE+PE)(BE﹣PE)
=(CE+PE)BP
=CP BP.
即BP PC=m2﹣n2.
31.【分析】[建立模型]
(1)先描点,再得出结论,然后用待定系数法求函数解析式;
(2)把x=12代入解析式求出y的值即可;
[解决问题]
把y=40代入解析式求出x即可.
【解答】解:[建立模型]
(1)描点,连线,
根据点的分布规律可知,h关于x的函数关系式满足一次函数,
设h关于x的函数关系式为h=kx+b,
则,
解得,
∴h关于x的函数关系式为h=1.4x+8.6;
(2)当x=12时,y=1.4×12+8.6=25.4,
∴这摞杯子的总高度25.4cm;
[解决问题]
当y=40时,1.4x+8.6=40,
解得x22.4,
∴一摞最多能叠22个杯子,可以一次性放进柜子里.
32.【分析】任务1:直接描点并作图,利用待定系数法求出函数关系式,并求出x的最大值和最小值;当y=70时求出a的值即可.
任务2:根据“背带的总长度为单层部分与双层部分的长度和”和x与y之间的函数关系式,用含x的代数式将背带的总长度表示出来,再由背带总长度与身高的比例关系列出等式,将h表示为x的函数的形式即可;
任务3:当背包的背带调节到最短时都为双层部分,求出此时x的值,从而求出手离地面的高度;设小明爸爸的身高为未知数,根据臂展与身高的关系及肩宽,将一条胳膊的长度用身高表示出来,头顶到肩膀的垂直高度、一条胳膊的长度、手离地面的高度之和为身高,利用此等量关系列方程求出身高,将其代入任务2中得到的函数关系式,求出对应x的值即可.
【解答】解:任务1:描点并作图如图所示:
根据图象可知,变量x、y满足一次函数关系.
设y=kx+b(k、b为常数,且k≠0),
将x=2,y=116和x=10,y=100代入y=kx+b,
得,解得,
∴y=﹣2x+120.
将x=a和y=70代入y=﹣2x+120,
得﹣2a+120=70,解得a=25;
当背带都为单层部分时,x=0;
当背带都为双层部分时,y=0,即﹣2x+120=0,解得x=60,
∴x的取值范围是0≤x≤60.
任务2:∵背带的总长度为单层部分与双层部分的长度和,
∴总长度为﹣2x+120+x=﹣x+120,
当单肩包背带长度调整为最佳背带总长度时,得,
∴hx+180(0≤x≤60).
任务3:由素材可知,当背包的背带调节到最短时都为双层部分,即x=60,y=0.
∵背包提在手上,且背包的悬挂点距地面高度为53.5cm,
∴手到地面的距离为(53.5)cm,即83.5cm.
设小明爸爸的身高为h cm.
∵臂展和身高一样,且肩宽为38cm,
∴小明爸爸一条胳膊的长度为cm,
∴h83.5=h,解得h=172,
根据任务2,得172x+180,解得x,
∴此时双层部分的长度为cm.
33.【分析】(1)利用待定系数法即可求出k的值;
(2)根据一次函数的图象特征即可求出k的取值范围;
(3)根据y1﹣y2=b+1,得(k﹣1)x=0,又k≠1,可求x的值.
【解答】解:(1)∵一次函数y1=kx+b过点(3,2)和(0,5),
∴,
解得,
∴k的值为﹣1;
(2)当一次函数y1=kx+b过点(3,2)和(0,0)时,
可得,
解得k,
∴当一次函数y1=kx+b不经过第四象限,
∴k的取值范围为0<k;
(3)∵y1﹣y2=b+1,
∴kx+b﹣x+1=b+1,
kx﹣x=0,
(k﹣1)x=0,
∵k≠1,
∴k﹣1≠0,
∴x=0.
34.【分析】(1)依据题意,设y=kt,再用待定系数法求函数表达式即可;
(2)依据题意,设CD的函数表达式为y=mt+n,由C(0.1,8),D(0.5,0)用待定系数法求函数表达式即可;
(3)依据题意,由(1)和(2)建立方程组,再解方程组求出方程组的解即可;
(4)依据题意,根据题意分四种情况讨论即可.
【解答】解:(1)设OA的函数表达式为y=kt,
把A(0.8,8)代入函数表达式得:8=0.8k,
解得k=10,
∴OA的函数表达式为y=10t.
(2)由图象知,C(0.1,8),D(0.5,0),
设CD的函数表达式为y=mt+n,
则,
解得,
∴CD的函数表达式为y=﹣20t+10.
(3)由题意,联立方程组,
解得,
∴点K的坐标为(,).
(4)当t≤0.1时,由图象知S=8﹣10t≥7,不合题意;
当0.1<t时,S=﹣20t+10﹣10t=﹣30t+10,
当S≤3时,t,
即t;
当t<0.5时,S=10t﹣(﹣20t+10)=30t﹣10,
当S≤3时,t,
即t;
当0.5<t≤0.8时,S=10t,
则5<S≤8.不符合题意;
综上,t的取值范围为t.
35.【分析】(1)①由等腰三角形的性质得出∠ABC=∠C=50°,则可求出答案;
②由等腰三角形的性质得出∠A=∠ADB,∠ABC=∠C=α,则可求出β,由三角形外角的性质可得出答案;
(2)过点B作BM⊥BC于点M,BN⊥AC于点N,由勾股定理可得出AM=4,由勾股定理得出25﹣x2=36﹣(5﹣x)2,则可得出答案.
【解答】解:(1)①∵AB=AC,
∴∠ABC=∠C=50°,
∴∠A=180°﹣∠ABC﹣∠C=80°,
∵BD=AB,
∴∠BDA=∠A=80°,
∴β=180°﹣∠A﹣∠BDA=20°;
②∵AB=BD,
∴∠A=∠ADB,
∴β=180°﹣2∠A,
又∵AB=AC,
∴∠ABC=∠C=α,
∴∠A=180°﹣2∠C=180°﹣2α,
∴β=180°﹣2(180°﹣2α)=4α﹣180°,
即β=4α﹣180°;
(2)过点B作AM⊥BC于点M,BN⊥AC于点N,
设AN=x,则CN=5﹣x,
∵AB=5,BC=6,
∴BM=CM=3,
∴AM4,
∵BN2=AB2﹣AN2=BC2﹣CN2,
∴25﹣x2=36﹣(5﹣x)2,
∴x,
∴AD=2AN.
36.【分析】(1)先利用直角三角形的两个锐角互余可得∠C=70°,再利用等腰三角形的性质可得∠HAD=∠ADH,然后利用等量代换可得∠HAD=∠ADH=∠C=70°,从而利用三角形内角和定理进行计算即可解答;
(2)①过点H作AE⊥AD,垂足为E,根据垂直定义可得∠BAC=∠HED=90°,然后利用AAS证明△ACB≌△EDH,从而可得AC=DE,再根据等腰三角形的三线合一性质可得AD=2DE,从而可得AD=2AC,即可解答;
②利用①的结论可得AD=2a,再利用直角三角形的斜边上的中线性质可得AD=CDBC,从而可得BC=DH=4a,∠C=∠CAD,进而可得∠CAD=∠ADH,然后利用内错角相等,两直线平行可得AC∥DK,从而可得点K是AB的中点,进而可得DK是△ABC的中位线,再利用三角形的中位线定理可得DKACa,最后利用线段的和差关系进行计算,即可解答.
【解答】解:(1)∵∠CAB=90°,∠B=20°,
∴∠C=90°﹣∠B=70°,
∵HA=HD,
∴∠HAD=∠ADH,
∵∠ADH=∠C,
∴∠HAD=∠ADH=∠C=70°,
∴∠H=180°﹣∠HAD﹣∠ADH=40°,
∴∠H度数为40°;
(2)①证明:过点H作AE⊥AD,垂足为E,
∴∠HED=90°,
∵∠BAC=90°,
∴∠BAC=∠HED=90°,
∵∠C=∠ADH,HD=BC,
∴△ACB≌△EDH(AAS),
∴AC=DE,
∵HA=HD,HE⊥AD,
∴AD=2DE,
∴AD=2AC;
②解:∵AC=a,AD=2AC,
∴AD=2a,
∵∠CAB=90°,点D是边BC的中点,
∴AD=CDBC,
∴BC=2AD=4a,
∴BC=DH=4a,
∵DA=DC,
∴∠C=∠CAD,
∴∠CAD=∠ADH,
∴AC∥DK,
∴点K是AB的中点,
∴DK是△ABC的中位线,
∴DKACa,
∴HK=DH﹣DK=4aaa,
∴HK的长为a.
37.【分析】(1)先证△ADH是等边三角形,可得AD=DH=AH,∠ADH=∠AHD=60°,由等腰三角形的性质可求∠HDC=30°,即可求解;
(2)由“HL”可证Rt△CEF≌Rt△BEG,可得∠BEG=∠CEF,可证∠BEC=∠GEF=90°,即可求解;
(3)由直角三角形的性质可得BC=2CD,BEBC,即可求解.
【解答】(1)证明:如图,取AC的中点H,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,∠DAC=60°,
∵ADABAC,点H是AC的中点,
∴AD=AH=HC,
∴△ADH是等边三角形,
∴AD=DH=AH,∠ADH=∠AHD=60°,
∴DH=HC,
∴∠HDC=∠HCD=30°,
∴∠ADC=90°,
∴AD⊥CD;
(2)解:如图,过点E作EF⊥直线DC于F,EG⊥AB于G,
又∵∠ADC=90°,
∴∠GEF=90°,
∵DE平分∠BDC,EF⊥DC,EG⊥AB,
∴EG=EF,
∵AB=AC,AE平分∠BAC,
∴AE垂直平分BC,
∴BE=CE,
∴Rt△CEF≌Rt△BEG((HL),
∴∠BEG=∠CEF,
∴∠BEC=∠GEF=90°,
又∵BE=CE,
∴∠EBC=45°,
∴∠DBE=30°+45°=75°;
(3)解:∵∠ADC=90°,∠DBC=30°,
∴BC=2CD,
∵BE=CE,∠BEC=90°,
∴BEBC,
∴BECD,
∴.
38.【分析】(1)根据等边三角形的性质,利用SAS即可证明△ABD≌△CBE;
(2)结合(1)根据等边三角形的性质即可求∠DCE的度数;
(3)结合(1)利用三角形的面积公式分别求出△ABD的面积=△BCE的面积=S1AF BFFD BF,△BCD的面积=S2AF BFFD BF,进而可以用含S1,S2的代数式表示△BFD的面积.
【解答】(1)证明:∵△ABC和△DBE都是等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABD=60°﹣∠DBC=∠CBE,
在△ABD和△CBE中,
,
∴△ABD≌△CBE(SAS);
(2)解:∵△ABC是等边三角形,
∴∠ACB=60°,
由(1)知:△ABD≌△CBE,
∴∠CEB=∠A=60°,
∴∠DCE=∠ABC+∠BCE=60°+60°=120°;
(3)解:∵△ABC是等边三角形,BF⊥AC,
∴AF=CF,
由(1)知:△ABD≌△CBE,
∴△ABD的面积=△BCE的面积=S1AD BF(AF+FD) BFAF BFFD BF,
∵△BCD的面积=S2CD BF(CF﹣FD) BF(AF﹣FD) BFAF BFFD BF,
∴S1﹣S2=(AF BFFD BF)﹣(AF BFFD BF)=FD BF,
∴△BFD的面积FD BF(S1﹣S2).
39.【分析】(1)根据折叠的性质得∠EDF=∠A=90°,∠AFE=∠DFE,根据三角形的内角和定理得到∠CFD=60°,∠AFE=∠DFE=60°,求得∠AEF=30°,根据勾股定理得到AEAF,于是得到AE:AF;
(2)根据三角形中线的定义得到AE=BEAB=3,根据勾股定理得到CE5,由折叠的性质得∠EDF=∠A=90°,AF=DF=AC﹣CF=4﹣CF,DE=AE=3,CD=2根据勾股定理得到AF,于是得到AE:AF=3:2;
(3)根据等边三角形的性质得到AB=BC=AC,∠A=∠B=∠ACB=60°,根据CE是AB边上的中线,求得AE=BEAC,∠AEC=∠BEC=90°,∠BCE=∠ACE∠ACB=30°,由折叠的性质得∠EDF=∠A=60°,AE=DE,AF=DF,设AE=x,则AC=2x,根据勾股定理得到CEx,求得AF=(1)x,于是得到AE:AF=x:(1)x.
【解答】解:(1)由折叠的性质得∠EDF=∠A=90°,∠AFE=∠DFE,
∵∠ACE=30°,
∴∠CFD=60°,∠AFE=∠DFE=60°,
∴∠AEF=30°,
∴EF=2AF,
在Rt△AEF中,AE2+AF2=EF2,
∴AE2+AF2=(2AE)2,
∴AEAF,
∴AE:AF;
(2)∵CE是AB边上的中线,
∴AE=BEAB=3,在Rt△AEC中,AE2+AC2=EC2,
∴CE5,
由折叠的性质得∠EDF=∠A=90°,AF=DF=AC﹣CF=4﹣CF,DE=AE=3,CD=2,
在Rt△CDF中,CD2+DF2=CF2,
∴22+AF2=(4﹣AF)2,
∴AF,
∴AE:AF=3:2;
(3)∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠ACB=60°,
∵CE是AB边上的中线,
∴AE=BEAC,∠AEC=∠BEC=90°,∠BCE=∠ACE∠ACB=30°,
由折叠的性质得∠EDF=∠A=60°,AE=DE,AF=DF,
∴∠CDF=120°,
∴∠CFD=∠DCF=30°,
∴DF=CD,
设AE=x,则AC=2x,
∴CEx,
∵AE=DE=x,
∴CE﹣DEx=CD=AE,
∴AF=(1)x,
∴AE:AF=x:(1)x.
40.【分析】(1)根据四边形ABCD是“对角互补四边形”,求得∠B+∠D=180°,根据题意列方程即可得到结论;
(2)①根据“对角互补四边形”的定义得到∠ABC=120°,根据角平分线的定义得到∠BOC=∠BOA=30°,当∠BCO=∠BOC=30°时,求得∠CBO=180°﹣30°﹣30°=120°=∠ABC(不符合题意,舍去),当∠CBO=∠BOC=30°时,求得∠BAN=∠BOA+∠ABO=120°;当∠CBO=∠OCB时,求得∠BAN=∠BOA+∠ABO=75°;
②如图②,过点B作BG⊥ON于G,BH⊥OM于H,根据已知条件得到OC:OA=n,根据四边形COAB是“对角互补四边形”,求得∠ABC=180°﹣∠MON=120°,根据全等三角形的性质得到CH=AG,解方程即可得到结论.
【解答】解:(1)∵四边形ABCD是“对角互补四边形”,
∴∠B+∠D=180°,
∵∠B=3∠D,
∴∠B+∠B=180°,
∴∠B=135°;
(2)①∵四边形COAB是“对角互补四边形”,∠MON=60°,
∴∠ABC=120°,
∵OB平分∠MON,
∴∠BOC=∠BOA=30°,
当∠BCO=∠BOC=30°时,
∴∠CBO=180°﹣30°﹣30°=120°=∠ABC(不符合题意,舍去),
当∠CBO=∠BOC=30°时,
∴∠ABO=120°﹣30°=90°,
∴∠BAN=∠BOA+∠ABO=120°;
当∠CBO=∠OCB时,
∴∠OBC75,∠ABO=120°﹣75°=45°,
∴∠BAN=∠BOA+∠ABO=75°.
综上所述:∠BAN的度数为120°或75°;
②如图②,过点B作BG⊥ON于G,BH⊥OM于H,
∵∠BOC=∠BOA=30°,
∴BG=BHOBm,OHm,
∴S△BOC:S△BOAOC BH:OA BG=n,
∴OC:OA=n,
∵四边形COAB是“对角互补四边形”,
∴∠ABC=180°﹣∠MON=120°,
∵∠BHO=∠BGO=90°,
∴∠HBG=180°﹣∠MON=120°,
∴∠CBH=∠ABG,
在△CBH与△ABG中,
,
∴△CBH≌△ABG(AAS),
∴CH=AG,
∴OC+CH=OA﹣AG,
∴OC+2CHOC,
∴(1)OC=2CH,
∴CHOC,
∵OH=OC+CH,
∴OCOCm,
∴OC.
【培优集训】2024年浙江省杭州市近2年八年级精选期末压轴真题集训
一.选择题
1.如图,在△ABC中,AE⊥BC于点E,BD⊥AC于点D,点F是AB的中点,连接DF,EF,设∠ACB=x°,∠DFE=y°,则( )
A. B.y=x﹣30 C.y=90﹣x D.y=180﹣2x
2.如图,已知AB∥CD,∠ACD=70°,CE平分∠ACD交AB于点E,点P为线段CE上一点,∠CAP与∠EAP度数之比为k、若△ACP为直角三角形,且AP>PE,则k的值为( )
A.1 B. C.或1 D.1或
3.如图,在△ABC中,AB=BC=AC,AE=CD,AD与BE相交于点P,BQ⊥AD于Q.则BP与BQ的关系为( )
A.BP2=2BQ2 B.3BP2=4BQ2 C.4BP2=3BQ2 D.2BP2=3BQ2
4.如图,在△ABC中,AB=AC,点D是边AC的中点,点E在边BC上(不与点B,C重合),连接DE.( )
A.若AC>2DE,则BE>3EC B.若AC<2DE,则EC>3BE
C.若BE>3EC,则AC>2DE D.若BE<3EC,则AC<2DE
5.如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
①BF=CF;
②若BE⊥AC,则CF=DF;
③连结EF,若BE⊥AC,则∠DFE=2∠ABE;
④若BE平分∠ABC,则FG.
A.①②③ B.③④ C.①②④ D.①②③④
6.如图,在Rt△ABC中,∠ACB=90°,分别以Rt△ABC的三边为边在AB的同侧作三个正方形,顶点H恰为DE的中点,若阴影部分(四边形KNCM)的面积为9,则正方形ABHK的面积为( )
A.50 B.49 C.48 D.45
7.如图,在等腰直角△ABC中,点E,F将斜边AC三等分,且AC=12,点P在△ABC的边上,则满足PE+PF=9的点P的个数是( )
A.0个 B.2个 C.4个 D.6个
8.如图,在△ABC中,CA=CB=8,AB=6,∠C<90°,点D,E,F分别在边BC,AC,AB上,连接DF,DE.已知点B和点E关于直线DF对称,若ED=CD,则CE的长为( )
A. B. C. D.
9.如图,在Rt△ACB中,∠ACB=90°,按下列步骤作图:
①分别以点B,C为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点D;
②以C为圆心,CD长为半径画弧交AB于点E.
方方探究得到以下两个结论:
①△BCE是等腰△;
②若AC=6,BC=8,则点E到AC的距离为,
则( )
A.结论①正确,结论②正确
B.结论①正确,结论②错误
C.结论①错误,结论②正确
D.结论①错误,结论②错误
10.将长方形纸片ABCD如图折叠,B,C两点恰好重合落在AD边上的同一点P处,折痕分别是MH,NG,若∠MPN=90°,PN=4,MN=5,分别记△PHM,△PNG,△PMN的面积为S1,S2,S3,则S1,S2,S3之间的数量关系是( )
A.S3=S1+S2 B.3S3=2S1+2S2
C.2S3=3S2﹣S1 D.S3=5S2﹣5S1
11.如图,在△ABC中,∠ACB=90°,首先沿着CD折叠,点B落在点E处,然后沿着FG折叠,使得点A与点E重合,则下列说法中( )
①EF⊥CE;
②若BC=3,AC=4,那么.
A.①正确,②正确 B.①正确,②错误
C.①错误,②正确 D.①错误,②错误
12.甲、乙两车从A地出发,匀速驶往B地.乙车出发1h后,甲车才沿相同的路线开始行驶.甲车先到达B地并停留30分钟后,又以原速按原路线返回,直至与乙车相遇.图中的折线段表示从开始到相遇止,两车之间的距离y(km)与甲车行驶的时间x(h)的函数关系的图象,则( )
A.甲车的速度是120km/h
B.A,B两地的距离是360km
C.乙车出发4.5h时甲车到达B地
D.甲车出发4.5h最终与乙车相遇
二.填空题
13.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,AE是BC边的中线.若∠B=30°,DE=1,则AC= .
14.若一次函数y=kx+b(k为常数且k≠0)的图象过点(2,﹣4),且经过第二、三、四象限.
(1)b= .(请用含k的代数式表示)
(2)若m=k+3b,则m的取值范围是 .
15.如图,在△ABC中,AB=AC,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点.
(1)若△DEF的周长是8,则△ABC的周长是 ;
(2)若AE:EC=3:2,则AF:EF= .
16.如图,在△BED中,BC⊥DE于点C,点A在BE上,连接AC,已知AB=AC=2,CD=1.若∠ABC+2∠CBD=90°,则AE= ,BD= .
17.如图,等边△ABC中,AO⊥BC,O为垂足且AO,E是线段AO上的一个动点,连接BE,线段BF与线段BE关于直线BA对称,连接AF、OF,在点E运动的过程中,当OF的长取得最小值时,AE的长为 .
18.如图,在等边△ABC中,D为BC延长线上一点,E为AB上一点,过点B作BF∥AC,连接DF,EF,且∠DFE=60°.若,BD=5,则BE的长度是 .
19.在一条笔直的公路上有A,B两地,甲骑自行车匀速从A地到B地,乙骑摩托车匀速从B地到A地,到达A地后立即按原路匀速返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象.若两人之间的距离不超过5km时,能够用无线电对讲机保持联系,甲、乙两人能够用无线电对讲机保持联系时.则x的取值范围是 .
20.清代数学家李锐在其著作《勾股算术细草》中利用三个正方形出入相补的方法证明了勾股定理.如图,在Rt△ABC中,∠ACB=90°,分别以AB,AC和BC为边,按如图所示的方式作正方形ABKH,ACIG和BCFD,KH与CI交于点J,AB与DF交于点E.若四边形BCFE和△HIJ的面积和为5,四边形ACJH和△BDE的面积和为12,则AC+BC的值为 .
21.如图,在矩形ABCD中,点E在边AD上,△CDE沿CE折叠得到△CFE,且点B,F,E三点共线,连接DF,若,DE=3,则AE= ,DF= .
22.如图,在长方形ABCD中,△AEF为等腰Rt△,且∠AEF=90°,点E在线段BC上,点F在线段CD上,若3(AB+BE)=2(AD+DF),则 .
23.如图,已知在Rt△ABC中,∠B=90°,AB=3,BC=4,点D,E分别在边BC,AC上,连接AD,DE.将△ABD沿AD翻折,将△DCE沿DE翻折,翻折后,点B,C分别落在点B′,C′处,且边DB′与DC′在同一直线上,连接AC′,当△ADC′是以AD为腰的等腰三角形时,则BD= .
24.如图,△ABC中,AB=AC,AD⊥BC于点D,DE平分∠ADC,交AC与点E,EF⊥AB于点F,且交AD于点G,若AG=2,BC=12,则AF= .
三.解答题
25.设两个不同的一次函数y1=kx+b,y2=bx+k(k,b是常数,且kb≠0).
(1)若函数y1的图象经过点(2,﹣1),函数y2的图象经过点(1,﹣3),求k,b的值.
(2)若函数y1的图象经过点(r,0),求证:函数y2的图象经过点;
(3)设y3=y1﹣y2,y4=y2﹣y1,当y3>y4时,求x的取值范围.
26.综合与实践:数学课上,老师让同学们根据下面情境提出问题并解答:
问题情境:如图1,在Rt△ABC中,AB=BC,∠ABC=90°,点P是斜边AC上动点,点E在直线BC上,满足PB=PE,过点E作EQ⊥AC,垂足为Q,设∠PBE=α.
圆圆同学提出的问题:探究PQ与AC之间的数量关系;
方方同学提出的问题:探究AP,PQ,QC之间的数量关系;
经过小组讨论,第一小组提出解决问题的思路:取AC中点D,连接BD,可以证明:△BDP≌△PQE,从而得到对应线段相等…
请你继续完成以下问题:
(1)特例探究:从特殊到一般是研究几何问题的常用方法,如图1,当α=60°时,请直接写出PQ与AC这两条线段长度之间的数量关系 ;
(2)数学思考:如图2,当45°≤α≤90°时,
①PQ与AC这两条线段长度之间的数量关系: ;
②探究AP,PQ,QC这三条线段长度之间的数量关系得: ;并写出探究过程;
(3)延伸拓展:如图3,当0°≤α<45°时,探究AP,PQ,QC这三条线段长度之间的数量关系得: ;并写出探究过程.
27.如图,在△ABC中,AB=AC,点D在边BC上(不与点B,C重合),且BD>CD,过点D作DP⊥BC,分别交BA的延长线和AC于点P和点Q.
(1)求证:AP=AQ.
(2)若点Q是线段DP的中点,探索AQ与QC的数量关系.
(3)若△ABC的形状和大小都确定,说说DP+DQ的值是否为定值,如果是定值,直接写出这个定值的几何意义;如果不是定值,说明理由.
28.综合与实践
问题情境:“综合与实践”课上,老师请同学们探索一次函数的图象与系数的关系.老师给出两个一次函数y1=ax﹣b,y2=bx﹣a(a,b均不为0,且a≠b),同学们利用图形计算器画出a,b不同取值下的两个一次函数的图象,并观察它们的交点位置.三个小组分别绘制了当a=1,b=2;a=2,b=﹣1;a=﹣1,b=﹣2时的函数图象,得到了不同情况下函数y和y2的图象的交点坐标.
数学思考:(Ⅰ)请从(1)当a=1,b=2时;(Ⅱ)当a=2,b=﹣1时;(Ⅲ)当a=﹣1,b=﹣2时,三组值中任选一组,求此时函数y1和y2的图象的交点坐标.
注:如果选择多组条件分别作答,按第一个解答计分.
深入探究:(2)老师请同学们经过思考,提出新的问题.
①“运河小组”提出问题:不论a,b如何取值,函数y1和y2的图象的交点的横坐标都是定值.请你证明结论,并求出这个定值.
②“武林小组”提出问题:若a>b,要比较y1和y2的大小,需要分类讨论.请你比较y1和y2的大小.
③不论a,b如何取值,当x等于某个正数时,函数y1和y2的值都存在某种确定的等量关系,请你直接写出结论.
29.如图,为了测量一条两岸平行的河流宽度,由于跨河测量困难,所以,三个数学研究小组设计了不同的方案,他们在河南岸的点B处,测得河北岸的一棵树底部A点恰好在点B的正北方向,测量方案如下表:
课题 测量河流宽度
工具 测量角度的仪器(仪器的高度忽略不计),标杆,皮尺等
小组 第一小组 第二小组 第三小组
测量方案 观测者从B点向正东走到C点,此时恰好测得:∠ACB=45° 观测者从B点向正东走到E点,O是BE的中点,继续从点E沿垂直于BE的EF方向走,直到点A,O,F在一条直线上.
测量示意图
(1)第一小组认为,河宽AB的长度就是线段 的长度.
(2)第二小组方案灵感来源于古希腊哲学家泰勒斯,他们认为只要测得EF的长就是所求河宽AB的长,你认为第二小组的方案可行吗?如果可行,请给出证明;如果不可行,请说明理由.
(3)请你代表第三小组,设计一个测量方案,把测量方案和测量示意图填入上表,然后指明你画的示意图中,只要测出哪条线段的长,就能推算出河宽AB长,并说明方案的可行性.
30.在△ABC中,AB=AC,点P为线段BC上任意一点(P与B,C不重合),连接AP.
(1)若BC=16,AB=10,
①求AP的最小值.
②当AP=7时,求BP的长.
(2)若AB=m,AP=n,请用含m,n的代数式表示BP PC,并说明理由.
31.综合与实践
【情境描述】
圆圆想把一些相同规格的塑料杯,尽可能多地放入高40cm的柜子里(如图1).她把杯子按如图这样整齐地叠放成一摞(如图2),但她不知道一摞最多能叠几个可以一次性放进柜子里.
【观察发现】
圆圆测量后发现,按这样叠放,这摞杯子的总高度随着杯子数量的变化而变化,记录的数据如下表所示:
杯子的数量x(只) 1 2 3 4 5 6 …
总高度h(cm) 10 11.4 12.8 14.2 15.6 17 …
【建立模型】
(1)请根据上表中的信息,在平面直角坐标系中描出对应点,观察这些点的分布规律,试求h关于x的函数表达式.
(2)当杯子的数量为12只时,求这摞杯子的总高度.
【解决问题】
请帮圆圆算一算,一摞最多能叠几个杯子,可以一次性放进柜子里?
32.综合与实践
生活中的数学:如何确定单肩包最佳背带长度
素材1 如图是一款单肩包,背带由双层部分、单层部分和调节扣构成.使用时可以通过调节扣加长或缩短单层部分的长度,使背带的总长度加长或缩短(总长度为单层部分与双层部分的长度和,其中调节扣的长度忽略不计).
素材2 对于该背包的背带长度进行测量,设双层的部分长度是x cm,单层部分的长度是y cm,得到如下数据: 双层部分长度x(cm)261014a单层部分长度y(cm)1161081009270
素材3 单肩包的最佳背带总长度与身高比例为2:3
素材4 小明爸爸准备购买此款背包.爸爸自然站立,将该背包的背带调节到最短提在手上,背带在背包的悬挂点离地面的高度为53.5cm;已知爸爸的臂展和身高一样,且肩宽为38cm,头顶到肩膀的垂直高度为总身高的.
任务1 在平面直角坐标系中,以所测得数据中的x为横坐标,以y为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量x、y是否满足一次函数关系.如果是,求出该函数的表达式,直接写出a值并确定x的取值范围.
任务2 设人身高为h,当单肩包背带长度调整为最佳背带总长度时,求此时人身高h与这款背包的背带双层部分的长度x之间的函数表达式.
任务3 当小明爸爸的单肩包背带长度调整为最佳背带总长度时.求此时双层部分的长度.
33.一次函数y1=kx+b(k≠0)恒过定点(3,2).
(1)若一次函数y1=kx+b还经过(0,5)点,求k的值;
(2)一次函数y1=kx+b不经过第四象限,求k的取值范围;
(3)另一函数y2=x﹣1,满足y1﹣y2=b+1,且k≠1,求x的值.
34.小王骑自行车从家出发沿公路匀速前往新华书店,小王妈妈骑电瓶车从新华书店出发沿同一条路回家,线段OA与折线B﹣C﹣D﹣E分别表示两人离家的距离y(km)与小王的行驶时间t(h)之间的函数关系的图象,请解决以下问题.
(1)求OA的函数表达式;
(2)求CD的函数表达式;
(3)求点K的坐标;
(4)设小王和妈妈两人之间的距离为S(km),当S≤3时,求t的取值范围.
35.如图,在△ABC中,AB=AC,点D在AC边上(不与A,C重合),连接BD,BD=AB.
(1)设∠C=α,∠ABD=β.
①当α=50°时,求β.
②请求出β与α的数量关系.
(2)若AB=5,BC=6,求AD的长.
36.如图,在Rt△ABC中,∠CAB=90°,点D是边BC的中点,以AD为底边向上作等腰△ADH,使得∠ADH=∠C,DH交AB于点K,
(1)若∠B=20°,求∠H度数;
(2)若HD=BC.
①求证:AD=2AC;
②设AC=a,求HK的长(用含a的代数式表示).
37.如图,在△ABC中,AB=AC,∠BAC=120°,延长BA至点D,使,连结CD,作∠BAC的平分线与∠BDC的平分线交于点E,连结EB,EC.
(1)求证:AD⊥CD;
(2)求∠DBE的度数;
(3)求的值.
38.如图1,已知△ABC和△DBE都是等边三角形,且点D在边AC上,AD>CD.
(1)求证:△ABD≌△CBE.
(2)求∠DCE的度数.
(3)如图2,过点B作BF⊥AC于点F,设△BCE的面积为S1,△BCD的面积为S2,求△BFD的面积(用含S1,S2的代数式表示).
39.【综合与实践】
问题情景:
在数学活动课上,老师展示一张直角三角形纸片,如图1,在Rt△ABC中,∠A=90°,AB=6,AC=4,点E,F分别在AB,AC上,将△AEF沿EF折叠得△DEF,使点A的对应点D落在线段CE上.各学习小组先解决老师提出的问题,然后又提出了新的数学问题,请你解决这些问题.
问题解决:
(1)老师提出问题:如图1,若∠ACE=30°,求AE:AF的值.
深入探究:
(2)如图2,勤学小组提出问题:若CE是AB边上的中线,求AE:AF的值.
拓展探究:
(3)如图3,奋进小组提出问题:将直角三角形纸片换成等边三角形纸片,即在等边△ABC中,若CE是AB边上的中线,求AE:AF的值.
40.【问题背景】如图①,在四边形ABCD中,∠A和∠C称为它的对角,若这个四边形满足:∠A+∠C=180°,则这个四边形叫作为“对角互补四边形”.
【问题解决】
(1)若四边形ABCD是“对角互补四边形”,且∠B=3∠D,求∠B的度数;
(2)如图②,∠MON=60°,OB平分∠MON,A是射线OM上一动点,C是射线OM上的动点,且四边形COAB是“对角互补四边形”.
①若△COB是等腰三角形,求∠BAN的度数;
②若OB=m,若S△BOC:S△BOA=n,求OC的长(用含m、n的代数式表示).
参考答案
一.选择题
1.【分析】由垂直的定义得到∠ADB=∠BEA=90°,根据直角三角形的性质得到AF=DF,BF=EF,根据等腰三角形的性质得到∠DAF=∠ADF,∠EFB=∠BEF,于是得到结论.
【解答】解:∵AE⊥BC于点E,BD⊥AC于点D,
∴∠ADB=∠BEA=90°,
∵点F是AB的中点,
∴AF=DF,BF=EF,
∴∠DAF=∠ADF,∠EBF=∠BEF,
∴∠AFD=180°﹣2∠CAB,∠BFE=180°﹣2∠ABC,
∴∠DFE=180°﹣∠AFD﹣∠BFE=2(∠CAB+∠CBA)﹣180°=2(180°﹣∠ACB)﹣180°=180°﹣2∠ACB,
∴y=180°﹣2x,
故选:D.
2.【分析】设∠EAP=x,则∠CAP=kx.根据角平分线定义及平行线的性质求出∠AEP=∠ECD=35°,根据题意求出x<35°,进而推出∠APC<70°,则∠CAP=kx=90°,据此求解即可.
【解答】解:设∠EAP=x,则∠CAP=kx.
∵CE平分∠ACD,∠ACD=70°,
∴∠ACE=∠ECD=35°,
∵AB∥CD,
∴∠AEP=∠ECD=35°,
∵AP>PE,
∴∠EAP<∠AEP,
即x<35°,
∴∠APC=∠EAP+∠AEP=x+35°<70°,
∵△ACP为直角三角形,
∴kx=90°,
∴∠ACP+∠APC=90°,
即35°+x+35°=90°,
解得x=20°,
∴,
故选:B.
3.【分析】由已知可得△ABC是等边三角形,从而得到∠BAC=∠C=60°,根据SAS即可判定△ADC≌△BEA,根据全等三角形的性质可得到∠ABE=∠CAD,再根据等角的性质即可求得∠BPQ=60°,再根据余角的性质得到∠PBQ=30°,根据在直角三角形中30°的角对的边是斜边的一半即可证得结果,由勾股定理可得出答案.
【解答】解:∵AB=BC=AC,
∴△ABC是等边三角形.
∴∠BAC=∠C=60°.
∵AB=AC,AE=CD,
∴△ADC≌△BEA(SAS),
∴∠ABE=∠CAD.
∵∠CAD+∠BAD=60°,
∴∠ABE+∠BAD=60°.
∴∠BPQ=60°.
∵BQ⊥AD,
∴∠PBQ=30°.
∴BP=2PQ,
∵∠BQP=90°,
∴BP2﹣PQ2=BQ2,
∴BQ2,
∴3BP2=4BQ2,
故选:B.
4.【分析】过点D作DF∥AB,过点D作DE′⊥BC于E′,可得DF是△ABC的中位线,可得AB=AC=2DF,则DF=DC,根据等腰三角形的性质得BC=2CF=4E′C,根据三角形角和边的关系即可求解.
【解答】解:过点D作DF∥AB,过点D作DE′⊥BC于E′,
∵点D是边AC的中点,
∴DF是△ABC的中位线,
∵AB=AC,
∴AB=AC=2DF,BF=CF,
∴DF=DC,
∵DE′⊥BC于E′,
∴CF=2E′C,DE′<DF,
∴BC=2CF=4E′C,
∴BE′=3E′C,
∵∠DFC=∠DEC+∠EDF,
∴DE>DF,
∴若AC>2DE,则BE>EC;若AC<2DE,则EC>BE,若BE>3EC,则AC>2DE;若BE<EC,则AC<2DE.
故选:C.
5.【分析】由“SAS”可证△BAE≌△CAD,可得∠ABE=∠ACD,可证∠GBC=∠GCB,可得BG=CG,则点G是BC的中垂线上,由线段垂直平分线的性质可得BF=CF,故①正确;
由全等三角形的性质可得∠ADC=∠AEB=90°,由直角三角形的性质可得CF=DF,故②正确;
由等腰三角形的性质和三角形内角和定理可得2∠DBF+2∠ECF﹣∠DFE=180°,由∠BAC+∠ABC+∠ACB=180°,可得∠DFE=2∠ABE,故③正确;
由角平分线的性质可证点G是角平分线的交点,可得点G到三边距离相等,由面积法可求FG,故④正确;即可求解.
【解答】解:在△BAE和△CAD中,
,
∴△BAE≌△CAD(SAS),
∴∠ABE=∠ACD,
∵AB=AC=5,
∴∠ABC=∠ACB,
∴∠GBC=∠GCB,
∴BG=CG,
∴点G是BC的中垂线上,
∵AB=AC,
∴点A在BC的中垂线上,
∴AG垂直平分BC,
∴BF=CF,故①正确;
若BE⊥AC,则∠AEB=90°,
∵△BAE≌△CAD,
∴∠ADC=∠AEB=90°,
∴∠BDC=90°,
又∵BF=CF,
∴CF=DF,故②正确;
如图,连接EF,
若BE⊥AC,则∠AEB=90°,
∵△BAE≌△CAD,
∴∠ADC=∠AEB=90°,
∴∠BDC=90°=∠BEC,
又∵BF=CF,
∴CF=DF=EF=BF,
∴∠DBF=∠BDF,∠FEC=∠FCE,
∴2∠DBF+∠DFB=180°,2∠ECF+∠EFC=180°,
又∵∠DFB+∠EFC+∠DFE=180°,
∴2∠DBF+2∠ECF﹣∠DFE=180°,
∵∠BAC+∠ABC+∠ACB=180°,
∴2∠BAC+2∠ABC+2∠ACB=360°,
∴2∠BAC+180°+∠DFE=360°,
∴2∠BAC+∠DFE=180°,
∵∠BAC+∠ABE=90°,
∴∠DFE=2∠ABE,故③正确,
若BE平分∠ABC,
∴∠ABE=∠CBE∠ABC,
∵∠ABE=∠ACD,∠GBC=∠GCB,
∴∠ACD=∠BCD,
∴点G是角平分线的交点,
∴点G到三边的距离为GF的长,
∵AB=AC=5,BC=6,BF=CF,
∴BF=CF=3,
∴AF4,
∵S△ABCBC AFAB GFAC GFCB GF,
∴FG,故④正确;
故选:D.
6.【分析】由正方形的性质推出AB=BH=AK,BC=BE=DE,∠ABH=∠BAK=90°,∠E=90°,由HL证明Rt△ABC≌Rt△HBE,得到AC=HE,由H是DE中点,得到BC=2AC,由余角的性质推出∠ABC=∠KAB,又AK=AB,∠K=∠BAK,即可证明△BAP≌△AKM(ASA),得到△BAP是的面积=△AKM的面积,因此△ABC的面积=阴影的面积=9,由三角形面积公式得到△ABC的面积AC BC=AC2=9,由勾股定理得到AB2=AC2+BC2=AC2+4AC2=5AC2=45,即可得到正方形ABHK的面积.
【解答】解:∵四边形ABHK,四边形BCDE是正方形,
∴AB=BH=AK,BC=BE=DE,∠ABH=∠BAK=90°,∠E=90°,
∴Rt△ABC≌Rt△HBE(HL),
∴AC=HE,
∵H是DE中点,
∴HEDE,
∴BC=2AC,
∵∠ACB=90°,∠BAK=90°,
∴∠ABC+∠BAC=∠MAK+∠BAC=90°,
∴∠ABC=∠KAB,
∵AK=AB,∠K=∠BAK,
∴△BAP≌△AKM(ASA),
∴△BAP是的面积=△AKM的面积,
∴△ABC的面积=阴影的面积=9,
∵△ABC的面积AC BC=AC2=9,
∴AB2=AC2+BC2=AC2+4AC2=5AC2=45,
∴正方形ABHK的面积=AB2=45.
故选:D.
7.【分析】作点F关于BC的对称点M,连接FM交BC于点N,连接EM交BC于点H,连接CM、BE、BF、FH,可得点H到点E和点F的距离之和最小,求出最小值即可解答.
【解答】解:如图,作点F关于BC的对称点M,连接FM交BC于点N,连接EM交BC于点H,连接CM、BE、BF、FH,
∵点E,F将对角线AC三等分,且AC=12,
∴EC=8,FC=4=AE,
∵点M与点F关于BC对称,
∴CF=CM=4,∠ACB=∠BCM=45°,
∴∠ACM=90°,
∴,
即EH+HM=EH+HF=4,
则在线段BC存在点H到点E和点F的距离之和最小为,
在点H右侧,当点P与点C重合时,则PE+PF=12,
∴点P在CH上时,,有一个点P使PE+PF=9,
在点H左侧,当点P与点B重合时,,
∵AB=BC,CF=AE,∠BAE=∠BCF,
∴△ABE≌△CBF(SAS),
∴,
∴BE+BF=4,
∴点P在BH上时,有一个点P使PE+PF=9,
∴在线段BC上的左右两边各有一个点P使PE+PF=9,
同理在线段AB、AC上也都存在两个点使PE+PF=9.
即共有6个点P满足PE+PF=9,
故选:D.
8.【分析】如图,连接EB,过点C作CJ⊥AB于点J.首先证明BE⊥AC,利用面积法求出BE,再利用勾股定理求出CE.
【解答】解:如图,连接EB,过点C作CJ⊥AB于点J.
∵B,E关于DF对称,
∴DB=DE,
∵ED=DC,
∴DB=DE=DC,
∴∠BEC=90°,
∴BE⊥AC,
∵CA=CB=8,CJ⊥AB,
∴AJ=JBAB=3,
∴CJ,
∴S△ABC AB CJ AC BE,
∴BE,
∴CE.
故选:B.
9.【分析】①错误,理由反证法判断即可;
②正确.求出AE,再利用平行线分线段成比例定理求解.
【解答】解:①错误.当∠B=30°时,E,A重合,△BCE明显不是等腰三角形;
②正确.
理由:过点C作CH⊥AB于点H,过点E作EG⊥AC于点G.
∵AC=6,BC=8,∠ACB=90°,
∴AB10,
∴CH,
∴AH,
由作图可知DA=DC=DB=5,
∵CE=CD=5,
∴EH,
∴AE=AH=EH,
∵S△ACE AC EG AE CH,
∴EG,故②正确.
故选:C.
10.【分析】根据折叠的性质和三角形的面积公式即可得到结论.
【解答】解:过P作PE⊥BC于E,如图:
∵∠MPN=90°,PN=4,MN=5,
∴PM3,
∵将长方形纸片ABCD如图折叠,B,C两点恰好重合落在AD边上的同一点P处,折痕分别是MH,NG,
∴B与P关于直线MH对称,C与P关于直线NG对称,
∴∠CNG=∠PNG,
∵AD∥BC,
∴∠CNG=∠PGN,
∴∠PNG=∠PGN,
∴PG=PN=4,
同理PH=PM,
∵HG∥MN,
∴PE⊥HG,
∴S1,
S2PG PE4.
S36,
∴A.S1+S2S3,故该选项不符合题意;
B.2S1+2S23S3,故该选项不符合题意;
C.3S2﹣S1S3,故该选项不符合题意;
D.5S2﹣5S1=24﹣18=6,故该选项符合题意;
故选:D.
11.【分析】由∠ACB=90°,得∠A+∠B=90°,由折叠得∠FEG=∠A,∠CED=∠B,则∠FEG+∠CED=∠A+∠B=90°,所以∠CEF=90°,则EF⊥CE,可判断①正确;由BC=3,AC=4,根据勾股定理求得AB=5,而∠BDC=∠EDC180°=90°,所以5CD3×4=S△ABC,求得CD,进而求得DE=DB,则AE=AB﹣2DE,所以AG=EG,由EF=AF,EC=BC=3,CF=4﹣AF,根据勾股定理得AF2+32=(4﹣AF)2,求得AF,而∠AGF=∠EGF180°=90°,所以FG,可判断②正确,于是得到问题的答案.
【解答】解:∵∠ACB=90°,
∴∠A+∠B=90°,
由折叠得∠FEG=∠A,∠CED=∠B,
∴∠FEG+∠CED=∠A+∠B=90°,
∴∠CEF=180°﹣(∠FEG+∠CED)=90°,
∴EF⊥CE,
故①正确;
∵BC=3,AC=4,
∴AB5,
∵∠BDC=∠EDC180°=90°,
∴CD⊥AB,
∴5CD3×4=S△ABC,
∴CD,
∴DE=DB,
∴AE=AB﹣2DE=5﹣2,
∴AG=EGAE,
∵EF2+EC2=CF2,EF=AF,EC=BC=3,CF=4﹣AF,
∴AF2+32=(4﹣AF)2,
解得AF,
∵∠AGF=∠EGF180°=90°,
∴FG,
故②正确,
故选:A.
12.【分析】由图象可知两车起始距离为60,从而得到乙车速度,根据图象变化规律和两车运动状态,得到相关未知量.
【解答】解:乙车先行1小时的路程是60千米,因此乙车的速度为60千米/小时,
甲车出发1.5小时就追上乙,因此速度差为60÷1.5=40千米/小时,
故甲车的速度为100千米/小时,故选项A不合题意;
甲车追上乙车后到两车距离为80千米需要时间为80÷40=2(小时),
甲车行全程需要2+1.5=3.5(小时),
全程为100×3.5=350千米,故选项B不合题意;
此时乙车出发3.5+1=4.5(小时),故选项C符合题意;
甲车休息小时准备返回时乙车行3.5+1+0.5=5(小时),
此时乙车距B地350﹣60×5=50(千米),
返回时相遇时间为50÷(100+60)小时,
此时甲车行驶的时间为3.5+0.5(h),故选项D不合题意.
故选:C.
二.填空题
13.【分析】先求出∠CAB=60°,则∠CAD=∠BAD=30°=∠B,根据含30°角的直角三角形的性质可得ACCD,AD=BD=2CD,则BC=3CD,由AE是BC边的中线得CEBCCD,根据DE=1即可求解.
【解答】解:∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD是∠BAC的平分线,
∴∠CAD=∠BAD=30°=∠B,
∴AD=BD,ACCD,AD=2CD,
∴AD=BD=2CD,
∴BC=3CD,
∵AE是BC边的中线,
∴CEBCCD,
∵DE=1,
∴CE﹣CDCD﹣CD=1,
∴CD=2,
∴ACCD=2,
故答案为:2.
14.【分析】(1)根据题意列方程即可得到结论;
(2)根据题意列不等式,解不等式即可得到结论.
【解答】解:(1)∵一次函数y=kx+b(k为常数且k≠0)的图象过点(2,﹣4),
∴﹣4=2k+b,
∴b=﹣2k﹣4,
故答案为:﹣2k﹣4;
(2)∵函数图形过第二、三、四象限,
∴k<0,b<0,
∴﹣2k﹣4<0,
解得﹣2<k<0,
∵m=k+3b,
∴m=﹣5k﹣12,
∴﹣12<﹣5k﹣12<﹣2,
即﹣12<m<﹣2,
故答案为:﹣12<m<﹣2.
15.【分析】(1)根据等腰三角形的性质和直角三角形斜边上的中线等于斜边的一半性质证明△ABC的周长是△DEF的周长的2倍解答即可;
(2)根据题意设AE=3x,EC=2x,利用勾股定理和直角三角形斜边上的中线等于斜边的一半的性质求得AF和EF的值,进而解答即可.
【解答】解:∵AB=AC,AF⊥BC,
∴BF=CF,
∵BE⊥AC,点F为BC的中点,
∴BC=2EF,
∵BE⊥AC,点D是AB的中点.
∴AB=2DE,
∵点F为BC的中点,点D是AB的中点,
∴DF为△ABC的中位线,
∴AC=2DF,
∴△ABC的周长是△DEF的周长的2倍,
∵△DEF的周长是8,
∴△ABC的周长是16,
故答案为:16;
(2)∵AE:EC=3:2,
∴设AE=3x,EC=2x,
则AC=AB=5x,
在Rt△ABE中,根据勾股定理可得:BE=4x,
在Rt△BCE中,
∵CE=2x,BE=4x,
∴BC=2x,
∵BC=2EF,
∴EFx,
∵BC×AF=AC×BE,
即:2x×AF=5x×4x,
解得:AF=2x,
∴AF:EF=2x:x=2:1,
故答案为:2:1,
16.【分析】根据直角三角形的性质、等腰三角形的性质得到∠E=∠ACE,得到AE=AC=2,设∠E=∠ACE=x,根据题意得到∠ABD=90°x=∠D,再根据勾股定理计算即可.
【解答】解:∵AB=AC,
∴∠ABC=∠ACB.
∵BC⊥DE,
∴∠BCE=90°.
∴∠E+∠EBC=90°,∠ACE+∠ACB=90°,
∴∠E=∠ACE,
∴AE=AC=AB=2,
设∠E=∠ACE=x,则∠ACB=∠ABC=90°﹣x.
∵∠ABC+2∠CBD=90°,
∴∠CBDx,
∴∠ABD=∠ABC+∠CBD=90°x=∠D,
∴DE=BE=AB+AE=4,
∴CE=DE﹣CD=3.
在Rt△BCE中,BC,
∴BD2,
故答案为:2,2.
17.【分析】过点O作OH⊥AF于H,连接OF.首先证明∠BAF=30°,推出点F的在射线AF上运动,根据垂线段最短可知,当点F与H重合时,OF的值最小,最小值=OH的长.
【解答】解:过点O作OH⊥AF于H,连接OF.
∵△ABC是等边三角形,AO⊥BC,
∴∠BAO=∠CAO∠BAC=30°
∵线段BF与线段BE关于直线BA对称,
∴∠BAF=∠BAE=30°,∠OAF=60°,
∴点F的在射线AF上运动,
根据垂线段最短可知,当点F与H重合时,OF的值最小,
在Rt△AHO中,
∵∠AOH=30°,
∴AHOA,
∴AE=AH.
故答案为:.
18.【分析】在AB的延长线上截取BG=BF,连接FG,证明△BFG为等边三角形,然后证明△DFB≌△EFG,即可解答.
【解答】解:如图,在AB的延长线上截取BG=BF,连接FG,
∵△ABC 是等边三角形,
∴∠A=∠ACB=60°,
∵BF∥AC,
∴∠DBF=∠ACB=60°,∠GBF=∠A=60°,
又∵BG=BF,
∴△BFG 为等边三角形,
∴∠GFB=∠G=60°=∠DBF,,
又∵∠DFE=60°=∠DBF,
∴∠DFB=∠EFG,
∴△DFB≌△EFG,
∴EG=DB=5,
∴.
故答案为:5.
19.【分析】利用待定系数法分别求出甲、乙两人离B地的距离y与行驶时间x之间的函数关系式;按照x不同的取值范围,根据二者y之差的绝对值不大于5,列绝对值不等式并求解即可.
【解答】解:设甲离B地的距离y与行驶时间x之间的函数关系式为y=k1x+b1(k1、b1为常数,且k1≠0).
将x=0,y=30和x=2,y=0代入y=k1x+b1,
得,解得,
∴y=﹣15x+30(0≤x≤2);
当0≤x<1时,设乙离B地的距离y与行驶时间x之间的函数关系式为y=k2x(k2为常数,且k2≠0).
将x=1,y=30代入y=k2x,得k2=30,
∴y=30x(0≤x<1);
当1≤x≤2时,设乙离B地的距离y与行驶时间x之间的函数关系式为y=k3x+b2(k3、b2为常数,且k3≠0).
将x=1,y=30和x=2,y=0代入y=k3x+b2,
得,解得,
∴y=﹣30x+60(1≤x≤2);
综上,乙离B地的距离y与行驶时间x之间的函数关系式为y.
①当0≤x<1时,若两人之间的距离不超过5km,则|﹣15x+30﹣30x|≤5,
经整理,得|9x﹣6|≤1,解得x;
②当1≤x≤2时,若两人之间的距离不超过5km,则|﹣15x+30﹣(﹣30x+60)|≤5,
经整理,得|3x﹣6|≤1,解得x,
∴x≤2;
综上,x的取值范围是x或x≤2,
故答案为:x或x≤2.
20.【分析】可证明△AEF与△HJI全等,进而得出△ABC的面积,再将所给的面积全部相加,得出正方形BCFD和梯形ACIH的面积之和,用AC和BC的长将其表示出来即可解决问题.
【解答】解:由题知,
令BC=a,AC=b,
∵四边形ABKH和四边形ACIG是正方形,
∴∠BAH=∠CAG=90°,AB=AH,AC=AG,
∴∠BAH﹣∠CAH=∠CAG﹣∠CAH,
即∠BAC=∠HAG.
在△BAC和△HAG中,
,
∴△BAC≌△HAG(SAS),
∴HG=BC=a.
又∵AF=b﹣a,IH=b﹣a,
∴AF=IH.
∵∠HAG+∠AHG=∠AHG+∠JHI=90°,
∴∠HAG=∠JHI,
∴∠BAC=∠JHI.
在△EAF和△JHI中,
,
∴△AEF≌△HJI(ASA),
∴S△AEF=S△HJI.
又∵四边形BCFE和△HIJ的面积和为5,
∴S四边形BCFE+S△AEF=5,
即S△ABC=5,
∴,
则ab=10.
又∵四边形BCFE和△HIJ的面积和为5,四边形ACJH和△BDE的面积和为12,
将四部分的面积相加得,
S正方形BDFC+S梯形ACIH=17,
∴a2+b2,
则a2+b2=22.
∴(a+b)2=a2+b2+2ab=22+2×10=42,
则a+b(舍负),
即AC+BC的值为.
故答案为:.
21.【分析】设CE交DF于H,AD=BC=x,AB=CD=y,在Rt△BFC中,()2+y2=x2①,在Rt△ABE中,y2+(x﹣3)2=()2②,①﹣②得:(x﹣3)2=x2,可解得AD,CD=y=4,故AE=AD﹣DE3;CE5,根据面积法有DHFH,故DF=DH+FH.
【解答】解:设CE交DF于H,如图:
设AD=BC=x,AB=CD=y,
∵△CDE沿CE折叠得到△CFE,
∴CF=CD=y,∠EDC=∠EFC=90°=∠BFC,EF=DE=3,
∵,
∴BF=BE﹣EF3,
在Rt△BFC中,BF2+CF2=BC2,
∴()2+y2=x2①,
在Rt△ABE中,AB2+AE2=BE2,
∴y2+(x﹣3)2=()2②,
①﹣②得:(x﹣3)2=x2,
解得x或x(舍去),
∴AD,CD=y4,
∴AE=AD﹣DE3;CE5,
∵△CDE沿CE折叠得到△CFE,
∴DF⊥CE,DH=FH,
∴2S△DCE=DE CD=CE DH,
∴DHFH,
∴DF=DH+FH;
故答案为:,.
22.【分析】利用矩形的性质和全等三角形的判定与性质得到△BAE≌△CEF,则AB=EC,BE=FC,代入运算得到AD=2DF,设DF=a,则AD=2a,设BA=x,则BE=BC﹣AB=2a﹣x,CF=x﹣a,利用BE=FC求得AB,利用三角形的面积公式和矩形的面积公式解答即可得出结论.
【解答】解:∵△AEF为等腰Rt△,且∠AEF=90°,
∴AE=EF,∠AEB+∠FEC=90°,
∵四边形ABCD为矩形,
∴∠B=∠C=90°,AD=BC,
∴∠BAE+∠BEA=90°,
∴∠BAE=∠CEF.
在△BAE和△CEF中,
,
∴△BAE≌△CEF(AAS),
∴AB=EC,BE=FC.
∵3(AB+BE)=2(AD+DF),
∴3(EC+BE)=2AD+2DF,
∴3AD=2AD+2DF,
∴AD=2DF,
设DF=a,则AD=2a,
设BA=x,则BE=BC﹣AB=2a﹣x,CF=x﹣a,
∴2a﹣x=x﹣a,
∴xa.
∵AFa,
∴AE=EFAFa.
∴.
故答案为:.
23.【分析】根据AD=DC'和AD=AC'两种情况展开讨论,当AD=DC',设BD=x可得DC=4﹣x,根据折叠的性质得AD=DC=4﹣x,再根据勾股定理建立方程,解方程即可得到答案;当AD=AC',可得B'是DC'的中点,设BD=x,DC=4﹣x,可得,根据折叠的性质得BD=DB',建立方程解方程即可得到答案.
【解答】解:当AD=DC'时,设BD=x,
得DC=4﹣x,
∵DC'=DC,
∴AD=DC=4﹣x,
在Rt△ABC中AB2+BD2=AD2,
∴9+x2=(4﹣x)2,
∴x;
当AD=AC'时,
∵AB'⊥DC',
∴B'是DC'的中点,
∵DC'=DC,
∴DB′=0.5DC,
设BD=x,则DC=4﹣x,
∴,
∵BD=DB',
∴,
∴x,
∴当BD或BD时,△ADC′是以AD为腰的等腰三角形.
故答案为:或.
24.【分析】连接BG,先证得△DGE≌△DCE(AAS),运用勾股定理可得AB=10,利用面积法可求得:GF,再运用勾股定理即可求得答案.
【解答】解:如图,连接BG,
∵DE平分∠ADC,
∴∠EDC=∠EDG,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,BD=CDBC=6,∠CAD+∠C=90°,
∵EF⊥AB,
∴∠BAD+∠AGF=90°,
又∵∠AGF=∠DGE,
∴∠DGE=∠C,
在△DGE和△DCE中,
,
∴△DGE≌△DCE(AAS),
∴DG=CD=6,
∴AD=AG+DG=2+6=8,
在Rt△ABD中,AB10,
∵S△ABGAB GFAG BD,
∴GF,
在Rt△AGF中,AF.
故答案为:.
三.解答题
25.【分析】(1)将点的坐标代入函数解析式,建立二元一次方程组即可解决问题.
(2)将点(r,0)代入y1,得出k,b,r的关系即可解决问题.
(3)先求出y3和y4,再用作差法即可解决问题.
【解答】(1)解:将点(2,﹣1)和(1,﹣3)分别代入y1和y2得,
,
解得,
所以k的值为2,b的值为﹣5.
(2)证明:因为函数y1的图象经过点(r,0),
所以kr+b=0.
将x代入y2得,
.
又因为kr+b=0,
所以k,
所以,
即y2=0,
所以函数y2的图象经过点().
(3)解:y3=y1﹣y2=kx+b﹣(bx+k)=(k﹣b)x+b﹣k,
y4=y2﹣y1=bx+k﹣(kx+b)=(b﹣k)x+k﹣b.
又因为y3>y4,
则y3﹣y4>0,
所以y3﹣y4=2(k﹣b)x+2(b﹣k)>0,
即(k﹣b)x>k﹣b.
所以当k>b时,x>1;
当k<b时,x<1;
当k=b时,不存在.
故k>b时,x>1;k<b时,x<1.
26.【分析】(1)取AC中点D,连接BD,先说明△PBE为等边三角形,再证明△BDP≌△PQE即可解答;
(2)①取AC的中点D,连接BD,证明△BDP≌△PQE即可解答;
②由①知AC=2PQ,结合AC=AP+PQ+QC,即可得到2PQ=AP+PQ+QC,进而得到答案;
(3)AP=QC+PQ,过B作BD⊥AC,证明△PDB≌△EQP得出BD=PQ,再根据线段直角的关系即可解答.
【解答】解:(1)取AC中点D,连接BD,
∵AB=BC,∠ABC=90°,D为中点,
∴∠ABD=∠CBD=∠BAC=∠BCA=45°,BD=AD=CDAC,∠BDA=∠CDB=90°,
当α=60°时,
∵PB=PE,
∴△PBE为等边三角形,
∴∠PBE=∠PEB=∠BPE=60°,
∴∠PBD=15°,
∴∠BPD=90°﹣15°=75°,
∴∠EPQ=75°﹣60°=15°=∠PBD,
∵∠PDB=∠PQE=90°,PB=PE,
∴△BDP≌△PQE(AAS),
∴BD=PQ,
∵BDAC,
∴PQAC;
故答案为:;
(2)①取AC的中点D,连接BD,
∵AB=BC,∠ABC=90°,D为中点,
∴∠ABD=∠CBD=∠BAC=∠BCA=45°,BD=AD=CDAC,∠BDA=∠CDB=90°,
∵PB=PE,
∴∠PBE=∠PEB,
∵∠PBE=∠DBC﹣∠DBP=45°﹣∠DBP,∠PEB=∠C﹣∠EPQ=45°﹣∠EPQ,
∴∠DBP=∠EPQ,
∵PB=PE,∠PDB=∠EQP,
∴△BDP≌△PQE(AAS),
∴BD=PQ,
∵BDAC,
∴PQAC;
故答案为:;
②AP+QC=PQ;
由①知AC=2PQ,
∵AC=AP+PQ+QC,
∴2PQ=AP+PQ+QC,
∴AP+QC=PQ;
故答案为:AP+QC=PQ;
(3)AP=QC+PQ,
过B作BD⊥AC,
∵∠DBP=45°﹣α,
在△PCE 中,∠QPE=45°﹣α,
∠DBP=∠QPE,
在△PDB与△EQP中,
,
∴△PDB≌△EQP(AAS),
∴QE=DP,PQ=BD=AD=CD,
在Rt△ABC中,AB=BC,∠ABC=90°,
∴BDAC,
∴PQAC,
∵PC=PQ﹣CQ,AP+PC=AC,
∴AP+PQ﹣CQ=AC=2PQ,
∴AP=QC+PQ.
27.【分析】(1)由等腰三角形的性质可得出结论;
(2)过点P作PE∥BC,交CA的延长线于点E,证明△EQP≌△CQD(AAS),由全等三角形的性质得出QE=QC,则可得出结论;
(3)方法一:过点A作AM⊥BC于点M,延长AM至E,使AM=ME,连接CE,延长QD交CE于点F,证明△AMB≌△EMC(SAS),得出∠B=∠ECM,证出PF=AE=2AM,DQ=DF,则可得出结论.
方法二:过A作PQ垂线,由等腰三角形的性质可得出结论.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵DP⊥BC,
∴∠B+∠P=∠C+∠CQD=90°,
∴∠AQP=∠CQD=∠P,
∴AP=AQ.
(2)解:QC=2AQ.
理由:过点P作PE∥BC,交CA的延长线于点E,
∴∠E=∠C,∠APE=∠B,
由题意,得∠E=∠APE,
∴AE=AP=AQ.
∴QE=2AQ.
∵点Q是线段DP的中点,
∴PQ=DQ,
∵∠EQP=∠DQC,
∴△EQP≌△CQD(AAS),
∴QE=QC,
∴QC=2AQ.
(3)解:DP+DQ的值是定值,这个定值是BC边上的高的2倍.
方法一:过点A作AM⊥BC于点M,延长AM至E,使AM=ME,连接CE,延长QD交CE于点F,
∵AB=AC,AM⊥BC,
∴BM=CM,
∵∠AMB=∠CME,AM=ME,
∴△AMB≌△EMC(SAS),
∴∠B=∠ECM,
∴AB∥CE,
∵AM⊥BC,PD⊥BC,
∴AM∥PD,
∴四边形AEFP是平行四边形,
∴PF=AE=2AM,
∵AM=ME,AM⊥CM,
∴AC=CE,
∴∠CAM=∠CEM,
∵AE∥QFD,
∴∠CAM=∠CQF,∠CEM=∠CFQ,
∴∠CQF=∠CFQ,
∴CQ=CF,
∴DQ=DF,
∴PD+DQ=PD+DF=PF=2AM.
即DP+DQ的值是定值,这个定值是BC边上的高的2倍.
方法二:过A作PQ垂线,由等腰三角形的性质可得出结论.
28.【分析】(1)数学思考:分别将三组数据代入解析式,联立方程组解答交点坐标即可;
(2)①联立解析式,求出x的值,根据a,b均不为0,且a≠b,得到x=﹣1为定值即可;
②令y1﹣y2≥0,则(a﹣b)x+a﹣b≥0,得x≥﹣1;令y1﹣y2<0,则(a﹣b)x+a﹣b<0得x<﹣1;
③两解析式相加得)=(a+b)(x﹣1),即x=1时,不论a,b如何取值,y1+y2=0.
【解答】解:(1)当a=1,b=2时;联立解析式,解得,交点坐标为(﹣1,﹣3);
当a=2,b=﹣1时;联立解析式,解得,交点坐标为(﹣1,﹣1);
当a=﹣1,b=﹣2时,联立解析式,解得,交点坐标为(﹣1,3).
(2)①联立解析式,
∴ax﹣b=bx﹣a,
∴(a﹣b)x=﹣(a﹣b),
∵a,b均不为0,且a≠b,
∴a﹣b≠0,
∴x1,
故y1和y2的图象的交点的横坐标都是定值﹣1.
②∵a>b,
∴a﹣b>0,
∴y1﹣y2=ax﹣b﹣(bx﹣a)=ax﹣b﹣bx+a=(a﹣b)x+a﹣b,
令y1﹣y2≥0,则(a﹣b)x+a﹣b≥0,
∴(a﹣b)x≥﹣(a﹣b),
∴x≥﹣1;
令y1﹣y2<0,则(a﹣b)x+a﹣b<0,
∴x<﹣1,
综上分析,当x≥﹣1时,y1≥y2;当x<﹣1时,y1<y2;
③y1+y2=ax﹣b+bx﹣a=(a+b)x﹣(a+b)=(a+b)(x﹣1),
∴当x﹣1=0时即x=1时,不论a,b如何取值,y1+y2=0.
29.【分析】(1)判定△ABC是等腰直角三角形,即可得到BC=AB,
(2)由ASA证明△ABO≌△FEO,推出EF=AB,
(3)由ASA证明△ABC≌△DBC,推出BD=AB.
【解答】解:(1)∵AB⊥BC,∠ACB=45°,
∴△ABC是等腰直角三角形,
∴BC=AB,
∴河宽AB的长度就是线段BC的长度.
故答案为:BC;
(2)第二小组的方案可行,理由如下:
∵O是BE中点,
∴OB=OE,
∵AB⊥BE,EF⊥BE,
∴∠ABO=∠FEO=90°,
在△ABO和△FEO中,
,
∴△ABO≌△FEO(ASA),
∴EF=AB,
∴河宽AB的长度就是线段EF的长度.
(3)见表格,
课题 测量河流宽度
工具 测量角度的仪器(仪器的高度忽略不计),标杆,皮尺等
小组 第一小组 第二小组 第三小组
测量方案 观测者从B点向正东走到C点,此时恰好测得:∠ACB=45° 观测者从B点向正东走到E点,O是BE的中点,继续从点E沿垂直于BE的EF方向走,直到点A,O,F在一条直线上. 观测者从B点向正西走到C点,使用测量角度的仪器测得∠BCD=∠ACB=65°,CD交AB延长线于D,
测量示意图
只要测出BD的长,就能推算出河宽AB长,理由如下:
∵AB⊥BC,
∴∠ABC=∠DBC=90°,
在△ABC和△DBC中,
,
∴△ABC≌△DBC(ASA),
∴BD=AB,
∴河宽AB的长等于线段BD的长.
30.【分析】(1)①过点A作AD⊥BC于点D,当点P与点D重合时,AP最小,由勾股定理可得出答案;
②由勾股定理求出PD,则可得出答案;
(2)过点A作AE⊥BC于点E,由勾股定理得出AB2=m2=AE2+BE2①,AP2=n2=AE2+PE2②,①﹣②可得出答案.
【解答】解:(1)①过点A作AD⊥BC于点D,
∵AB=AC,BC=16,
∴BD=CD=8,
∵AB=10,
∴6,
当点P与点D重合时,AP最小,
∴AP的最小值为6;
②∵PA=7,AD=6,
∴PD,
∴BP=BD﹣DP=8或BP=BD+DP=8;
(2)过点A作AE⊥BC于点E,由(1)可知BE=CE,
在Rt△ABE中,AB2=m2=AE2+BE2①,
在Rt△APE中,AP2=n2=AE2+PE2②,
①﹣②得,
m2﹣n2=BE2﹣PE2=(BE+PE)(BE﹣PE)
=(CE+PE)BP
=CP BP.
即BP PC=m2﹣n2.
31.【分析】[建立模型]
(1)先描点,再得出结论,然后用待定系数法求函数解析式;
(2)把x=12代入解析式求出y的值即可;
[解决问题]
把y=40代入解析式求出x即可.
【解答】解:[建立模型]
(1)描点,连线,
根据点的分布规律可知,h关于x的函数关系式满足一次函数,
设h关于x的函数关系式为h=kx+b,
则,
解得,
∴h关于x的函数关系式为h=1.4x+8.6;
(2)当x=12时,y=1.4×12+8.6=25.4,
∴这摞杯子的总高度25.4cm;
[解决问题]
当y=40时,1.4x+8.6=40,
解得x22.4,
∴一摞最多能叠22个杯子,可以一次性放进柜子里.
32.【分析】任务1:直接描点并作图,利用待定系数法求出函数关系式,并求出x的最大值和最小值;当y=70时求出a的值即可.
任务2:根据“背带的总长度为单层部分与双层部分的长度和”和x与y之间的函数关系式,用含x的代数式将背带的总长度表示出来,再由背带总长度与身高的比例关系列出等式,将h表示为x的函数的形式即可;
任务3:当背包的背带调节到最短时都为双层部分,求出此时x的值,从而求出手离地面的高度;设小明爸爸的身高为未知数,根据臂展与身高的关系及肩宽,将一条胳膊的长度用身高表示出来,头顶到肩膀的垂直高度、一条胳膊的长度、手离地面的高度之和为身高,利用此等量关系列方程求出身高,将其代入任务2中得到的函数关系式,求出对应x的值即可.
【解答】解:任务1:描点并作图如图所示:
根据图象可知,变量x、y满足一次函数关系.
设y=kx+b(k、b为常数,且k≠0),
将x=2,y=116和x=10,y=100代入y=kx+b,
得,解得,
∴y=﹣2x+120.
将x=a和y=70代入y=﹣2x+120,
得﹣2a+120=70,解得a=25;
当背带都为单层部分时,x=0;
当背带都为双层部分时,y=0,即﹣2x+120=0,解得x=60,
∴x的取值范围是0≤x≤60.
任务2:∵背带的总长度为单层部分与双层部分的长度和,
∴总长度为﹣2x+120+x=﹣x+120,
当单肩包背带长度调整为最佳背带总长度时,得,
∴hx+180(0≤x≤60).
任务3:由素材可知,当背包的背带调节到最短时都为双层部分,即x=60,y=0.
∵背包提在手上,且背包的悬挂点距地面高度为53.5cm,
∴手到地面的距离为(53.5)cm,即83.5cm.
设小明爸爸的身高为h cm.
∵臂展和身高一样,且肩宽为38cm,
∴小明爸爸一条胳膊的长度为cm,
∴h83.5=h,解得h=172,
根据任务2,得172x+180,解得x,
∴此时双层部分的长度为cm.
33.【分析】(1)利用待定系数法即可求出k的值;
(2)根据一次函数的图象特征即可求出k的取值范围;
(3)根据y1﹣y2=b+1,得(k﹣1)x=0,又k≠1,可求x的值.
【解答】解:(1)∵一次函数y1=kx+b过点(3,2)和(0,5),
∴,
解得,
∴k的值为﹣1;
(2)当一次函数y1=kx+b过点(3,2)和(0,0)时,
可得,
解得k,
∴当一次函数y1=kx+b不经过第四象限,
∴k的取值范围为0<k;
(3)∵y1﹣y2=b+1,
∴kx+b﹣x+1=b+1,
kx﹣x=0,
(k﹣1)x=0,
∵k≠1,
∴k﹣1≠0,
∴x=0.
34.【分析】(1)依据题意,设y=kt,再用待定系数法求函数表达式即可;
(2)依据题意,设CD的函数表达式为y=mt+n,由C(0.1,8),D(0.5,0)用待定系数法求函数表达式即可;
(3)依据题意,由(1)和(2)建立方程组,再解方程组求出方程组的解即可;
(4)依据题意,根据题意分四种情况讨论即可.
【解答】解:(1)设OA的函数表达式为y=kt,
把A(0.8,8)代入函数表达式得:8=0.8k,
解得k=10,
∴OA的函数表达式为y=10t.
(2)由图象知,C(0.1,8),D(0.5,0),
设CD的函数表达式为y=mt+n,
则,
解得,
∴CD的函数表达式为y=﹣20t+10.
(3)由题意,联立方程组,
解得,
∴点K的坐标为(,).
(4)当t≤0.1时,由图象知S=8﹣10t≥7,不合题意;
当0.1<t时,S=﹣20t+10﹣10t=﹣30t+10,
当S≤3时,t,
即t;
当t<0.5时,S=10t﹣(﹣20t+10)=30t﹣10,
当S≤3时,t,
即t;
当0.5<t≤0.8时,S=10t,
则5<S≤8.不符合题意;
综上,t的取值范围为t.
35.【分析】(1)①由等腰三角形的性质得出∠ABC=∠C=50°,则可求出答案;
②由等腰三角形的性质得出∠A=∠ADB,∠ABC=∠C=α,则可求出β,由三角形外角的性质可得出答案;
(2)过点B作BM⊥BC于点M,BN⊥AC于点N,由勾股定理可得出AM=4,由勾股定理得出25﹣x2=36﹣(5﹣x)2,则可得出答案.
【解答】解:(1)①∵AB=AC,
∴∠ABC=∠C=50°,
∴∠A=180°﹣∠ABC﹣∠C=80°,
∵BD=AB,
∴∠BDA=∠A=80°,
∴β=180°﹣∠A﹣∠BDA=20°;
②∵AB=BD,
∴∠A=∠ADB,
∴β=180°﹣2∠A,
又∵AB=AC,
∴∠ABC=∠C=α,
∴∠A=180°﹣2∠C=180°﹣2α,
∴β=180°﹣2(180°﹣2α)=4α﹣180°,
即β=4α﹣180°;
(2)过点B作AM⊥BC于点M,BN⊥AC于点N,
设AN=x,则CN=5﹣x,
∵AB=5,BC=6,
∴BM=CM=3,
∴AM4,
∵BN2=AB2﹣AN2=BC2﹣CN2,
∴25﹣x2=36﹣(5﹣x)2,
∴x,
∴AD=2AN.
36.【分析】(1)先利用直角三角形的两个锐角互余可得∠C=70°,再利用等腰三角形的性质可得∠HAD=∠ADH,然后利用等量代换可得∠HAD=∠ADH=∠C=70°,从而利用三角形内角和定理进行计算即可解答;
(2)①过点H作AE⊥AD,垂足为E,根据垂直定义可得∠BAC=∠HED=90°,然后利用AAS证明△ACB≌△EDH,从而可得AC=DE,再根据等腰三角形的三线合一性质可得AD=2DE,从而可得AD=2AC,即可解答;
②利用①的结论可得AD=2a,再利用直角三角形的斜边上的中线性质可得AD=CDBC,从而可得BC=DH=4a,∠C=∠CAD,进而可得∠CAD=∠ADH,然后利用内错角相等,两直线平行可得AC∥DK,从而可得点K是AB的中点,进而可得DK是△ABC的中位线,再利用三角形的中位线定理可得DKACa,最后利用线段的和差关系进行计算,即可解答.
【解答】解:(1)∵∠CAB=90°,∠B=20°,
∴∠C=90°﹣∠B=70°,
∵HA=HD,
∴∠HAD=∠ADH,
∵∠ADH=∠C,
∴∠HAD=∠ADH=∠C=70°,
∴∠H=180°﹣∠HAD﹣∠ADH=40°,
∴∠H度数为40°;
(2)①证明:过点H作AE⊥AD,垂足为E,
∴∠HED=90°,
∵∠BAC=90°,
∴∠BAC=∠HED=90°,
∵∠C=∠ADH,HD=BC,
∴△ACB≌△EDH(AAS),
∴AC=DE,
∵HA=HD,HE⊥AD,
∴AD=2DE,
∴AD=2AC;
②解:∵AC=a,AD=2AC,
∴AD=2a,
∵∠CAB=90°,点D是边BC的中点,
∴AD=CDBC,
∴BC=2AD=4a,
∴BC=DH=4a,
∵DA=DC,
∴∠C=∠CAD,
∴∠CAD=∠ADH,
∴AC∥DK,
∴点K是AB的中点,
∴DK是△ABC的中位线,
∴DKACa,
∴HK=DH﹣DK=4aaa,
∴HK的长为a.
37.【分析】(1)先证△ADH是等边三角形,可得AD=DH=AH,∠ADH=∠AHD=60°,由等腰三角形的性质可求∠HDC=30°,即可求解;
(2)由“HL”可证Rt△CEF≌Rt△BEG,可得∠BEG=∠CEF,可证∠BEC=∠GEF=90°,即可求解;
(3)由直角三角形的性质可得BC=2CD,BEBC,即可求解.
【解答】(1)证明:如图,取AC的中点H,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,∠DAC=60°,
∵ADABAC,点H是AC的中点,
∴AD=AH=HC,
∴△ADH是等边三角形,
∴AD=DH=AH,∠ADH=∠AHD=60°,
∴DH=HC,
∴∠HDC=∠HCD=30°,
∴∠ADC=90°,
∴AD⊥CD;
(2)解:如图,过点E作EF⊥直线DC于F,EG⊥AB于G,
又∵∠ADC=90°,
∴∠GEF=90°,
∵DE平分∠BDC,EF⊥DC,EG⊥AB,
∴EG=EF,
∵AB=AC,AE平分∠BAC,
∴AE垂直平分BC,
∴BE=CE,
∴Rt△CEF≌Rt△BEG((HL),
∴∠BEG=∠CEF,
∴∠BEC=∠GEF=90°,
又∵BE=CE,
∴∠EBC=45°,
∴∠DBE=30°+45°=75°;
(3)解:∵∠ADC=90°,∠DBC=30°,
∴BC=2CD,
∵BE=CE,∠BEC=90°,
∴BEBC,
∴BECD,
∴.
38.【分析】(1)根据等边三角形的性质,利用SAS即可证明△ABD≌△CBE;
(2)结合(1)根据等边三角形的性质即可求∠DCE的度数;
(3)结合(1)利用三角形的面积公式分别求出△ABD的面积=△BCE的面积=S1AF BFFD BF,△BCD的面积=S2AF BFFD BF,进而可以用含S1,S2的代数式表示△BFD的面积.
【解答】(1)证明:∵△ABC和△DBE都是等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABD=60°﹣∠DBC=∠CBE,
在△ABD和△CBE中,
,
∴△ABD≌△CBE(SAS);
(2)解:∵△ABC是等边三角形,
∴∠ACB=60°,
由(1)知:△ABD≌△CBE,
∴∠CEB=∠A=60°,
∴∠DCE=∠ABC+∠BCE=60°+60°=120°;
(3)解:∵△ABC是等边三角形,BF⊥AC,
∴AF=CF,
由(1)知:△ABD≌△CBE,
∴△ABD的面积=△BCE的面积=S1AD BF(AF+FD) BFAF BFFD BF,
∵△BCD的面积=S2CD BF(CF﹣FD) BF(AF﹣FD) BFAF BFFD BF,
∴S1﹣S2=(AF BFFD BF)﹣(AF BFFD BF)=FD BF,
∴△BFD的面积FD BF(S1﹣S2).
39.【分析】(1)根据折叠的性质得∠EDF=∠A=90°,∠AFE=∠DFE,根据三角形的内角和定理得到∠CFD=60°,∠AFE=∠DFE=60°,求得∠AEF=30°,根据勾股定理得到AEAF,于是得到AE:AF;
(2)根据三角形中线的定义得到AE=BEAB=3,根据勾股定理得到CE5,由折叠的性质得∠EDF=∠A=90°,AF=DF=AC﹣CF=4﹣CF,DE=AE=3,CD=2根据勾股定理得到AF,于是得到AE:AF=3:2;
(3)根据等边三角形的性质得到AB=BC=AC,∠A=∠B=∠ACB=60°,根据CE是AB边上的中线,求得AE=BEAC,∠AEC=∠BEC=90°,∠BCE=∠ACE∠ACB=30°,由折叠的性质得∠EDF=∠A=60°,AE=DE,AF=DF,设AE=x,则AC=2x,根据勾股定理得到CEx,求得AF=(1)x,于是得到AE:AF=x:(1)x.
【解答】解:(1)由折叠的性质得∠EDF=∠A=90°,∠AFE=∠DFE,
∵∠ACE=30°,
∴∠CFD=60°,∠AFE=∠DFE=60°,
∴∠AEF=30°,
∴EF=2AF,
在Rt△AEF中,AE2+AF2=EF2,
∴AE2+AF2=(2AE)2,
∴AEAF,
∴AE:AF;
(2)∵CE是AB边上的中线,
∴AE=BEAB=3,在Rt△AEC中,AE2+AC2=EC2,
∴CE5,
由折叠的性质得∠EDF=∠A=90°,AF=DF=AC﹣CF=4﹣CF,DE=AE=3,CD=2,
在Rt△CDF中,CD2+DF2=CF2,
∴22+AF2=(4﹣AF)2,
∴AF,
∴AE:AF=3:2;
(3)∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠ACB=60°,
∵CE是AB边上的中线,
∴AE=BEAC,∠AEC=∠BEC=90°,∠BCE=∠ACE∠ACB=30°,
由折叠的性质得∠EDF=∠A=60°,AE=DE,AF=DF,
∴∠CDF=120°,
∴∠CFD=∠DCF=30°,
∴DF=CD,
设AE=x,则AC=2x,
∴CEx,
∵AE=DE=x,
∴CE﹣DEx=CD=AE,
∴AF=(1)x,
∴AE:AF=x:(1)x.
40.【分析】(1)根据四边形ABCD是“对角互补四边形”,求得∠B+∠D=180°,根据题意列方程即可得到结论;
(2)①根据“对角互补四边形”的定义得到∠ABC=120°,根据角平分线的定义得到∠BOC=∠BOA=30°,当∠BCO=∠BOC=30°时,求得∠CBO=180°﹣30°﹣30°=120°=∠ABC(不符合题意,舍去),当∠CBO=∠BOC=30°时,求得∠BAN=∠BOA+∠ABO=120°;当∠CBO=∠OCB时,求得∠BAN=∠BOA+∠ABO=75°;
②如图②,过点B作BG⊥ON于G,BH⊥OM于H,根据已知条件得到OC:OA=n,根据四边形COAB是“对角互补四边形”,求得∠ABC=180°﹣∠MON=120°,根据全等三角形的性质得到CH=AG,解方程即可得到结论.
【解答】解:(1)∵四边形ABCD是“对角互补四边形”,
∴∠B+∠D=180°,
∵∠B=3∠D,
∴∠B+∠B=180°,
∴∠B=135°;
(2)①∵四边形COAB是“对角互补四边形”,∠MON=60°,
∴∠ABC=120°,
∵OB平分∠MON,
∴∠BOC=∠BOA=30°,
当∠BCO=∠BOC=30°时,
∴∠CBO=180°﹣30°﹣30°=120°=∠ABC(不符合题意,舍去),
当∠CBO=∠BOC=30°时,
∴∠ABO=120°﹣30°=90°,
∴∠BAN=∠BOA+∠ABO=120°;
当∠CBO=∠OCB时,
∴∠OBC75,∠ABO=120°﹣75°=45°,
∴∠BAN=∠BOA+∠ABO=75°.
综上所述:∠BAN的度数为120°或75°;
②如图②,过点B作BG⊥ON于G,BH⊥OM于H,
∵∠BOC=∠BOA=30°,
∴BG=BHOBm,OHm,
∴S△BOC:S△BOAOC BH:OA BG=n,
∴OC:OA=n,
∵四边形COAB是“对角互补四边形”,
∴∠ABC=180°﹣∠MON=120°,
∵∠BHO=∠BGO=90°,
∴∠HBG=180°﹣∠MON=120°,
∴∠CBH=∠ABG,
在△CBH与△ABG中,
,
∴△CBH≌△ABG(AAS),
∴CH=AG,
∴OC+CH=OA﹣AG,
∴OC+2CHOC,
∴(1)OC=2CH,
∴CHOC,
∵OH=OC+CH,
∴OCOCm,
∴OC.
同课章节目录
