人教版2024七年级下册数学7.1.1 两条直线相交 教学课件( 共25张PPT)
文档属性
| 名称 | 人教版2024七年级下册数学7.1.1 两条直线相交 教学课件( 共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-21 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
7.1.1 两条直线相交
第七章 相交线与平行线
7.1 相交线
2024人教版七年级下册
学习目标
借助实际物体理解邻补角,对顶角的概念,初步发展抽象能力.
一
经历度量,几何画板验证,演绎证明等过程探索邻补角,对顶角的性质,感悟具有传递性的数学逻辑, 形成几何直观和推理能力.
二
三
运用邻补角,对顶角的性质解决中考题,进一步发展运算能力和推理能力.
1
情景引入
目录
2
合作探究
3
典例分析
5
归纳总结
4
巩固练习
6
感受中考
7
小结梳理
8
布置作业
情景引入
问题1 观察下列图片,你能否看到相交线?
问题2 你能再举出一些相交线的实例吗?
情景引入
问题3 取两根木条a、b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型. 在转动木条的过程中,它们所成的角也在变化,你能发现这些角之间不变的关系吗?
a
b
合作探究
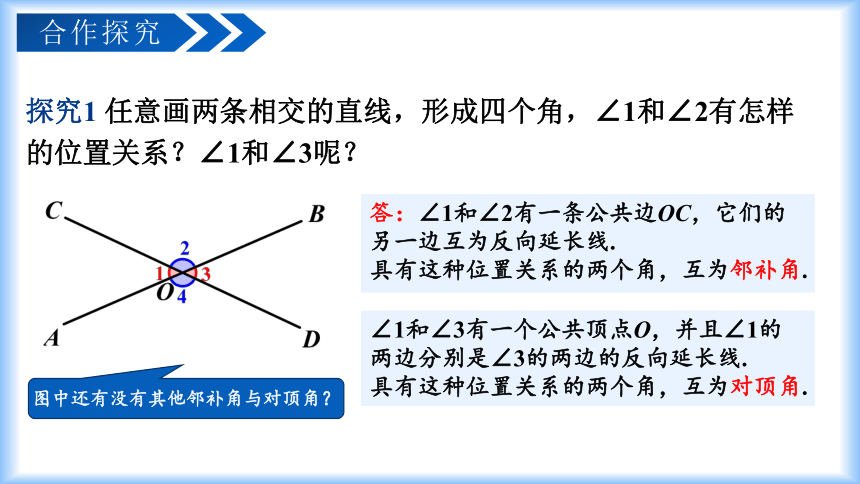
探究1 任意画两条相交的直线,形成四个角,∠1和∠2有怎样的位置关系?∠1和∠3呢?
答:∠1和∠2有一条公共边OC,它们的另一边互为反向延长线.
具有这种位置关系的两个角,互为邻补角.
图中还有没有其他邻补角与对顶角?
∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线.
具有这种位置关系的两个角,互为对顶角.
巩固练习
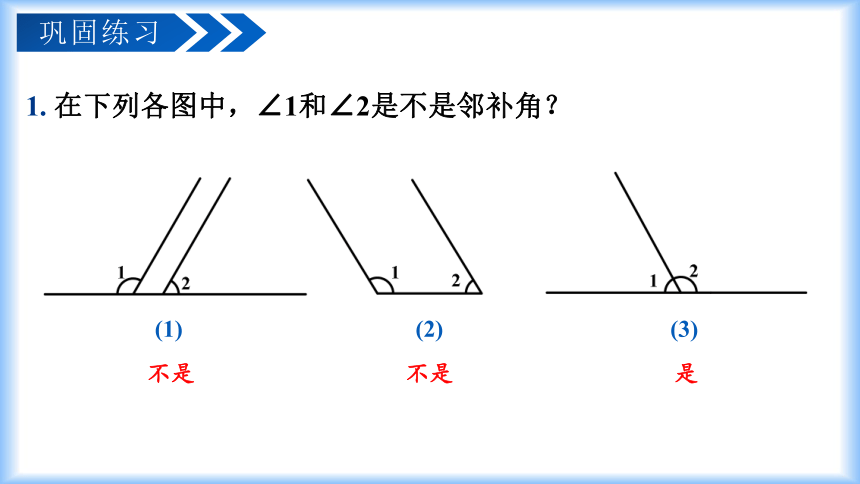
1. 在下列各图中,∠1和∠2是不是邻补角?
(1) (2) (3)
不是
不是
是
巩固练习
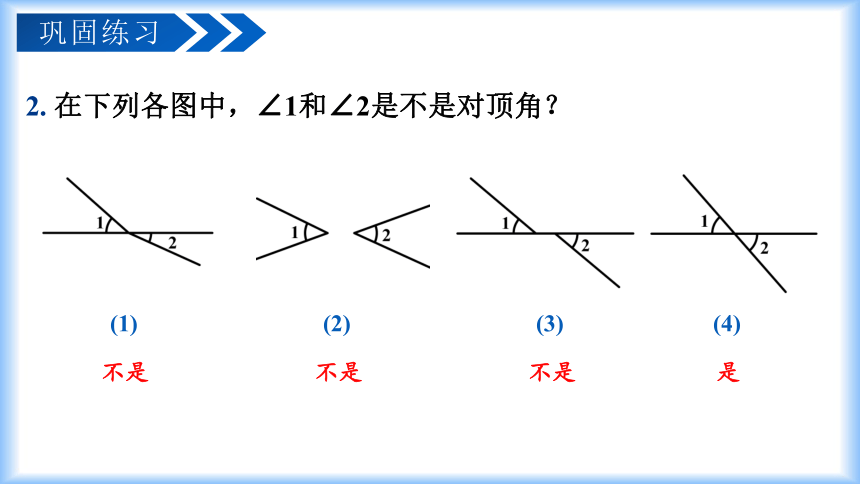
2. 在下列各图中,∠1和∠2是不是对顶角?
(1) (2) (3) (4)
不是
不是
是
不是
合作探究
探究2 分别量一下各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
答:∠1和∠2互补. ∠1和∠3相等.
改变两条直线相交所成的角的大小,上述关系还保持吗,为什么?
画板验证
合作探究
探究3 你能用数学的语言说明∠1=∠3吗?
证明:
因为 ∠1与∠2互补,∠3与∠2互补,
所以 ∠1=∠3(同角的补角相等).
合作探究
对顶角的性质:对顶角相等.
典例分析
例1 如图,直线a,b相交,∠1=40 ,求∠2,∠3,∠4的度数.
解:由∠1和∠2互为邻补角得
∠2=180 -∠1=180 -40 =140 .
由对顶角相等,得
∠3=∠1=40 ,∠4=∠2=140 .
典例分析
变式1 若∠1+∠3= 80 ,求各个角的度数.
解:由对顶角相等,得∠1=∠3,
因为∠1+∠3= 80 ,所以∠1=∠3=40 .
由∠1和∠2互为邻补角,得
∠2=180°-∠1=180°-40°=140°.
由对顶角相等,得∠4=∠2=140°.
典例分析
变式2 若∠2是∠1的 3倍,求各个角的度数.
解:由∠1和∠2互为邻补角,得
∠1+∠2= 180 ,
所以∠1+3∠1= 180 ,
所以∠1=45 ,∠2=135 .
由对顶角相等,得
∠3=∠1=45 ,∠4=∠2=135 .
典例分析
变式3 若 1 : 2 = 3 : 7 ,求各个角的度数.
解:由∠1和∠2互为邻补角,得
∠1+∠2= 180 ,
所以∠1= 180 × =54 ,
∠2= 180 × =126 ,
由对顶角相等,得
∠3=∠1=54 ,∠4=∠2=126 .
巩固练习
1. 图中是对顶角量角器,你能说出用它测量角的度数的原理吗?
答:对顶角相等.
巩固练习
2. 如图,在相交线的模型中,如果两根木条a,b所成的角中有一个角∠α=35 ,其他三个角分别等于多少度?如果∠α等于90 ,115 ,m 呢?请思考以上问题,并填写下表.
∠α的度数 ∠1的度数 ∠2的度数 ∠3的度数
35 35 145 145
90 90 90 90
115 115 65 65
m m (180-m) (180-m)
巩固练习
3. 如图,直线AB,CD相交于点O,∠AOC :∠BOC=2 : 7,则∠BOC= ,∠AOD= .
140
40
归纳总结
两条直线相交 分类 位置关系 数量关系 名称
∠1与∠2 ∠2与∠3 ∠3与∠4 ∠4与∠1 ①有公共顶点 ②有一条公共边 ③另一边互为反向延长线 互补 邻补角
∠1与∠3 ∠2与∠4 ①有公共顶点 ②两边互为反向延长线 相等 对顶角
感受中考
1. (2024广西)已知∠1与∠2为对顶角,∠1=35 ,则∠2= .
2. (2023青海)如图,直线AB,CD相交于点O,∠AOD=140 ,则∠AOC的度数是( )
A.40 B.50 C.60 D.70
35
A
感受中考
3. (2024日照)如图,直线AB,CD相交于点O.若∠1=40 ,∠2=
120 ,则∠COM的度数为( )
A.70 B.80 C.90 D.100
B
感受中考
4. (2021益阳)如图,AB与CD相交于点O,OE是∠AOC的平分线,且OC恰好平分∠EOB,则∠AOD= 度.
60
小结梳理
两条直线相交
对顶角
邻补角
定义
性质
定义
性质
布置作业
必做题:习题7.1 第1题,第5题.
1
选做题:观察下列各图,寻找对顶角(不含平角)
(1)如图a,图中共有 对对顶角;
(2)如图b,图中共有 对对顶角;
(3)如图c,图中共有 对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之
间的关系,猜测:若有n条直线相交于一点,则可
形成 对对顶角;
(5)若有10条直线相交于一点,则可形成 对
对顶角.
2
图a
图b
图c
谢谢观看!
2024人教版七年级下册
7.1.1 两条直线相交
第七章 相交线与平行线
7.1 相交线
2024人教版七年级下册
学习目标
借助实际物体理解邻补角,对顶角的概念,初步发展抽象能力.
一
经历度量,几何画板验证,演绎证明等过程探索邻补角,对顶角的性质,感悟具有传递性的数学逻辑, 形成几何直观和推理能力.
二
三
运用邻补角,对顶角的性质解决中考题,进一步发展运算能力和推理能力.
1
情景引入
目录
2
合作探究
3
典例分析
5
归纳总结
4
巩固练习
6
感受中考
7
小结梳理
8
布置作业
情景引入
问题1 观察下列图片,你能否看到相交线?
问题2 你能再举出一些相交线的实例吗?
情景引入
问题3 取两根木条a、b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型. 在转动木条的过程中,它们所成的角也在变化,你能发现这些角之间不变的关系吗?
a
b
合作探究
探究1 任意画两条相交的直线,形成四个角,∠1和∠2有怎样的位置关系?∠1和∠3呢?
答:∠1和∠2有一条公共边OC,它们的另一边互为反向延长线.
具有这种位置关系的两个角,互为邻补角.
图中还有没有其他邻补角与对顶角?
∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线.
具有这种位置关系的两个角,互为对顶角.
巩固练习
1. 在下列各图中,∠1和∠2是不是邻补角?
(1) (2) (3)
不是
不是
是
巩固练习
2. 在下列各图中,∠1和∠2是不是对顶角?
(1) (2) (3) (4)
不是
不是
是
不是
合作探究
探究2 分别量一下各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
答:∠1和∠2互补. ∠1和∠3相等.
改变两条直线相交所成的角的大小,上述关系还保持吗,为什么?
画板验证
合作探究
探究3 你能用数学的语言说明∠1=∠3吗?
证明:
因为 ∠1与∠2互补,∠3与∠2互补,
所以 ∠1=∠3(同角的补角相等).
合作探究
对顶角的性质:对顶角相等.
典例分析
例1 如图,直线a,b相交,∠1=40 ,求∠2,∠3,∠4的度数.
解:由∠1和∠2互为邻补角得
∠2=180 -∠1=180 -40 =140 .
由对顶角相等,得
∠3=∠1=40 ,∠4=∠2=140 .
典例分析
变式1 若∠1+∠3= 80 ,求各个角的度数.
解:由对顶角相等,得∠1=∠3,
因为∠1+∠3= 80 ,所以∠1=∠3=40 .
由∠1和∠2互为邻补角,得
∠2=180°-∠1=180°-40°=140°.
由对顶角相等,得∠4=∠2=140°.
典例分析
变式2 若∠2是∠1的 3倍,求各个角的度数.
解:由∠1和∠2互为邻补角,得
∠1+∠2= 180 ,
所以∠1+3∠1= 180 ,
所以∠1=45 ,∠2=135 .
由对顶角相等,得
∠3=∠1=45 ,∠4=∠2=135 .
典例分析
变式3 若 1 : 2 = 3 : 7 ,求各个角的度数.
解:由∠1和∠2互为邻补角,得
∠1+∠2= 180 ,
所以∠1= 180 × =54 ,
∠2= 180 × =126 ,
由对顶角相等,得
∠3=∠1=54 ,∠4=∠2=126 .
巩固练习
1. 图中是对顶角量角器,你能说出用它测量角的度数的原理吗?
答:对顶角相等.
巩固练习
2. 如图,在相交线的模型中,如果两根木条a,b所成的角中有一个角∠α=35 ,其他三个角分别等于多少度?如果∠α等于90 ,115 ,m 呢?请思考以上问题,并填写下表.
∠α的度数 ∠1的度数 ∠2的度数 ∠3的度数
35 35 145 145
90 90 90 90
115 115 65 65
m m (180-m) (180-m)
巩固练习
3. 如图,直线AB,CD相交于点O,∠AOC :∠BOC=2 : 7,则∠BOC= ,∠AOD= .
140
40
归纳总结
两条直线相交 分类 位置关系 数量关系 名称
∠1与∠2 ∠2与∠3 ∠3与∠4 ∠4与∠1 ①有公共顶点 ②有一条公共边 ③另一边互为反向延长线 互补 邻补角
∠1与∠3 ∠2与∠4 ①有公共顶点 ②两边互为反向延长线 相等 对顶角
感受中考
1. (2024广西)已知∠1与∠2为对顶角,∠1=35 ,则∠2= .
2. (2023青海)如图,直线AB,CD相交于点O,∠AOD=140 ,则∠AOC的度数是( )
A.40 B.50 C.60 D.70
35
A
感受中考
3. (2024日照)如图,直线AB,CD相交于点O.若∠1=40 ,∠2=
120 ,则∠COM的度数为( )
A.70 B.80 C.90 D.100
B
感受中考
4. (2021益阳)如图,AB与CD相交于点O,OE是∠AOC的平分线,且OC恰好平分∠EOB,则∠AOD= 度.
60
小结梳理
两条直线相交
对顶角
邻补角
定义
性质
定义
性质
布置作业
必做题:习题7.1 第1题,第5题.
1
选做题:观察下列各图,寻找对顶角(不含平角)
(1)如图a,图中共有 对对顶角;
(2)如图b,图中共有 对对顶角;
(3)如图c,图中共有 对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之
间的关系,猜测:若有n条直线相交于一点,则可
形成 对对顶角;
(5)若有10条直线相交于一点,则可形成 对
对顶角.
2
图a
图b
图c
谢谢观看!
2024人教版七年级下册
同课章节目录
