【集中培优】浙江省温州市近5年各区九年级上册精选期末压轴真题集中训练卷(含解析)
文档属性
| 名称 | 【集中培优】浙江省温州市近5年各区九年级上册精选期末压轴真题集中训练卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-20 14:51:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【集中培优】浙江省温州市近5年各区九年级上册期末压轴真题集中训练卷
一.选择题
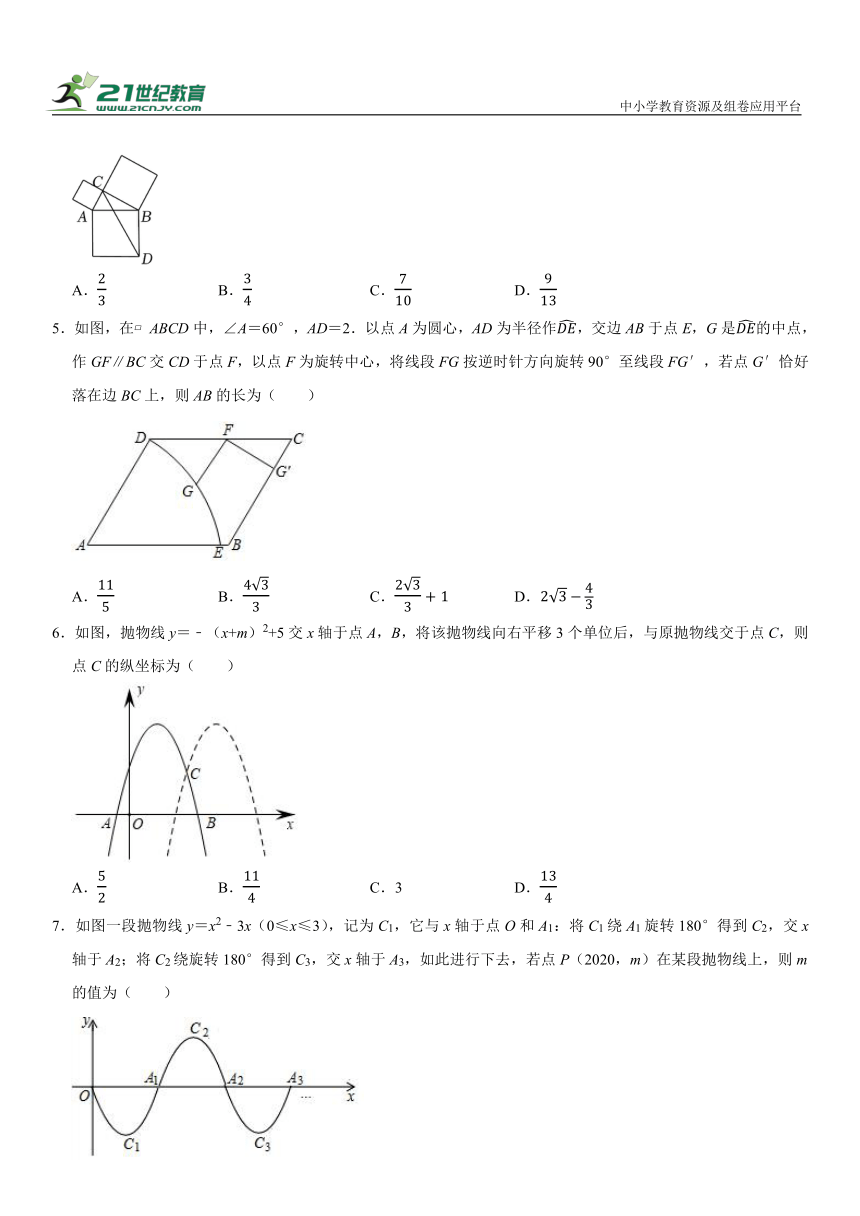
1.公元三世纪中期,我国魏晋时期的数学家刘徽创立了“割圆术”,为计算圆周率建立了严密的理论和完善的算法,所谓“割圆术”,是通过不断倍增圆内接正多边形的边数,间接求出圆面积和周长的方法.如图,在半径为2的圆内作两个正方形,得到一个正八边形,则阴影部分的面积是( )
A. B. C.24﹣16 D.48﹣32
2.如图,点P在⊙O的直径AB上,作正方形PCDE和正方形PFGH,其中点D,G在直径所在直线上,点C,E,F,H都在⊙O上,若两个正方形的面积之和为16,OP,则DG的长是( )
A.6 B.2 C.7 D.4
3.我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A.1 B. C. D.
4.如图,在△ABC中,∠ACB=90°,分别以AB,AC,BC为边向外作正方形.连结CD,若sin∠BCD,则tan∠CDB的值为( )
A. B. C. D.
5.如图,在 ABCD中,∠A=60°,AD=2.以点A为圆心,AD为半径作,交边AB于点E,G是的中点,作GF∥BC交CD于点F,以点F为旋转中心,将线段FG按逆时针方向旋转90°至线段FG′,若点G′恰好落在边BC上,则AB的长为( )
A. B. C. D.
6.如图,抛物线y=﹣(x+m)2+5交x轴于点A,B,将该抛物线向右平移3个单位后,与原抛物线交于点C,则点C的纵坐标为( )
A. B. C.3 D.
7.如图一段抛物线y=x2﹣3x(0≤x≤3),记为C1,它与x轴于点O和A1:将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕旋转180°得到C3,交x轴于A3,如此进行下去,若点P(2020,m)在某段抛物线上,则m的值为( )
A.0 B. C.2 D.﹣2
8.如图,点A,B的坐标分别为(0,8),(10,0),动点C,D分别在OA,OB上且CD=8,以CD为直径作⊙P交AB于点E,F.动点C从点O向终点A的运动过程中,线段EF长的变化情况为( )
A.一直不变 B.一直变大
C.先变小再变大 D.先变大再变小
9.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,连接CG交AB于点M,连接CE,CH.若CH=2CE,则的值为( )
A. B. C. D.
10.如图,抛物线的图象与x轴交于点A,B,交y轴于点C,动点P在射线AB运动,作△BCP的外接圆⊙M,当圆心M落在该抛物线上时,则AP的值( )
A.3 B.4 C.5 D.3.5
11.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示,过点G作GD的垂线交AB于点I,若GIGD,则的值为( )
A. B. C. D.
12.如图,一个装有液体的锥形瓶轴截面是轴对称图形,底部BC=20cm,当BC处于水平位置时,液面宽AD=10cm,液体高度DE=6cm,此时往瓶中再倒入一些液体,液面上升到宽GF=6cm,则此时液体的高度FH为( )
A.9.6 B.9.2 C.8.4 D.7
二.填空题
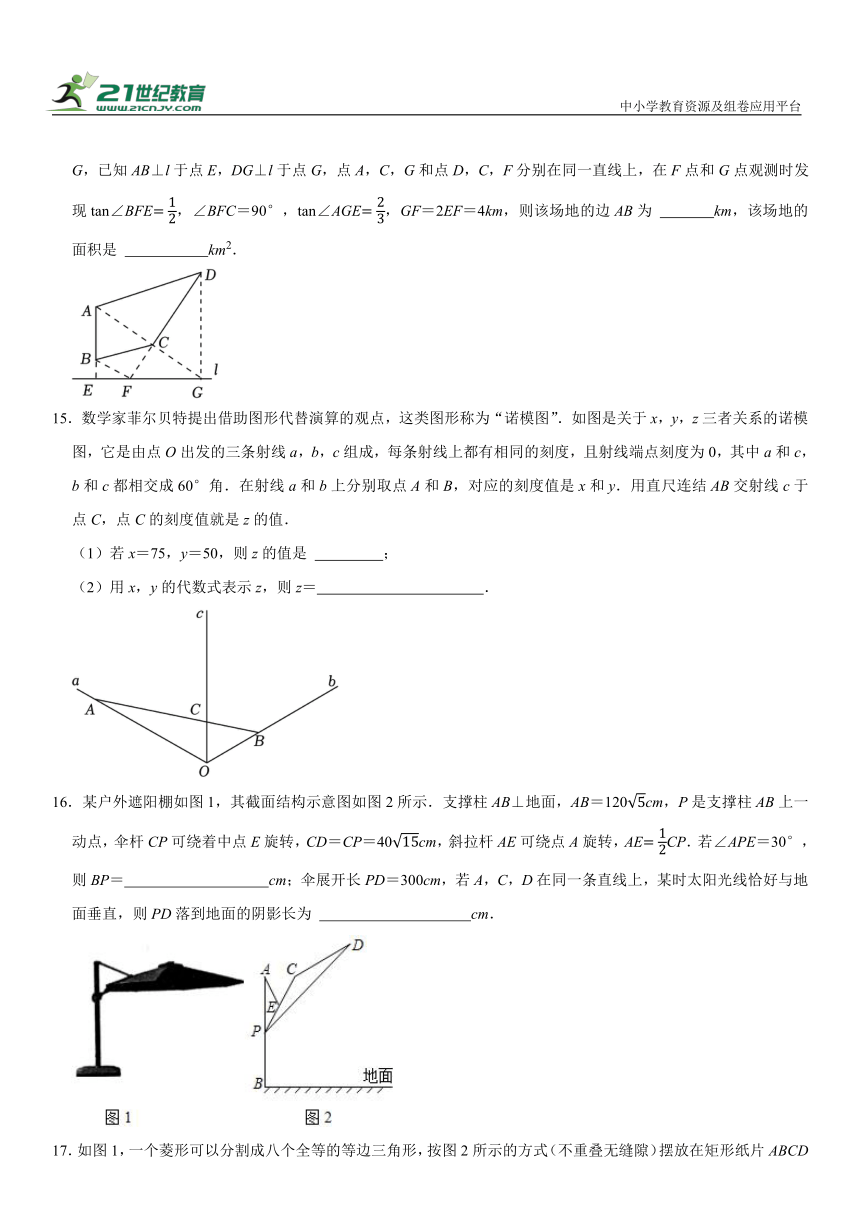
13.【情境】图1是某庭院所砌的一堵带有月洞门的墙,其设计图(图2)是轴对称图形,对称轴GH交圆弧于点G,墙面ABCD为正方形,门洞上方匾额的中点M,N,P,Q分别是上方两个矩形对角线的交点.已知AB米,EF米,GH米,EK米.
【问题】月洞门所在圆的半径为 米,匾额的长与宽之比为 .
14.如图,在一段笔直公路l的一侧有一块四边形场地ABCD,为了估测该场地的大小,在公路l上依次取E,F,G,已知AB⊥l于点E,DG⊥l于点G,点A,C,G和点D,C,F分别在同一直线上,在F点和G点观测时发现tan∠BFE,∠BFC=90°,tan∠AGE,GF=2EF=4km,则该场地的边AB为 km,该场地的面积是 km2.
15.数学家菲尔贝特提出借助图形代替演算的观点,这类图形称为“诺模图”.如图是关于x,y,z三者关系的诺模图,它是由点O出发的三条射线a,b,c组成,每条射线上都有相同的刻度,且射线端点刻度为0,其中a和c,b和c都相交成60°角.在射线a和b上分别取点A和B,对应的刻度值是x和y.用直尺连结AB交射线c于点C,点C的刻度值就是z的值.
(1)若x=75,y=50,则z的值是 ;
(2)用x,y的代数式表示z,则z= .
16.某户外遮阳棚如图1,其截面结构示意图如图2所示.支撑柱AB⊥地面,AB=120cm,P是支撑柱AB上一动点,伞杆CP可绕着中点E旋转,CD=CP=40cm,斜拉杆AE可绕点A旋转,AECP.若∠APE=30°,则BP= cm;伞展开长PD=300cm,若A,C,D在同一条直线上,某时太阳光线恰好与地面垂直,则PD落到地面的阴影长为 cm.
17.如图1,一个菱形可以分割成八个全等的等边三角形,按图2所示的方式(不重叠无缝隙)摆放在矩形纸片ABCD内,顶点E,F,G,H,M,N均恰好落在矩形ABCD的边上,若菱形的边长为4,则FG的长为 ,BC的长为 .
18.如图,正六边形ABCDEF的边长为2,点P在对角线AC上,∠EDP=75°,PQ⊥EF于点Q,则PQ的长是 ;过点Q作QG∥ED交DP于点G,则△PQG的面积为 .
19.如图,AB是半圆O的直径,D是半圆O上一点,C是的中点,连接AC交BD于点E,连接AD,若BE=4DE,CE=6,则AB的长为 .
20.如图,AC是⊙O的直径,弦BD⊥AC于点E,连接BC过点O作OF⊥BC于点F,若BD=12cm,AE=4cm,则OF的长度是 cm.
21.图甲是小张同学设计的带图案的花边作品,该作品由形如图乙的矩形图案设计拼接面成(不重叠,无缝隙).图乙中,点E、F、G、H分别为矩形AB、BC、CD、DA的中点,若AB=4,BC=6,则图乙中阴影部分的面积为
.
22.图1是某游乐园的海盗船,A,B两位同学坐在海盗船上的示意图如图2,开始状态下OA=OB,且A,B离地高度相等,水平距离AB为5米,当B同学摆动到最低位置B'时,他的高度下降了0.5米,A同学也随之旋转至A'的位置,此时,B同学离顶端O的距离OB'为 米,A同学的高度上升了 米.
23.如图1是一款重型订书机,其结构示意图如图2所示.其主体部分为矩形EFGH,由支撑杆CD垂直固定于底座AB上,且可以绕点D旋转.压杆MN与伸缩片PG连接,点M在HG上,MN可绕点M旋转,PG⊥HG,DF=8cm,GF=2cm,不使用时,EF∥AB,G是PF中点,且点D在NM的延长线上,则MG= cm,使用时如图3,按压MN使得MN∥AB,此时点F落在AB上,若CD=2cm,则压杆MN到底座AB的距离为 cm.
24.如图是一款上铺的收纳挂篮(如图1),其侧截面可看作直角梯形,现有一长方体形状的物体放置在该挂篮中,当物体如图2放置时,AB∥PQ.正方形DMEC为露出挂篮部分,此时S正方形DMEC=400cm2,当物体如图3放置时,B'与Q重合,四边形为D′FNC′露出挂篮部分,此时S四边形D′C′NF=200cm2,且D′FC′NMF,则D′到PQ的距离为 .
25.如图1是安装“摩擦铰链”的平开窗,如图2,点C、D、E是窗框AB上的定点,AC=5cm,CD=8cm,DE=26,BE=13cm,转轴H、F分别是窗门底部MN和支架HE上的定点,且HF=AC,滑点P在轨道CD上运动,当点P运动到点C时,窗户关闭(窗门底部MN与面框AB重合):如图3,当窗户开到最大时,点P与D重合,此时∠PFE=90°,PF<EF,则PF= cm,此时点N到AB的距离为 cm.
三.解答题
26.综合与实践:设计公交车停靠站的扩建方案.
【素材1】:图1为某公交车停靠站,顶棚截面由若干段形状相同的抛物线拼接而成.图2为某段结构示意图,C1,C2皆为轴对称图形,且关于点M成中心对称,该段结构水平宽度为8米.
【素材2】:图3为停靠站部分截面示意图,两根长为2.5米的立柱M1N1,M2N2竖直立于地面并支撑在对称中心M1,M2处.小温将长为2.8米的竹竿AB竖直立于地面,当点A触碰到顶棚时,测得N2B为1米.
【素材3】:将顶棚扩建,要求截面为轴对称图形,且水平宽度为27米.计划在顶棚两个末端到地面之间加装垂直于地面的挡风板.
【任务】:
(1)确定中心:求图2中点M到该结构最低点的水平距离l;
(2)确定形状:在图3中建立合适的直角坐标系,求C1的函数表达式;
(3)确定高度:求挡风板的高度.
27.如图,在△ABC中,∠ACB=90°,点D在BC边上,△ACD的外接圆⊙O交AB于点E,,过点C作CG⊥AD于点G,延长CG交AB于点F.
(1)求证:∠FAC=∠ACG;
(2)求证:;
(3)若CF=3FG,,求BD的长.
28.如图1,在矩形ABCD中,AB=4,BC=3,P是AB上一动点(不与A,B重合),点E在CD上,AP=CE,以PE为直径的⊙O交AB于另一点F,设AP=x.
(1)若点P在F的左侧,用含x的代数式表示PF的长.
(2)在(1)条件下,⊙O与BC相切时,求PF的长.
(3)如图2,O′是点O关于EF的对称点.
①若PO′所在的直线经过矩形ABCD的一个顶点时,求所有满足条件的x的值.
②当点O′落在⊙O内时,直接写出x的取值范围.
29.如图,在⊙O中,直径AB=10,弦BC=6,点D在BC的延长线上,线段AD
交⊙O于点E,过点E作EF∥BC分别交⊙O,AB于点F,G,连结BF.
(1)求证:△ABD∽△FGB.
(2)当△FGB为等腰三角形时,求CD的长.
(3)当∠D=45°时,求EG:FG的值.
30.根据素材解决问题.
设计货船通过圆形拱桥的方案
素材1 图1中有一座圆拱石桥,图2是其圆形桥拱的示意图,测得水面宽AB=16m,拱顶离水面的距离CD=4m.
素材2 如图3,一艘货船露出水面部分的横截面为矩形EFGH,测得EF=3m,EH=10m.因水深足够,货船可以根据需要运载货物.据调查,船身下降的高度y(米)与货船增加的载重量x(吨)满足函数关系式.
问题解决
任务1 确定桥拱半径 求圆形桥拱的半径
任务2 拟定设计方案 根据图3状态,货船能否通过圆形拱桥?若能,最多还能卸载多少吨货物?若不能,至少要增加多少吨货物才能通过?
31.如图,在Rt△ABC中,∠CAB=90°,AC=3,AB=4,AD⊥BC于点D,射线CE平行AB交AD的延长线于点E,P是射线CE上一点(在点E的右侧),连结AP交BC于点F.
(1)求证:△ACE∽△BAC.
(2)若,求的值.
(3)以PF为直径的圆经过△BDE中的某一个顶点时,求所有满足条件的EP的长.
32.如图,在△ABC中,∠C=90°,D为边BC上一点,DE⊥AB于点E,以DE为直径的⊙O分别交线段BD,AD于点F,G,连结EF,EG.
(1)求证:△DEF∽△ABC.
(2)若AC=6,BC=8,当DG与四边形DGEF其它三边中的一边相等时,求所有满足条件的BD的长.
(3)当AC=BC时,连结OC交AD于点H,记△DOH的面积为S1,△ACH的面积为S2,若OC∥EG,则的值为 .(在横线上直接写出答案)
33.如图,点A,B都在x轴上,过点A作x轴的垂线交抛物线y=﹣x2+4x于点C,过点B作x轴的垂线交该抛物线于点D,点C,D都在第一象限,点D在点C的右侧,DE⊥AC于点E,连接CD,BE,CD∥EB.
(1)若OA=2,求AB的长.
(2)若点A是线段OB的中点,求点E的坐标.
(3)根据(2)的条件,连接OD,动点P在线段OB上,作PQ⊥OD交OD于点Q.当△PDQ与△CDE相似时,求的值.
34.如图,在矩形ABCD中,AB=6,BC=8,点E,F分别在边BC,AB上,AF=BE=2,连接DE,DF.动点M在EF上从点E向终点F匀速运动,同时,动点N在射线CD上从点C沿CD方向匀速运动,当点M运动到EF的中点时,点N恰好与点D重合,点M到达终点时,M,N同时停止运动.
(1)求EF的长.
(2)设CN=x,EM=y,求y关于x的函数表达式,并写出自变量x的取值范围.
(3)连接MN,当MN与△DEF的一边平行时,求CN的长.
35.如图,抛物线yx2+2x+6交x轴于A,B两点(点A在点B的右侧),交y轴于点C,顶点为D,对称轴分别交x轴、线段AC于点E、F.
(1)求抛物线的对称轴及点A的坐标;
(2)连接AD,CD,求△ACD的面积;
(3)设动点P从点D出发,沿线段DE匀速向终点E运动,取△ACD一边的两端点和点P,若以这三点为顶点的三角形是等腰三角形,且P为顶角顶点,求所有满足条件的点P的坐标.
36.如图,在 ABCD中,AB=4,BC=8,∠ABC=60°.点P是边BC上一动点,作△PAB的外接圆⊙O交BD于E.
(1)如图1,当PB=3时,求PA的长以及⊙O的半径;
(2)如图2,当∠APB=2∠PBE时,求证:AE平分∠PAD;
(3)当AE与△ABD的某一条边垂直时,求所有满足条件的⊙O的半径.
37.如图,在矩形ABCD中,E为AD边中点,BE的中垂线分别交AB,BE,CD,BC的延长线于点F,H,G,N,延长FE交CD的延长线于点M.
(1)证明:△ABE∽△CNG.
(2)连接BG,当AB=CN时,求∠EBG的度数.
(3)当BC=CN时,求AD:AB的值.
38.如图,矩形ABCD中,BC=8,点F是AB边上一点(不与点B重合),△BCF的外接圆交对角线BD于点E,连结CF交BD于点G.
(1)求证:∠ECG=∠BDC.
(2)当AB=6时,在点F的整个运动过程中,
①连结EF,若BF时,求CE的长.
②当△CGE为等腰三角形时,求所有满足条件的CG的长.
直接写出答案CG为 .
39.如图,Rt△ABC中,∠ACB=90°,点D是斜边AB上一点,⊙O为△ACD的外接圆,BC交⊙O于点F,连结FD并延长至点E,使AE∥BC.
(1)当∠EAF=70°时,求∠CDF的度数;
(2)若AC=4,BC=6,当△ACD为等腰三角形时,求CF的长;
(3)设,若△AEF的外心I恰好落在⊙O上,求k的值.
40.如图1,在菱形ABCD中,∠B为锐角,点P,H分别在边AD,CB上,且DP=BH,在AB边上取点M,N(点N在BM之间)使AM=5BN.点P从点D匀速运动到点A时,点Q恰好从点M匀速运动到点N,连结PQ,PH分别交对角线AC于E,F,记QM=x,AP=y,已知y=﹣2x+12.
(1)①请判断PF与FH的大小关系,并说明理由;
②求AD,BN的长;
(2)如图2,连结QF,当四边形FQBH中有两边平行时,求AE:EC的值;
(3)若∠B=60°,连结QH,求△FQH面积的最小值.
参考答案
一.选择题
1.【分析】如图,连接OA,OB.设AF=EF=EG=BG=x,则FGx.构建方程求出x,可得结论.
【解答】解:如图,连接OA,OB.设AF=EF=EG=BG=x,则FGx.
由对称性可知四个阴影部分是全等的等腰直角三角形,
∵△AOB是等腰直角三角形,OA=OB=2,
∴AB=2,
∴2xx=2,
∴x=22,
∴阴影部分的面积=4(2)×(22)=24﹣16.
故选:C.
2.【分析】设正方形PFGH的边长是x,由条件得到x2+(x+2)2=16,从而求出正方形PFGH的边长,得到正方形PCDE的边长,进一步求出PD,PG的长,即可求出DG的长.
【解答】解:作OK⊥PC于K,设正方形PFGH的边长是x,
∵四边形PCDE是正方形,
∴∠CPD=45°,
∵∠OKP=90°,
∴△KOP是等腰直角三角形,
∴PKOP=1,
∴CK=FK=x+1,
∴PC=CK+PK=x+2,
∵两个正方形的面积之和为16,
∴x2+(x+2)2=16,
∴x1或x1(舍),
∴PC=x+21,PH=x1,
∴PDPC,PGPH,
∴DG=PD+PG=2.
故选:B.
3.【分析】根据正多边形与圆的对称性、垂径定理以及正多边形与圆的计算,可求出∠AOD=120°,∠BOC=90°,由直角三角形的边角关系求出OM、AM、BM,根据三角形的面积公式进行计算即可.
【解答】解:如图,连接OA、OB、OC、OD,过点O作OM⊥AD,垂足为M,
由圆的对称性可知,点A、点D是⊙O的三等分点,四边形BCFE是正方形,
∴∠AOD360°=120°,∠BOC360°=90°,
在Rt△AOM中,OA=2,∠AOM=60°,
∴OMOA=1,AMOA,
在Rt△BOM中,∠BOM=45°,OM=1,
∴BM=OM=1,
∴AB=AM﹣BM1,
∴8个阴影三角形的面积和为:(1)(1)×8=16﹣8,
故选:C.
4.【分析】过点B作BE⊥CD于点E,过点C作CF⊥AB于点F,可得△ABC,△BED,△BEC,△BCF都是直角三角形,根据sin∠BCE,设BE=3a,BC=5a,得CE4a,过点C作DB延长线于点G,得矩形CFBG,设AC=x,AB=y,然后利用勾股定理和三角形的面积可得a,进而利用锐角三角函数即可解决问题.
【解答】解:如图,过点B作BE⊥CD于点E,过点C作CF⊥AB于点F,
∴△ABC,△BED,△BEC,△BCF都是直角三角形,
∵sin∠BCD,
∴sin∠BCE,
设BE=3a,BC=5a,
∴CE4a,
过点C作DB延长线于点G,得矩形CFBG,
∴BF=CG,
设AC=x,AB=y,
在Rt△ABC中,根据勾股定理,得
AB2﹣AC2=BC2,
∴y2﹣x2=25a2,
∵S△ABCAB CFAC BC,
∴y CF=5ax,
∴CF,
在Rt△BCF中,根据勾股定理,得
BFaa,
∴BF=CGa,
在正方形ABDH中,AB=BD=y,
在Rt△BDE中,根据勾股定理,得
DE,
∴CD=CE+ED=4,
∵S△CBDCD BEBD CG,
∴CD BE=BD CG,
∴(4)×3=ya,
∴a,
∴tan∠CDB=tan∠EDB.
故选:D.
5.【分析】连接AG,过点D作DT⊥AB于T,过点G作GN⊥AB于N,交CD于M.想办法求出DM,FM,CF,可得结论.
【解答】解:连接AG,过点D作DT⊥AB于T,过点G作GN⊥AB于N,交CD于M.
在Rt△ADT中,AD=2,∠DAT=60°,
∴AT=AD cos60°=1,DTAT,
∵,
∴∠DAG=∠GAB=30°,
在Rt△AGN中,GNAG=1,ANGN,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵DT⊥AB,
∴DT⊥CD,
∴∠DTN=∠MNT=∠TDM=90°,
∴DT=MN,DM=TN=AN﹣AT1,
∴GM=MN﹣GN1,
∵AD∥FG,
∴∠ADF+∠DFG=180°,
∵∠ADC=180°﹣∠DAB=120°,
∴∠GFM=60°,
∴FM1,
∴FG=FG′=2FM=2,
∵∠C=∠DAB=60°,
∴CF,
∴AB=CD=DM+FM+CF1+12,
故选:D.
6.【分析】将抛物线y=﹣(x+m)2+5向右平移3个单位后得到y=﹣(x+m﹣3)2+5,然后联立组成方程组求解即可.
【解答】解:将抛物线y=﹣(x+m)2+5向右平移3个单位后得到y=﹣(x+m﹣3)2+5,
根据题意得:,
解得:,
∴交点C的坐标为(,),
故选:B.
7.【分析】利用二次函数图象上点的坐标特征可得出点A1的坐标,结合旋转的性质可得出点A2的坐标,观察图形可知:图象上点以6(横坐标)为周期变化,结合2020=336×6+4可知点P的纵坐标和当x=4时的纵坐标相等,由旋转的性质结合二次函数图象上点的坐标特征,即可求出m的值,此题得解.
【解答】解:当y=0时,x2﹣3x=0,
解得:x1=0,x2=3,
∴点A1的坐标为(3,0).
由旋转的性质,可知:点A2的坐标为(6,0).
∵2020=336×6+4,
∴当x=4时,y=m.
由图象可知:当x=2时的y值与当x=4时的y值互为相反数,
∴m=﹣(2×2﹣3×2)=2.
故选:C.
8.【分析】如图,连接OP,PF,作PH⊥AB于H.点P的运动轨迹是以O为圆心、OP为半径的⊙O,易知EF=2FH=2,观察图形可知PH的值由大变小再变大,推出EF的值由小变大再变小.
【解答】解:如图,连接OP,PF,作PH⊥AB于H.
∵CD=8,∠COD=90°,
∴OPCD=4,
∴点P的运动轨迹是以O为圆心OP为半径的⊙O,
∵PH⊥EF,
∴EH=FH,
∴EF=2FH=2,
观察图形可知PH的值由大变小再变大,
∴EF的值由小变大再变小,
故选:D.
9.【分析】过C作CN⊥AB于N,判定△ACE∽△BCH,即可得到;设AC=a,再根据勾股定理以及面积法即可得到AB与CN的长,进而得出AN的长;再根据△CNM∽△GBM,即可得到MN和BM的长,进而得出答案.
【解答】解:如图所示,过C作CN⊥AB于N,
由题可得,∠CAE=∠CBH=90°,∠ACE=∠BCH=45°,
∴△ACE∽△BCH,
∴,
设AC=a,则BC=2a,ABa,CNa,
Rt△ACN中,ANa,
∴BNaaa,
∵∠CNM=∠GBM=90°,∠CMN=∠GMB,
∴△CNM∽△GBM,
∴,
∴MNBNa,BMNBa,
∴AM=AN+MNa,
∴,
故选:B.
10.【分析】△PBC的外接圆的圆心在线段BC的垂直平分线y=﹣x上,求出直线y=﹣x与抛物线的交点,即可推出点M坐标,由此即可解决问题.
【解答】解:∵△PBC的外接圆的圆心在线段BC的垂直平分线y=﹣x上,
由,
解得或(舍弃),
∴点M坐标为(2,﹣2),
如图1中,作MN⊥AB于N,
∵MP=MB,NM⊥PB,
∴PN=NB=1,
∴OP=1,AP=3,
∴当AP=3时圆心在抛物线上.
故选:A.
11.【分析】设AF=BG=DE=CH=a,DH=BF=AE=CG=b,由相似三角形的性质可求a=2b,由正方形的面积公式可求解.
【解答】解:如图,过点I作IN⊥BG于N,
设AF=BG=DE=CH=a,DH=BF=AE=CG=b,
则HG=EH=a﹣b,
∵∠FGH=∠IGD=90°,
∴∠DGH=∠IGF,
又∵∠ING=∠GHD=90°,
∴△DHG∽△ING,
∴,
∵GIGD,
∴INDHb,GNGH(a﹣b),
∴BN=a(a﹣b)ba,
∵∠ABF=∠IBN,∠AFB=∠INB=90°,
∴△AFB∽△INB,
∴,
∴,
∴a=2b,
∴S正方形EFGH=HG2=(a﹣b)2=b2,
∵S正方形ABCD=AD2=AE2+DE2=5b2,
∴,
故选:A.
12.【分析】根据等腰三角形的性质可得CE=(20﹣10)÷2=5(cm),CH=(20﹣6)÷2=7(cm),再根据△CDE∽△CFH解答即可.
【解答】解:由题意得,CE=(20﹣10)÷2=5(cm),CH=(20﹣6)÷2=7(cm),
在△CDE和△CFH中,
∵∠C=∠C,∠CED=∠CHF=90°,
∴△CDE∽△CFH,
∴,
即,
解得FH=8.4(cm).
故选:C.
二.填空题
13.【分析】如图,设圆心为O,连接OK,根据轴对称图形的性质可得KIEF,OI=GH﹣GO﹣EK,再根据勾股定理即可求解;利用△PLQ∽△RSC的对应边成比例得出,分别求出CS,RS即可求解.
【解答】解:如图,设圆心为O,连接OK,
由轴对称图形的性质可得KIEF,OI=GH﹣GO﹣EKr,
在Rt△KOI中,r2=(r)2+()2,
解得r;
根据矩形的性质可得△PLQ∽△RSC,
∴,即,
根据题意可得AD,AE=FB(),
∴CS,RS,
∴,
∴,
∵匾额的长为2PL,宽为2QL,
∴匾额的长与宽之比为,
故答案为:,7:3.
14.【分析】根据题目中的数据,利用锐角三角函数可以求得AB的长,再根据题意,作出合适的辅助线,求出BE、EF、BF、FC、FG、DG的长,然后根据S四边形ABCD=S梯形AEGD﹣S△BEF﹣S△BFC﹣S△DFG,代入数据计算即可.
【解答】解:∵GF=2EF=4km,EG=EF+FG,
∴EF=2km,EG=6km,
∵tan∠BFE,tan∠AGE,∠AEG=90°,∠BEF=90°,
∴AE=4km,BE=1km,
∴BF(km),AB=AE﹣BE=4﹣1=3(km),
∵∠BFC=90°,∠DGF=90°,
∴∠BFE+∠DFG=90°,∠DFG+∠FDG=90°,
∴∠BFE=∠FDG,
∴tan∠FDG,
∴DG8(km),
作CM⊥AB交AB于点M,作CN⊥EG交EG于点N,如图所示,
则ME=CN,MC=EN,
∵MC∥EG,tan∠AGE,
∴tan∠ACM,
设AM=2a,则MC=3a,ME=4﹣2a,
∵CN⊥EG,DG⊥EG,tan∠BFE,∠BFE=∠FDG,CN=ME=4﹣2a,
∴∠FDG=∠FCN,
∴,
∴FN=2﹣a,
∴GN=FG﹣FN=4﹣(2﹣a)=2+a,
∵tan∠CGN,
∴,
解得a=1,
∴CN=2km,FN=1km,
∴FC(km),
∴S四边形ABCD=S梯形AEGD﹣S△BEF﹣S△BFC﹣S△DFG16.5(km2),
故答案为:3,16.5.
15.【分析】在a上取点D,在b上取点E,使OD=OC=OE,连接CD,CE,根据a和c,b和c都相交成60°角,可得△COD,△COE都是等边三角形,∠AOB=120°,即可证明△ABO∽△CBE,可得,
(1)当x=75,y=50时,,解得z=30;
(2)由得:z.
【解答】解:在a上取点D,在b上取点E,使OD=OC=OE,连接CD,CE,如图:
∵a和c,b和c都相交成60°角,
∴△COD,△COE都是等边三角形,∠AOB=120°,
∴∠CEO=60°,∠BAO=60°﹣∠ABO,OD=OC=OE=z,
∴∠BCE=60°﹣∠CBE=∠BAO,
∵∠ABO=∠CBE,
∴△ABO∽△CBE,
∴,即,
(1)当x=75,y=50时,
,
解得z=30,
故答案为:30;
(2)由得:z,
故答案为:.
16.【分析】(1)先过点E作EF⊥AP构造出含30度角的直角三角形,利用其性质得到线段长度,再利用等腰三角形的性质得到AP,最后根据图象利用AB﹣AP即可求解;
(2)首先根据题意画图,明确求出AD即所得,设出AC长度,利用两个直角形的公共边,结合勾股定理列出方程求解,最后利用线段相加即可解决.
【解答】解(1)如图,过点E作EF⊥AP,垂足为F,
∵E是PC的中点,
∴PE=ECPC=20cm,
又∵AEPC,
∴AE=PE=CE=20cm,
在Rt△PEF中,∠APE=30°,PE=20cm,
∴PF=PE cos∠APE
=20
=30(cm),
∵AE=PE,EF⊥AB,
∴AP=2PF=60cm,
∴BP=AB﹣AP
=12060
=60(cm).
(2)由题意可知,当A、C、D三点共线时,此时AC⊥AP,
如图所示:过点D作DF⊥地面,交地面水平线为F,
∵∠DAP=∠B=∠DFB=90°,
∴四边形ABFD为矩形,
∴AD=BF,
设AC=x,
在Rt△ACP和Rt△PDA中,
∴CP2﹣AC2=DP2﹣DA2,
∴,
解得x,
∴BF=AD=AC+CD(cm),
∴当太阳光线恰好与地面垂直,则PD落在地面上的阴影为cm.
故答案为:;.
17.【分析】连接FN交EK于点O,过点O作PQ⊥BC于点P,交AD于点Q,证明四边形ABPQ是矩形,四边形ENKF是菱形,利用勾股定理求出FG的长;然后根据S△OFGOP FGOF OG,求出OP,由△GOP∽△GEB,求出BE,再证明△ANE≌△CGH,进而可以解决问题.
【解答】解:如图,连接FN交EK于点O,过点O作PQ⊥BC于点P,交AD于点Q,
∴∠QPB=90°,
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,
∴∠AQP=90°,
∴四边形ABPQ是矩形,
∴AB=QP,
∵△ENK和△EFK都是全等的等边三角形,
∴∠EFK=∠ENK=60°,EF=FK=NK=EN=EK=2,
∴四边形ENKF是菱形,
∴NF⊥EK,OE=OKEK=1,OF=ONFN,∠EFN∠EFK=30°,
∴OF,
∵OG=OK+KG=1+4=5,
∴FG2,
∵S△OFGOP FGOF OG,
∴2OP=5,
∴OP,
∴AB=PQ=2OP,
∵OP∥BE,
∴△GOP∽△GEB,
∴,
∴,
∴BE,
∴AE=AB﹣BE,
∴AN,
∵BF,
∵AD∥BC,EN∥GH,
∴∠ANE=∠CGH,
在△ANE和△CGH中,
,
∴△ANE≌△CGH(AAS),
∴CG=AN,
∴BC=BF+FG+CG2.
故答案为:2;.
18.【分析】如图1中,过点E作EJ⊥AC于J,过点D作DK⊥EJ于K,过点Q作QM⊥EJ于M,过点P作PN⊥QM于N,则四边形PNMJ是矩形,四边形DKJC是矩形,设PQ=m.用两种方法求出EJ,构建方程求出m,即可解决问题.
【解答】解:如图1中,过点E作EJ⊥AC于J,过点D作DK⊥EJ于K,过点Q作QM⊥EJ于M,过点P作PN⊥QM于N,则四边形PNMJ是矩形,四边形DKJC是矩形,设PQ=m.
∵∠DEF=∠EDC=120°,∠EDP=75°,
∴∠PDC=45°,
∵∠DCP=90°,
∴∠CDP=∠CPD=45°,
∴CP=CD=2,
∵PQ⊥EF,
∴∠PQE=90°,
∴∠DPQ=360°﹣75°﹣120°﹣90°=75°,
∵∠DPN=45°,
∴∠QPN=30°,
∴NQm,PN=MJm,
在Rt△DEM中,∠EDM=30°,DE=2,
∴EK=1,
∵EM+PN=3,
∴PNm,
∵DK=CJ,
∴MN=PJ=2,
∴QMm+2,
∵∠EQM=30°,
∴EMQM(m+2),
∴3(m+2)m,
∴m=21,
∴PQ=21,
如图2中,过点G作GH⊥PQ于H.
∵QG∥DE,
∴∠QGP=∠EDP=75°,
∵∠QPG=75°,
∴∠QGP=∠QPG,
∴GQ=QP,∠GQP=30°,
∴GHQG,
∴S△PQG PQ GH(21).
故答案为:21,.
19.【分析】如图,连接OC交BD于K.设DE=k.BE=4k,则DK=BK=2.5k,EK=1.5k,由AD∥CK,推出AE:EC=DE:EK,可得AE=4,由△ECK∽△EBC,推出EC2=EK EB,求出k即可解决问题.
【解答】解:如图,连接OC交BD于K,连接BC.
∵,
∴OC⊥BD,
∵BE=4DE,
∴可以假设DE=k.BE=4k,则DK=BK=2.5k,EK=1.5k,
∵AB是直径,
∴∠ADK=∠DKC=∠ACB=90°,
∴AD∥CK,
∴AE:EC=DE:EK,
∴AE:6=k:1.5k,
∴AE=4,
∵△ECK∽△EBC,
∴EC2=EK EB,
∴36=1.5k×4k,
∵k>0,
∴k,
∴BC2,
∴AB4.
故答案为4.
20.【分析】连接OB,根据垂径定理求出BE,根据勾股定理求出OB,再根据勾股定理计算即可.
【解答】解:连接OB,
∵AC是⊙O的直径,弦BD⊥AC,
∴BEBD=6cm,
在Rt△OEB中,OB2=OE2+BE2,即OB2=(OB﹣4)2+62,
解得,OB,
则EC=AC﹣AE=9,
BC3,
∵OF⊥BC,
∴CFBC,
∴OF(cm),
故答案为.
21.【分析】因为S阴=S菱形PHQF﹣2S△HTN,想办法求出菱形PHQF的面积,△HTN的面积即可解决问题.
【解答】解:如图,设FM=HN=a.
由题意点E、F、G、H分别为矩形AB、BC、CD、DA的中点,可得四边形HQFP是菱形,它的面积S矩形ABCD4×6=6,
∵FM∥BJ,CF=FB,
∴CM=MJ,
∴BJ=2FM=2a,
∵EJ∥AN,AE=EB,
∴BJ=JN=2a,
∵S△HBC 6 4=12,HJBH,
∴S△HCJ12,
∵TN∥CJ,
∴△HTN∽△HCJ,
∴()2,
∴S△HTN,
∴S阴=S菱形PHQF﹣2S△HTN=6,
故答案为.
22.【分析】由题意可得在三角形OAC为直角三角形,设OA=OB=OB'=x,则根据勾股定理得方程:,解得x;过点A'作A'D⊥OB'于点D,设B'D=m,则ODm,在直角三角形OA'D中,可得:AD2=OA'2﹣OD2,在直角三角形A'DB'中,由勾股定理有AD2=A'B'2﹣B'D2,从而可建立方程,解出m的值,最后A同学的高度上升的高度即为DC=OC﹣OD可求.
【解答】解:设AB与OB'交于点C,由题意可得OB'⊥AB,
在直角三角形OAC中,设OA=OB=OB'=x,
根据勾股定理得方程:
,解得:x.
过点A'作A'D⊥OB'于点D,
设B'D=m,则ODm,
在直角三角形OA'D中,由勾股定理有:
AD2=OA'2﹣OD2,
在直角三角形A'DB'中,由勾股定理有:
AD2=A'B'2﹣B'D2=25﹣m2,
∴25﹣m2,
解得:m,
即B'D,
∴DC=OC﹣OD=()﹣().
故答案为:,.
23.【分析】如图2,延长NM,则NM过点D,由三角形中位线定理可得MG的长度,如图3,过点P作PK⊥AB于K,可得∠PFK=∠CDF=∠MPF,在Rt△CDF中,CF2,知tan∠CDF,故tan∠MPF,可得PG,PF=PG+GF,由△CDF∽△KFP,得,即可得压杆MN到底座AB的距离为cm.
【解答】解:如图2,延长NM,则NM过点D,
∵四边形EFGH是矩形,
∴HG∥EF,即MG∥DF,
∵G是PF中点,
∴MG是△PDF的中位线,
∴MGDF8=4(cm),
如图3,过点P作PK⊥AB于K,
∵MN∥AB,
∴PK⊥MN,∠MPF=∠PFK,
∵∠DFP=∠DCF=90°,
∴∠CDF+∠DFC=∠PFK+∠DFC=90°,
∴∠PFK=∠CDF=∠MPF,
在Rt△CDF中,CF2,
∴tan∠CDF,
∴tan∠MPF,即,
∴,
解得PG,
∴PF=PG+GF2,
∵∠CDF=∠PFK,∠DCF=90°=∠PKF,
∴△CDF∽△KFP,
∴,即,
解得PK(cm),
∴压杆MN到底座AB的距离为cm,
故答案为:4,.
24.【分析】过点N作NG⊥A′D′于G,过点D′作D′H⊥PQ于H,交MN于T,过点A′作A′K⊥D′H于K,利用正方形面积和梯形面积求得:C′D′=CD=A′Q=20cm,C′N=8cm,D′F=12cm,MF=C′N=8cm,运用勾股定理求得FN=4,再根据△D′FT∽△NFG,△A′FM∽△NFG,即可求得答案.
【解答】解:∵S正方形DMEC=400cm2,
∴CD=DM=AB=20cm,
∴C′D′=CD=A′Q=20cm,
∵S四边形D′C′NF=200cm2,D′FC′N,
∴(D′F+C′N)×C′D′=200,
即C′N×20=200,
∴C′N=8cm,
∴D′F=12cm,
∴MF=C′N=8cm,
过点N作NG⊥A′D′于G,过点D′作D′H⊥PQ于H,交MN于T,
过点A′作A′K⊥D′H于K,
则D′G=C′N=8cm,FG=4cm,NG=20cm,
∴FN4,
∵∠NFG=∠D′FT,∠D′TF=∠NGF=90°,
∴△D′FT∽△NFG,
∴,即,
∴D′T,
∵∠NFG=∠A′FM,∠NGF=∠M=90°,
∴△A′FM∽△NFG,
∴,即,
∴A′M=40,A′F=8,
∵∠M=∠P=∠FA′Q=90°,
∴∠MA′F+∠QA′P=∠QA′P+∠A′QP=90°,
∴∠MA′F=∠A′QP,
∴△A′FM∽△QA′P,
∴,即,
∴A′P,
∵四边形A′PHK、A′KTM为矩形,
∴TK=A′M=40,KH=A′P,
∴D′H=D′T+TK+KH4040,
故答案为:40.
25.【分析】根据题意,由勾股定理得到DF=10cm,再利用等角三角函数也相等列出关系式计算出点N到AB的距离即可.
【解答】解:由题意可知:MD+DF+FE=AE,AC=MD=HF=5cm,
∴DF+FE=CE=34cm,
设DF=x cm,则FE=(34﹣x)cm,
∵∠DFE=90°,
DF2+FE2=DE2即x2+(34﹣x)2=262,
解得:x=10,
∴DF=10cm即PF=10cm.
∴EF=34﹣x=24cm,MN=AB=5+8+26+13=52cm,
过点N作NG⊥AB,垂足为G,延长NM交AB于点J,
∵HF∥MD,
∴∠MDJ=∠FEP,即tan∠MDJ=tan∠FEP
∵MD=5cm,
∴MJcm.
∴NJ=MJ+MNcm,
∵∠JNG=∠DEF,
∴cos∠JNG=cos∠DEF,
∴NG.
故答案为:10;.
三.解答题
26.【分析】(1)根据轴对称性图形的性质和抛物线的对称性可得中点M到该结构最低点的水平距离为8÷2÷2=2(米);
(2)以M2点为原点建立坐标系,设抛物线C1的解析式为y=a(x﹣2)2+h,将(0,0),(1,0.3)代入,即可求函数的解析式;
(3)分两种情况讨论:①当x=1.5+2=3.5时,y=0.175,则h=2.5+0.275=3.125(米);②当x=2.5﹣2=0.5时,y=0.625,h=2.5+0.625=3.125(米).
【解答】解:(1)∵C1,C2皆为轴对称图形,且关于点M成中心对称,水平宽度为8米,
∴8÷2÷2=2(米),
∴中点M到该结构最低点的水平距离l为2米;
(2)以M2点为原点,如图建立平面直角坐标系,
∵C1过点(0,0),(1,0.3),对称轴为直线x=2,
∴设抛物线C1的解析式为y=a(x﹣2)2+h,
将(0,0),(1,0.3)代入,
∴,
解得,
∴抛物线C1的解析式为y=﹣0.1(x﹣2)2+0.4;
(3)方法一:27﹣8×3=3(米),3÷2=1.5(米),
①如图,
当x=1.5+2=3.5时,y=﹣0.1×(3.5﹣2)2+0.4=0.175,
∴h=2.5+0.175=2.675(米);
②如图,
当x=1.5﹣2=﹣0.5时,y=0.1×(0.5+2)2﹣0.4=﹣0.175,
∴h=2.5+(﹣0.175)=2.325(米);
综上所述:挡风板的高度为2.675米或2.325米.
方法二:由图形为轴对称图形可知,图形必由若干个图2结构和一个C1或者C2构成:
4+8×3=28,28﹣27=1,1÷2=0.5米,
只需将x=0.5以及x=﹣0.5相应代入C1、C2即可,
y0.1(0.5﹣2)2+0.4=0.175米,
∴h=2.5+y=2.675米,
y0.1(﹣0.5+2)2﹣0.4=﹣0.175米,
∴h=2.5+y=2.325(米);
综上所述:挡风板的高度为2.675米或2.325米.
27.【分析】(1)由余角的性质可得∠ADC=∠ACG,由圆周角定理可得∠FAC=∠ADC,即可求解;
(2)通过证明△AGC∽△BCA,可得;
(3)由勾股定理可求FG,AG的长,通过证明△AGC∽△CGD,可得,可求DG的长,即可求解.
【解答】(1)证明:∵DA是直径,
∴∠ACD=90°,
∴∠CAD+∠ADC=90°,
∵CG⊥AD,
∴∠AGC=90°,
∴∠CAD+∠ACG=90°,
∴∠ADC=∠ACG,
∵,
∴∠FAC=∠ADC,
∴∠FAC=∠ACG;
(2)证明:∵∠FAC=∠ACG,∠ACB=∠AGC=90°,
∴△AGC∽△BCA,
∴;
(3)解:∵∠FAC=∠FCA,
∴AF=CF,
∵CF=3FG,
∴CG=2FG,AF=FC=3FG,
∴AG2FG,
∵AC2=AG2+GC2,
∴12=8FG2+4FG2,
∴FG=1(负值舍去),
∴AG=2,CG=2,
∵,
∴,
∴BC=2,
∵∠ADC=∠ACG,∠AGC=∠DGC,
∴△AGC∽△CGD,
∴,
∴2×2=2GD,
∴GD,
∴CD,
∴BD=BC﹣CD.
28.【分析】(1)先根据直径所对的圆周角是直角可得EF⊥AB,再证得四边形BCEF是矩形,得出BF=CE=x,即可得出答案;
(2)如图1,连接OG交EF于H,由切线性质可得OG⊥BC,利用三角形中位线定理和勾股定理即可求得答案;
(3)①分两种情况:当PO′所在直线经过点C时,当PO′所在直线经过点D时,分别建立方程求解即可;
②分两种情况:当点O′在点O右侧时,当点O′在点O左侧时,分别求得x的值即可得出答案.
【解答】解:(1)由题意得:AB=4,CE=AP=x,
∵PE是⊙O的直径,
∴EF⊥AB,即∠PFE=∠BFE=90°,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠B=∠C=∠BFE=90°,
∴四边形BCEF是矩形,
∴BF=CE=x,
∴PF=AB﹣AP﹣BF=4﹣x﹣x=4﹣2x.
(2)在(1)条件下,⊙O与BC相切于G,如图1,连接OG交EF于H,
则OG⊥BC,
∵EF∥BC,
∴OH⊥EF,
∴OH是△PEF的中位线,
∴OHPF(4﹣2x)=2﹣x,
∵HG=BF=x,
∴OG=OH+GH=2﹣x+x=2,
∴PE=2OG=4,EF=BC=3,
在Rt△PEF中,PF.
(3)①当PO′所在直线经过点C时,如图2,
由题意得,OO′CE,OO′=PF,
∴PFCE,即4﹣2xx,
解得:x;
当PO′所在直线经过点D时,如图3,
此时,PF=2x﹣4,DE=4﹣x,
OO′DE,OO′=PF,
∴PFDE,即2x﹣4(4﹣x),
解得:x,
综上所述,PO′所在直线经过矩形ABCD的一个顶点时,x或.
②当点O′落在⊙O内时,x的取值范围为x.
当点O′在点O右侧时,如图4,
∵OE=2OM=PF,EFPF,
∴3(4﹣2x),
解得:x;
当点O′在点O左侧时,如图5,
同理可得:EFPF,
∴3(2x﹣4),
解得:x;
综上所述,当点O′落在⊙O内时,x的取值范围为x.
29.【分析】(1)可证明△AGE∽△ABD,△AGE∽△FGB,进而得出结论;
(2)可讨论△ABD是等腰三角形,分为BD=AB,AD=AB和AD=BD;当BD=AB=10时,易得CD=4,当AD=AB时,连接AC,可得CD=BC=6,当AD=BD时,连接OD,可证明△ABC∽△DBO,进而得出结果;
(3)连接BE和AC,可求得CD和AD,DE,AE,进而根据△AGE∽△ABD,求得EG和AG,BG的长,根据△ABD∽△FGB可求得FG,进而得出结果.
【解答】(1)证明:∵EF∥BD,
∴∠AGE=∠ABD,∠AEC=∠D,
∴△AGE∽△ABD,
∵∠AEF=∠ABF,∠F=∠BAE,
∴△AGE∽△FGB,
∴△ABD∽△FGB;
(2)解:由①得,
△ABD∽△FGB,
∵△FGB是等腰三角形,
∴△ABD是等腰三角形,
如图1,
当AB=AD时,连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴CD=BC=6,
如图2,
当AD=BD时,连接OD,AC,
∵OA=OB,
∴DO⊥AB,
∴∠BOD=90°,
∵∠ACB=90°,
∴∠ACB=∠BOD,AC8,
∵∠B=∠B,
∴△ABC∽△DBO,
∴,
∴,
∴BD,
∴CD=BD﹣BC,
当BD=AB=10时,CD=BD﹣BC=10﹣6=4,
综上所述:CD=6或或4;
(3)解:如图,
连接BE,AC,
∵AB是⊙O的直径,
∴∠BED=∠AEB=90°,∠ACD=∠ACB=90°,
∴CD=AC tanD=AC=8,AD8,
∴BD=BC+CD=14,
∴DE=BD cosD=14 cos45°=7,
∴AE=AD﹣DE=8,
由(1)知,
△AGE∽△ABD,△ABD∽△FGB;
∴,,
∴,
∴EG,AG,
∴BG=AB﹣AG=10,,
∴FG,
∴.
30.【分析】任务1,设 圆心为点O,则点O在CD延长线上,延长CD,则CD经过点O,连结AO,设桥拱的半径为r m,则OD=(r﹣4)m,由勾股定理,垂径定理,列出关于半径的方程,即可解决问题;
任务2,由勾股定理得到货船不能通过圆形桥拱,通过计算,即可得到需要增加的货物的吨数.
【解答】解:任务1,设圆心为点O,则点O在CD延长线上,延长CD,则CD经过点O,连接AO,如图,
设桥拱的半径为r m,则OD=(r﹣4)m,
∵OC⊥AB,
∴m,
∵OD2+AD2=OA2,
∴(r﹣4)2+82=r2,
∴r=10,
∴圆形拱桥的半径为10m.
任务2,根据图3状态,货船不能通过圆形桥拱,至少要增加吨的货物才能通过.理由:
当EH是⊙O的弦时,EH与OC的交点为M,连接OE,OH,如图,
∵四边形EFGH为矩形,
∴EH∥FG,
∵OC⊥AB,
∴OM⊥EH.
∴,
∴m,
∵OD=6m,
∴,
∴根据图3状态,货船不能通过圆形桥拱,
∴船在水面部分可以下降的高度m.
∵,
∴吨,
∴至少要增加吨的货物才能通过.
31.【分析】(1)利用同角的余角相等可得∠CEA=∠ACB,可证明结论;
(2)由(1)得△ACE∽△BAC,得,则CE,EP,从而得出CP的长,再利用△CFP∽△BFA,可得;
(3)分以PF为直径的圆经过△BDE中的一个顶点D或E或B,分别画出图形,利用相似三角形的判定与性质进行解题.
【解答】(1)证明:∵CE∥AB,
∴∠CAB+∠ACE=180°,
∵∠CAB=90°,
∴∠ACE=90°,
∴∠ACB+∠ECD=90°,
∵AD⊥BC,
∴∠CDE=90°,
∴∠AEC+∠ECD=90°,
∴∠CEA=∠ACB,
∴△ACE∽△BAC;
(2)解:由(1)得△ACE∽△BAC,
∴,
∴,
∴CE,
∵,
∴EP,
∴CP=CE+EP=6,
∵CP∥AB,
∴△CFP∽△BFA,
∴;
(3)解:当以PF为直径的圆经过△BDE中的一个顶点D时,
AP与AE重合,点P与点E重合,不符合题意,
当以PF为直径的圆经过△BDE中的一个顶点E时,
连接EF,则∠PEF=90°,
∵∠PCA=90°,
∴EF∥AC,
∴△PEF∽△PCA,
∴,
∵∠FCE=∠CBA,
∴tan∠FCE=tan∠CBA,
∵tan∠FCE,tan,
∴,
∴EF,
由(1)知,CE,
∵PC=PE+CE=PE,,
∴,
∴PE;
以PF为直径的圆经过△BDE中的一个顶点B时,
连接BP,
则∠FBP=90°,BP⊥BC,
∵AE⊥BC,
∴BP∥AE,
∵EP∥AB,
∴四边形EABP是平行四边形,
∴EP=AB=4,
综上所述,满足条件的EP的长为4或.
32.【分析】(1)可证∠EDF=∠BAC,∠EFD=∠C=90°,从而命题得证;
(2)分为三种情形讨论:当DG=DF时,转化为BD=AD求解,当EG=DG时,解斜三角形ABD:已知∠B,∠BAD=45°,AB=10,当DG=EF,可推出四边形EFDG是矩形,此时∠ADB=90°,此时点D和点C重合,从而得出结果.
【解答】(1)证明:∵DE⊥AB,
∴∠BED=90°,
∴∠EDF+∠B=90°,
∵∠=90°,
∴∠B+∠BAC=90°,
∴∠EDF=∠BAC,
∵DE是⊙O的直径,
∴∠DFE=90°,
∴∠EFD=∠C,
∴△DEF∽△ABC;
(2)当DG=DF时,,
∴∠FED=∠DEG,
∵DE是⊙O的直径,
∴∠EFD=∠EGD=90°,
∴∠EDF=∠EDA,
∵DE⊥AB,
∴∠AED=∠BED=90°,
∴∠B=∠BAD,
∴AD=BD,
在Rt△ACD中,
∵CD2+AC2=AD2,
∴(8﹣BD)2+62=BD2,
∴BD,
当DG=EG时,
∵∠EGD=90°,
∴∠EDG=∠DEG=45°,
∵∠AED=90°,
∴∠BAD=90°﹣∠EDG=45°,
∴DE=AE,
∵∠B=∠B,∠BED=∠ACB=90°,
∴△BED∽△BCA,
∴,
∴,
∴BE
∵BE+AE=10,
∴,
∴DE,
∴,
∴BD,
当DG=EF时,
∴,
∴∠EDF=∠DEG,
∵∠EFD=∠EGD=90°,
∴∠FED=∠EDG,
∴EF∥DG,
∴四边形EFDG是平行四边形,
∴ EFDG是矩形,
∴∠FDG=90°,
∵∠C=90°,
∴此时点D和C重合,
∴BD=8,
综上所述:BD或或8;
(3)如图
作OV⊥BC于V,
∴∠OVC=90°,
C∥EG,∠EGD=90°,
∴∠AHC=90°,
∴∠DAC+∠ACH=90°,
∵∠ACB=90°,
∴∠OCV+∠ACH=90°,
∴∠OCV=∠DAC,
∵∠ONC=∠ACD=90°,
∴△OCV∽△DAC,
∴,
设CD=a,AC=BC=b,
在等腰直角三角形BDE中,
DE,
∴OD,
在等腰直角三角形DOV中,
OV=DV,
∴VC=VD+CD,
∴,
∴b=3a,
∴AC=3a,OV,
∴tan∠OCV=tan∠DAC,
∴sin∠OVC=sin∠DAC,
cos∠OVC=cos∠DAC,
∵S△COD,
∴DH=a sin∠OCVa,
CHa,AH,
∴S△CDH,
S△ACH,
∴S△DOH,
∴,
故答案为:.
33.【分析】(1)先证明四边形BDCE是平行四边形,得出A(2,0),将x=2代入y=﹣x2+4x,得C(2,4),根据DB=AE=2,建立方程求解即可;
(2)设OA=t,则OB=2t,可得C(t,﹣t2+4t),D(2t,﹣4t2+8t),由DB=AE=CE,建立方程求解,可得出答案;
(3)如图,连接OD,PD,过点P作PQ⊥OD于点Q,分两种情况进行讨论:①若△PQD∽△DEC,②若△PQD∽△CED,即可得出答案.
【解答】解:(1)∵AC⊥x轴,BD⊥x轴,
∴AC∥BD,
∵CD∥EB,
∴四边形BDCE是平行四边形,
∴DB=AE,
∴AE=CE,
∵OA=2,
∴A(2,0),
当x=2时,y=﹣x2+4x=﹣22+4×2=4,
∴C(2,4),
∴AC=4,AE=2,DB=AE=2,
令y=2,得﹣x2+4x=2,
解得:x1=2(舍去),x2=2,
∴D(2,2),B(2,0),
∴AB=22;
(2)设OA=t,则OB=2t,
∴C(t,﹣t2+4t),D(2t,﹣4t2+8t),
∵DB=AE=CE,
∴﹣t2+4t=2(﹣4t2+8t),
∴t1,t2=0(不符合题意,舍去),
∴﹣4t2+8t=﹣4×()2+8,
∴E(,);
(3)如图,连接OD,PD,过点P作PQ⊥OD于点Q,
在(2)的条件下:C(,),D(,),
①若△PQD∽△DEC,
则:,
而tan∠DOB:,
∴::;
②若△PQD∽△CED,
则:,
而,
∴::2,
综上所述,的值为或2.
34.【分析】(1)在Rt△BEF中,利用勾股定理即可解决问题.
(2)根据速度比相等构建关系式解决问题即可.
(3)分两种情形如图3﹣1中,当MN∥DF,延长FE交DC的延长线于H.如图3﹣2中,当MN∥DE,分别利用平行线分线段成比例定理构建方程解决问题即可.
【解答】解:(1)∵四边形ABCD是矩形,
∴∠B=90°,AB=CD=6,AD=BC=8,
∵AF=BE=2,
∴BF=6﹣2=4,
∴EF2.
(2)由题意:,
∴
∴yx(0≤x≤12).
(3)如图3﹣1中,延长FE交DC的延长线于H.
∵BF∥CH,
∴△EFB∽△EHC,
∴,
∴,
∴EH=6,CH=12,
当MN∥DF时,,
∴,
∵yx,
解得x.
如图3﹣2中,当MN∥DE时,,
∴,
∵yx,
解得x=12,
综上所述,满足条件的CN的值为或12.
35.【分析】(1)令y=0,得到x2+2x+6=0,解得x=﹣2或6,则A(6,0),由对称轴公式计算即可;
(2)求出直线AC的解析式,求出F(2,4),则S△ACDDF×OA可求出答案;
(3)分三种情况,当AC,CD和AD分别为底边时,画出图形,可由等腰三角形的性质求出顶点P的坐标即可.
【解答】解:(1)对于抛物线yx2+2x+6令y=0,得到x2+2x+6=0,解得x=﹣2或6,
∴B(﹣2,0),A(6,0),
令x=0,得到y=6,
∴C(0,6),
∴抛物线的对称轴x2,A(6,0).
(2)∵yx2+2x+68,
∴抛物线的顶点坐标D(2,8),
设直线AC的解析式为y=kx+6,
∴0=6k+6,
∴k=﹣1,
∴直线AC的解析式为y=﹣x+6,
∴F(2,4),
∴DF=4,
∴S△ACDDF OA4×6=12;
(3)如图1,过点O作OM⊥AC交DE于点P,交AC于点M,
∵A(6,0),C(0,6),
∴OA=OC=6,
∴CM=AM,
∴CP=AP,
此时AC为等腰三角形ACP的底边,
∴OE=PE=2.
∴P(2,2),
如图2,过点C作CP⊥DE于点P,
∵OC=6,DE=8,
∴PD=DE﹣PE=2,
∴PD=PC,
此时△PCD是以CD为底边的等腰直角三角形,
∴P(2,6),
如图3,作AD的垂直平分线交DE于点P,
则PD=PA,
设PD=x,则PE=8﹣x,在Rt△PAE中,PE2+AE2=PA2,
∴(8﹣x)2+42=x2,
解得x=5,
∴PE=8﹣5=3,
∴P(2,3),
综合以上可得点P的坐标为(2,2)或(2,6)或(2,3).
36.【分析】(1)过点A作BP的垂线,作直径AM,先在Rt△ABH中求出BH,AH的长,再在Rt△AHP中用勾股定理求出AP的长,在Rt△AMP中通过锐角三角函数求出直径AM的长,即求出半径的值;
(2)证∠APB=∠PAD=2∠PAE,即可推出结论;
(3)分三种情况:当AE⊥BD时,AB是⊙O的直径,可直接求出半径;当AE⊥AD时,连接OB,OE,延长AE交BC于F,通过证△BFE∽△DAE,求出BE的长,再证△OBE是等边三角形,即得到半径的值;当AE⊥AB时,过点D作BC的垂线,通过证△BPE∽△BND,求出PE,AE的长,再利用勾股定理求出直径BE的长,即可得到半径的值.
【解答】解:(1)如图1,过点A作BP的垂线,垂足为H,作直径AM,连接MP,
在Rt△ABH中,∠ABH=60°,
∴∠BAH=30°,
∴BHAB=2,AH=AB sin60°=2,
∴HP=BP﹣BH=1,
∴在Rt△AHP中,
AP,
∵AB是直径,
∴∠APM=90°,
在Rt△AMP中,∠M=∠ABP=60°,
∴AM,
∴⊙O的半径为,
即PA的长为,⊙O的半径为;
(2)当∠APB=2∠PBE时,
∵∠PBE=∠PAE,
∴∠APB=2∠PAE,
在平行四边形ABCD中,AD∥BC,
∴∠APB=∠PAD,
∴∠PAD=2∠PAE,
∴∠PAE=∠DAE,
∴AE平分∠PAD;
(3)①如图3﹣1,当AE⊥BD时,∠AEB=90°,
∴AB是⊙O的直径,
∴rAB=2;
②如图3﹣2,当AE⊥AD时,连接OB,OE,延长AE交BC于F,
∵AD∥BC,
∴AF⊥BC,△BFE∽△DAE,
∴,
在Rt△ABF中,∠ABF=60°,
∴AF=AB sin60°=2,BFAB=2,
∴,
∴EF,
在Rt△BFE中,
BE,
∵∠BOE=2∠BAE=60°,OB=OE,
∴△OBE是等边三角形,
∴r;
③当AE⊥AB时,∠BAE=90°,
∴AE为⊙O的直径,
∴∠BPE=90°,
如图3﹣3,过点D作BC的垂线,交BC的延长线于点N,延长PE交AD于点Q,
在Rt△DCN中,∠DCN=60°,DC=4,
∴DN=DC sin60°=2,CNCD=2,
∴PQ=DN=2,
设QE=x,则PE=2x,
在Rt△AEQ中,∠QAE=∠BAD﹣∠BAE=30°,
∴AE=2QE=2x,
∵PE∥DN,
∴△BPE∽△BND,
∴,
∴,
∴BP=10x,
在Rt△ABE与Rt△BPE中,
AB2+AE2=BP2+PE2,
∴16+4x2=(10x)2+(2x)2,
解得,x1=6(舍),x2,
∴AE=2,
∴BE2,
∴r,
∴⊙O的半径为2或或.
37.【分析】(1)由垂直定义得∠HFB+∠HBF=90°.由矩形性质及相似三角形的判定可得结论;
(2)连接EG,根据相似三角形性质及中点定义得EG=BG.由HL得Rt△DEG≌Rt△CGB,然后根据全等三角形的性质及等腰三角形的性质可得答案;
(3)连接EN交CD于点P,由中点定义得,根据相似三角形的判定与性质得.设DE=a,则BC=CN=2a,EN=BN=BC+CN=4a,最后根据比例线段可得答案.
【解答】解:(1)∵BE⊥FN,
∴∠BHF=90°,
∴∠HFB+∠HBF=90°.
在矩形ABCD中,∠ABC=∠A=∠BCD=90°,
∴∠HFB+∠N=90°,∠NCG=90°,
∴∠HBF=∠N,∠A=∠NCG,
∴△ABE∽△CNG.
(2)如图1,连接EG,
∵△ABE∽△CNG,
∴AB=CN,
∴△ABE≌△CNG,
∴AE=CG,
∵E为AD边中点,
∴DE=AE=CG.
∵FN是BE的中垂线,
∴EG=BG.
∵∠D=∠BCD=90°,
∴Rt△DEG≌Rt△CGB(HL),
∴∠DGE=∠CBG.
∵∠CBG+∠CGB=90°,
∴∠DGE+∠CGB=90°,
∴∠BGE=90°,
∴△BGE是等腰直角三角形,
∴∠EBG=45°.
(3)法1:如图2,连接EN交CD于点P,
∵FN是BE的中垂线,
∴EN=BN,
∵E为AD边中点,
∴,
∵AD∥BC,
∴△DEP∽△CNP,
∴.
设DE=a,则BC=CN=2a,EN=BN=BC+CN=4a,
∴,
∴,
∴,
∴.
法2:(略解)由△CNG∽△BNF得.
易证得△MED≌△FEA,
∴DM=AF,ME=FE.
设CG=a,则ME=FE=BF=2a,MF=MG=4a,
∴CM=5a,
∵MC+BF=7a,即2AB=7a,
∴,,
∴,
∴,
∴.
法3:(如图,略解)作GK⊥AB于点K,
易证得△MFG∽△GFB,
∴,
∴.
设FK=BK=a,则EF=BF=2a,,
在Rt△GKF中,,
∴,
∴,
∴,
∴,
∴.
38.【分析】(1)根据平行线的性质得出∠ABD=∠BDC,根据圆周角定理得出∠ABD=∠ECG,即可证得结论;
(2)根据勾股定理求得BD=10,
①连接EF,根据圆周角定理得出∠CEF=∠BCD=90°,∠EFC=∠CBD.即可得出sin∠EFC=sin∠CBD,得出,根据勾股定理得到CF=6,即可求得CE的长;
②分三种情况讨论,由等腰三角形的性质及相似三角形的性质可得出答案.
【解答】(1)证明:∵AB∥CD.
∴∠ABD=∠BDC,
∵∠ABD=∠ECG,
∴∠ECG=∠BDC.
(2)解:①∵AB=CD=6,AD=BC=8,
∴BD10,
如图1,连接EF,则∠CEF=∠BCD=90°,
∵∠EFC=∠CBD.
∴sin∠EFC=sin∠CBD,
∴,
∴CF6,
∴CE.
②分三种情况:Ⅰ、当EG=CG时,∠GEC=∠GCE=∠ABD=∠BDC.
∴E与D重合,CG=DG,
∴G为BD的中点,
∴CGBD=5.
Ⅱ、当GE=CE时,
∴∠EGC=∠ECG=∠ABD=∠GDC,
∴CG=CD=6.
Ⅲ、如图2,当CG=CE时,
∴∠GEC=∠EGC=∠BFC=∠GCD,
∴CD=DG=6,
∴BG=BF=4,
∴FC4,
∵BF∥CD,
∴△FBG∽△CDG,
∴,
∴,
∴CG,
综上所述,CG的长为5或6或.
故答案为:5或6或.
39.【分析】(1)根据平行线的性质得∠AFC=∠EAF=70°,由圆周角定理得∠AFC=∠ADC=70°,∠ADF=90°,即可得出答案;
(2)分三种情况:①AD=CD时,②AC=AD时,③AC=CD时,根据相似三角形的判定和性质分别求解即可;
(3)连接AI、FI,连接DO并延长交⊙O于G,连接CG,根据AF是⊙O的直径,△AEF的外心I恰好落在⊙O上得出∠AIF=90°,由圆周角定理得∠AEF∠AIF=45°,根据平行线的性质以及直角三角形的性质可得∠CAB=∠CGD=45°,可得出△DCG是等腰直角三角形,即可得出答案.
【解答】解:(1)∵AE∥BC,∠EAF=70°,
∴∠AFC=∠EAF=70°,
∵∠ACB=90°,
∴AF是⊙O的直径,
∴∠ADF=90°,
∴∠ADC=∠AFC=70°,
∴∠CDF=∠ADF﹣∠ADC=90°﹣70°=20°;
(2)∵∠ACB=90°,AC=4,BC=6,
∴AB2,
当△ACD为等腰三角形时,分三种情况:
①AD=CD时,
∵AD=CD,
∴∠CAD=∠ACD,
∵∠ACB=90°,
∴∠CAD+∠B=∠ACD+∠BCD=90°,
∴∠B=∠BCD,
∴CD=BD,
∵AD=CD,
∴AD=BDAB,
∵∠B=∠B,∠ACB=∠FDB=90°,
∴△ACB∽△FDB,
∴,即,
∴BF,
∴CF=BC﹣BF=6;
②AC=AD时,
∵AC=AD=4,
∴∠ADC=∠ACD,BD=24,
∵∠ACB=∠ADF=90°,
∴∠ADC+∠CDF=∠ACD+∠BCD=90°,
∴∠CDF=∠BCD,
∴CF=DF,
∵∠B=∠B,∠ACB=∠FDB=90°,
∴△ACB∽△FDB,
∴,即,
∴DF,
∴CF=DF;
③AC=CD时,
∵AC=CD=4,
∴∠ADC=∠CAD,
∵∠ACB=∠ADF=90°,
∴∠ADC+∠CDF=∠CAD+∠B=90°,
∴∠CDF=∠B,
∵∠DCF=∠BCD,
∴△DCF∽△BCD,
∴,即,
∴CF;
综上,CF的长为或或;
(3)连接AI、FI,连接DO并延长交⊙O于G,连接CG,
∵AF是⊙O的直径,△AEF的外心I恰好落在⊙O上,
∴∠AIF=90°,
∴∠AEF∠AIF=45°,
∵AE∥BC,
∴∠EFB=∠AEF=45°,
∵∠BDF=90°,
∴∠B=45°,
∵∠ACB=90°,
∴∠CAB=45°,
∴∠CGD=45°,
∵GD是⊙O的直径,
∴∠DCG=90°,DG=AF,
∴△DCG是等腰直角三角形,
∴,
∴,
∵k,
∴k.
40.【分析】(1)①根据菱形的性质和全等三角形的判定证得△PDF≌△HBF,再根据全等三角形的性质即可解答;
②根据题意,分别令x=0,y=0即可求解;
(2)分BF∥QH和FQ∥BH两种情况讨论解答即可;
(3)连接QH.过点F作FK⊥BC于点K,FJ⊥AB于点J,过点Q作QT⊥BC于T.则S△FQH=S△ABC﹣S△QBH﹣S△AQF﹣S△CFH,由二次函数求最值的方法求解即可.
【解答】解:(1)①结论:PF=PH.理由如下:
∵ABCD是菱形,
∴AD∥BC,AD=BC,
∵PD=BH,
∴∠PAF=∠FCH,AP=CH,
又∵∠AFP=∠HFC,
∴△AFP≌△HFC(AAS),
∴PF=FH;
②当x=0代入y=﹣2x+12得y=12,即AD=12,
当y=0代入y=﹣2x+12,得x=6,即MN=6,
∵AM=5BN,AB=AD=12,
∴5BN+BN+6=12,
∴BN=1;
(2)①当FQ∥BH时,如图2,
∵AF=FC,
∴AQ=QB,
∴QF是△ABC的中位线,
∴AQ=6,而AM=5,
∴MQ=1,
∴x=1,y=10,
∴AP=10,QF=6,
∵AP∥QF,
∴△AEP∽△QEF,
∴AE:EF=10:6=5:3,
∴AE:EC=5:11;
②当FH∥BQ时,如图2,
∵AP∥BC,
∴ABHP是平行四边形,
∴12﹣y=y,y=6 代入得x=3,
∴AQ=8,
∵PF=6,△AQE∽△PFE,
∴AE:EF=4:3,
∴AE:EC=4:10=2:5;
(3)连接QH.过点F作FK⊥BC于点K,FJ⊥AB于点J,过点Q作QT⊥BC于T.
由题意,CH=AP=﹣2x+12,BQ=7﹣x,AQ=5+x,
∵AB=BC,∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=BC=12,
∴FA=FC=6,
∴QT(7﹣x),FJ=FK6=3,
∵S△FQH=S△ABC﹣S△BQH﹣S△AQF﹣S△FCH
=362x(7﹣x)(﹣2x+12)×3(5+x)×3
(x﹣2)2,
∵0,
∴x=2时,△FQH的面积最小,最小值为.
【集中培优】浙江省温州市近5年各区九年级上册期末压轴真题集中训练卷
一.选择题
1.公元三世纪中期,我国魏晋时期的数学家刘徽创立了“割圆术”,为计算圆周率建立了严密的理论和完善的算法,所谓“割圆术”,是通过不断倍增圆内接正多边形的边数,间接求出圆面积和周长的方法.如图,在半径为2的圆内作两个正方形,得到一个正八边形,则阴影部分的面积是( )
A. B. C.24﹣16 D.48﹣32
2.如图,点P在⊙O的直径AB上,作正方形PCDE和正方形PFGH,其中点D,G在直径所在直线上,点C,E,F,H都在⊙O上,若两个正方形的面积之和为16,OP,则DG的长是( )
A.6 B.2 C.7 D.4
3.我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A.1 B. C. D.
4.如图,在△ABC中,∠ACB=90°,分别以AB,AC,BC为边向外作正方形.连结CD,若sin∠BCD,则tan∠CDB的值为( )
A. B. C. D.
5.如图,在 ABCD中,∠A=60°,AD=2.以点A为圆心,AD为半径作,交边AB于点E,G是的中点,作GF∥BC交CD于点F,以点F为旋转中心,将线段FG按逆时针方向旋转90°至线段FG′,若点G′恰好落在边BC上,则AB的长为( )
A. B. C. D.
6.如图,抛物线y=﹣(x+m)2+5交x轴于点A,B,将该抛物线向右平移3个单位后,与原抛物线交于点C,则点C的纵坐标为( )
A. B. C.3 D.
7.如图一段抛物线y=x2﹣3x(0≤x≤3),记为C1,它与x轴于点O和A1:将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕旋转180°得到C3,交x轴于A3,如此进行下去,若点P(2020,m)在某段抛物线上,则m的值为( )
A.0 B. C.2 D.﹣2
8.如图,点A,B的坐标分别为(0,8),(10,0),动点C,D分别在OA,OB上且CD=8,以CD为直径作⊙P交AB于点E,F.动点C从点O向终点A的运动过程中,线段EF长的变化情况为( )
A.一直不变 B.一直变大
C.先变小再变大 D.先变大再变小
9.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,连接CG交AB于点M,连接CE,CH.若CH=2CE,则的值为( )
A. B. C. D.
10.如图,抛物线的图象与x轴交于点A,B,交y轴于点C,动点P在射线AB运动,作△BCP的外接圆⊙M,当圆心M落在该抛物线上时,则AP的值( )
A.3 B.4 C.5 D.3.5
11.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示,过点G作GD的垂线交AB于点I,若GIGD,则的值为( )
A. B. C. D.
12.如图,一个装有液体的锥形瓶轴截面是轴对称图形,底部BC=20cm,当BC处于水平位置时,液面宽AD=10cm,液体高度DE=6cm,此时往瓶中再倒入一些液体,液面上升到宽GF=6cm,则此时液体的高度FH为( )
A.9.6 B.9.2 C.8.4 D.7
二.填空题
13.【情境】图1是某庭院所砌的一堵带有月洞门的墙,其设计图(图2)是轴对称图形,对称轴GH交圆弧于点G,墙面ABCD为正方形,门洞上方匾额的中点M,N,P,Q分别是上方两个矩形对角线的交点.已知AB米,EF米,GH米,EK米.
【问题】月洞门所在圆的半径为 米,匾额的长与宽之比为 .
14.如图,在一段笔直公路l的一侧有一块四边形场地ABCD,为了估测该场地的大小,在公路l上依次取E,F,G,已知AB⊥l于点E,DG⊥l于点G,点A,C,G和点D,C,F分别在同一直线上,在F点和G点观测时发现tan∠BFE,∠BFC=90°,tan∠AGE,GF=2EF=4km,则该场地的边AB为 km,该场地的面积是 km2.
15.数学家菲尔贝特提出借助图形代替演算的观点,这类图形称为“诺模图”.如图是关于x,y,z三者关系的诺模图,它是由点O出发的三条射线a,b,c组成,每条射线上都有相同的刻度,且射线端点刻度为0,其中a和c,b和c都相交成60°角.在射线a和b上分别取点A和B,对应的刻度值是x和y.用直尺连结AB交射线c于点C,点C的刻度值就是z的值.
(1)若x=75,y=50,则z的值是 ;
(2)用x,y的代数式表示z,则z= .
16.某户外遮阳棚如图1,其截面结构示意图如图2所示.支撑柱AB⊥地面,AB=120cm,P是支撑柱AB上一动点,伞杆CP可绕着中点E旋转,CD=CP=40cm,斜拉杆AE可绕点A旋转,AECP.若∠APE=30°,则BP= cm;伞展开长PD=300cm,若A,C,D在同一条直线上,某时太阳光线恰好与地面垂直,则PD落到地面的阴影长为 cm.
17.如图1,一个菱形可以分割成八个全等的等边三角形,按图2所示的方式(不重叠无缝隙)摆放在矩形纸片ABCD内,顶点E,F,G,H,M,N均恰好落在矩形ABCD的边上,若菱形的边长为4,则FG的长为 ,BC的长为 .
18.如图,正六边形ABCDEF的边长为2,点P在对角线AC上,∠EDP=75°,PQ⊥EF于点Q,则PQ的长是 ;过点Q作QG∥ED交DP于点G,则△PQG的面积为 .
19.如图,AB是半圆O的直径,D是半圆O上一点,C是的中点,连接AC交BD于点E,连接AD,若BE=4DE,CE=6,则AB的长为 .
20.如图,AC是⊙O的直径,弦BD⊥AC于点E,连接BC过点O作OF⊥BC于点F,若BD=12cm,AE=4cm,则OF的长度是 cm.
21.图甲是小张同学设计的带图案的花边作品,该作品由形如图乙的矩形图案设计拼接面成(不重叠,无缝隙).图乙中,点E、F、G、H分别为矩形AB、BC、CD、DA的中点,若AB=4,BC=6,则图乙中阴影部分的面积为
.
22.图1是某游乐园的海盗船,A,B两位同学坐在海盗船上的示意图如图2,开始状态下OA=OB,且A,B离地高度相等,水平距离AB为5米,当B同学摆动到最低位置B'时,他的高度下降了0.5米,A同学也随之旋转至A'的位置,此时,B同学离顶端O的距离OB'为 米,A同学的高度上升了 米.
23.如图1是一款重型订书机,其结构示意图如图2所示.其主体部分为矩形EFGH,由支撑杆CD垂直固定于底座AB上,且可以绕点D旋转.压杆MN与伸缩片PG连接,点M在HG上,MN可绕点M旋转,PG⊥HG,DF=8cm,GF=2cm,不使用时,EF∥AB,G是PF中点,且点D在NM的延长线上,则MG= cm,使用时如图3,按压MN使得MN∥AB,此时点F落在AB上,若CD=2cm,则压杆MN到底座AB的距离为 cm.
24.如图是一款上铺的收纳挂篮(如图1),其侧截面可看作直角梯形,现有一长方体形状的物体放置在该挂篮中,当物体如图2放置时,AB∥PQ.正方形DMEC为露出挂篮部分,此时S正方形DMEC=400cm2,当物体如图3放置时,B'与Q重合,四边形为D′FNC′露出挂篮部分,此时S四边形D′C′NF=200cm2,且D′FC′NMF,则D′到PQ的距离为 .
25.如图1是安装“摩擦铰链”的平开窗,如图2,点C、D、E是窗框AB上的定点,AC=5cm,CD=8cm,DE=26,BE=13cm,转轴H、F分别是窗门底部MN和支架HE上的定点,且HF=AC,滑点P在轨道CD上运动,当点P运动到点C时,窗户关闭(窗门底部MN与面框AB重合):如图3,当窗户开到最大时,点P与D重合,此时∠PFE=90°,PF<EF,则PF= cm,此时点N到AB的距离为 cm.
三.解答题
26.综合与实践:设计公交车停靠站的扩建方案.
【素材1】:图1为某公交车停靠站,顶棚截面由若干段形状相同的抛物线拼接而成.图2为某段结构示意图,C1,C2皆为轴对称图形,且关于点M成中心对称,该段结构水平宽度为8米.
【素材2】:图3为停靠站部分截面示意图,两根长为2.5米的立柱M1N1,M2N2竖直立于地面并支撑在对称中心M1,M2处.小温将长为2.8米的竹竿AB竖直立于地面,当点A触碰到顶棚时,测得N2B为1米.
【素材3】:将顶棚扩建,要求截面为轴对称图形,且水平宽度为27米.计划在顶棚两个末端到地面之间加装垂直于地面的挡风板.
【任务】:
(1)确定中心:求图2中点M到该结构最低点的水平距离l;
(2)确定形状:在图3中建立合适的直角坐标系,求C1的函数表达式;
(3)确定高度:求挡风板的高度.
27.如图,在△ABC中,∠ACB=90°,点D在BC边上,△ACD的外接圆⊙O交AB于点E,,过点C作CG⊥AD于点G,延长CG交AB于点F.
(1)求证:∠FAC=∠ACG;
(2)求证:;
(3)若CF=3FG,,求BD的长.
28.如图1,在矩形ABCD中,AB=4,BC=3,P是AB上一动点(不与A,B重合),点E在CD上,AP=CE,以PE为直径的⊙O交AB于另一点F,设AP=x.
(1)若点P在F的左侧,用含x的代数式表示PF的长.
(2)在(1)条件下,⊙O与BC相切时,求PF的长.
(3)如图2,O′是点O关于EF的对称点.
①若PO′所在的直线经过矩形ABCD的一个顶点时,求所有满足条件的x的值.
②当点O′落在⊙O内时,直接写出x的取值范围.
29.如图,在⊙O中,直径AB=10,弦BC=6,点D在BC的延长线上,线段AD
交⊙O于点E,过点E作EF∥BC分别交⊙O,AB于点F,G,连结BF.
(1)求证:△ABD∽△FGB.
(2)当△FGB为等腰三角形时,求CD的长.
(3)当∠D=45°时,求EG:FG的值.
30.根据素材解决问题.
设计货船通过圆形拱桥的方案
素材1 图1中有一座圆拱石桥,图2是其圆形桥拱的示意图,测得水面宽AB=16m,拱顶离水面的距离CD=4m.
素材2 如图3,一艘货船露出水面部分的横截面为矩形EFGH,测得EF=3m,EH=10m.因水深足够,货船可以根据需要运载货物.据调查,船身下降的高度y(米)与货船增加的载重量x(吨)满足函数关系式.
问题解决
任务1 确定桥拱半径 求圆形桥拱的半径
任务2 拟定设计方案 根据图3状态,货船能否通过圆形拱桥?若能,最多还能卸载多少吨货物?若不能,至少要增加多少吨货物才能通过?
31.如图,在Rt△ABC中,∠CAB=90°,AC=3,AB=4,AD⊥BC于点D,射线CE平行AB交AD的延长线于点E,P是射线CE上一点(在点E的右侧),连结AP交BC于点F.
(1)求证:△ACE∽△BAC.
(2)若,求的值.
(3)以PF为直径的圆经过△BDE中的某一个顶点时,求所有满足条件的EP的长.
32.如图,在△ABC中,∠C=90°,D为边BC上一点,DE⊥AB于点E,以DE为直径的⊙O分别交线段BD,AD于点F,G,连结EF,EG.
(1)求证:△DEF∽△ABC.
(2)若AC=6,BC=8,当DG与四边形DGEF其它三边中的一边相等时,求所有满足条件的BD的长.
(3)当AC=BC时,连结OC交AD于点H,记△DOH的面积为S1,△ACH的面积为S2,若OC∥EG,则的值为 .(在横线上直接写出答案)
33.如图,点A,B都在x轴上,过点A作x轴的垂线交抛物线y=﹣x2+4x于点C,过点B作x轴的垂线交该抛物线于点D,点C,D都在第一象限,点D在点C的右侧,DE⊥AC于点E,连接CD,BE,CD∥EB.
(1)若OA=2,求AB的长.
(2)若点A是线段OB的中点,求点E的坐标.
(3)根据(2)的条件,连接OD,动点P在线段OB上,作PQ⊥OD交OD于点Q.当△PDQ与△CDE相似时,求的值.
34.如图,在矩形ABCD中,AB=6,BC=8,点E,F分别在边BC,AB上,AF=BE=2,连接DE,DF.动点M在EF上从点E向终点F匀速运动,同时,动点N在射线CD上从点C沿CD方向匀速运动,当点M运动到EF的中点时,点N恰好与点D重合,点M到达终点时,M,N同时停止运动.
(1)求EF的长.
(2)设CN=x,EM=y,求y关于x的函数表达式,并写出自变量x的取值范围.
(3)连接MN,当MN与△DEF的一边平行时,求CN的长.
35.如图,抛物线yx2+2x+6交x轴于A,B两点(点A在点B的右侧),交y轴于点C,顶点为D,对称轴分别交x轴、线段AC于点E、F.
(1)求抛物线的对称轴及点A的坐标;
(2)连接AD,CD,求△ACD的面积;
(3)设动点P从点D出发,沿线段DE匀速向终点E运动,取△ACD一边的两端点和点P,若以这三点为顶点的三角形是等腰三角形,且P为顶角顶点,求所有满足条件的点P的坐标.
36.如图,在 ABCD中,AB=4,BC=8,∠ABC=60°.点P是边BC上一动点,作△PAB的外接圆⊙O交BD于E.
(1)如图1,当PB=3时,求PA的长以及⊙O的半径;
(2)如图2,当∠APB=2∠PBE时,求证:AE平分∠PAD;
(3)当AE与△ABD的某一条边垂直时,求所有满足条件的⊙O的半径.
37.如图,在矩形ABCD中,E为AD边中点,BE的中垂线分别交AB,BE,CD,BC的延长线于点F,H,G,N,延长FE交CD的延长线于点M.
(1)证明:△ABE∽△CNG.
(2)连接BG,当AB=CN时,求∠EBG的度数.
(3)当BC=CN时,求AD:AB的值.
38.如图,矩形ABCD中,BC=8,点F是AB边上一点(不与点B重合),△BCF的外接圆交对角线BD于点E,连结CF交BD于点G.
(1)求证:∠ECG=∠BDC.
(2)当AB=6时,在点F的整个运动过程中,
①连结EF,若BF时,求CE的长.
②当△CGE为等腰三角形时,求所有满足条件的CG的长.
直接写出答案CG为 .
39.如图,Rt△ABC中,∠ACB=90°,点D是斜边AB上一点,⊙O为△ACD的外接圆,BC交⊙O于点F,连结FD并延长至点E,使AE∥BC.
(1)当∠EAF=70°时,求∠CDF的度数;
(2)若AC=4,BC=6,当△ACD为等腰三角形时,求CF的长;
(3)设,若△AEF的外心I恰好落在⊙O上,求k的值.
40.如图1,在菱形ABCD中,∠B为锐角,点P,H分别在边AD,CB上,且DP=BH,在AB边上取点M,N(点N在BM之间)使AM=5BN.点P从点D匀速运动到点A时,点Q恰好从点M匀速运动到点N,连结PQ,PH分别交对角线AC于E,F,记QM=x,AP=y,已知y=﹣2x+12.
(1)①请判断PF与FH的大小关系,并说明理由;
②求AD,BN的长;
(2)如图2,连结QF,当四边形FQBH中有两边平行时,求AE:EC的值;
(3)若∠B=60°,连结QH,求△FQH面积的最小值.
参考答案
一.选择题
1.【分析】如图,连接OA,OB.设AF=EF=EG=BG=x,则FGx.构建方程求出x,可得结论.
【解答】解:如图,连接OA,OB.设AF=EF=EG=BG=x,则FGx.
由对称性可知四个阴影部分是全等的等腰直角三角形,
∵△AOB是等腰直角三角形,OA=OB=2,
∴AB=2,
∴2xx=2,
∴x=22,
∴阴影部分的面积=4(2)×(22)=24﹣16.
故选:C.
2.【分析】设正方形PFGH的边长是x,由条件得到x2+(x+2)2=16,从而求出正方形PFGH的边长,得到正方形PCDE的边长,进一步求出PD,PG的长,即可求出DG的长.
【解答】解:作OK⊥PC于K,设正方形PFGH的边长是x,
∵四边形PCDE是正方形,
∴∠CPD=45°,
∵∠OKP=90°,
∴△KOP是等腰直角三角形,
∴PKOP=1,
∴CK=FK=x+1,
∴PC=CK+PK=x+2,
∵两个正方形的面积之和为16,
∴x2+(x+2)2=16,
∴x1或x1(舍),
∴PC=x+21,PH=x1,
∴PDPC,PGPH,
∴DG=PD+PG=2.
故选:B.
3.【分析】根据正多边形与圆的对称性、垂径定理以及正多边形与圆的计算,可求出∠AOD=120°,∠BOC=90°,由直角三角形的边角关系求出OM、AM、BM,根据三角形的面积公式进行计算即可.
【解答】解:如图,连接OA、OB、OC、OD,过点O作OM⊥AD,垂足为M,
由圆的对称性可知,点A、点D是⊙O的三等分点,四边形BCFE是正方形,
∴∠AOD360°=120°,∠BOC360°=90°,
在Rt△AOM中,OA=2,∠AOM=60°,
∴OMOA=1,AMOA,
在Rt△BOM中,∠BOM=45°,OM=1,
∴BM=OM=1,
∴AB=AM﹣BM1,
∴8个阴影三角形的面积和为:(1)(1)×8=16﹣8,
故选:C.
4.【分析】过点B作BE⊥CD于点E,过点C作CF⊥AB于点F,可得△ABC,△BED,△BEC,△BCF都是直角三角形,根据sin∠BCE,设BE=3a,BC=5a,得CE4a,过点C作DB延长线于点G,得矩形CFBG,设AC=x,AB=y,然后利用勾股定理和三角形的面积可得a,进而利用锐角三角函数即可解决问题.
【解答】解:如图,过点B作BE⊥CD于点E,过点C作CF⊥AB于点F,
∴△ABC,△BED,△BEC,△BCF都是直角三角形,
∵sin∠BCD,
∴sin∠BCE,
设BE=3a,BC=5a,
∴CE4a,
过点C作DB延长线于点G,得矩形CFBG,
∴BF=CG,
设AC=x,AB=y,
在Rt△ABC中,根据勾股定理,得
AB2﹣AC2=BC2,
∴y2﹣x2=25a2,
∵S△ABCAB CFAC BC,
∴y CF=5ax,
∴CF,
在Rt△BCF中,根据勾股定理,得
BFaa,
∴BF=CGa,
在正方形ABDH中,AB=BD=y,
在Rt△BDE中,根据勾股定理,得
DE,
∴CD=CE+ED=4,
∵S△CBDCD BEBD CG,
∴CD BE=BD CG,
∴(4)×3=ya,
∴a,
∴tan∠CDB=tan∠EDB.
故选:D.
5.【分析】连接AG,过点D作DT⊥AB于T,过点G作GN⊥AB于N,交CD于M.想办法求出DM,FM,CF,可得结论.
【解答】解:连接AG,过点D作DT⊥AB于T,过点G作GN⊥AB于N,交CD于M.
在Rt△ADT中,AD=2,∠DAT=60°,
∴AT=AD cos60°=1,DTAT,
∵,
∴∠DAG=∠GAB=30°,
在Rt△AGN中,GNAG=1,ANGN,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵DT⊥AB,
∴DT⊥CD,
∴∠DTN=∠MNT=∠TDM=90°,
∴DT=MN,DM=TN=AN﹣AT1,
∴GM=MN﹣GN1,
∵AD∥FG,
∴∠ADF+∠DFG=180°,
∵∠ADC=180°﹣∠DAB=120°,
∴∠GFM=60°,
∴FM1,
∴FG=FG′=2FM=2,
∵∠C=∠DAB=60°,
∴CF,
∴AB=CD=DM+FM+CF1+12,
故选:D.
6.【分析】将抛物线y=﹣(x+m)2+5向右平移3个单位后得到y=﹣(x+m﹣3)2+5,然后联立组成方程组求解即可.
【解答】解:将抛物线y=﹣(x+m)2+5向右平移3个单位后得到y=﹣(x+m﹣3)2+5,
根据题意得:,
解得:,
∴交点C的坐标为(,),
故选:B.
7.【分析】利用二次函数图象上点的坐标特征可得出点A1的坐标,结合旋转的性质可得出点A2的坐标,观察图形可知:图象上点以6(横坐标)为周期变化,结合2020=336×6+4可知点P的纵坐标和当x=4时的纵坐标相等,由旋转的性质结合二次函数图象上点的坐标特征,即可求出m的值,此题得解.
【解答】解:当y=0时,x2﹣3x=0,
解得:x1=0,x2=3,
∴点A1的坐标为(3,0).
由旋转的性质,可知:点A2的坐标为(6,0).
∵2020=336×6+4,
∴当x=4时,y=m.
由图象可知:当x=2时的y值与当x=4时的y值互为相反数,
∴m=﹣(2×2﹣3×2)=2.
故选:C.
8.【分析】如图,连接OP,PF,作PH⊥AB于H.点P的运动轨迹是以O为圆心、OP为半径的⊙O,易知EF=2FH=2,观察图形可知PH的值由大变小再变大,推出EF的值由小变大再变小.
【解答】解:如图,连接OP,PF,作PH⊥AB于H.
∵CD=8,∠COD=90°,
∴OPCD=4,
∴点P的运动轨迹是以O为圆心OP为半径的⊙O,
∵PH⊥EF,
∴EH=FH,
∴EF=2FH=2,
观察图形可知PH的值由大变小再变大,
∴EF的值由小变大再变小,
故选:D.
9.【分析】过C作CN⊥AB于N,判定△ACE∽△BCH,即可得到;设AC=a,再根据勾股定理以及面积法即可得到AB与CN的长,进而得出AN的长;再根据△CNM∽△GBM,即可得到MN和BM的长,进而得出答案.
【解答】解:如图所示,过C作CN⊥AB于N,
由题可得,∠CAE=∠CBH=90°,∠ACE=∠BCH=45°,
∴△ACE∽△BCH,
∴,
设AC=a,则BC=2a,ABa,CNa,
Rt△ACN中,ANa,
∴BNaaa,
∵∠CNM=∠GBM=90°,∠CMN=∠GMB,
∴△CNM∽△GBM,
∴,
∴MNBNa,BMNBa,
∴AM=AN+MNa,
∴,
故选:B.
10.【分析】△PBC的外接圆的圆心在线段BC的垂直平分线y=﹣x上,求出直线y=﹣x与抛物线的交点,即可推出点M坐标,由此即可解决问题.
【解答】解:∵△PBC的外接圆的圆心在线段BC的垂直平分线y=﹣x上,
由,
解得或(舍弃),
∴点M坐标为(2,﹣2),
如图1中,作MN⊥AB于N,
∵MP=MB,NM⊥PB,
∴PN=NB=1,
∴OP=1,AP=3,
∴当AP=3时圆心在抛物线上.
故选:A.
11.【分析】设AF=BG=DE=CH=a,DH=BF=AE=CG=b,由相似三角形的性质可求a=2b,由正方形的面积公式可求解.
【解答】解:如图,过点I作IN⊥BG于N,
设AF=BG=DE=CH=a,DH=BF=AE=CG=b,
则HG=EH=a﹣b,
∵∠FGH=∠IGD=90°,
∴∠DGH=∠IGF,
又∵∠ING=∠GHD=90°,
∴△DHG∽△ING,
∴,
∵GIGD,
∴INDHb,GNGH(a﹣b),
∴BN=a(a﹣b)ba,
∵∠ABF=∠IBN,∠AFB=∠INB=90°,
∴△AFB∽△INB,
∴,
∴,
∴a=2b,
∴S正方形EFGH=HG2=(a﹣b)2=b2,
∵S正方形ABCD=AD2=AE2+DE2=5b2,
∴,
故选:A.
12.【分析】根据等腰三角形的性质可得CE=(20﹣10)÷2=5(cm),CH=(20﹣6)÷2=7(cm),再根据△CDE∽△CFH解答即可.
【解答】解:由题意得,CE=(20﹣10)÷2=5(cm),CH=(20﹣6)÷2=7(cm),
在△CDE和△CFH中,
∵∠C=∠C,∠CED=∠CHF=90°,
∴△CDE∽△CFH,
∴,
即,
解得FH=8.4(cm).
故选:C.
二.填空题
13.【分析】如图,设圆心为O,连接OK,根据轴对称图形的性质可得KIEF,OI=GH﹣GO﹣EK,再根据勾股定理即可求解;利用△PLQ∽△RSC的对应边成比例得出,分别求出CS,RS即可求解.
【解答】解:如图,设圆心为O,连接OK,
由轴对称图形的性质可得KIEF,OI=GH﹣GO﹣EKr,
在Rt△KOI中,r2=(r)2+()2,
解得r;
根据矩形的性质可得△PLQ∽△RSC,
∴,即,
根据题意可得AD,AE=FB(),
∴CS,RS,
∴,
∴,
∵匾额的长为2PL,宽为2QL,
∴匾额的长与宽之比为,
故答案为:,7:3.
14.【分析】根据题目中的数据,利用锐角三角函数可以求得AB的长,再根据题意,作出合适的辅助线,求出BE、EF、BF、FC、FG、DG的长,然后根据S四边形ABCD=S梯形AEGD﹣S△BEF﹣S△BFC﹣S△DFG,代入数据计算即可.
【解答】解:∵GF=2EF=4km,EG=EF+FG,
∴EF=2km,EG=6km,
∵tan∠BFE,tan∠AGE,∠AEG=90°,∠BEF=90°,
∴AE=4km,BE=1km,
∴BF(km),AB=AE﹣BE=4﹣1=3(km),
∵∠BFC=90°,∠DGF=90°,
∴∠BFE+∠DFG=90°,∠DFG+∠FDG=90°,
∴∠BFE=∠FDG,
∴tan∠FDG,
∴DG8(km),
作CM⊥AB交AB于点M,作CN⊥EG交EG于点N,如图所示,
则ME=CN,MC=EN,
∵MC∥EG,tan∠AGE,
∴tan∠ACM,
设AM=2a,则MC=3a,ME=4﹣2a,
∵CN⊥EG,DG⊥EG,tan∠BFE,∠BFE=∠FDG,CN=ME=4﹣2a,
∴∠FDG=∠FCN,
∴,
∴FN=2﹣a,
∴GN=FG﹣FN=4﹣(2﹣a)=2+a,
∵tan∠CGN,
∴,
解得a=1,
∴CN=2km,FN=1km,
∴FC(km),
∴S四边形ABCD=S梯形AEGD﹣S△BEF﹣S△BFC﹣S△DFG16.5(km2),
故答案为:3,16.5.
15.【分析】在a上取点D,在b上取点E,使OD=OC=OE,连接CD,CE,根据a和c,b和c都相交成60°角,可得△COD,△COE都是等边三角形,∠AOB=120°,即可证明△ABO∽△CBE,可得,
(1)当x=75,y=50时,,解得z=30;
(2)由得:z.
【解答】解:在a上取点D,在b上取点E,使OD=OC=OE,连接CD,CE,如图:
∵a和c,b和c都相交成60°角,
∴△COD,△COE都是等边三角形,∠AOB=120°,
∴∠CEO=60°,∠BAO=60°﹣∠ABO,OD=OC=OE=z,
∴∠BCE=60°﹣∠CBE=∠BAO,
∵∠ABO=∠CBE,
∴△ABO∽△CBE,
∴,即,
(1)当x=75,y=50时,
,
解得z=30,
故答案为:30;
(2)由得:z,
故答案为:.
16.【分析】(1)先过点E作EF⊥AP构造出含30度角的直角三角形,利用其性质得到线段长度,再利用等腰三角形的性质得到AP,最后根据图象利用AB﹣AP即可求解;
(2)首先根据题意画图,明确求出AD即所得,设出AC长度,利用两个直角形的公共边,结合勾股定理列出方程求解,最后利用线段相加即可解决.
【解答】解(1)如图,过点E作EF⊥AP,垂足为F,
∵E是PC的中点,
∴PE=ECPC=20cm,
又∵AEPC,
∴AE=PE=CE=20cm,
在Rt△PEF中,∠APE=30°,PE=20cm,
∴PF=PE cos∠APE
=20
=30(cm),
∵AE=PE,EF⊥AB,
∴AP=2PF=60cm,
∴BP=AB﹣AP
=12060
=60(cm).
(2)由题意可知,当A、C、D三点共线时,此时AC⊥AP,
如图所示:过点D作DF⊥地面,交地面水平线为F,
∵∠DAP=∠B=∠DFB=90°,
∴四边形ABFD为矩形,
∴AD=BF,
设AC=x,
在Rt△ACP和Rt△PDA中,
∴CP2﹣AC2=DP2﹣DA2,
∴,
解得x,
∴BF=AD=AC+CD(cm),
∴当太阳光线恰好与地面垂直,则PD落在地面上的阴影为cm.
故答案为:;.
17.【分析】连接FN交EK于点O,过点O作PQ⊥BC于点P,交AD于点Q,证明四边形ABPQ是矩形,四边形ENKF是菱形,利用勾股定理求出FG的长;然后根据S△OFGOP FGOF OG,求出OP,由△GOP∽△GEB,求出BE,再证明△ANE≌△CGH,进而可以解决问题.
【解答】解:如图,连接FN交EK于点O,过点O作PQ⊥BC于点P,交AD于点Q,
∴∠QPB=90°,
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,
∴∠AQP=90°,
∴四边形ABPQ是矩形,
∴AB=QP,
∵△ENK和△EFK都是全等的等边三角形,
∴∠EFK=∠ENK=60°,EF=FK=NK=EN=EK=2,
∴四边形ENKF是菱形,
∴NF⊥EK,OE=OKEK=1,OF=ONFN,∠EFN∠EFK=30°,
∴OF,
∵OG=OK+KG=1+4=5,
∴FG2,
∵S△OFGOP FGOF OG,
∴2OP=5,
∴OP,
∴AB=PQ=2OP,
∵OP∥BE,
∴△GOP∽△GEB,
∴,
∴,
∴BE,
∴AE=AB﹣BE,
∴AN,
∵BF,
∵AD∥BC,EN∥GH,
∴∠ANE=∠CGH,
在△ANE和△CGH中,
,
∴△ANE≌△CGH(AAS),
∴CG=AN,
∴BC=BF+FG+CG2.
故答案为:2;.
18.【分析】如图1中,过点E作EJ⊥AC于J,过点D作DK⊥EJ于K,过点Q作QM⊥EJ于M,过点P作PN⊥QM于N,则四边形PNMJ是矩形,四边形DKJC是矩形,设PQ=m.用两种方法求出EJ,构建方程求出m,即可解决问题.
【解答】解:如图1中,过点E作EJ⊥AC于J,过点D作DK⊥EJ于K,过点Q作QM⊥EJ于M,过点P作PN⊥QM于N,则四边形PNMJ是矩形,四边形DKJC是矩形,设PQ=m.
∵∠DEF=∠EDC=120°,∠EDP=75°,
∴∠PDC=45°,
∵∠DCP=90°,
∴∠CDP=∠CPD=45°,
∴CP=CD=2,
∵PQ⊥EF,
∴∠PQE=90°,
∴∠DPQ=360°﹣75°﹣120°﹣90°=75°,
∵∠DPN=45°,
∴∠QPN=30°,
∴NQm,PN=MJm,
在Rt△DEM中,∠EDM=30°,DE=2,
∴EK=1,
∵EM+PN=3,
∴PNm,
∵DK=CJ,
∴MN=PJ=2,
∴QMm+2,
∵∠EQM=30°,
∴EMQM(m+2),
∴3(m+2)m,
∴m=21,
∴PQ=21,
如图2中,过点G作GH⊥PQ于H.
∵QG∥DE,
∴∠QGP=∠EDP=75°,
∵∠QPG=75°,
∴∠QGP=∠QPG,
∴GQ=QP,∠GQP=30°,
∴GHQG,
∴S△PQG PQ GH(21).
故答案为:21,.
19.【分析】如图,连接OC交BD于K.设DE=k.BE=4k,则DK=BK=2.5k,EK=1.5k,由AD∥CK,推出AE:EC=DE:EK,可得AE=4,由△ECK∽△EBC,推出EC2=EK EB,求出k即可解决问题.
【解答】解:如图,连接OC交BD于K,连接BC.
∵,
∴OC⊥BD,
∵BE=4DE,
∴可以假设DE=k.BE=4k,则DK=BK=2.5k,EK=1.5k,
∵AB是直径,
∴∠ADK=∠DKC=∠ACB=90°,
∴AD∥CK,
∴AE:EC=DE:EK,
∴AE:6=k:1.5k,
∴AE=4,
∵△ECK∽△EBC,
∴EC2=EK EB,
∴36=1.5k×4k,
∵k>0,
∴k,
∴BC2,
∴AB4.
故答案为4.
20.【分析】连接OB,根据垂径定理求出BE,根据勾股定理求出OB,再根据勾股定理计算即可.
【解答】解:连接OB,
∵AC是⊙O的直径,弦BD⊥AC,
∴BEBD=6cm,
在Rt△OEB中,OB2=OE2+BE2,即OB2=(OB﹣4)2+62,
解得,OB,
则EC=AC﹣AE=9,
BC3,
∵OF⊥BC,
∴CFBC,
∴OF(cm),
故答案为.
21.【分析】因为S阴=S菱形PHQF﹣2S△HTN,想办法求出菱形PHQF的面积,△HTN的面积即可解决问题.
【解答】解:如图,设FM=HN=a.
由题意点E、F、G、H分别为矩形AB、BC、CD、DA的中点,可得四边形HQFP是菱形,它的面积S矩形ABCD4×6=6,
∵FM∥BJ,CF=FB,
∴CM=MJ,
∴BJ=2FM=2a,
∵EJ∥AN,AE=EB,
∴BJ=JN=2a,
∵S△HBC 6 4=12,HJBH,
∴S△HCJ12,
∵TN∥CJ,
∴△HTN∽△HCJ,
∴()2,
∴S△HTN,
∴S阴=S菱形PHQF﹣2S△HTN=6,
故答案为.
22.【分析】由题意可得在三角形OAC为直角三角形,设OA=OB=OB'=x,则根据勾股定理得方程:,解得x;过点A'作A'D⊥OB'于点D,设B'D=m,则ODm,在直角三角形OA'D中,可得:AD2=OA'2﹣OD2,在直角三角形A'DB'中,由勾股定理有AD2=A'B'2﹣B'D2,从而可建立方程,解出m的值,最后A同学的高度上升的高度即为DC=OC﹣OD可求.
【解答】解:设AB与OB'交于点C,由题意可得OB'⊥AB,
在直角三角形OAC中,设OA=OB=OB'=x,
根据勾股定理得方程:
,解得:x.
过点A'作A'D⊥OB'于点D,
设B'D=m,则ODm,
在直角三角形OA'D中,由勾股定理有:
AD2=OA'2﹣OD2,
在直角三角形A'DB'中,由勾股定理有:
AD2=A'B'2﹣B'D2=25﹣m2,
∴25﹣m2,
解得:m,
即B'D,
∴DC=OC﹣OD=()﹣().
故答案为:,.
23.【分析】如图2,延长NM,则NM过点D,由三角形中位线定理可得MG的长度,如图3,过点P作PK⊥AB于K,可得∠PFK=∠CDF=∠MPF,在Rt△CDF中,CF2,知tan∠CDF,故tan∠MPF,可得PG,PF=PG+GF,由△CDF∽△KFP,得,即可得压杆MN到底座AB的距离为cm.
【解答】解:如图2,延长NM,则NM过点D,
∵四边形EFGH是矩形,
∴HG∥EF,即MG∥DF,
∵G是PF中点,
∴MG是△PDF的中位线,
∴MGDF8=4(cm),
如图3,过点P作PK⊥AB于K,
∵MN∥AB,
∴PK⊥MN,∠MPF=∠PFK,
∵∠DFP=∠DCF=90°,
∴∠CDF+∠DFC=∠PFK+∠DFC=90°,
∴∠PFK=∠CDF=∠MPF,
在Rt△CDF中,CF2,
∴tan∠CDF,
∴tan∠MPF,即,
∴,
解得PG,
∴PF=PG+GF2,
∵∠CDF=∠PFK,∠DCF=90°=∠PKF,
∴△CDF∽△KFP,
∴,即,
解得PK(cm),
∴压杆MN到底座AB的距离为cm,
故答案为:4,.
24.【分析】过点N作NG⊥A′D′于G,过点D′作D′H⊥PQ于H,交MN于T,过点A′作A′K⊥D′H于K,利用正方形面积和梯形面积求得:C′D′=CD=A′Q=20cm,C′N=8cm,D′F=12cm,MF=C′N=8cm,运用勾股定理求得FN=4,再根据△D′FT∽△NFG,△A′FM∽△NFG,即可求得答案.
【解答】解:∵S正方形DMEC=400cm2,
∴CD=DM=AB=20cm,
∴C′D′=CD=A′Q=20cm,
∵S四边形D′C′NF=200cm2,D′FC′N,
∴(D′F+C′N)×C′D′=200,
即C′N×20=200,
∴C′N=8cm,
∴D′F=12cm,
∴MF=C′N=8cm,
过点N作NG⊥A′D′于G,过点D′作D′H⊥PQ于H,交MN于T,
过点A′作A′K⊥D′H于K,
则D′G=C′N=8cm,FG=4cm,NG=20cm,
∴FN4,
∵∠NFG=∠D′FT,∠D′TF=∠NGF=90°,
∴△D′FT∽△NFG,
∴,即,
∴D′T,
∵∠NFG=∠A′FM,∠NGF=∠M=90°,
∴△A′FM∽△NFG,
∴,即,
∴A′M=40,A′F=8,
∵∠M=∠P=∠FA′Q=90°,
∴∠MA′F+∠QA′P=∠QA′P+∠A′QP=90°,
∴∠MA′F=∠A′QP,
∴△A′FM∽△QA′P,
∴,即,
∴A′P,
∵四边形A′PHK、A′KTM为矩形,
∴TK=A′M=40,KH=A′P,
∴D′H=D′T+TK+KH4040,
故答案为:40.
25.【分析】根据题意,由勾股定理得到DF=10cm,再利用等角三角函数也相等列出关系式计算出点N到AB的距离即可.
【解答】解:由题意可知:MD+DF+FE=AE,AC=MD=HF=5cm,
∴DF+FE=CE=34cm,
设DF=x cm,则FE=(34﹣x)cm,
∵∠DFE=90°,
DF2+FE2=DE2即x2+(34﹣x)2=262,
解得:x=10,
∴DF=10cm即PF=10cm.
∴EF=34﹣x=24cm,MN=AB=5+8+26+13=52cm,
过点N作NG⊥AB,垂足为G,延长NM交AB于点J,
∵HF∥MD,
∴∠MDJ=∠FEP,即tan∠MDJ=tan∠FEP
∵MD=5cm,
∴MJcm.
∴NJ=MJ+MNcm,
∵∠JNG=∠DEF,
∴cos∠JNG=cos∠DEF,
∴NG.
故答案为:10;.
三.解答题
26.【分析】(1)根据轴对称性图形的性质和抛物线的对称性可得中点M到该结构最低点的水平距离为8÷2÷2=2(米);
(2)以M2点为原点建立坐标系,设抛物线C1的解析式为y=a(x﹣2)2+h,将(0,0),(1,0.3)代入,即可求函数的解析式;
(3)分两种情况讨论:①当x=1.5+2=3.5时,y=0.175,则h=2.5+0.275=3.125(米);②当x=2.5﹣2=0.5时,y=0.625,h=2.5+0.625=3.125(米).
【解答】解:(1)∵C1,C2皆为轴对称图形,且关于点M成中心对称,水平宽度为8米,
∴8÷2÷2=2(米),
∴中点M到该结构最低点的水平距离l为2米;
(2)以M2点为原点,如图建立平面直角坐标系,
∵C1过点(0,0),(1,0.3),对称轴为直线x=2,
∴设抛物线C1的解析式为y=a(x﹣2)2+h,
将(0,0),(1,0.3)代入,
∴,
解得,
∴抛物线C1的解析式为y=﹣0.1(x﹣2)2+0.4;
(3)方法一:27﹣8×3=3(米),3÷2=1.5(米),
①如图,
当x=1.5+2=3.5时,y=﹣0.1×(3.5﹣2)2+0.4=0.175,
∴h=2.5+0.175=2.675(米);
②如图,
当x=1.5﹣2=﹣0.5时,y=0.1×(0.5+2)2﹣0.4=﹣0.175,
∴h=2.5+(﹣0.175)=2.325(米);
综上所述:挡风板的高度为2.675米或2.325米.
方法二:由图形为轴对称图形可知,图形必由若干个图2结构和一个C1或者C2构成:
4+8×3=28,28﹣27=1,1÷2=0.5米,
只需将x=0.5以及x=﹣0.5相应代入C1、C2即可,
y0.1(0.5﹣2)2+0.4=0.175米,
∴h=2.5+y=2.675米,
y0.1(﹣0.5+2)2﹣0.4=﹣0.175米,
∴h=2.5+y=2.325(米);
综上所述:挡风板的高度为2.675米或2.325米.
27.【分析】(1)由余角的性质可得∠ADC=∠ACG,由圆周角定理可得∠FAC=∠ADC,即可求解;
(2)通过证明△AGC∽△BCA,可得;
(3)由勾股定理可求FG,AG的长,通过证明△AGC∽△CGD,可得,可求DG的长,即可求解.
【解答】(1)证明:∵DA是直径,
∴∠ACD=90°,
∴∠CAD+∠ADC=90°,
∵CG⊥AD,
∴∠AGC=90°,
∴∠CAD+∠ACG=90°,
∴∠ADC=∠ACG,
∵,
∴∠FAC=∠ADC,
∴∠FAC=∠ACG;
(2)证明:∵∠FAC=∠ACG,∠ACB=∠AGC=90°,
∴△AGC∽△BCA,
∴;
(3)解:∵∠FAC=∠FCA,
∴AF=CF,
∵CF=3FG,
∴CG=2FG,AF=FC=3FG,
∴AG2FG,
∵AC2=AG2+GC2,
∴12=8FG2+4FG2,
∴FG=1(负值舍去),
∴AG=2,CG=2,
∵,
∴,
∴BC=2,
∵∠ADC=∠ACG,∠AGC=∠DGC,
∴△AGC∽△CGD,
∴,
∴2×2=2GD,
∴GD,
∴CD,
∴BD=BC﹣CD.
28.【分析】(1)先根据直径所对的圆周角是直角可得EF⊥AB,再证得四边形BCEF是矩形,得出BF=CE=x,即可得出答案;
(2)如图1,连接OG交EF于H,由切线性质可得OG⊥BC,利用三角形中位线定理和勾股定理即可求得答案;
(3)①分两种情况:当PO′所在直线经过点C时,当PO′所在直线经过点D时,分别建立方程求解即可;
②分两种情况:当点O′在点O右侧时,当点O′在点O左侧时,分别求得x的值即可得出答案.
【解答】解:(1)由题意得:AB=4,CE=AP=x,
∵PE是⊙O的直径,
∴EF⊥AB,即∠PFE=∠BFE=90°,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠B=∠C=∠BFE=90°,
∴四边形BCEF是矩形,
∴BF=CE=x,
∴PF=AB﹣AP﹣BF=4﹣x﹣x=4﹣2x.
(2)在(1)条件下,⊙O与BC相切于G,如图1,连接OG交EF于H,
则OG⊥BC,
∵EF∥BC,
∴OH⊥EF,
∴OH是△PEF的中位线,
∴OHPF(4﹣2x)=2﹣x,
∵HG=BF=x,
∴OG=OH+GH=2﹣x+x=2,
∴PE=2OG=4,EF=BC=3,
在Rt△PEF中,PF.
(3)①当PO′所在直线经过点C时,如图2,
由题意得,OO′CE,OO′=PF,
∴PFCE,即4﹣2xx,
解得:x;
当PO′所在直线经过点D时,如图3,
此时,PF=2x﹣4,DE=4﹣x,
OO′DE,OO′=PF,
∴PFDE,即2x﹣4(4﹣x),
解得:x,
综上所述,PO′所在直线经过矩形ABCD的一个顶点时,x或.
②当点O′落在⊙O内时,x的取值范围为x.
当点O′在点O右侧时,如图4,
∵OE=2OM=PF,EFPF,
∴3(4﹣2x),
解得:x;
当点O′在点O左侧时,如图5,
同理可得:EFPF,
∴3(2x﹣4),
解得:x;
综上所述,当点O′落在⊙O内时,x的取值范围为x.
29.【分析】(1)可证明△AGE∽△ABD,△AGE∽△FGB,进而得出结论;
(2)可讨论△ABD是等腰三角形,分为BD=AB,AD=AB和AD=BD;当BD=AB=10时,易得CD=4,当AD=AB时,连接AC,可得CD=BC=6,当AD=BD时,连接OD,可证明△ABC∽△DBO,进而得出结果;
(3)连接BE和AC,可求得CD和AD,DE,AE,进而根据△AGE∽△ABD,求得EG和AG,BG的长,根据△ABD∽△FGB可求得FG,进而得出结果.
【解答】(1)证明:∵EF∥BD,
∴∠AGE=∠ABD,∠AEC=∠D,
∴△AGE∽△ABD,
∵∠AEF=∠ABF,∠F=∠BAE,
∴△AGE∽△FGB,
∴△ABD∽△FGB;
(2)解:由①得,
△ABD∽△FGB,
∵△FGB是等腰三角形,
∴△ABD是等腰三角形,
如图1,
当AB=AD时,连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴CD=BC=6,
如图2,
当AD=BD时,连接OD,AC,
∵OA=OB,
∴DO⊥AB,
∴∠BOD=90°,
∵∠ACB=90°,
∴∠ACB=∠BOD,AC8,
∵∠B=∠B,
∴△ABC∽△DBO,
∴,
∴,
∴BD,
∴CD=BD﹣BC,
当BD=AB=10时,CD=BD﹣BC=10﹣6=4,
综上所述:CD=6或或4;
(3)解:如图,
连接BE,AC,
∵AB是⊙O的直径,
∴∠BED=∠AEB=90°,∠ACD=∠ACB=90°,
∴CD=AC tanD=AC=8,AD8,
∴BD=BC+CD=14,
∴DE=BD cosD=14 cos45°=7,
∴AE=AD﹣DE=8,
由(1)知,
△AGE∽△ABD,△ABD∽△FGB;
∴,,
∴,
∴EG,AG,
∴BG=AB﹣AG=10,,
∴FG,
∴.
30.【分析】任务1,设 圆心为点O,则点O在CD延长线上,延长CD,则CD经过点O,连结AO,设桥拱的半径为r m,则OD=(r﹣4)m,由勾股定理,垂径定理,列出关于半径的方程,即可解决问题;
任务2,由勾股定理得到货船不能通过圆形桥拱,通过计算,即可得到需要增加的货物的吨数.
【解答】解:任务1,设圆心为点O,则点O在CD延长线上,延长CD,则CD经过点O,连接AO,如图,
设桥拱的半径为r m,则OD=(r﹣4)m,
∵OC⊥AB,
∴m,
∵OD2+AD2=OA2,
∴(r﹣4)2+82=r2,
∴r=10,
∴圆形拱桥的半径为10m.
任务2,根据图3状态,货船不能通过圆形桥拱,至少要增加吨的货物才能通过.理由:
当EH是⊙O的弦时,EH与OC的交点为M,连接OE,OH,如图,
∵四边形EFGH为矩形,
∴EH∥FG,
∵OC⊥AB,
∴OM⊥EH.
∴,
∴m,
∵OD=6m,
∴,
∴根据图3状态,货船不能通过圆形桥拱,
∴船在水面部分可以下降的高度m.
∵,
∴吨,
∴至少要增加吨的货物才能通过.
31.【分析】(1)利用同角的余角相等可得∠CEA=∠ACB,可证明结论;
(2)由(1)得△ACE∽△BAC,得,则CE,EP,从而得出CP的长,再利用△CFP∽△BFA,可得;
(3)分以PF为直径的圆经过△BDE中的一个顶点D或E或B,分别画出图形,利用相似三角形的判定与性质进行解题.
【解答】(1)证明:∵CE∥AB,
∴∠CAB+∠ACE=180°,
∵∠CAB=90°,
∴∠ACE=90°,
∴∠ACB+∠ECD=90°,
∵AD⊥BC,
∴∠CDE=90°,
∴∠AEC+∠ECD=90°,
∴∠CEA=∠ACB,
∴△ACE∽△BAC;
(2)解:由(1)得△ACE∽△BAC,
∴,
∴,
∴CE,
∵,
∴EP,
∴CP=CE+EP=6,
∵CP∥AB,
∴△CFP∽△BFA,
∴;
(3)解:当以PF为直径的圆经过△BDE中的一个顶点D时,
AP与AE重合,点P与点E重合,不符合题意,
当以PF为直径的圆经过△BDE中的一个顶点E时,
连接EF,则∠PEF=90°,
∵∠PCA=90°,
∴EF∥AC,
∴△PEF∽△PCA,
∴,
∵∠FCE=∠CBA,
∴tan∠FCE=tan∠CBA,
∵tan∠FCE,tan,
∴,
∴EF,
由(1)知,CE,
∵PC=PE+CE=PE,,
∴,
∴PE;
以PF为直径的圆经过△BDE中的一个顶点B时,
连接BP,
则∠FBP=90°,BP⊥BC,
∵AE⊥BC,
∴BP∥AE,
∵EP∥AB,
∴四边形EABP是平行四边形,
∴EP=AB=4,
综上所述,满足条件的EP的长为4或.
32.【分析】(1)可证∠EDF=∠BAC,∠EFD=∠C=90°,从而命题得证;
(2)分为三种情形讨论:当DG=DF时,转化为BD=AD求解,当EG=DG时,解斜三角形ABD:已知∠B,∠BAD=45°,AB=10,当DG=EF,可推出四边形EFDG是矩形,此时∠ADB=90°,此时点D和点C重合,从而得出结果.
【解答】(1)证明:∵DE⊥AB,
∴∠BED=90°,
∴∠EDF+∠B=90°,
∵∠=90°,
∴∠B+∠BAC=90°,
∴∠EDF=∠BAC,
∵DE是⊙O的直径,
∴∠DFE=90°,
∴∠EFD=∠C,
∴△DEF∽△ABC;
(2)当DG=DF时,,
∴∠FED=∠DEG,
∵DE是⊙O的直径,
∴∠EFD=∠EGD=90°,
∴∠EDF=∠EDA,
∵DE⊥AB,
∴∠AED=∠BED=90°,
∴∠B=∠BAD,
∴AD=BD,
在Rt△ACD中,
∵CD2+AC2=AD2,
∴(8﹣BD)2+62=BD2,
∴BD,
当DG=EG时,
∵∠EGD=90°,
∴∠EDG=∠DEG=45°,
∵∠AED=90°,
∴∠BAD=90°﹣∠EDG=45°,
∴DE=AE,
∵∠B=∠B,∠BED=∠ACB=90°,
∴△BED∽△BCA,
∴,
∴,
∴BE
∵BE+AE=10,
∴,
∴DE,
∴,
∴BD,
当DG=EF时,
∴,
∴∠EDF=∠DEG,
∵∠EFD=∠EGD=90°,
∴∠FED=∠EDG,
∴EF∥DG,
∴四边形EFDG是平行四边形,
∴ EFDG是矩形,
∴∠FDG=90°,
∵∠C=90°,
∴此时点D和C重合,
∴BD=8,
综上所述:BD或或8;
(3)如图
作OV⊥BC于V,
∴∠OVC=90°,
C∥EG,∠EGD=90°,
∴∠AHC=90°,
∴∠DAC+∠ACH=90°,
∵∠ACB=90°,
∴∠OCV+∠ACH=90°,
∴∠OCV=∠DAC,
∵∠ONC=∠ACD=90°,
∴△OCV∽△DAC,
∴,
设CD=a,AC=BC=b,
在等腰直角三角形BDE中,
DE,
∴OD,
在等腰直角三角形DOV中,
OV=DV,
∴VC=VD+CD,
∴,
∴b=3a,
∴AC=3a,OV,
∴tan∠OCV=tan∠DAC,
∴sin∠OVC=sin∠DAC,
cos∠OVC=cos∠DAC,
∵S△COD,
∴DH=a sin∠OCVa,
CHa,AH,
∴S△CDH,
S△ACH,
∴S△DOH,
∴,
故答案为:.
33.【分析】(1)先证明四边形BDCE是平行四边形,得出A(2,0),将x=2代入y=﹣x2+4x,得C(2,4),根据DB=AE=2,建立方程求解即可;
(2)设OA=t,则OB=2t,可得C(t,﹣t2+4t),D(2t,﹣4t2+8t),由DB=AE=CE,建立方程求解,可得出答案;
(3)如图,连接OD,PD,过点P作PQ⊥OD于点Q,分两种情况进行讨论:①若△PQD∽△DEC,②若△PQD∽△CED,即可得出答案.
【解答】解:(1)∵AC⊥x轴,BD⊥x轴,
∴AC∥BD,
∵CD∥EB,
∴四边形BDCE是平行四边形,
∴DB=AE,
∴AE=CE,
∵OA=2,
∴A(2,0),
当x=2时,y=﹣x2+4x=﹣22+4×2=4,
∴C(2,4),
∴AC=4,AE=2,DB=AE=2,
令y=2,得﹣x2+4x=2,
解得:x1=2(舍去),x2=2,
∴D(2,2),B(2,0),
∴AB=22;
(2)设OA=t,则OB=2t,
∴C(t,﹣t2+4t),D(2t,﹣4t2+8t),
∵DB=AE=CE,
∴﹣t2+4t=2(﹣4t2+8t),
∴t1,t2=0(不符合题意,舍去),
∴﹣4t2+8t=﹣4×()2+8,
∴E(,);
(3)如图,连接OD,PD,过点P作PQ⊥OD于点Q,
在(2)的条件下:C(,),D(,),
①若△PQD∽△DEC,
则:,
而tan∠DOB:,
∴::;
②若△PQD∽△CED,
则:,
而,
∴::2,
综上所述,的值为或2.
34.【分析】(1)在Rt△BEF中,利用勾股定理即可解决问题.
(2)根据速度比相等构建关系式解决问题即可.
(3)分两种情形如图3﹣1中,当MN∥DF,延长FE交DC的延长线于H.如图3﹣2中,当MN∥DE,分别利用平行线分线段成比例定理构建方程解决问题即可.
【解答】解:(1)∵四边形ABCD是矩形,
∴∠B=90°,AB=CD=6,AD=BC=8,
∵AF=BE=2,
∴BF=6﹣2=4,
∴EF2.
(2)由题意:,
∴
∴yx(0≤x≤12).
(3)如图3﹣1中,延长FE交DC的延长线于H.
∵BF∥CH,
∴△EFB∽△EHC,
∴,
∴,
∴EH=6,CH=12,
当MN∥DF时,,
∴,
∵yx,
解得x.
如图3﹣2中,当MN∥DE时,,
∴,
∵yx,
解得x=12,
综上所述,满足条件的CN的值为或12.
35.【分析】(1)令y=0,得到x2+2x+6=0,解得x=﹣2或6,则A(6,0),由对称轴公式计算即可;
(2)求出直线AC的解析式,求出F(2,4),则S△ACDDF×OA可求出答案;
(3)分三种情况,当AC,CD和AD分别为底边时,画出图形,可由等腰三角形的性质求出顶点P的坐标即可.
【解答】解:(1)对于抛物线yx2+2x+6令y=0,得到x2+2x+6=0,解得x=﹣2或6,
∴B(﹣2,0),A(6,0),
令x=0,得到y=6,
∴C(0,6),
∴抛物线的对称轴x2,A(6,0).
(2)∵yx2+2x+68,
∴抛物线的顶点坐标D(2,8),
设直线AC的解析式为y=kx+6,
∴0=6k+6,
∴k=﹣1,
∴直线AC的解析式为y=﹣x+6,
∴F(2,4),
∴DF=4,
∴S△ACDDF OA4×6=12;
(3)如图1,过点O作OM⊥AC交DE于点P,交AC于点M,
∵A(6,0),C(0,6),
∴OA=OC=6,
∴CM=AM,
∴CP=AP,
此时AC为等腰三角形ACP的底边,
∴OE=PE=2.
∴P(2,2),
如图2,过点C作CP⊥DE于点P,
∵OC=6,DE=8,
∴PD=DE﹣PE=2,
∴PD=PC,
此时△PCD是以CD为底边的等腰直角三角形,
∴P(2,6),
如图3,作AD的垂直平分线交DE于点P,
则PD=PA,
设PD=x,则PE=8﹣x,在Rt△PAE中,PE2+AE2=PA2,
∴(8﹣x)2+42=x2,
解得x=5,
∴PE=8﹣5=3,
∴P(2,3),
综合以上可得点P的坐标为(2,2)或(2,6)或(2,3).
36.【分析】(1)过点A作BP的垂线,作直径AM,先在Rt△ABH中求出BH,AH的长,再在Rt△AHP中用勾股定理求出AP的长,在Rt△AMP中通过锐角三角函数求出直径AM的长,即求出半径的值;
(2)证∠APB=∠PAD=2∠PAE,即可推出结论;
(3)分三种情况:当AE⊥BD时,AB是⊙O的直径,可直接求出半径;当AE⊥AD时,连接OB,OE,延长AE交BC于F,通过证△BFE∽△DAE,求出BE的长,再证△OBE是等边三角形,即得到半径的值;当AE⊥AB时,过点D作BC的垂线,通过证△BPE∽△BND,求出PE,AE的长,再利用勾股定理求出直径BE的长,即可得到半径的值.
【解答】解:(1)如图1,过点A作BP的垂线,垂足为H,作直径AM,连接MP,
在Rt△ABH中,∠ABH=60°,
∴∠BAH=30°,
∴BHAB=2,AH=AB sin60°=2,
∴HP=BP﹣BH=1,
∴在Rt△AHP中,
AP,
∵AB是直径,
∴∠APM=90°,
在Rt△AMP中,∠M=∠ABP=60°,
∴AM,
∴⊙O的半径为,
即PA的长为,⊙O的半径为;
(2)当∠APB=2∠PBE时,
∵∠PBE=∠PAE,
∴∠APB=2∠PAE,
在平行四边形ABCD中,AD∥BC,
∴∠APB=∠PAD,
∴∠PAD=2∠PAE,
∴∠PAE=∠DAE,
∴AE平分∠PAD;
(3)①如图3﹣1,当AE⊥BD时,∠AEB=90°,
∴AB是⊙O的直径,
∴rAB=2;
②如图3﹣2,当AE⊥AD时,连接OB,OE,延长AE交BC于F,
∵AD∥BC,
∴AF⊥BC,△BFE∽△DAE,
∴,
在Rt△ABF中,∠ABF=60°,
∴AF=AB sin60°=2,BFAB=2,
∴,
∴EF,
在Rt△BFE中,
BE,
∵∠BOE=2∠BAE=60°,OB=OE,
∴△OBE是等边三角形,
∴r;
③当AE⊥AB时,∠BAE=90°,
∴AE为⊙O的直径,
∴∠BPE=90°,
如图3﹣3,过点D作BC的垂线,交BC的延长线于点N,延长PE交AD于点Q,
在Rt△DCN中,∠DCN=60°,DC=4,
∴DN=DC sin60°=2,CNCD=2,
∴PQ=DN=2,
设QE=x,则PE=2x,
在Rt△AEQ中,∠QAE=∠BAD﹣∠BAE=30°,
∴AE=2QE=2x,
∵PE∥DN,
∴△BPE∽△BND,
∴,
∴,
∴BP=10x,
在Rt△ABE与Rt△BPE中,
AB2+AE2=BP2+PE2,
∴16+4x2=(10x)2+(2x)2,
解得,x1=6(舍),x2,
∴AE=2,
∴BE2,
∴r,
∴⊙O的半径为2或或.
37.【分析】(1)由垂直定义得∠HFB+∠HBF=90°.由矩形性质及相似三角形的判定可得结论;
(2)连接EG,根据相似三角形性质及中点定义得EG=BG.由HL得Rt△DEG≌Rt△CGB,然后根据全等三角形的性质及等腰三角形的性质可得答案;
(3)连接EN交CD于点P,由中点定义得,根据相似三角形的判定与性质得.设DE=a,则BC=CN=2a,EN=BN=BC+CN=4a,最后根据比例线段可得答案.
【解答】解:(1)∵BE⊥FN,
∴∠BHF=90°,
∴∠HFB+∠HBF=90°.
在矩形ABCD中,∠ABC=∠A=∠BCD=90°,
∴∠HFB+∠N=90°,∠NCG=90°,
∴∠HBF=∠N,∠A=∠NCG,
∴△ABE∽△CNG.
(2)如图1,连接EG,
∵△ABE∽△CNG,
∴AB=CN,
∴△ABE≌△CNG,
∴AE=CG,
∵E为AD边中点,
∴DE=AE=CG.
∵FN是BE的中垂线,
∴EG=BG.
∵∠D=∠BCD=90°,
∴Rt△DEG≌Rt△CGB(HL),
∴∠DGE=∠CBG.
∵∠CBG+∠CGB=90°,
∴∠DGE+∠CGB=90°,
∴∠BGE=90°,
∴△BGE是等腰直角三角形,
∴∠EBG=45°.
(3)法1:如图2,连接EN交CD于点P,
∵FN是BE的中垂线,
∴EN=BN,
∵E为AD边中点,
∴,
∵AD∥BC,
∴△DEP∽△CNP,
∴.
设DE=a,则BC=CN=2a,EN=BN=BC+CN=4a,
∴,
∴,
∴,
∴.
法2:(略解)由△CNG∽△BNF得.
易证得△MED≌△FEA,
∴DM=AF,ME=FE.
设CG=a,则ME=FE=BF=2a,MF=MG=4a,
∴CM=5a,
∵MC+BF=7a,即2AB=7a,
∴,,
∴,
∴,
∴.
法3:(如图,略解)作GK⊥AB于点K,
易证得△MFG∽△GFB,
∴,
∴.
设FK=BK=a,则EF=BF=2a,,
在Rt△GKF中,,
∴,
∴,
∴,
∴,
∴.
38.【分析】(1)根据平行线的性质得出∠ABD=∠BDC,根据圆周角定理得出∠ABD=∠ECG,即可证得结论;
(2)根据勾股定理求得BD=10,
①连接EF,根据圆周角定理得出∠CEF=∠BCD=90°,∠EFC=∠CBD.即可得出sin∠EFC=sin∠CBD,得出,根据勾股定理得到CF=6,即可求得CE的长;
②分三种情况讨论,由等腰三角形的性质及相似三角形的性质可得出答案.
【解答】(1)证明:∵AB∥CD.
∴∠ABD=∠BDC,
∵∠ABD=∠ECG,
∴∠ECG=∠BDC.
(2)解:①∵AB=CD=6,AD=BC=8,
∴BD10,
如图1,连接EF,则∠CEF=∠BCD=90°,
∵∠EFC=∠CBD.
∴sin∠EFC=sin∠CBD,
∴,
∴CF6,
∴CE.
②分三种情况:Ⅰ、当EG=CG时,∠GEC=∠GCE=∠ABD=∠BDC.
∴E与D重合,CG=DG,
∴G为BD的中点,
∴CGBD=5.
Ⅱ、当GE=CE时,
∴∠EGC=∠ECG=∠ABD=∠GDC,
∴CG=CD=6.
Ⅲ、如图2,当CG=CE时,
∴∠GEC=∠EGC=∠BFC=∠GCD,
∴CD=DG=6,
∴BG=BF=4,
∴FC4,
∵BF∥CD,
∴△FBG∽△CDG,
∴,
∴,
∴CG,
综上所述,CG的长为5或6或.
故答案为:5或6或.
39.【分析】(1)根据平行线的性质得∠AFC=∠EAF=70°,由圆周角定理得∠AFC=∠ADC=70°,∠ADF=90°,即可得出答案;
(2)分三种情况:①AD=CD时,②AC=AD时,③AC=CD时,根据相似三角形的判定和性质分别求解即可;
(3)连接AI、FI,连接DO并延长交⊙O于G,连接CG,根据AF是⊙O的直径,△AEF的外心I恰好落在⊙O上得出∠AIF=90°,由圆周角定理得∠AEF∠AIF=45°,根据平行线的性质以及直角三角形的性质可得∠CAB=∠CGD=45°,可得出△DCG是等腰直角三角形,即可得出答案.
【解答】解:(1)∵AE∥BC,∠EAF=70°,
∴∠AFC=∠EAF=70°,
∵∠ACB=90°,
∴AF是⊙O的直径,
∴∠ADF=90°,
∴∠ADC=∠AFC=70°,
∴∠CDF=∠ADF﹣∠ADC=90°﹣70°=20°;
(2)∵∠ACB=90°,AC=4,BC=6,
∴AB2,
当△ACD为等腰三角形时,分三种情况:
①AD=CD时,
∵AD=CD,
∴∠CAD=∠ACD,
∵∠ACB=90°,
∴∠CAD+∠B=∠ACD+∠BCD=90°,
∴∠B=∠BCD,
∴CD=BD,
∵AD=CD,
∴AD=BDAB,
∵∠B=∠B,∠ACB=∠FDB=90°,
∴△ACB∽△FDB,
∴,即,
∴BF,
∴CF=BC﹣BF=6;
②AC=AD时,
∵AC=AD=4,
∴∠ADC=∠ACD,BD=24,
∵∠ACB=∠ADF=90°,
∴∠ADC+∠CDF=∠ACD+∠BCD=90°,
∴∠CDF=∠BCD,
∴CF=DF,
∵∠B=∠B,∠ACB=∠FDB=90°,
∴△ACB∽△FDB,
∴,即,
∴DF,
∴CF=DF;
③AC=CD时,
∵AC=CD=4,
∴∠ADC=∠CAD,
∵∠ACB=∠ADF=90°,
∴∠ADC+∠CDF=∠CAD+∠B=90°,
∴∠CDF=∠B,
∵∠DCF=∠BCD,
∴△DCF∽△BCD,
∴,即,
∴CF;
综上,CF的长为或或;
(3)连接AI、FI,连接DO并延长交⊙O于G,连接CG,
∵AF是⊙O的直径,△AEF的外心I恰好落在⊙O上,
∴∠AIF=90°,
∴∠AEF∠AIF=45°,
∵AE∥BC,
∴∠EFB=∠AEF=45°,
∵∠BDF=90°,
∴∠B=45°,
∵∠ACB=90°,
∴∠CAB=45°,
∴∠CGD=45°,
∵GD是⊙O的直径,
∴∠DCG=90°,DG=AF,
∴△DCG是等腰直角三角形,
∴,
∴,
∵k,
∴k.
40.【分析】(1)①根据菱形的性质和全等三角形的判定证得△PDF≌△HBF,再根据全等三角形的性质即可解答;
②根据题意,分别令x=0,y=0即可求解;
(2)分BF∥QH和FQ∥BH两种情况讨论解答即可;
(3)连接QH.过点F作FK⊥BC于点K,FJ⊥AB于点J,过点Q作QT⊥BC于T.则S△FQH=S△ABC﹣S△QBH﹣S△AQF﹣S△CFH,由二次函数求最值的方法求解即可.
【解答】解:(1)①结论:PF=PH.理由如下:
∵ABCD是菱形,
∴AD∥BC,AD=BC,
∵PD=BH,
∴∠PAF=∠FCH,AP=CH,
又∵∠AFP=∠HFC,
∴△AFP≌△HFC(AAS),
∴PF=FH;
②当x=0代入y=﹣2x+12得y=12,即AD=12,
当y=0代入y=﹣2x+12,得x=6,即MN=6,
∵AM=5BN,AB=AD=12,
∴5BN+BN+6=12,
∴BN=1;
(2)①当FQ∥BH时,如图2,
∵AF=FC,
∴AQ=QB,
∴QF是△ABC的中位线,
∴AQ=6,而AM=5,
∴MQ=1,
∴x=1,y=10,
∴AP=10,QF=6,
∵AP∥QF,
∴△AEP∽△QEF,
∴AE:EF=10:6=5:3,
∴AE:EC=5:11;
②当FH∥BQ时,如图2,
∵AP∥BC,
∴ABHP是平行四边形,
∴12﹣y=y,y=6 代入得x=3,
∴AQ=8,
∵PF=6,△AQE∽△PFE,
∴AE:EF=4:3,
∴AE:EC=4:10=2:5;
(3)连接QH.过点F作FK⊥BC于点K,FJ⊥AB于点J,过点Q作QT⊥BC于T.
由题意,CH=AP=﹣2x+12,BQ=7﹣x,AQ=5+x,
∵AB=BC,∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=BC=12,
∴FA=FC=6,
∴QT(7﹣x),FJ=FK6=3,
∵S△FQH=S△ABC﹣S△BQH﹣S△AQF﹣S△FCH
=362x(7﹣x)(﹣2x+12)×3(5+x)×3
(x﹣2)2,
∵0,
∴x=2时,△FQH的面积最小,最小值为.
同课章节目录
