湖南省岳阳市云溪区2024-2025学年高三上学期11月期中考试 数学(含答案)
文档属性
| 名称 | 湖南省岳阳市云溪区2024-2025学年高三上学期11月期中考试 数学(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-20 15:35:00 | ||
图片预览




文档简介
1
2024年高三上学期数学期中考试试卷
一、单选题(共4小题,每小题5分,总分40分)
1. 设集合,,则()
A. B.
C. D.
2. 复数的共轭复数在复平面上对应的点位于()
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
3. 为了让自己渐渐养成爱运动的习惯,小张11月1日运动了2分钟,从第二天开始,每天运动的时长比前一天多2分钟,则从11月1日到11月15日,小张运动的总时长为()
A. 3.5小时 B. 246分钟
C. 4小时 D. 250分钟
4. 已知同一平面内的单位向量满足,则()
A. B. C. D.
5. 已知函数的定义域为,设的导函数是,且恒成立,则()
A B.
C. D.
6. 将函数图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数的图象.若的图象关于点对称,则的最小值为()
A. B. C. D.
7. 已知定义域为为奇函数,为偶函数,若当时,,则()
A. B. 0 C. 1 D. e
8. 已知可导函数的定义域为,为奇函数,设是的导函数,若为奇函数,且,则()
A. -1012 B. -506
C. 506 D. 1012
二、多选题(共4小题,每小题5分,总分20分)
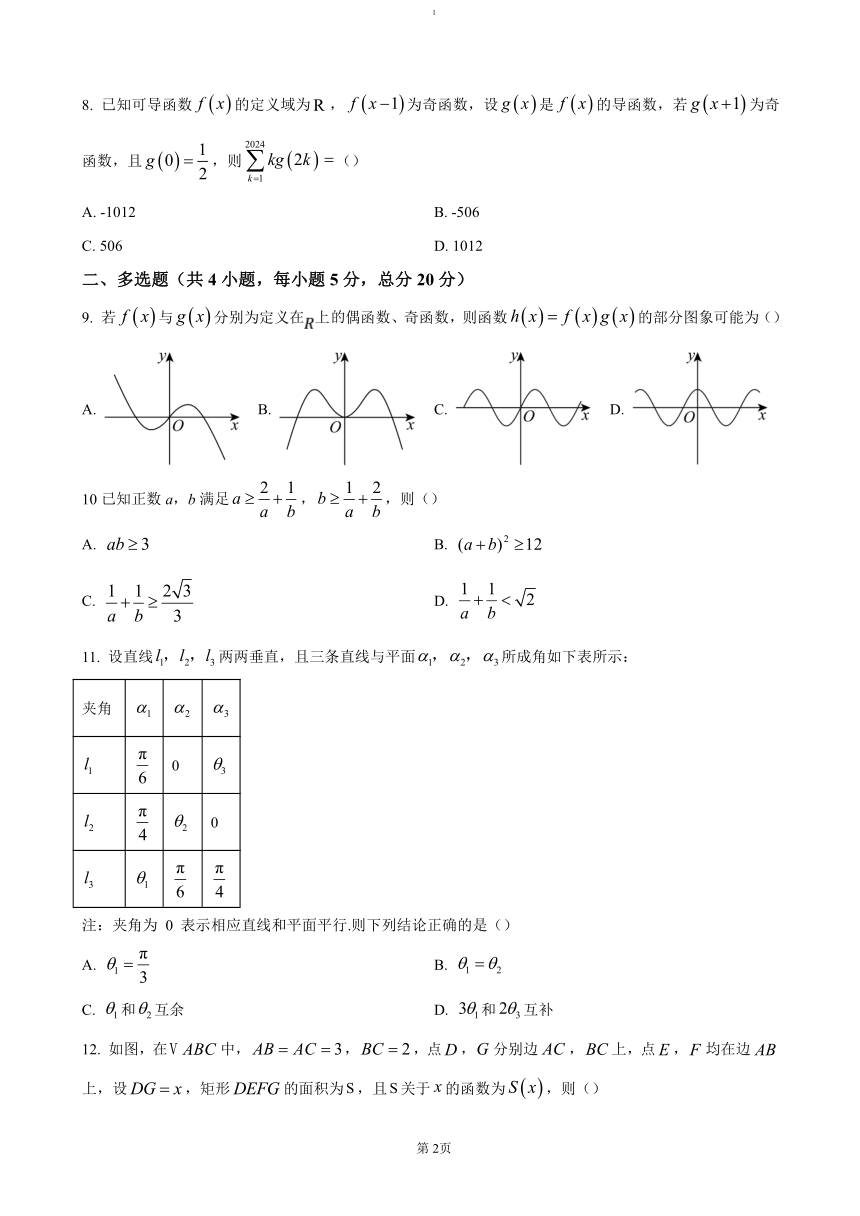
9. 若与分别为定义在上偶函数、奇函数,则函数的部分图象可能为()
A. B. C. D.
10已知正数a,b满足,,则()
A. B.
C. D.
11. 设直线两两垂直,且三条直线与平面所成角如下表所示:
夹角
0
0
注:夹角为 0 表示相应直线和平面平行.则下列结论正确的是()
A. B.
C. 和互余 D. 和互补
12. 如图,在中,,,点,分别边,上,点,均在边上,设,矩形的面积为,且关于的函数为,则()
A. 内切圆的半径为 B.
C. 先增后减 D. 的最大值为
三、填空题(共4小题,每小题5分,总分20分)
13. 已知,,,则________.
14. 已知圆,点在直线上运动,以线段为直径的圆与圆相交于两点,则直线过定点______.
15. 将一副三角板按如图所示的位置拼接:含角的三角板的长直角边与含角的三角板的斜边恰好重合.与相交于点.若,则___________.
16. 某同学喜爱篮球和跑步运动.在暑假期间,该同学下午去打篮球的概率为.若该同学下午去打篮球,则晚上一定去跑步;若下午不去打篮球,则晚上去跑步的概率为.已知该同学在某天晚上去跑步,则下午打过篮球的概率为__________.
四、解答题(共4小题,总分70分)
17. 锐角的三个内角是,满足,的外接圆的圆心为,半径是 1 .
(1)求角的大小及的值;
(2)求的取值范围.
18. 设数列的前n项和为,,.
(1)求的通项公式;
(2)若,求数列的前n项和.
19. 甲同学现参加一项答题活动,其每轮答题答对的概率均为,且每轮答题结果相互独立.若每轮答题答对得5分,答错得0分,记第轮答题后甲同学的总得分为,其中.
(1)求;
(2)若乙同学也参加该答题活动,其每轮答题答对的概率均为,并选择另一种答题方式答题:从第1轮答题开始,若本轮答对,则得20分,并继续答题;若本轮答错,则得0分,并终止答题,记乙同学的总得分为.证明:当时,.
20. 已知椭圆的中心在原点,焦点在轴上,离心率为,以的四个顶点为顶点的平行四边形的面积为,直线与椭圆交于两点(不与椭圆的顶点重合).
(1)求的标准方程;
(2)若以为直径的圆经过原点,求证:直线与圆相切;
(3)若动直线过点,点关于轴的对称点为,直线与轴的交点为,求面积的最大值.
21. 若存在有限个,使得,且不是偶函数,则称为“缺陷偶函数”,称为的偶点.
(1)证明:为“缺陷偶函数”,且偶点唯一.
(2)对任意x,,函数,都满足.
①若“缺陷偶函数”,证明:函数有2个极值点.
②若,证明:当时,.
参考数据:,.
2024年高三上学期数学期中考试试卷
一、单选题(共4小题,每小题5分,总分40分)
1.
【答案】B
2.
【答案】D
3.
【答案】C
4.
【答案】D
5.
【答案】C
6.
【答案】A
7.
【答案】C
8.
【答案】D
二、多选题(共4小题,每小题5分,总分20分)
9.
【答案】AC
10.
【答案】ABD
11.
【答案】CD
12.
【答案】ACD
三、填空题(共4小题,每小题5分,总分20分)
13.【答案】
14.【答案】
15.
【答案】
16.【答案】
四、解答题(共4小题,总分70分)
17.
【小问1详解】
(1) 由,
得,
;
由正弦定理得,
即,又锐角中,,
,
由圆周角定理可得,,
又,
.
【小问2详解】
.
是锐角三角形,
,
,又在上单调递减,
所以,即.
故的取值范围是.
18.
【小问1详解】
由,得,
两式相减得,即.
因为,所以,得,满足.
所以是首项为8,公比为4的等比数列,,.
【小问2详解】
因为,
所以.
所以.
故数列的前n项和为,.
19.
【小问1详解】
设,故,
∴,
故;
【小问2详解】
由(1)知,记乙同学的答题次数为,且的所有可能取值为,
且,
∴,
且,
,
∴当时,.
20.
【分析】(1)根据面积和离心率得和,即可求解,
(2)联立直线与椭圆方程得韦达定理,根据,得,代入化简可得,根据点到直线距离公式即可求证,
(3)联立直线与椭圆方程得到韦达定理,根据三点共线可得,即,化简可得为定点,即可利用三角形面积关系得表达式,结合基本不等式求解最值.
【小问1详解】
设椭圆的长半轴长为,短半轴长为,半焦距为 .
由已知,,即,又,
由可得: ,
因为的焦点在轴上,所以的标准方程是
【小问2详解】
当直线有斜率时,设直线的方程为,
以为直径的圆经过原点,即,
设,所以,
联立方程,得,即,
,
化简得,
设到直线距离为,则,
所以直线与圆相切.
当直线无斜率时,设直线方程为,与椭圆方程联立可得,,
由于为直径的圆经过原点,故,
故圆的圆心到直线的距离,故直线与圆相切.
综上,直线与圆相切.
【小问3详解】
设直线的方程为,代入椭圆方程,得,
即 . 设点,
则 .
因为点关于轴对称,则. 设点,
因为三点共线,则,即,
即,即,得
所以点为定点,,
.
令,则 .
当且仅当时取等号,所以的面积的最大值为 .
21.
【分析】(1)根据,即可解方程求解,
(2)①根据,取,可得,即可对求导,根据导函数的正负确定函数单调性,结合极值定义求证,②利用放缩法,先证明故,构造,求导,确定函数的最值即可求解.
【小问1详解】
由可得,
由可得,解得,
所以为“缺陷偶函数”,且偶点唯一,且为0,
【小问2详解】
由可得对任意x,,恒成立,
所以存在常数,使得,
令,则,且,
解得,
①,则,
由于是“缺陷偶函数”,故,
即,即,
则,得,
,
由于,所以有两个不相等的实数根,不妨设,
当或时,,单调递增,
当时,,单调递减,
所以有两个极值点.
②若,即,则,故,
当时,要证,只需要证. ,
因,故,
只需证,
令,
当单调递减,当单调递增,
故,
所以,从而,故,
时,得证.
PAGE
第12页
2024年高三上学期数学期中考试试卷
一、单选题(共4小题,每小题5分,总分40分)
1. 设集合,,则()
A. B.
C. D.
2. 复数的共轭复数在复平面上对应的点位于()
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
3. 为了让自己渐渐养成爱运动的习惯,小张11月1日运动了2分钟,从第二天开始,每天运动的时长比前一天多2分钟,则从11月1日到11月15日,小张运动的总时长为()
A. 3.5小时 B. 246分钟
C. 4小时 D. 250分钟
4. 已知同一平面内的单位向量满足,则()
A. B. C. D.
5. 已知函数的定义域为,设的导函数是,且恒成立,则()
A B.
C. D.
6. 将函数图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数的图象.若的图象关于点对称,则的最小值为()
A. B. C. D.
7. 已知定义域为为奇函数,为偶函数,若当时,,则()
A. B. 0 C. 1 D. e
8. 已知可导函数的定义域为,为奇函数,设是的导函数,若为奇函数,且,则()
A. -1012 B. -506
C. 506 D. 1012
二、多选题(共4小题,每小题5分,总分20分)
9. 若与分别为定义在上偶函数、奇函数,则函数的部分图象可能为()
A. B. C. D.
10已知正数a,b满足,,则()
A. B.
C. D.
11. 设直线两两垂直,且三条直线与平面所成角如下表所示:
夹角
0
0
注:夹角为 0 表示相应直线和平面平行.则下列结论正确的是()
A. B.
C. 和互余 D. 和互补
12. 如图,在中,,,点,分别边,上,点,均在边上,设,矩形的面积为,且关于的函数为,则()
A. 内切圆的半径为 B.
C. 先增后减 D. 的最大值为
三、填空题(共4小题,每小题5分,总分20分)
13. 已知,,,则________.
14. 已知圆,点在直线上运动,以线段为直径的圆与圆相交于两点,则直线过定点______.
15. 将一副三角板按如图所示的位置拼接:含角的三角板的长直角边与含角的三角板的斜边恰好重合.与相交于点.若,则___________.
16. 某同学喜爱篮球和跑步运动.在暑假期间,该同学下午去打篮球的概率为.若该同学下午去打篮球,则晚上一定去跑步;若下午不去打篮球,则晚上去跑步的概率为.已知该同学在某天晚上去跑步,则下午打过篮球的概率为__________.
四、解答题(共4小题,总分70分)
17. 锐角的三个内角是,满足,的外接圆的圆心为,半径是 1 .
(1)求角的大小及的值;
(2)求的取值范围.
18. 设数列的前n项和为,,.
(1)求的通项公式;
(2)若,求数列的前n项和.
19. 甲同学现参加一项答题活动,其每轮答题答对的概率均为,且每轮答题结果相互独立.若每轮答题答对得5分,答错得0分,记第轮答题后甲同学的总得分为,其中.
(1)求;
(2)若乙同学也参加该答题活动,其每轮答题答对的概率均为,并选择另一种答题方式答题:从第1轮答题开始,若本轮答对,则得20分,并继续答题;若本轮答错,则得0分,并终止答题,记乙同学的总得分为.证明:当时,.
20. 已知椭圆的中心在原点,焦点在轴上,离心率为,以的四个顶点为顶点的平行四边形的面积为,直线与椭圆交于两点(不与椭圆的顶点重合).
(1)求的标准方程;
(2)若以为直径的圆经过原点,求证:直线与圆相切;
(3)若动直线过点,点关于轴的对称点为,直线与轴的交点为,求面积的最大值.
21. 若存在有限个,使得,且不是偶函数,则称为“缺陷偶函数”,称为的偶点.
(1)证明:为“缺陷偶函数”,且偶点唯一.
(2)对任意x,,函数,都满足.
①若“缺陷偶函数”,证明:函数有2个极值点.
②若,证明:当时,.
参考数据:,.
2024年高三上学期数学期中考试试卷
一、单选题(共4小题,每小题5分,总分40分)
1.
【答案】B
2.
【答案】D
3.
【答案】C
4.
【答案】D
5.
【答案】C
6.
【答案】A
7.
【答案】C
8.
【答案】D
二、多选题(共4小题,每小题5分,总分20分)
9.
【答案】AC
10.
【答案】ABD
11.
【答案】CD
12.
【答案】ACD
三、填空题(共4小题,每小题5分,总分20分)
13.【答案】
14.【答案】
15.
【答案】
16.【答案】
四、解答题(共4小题,总分70分)
17.
【小问1详解】
(1) 由,
得,
;
由正弦定理得,
即,又锐角中,,
,
由圆周角定理可得,,
又,
.
【小问2详解】
.
是锐角三角形,
,
,又在上单调递减,
所以,即.
故的取值范围是.
18.
【小问1详解】
由,得,
两式相减得,即.
因为,所以,得,满足.
所以是首项为8,公比为4的等比数列,,.
【小问2详解】
因为,
所以.
所以.
故数列的前n项和为,.
19.
【小问1详解】
设,故,
∴,
故;
【小问2详解】
由(1)知,记乙同学的答题次数为,且的所有可能取值为,
且,
∴,
且,
,
∴当时,.
20.
【分析】(1)根据面积和离心率得和,即可求解,
(2)联立直线与椭圆方程得韦达定理,根据,得,代入化简可得,根据点到直线距离公式即可求证,
(3)联立直线与椭圆方程得到韦达定理,根据三点共线可得,即,化简可得为定点,即可利用三角形面积关系得表达式,结合基本不等式求解最值.
【小问1详解】
设椭圆的长半轴长为,短半轴长为,半焦距为 .
由已知,,即,又,
由可得: ,
因为的焦点在轴上,所以的标准方程是
【小问2详解】
当直线有斜率时,设直线的方程为,
以为直径的圆经过原点,即,
设,所以,
联立方程,得,即,
,
化简得,
设到直线距离为,则,
所以直线与圆相切.
当直线无斜率时,设直线方程为,与椭圆方程联立可得,,
由于为直径的圆经过原点,故,
故圆的圆心到直线的距离,故直线与圆相切.
综上,直线与圆相切.
【小问3详解】
设直线的方程为,代入椭圆方程,得,
即 . 设点,
则 .
因为点关于轴对称,则. 设点,
因为三点共线,则,即,
即,即,得
所以点为定点,,
.
令,则 .
当且仅当时取等号,所以的面积的最大值为 .
21.
【分析】(1)根据,即可解方程求解,
(2)①根据,取,可得,即可对求导,根据导函数的正负确定函数单调性,结合极值定义求证,②利用放缩法,先证明故,构造,求导,确定函数的最值即可求解.
【小问1详解】
由可得,
由可得,解得,
所以为“缺陷偶函数”,且偶点唯一,且为0,
【小问2详解】
由可得对任意x,,恒成立,
所以存在常数,使得,
令,则,且,
解得,
①,则,
由于是“缺陷偶函数”,故,
即,即,
则,得,
,
由于,所以有两个不相等的实数根,不妨设,
当或时,,单调递增,
当时,,单调递减,
所以有两个极值点.
②若,即,则,故,
当时,要证,只需要证. ,
因,故,
只需证,
令,
当单调递减,当单调递增,
故,
所以,从而,故,
时,得证.
PAGE
第12页
同课章节目录
