山东省宁津县育新中学2016届九年级下学期第一次月考数学试题
文档属性
| 名称 | 山东省宁津县育新中学2016届九年级下学期第一次月考数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 222.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-07 00:00:00 | ||
图片预览


文档简介
育新中学初三数学第一次月考试题
满分120分,时间120分钟
一、选择题(每小题3分,共36分)
一、选择题(本大题共12小题,每小题3分,满分36分,)
1. 3的倒数是【 】
A. B. C.3 D.﹣3
2. 下列大学的校徽图案是轴对称图形的是( )
A.清华大学 B.北京大学 C.中国人民大学 D.浙江大学
3. 下面的几何体中,主视图为三角形的是( )
A. B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
4. 餐桌边的一蔬一饭,舌尖上的一饮一酌 ( http: / / www.21cnjy.com ),实属来之不易,舌尖上的浪费让人触目惊心.据统计,中国每年浪费的食物总量折合粮食约500亿千克,这个数据用科学记数法表示为( )
A.5×1010千克 B.50×109千克 C.5×109千克 D.0.5×1011千克
5. 如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
A.35° B.45° C.55° D.65°
6. 一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集( ) 第5题图
A.x>1 B x≥1 C. x>3 D.x≥3
7. 如图,在 ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF: FC等于( )
A.3:2 B.3:1 C.1:1 D.1:2
8. 春节期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )
A.2小时 B.2.2小时
C.2.25小时 D.2.4小时
9.为了调查某小区居民的用水情况,随机抽查了若干户家庭的月用水量,结果如下表:
月用水量(吨) 3 4 5 8
户 数 2 3 4 1
则关于这若干户家庭的月用水量,下列说法错误的是( )
A.众数是4 B.平均数是4.6
C.调查了10户家庭的月用水量 D.中位数是4.5
10. 用直尺和圆规作一个以线段为边的菱形,作图痕迹如图所示,能得到四边形是菱形的依据是( )
A.一组邻边相等的四边形是菱形 B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
11.某工厂现在平均每天比原计划多生产50 ( http: / / www.21cnjy.com )台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )
A. B. C. D.
12. 下列图形中,阴影部分面积最大的是:( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二、填空题(本大题共5小题,每小题4分,满分20分,)
13. 因式分解:x3﹣5x2+6x= .
14. 若实数m,n满足 .则 = 。
15.一副量角器与一块含30°锐角的三角板 ( http: / / www.21cnjy.com )如图所示放置,三角板的顶点C恰好落在量角器的直径MN上,顶点A,B恰好落在量角器的圆弧上,且AB∥MN. 若AB=8,则量角器的直径MN= .
16.若α、β是一元二次方程的两根,则=
17.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x ﹣1 0 1 3
y ﹣1 3 5 3
下列结论:
(1)ac<0; (2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的的是_________;(填序号)
三.解答题(共64分)
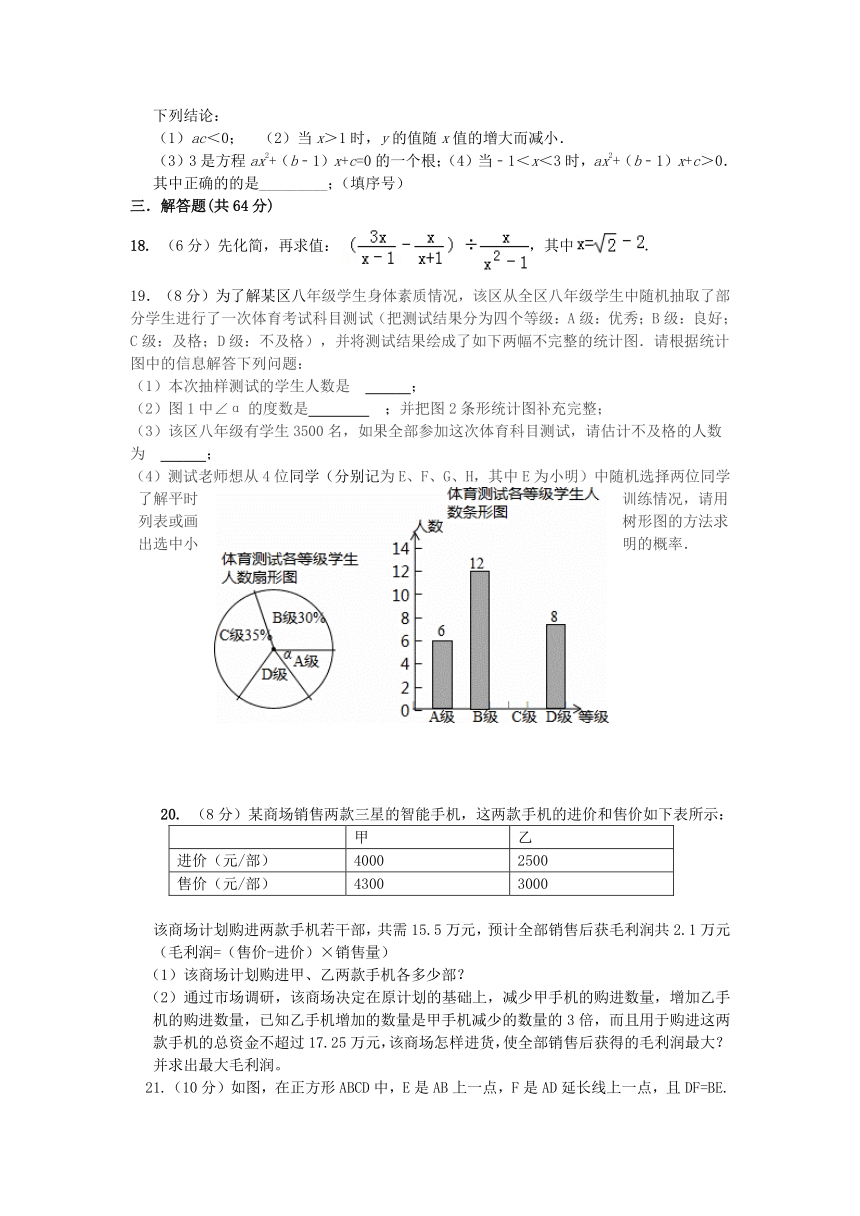
18. (6分)先化简,再求值:,其中.
19.(8分)为了解某区八 ( http: / / www.21cnjy.com )年级学生身体素质情况,该区从全区八年级学生中随机抽取了部分学生进行了一次体育考试科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)图1中∠α的度数是 ;并把图2条形统计图补充完整;
(3)该区八年级有学生3500名,如果全部参加这次体育科目测试,请估计不及格的人数为 ;
(4)测试老师想从4位同学(分别记 ( http: / / www.21cnjy.com )为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
20. (8分)某商场销售两款三星的智能手机,这两款手机的进价和售价如下表所示:
甲 乙
进价(元/部) 4000 2500
售价(元/部) 4300 3000
该商场计划购进两款手机若干部,共需15.5万元,预计全部销售后获毛利润共2.1万元(毛利润=(售价-进价)×销售量)
(1)该商场计划购进甲、乙两款手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲手机的购进数量,增加乙手机的购进数量,已知乙手机增加的数量是甲手机减少的数量的3倍,而且用于购进这两款手机的总资金不超过17.25万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润。
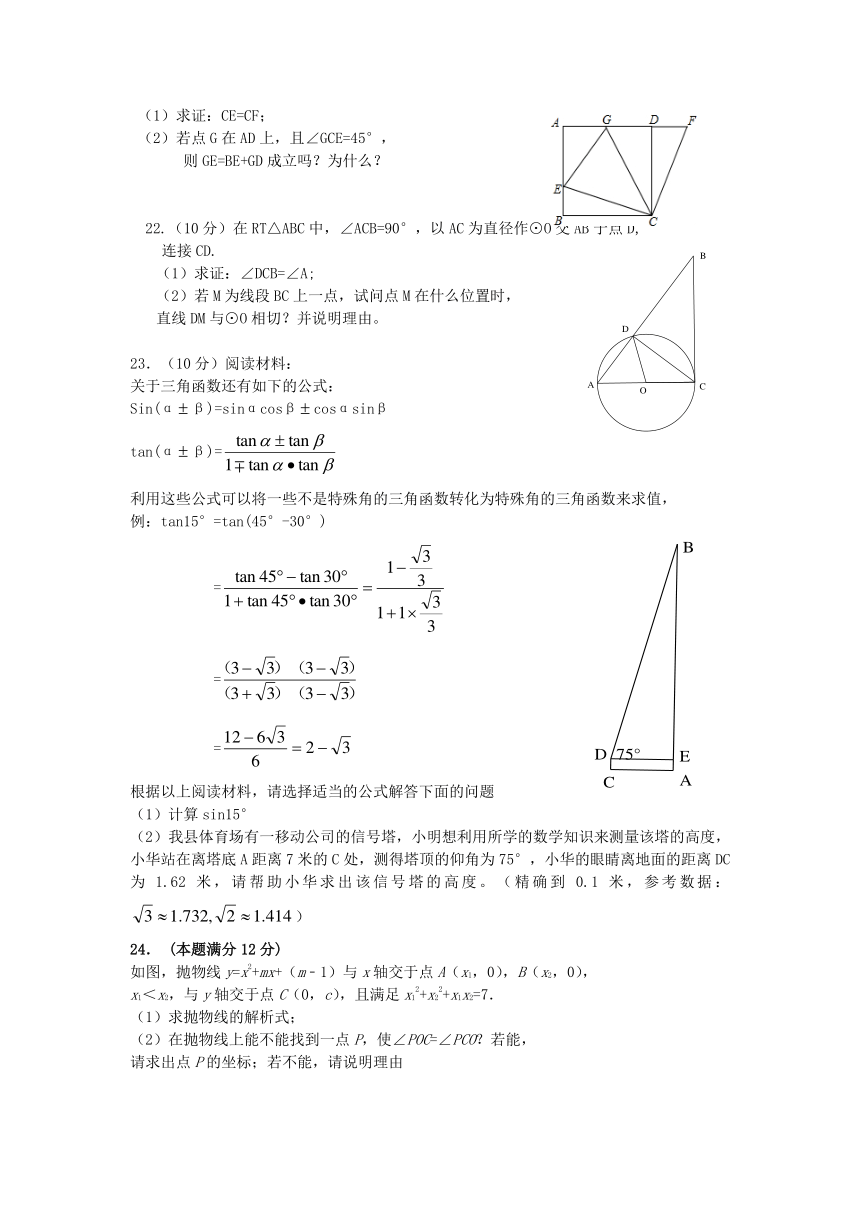
21.(10分)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,
则GE=BE+GD成立吗?为什么?
22.(10分)在RT△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,
连接CD.
(1)求证:∠DCB=∠A;
(2)若M为线段BC上一点,试问点M在什么位置时,
直线DM与⊙O相切?并说明理由。
23.(10分)阅读材料:
关于三角函数还有如下的公式:
Sin(αβ)=sinαcosβcosαsinβ
tan(αβ)=
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,
例:tan15°=tan(45°-30°)
=
=
=
根据以上阅读材料,请选择适当的公式解答下面的问题
(1)计算sin15°
(2)我县体育场有一移动公司的信号塔,小明想利用所学的数学知识来测量该塔的高度,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出该信号塔的高度。(精确到0.1米,参考数据:)
24. (本题满分12分)
如图,抛物线y=x2+mx+(m﹣1)与x轴交于点A(x1,0),B(x2,0),
x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,
请求出点P的坐标;若不能,请说明理由
初三月考数学答案
选择题(每题3分)
1—5 DBCAA 6-10 CDCAB 11-12 AC
二、填空题(每题4分)
13、X(X-2)(X-3) 14、 15、10 16、4 17、(1)(3)(4)
三、解答题
18、 化简:2X+4 …………………………………………………….. 4分
结果:2 …………………………………………………….. 6分
19、(1)40 …………………………………………………….. 2分
(2)54°………….. 3分 补图…………….. 4分
(3)1100 …………………………………………………….. 6分
(4) …………………………………………………….. 8分
20、解:(1)设商场计划购进甲种手机x部,乙种手机y部,由题意,得
…………………………………………………….. 2分
解得:x=
答:商场计划购进甲种手机20部,乙种手机30部;………………………….. 3分
(2)设甲种手机减少a部,则乙种 ( http: / / www.21cnjy.com )手机增加3a部,由题意,得
0.4(20-a)+0.25(30+3a)≤17.25,
解得:a≤5. ……………………………………………………. 5分
设全部销售后获得的毛利润为W万元,由题意,得
W=0.03(20-a)+0.05(30+3a)
=0.12a+2.1…
∵k=0.12>0,
∴W随a的增大而增大, ( http: / / www.21cnjy.com )
∴当a=5时,W最大=2.7.
答:当该商场购进甲种手机15部,乙种手机45部时,全部销售后获利最大.最大毛利润为2.7万元. …………………………………………………….. 8分
21、解:(1)证明:在正方形ABCD中,
∴AB=BC=CD=AD,∠A=∠B=∠BCD=∠ADC.…………………………………………………….. 1分
∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF(SAS), ………………………………………………….. 3分
∴CE=CF. …………………………………………………….. 4分
(2)GE=BE+GD …………………………………………………….. 5分
∵△CBE≌△CDF,
∴∠BCE=∠DCF. …………………………………………………….. 6分
∵∠GCE=45°,
∴∠BCE+∠GCD=45°
∴∠GCD+∠DCF=∠GCF=45°, …………………………………………………….. 8分
∴∠GCF=∠GCE,CG=CG,
∴△GCE≌△GCF,
∴GE=GF,
∵GF=GD+DF,
∴GE=GD+DF,
∴GE=GD+BE. …………………………………………………….. 10分
22、
证明:
∵AC为⊙O的直径
∴∠ADC=90°
∴∠A+∠ACD=90°
∴∠DCB=∠A …………………………………………….. 2分
∵△ABC为直角三角形
∴ ∠DCB+∠ACD=90° ………………………………………….. 4分
解:当M为BC的中点时。
∵当DM为⊙O的切线时,
∴DM=MC
∴∠MDC=∠MCD ………………………………………….. 7分
∵∠BDC=90°
∴∠MDC+∠BDM=∠MCD+∠B=90°
∴∠BDM=∠B
∴MD=MB ………………………………………….. 9分
∴MD=MB=MC
∴M为BC的中点。 ………………………………………….. 10分
23、
解:(1)
………………………………………….. 4分
在RT△BDE中,
DE=AC=7
∠BDE=75°
tan∠BDE=
∴BE=DEtan∠BDE
=DEtan75° ………………………………………….. 6分
∵tan75°=tan(45°+30°)
………………………………………….. 8分
∴BE=7(2+)≈26.12
∴信号塔AB的高度≈26.12+1.62≈27.7(米)……………….10分
答:该信号塔AB的高度约为27.7米。
24、
.(本题12分)
解(1)依题意:x1+x2=﹣m,x1x2=m﹣1,
∵x1+x2+x1x2=7,
∴(x1+x2)2﹣x1x2=7,
∴(﹣m)2﹣(m﹣1)=7,
即m2﹣m﹣6=0,
解得m1=﹣2,m2=3,…………………3分
∵c=m﹣1<0,∴m=3不合题意
∴m=﹣2
抛物线的解析式是y=x2﹣2x﹣3;…………………5分
( http: / / www.21cnjy.com )
(2)能 …………………6分
如图,设p是抛物线上的一点,连接PO,PC,过点P作y轴的垂线,垂足为D.
若∠POC=∠PCO
则PD应是线段OC的垂直平分线 …………………8分
∵C的坐标为(0,﹣3)
∴D的坐标为(0,﹣)
∴P的纵坐标应是﹣
令x2﹣2x﹣3=,解得,x1=,x2= …………………10分
因此所求点P的坐标是(,﹣),(,﹣)…………………12分
(第10题)
(第15题)
满分120分,时间120分钟
一、选择题(每小题3分,共36分)
一、选择题(本大题共12小题,每小题3分,满分36分,)
1. 3的倒数是【 】
A. B. C.3 D.﹣3
2. 下列大学的校徽图案是轴对称图形的是( )
A.清华大学 B.北京大学 C.中国人民大学 D.浙江大学
3. 下面的几何体中,主视图为三角形的是( )
A. B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
4. 餐桌边的一蔬一饭,舌尖上的一饮一酌 ( http: / / www.21cnjy.com ),实属来之不易,舌尖上的浪费让人触目惊心.据统计,中国每年浪费的食物总量折合粮食约500亿千克,这个数据用科学记数法表示为( )
A.5×1010千克 B.50×109千克 C.5×109千克 D.0.5×1011千克
5. 如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
A.35° B.45° C.55° D.65°
6. 一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集( ) 第5题图
A.x>1 B x≥1 C. x>3 D.x≥3
7. 如图,在 ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF: FC等于( )
A.3:2 B.3:1 C.1:1 D.1:2
8. 春节期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )
A.2小时 B.2.2小时
C.2.25小时 D.2.4小时
9.为了调查某小区居民的用水情况,随机抽查了若干户家庭的月用水量,结果如下表:
月用水量(吨) 3 4 5 8
户 数 2 3 4 1
则关于这若干户家庭的月用水量,下列说法错误的是( )
A.众数是4 B.平均数是4.6
C.调查了10户家庭的月用水量 D.中位数是4.5
10. 用直尺和圆规作一个以线段为边的菱形,作图痕迹如图所示,能得到四边形是菱形的依据是( )
A.一组邻边相等的四边形是菱形 B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
11.某工厂现在平均每天比原计划多生产50 ( http: / / www.21cnjy.com )台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )
A. B. C. D.
12. 下列图形中,阴影部分面积最大的是:( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二、填空题(本大题共5小题,每小题4分,满分20分,)
13. 因式分解:x3﹣5x2+6x= .
14. 若实数m,n满足 .则 = 。
15.一副量角器与一块含30°锐角的三角板 ( http: / / www.21cnjy.com )如图所示放置,三角板的顶点C恰好落在量角器的直径MN上,顶点A,B恰好落在量角器的圆弧上,且AB∥MN. 若AB=8,则量角器的直径MN= .
16.若α、β是一元二次方程的两根,则=
17.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x ﹣1 0 1 3
y ﹣1 3 5 3
下列结论:
(1)ac<0; (2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的的是_________;(填序号)
三.解答题(共64分)
18. (6分)先化简,再求值:,其中.
19.(8分)为了解某区八 ( http: / / www.21cnjy.com )年级学生身体素质情况,该区从全区八年级学生中随机抽取了部分学生进行了一次体育考试科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)图1中∠α的度数是 ;并把图2条形统计图补充完整;
(3)该区八年级有学生3500名,如果全部参加这次体育科目测试,请估计不及格的人数为 ;
(4)测试老师想从4位同学(分别记 ( http: / / www.21cnjy.com )为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
20. (8分)某商场销售两款三星的智能手机,这两款手机的进价和售价如下表所示:
甲 乙
进价(元/部) 4000 2500
售价(元/部) 4300 3000
该商场计划购进两款手机若干部,共需15.5万元,预计全部销售后获毛利润共2.1万元(毛利润=(售价-进价)×销售量)
(1)该商场计划购进甲、乙两款手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲手机的购进数量,增加乙手机的购进数量,已知乙手机增加的数量是甲手机减少的数量的3倍,而且用于购进这两款手机的总资金不超过17.25万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润。
21.(10分)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,
则GE=BE+GD成立吗?为什么?
22.(10分)在RT△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,
连接CD.
(1)求证:∠DCB=∠A;
(2)若M为线段BC上一点,试问点M在什么位置时,
直线DM与⊙O相切?并说明理由。
23.(10分)阅读材料:
关于三角函数还有如下的公式:
Sin(αβ)=sinαcosβcosαsinβ
tan(αβ)=
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,
例:tan15°=tan(45°-30°)
=
=
=
根据以上阅读材料,请选择适当的公式解答下面的问题
(1)计算sin15°
(2)我县体育场有一移动公司的信号塔,小明想利用所学的数学知识来测量该塔的高度,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出该信号塔的高度。(精确到0.1米,参考数据:)
24. (本题满分12分)
如图,抛物线y=x2+mx+(m﹣1)与x轴交于点A(x1,0),B(x2,0),
x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,
请求出点P的坐标;若不能,请说明理由
初三月考数学答案
选择题(每题3分)
1—5 DBCAA 6-10 CDCAB 11-12 AC
二、填空题(每题4分)
13、X(X-2)(X-3) 14、 15、10 16、4 17、(1)(3)(4)
三、解答题
18、 化简:2X+4 …………………………………………………….. 4分
结果:2 …………………………………………………….. 6分
19、(1)40 …………………………………………………….. 2分
(2)54°………….. 3分 补图…………….. 4分
(3)1100 …………………………………………………….. 6分
(4) …………………………………………………….. 8分
20、解:(1)设商场计划购进甲种手机x部,乙种手机y部,由题意,得
…………………………………………………….. 2分
解得:x=
答:商场计划购进甲种手机20部,乙种手机30部;………………………….. 3分
(2)设甲种手机减少a部,则乙种 ( http: / / www.21cnjy.com )手机增加3a部,由题意,得
0.4(20-a)+0.25(30+3a)≤17.25,
解得:a≤5. ……………………………………………………. 5分
设全部销售后获得的毛利润为W万元,由题意,得
W=0.03(20-a)+0.05(30+3a)
=0.12a+2.1…
∵k=0.12>0,
∴W随a的增大而增大, ( http: / / www.21cnjy.com )
∴当a=5时,W最大=2.7.
答:当该商场购进甲种手机15部,乙种手机45部时,全部销售后获利最大.最大毛利润为2.7万元. …………………………………………………….. 8分
21、解:(1)证明:在正方形ABCD中,
∴AB=BC=CD=AD,∠A=∠B=∠BCD=∠ADC.…………………………………………………….. 1分
∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF(SAS), ………………………………………………….. 3分
∴CE=CF. …………………………………………………….. 4分
(2)GE=BE+GD …………………………………………………….. 5分
∵△CBE≌△CDF,
∴∠BCE=∠DCF. …………………………………………………….. 6分
∵∠GCE=45°,
∴∠BCE+∠GCD=45°
∴∠GCD+∠DCF=∠GCF=45°, …………………………………………………….. 8分
∴∠GCF=∠GCE,CG=CG,
∴△GCE≌△GCF,
∴GE=GF,
∵GF=GD+DF,
∴GE=GD+DF,
∴GE=GD+BE. …………………………………………………….. 10分
22、
证明:
∵AC为⊙O的直径
∴∠ADC=90°
∴∠A+∠ACD=90°
∴∠DCB=∠A …………………………………………….. 2分
∵△ABC为直角三角形
∴ ∠DCB+∠ACD=90° ………………………………………….. 4分
解:当M为BC的中点时。
∵当DM为⊙O的切线时,
∴DM=MC
∴∠MDC=∠MCD ………………………………………….. 7分
∵∠BDC=90°
∴∠MDC+∠BDM=∠MCD+∠B=90°
∴∠BDM=∠B
∴MD=MB ………………………………………….. 9分
∴MD=MB=MC
∴M为BC的中点。 ………………………………………….. 10分
23、
解:(1)
………………………………………….. 4分
在RT△BDE中,
DE=AC=7
∠BDE=75°
tan∠BDE=
∴BE=DEtan∠BDE
=DEtan75° ………………………………………….. 6分
∵tan75°=tan(45°+30°)
………………………………………….. 8分
∴BE=7(2+)≈26.12
∴信号塔AB的高度≈26.12+1.62≈27.7(米)……………….10分
答:该信号塔AB的高度约为27.7米。
24、
.(本题12分)
解(1)依题意:x1+x2=﹣m,x1x2=m﹣1,
∵x1+x2+x1x2=7,
∴(x1+x2)2﹣x1x2=7,
∴(﹣m)2﹣(m﹣1)=7,
即m2﹣m﹣6=0,
解得m1=﹣2,m2=3,…………………3分
∵c=m﹣1<0,∴m=3不合题意
∴m=﹣2
抛物线的解析式是y=x2﹣2x﹣3;…………………5分
( http: / / www.21cnjy.com )
(2)能 …………………6分
如图,设p是抛物线上的一点,连接PO,PC,过点P作y轴的垂线,垂足为D.
若∠POC=∠PCO
则PD应是线段OC的垂直平分线 …………………8分
∵C的坐标为(0,﹣3)
∴D的坐标为(0,﹣)
∴P的纵坐标应是﹣
令x2﹣2x﹣3=,解得,x1=,x2= …………………10分
因此所求点P的坐标是(,﹣),(,﹣)…………………12分
(第10题)
(第15题)
同课章节目录
