人教版初中数学七年级上册 5.1.2 等式的性质 课件(共20张PPT)
文档属性
| 名称 | 人教版初中数学七年级上册 5.1.2 等式的性质 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-22 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第五章 一元一次方程
5.1 方程
第2课时 等式的性质
1.理解和掌握等式的性质.(重)
2.能正确应用等式的性质把简单的一元一次方程化成“x=m”的形式,体会化归思想.(难)
方程
解方程
(方程的解)
一元一次方程
如何求一元一次方程的解?
用观察的方法我们可以求出像x+1=3这样的简单一元一次方程的解.你能用这种方法求出下列方程的解吗?
(1)3x-5=22;(2)0.28-0.13y=0.27y+1.
用估算的方法解比较复杂的方程是困难的.因此,我们还要讨论怎样解方程.
像m+n=n+m,x+2x=3x,3×3+1=5×2,3x+1=5y这样的式子,都是等式.我们可以用a=b表示一般的等式.
首先,给出关于等式的两个基本事实:
等式两边可以交换.如果a=b,那么b=a.
相等关系可以传递.如果a=b,b=c,那么a=c.
学生活动一 【一起探究】
思考:在小学,我们已经知道:
等式两边同时加(或减)同一个正数,同时乘同一个正数,或同时除以同一个不为0的正数,结果仍相等.
引入负数后,这些性质还成立吗?
你可以用具体的数试一试.
等式两边同时加(或减)同一个数(或式子),结果仍相等.
例如:对于等式a=b,在等式两边都加上 -5,
计算a+(-5)与b+(-5)的值.
当a=b=2时,a+(-5)=2+(-5)= ;
b+(-5)=2+(-5)= .
因此,当引入负数后,这条性质仍然成立.
可见,a+(-5) b+(-5)
类似地,a-(-5) b-(-5)
等式两边同时乘同一个数,或除以同一个不为0的数,结果仍相等.
例如:对于等式a=b,在等式两边都乘以-5,
计算a×(-5)与b×(-5)的值,
当a=b=( )时,a×(-5)=( )×(-5)=( );
b×(-5)=( )×(-5)=( ).
因此,当引入负数后,这条性质也成立.
可见,a×(-5) b×(-5)
类似地,a÷(-5) b÷(-5)
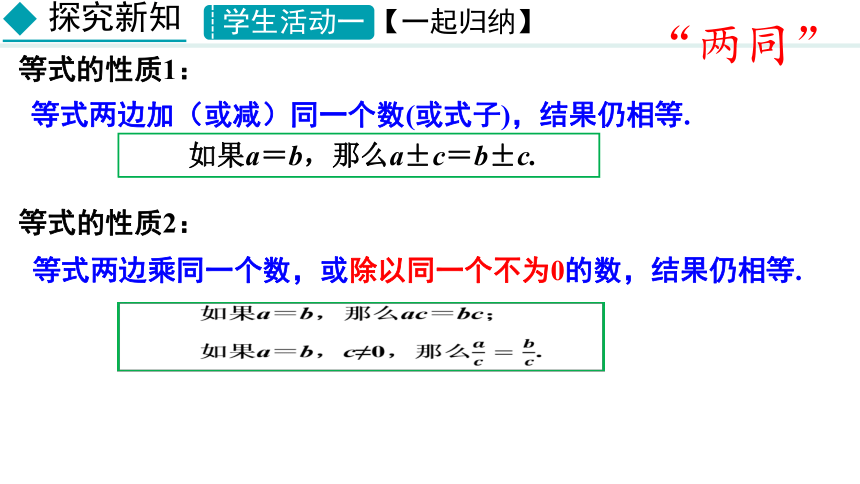
等式的性质1:
等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,那么a±c=b±c.
学生活动一 【一起归纳】
等式的性质2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc;
如果a=b,c≠0,那么.
“两同”
根据等式的性质填空,并说明依据:
(1)如果2x=5-x,那么2x+ =5;
(2)如果m+2n=5+2n,那么m= ;
(3)如果x=-4,那么 ·x=28;
(4)如果3m=4n,那么 m= ·n.
学生活动二 【一起探究】
根据等式的性质1,等式两边加x,结果仍相等.
x
根据等式的性质1,等式两边减2n,结果仍相等.
5
根据等式的性质2,等式两边乘-7,结果仍相等.
根据等式的性质2,等式两边除以2,结果仍相等.
-7
2
用适当的数或整式填空,使所得结果仍是等式,并说明是根据哪条性质以及怎样变形的:
(1)如果3x=-2x-1,那么3x+ =-1;两边同时 ,
根据是 ;
(2)如果x=5,那么x= ;两边同时 ,
根据是 ;
学生活动三 【一起探究】
2x
加2x
等式的性质1
10
乘2
等式的性质2
(3)如果x-2=x- ,那么x- =- + ;
两边同时 ,根据是 .
加(2-x)
x
2
等式的性质1
利用等式的性质解下列方程:
(1)x+7=26; (2)-5x=20; (3)- x-5=4.
化归思想
以x为未知数的方程
转化
等式的性质
x=m(常数)
检验
1.用适当的数或整式填空,使所得的式子仍是等式,并注明根据.
(1)如果x+2=3,那么x=3+_____,根据是______________;
(2)如果4x=3x-7,那么4x-____=-7,根据是__________;
(3)如果-2x=6,那么x=_____,根据是______________;
(4)如果 x=-4,那么____=-8,根据是____________.
(-2)
等式的性质1
3x
等式的性质1
-3
等式的性质2
x
等式的性质2
2.由x+2=0得x=-3可分两步,按步骤完成下列填空:
第一步:根据等式的性质___,等式两边____得到x=-2;
第二步:根据等式的性质___,等式两边____得到x=-3.
1
减2
2
3.利用等式的性质解方程:
(1)x-4=1; (2)3x+5=0.(需检验)
解:x=5
乘
解:x=-
已知2x2-3=5,你能求出x2+3的值吗?
解: 由2x2-3=5,
得 2x2-3+3=5+3,
x2=4,
所以x2+3=7.
拓展
1.如果mx=my,那么下列等式中不一定成立的是 ( )
A.mx+1=my+1 B.mx-3=my-3
C.- mx=- my D.x=y
D
2.下列方程的变形,符合等式的性质的是 ( )
A.由2x-3=7得2x=7-3 B.由-3x=5得x=5+3
C.由2x-3=x-1得2x-x=-1-3
D.由- x=1得x=-4
D
3.若a-9=2017-b,则a+b=________.
4.若a=b,则下列等式:①-a=-b;②2-a=2-b;
③ = ;④a2=b2;⑤ =1.其中正确的有_______.(填序号)
①②④
2026
5.利用等式的性质解方程:2x-3=1.
x=2.
自由选择下面的角度,对今天的学习进行总结概括:
今天我学到了……
我体验到了……
我感到骄傲的是……
我的学习经验是……
我想进一步探究的是……
?
后续研究的经验和方法
数与式
等式
方程、不等式
性质
应用
定义
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b,c≠0,那么.
解一元一次方程
思想方法
类比法
化归思想
函数
课后作业
基础性作业:课本117页练习第1、2题( )
提升性作业:( )
小明学习了《等式的性质》后对小亮说:“我发现4可以等于3,你看这里有一个方程4x-2=3x-2,等式的两边同时加上2,得4x=3x,然后等式的两边再同时除以x,得4=3.”
(1)请你想一想,小明的说法对吗?为什么?
(2)你能求出方程4x-2=3x-2的解吗?
实践性作业:( )
列举你在生活中遇到的可以用等式的性质来解释的问题.
第五章 一元一次方程
5.1 方程
第2课时 等式的性质
1.理解和掌握等式的性质.(重)
2.能正确应用等式的性质把简单的一元一次方程化成“x=m”的形式,体会化归思想.(难)
方程
解方程
(方程的解)
一元一次方程
如何求一元一次方程的解?
用观察的方法我们可以求出像x+1=3这样的简单一元一次方程的解.你能用这种方法求出下列方程的解吗?
(1)3x-5=22;(2)0.28-0.13y=0.27y+1.
用估算的方法解比较复杂的方程是困难的.因此,我们还要讨论怎样解方程.
像m+n=n+m,x+2x=3x,3×3+1=5×2,3x+1=5y这样的式子,都是等式.我们可以用a=b表示一般的等式.
首先,给出关于等式的两个基本事实:
等式两边可以交换.如果a=b,那么b=a.
相等关系可以传递.如果a=b,b=c,那么a=c.
学生活动一 【一起探究】
思考:在小学,我们已经知道:
等式两边同时加(或减)同一个正数,同时乘同一个正数,或同时除以同一个不为0的正数,结果仍相等.
引入负数后,这些性质还成立吗?
你可以用具体的数试一试.
等式两边同时加(或减)同一个数(或式子),结果仍相等.
例如:对于等式a=b,在等式两边都加上 -5,
计算a+(-5)与b+(-5)的值.
当a=b=2时,a+(-5)=2+(-5)= ;
b+(-5)=2+(-5)= .
因此,当引入负数后,这条性质仍然成立.
可见,a+(-5) b+(-5)
类似地,a-(-5) b-(-5)
等式两边同时乘同一个数,或除以同一个不为0的数,结果仍相等.
例如:对于等式a=b,在等式两边都乘以-5,
计算a×(-5)与b×(-5)的值,
当a=b=( )时,a×(-5)=( )×(-5)=( );
b×(-5)=( )×(-5)=( ).
因此,当引入负数后,这条性质也成立.
可见,a×(-5) b×(-5)
类似地,a÷(-5) b÷(-5)
等式的性质1:
等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,那么a±c=b±c.
学生活动一 【一起归纳】
等式的性质2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc;
如果a=b,c≠0,那么.
“两同”
根据等式的性质填空,并说明依据:
(1)如果2x=5-x,那么2x+ =5;
(2)如果m+2n=5+2n,那么m= ;
(3)如果x=-4,那么 ·x=28;
(4)如果3m=4n,那么 m= ·n.
学生活动二 【一起探究】
根据等式的性质1,等式两边加x,结果仍相等.
x
根据等式的性质1,等式两边减2n,结果仍相等.
5
根据等式的性质2,等式两边乘-7,结果仍相等.
根据等式的性质2,等式两边除以2,结果仍相等.
-7
2
用适当的数或整式填空,使所得结果仍是等式,并说明是根据哪条性质以及怎样变形的:
(1)如果3x=-2x-1,那么3x+ =-1;两边同时 ,
根据是 ;
(2)如果x=5,那么x= ;两边同时 ,
根据是 ;
学生活动三 【一起探究】
2x
加2x
等式的性质1
10
乘2
等式的性质2
(3)如果x-2=x- ,那么x- =- + ;
两边同时 ,根据是 .
加(2-x)
x
2
等式的性质1
利用等式的性质解下列方程:
(1)x+7=26; (2)-5x=20; (3)- x-5=4.
化归思想
以x为未知数的方程
转化
等式的性质
x=m(常数)
检验
1.用适当的数或整式填空,使所得的式子仍是等式,并注明根据.
(1)如果x+2=3,那么x=3+_____,根据是______________;
(2)如果4x=3x-7,那么4x-____=-7,根据是__________;
(3)如果-2x=6,那么x=_____,根据是______________;
(4)如果 x=-4,那么____=-8,根据是____________.
(-2)
等式的性质1
3x
等式的性质1
-3
等式的性质2
x
等式的性质2
2.由x+2=0得x=-3可分两步,按步骤完成下列填空:
第一步:根据等式的性质___,等式两边____得到x=-2;
第二步:根据等式的性质___,等式两边____得到x=-3.
1
减2
2
3.利用等式的性质解方程:
(1)x-4=1; (2)3x+5=0.(需检验)
解:x=5
乘
解:x=-
已知2x2-3=5,你能求出x2+3的值吗?
解: 由2x2-3=5,
得 2x2-3+3=5+3,
x2=4,
所以x2+3=7.
拓展
1.如果mx=my,那么下列等式中不一定成立的是 ( )
A.mx+1=my+1 B.mx-3=my-3
C.- mx=- my D.x=y
D
2.下列方程的变形,符合等式的性质的是 ( )
A.由2x-3=7得2x=7-3 B.由-3x=5得x=5+3
C.由2x-3=x-1得2x-x=-1-3
D.由- x=1得x=-4
D
3.若a-9=2017-b,则a+b=________.
4.若a=b,则下列等式:①-a=-b;②2-a=2-b;
③ = ;④a2=b2;⑤ =1.其中正确的有_______.(填序号)
①②④
2026
5.利用等式的性质解方程:2x-3=1.
x=2.
自由选择下面的角度,对今天的学习进行总结概括:
今天我学到了……
我体验到了……
我感到骄傲的是……
我的学习经验是……
我想进一步探究的是……
?
后续研究的经验和方法
数与式
等式
方程、不等式
性质
应用
定义
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b,c≠0,那么.
解一元一次方程
思想方法
类比法
化归思想
函数
课后作业
基础性作业:课本117页练习第1、2题( )
提升性作业:( )
小明学习了《等式的性质》后对小亮说:“我发现4可以等于3,你看这里有一个方程4x-2=3x-2,等式的两边同时加上2,得4x=3x,然后等式的两边再同时除以x,得4=3.”
(1)请你想一想,小明的说法对吗?为什么?
(2)你能求出方程4x-2=3x-2的解吗?
实践性作业:( )
列举你在生活中遇到的可以用等式的性质来解释的问题.
同课章节目录
