人教版数学九年级上册 22.1 二次函数的图像 第二十二章 二次函数 课件(共26张PPT)
文档属性
| 名称 | 人教版数学九年级上册 22.1 二次函数的图像 第二十二章 二次函数 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-22 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
第二十二章 二次函数
人教版·九年级·上册·第二十二章·二次函数
河上架起的拱桥
图片欣赏
雨后天空的彩虹
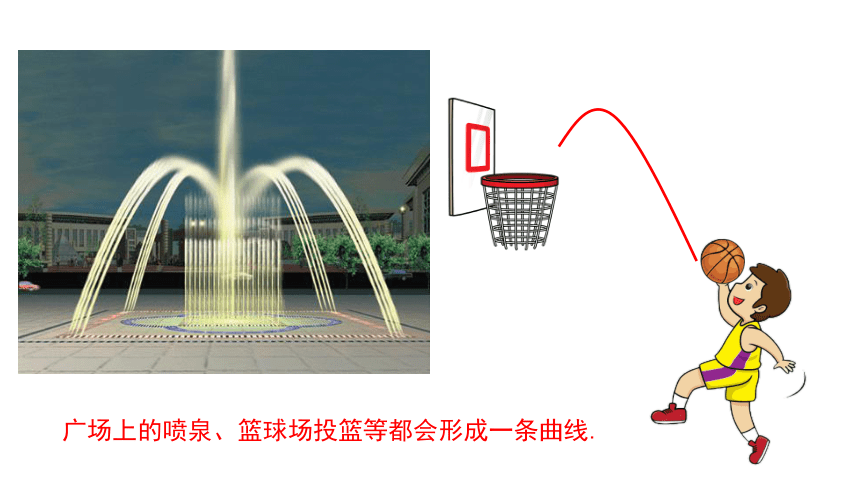
广场上的喷泉、篮球场投篮等都会形成一条曲线.
函数的
定义
类比与归纳
数形结合
转化
一次函数
二次函数
反比例函数
解析式与图像
函数与方程
、不等式
两个变量之间的关系
运动变化的观点看函数
系数与函数图像的关系
一次函数
二次函数
反比例函数
函数概念
实际问题
图象
性质
代数式
坐标系
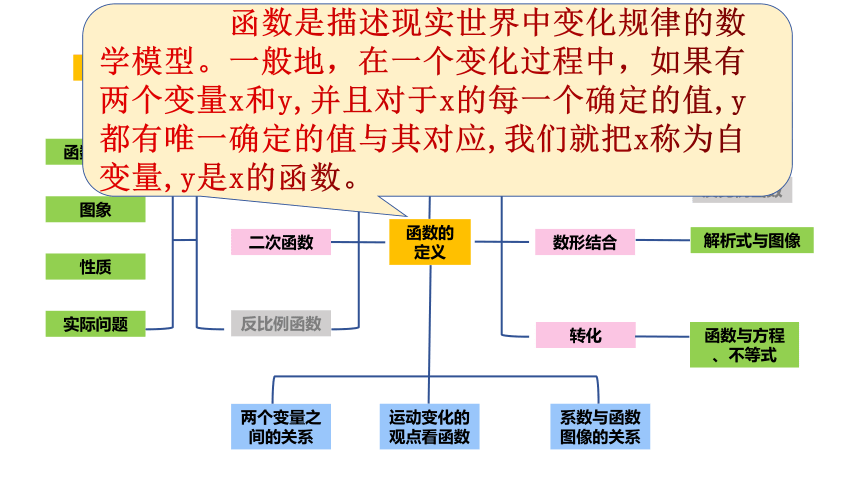
函数是描述现实世界中变化规律的数学模型。一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,我们就把x称为自变量,y是x的函数。
22.1.1 二次函数
人教版·九年级·上册·第二十二章·二次函数
学习目标
1.理解掌握二次函数的概念和一般形式.(重点)
2.会利用二次函数的概念解决问题.
3.会列二次函数表达式解决实际问题.(难点)
请同学们完成学案中的三个问题.
创设问题情景 导入新课
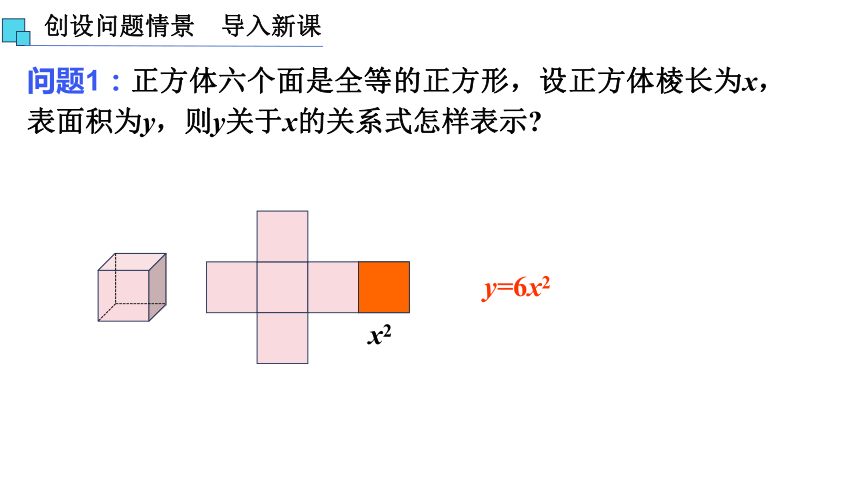
问题1:正方体六个面是全等的正方形,设正方体棱长为x,表面积为y,则y关于x的关系式怎样表示
x2
y=6x2
创设问题情景 导入新课
问题2:n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数m与球队数n有什么关系
【分析】每个球队与其他_____个球队各比赛一场.
(n-1)
m= n(n-1)
m= n2- n
创设问题情景 导入新课
问题3:某种产品现在的年产量为20 t,计划今后两年增加产量. 如果每年都比上一年的产量增加x倍,那么两年后这种产品的年产量y将随计划所定的x值而确定,y与x之间的关系应怎样表示
【分析】一年后的产量:
20(1+x) t
两年后的产量:
20(1+x)(1+x) t
y=20(1+x)2
y=20x2+40x+20
创设问题情景 导入新课
观察上面的三个关系式,请同学们思考以下问题:
①三个问题中的关系式是不是函数关系?如果是,每个函数关系式分别有几个变量?其中哪些是自变量?
②三个问题中的函数具有什么共同特征?
自主探究
1.函数关系式都是整式;
2.函数都是用自变量的二次式表示的.
y=6x2
m= n2- n
y=20x2+40x+20
二次函数
二次
(一元)二次方程
函数
一次函数
ax2+bx+c=0(a≠0)
y=kx+b
(k,b是常数,k≠0)
二次函数的概念:
二次函数的概念:
一般地,形如y=ax +bx+c(a,b,c为常数,a≠0)的函数,叫做二次函数.其中x是自变量,的函数.
归纳总结 得出概念
(1)“ ax ”、“ bx ”、“ c ”分别称为什么项
其中“ab ”分别是什么?
(2)为什么“a”? b、c 可以等于0吗?
我来当小老师
二次函数的概念:
一般地,形如y=ax +bx+c(a,b,c为常数,a≠0)的函数,叫做二次函数.其中x是自变量,的函数.
归纳总结 得出概念
二次项
一次项
常数项
是二次项系数
b是一次项系数
二次函数的一般式
任何一个二次函数的解析式都可以化为一般式
我来当小老师
(1)“ ax ”、“ bx ”、“ c ”分别称为什么项
其中“ab ”分别是什么?
二次函数的一般形式:
y=ax +bx+c(a,b,c为常数,a≠0)
二次函数的特殊形式:
当b=0,c=0时,
当c=0时,
当b=0时,
我来当小老师
(2)为什么“a”? b、c 可以等于0吗?
y=ax2(a≠0)
y=ax2+bx(a≠0)
y=ax2+c(a≠0)
温馨提示:
(1)函数解析式是整式;
(2)化简整理后自变量的最高次数是2,可以没有一次项 和常数项;
(3)二次项系数不为0,即a≠0, b,c任意.
归纳总结 理解概念
例1: 判断下列函数中,哪些是二次函数?若是二次函数,请指出二次项系数、一次项系数、常数项。
×
×
×
×
×
×
√
√
例题讲解
1.说出下列二次函数的二次项系数、一次项系数、常数项.
(1)y=-x2+58x-112;
2.指出下列函数 y=ax +bx+c 中的 a、b、c.
(1)y=-3x2-x-1;
请同学们口答下列问题.
看谁反应快?
(2)y=πx2.
(2)y=-6+5x2;
(3)y=x(1+x).
例2
(1)m取什么值时,此函数是正比例函数?
(2) m取什么值时,此函数是二次函数?
解:
(1)由题可知,
解得
(2)由题可知,
解得
m=3.
例题讲解
1.已知: ,k取什么值时,y是x的二次函数?
解:当 k =2且k+2≠0,即k= 2时, y是x的二次函数.
变式训练
解:
由题意得:
一农民用 40 m 长的篱笆围成一个一边靠墙(墙足够长)的长方形菜园,和墙垂直的一边长为 x m,菜园的面积为 y m2,求y与x之间的函数关系式,并说出自变量的取值范围.当 x=12 m 时,计算菜园的面积.
x m
y m2
x m
(40-2x) m
解:由题意得:y=x(40-2x).
即:y=-2x2+40x
当 x=12 m 时,菜园的面积为:
y=-2x2+40x=-2×122+40×12=192 (m2).
生活问题数学化
(0谈谈你的收获......
课堂小结
二次函数
定 义
一般形式
特殊形式
右边是整式;
自变量的最高次数是2;
二次项系数a≠0
y=ax2+bx+c(a≠0,a,b,c是常数)
y=ax2;
y=ax2+bx;
y=ax2+c(a≠0,a,b,c是常数)
课堂小结
C组:同步练习册8,9题.
AB组:教材第29页练习第1题,教材第41页习题22.1第1,2题.
A组:同步练习册11,12,13题.
课后作业
谢 谢!
第二十二章 二次函数
人教版·九年级·上册·第二十二章·二次函数
河上架起的拱桥
图片欣赏
雨后天空的彩虹
广场上的喷泉、篮球场投篮等都会形成一条曲线.
函数的
定义
类比与归纳
数形结合
转化
一次函数
二次函数
反比例函数
解析式与图像
函数与方程
、不等式
两个变量之间的关系
运动变化的观点看函数
系数与函数图像的关系
一次函数
二次函数
反比例函数
函数概念
实际问题
图象
性质
代数式
坐标系
函数是描述现实世界中变化规律的数学模型。一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,我们就把x称为自变量,y是x的函数。
22.1.1 二次函数
人教版·九年级·上册·第二十二章·二次函数
学习目标
1.理解掌握二次函数的概念和一般形式.(重点)
2.会利用二次函数的概念解决问题.
3.会列二次函数表达式解决实际问题.(难点)
请同学们完成学案中的三个问题.
创设问题情景 导入新课
问题1:正方体六个面是全等的正方形,设正方体棱长为x,表面积为y,则y关于x的关系式怎样表示
x2
y=6x2
创设问题情景 导入新课
问题2:n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数m与球队数n有什么关系
【分析】每个球队与其他_____个球队各比赛一场.
(n-1)
m= n(n-1)
m= n2- n
创设问题情景 导入新课
问题3:某种产品现在的年产量为20 t,计划今后两年增加产量. 如果每年都比上一年的产量增加x倍,那么两年后这种产品的年产量y将随计划所定的x值而确定,y与x之间的关系应怎样表示
【分析】一年后的产量:
20(1+x) t
两年后的产量:
20(1+x)(1+x) t
y=20(1+x)2
y=20x2+40x+20
创设问题情景 导入新课
观察上面的三个关系式,请同学们思考以下问题:
①三个问题中的关系式是不是函数关系?如果是,每个函数关系式分别有几个变量?其中哪些是自变量?
②三个问题中的函数具有什么共同特征?
自主探究
1.函数关系式都是整式;
2.函数都是用自变量的二次式表示的.
y=6x2
m= n2- n
y=20x2+40x+20
二次函数
二次
(一元)二次方程
函数
一次函数
ax2+bx+c=0(a≠0)
y=kx+b
(k,b是常数,k≠0)
二次函数的概念:
二次函数的概念:
一般地,形如y=ax +bx+c(a,b,c为常数,a≠0)的函数,叫做二次函数.其中x是自变量,的函数.
归纳总结 得出概念
(1)“ ax ”、“ bx ”、“ c ”分别称为什么项
其中“ab ”分别是什么?
(2)为什么“a”? b、c 可以等于0吗?
我来当小老师
二次函数的概念:
一般地,形如y=ax +bx+c(a,b,c为常数,a≠0)的函数,叫做二次函数.其中x是自变量,的函数.
归纳总结 得出概念
二次项
一次项
常数项
是二次项系数
b是一次项系数
二次函数的一般式
任何一个二次函数的解析式都可以化为一般式
我来当小老师
(1)“ ax ”、“ bx ”、“ c ”分别称为什么项
其中“ab ”分别是什么?
二次函数的一般形式:
y=ax +bx+c(a,b,c为常数,a≠0)
二次函数的特殊形式:
当b=0,c=0时,
当c=0时,
当b=0时,
我来当小老师
(2)为什么“a”? b、c 可以等于0吗?
y=ax2(a≠0)
y=ax2+bx(a≠0)
y=ax2+c(a≠0)
温馨提示:
(1)函数解析式是整式;
(2)化简整理后自变量的最高次数是2,可以没有一次项 和常数项;
(3)二次项系数不为0,即a≠0, b,c任意.
归纳总结 理解概念
例1: 判断下列函数中,哪些是二次函数?若是二次函数,请指出二次项系数、一次项系数、常数项。
×
×
×
×
×
×
√
√
例题讲解
1.说出下列二次函数的二次项系数、一次项系数、常数项.
(1)y=-x2+58x-112;
2.指出下列函数 y=ax +bx+c 中的 a、b、c.
(1)y=-3x2-x-1;
请同学们口答下列问题.
看谁反应快?
(2)y=πx2.
(2)y=-6+5x2;
(3)y=x(1+x).
例2
(1)m取什么值时,此函数是正比例函数?
(2) m取什么值时,此函数是二次函数?
解:
(1)由题可知,
解得
(2)由题可知,
解得
m=3.
例题讲解
1.已知: ,k取什么值时,y是x的二次函数?
解:当 k =2且k+2≠0,即k= 2时, y是x的二次函数.
变式训练
解:
由题意得:
一农民用 40 m 长的篱笆围成一个一边靠墙(墙足够长)的长方形菜园,和墙垂直的一边长为 x m,菜园的面积为 y m2,求y与x之间的函数关系式,并说出自变量的取值范围.当 x=12 m 时,计算菜园的面积.
x m
y m2
x m
(40-2x) m
解:由题意得:y=x(40-2x).
即:y=-2x2+40x
当 x=12 m 时,菜园的面积为:
y=-2x2+40x=-2×122+40×12=192 (m2).
生活问题数学化
(0
课堂小结
二次函数
定 义
一般形式
特殊形式
右边是整式;
自变量的最高次数是2;
二次项系数a≠0
y=ax2+bx+c(a≠0,a,b,c是常数)
y=ax2;
y=ax2+bx;
y=ax2+c(a≠0,a,b,c是常数)
课堂小结
C组:同步练习册8,9题.
AB组:教材第29页练习第1题,教材第41页习题22.1第1,2题.
A组:同步练习册11,12,13题.
课后作业
谢 谢!
同课章节目录
