期末高频考点检测卷(含答案)-数学六年级上册北师大版
文档属性
| 名称 | 期末高频考点检测卷(含答案)-数学六年级上册北师大版 |
|
|
| 格式 | docx | ||
| 文件大小 | 824.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-20 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末高频考点检测卷-数学六年级上册北师大版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个立体图形,从上面看到的形状是,从左面看到的形状是。搭这样的立体图形,最少需要______个小正方体,最多可以有______个小正方体。横线上应填的正确答案是( )。
A.4,7 B.5,6 C.5,7 D.6,7
2.下面图形中阴影部分的面积占整幅图面积的25%的是( )。
A. B. C. D.
3.180千克的相当于100千克的( )。
A. B. C. D.
4.一块手表的分针长7毫米,从9时到10时,分针尖端走过了( )毫米。
A.21.98 B.43.96 C.87.92 D.153.86
5.下图是某本杂志的内容统计情况。这本杂志共208页,体育版约占( )页。
A.10 B.30 C.50 D.100
6.男生比女生少,男、女生的人数之比是( )。
A.4∶5 B.5∶4 C.1∶5 D.5∶1
7.配制一种消毒液,其中药粉与水质量的比是,现在有这种药粉7.5千克,需要水( )千克。
A.1500 B.750 C.600 D.500
8.一款电子手表原价400元,现按八折出售,现在的价格比原来便宜了( )元。
A.480 B.320 C.80 D.32
二、填空题
9.一个立体图形,从正面看的形状是,从左面看的形状是,搭这样的立体图形,最少需要( )个。最多可以有( )个小正方体。
10.某游泳池有A、B两个注水口,用A口注水需要5小时注满游泳池,用B口注水需要3小时注满游泳池。如果用A、B两个注水口同时注水,需要( )小时能注这个游泳池的。
11.六(2)班对全班40人开展“我最喜爱的职业”调查活动,并将调查结果绘制成下面的扇形统计图。
(1)选择( )的人最多,占调查总人数的( )%,有( )人。
(2)选择教师的比选择律师的多占调查总人数的( )%,多( )人。
(3)选择公务员的和选择医生的共占调查总人数的( )%,共( )人。
12.如图,图中长方形的长与宽的比是( ),比值是( )。
13.把25克糖融化在100克水中,糖的质量占糖水质量的( )%,如果从中取出80克糖水,这些糖水中含有糖( )克。
14.王老师把28000元钱存入银行,定期一年,年利率是2.15%,到期后,他把得到的利息全部捐给了敬老院。王老师捐了( )元。
15.一个半圆的半径是4厘米,周长是( )厘米,面积是( )平方厘米。
16.在一个长8厘米,宽4厘米长方形纸板上剪一个最大的圆,圆的面积是( )平方分米,周长是( )分米。
三、判断题
17.一杯糖水,糖与水的质量比是1∶4,喝掉一半后,糖与水的质量比是1∶2。( )
18.一个圆有无数条对称轴,两个圆组成的图形也有无数条对称轴。( )
19.希望小学要统计各年级戴眼镜的人数,绘制扇形统计图比较合适。( )
20.一项工作由甲乙两人单独做,所用时间比是3∶2,那么他们工作效率的比是2∶3。( )
21.津津看一本课外书,第一天看了全书的,第二天看了全书的,第二天比第一天多看了6页。这本课外书共有120页。( )
四、计算题
22.直接写出得数。
23.用你喜欢的方法计算下面各题,要写出计算过程。
24.解方程。
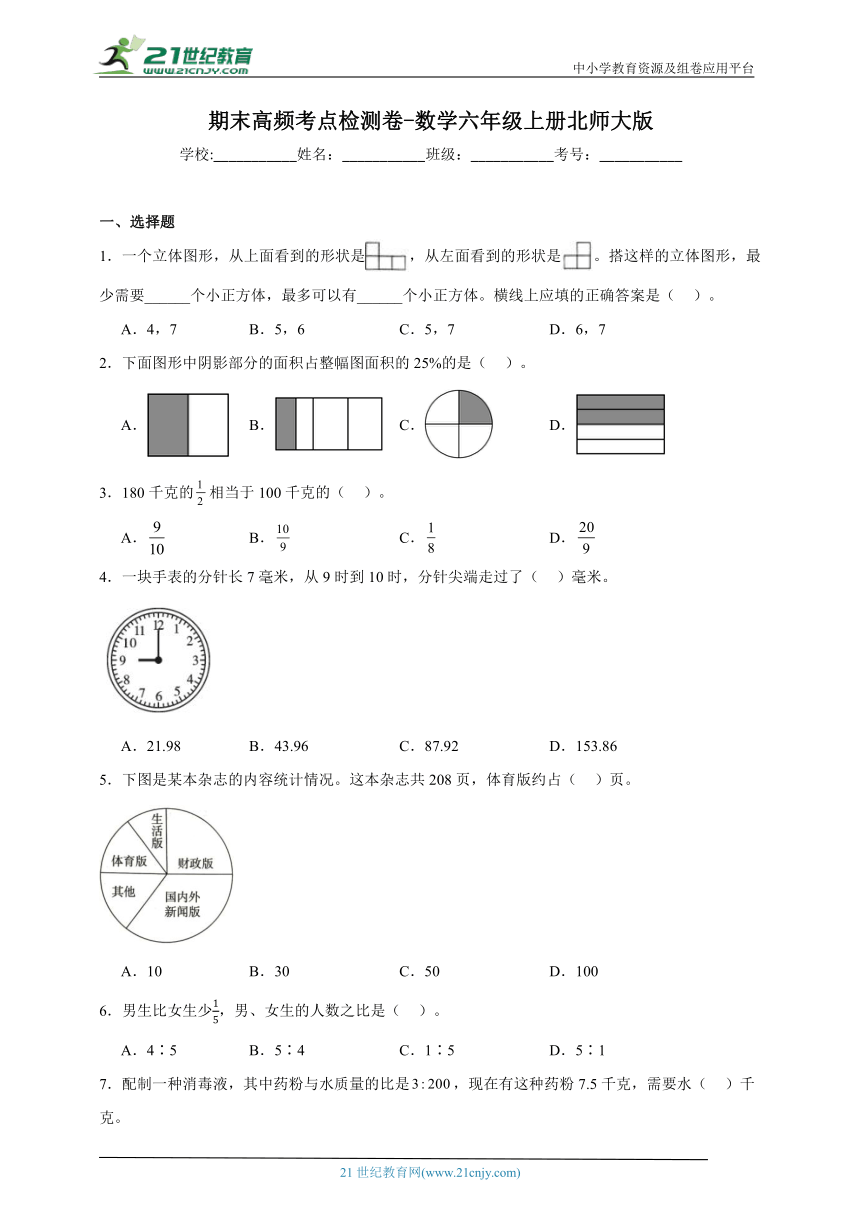
25.看图计算阴影部分的面积。(单位:cm)
五、作图题
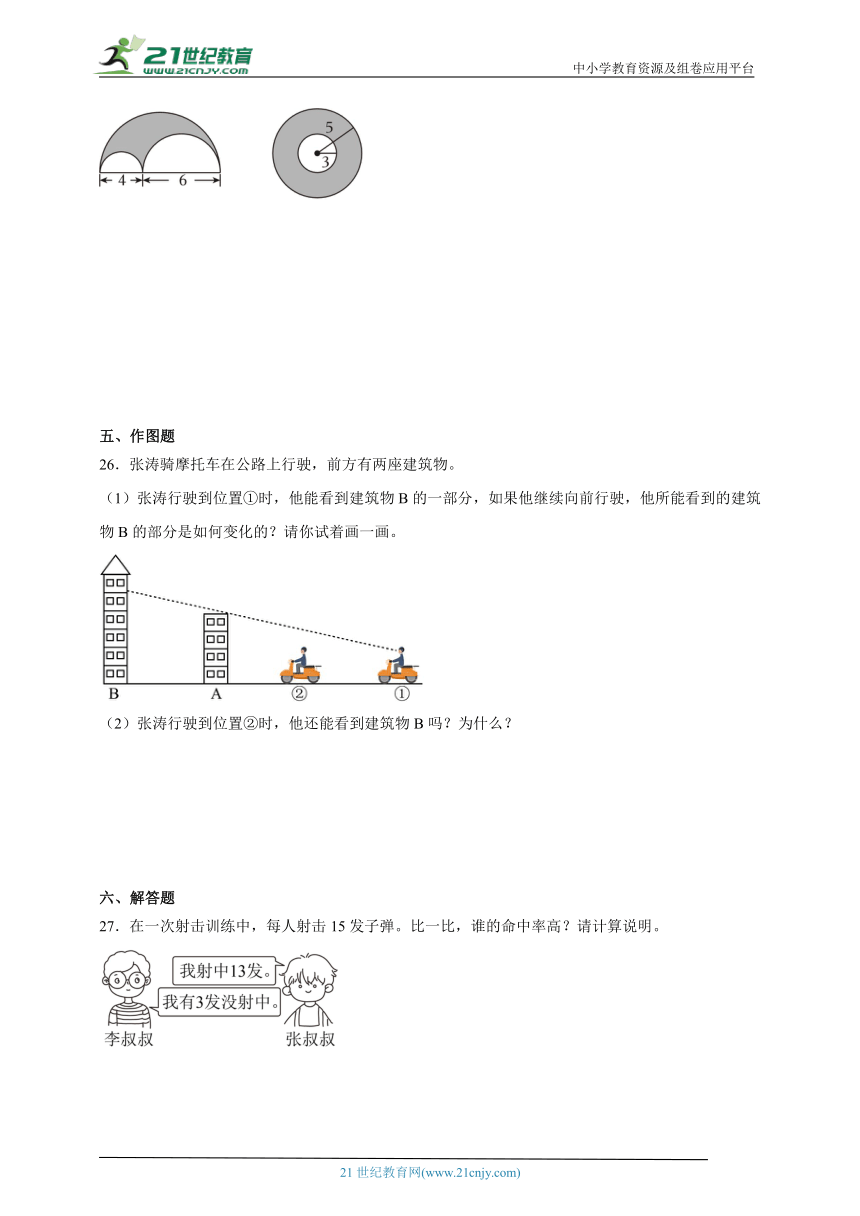
26.张涛骑摩托车在公路上行驶,前方有两座建筑物。
(1)张涛行驶到位置①时,他能看到建筑物B的一部分,如果他继续向前行驶,他所能看到的建筑物B的部分是如何变化的?请你试着画一画。
(2)张涛行驶到位置②时,他还能看到建筑物B吗?为什么?
六、解答题
27.在一次射击训练中,每人射击15发子弹。比一比,谁的命中率高?请计算说明。
28.甲、乙两地相距720千米,客车和货车分别从两地同时相对开出,经过4小时相遇,客车和货车速度比是5∶4,客车每小时行驶多少千米?
29.《诗经》是中国最早的一部诗歌总集,总共有305篇诗歌,又称“诗三百”,分为《风》《雅》《颂》三部分。《风》占总篇数的,《雅》的篇数比《风》的少,《雅》有多少篇?
30.在一次“爱心助学”捐款活动中,一班所有同学都拿出零花钱踊跃捐款。学生的捐款金额有5元、10元、15元、20元四种情况。根据统计数据绘制了图①和图②两幅尚不完整的统计图。
(1)一班共有多少人?
(2)请你将图②补充完整。
(3)捐款15元的人数比捐款20元的多百分之几?
31.在解决“有两个半径分别为5厘米和3厘米的圆(如下图所示),分别写出两个圆的直径、周长以及面积的比”这个问题时,王亮说这两个圆的直径、周长以及面积的比一样,都是5∶3,你认为王亮说得对吗?请写出你的判断理由。
32.下图是某小学的田径场示意图,跑道分为直道和弯道,其中弯道部分是半圆形。
(1)请计算阴影部分的活动场地面积。
(2)如果你沿着最内圈跑道跑1圈,要跑多少米?
(3)如果每条跑道的宽度是1.2米,那么进行400米跑步比赛时,第二跑道与第一跑道的起跑线(起跑线设在直道上)应相距多少米?
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C C A B B A D C
1.C
【分析】从上面看到的形状是说明第一层有4个小正方体,从左面看到的形状是,说明第二层最少有1个小正方体,最多有3个小正方体。两层的个数相加即可得解。
【详解】(个)
(个)
搭这样的立体图形,最少需要5个小正方体,最多可以有7个小正方体。
故答案为:C
2.C
【分析】根据25%=,阴影部分面积占整幅图面积的25%,也就是把整幅图平均分成4份, 阴影部分占其中的1份,据此解答。
【详解】A.将图形平均分成2份,阴影部分占1份,该选项不符合题意;
B.不是平均分,不能用分数或百分数25%来表示,该选项不符合题意;
C.将图形平均分成4份,阴影部分占1份,该选项符合题意;
D.将图形平均分成4份,阴影部分占2份,该选项不符合题意;
故答案为:C
3.A
【分析】将180千克看成单位“1”,先用乘法求出180的是180×千克;再用180×除以100即可求出180千克的相当于100千克的几分之几;据此解答。
【详解】180×÷100
=90÷100
=
即180千克的相当于100千克的。
故答案为:A
【点睛】求一个数的几分之几是多少用乘法,求一个数是另一个数的几分之几用除法。
4.B
【分析】观察图形可知,从9时到10时,分针走一圈,分针尖端走过的路程是一个半径是7毫米的圆的周长,根据圆的周长公式:周长=π×半径×2,代入数据,即可解答。
【详解】3.14×7×2
=21.98×2
=43.96(毫米)
一块手表的分针长7毫米,从9时到10时,分针尖端走过了43.96毫米。
故答案为:B
【点睛】本题考查圆的周长公式的应用,关键明确:无论从9时到10时,还是从10时到11时,分针的针尖要绕钟面旋转1周。
5.B
【分析】由图可知,体育版和生活版一共占扇形的25%,其中体育版占的百分比明显大于生活版,求一个数的百分之几是多少,用乘法,据此求出体育版和生活版的页数和,再用页数和除以2,体育版应该大于页数和的一半,结合选项即可解答。
【详解】208×25%=52(页)
52÷2=26(页)
结合选项中的数据可知,30页符合题意。
故答案为:B
6.A
【分析】把女生人数看作单位“1”,男生比女生少,则男生人数是女生的(),用男生人数比女生人数,化简比即可。
【详解】
因此男、女生的人数之比是4∶5。
故答案为:A
7.D
【分析】把这种药粉的质量看作单位“1”,则需要水的质量是药粉质量的,根据分数乘法的意义,用药粉的质量(7.5千克)×,就是需要水的质量,据此解答。
【详解】7.5×=500(千克)
配制一种消毒液,其中药粉与水质量的比是,现在有这种药粉7.5千克,需要水500千克。
故答案为:D
【点睛】本题考查比的应用,关键是把比转化成分数,再根据分数乘法的意义进行解答。
8.C
【分析】把原价看作单位“1”,现按八折出售,即现在售价是原价的80%,利用1减去80%就是便宜的折扣,再利用原价乘便宜的折扣即可。
【详解】
(元),即现在的价格比原来便宜了80元。
故答案为:C
9. 4 7
【分析】最少需要几个小正方体,那么正面第一排有两个小正方体,中间是空的,第二排有两个小正方体叠在一起放在中间;最多需要几个小正方体,那么正面的第一排要有三个正方体排成一行,第二排也有三个正方体排成一行,同时中间还有叠加一个小正方体,据此解答。
【详解】1+3=4(个)
1+6=7(个)
一个立体图形,从正面看的形状是,从左面看的形状是,搭这样的立体图形,最少需要4个。最多可以有7个小正方体。
10.//1.5
【分析】看成工程问题进行分析,将注水总量,即工作总量看作单位“1”,时间分之一可以看作效率,这个游泳池的÷两个注水口的效率和=同时注水需要的时间,据此列式计算。
【详解】
(小时)
如果用A、B两个注水口同时注水,需要小时能注这个游泳池的。
11.(1) 公务员 25 10
(2) 5 2
(3) 45 18
【分析】理解扇形统计图的特点,用整个圆表示调查全班的总人数,用圆内面积大小不同的扇形表示各部分量占总量的百分比。
(1)扇形面积越大表示所占百分比越大,从扇形统计图中可以看出最喜欢公务员的人最多,因为它的扇形面积最大,所占百分比是25%,根据求一个数的百分之几是多少,用乘法计算,即可求出喜欢公务员的人数;
(2)选择教师的百分比是17.5%,选择律师的百分比是12.5%,先求出选择教师的比选择律师的多占调查总人数的百分比,再根据求一个数的百分之几是多少,用乘法计算,即可求出选择教师的比选择律师多的人数;
(3)选择公务员的占总人数的25%,选择医生的占总人数的20%,先求选择公务员和选择医生的人数共占总人数的百分比,再根据求一个数的百分之几是多少,用乘法计算,即可求出选择公务员的和选择医生的总人数。
【详解】(1)40×25%=10(人)
即选择公务员的人最多,占调查总人数的25%,有10人。
(2)17.5%-12.5%=5%
40×5%=2(人)
即选择教师的比选择律师的多占调查总人数的5%,多2人。
(3)25%+20%=45%
40×45%=18(人)
即选择公务员的和选择医生的共占调查总人数的45%,共18人。
12. 4∶3
【分析】假设每个小正方形的边长为1,则该长方形的长为4,宽为3,用长方形的长∶宽即可;再用比的前项除以比的后项即可求出比值。
【详解】假设每个小正方形的边长为1。
(1×4)∶(1×3)
=4∶3
4∶3
=4÷3
=
长方形的长与宽的比是4∶3,比值是。
13. 20 16
【分析】先用糖的质量+水的质量,求出糖水的质量;再用糖的质量÷糖水的质量×100%,代入数据,求出糖的质量占糖水质量的百分之几;再用取出糖水的质量×糖的质量占糖水质量的百分比,即可解答。
【详解】25÷(25+100)×100%
=25÷125×100%
=0.2×100%
=20%
80×20%=16(克)
把25克糖融化在100克水中,糖的质量占糖水质量的20%,如果从中取出80克糖水,这些糖水中含有糖16克。
14.602
【分析】到期取款时银行多支付的钱叫利息,根据利息=本金×利率×存期,列式计算即可。
【详解】28000×2.15%×1
=28000×0.0215×1
=602(元)
王老师捐了602元。
15. 20.56 25.12
【分析】半圆的周长C=πr+2r,半圆的面积S=πr2÷2,据此解答。
【详解】3.14×4+2×4
=12.56+8
=20.56(厘米),周长是20.56厘米;
3.14×42÷2
=50.24÷2
=25.12(平方厘米),面积是25.12平方厘米。
【点睛】此题考查了半圆的周长和面积计算,注意计算周长时需要用圆周长的一半加直径。
16. 0.1256 1.256
【分析】由题意可知:最大圆的直径是4厘米,带入圆的面积、周长公式计算即可。
【详解】最大圆的直径是4厘米
面积:3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
12.56平方厘米=0.1256平方分米
3.14×4=12.56(厘米)
12.56厘米=1.256分米
【点睛】本题主要考查圆的周长、面积公式,明确圆的直径是解题的关键。
17.×
【分析】一杯糖水,糖与水的比是1∶4,喝掉一半后,糖和水都变成原来的一半,糖与水的比是不变的,即还是1∶4,据此分析选择。
【详解】1∶4=(1÷2)∶(4÷2)=1∶4
一杯糖水,糖与水的比是1∶4,喝掉一半后,糖与水的比是1∶4;原题说法错误;
故答案为:×
【点睛】解答本题关键是理解:喝掉一半后,糖与水的比是不变的。
18.×
【分析】两个圆组成的图形,对称轴的条数取决于两个圆的位置关系。当两个圆组成同心圆时,有无数条对称轴,如下图所示;当两个圆不组成同心圆时,只有一条对称轴,如下图所示。据此解答即可。
【详解】由分析可知:
一个圆有无数条对称轴,两个圆组成的图形也有无数条对称轴。
原说法错误。
故答案为:×
19.×
【分析】条形统计图可以清楚地看出数量的多少。
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
扇形统计图表示各部分数量与总数之间的关系。
【详解】希望小学要统计各年级戴眼镜的人数,绘制条形统计图比较合适。
原题说法错误。
故答案为:×
20.√
【分析】根据题意,甲乙两人单独做,所用时间比是3∶2,即把甲单独完成这项工作需要3小时,乙单独完成这项工作需要2小时;把这项工作看作单位“1”,根据工作效率=工作总量÷工作时间,用1÷3,求出甲的工作效率;用1÷2,求出乙的工作效率;再根据比的意义,用甲的工作效率∶乙的工作效率,化简,即可解答。
【详解】(1÷3)∶(1÷2)
=∶
=(×6)∶(×6)
=2∶3
一项工作由甲乙两人单独做,所用时间比是3∶2,那么他们工作效率的比是2∶3。
原题干说法正确。
故答案为:√
21.√
【分析】将第二天看的分率减去第一天看的分率,求出第二天比第一天多看了全书的几分之几。将全书看作单位“1”,将第二天比第一天多看了的页数除以对应的分率,求出总页数。
【详解】6÷(-)
=6÷(-)
=6÷
=6×20
=120(页)
所以,这本课外书共有120页。原说法正确。
故答案为:√
22.18;1.05;16;6
9;3.5;;
【详解】略
23.90;;5
【分析】(1)先把8拆成2×4,即,再根据乘法结合律(a×b)×c=a×(b×c),把变成,然后按照运算顺序计算;
(2)先算乘法,再算加法;
(3)先把62.5%化成,即,再根据乘法分配律a×c+b×c=(a+b)×c,把变成,然后按照运算顺序计算。
【详解】(1)
(2)
(3)
24.x=40;x=3.75
【分析】44+120%x=92,根据等式的性质1,方程两边同时减去44,再根据等式的性质2,方程两边同时除以120%即可;
30%x-x=,先化简方程左边含有未知数的算式,即求出30%-的差,再根据等式的性质2,方程两边同时除以30%-的差即可。
【详解】44+120%x=92
解:44-44+120%x=92-44
120%x=48
120%x÷120%=48÷120%
x=40
30%x-x=
解:0.3x-0.2x=
0.1x=
0.1x÷0.1=0.375÷0.1
x=3.75
25.18.84cm2;50.24cm2
【分析】第一个阴影部分的面积=大半圆的面积-两个小半圆的面积,半圆面积=圆周率×半径的平方÷2;
第二个阴影部分是个圆环,根据圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),列式计算即可。
【详解】3.14×[(4+6)÷2]2÷2-3.14×(4÷2)2÷2-3.14×(6÷2)2÷2
=3.14×[10÷2]2÷2-3.14×22÷2-3.14×32÷2
=3.14×52÷2-3.14×4÷2-3.14×9÷2
=3.14×25÷2-6.28-14.13
=39.25-6.28-14.13
=18.84(cm2)
3.14×(52-32)
=3.14×(25-9)
=3.14×16
=50.24(cm2)
26.(1)图见详解;他发现建筑物B逐渐消失
(2)不能;原因见详解
【分析】(1)在②的位置时,过张涛的眼睛和A建筑物的顶端作射线与A建筑物相交,A建筑物射线以上的部分是张涛能够看到的部分,如果张涛继续向前行驶,张涛看到建筑物B的部分越来越少,直到看不见,据此解答。
(2)根据张涛的眼睛和A建筑物的顶端作射线与A建筑物相交,A建筑物射线以上的部分是张涛能够看到的部分,建筑物B是不是在张涛能看到的部分,在张涛能看到的部分,就能看到,不在张涛能看到的部分,就不能看到,据此解答。
【详解】(1)如图:
他发现建筑物B逐渐消失。
(2)不能,因为建筑物A挡住了张涛的视线。
27.李叔叔
【分析】根据命中率=射中子弹数÷射击子弹的总数量×100%,分别求出李叔叔和张叔叔的命中率,再进行比较,即可解答。
【详解】李叔叔:13÷15×100%
≈0.87×100%
=87%
张叔叔:(15-3)÷15×100%
=12÷15×100%
=0.8×100%
=80%
因为87%>80%,所以李叔叔命中率高。
答:李叔叔命中率高。
28.100千米
【分析】根据速度=路程÷时间,用甲、乙两地的距离÷4,求出客车和货车的速度和;再根据客车和货车速度比是5∶4,即客车速度是客车和货车速度和的,用客车和货车的速度和×,即可求出客车的速度。
【详解】720÷4×
=180×
=100(千米)
答:客车每小时行驶100千米。
29.105篇
【分析】把《诗经》总篇数看作单位“1”,《风》占总篇数的,用《诗经》总篇数×,求出《风》的篇数,再把《风》的篇数看作单位“1”,《雅》的篇数比《风》的少,即《雅》的篇数是《风》的(1-),用《风》的篇数×(1-),即可求出《雅》的篇数。
【详解】305××(1-)
=160×
=105(篇)
答:《雅》有105篇。
30.(1)50人(2)见详解(3)60%
【分析】(1)根据图①和图②可知,捐款金额是15元的有16人,占全班总人数的32%,利用已知一个数的百分之几是多少,求这个数,用除法计算。
(2)根据求一个数的百分之几是多少,用乘法计算;捐款金额是20元的人数占全班总人数的20%,用全班人数乘20%计算出捐款20元的人数;再用总人数分别减去捐款5元、15元和20元的人数,所得结果即为捐款10元的人数,据此可将图②补充完整。
(3)用捐款15元的人数减去捐款20元的人数,所得差除以捐款20元的人数,最后乘100%即可。
【详解】(1)16÷32%
=16÷0.32
=50(人)
答:一班共有50人。
(2)50×20%
=50×0.2
=10(人)
50-6-16-10=18(人)
因此捐款10元的有18人,捐款20元的有10人,如图所示:
(3)(16-10)÷10×100%
=6÷10×100%
=0.6×100%
=60%
答:捐款15元的人数比捐款20元的多60%。
31.不对;理由见详解
【分析】已知两个圆的半径分别为5厘米和3厘米,根据圆的直径d=2r,圆的周长C=πd,圆的面积S=πr2,分别求出这两个圆的直径、周长和面积,再根据比的意义,写出两个圆的直径的比、周长的比和面积的比,并化简比,据此判断王亮的说法是否正确。
【详解】5×2=10(厘米)
3×2=6(厘米)
π×10=10π(厘米)
π×6=6π(厘米)
π×52=25π(平方厘米)
π×32=9π(平方厘米)
10∶6=(10÷2)∶(6÷2)=5∶3
10π∶6π=(10π÷2π)∶(6π÷2π)=5∶3
25π∶9π=(25π÷π)∶(9π÷π)=25∶9
答:王亮说得不对。因为这两个圆的直径、周长的比都是5∶3,但面积的比是25∶9。
32.(1)6962.5平方米
(2)357米
(3)7.536米
【分析】(1)阴影部分的活动场面积等于直径是50米的圆的面积与长是100米,宽是50米的长方形面积的和;根据圆的面积公式:面积=π×半径2,长方形面积公式:面积=长×宽,代入数据,即可解答。
(2)沿最内圈跑即求最内圈的周长,即长方形的两个长的和与直径是50米的圆的周长的和;根据圆的周长公式:周长=π×直径,代入数据,即可解答。
(3)第二跑道的周长等于直径是(50+1.2)米的圆的周长+2条长方形的长的和;第一跑道的周长等于直径是50米的圆的周长+2条长方形的长的和,求第二跑道与第一跑到的起跑线应相差多少米,就是求直径是(50+1.2×2)米的圆的周长与直径是50米的圆的周长的差,把数据代入圆的周长公式,分别求出两个圆的周长,再相减,即可解答。
【详解】(1)3.14×(50÷2)2+50×100
=3.14×252+5000
=3.14×625+5000
=1962.5+5000
=6962.5(平方米)
答:阴影部分的活动场地面积是6962.5平方米。
(2)3.14×50+100×2
=157+200
=357(米)
答:沿着最内圈跑道跑一圈要跑357米。
(3)3.14×(50+1.2×2)-3.14×50
=3.14×(50+2.4)-157
=3.14×52.4-157
=164.536-157
=7.536(米)
答:第二跑道与第一跑道的起跑线应相距7.536米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末高频考点检测卷-数学六年级上册北师大版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个立体图形,从上面看到的形状是,从左面看到的形状是。搭这样的立体图形,最少需要______个小正方体,最多可以有______个小正方体。横线上应填的正确答案是( )。
A.4,7 B.5,6 C.5,7 D.6,7
2.下面图形中阴影部分的面积占整幅图面积的25%的是( )。
A. B. C. D.
3.180千克的相当于100千克的( )。
A. B. C. D.
4.一块手表的分针长7毫米,从9时到10时,分针尖端走过了( )毫米。
A.21.98 B.43.96 C.87.92 D.153.86
5.下图是某本杂志的内容统计情况。这本杂志共208页,体育版约占( )页。
A.10 B.30 C.50 D.100
6.男生比女生少,男、女生的人数之比是( )。
A.4∶5 B.5∶4 C.1∶5 D.5∶1
7.配制一种消毒液,其中药粉与水质量的比是,现在有这种药粉7.5千克,需要水( )千克。
A.1500 B.750 C.600 D.500
8.一款电子手表原价400元,现按八折出售,现在的价格比原来便宜了( )元。
A.480 B.320 C.80 D.32
二、填空题
9.一个立体图形,从正面看的形状是,从左面看的形状是,搭这样的立体图形,最少需要( )个。最多可以有( )个小正方体。
10.某游泳池有A、B两个注水口,用A口注水需要5小时注满游泳池,用B口注水需要3小时注满游泳池。如果用A、B两个注水口同时注水,需要( )小时能注这个游泳池的。
11.六(2)班对全班40人开展“我最喜爱的职业”调查活动,并将调查结果绘制成下面的扇形统计图。
(1)选择( )的人最多,占调查总人数的( )%,有( )人。
(2)选择教师的比选择律师的多占调查总人数的( )%,多( )人。
(3)选择公务员的和选择医生的共占调查总人数的( )%,共( )人。
12.如图,图中长方形的长与宽的比是( ),比值是( )。
13.把25克糖融化在100克水中,糖的质量占糖水质量的( )%,如果从中取出80克糖水,这些糖水中含有糖( )克。
14.王老师把28000元钱存入银行,定期一年,年利率是2.15%,到期后,他把得到的利息全部捐给了敬老院。王老师捐了( )元。
15.一个半圆的半径是4厘米,周长是( )厘米,面积是( )平方厘米。
16.在一个长8厘米,宽4厘米长方形纸板上剪一个最大的圆,圆的面积是( )平方分米,周长是( )分米。
三、判断题
17.一杯糖水,糖与水的质量比是1∶4,喝掉一半后,糖与水的质量比是1∶2。( )
18.一个圆有无数条对称轴,两个圆组成的图形也有无数条对称轴。( )
19.希望小学要统计各年级戴眼镜的人数,绘制扇形统计图比较合适。( )
20.一项工作由甲乙两人单独做,所用时间比是3∶2,那么他们工作效率的比是2∶3。( )
21.津津看一本课外书,第一天看了全书的,第二天看了全书的,第二天比第一天多看了6页。这本课外书共有120页。( )
四、计算题
22.直接写出得数。
23.用你喜欢的方法计算下面各题,要写出计算过程。
24.解方程。
25.看图计算阴影部分的面积。(单位:cm)
五、作图题
26.张涛骑摩托车在公路上行驶,前方有两座建筑物。
(1)张涛行驶到位置①时,他能看到建筑物B的一部分,如果他继续向前行驶,他所能看到的建筑物B的部分是如何变化的?请你试着画一画。
(2)张涛行驶到位置②时,他还能看到建筑物B吗?为什么?
六、解答题
27.在一次射击训练中,每人射击15发子弹。比一比,谁的命中率高?请计算说明。
28.甲、乙两地相距720千米,客车和货车分别从两地同时相对开出,经过4小时相遇,客车和货车速度比是5∶4,客车每小时行驶多少千米?
29.《诗经》是中国最早的一部诗歌总集,总共有305篇诗歌,又称“诗三百”,分为《风》《雅》《颂》三部分。《风》占总篇数的,《雅》的篇数比《风》的少,《雅》有多少篇?
30.在一次“爱心助学”捐款活动中,一班所有同学都拿出零花钱踊跃捐款。学生的捐款金额有5元、10元、15元、20元四种情况。根据统计数据绘制了图①和图②两幅尚不完整的统计图。
(1)一班共有多少人?
(2)请你将图②补充完整。
(3)捐款15元的人数比捐款20元的多百分之几?
31.在解决“有两个半径分别为5厘米和3厘米的圆(如下图所示),分别写出两个圆的直径、周长以及面积的比”这个问题时,王亮说这两个圆的直径、周长以及面积的比一样,都是5∶3,你认为王亮说得对吗?请写出你的判断理由。
32.下图是某小学的田径场示意图,跑道分为直道和弯道,其中弯道部分是半圆形。
(1)请计算阴影部分的活动场地面积。
(2)如果你沿着最内圈跑道跑1圈,要跑多少米?
(3)如果每条跑道的宽度是1.2米,那么进行400米跑步比赛时,第二跑道与第一跑道的起跑线(起跑线设在直道上)应相距多少米?
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C C A B B A D C
1.C
【分析】从上面看到的形状是说明第一层有4个小正方体,从左面看到的形状是,说明第二层最少有1个小正方体,最多有3个小正方体。两层的个数相加即可得解。
【详解】(个)
(个)
搭这样的立体图形,最少需要5个小正方体,最多可以有7个小正方体。
故答案为:C
2.C
【分析】根据25%=,阴影部分面积占整幅图面积的25%,也就是把整幅图平均分成4份, 阴影部分占其中的1份,据此解答。
【详解】A.将图形平均分成2份,阴影部分占1份,该选项不符合题意;
B.不是平均分,不能用分数或百分数25%来表示,该选项不符合题意;
C.将图形平均分成4份,阴影部分占1份,该选项符合题意;
D.将图形平均分成4份,阴影部分占2份,该选项不符合题意;
故答案为:C
3.A
【分析】将180千克看成单位“1”,先用乘法求出180的是180×千克;再用180×除以100即可求出180千克的相当于100千克的几分之几;据此解答。
【详解】180×÷100
=90÷100
=
即180千克的相当于100千克的。
故答案为:A
【点睛】求一个数的几分之几是多少用乘法,求一个数是另一个数的几分之几用除法。
4.B
【分析】观察图形可知,从9时到10时,分针走一圈,分针尖端走过的路程是一个半径是7毫米的圆的周长,根据圆的周长公式:周长=π×半径×2,代入数据,即可解答。
【详解】3.14×7×2
=21.98×2
=43.96(毫米)
一块手表的分针长7毫米,从9时到10时,分针尖端走过了43.96毫米。
故答案为:B
【点睛】本题考查圆的周长公式的应用,关键明确:无论从9时到10时,还是从10时到11时,分针的针尖要绕钟面旋转1周。
5.B
【分析】由图可知,体育版和生活版一共占扇形的25%,其中体育版占的百分比明显大于生活版,求一个数的百分之几是多少,用乘法,据此求出体育版和生活版的页数和,再用页数和除以2,体育版应该大于页数和的一半,结合选项即可解答。
【详解】208×25%=52(页)
52÷2=26(页)
结合选项中的数据可知,30页符合题意。
故答案为:B
6.A
【分析】把女生人数看作单位“1”,男生比女生少,则男生人数是女生的(),用男生人数比女生人数,化简比即可。
【详解】
因此男、女生的人数之比是4∶5。
故答案为:A
7.D
【分析】把这种药粉的质量看作单位“1”,则需要水的质量是药粉质量的,根据分数乘法的意义,用药粉的质量(7.5千克)×,就是需要水的质量,据此解答。
【详解】7.5×=500(千克)
配制一种消毒液,其中药粉与水质量的比是,现在有这种药粉7.5千克,需要水500千克。
故答案为:D
【点睛】本题考查比的应用,关键是把比转化成分数,再根据分数乘法的意义进行解答。
8.C
【分析】把原价看作单位“1”,现按八折出售,即现在售价是原价的80%,利用1减去80%就是便宜的折扣,再利用原价乘便宜的折扣即可。
【详解】
(元),即现在的价格比原来便宜了80元。
故答案为:C
9. 4 7
【分析】最少需要几个小正方体,那么正面第一排有两个小正方体,中间是空的,第二排有两个小正方体叠在一起放在中间;最多需要几个小正方体,那么正面的第一排要有三个正方体排成一行,第二排也有三个正方体排成一行,同时中间还有叠加一个小正方体,据此解答。
【详解】1+3=4(个)
1+6=7(个)
一个立体图形,从正面看的形状是,从左面看的形状是,搭这样的立体图形,最少需要4个。最多可以有7个小正方体。
10.//1.5
【分析】看成工程问题进行分析,将注水总量,即工作总量看作单位“1”,时间分之一可以看作效率,这个游泳池的÷两个注水口的效率和=同时注水需要的时间,据此列式计算。
【详解】
(小时)
如果用A、B两个注水口同时注水,需要小时能注这个游泳池的。
11.(1) 公务员 25 10
(2) 5 2
(3) 45 18
【分析】理解扇形统计图的特点,用整个圆表示调查全班的总人数,用圆内面积大小不同的扇形表示各部分量占总量的百分比。
(1)扇形面积越大表示所占百分比越大,从扇形统计图中可以看出最喜欢公务员的人最多,因为它的扇形面积最大,所占百分比是25%,根据求一个数的百分之几是多少,用乘法计算,即可求出喜欢公务员的人数;
(2)选择教师的百分比是17.5%,选择律师的百分比是12.5%,先求出选择教师的比选择律师的多占调查总人数的百分比,再根据求一个数的百分之几是多少,用乘法计算,即可求出选择教师的比选择律师多的人数;
(3)选择公务员的占总人数的25%,选择医生的占总人数的20%,先求选择公务员和选择医生的人数共占总人数的百分比,再根据求一个数的百分之几是多少,用乘法计算,即可求出选择公务员的和选择医生的总人数。
【详解】(1)40×25%=10(人)
即选择公务员的人最多,占调查总人数的25%,有10人。
(2)17.5%-12.5%=5%
40×5%=2(人)
即选择教师的比选择律师的多占调查总人数的5%,多2人。
(3)25%+20%=45%
40×45%=18(人)
即选择公务员的和选择医生的共占调查总人数的45%,共18人。
12. 4∶3
【分析】假设每个小正方形的边长为1,则该长方形的长为4,宽为3,用长方形的长∶宽即可;再用比的前项除以比的后项即可求出比值。
【详解】假设每个小正方形的边长为1。
(1×4)∶(1×3)
=4∶3
4∶3
=4÷3
=
长方形的长与宽的比是4∶3,比值是。
13. 20 16
【分析】先用糖的质量+水的质量,求出糖水的质量;再用糖的质量÷糖水的质量×100%,代入数据,求出糖的质量占糖水质量的百分之几;再用取出糖水的质量×糖的质量占糖水质量的百分比,即可解答。
【详解】25÷(25+100)×100%
=25÷125×100%
=0.2×100%
=20%
80×20%=16(克)
把25克糖融化在100克水中,糖的质量占糖水质量的20%,如果从中取出80克糖水,这些糖水中含有糖16克。
14.602
【分析】到期取款时银行多支付的钱叫利息,根据利息=本金×利率×存期,列式计算即可。
【详解】28000×2.15%×1
=28000×0.0215×1
=602(元)
王老师捐了602元。
15. 20.56 25.12
【分析】半圆的周长C=πr+2r,半圆的面积S=πr2÷2,据此解答。
【详解】3.14×4+2×4
=12.56+8
=20.56(厘米),周长是20.56厘米;
3.14×42÷2
=50.24÷2
=25.12(平方厘米),面积是25.12平方厘米。
【点睛】此题考查了半圆的周长和面积计算,注意计算周长时需要用圆周长的一半加直径。
16. 0.1256 1.256
【分析】由题意可知:最大圆的直径是4厘米,带入圆的面积、周长公式计算即可。
【详解】最大圆的直径是4厘米
面积:3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
12.56平方厘米=0.1256平方分米
3.14×4=12.56(厘米)
12.56厘米=1.256分米
【点睛】本题主要考查圆的周长、面积公式,明确圆的直径是解题的关键。
17.×
【分析】一杯糖水,糖与水的比是1∶4,喝掉一半后,糖和水都变成原来的一半,糖与水的比是不变的,即还是1∶4,据此分析选择。
【详解】1∶4=(1÷2)∶(4÷2)=1∶4
一杯糖水,糖与水的比是1∶4,喝掉一半后,糖与水的比是1∶4;原题说法错误;
故答案为:×
【点睛】解答本题关键是理解:喝掉一半后,糖与水的比是不变的。
18.×
【分析】两个圆组成的图形,对称轴的条数取决于两个圆的位置关系。当两个圆组成同心圆时,有无数条对称轴,如下图所示;当两个圆不组成同心圆时,只有一条对称轴,如下图所示。据此解答即可。
【详解】由分析可知:
一个圆有无数条对称轴,两个圆组成的图形也有无数条对称轴。
原说法错误。
故答案为:×
19.×
【分析】条形统计图可以清楚地看出数量的多少。
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
扇形统计图表示各部分数量与总数之间的关系。
【详解】希望小学要统计各年级戴眼镜的人数,绘制条形统计图比较合适。
原题说法错误。
故答案为:×
20.√
【分析】根据题意,甲乙两人单独做,所用时间比是3∶2,即把甲单独完成这项工作需要3小时,乙单独完成这项工作需要2小时;把这项工作看作单位“1”,根据工作效率=工作总量÷工作时间,用1÷3,求出甲的工作效率;用1÷2,求出乙的工作效率;再根据比的意义,用甲的工作效率∶乙的工作效率,化简,即可解答。
【详解】(1÷3)∶(1÷2)
=∶
=(×6)∶(×6)
=2∶3
一项工作由甲乙两人单独做,所用时间比是3∶2,那么他们工作效率的比是2∶3。
原题干说法正确。
故答案为:√
21.√
【分析】将第二天看的分率减去第一天看的分率,求出第二天比第一天多看了全书的几分之几。将全书看作单位“1”,将第二天比第一天多看了的页数除以对应的分率,求出总页数。
【详解】6÷(-)
=6÷(-)
=6÷
=6×20
=120(页)
所以,这本课外书共有120页。原说法正确。
故答案为:√
22.18;1.05;16;6
9;3.5;;
【详解】略
23.90;;5
【分析】(1)先把8拆成2×4,即,再根据乘法结合律(a×b)×c=a×(b×c),把变成,然后按照运算顺序计算;
(2)先算乘法,再算加法;
(3)先把62.5%化成,即,再根据乘法分配律a×c+b×c=(a+b)×c,把变成,然后按照运算顺序计算。
【详解】(1)
(2)
(3)
24.x=40;x=3.75
【分析】44+120%x=92,根据等式的性质1,方程两边同时减去44,再根据等式的性质2,方程两边同时除以120%即可;
30%x-x=,先化简方程左边含有未知数的算式,即求出30%-的差,再根据等式的性质2,方程两边同时除以30%-的差即可。
【详解】44+120%x=92
解:44-44+120%x=92-44
120%x=48
120%x÷120%=48÷120%
x=40
30%x-x=
解:0.3x-0.2x=
0.1x=
0.1x÷0.1=0.375÷0.1
x=3.75
25.18.84cm2;50.24cm2
【分析】第一个阴影部分的面积=大半圆的面积-两个小半圆的面积,半圆面积=圆周率×半径的平方÷2;
第二个阴影部分是个圆环,根据圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),列式计算即可。
【详解】3.14×[(4+6)÷2]2÷2-3.14×(4÷2)2÷2-3.14×(6÷2)2÷2
=3.14×[10÷2]2÷2-3.14×22÷2-3.14×32÷2
=3.14×52÷2-3.14×4÷2-3.14×9÷2
=3.14×25÷2-6.28-14.13
=39.25-6.28-14.13
=18.84(cm2)
3.14×(52-32)
=3.14×(25-9)
=3.14×16
=50.24(cm2)
26.(1)图见详解;他发现建筑物B逐渐消失
(2)不能;原因见详解
【分析】(1)在②的位置时,过张涛的眼睛和A建筑物的顶端作射线与A建筑物相交,A建筑物射线以上的部分是张涛能够看到的部分,如果张涛继续向前行驶,张涛看到建筑物B的部分越来越少,直到看不见,据此解答。
(2)根据张涛的眼睛和A建筑物的顶端作射线与A建筑物相交,A建筑物射线以上的部分是张涛能够看到的部分,建筑物B是不是在张涛能看到的部分,在张涛能看到的部分,就能看到,不在张涛能看到的部分,就不能看到,据此解答。
【详解】(1)如图:
他发现建筑物B逐渐消失。
(2)不能,因为建筑物A挡住了张涛的视线。
27.李叔叔
【分析】根据命中率=射中子弹数÷射击子弹的总数量×100%,分别求出李叔叔和张叔叔的命中率,再进行比较,即可解答。
【详解】李叔叔:13÷15×100%
≈0.87×100%
=87%
张叔叔:(15-3)÷15×100%
=12÷15×100%
=0.8×100%
=80%
因为87%>80%,所以李叔叔命中率高。
答:李叔叔命中率高。
28.100千米
【分析】根据速度=路程÷时间,用甲、乙两地的距离÷4,求出客车和货车的速度和;再根据客车和货车速度比是5∶4,即客车速度是客车和货车速度和的,用客车和货车的速度和×,即可求出客车的速度。
【详解】720÷4×
=180×
=100(千米)
答:客车每小时行驶100千米。
29.105篇
【分析】把《诗经》总篇数看作单位“1”,《风》占总篇数的,用《诗经》总篇数×,求出《风》的篇数,再把《风》的篇数看作单位“1”,《雅》的篇数比《风》的少,即《雅》的篇数是《风》的(1-),用《风》的篇数×(1-),即可求出《雅》的篇数。
【详解】305××(1-)
=160×
=105(篇)
答:《雅》有105篇。
30.(1)50人(2)见详解(3)60%
【分析】(1)根据图①和图②可知,捐款金额是15元的有16人,占全班总人数的32%,利用已知一个数的百分之几是多少,求这个数,用除法计算。
(2)根据求一个数的百分之几是多少,用乘法计算;捐款金额是20元的人数占全班总人数的20%,用全班人数乘20%计算出捐款20元的人数;再用总人数分别减去捐款5元、15元和20元的人数,所得结果即为捐款10元的人数,据此可将图②补充完整。
(3)用捐款15元的人数减去捐款20元的人数,所得差除以捐款20元的人数,最后乘100%即可。
【详解】(1)16÷32%
=16÷0.32
=50(人)
答:一班共有50人。
(2)50×20%
=50×0.2
=10(人)
50-6-16-10=18(人)
因此捐款10元的有18人,捐款20元的有10人,如图所示:
(3)(16-10)÷10×100%
=6÷10×100%
=0.6×100%
=60%
答:捐款15元的人数比捐款20元的多60%。
31.不对;理由见详解
【分析】已知两个圆的半径分别为5厘米和3厘米,根据圆的直径d=2r,圆的周长C=πd,圆的面积S=πr2,分别求出这两个圆的直径、周长和面积,再根据比的意义,写出两个圆的直径的比、周长的比和面积的比,并化简比,据此判断王亮的说法是否正确。
【详解】5×2=10(厘米)
3×2=6(厘米)
π×10=10π(厘米)
π×6=6π(厘米)
π×52=25π(平方厘米)
π×32=9π(平方厘米)
10∶6=(10÷2)∶(6÷2)=5∶3
10π∶6π=(10π÷2π)∶(6π÷2π)=5∶3
25π∶9π=(25π÷π)∶(9π÷π)=25∶9
答:王亮说得不对。因为这两个圆的直径、周长的比都是5∶3,但面积的比是25∶9。
32.(1)6962.5平方米
(2)357米
(3)7.536米
【分析】(1)阴影部分的活动场面积等于直径是50米的圆的面积与长是100米,宽是50米的长方形面积的和;根据圆的面积公式:面积=π×半径2,长方形面积公式:面积=长×宽,代入数据,即可解答。
(2)沿最内圈跑即求最内圈的周长,即长方形的两个长的和与直径是50米的圆的周长的和;根据圆的周长公式:周长=π×直径,代入数据,即可解答。
(3)第二跑道的周长等于直径是(50+1.2)米的圆的周长+2条长方形的长的和;第一跑道的周长等于直径是50米的圆的周长+2条长方形的长的和,求第二跑道与第一跑到的起跑线应相差多少米,就是求直径是(50+1.2×2)米的圆的周长与直径是50米的圆的周长的差,把数据代入圆的周长公式,分别求出两个圆的周长,再相减,即可解答。
【详解】(1)3.14×(50÷2)2+50×100
=3.14×252+5000
=3.14×625+5000
=1962.5+5000
=6962.5(平方米)
答:阴影部分的活动场地面积是6962.5平方米。
(2)3.14×50+100×2
=157+200
=357(米)
答:沿着最内圈跑道跑一圈要跑357米。
(3)3.14×(50+1.2×2)-3.14×50
=3.14×(50+2.4)-157
=3.14×52.4-157
=164.536-157
=7.536(米)
答:第二跑道与第一跑道的起跑线应相距7.536米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
