期末能力提升卷(含解析)-2024-2025学年数学八年级上册苏科版
文档属性
| 名称 | 期末能力提升卷(含解析)-2024-2025学年数学八年级上册苏科版 |

|
|
| 格式 | docx | ||
| 文件大小 | 703.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-20 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末能力提升卷-2024-2025学年数学八年级上册苏科版
一.选择题(共8小题)
1.(2023秋 南充校级期末)下面是大疆科技、华为集团、太极股份和凤凰光学四个杰出科技企业的标志,其中是轴对称图形的是( )
A. B. C. D.
2.(2023秋 慈利县期末)下列各数中,不是无理数的是( )
A. B.π
C. D.0.1010010001
3.(2024春 韩城市期末)8的立方根是( )
A.±4 B.2 C.4 D.±2
4.(2023秋 文昌校级期末)下列函数(其中x是自变量)中,不是正比例函数的个数有( )
①y=﹣x;②y+2=2(x+1);③y=k2x(k是常数);④y2=x2.
A.1个 B.2个 C.3个 D.4个
5.(2023秋 东莞市校级期末)2002年国际数学家大会在北京召开,如图①是大会会标,会标中央图案是经过艺术处理的,它标志着中国古代数学的成就.如图②是我国古代数学家赵爽为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是( )
A.三角形内角和定理 B.三角形全等
C.勾股定理 D.轴对称图形
6.(2023秋 安徽期末)如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=3cm,CDBC,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0<t<10),连接DE,当△BDE是直角三角形时,t的值最多有( )个
A.1 B.2 C.3 D.4
7.(2023秋 阳城县期末)如图,等腰直角三角形DEF的斜边中点O与等腰直角三角形ABC的斜边中点重合,D,E两点分别在AB、BC上,若AB=4,AD=1,则△DEF的面积为( )
A.3 B.4 C.5 D.6
8.(2023秋 灵武市期末)在同一平面直角坐标系中,一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图象如图所示,则下列结论错误的是( )
A.y1随x的增大而增大
B.b<n
C.当x<2时,y1>y2
D.关于x,y的方程组的解为
二.填空题(共7小题)
9.(2024春 江都区期末)比较大小: .
10.(2023秋 金安区校级期末)在平面直角坐标系中,点P(2,2)到x轴的距离是 .
11.(2023秋 临潼区期末)如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若△ABC的周长26cm,△AEC的周长18cm,则AB的长为 .
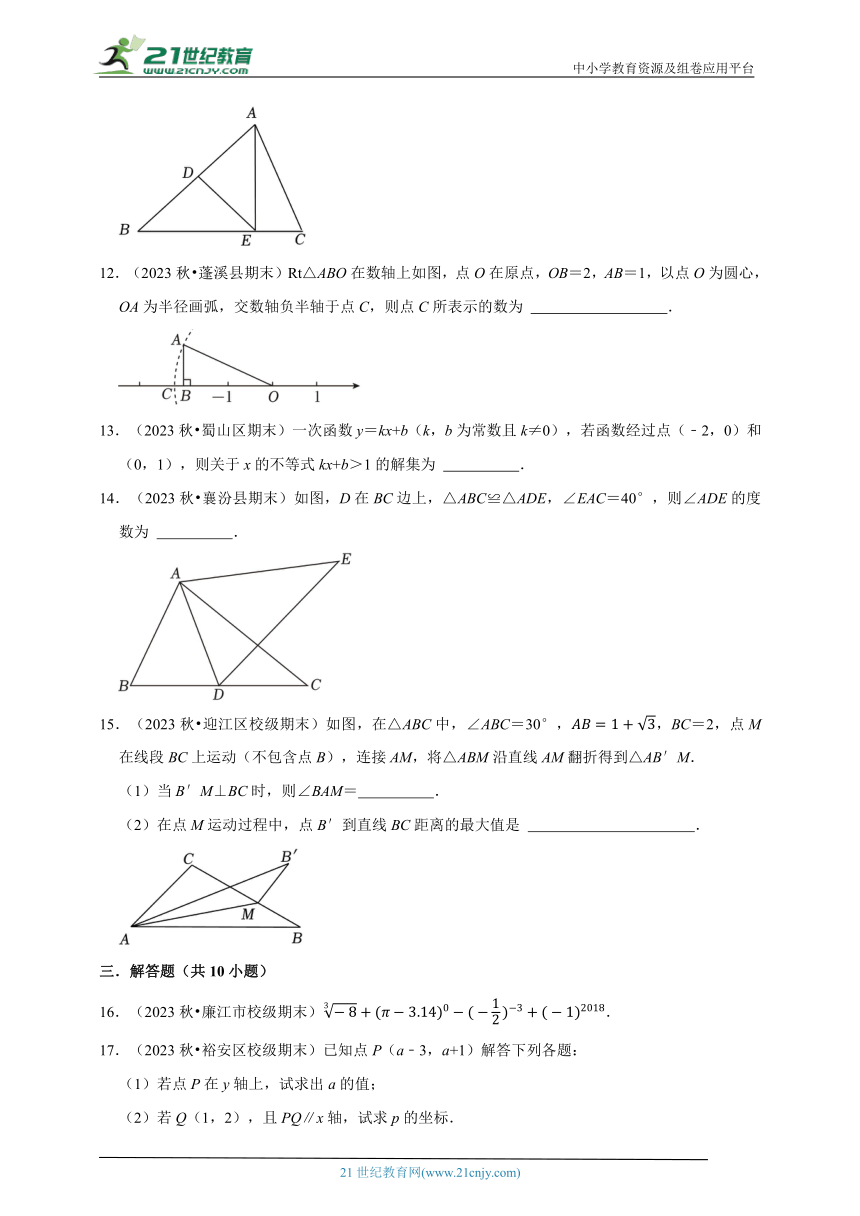
12.(2023秋 蓬溪县期末)Rt△ABO在数轴上如图,点O在原点,OB=2,AB=1,以点O为圆心,OA为半径画弧,交数轴负半轴于点C,则点C所表示的数为 .
13.(2023秋 蜀山区期末)一次函数y=kx+b(k,b为常数且k≠0),若函数经过点(﹣2,0)和(0,1),则关于x的不等式kx+b>1的解集为 .
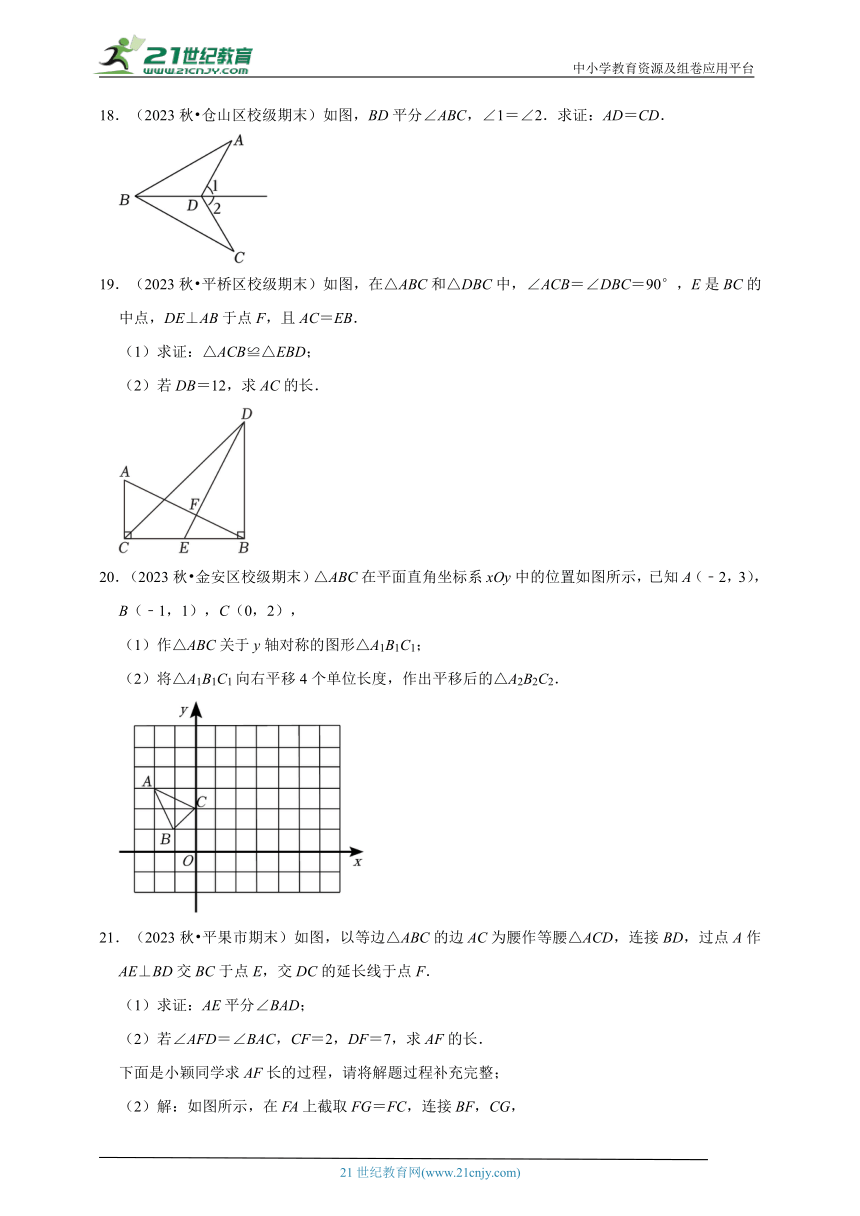
14.(2023秋 襄汾县期末)如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠ADE的度数为 .
15.(2023秋 迎江区校级期末)如图,在△ABC中,∠ABC=30°,,BC=2,点M在线段BC上运动(不包含点B),连接AM,将△ABM沿直线AM翻折得到△AB′M.
(1)当B′M⊥BC时,则∠BAM= .
(2)在点M运动过程中,点B′到直线BC距离的最大值是 .
三.解答题(共10小题)
16.(2023秋 廉江市校级期末).
17.(2023秋 裕安区校级期末)已知点P(a﹣3,a+1)解答下列各题:
(1)若点P在y轴上,试求出a的值;
(2)若Q(1,2),且PQ∥x轴,试求p的坐标.
18.(2023秋 仓山区校级期末)如图,BD平分∠ABC,∠1=∠2.求证:AD=CD.
19.(2023秋 平桥区校级期末)如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB于点F,且AC=EB.
(1)求证:△ACB≌△EBD;
(2)若DB=12,求AC的长.
20.(2023秋 金安区校级期末)△ABC在平面直角坐标系xOy中的位置如图所示,已知A(﹣2,3),B(﹣1,1),C(0,2),
(1)作△ABC关于y轴对称的图形△A1B1C1;
(2)将△A1B1C1向右平移4个单位长度,作出平移后的△A2B2C2.
21.(2023秋 平果市期末)如图,以等边△ABC的边AC为腰作等腰△ACD,连接BD,过点A作AE⊥BD交BC于点E,交DC的延长线于点F.
(1)求证:AE平分∠BAD;
(2)若∠AFD=∠BAC,CF=2,DF=7,求AF的长.
下面是小颖同学求AF长的过程,请将解题过程补充完整;
(2)解:如图所示,在FA上截取FG=FC,连接BF,CG,
∵∠AFD=∠BAC=60°,FG=FC,∴△FCG是等边三角形,
∴ .
∵△ABC是等边三角形,
∴BC=AC,∠ACB=∠GCF=60°,
∴ ,
在△ACG和△BCF中,
,
∴△ACG≌△BCF,
∴ .
由(1)知AF为BD的垂直平分线,
∴BF=FD,
∴ .
∴AF=AG+FG=DF+CF=7+2=9.
22.(2023秋 瑞金市期末)如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为20,求BC的长.
23.(2023秋 万安县期末)如图,直线y=2x+4与x轴交于点A,与y轴交于点B,点C是OB的中点.
(1)求点C的坐标;
(2)在x轴上找一点D,使得S△ACD=S△ABC,求点D的坐标;
(3)在x轴上是否存在一点P,使得△ABP是直角三角形?若存在,请写出点P的坐标;若不存在,请说明理由.
24.(2023秋 安庆期末)某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元,
(1)求A、B两种奖品单价各是多少元?
(2)学校计过购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍.设购买A种奖品m件,购买费用为w元,写出w(元)与m(件)之间的函数表达式,并求最少费用w的值.
25.(2023秋 长治期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.
(1)如图1,连接CE,求证:△BCE是等边三角形;
(2)如图2,点M为CE上一点,连接BM,作等边△BMN,连接EN,求证:EN∥BC;
(3)如图3,点P为线段AD上一点,连接BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间的数量关系,并证明.
期末能力提升卷-2024-2025学年数学八年级上册苏科版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8
答案 B C B B C C C C
一.选择题(共8小题)
1.(2023秋 南充校级期末)下面是大疆科技、华为集团、太极股份和凤凰光学四个杰出科技企业的标志,其中是轴对称图形的是( )
A. B. C. D.
【解答】解:选项A、C、D的图形均不能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形.
选项B的图形能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
故选:B.
2.(2023秋 慈利县期末)下列各数中,不是无理数的是( )
A. B.π
C. D.0.1010010001
【解答】解:由无理数的概念可知:...均是无理数,
是分数,不是无理数,
故选:C.
3.(2024春 韩城市期末)8的立方根是( )
A.±4 B.2 C.4 D.±2
【解答】解:∵23=8,∴,
故选:B.
4.(2023秋 文昌校级期末)下列函数(其中x是自变量)中,不是正比例函数的个数有( )
①y=﹣x;②y+2=2(x+1);③y=k2x(k是常数);④y2=x2.
A.1个 B.2个 C.3个 D.4个
【解答】解:①y=﹣x是正比例函数;
②y+2=2(x+1),整理得y=2x,是正比例函数;
③y=k2x(k是常数),当k=0时,不是函数,当k≠0时,是正比例函数;
④y2=x2,不是函数;
所以不是正比例函数的个数有2个,
故选:B.
5.(2023秋 东莞市校级期末)2002年国际数学家大会在北京召开,如图①是大会会标,会标中央图案是经过艺术处理的,它标志着中国古代数学的成就.如图②是我国古代数学家赵爽为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是( )
A.三角形内角和定理 B.三角形全等
C.勾股定理 D.轴对称图形
【解答】解:∵“弦图”是利用面积关系证明勾股定理的,
∴“弦图”解决的数学问题是:勾股定理.
故选:C.
6.(2023秋 安徽期末)如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=3cm,CDBC,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0<t<10),连接DE,当△BDE是直角三角形时,t的值最多有( )个
A.1 B.2 C.3 D.4
【解答】解:∵∠C=90°,BC=3cm,∠B=60°,
∴AB=2BC=6cm,
①当∠EDB=90°时,
∵BC=3cm,CDBC,
∴BD=2cm,
∵∠C=90°,
∴∠EDB=∠C,
∵∠B=∠B,
∴△BDE∽△BCA,
∴,
∴,
解得:BE=4,
即AE=6﹣4=2(cm),
当从A到E时,时间t=2秒,
当从A到B再到E时,时间t=6+4=10秒,
∵0<t<10,此时舍去;
②当∠BED=90°时,
∵∠DEB=∠C=90°,∠B=∠B,
∴△BED∽△BCA,
∴,
∴,
解得:BE=1(cm),
∴AE=5cm,
当从A到E时,时间t=5秒,
当从A到B再到E时,时间t=6+1=7(秒),
综合上述,时间t=2或5或7共3个,
故选:C.
7.(2023秋 阳城县期末)如图,等腰直角三角形DEF的斜边中点O与等腰直角三角形ABC的斜边中点重合,D,E两点分别在AB、BC上,若AB=4,AD=1,则△DEF的面积为( )
A.3 B.4 C.5 D.6
【解答】解:连接BO,EO,
∵△ABC是等腰直角三角形,O是斜边AC的中点,
∴OB⊥AC,OBAC,
∴OB=OA,
同理:OE⊥DF,OE=OD,
∵∠AOD+∠BOD=∠BOE+∠BOD=90°,
∴∠BOE=∠AOD,
在△OBE和△OAD中,
,
∴△OBE≌△OAD(SAS),
∴BE=AD=1,
∵BD=AB﹣AD=4﹣1=3,
∵∠DBE=90°,
∴DE,
∵△DEF是等腰直角三角形,
∴EF=DE,
∴△DEF的面积DE×EFDE2=5.
故选:C.
8.(2023秋 灵武市期末)在同一平面直角坐标系中,一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图象如图所示,则下列结论错误的是( )
A.y1随x的增大而增大
B.b<n
C.当x<2时,y1>y2
D.关于x,y的方程组的解为
【解答】解:A、y1随x的增大而增大,故选项A正确;
B、由图象可知,一次函数y1=ax+b(a≠0)的图象与y轴的交点在y2=mx+n(m≠0)的图象与y轴的交点的下方,即b<n,故选项B正确;
C、由图象可知:当x<2时,y1<y2,故选项C错误;
D、由图象可知,两条直线的交点为(2,3),
∴关于x,y的方程组的解为;
故选项D正确;
故选:C.
二.填空题(共7小题)
9.(2024春 江都区期末)比较大小: > .
【解答】解:∵,,18<12,
∴.
故答案为:>.
10.(2023秋 金安区校级期末)在平面直角坐标系中,点P(2,2)到x轴的距离是 2 .
【解答】解:点P(2,2)到x轴的距离是其纵坐标的绝对值,
所以点P(2,2)到x轴的距离为2,
故答案为:2.
11.(2023秋 临潼区期末)如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若△ABC的周长26cm,△AEC的周长18cm,则AB的长为 8cm .
【解答】解:∵AB的垂直平分线交AB于点D,交BC于点E,
∴AE=BE,
∵△ABC的周长是26cm,
∴BC+AB+AC=26(cm),
∵△AEC的周长18cm,
∴AC+AE+EC=18(cm),
∴BC+AC=18(cm),
∴AB=8(cm),
故答案为:8cm.
12.(2023秋 蓬溪县期末)Rt△ABO在数轴上如图,点O在原点,OB=2,AB=1,以点O为圆心,OA为半径画弧,交数轴负半轴于点C,则点C所表示的数为 .
【解答】解:由题意得,OB=2,AB=1,∠ABO=90°,OC=OA,
∴,
∴,
∵点C在点O左侧,
∴点C所表示的数为,
故答案为:.
13.(2023秋 蜀山区期末)一次函数y=kx+b(k,b为常数且k≠0),若函数经过点(﹣2,0)和(0,1),则关于x的不等式kx+b>1的解集为 x>0 .
【解答】解:如图所示,即为一次函数y=kx+b的函数图象,
由函数图象可知,当一次函数的函数值大于1时自变量的取值范围为x>0,
∴关于x的不等式kx+b>1的解集为x>0,
故答案为:x>0.
14.(2023秋 襄汾县期末)如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠ADE的度数为 70° .
【解答】解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,AB=AD,∠ADE=∠B,
∴∠EAC=∠DAB=40°,
∴△ABD中,∠B(180°﹣∠BAD)=70°,
∴∠ADE=∠B=70°,
故答案为:70°.
15.(2023秋 迎江区校级期末)如图,在△ABC中,∠ABC=30°,,BC=2,点M在线段BC上运动(不包含点B),连接AM,将△ABM沿直线AM翻折得到△AB′M.
(1)当B′M⊥BC时,则∠BAM= 15° .
(2)在点M运动过程中,点B′到直线BC距离的最大值是 .
【解答】解:(1)如图,
由折叠性质可知:∠B=∠B′=30°,∠AMB=∠AMB′,
∵∠AMB+∠AMB′+∠BMB′=360°,
∴∠AMB=∠AMB′=135°,
∵∠BAM+∠AMB+∠B=180°,
∴∠BAM=15°,
故答案为:15°;
(2)如图,AB′=AB,当垂足E在线段AB′上时,点B′到直线BC距离的最大;
∴∠AEM=∠B′EM=90°,
由折叠性质可知:∠BAM=∠B′AM,∠B=∠B′=30°,
∴∠BAE=60°,
∴∠EAM=∠BAM=∠B′=30°,
∴,
故答案为:.
三.解答题(共10小题)
16.(2023秋 廉江市校级期末).
【解答】解:原式=﹣2+1﹣(﹣8)+1
=﹣1+8+1
=8.
17.(2023秋 裕安区校级期末)已知点P(a﹣3,a+1)解答下列各题:
(1)若点P在y轴上,试求出a的值;
(2)若Q(1,2),且PQ∥x轴,试求p的坐标.
【解答】解:(1)∵点P(a﹣3,a+1)在y轴上,
∴a﹣3=0,
解得a=3;
(2)∵点P(a﹣3,a+1),Q(1,2),且PQ∥x轴,
∴a+1=2,
解得a=1,
∴a﹣3=1﹣3=﹣2,
∴P(﹣2,2).
18.(2023秋 仓山区校级期末)如图,BD平分∠ABC,∠1=∠2.求证:AD=CD.
【解答】证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠1=∠2,
∴180°﹣∠1=180°﹣∠2,
∴∠ADB=∠CDB,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(ASA),
∴AD=CD.
19.(2023秋 平桥区校级期末)如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB于点F,且AC=EB.
(1)求证:△ACB≌△EBD;
(2)若DB=12,求AC的长.
【解答】(1)证明:∵∠ACB=∠DBC=90°,DE⊥AB,
∴∠DEB+∠ABC=90°,∠A+∠ABC=90°,
∴∠DEB=∠A.
在△ACB和△EBD中,
,
∴△ACB≌△EBD(ASA);
(2)解:∵△ACB≌△EBD,
∴BC=DB,AC=EB.
∵E是BC的中点,
∴EBBC.
∵DB=12,BC=DB,
∴BC=12,
∴AC=EBBC=6.
20.(2023秋 金安区校级期末)△ABC在平面直角坐标系xOy中的位置如图所示,已知A(﹣2,3),B(﹣1,1),C(0,2),
(1)作△ABC关于y轴对称的图形△A1B1C1;
(2)将△A1B1C1向右平移4个单位长度,作出平移后的△A2B2C2.
【解答】解:(1)如图1,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
21.(2023秋 平果市期末)如图,以等边△ABC的边AC为腰作等腰△ACD,连接BD,过点A作AE⊥BD交BC于点E,交DC的延长线于点F.
(1)求证:AE平分∠BAD;
(2)若∠AFD=∠BAC,CF=2,DF=7,求AF的长.
下面是小颖同学求AF长的过程,请将解题过程补充完整;
(2)解:如图所示,在FA上截取FG=FC,连接BF,CG,
∵∠AFD=∠BAC=60°,FG=FC,∴△FCG是等边三角形,
∴ CG=CF .
∵△ABC是等边三角形,
∴BC=AC,∠ACB=∠GCF=60°,
∴ ∠ACG=60°﹣∠BCG=∠BCF ,
在△ACG和△BCF中,
,
∴△ACG≌△BCF,
∴ AG=BF .
由(1)知AF为BD的垂直平分线,
∴BF=FD,
∴ AG=DF .
∴AF=AG+FG=DF+CF=7+2=9.
【解答】(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,
∵△ACD是等腰三角形,
∴AC=AD,
∴AB=AD,即△ABD是等腰三角形,
∵AG⊥BD,
∴AG平分∠BAD,
∵点E是AG线段上的一点,即点A,G,E三点共线,
∴AE平分∠BAD;
(2)解:如图所示,在FA上截取FG=FC,连接BF,CG,
∵∠AFD=∠BAC=60°,FG=FC,
∴△FCG是等边三角形,
∴CG=CF,
∵△ABC是等边三角形,
∴BC=AC,∠ACB=∠GCF=60°,
∴∠ACG=60°﹣∠BCG=∠BCF,
在△ACG和△BCF中,
,
∴△ACG≌△BCF(SAS),
∴AG=BF,
由(1)可知AF为BD的垂直平分线,
∴BF=FD,
∴AG=DF,
∴AF=AG+FG=DF+CF=7+2=9.
故答案为:CG=CF,∠ACG=60°﹣∠BCG=∠BCF,AG=BF,AG=DF.
22.(2023秋 瑞金市期末)如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为20,求BC的长.
【解答】解:(1)∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣30°﹣50°=100°;
∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30°,
同理可得,∠FAC=∠ACB=50°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=100°﹣30°﹣50°=20°;
(2)∵△DAF的周长为20,
∴DA+DF+FA=20,
由(1)可知,DA=DB,FA=FC,
∴BC=DB+DF+FC=DA+DF+FA=20.
23.(2023秋 万安县期末)如图,直线y=2x+4与x轴交于点A,与y轴交于点B,点C是OB的中点.
(1)求点C的坐标;
(2)在x轴上找一点D,使得S△ACD=S△ABC,求点D的坐标;
(3)在x轴上是否存在一点P,使得△ABP是直角三角形?若存在,请写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵直线y=2x+4与x轴交于点A,与y轴交于点B,
当x=0时,y=4;当y=0时,x=﹣2,
∴B(0,4),A(﹣2,0),
∵点C是OB的中点,
∴C(0,2);
(2)∵OA=2,OC=2,BC=OB﹣OC=4﹣2=2,
∴S△ABC=BC OA 2×22,
∵S△ACD=S△ABC,
∴S△ACD=AD OC AD×22,
∴AD=2,
当点D在点A左侧时,OD=OA+AD=2+2=4,
∴D(﹣4,0),
当点D在点A右侧时,OD=OA﹣AD=2﹣2=0,
∴D(0,0),
综上,D(﹣4,0)或(0,0);
(3)存在,设点P的坐标为(m,0),
①∠APB=90°时,点P与原点重合,坐标为(0,0);
②∠ABP=90°时,则AP2=AB2+BP2,
∵AP=m+2,AB2=OA2+OB2=22+42=20,BP2=OB2+OP2=42+m2,
∴(m+2)2=20+42+m2,
解得m=8,
∴P(8,0),
综上,P(0,0)或(8,0).
24.(2023秋 安庆期末)某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元,
(1)求A、B两种奖品单价各是多少元?
(2)学校计过购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍.设购买A种奖品m件,购买费用为w元,写出w(元)与m(件)之间的函数表达式,并求最少费用w的值.
【解答】解(1)设A奖品的单价是x元,B奖品的单价是y元,由题意,得
,
解得,
答:A奖品的单价是10元,B奖品的单价是15元;
(2)由题意,得
w=10m+15(100﹣m)=﹣5m+1500
∴,
解得:70≤m≤75.
∵m是整数,
∴m=70,71,72,73,74,75.
∵w=﹣5m+1500,
∴k=﹣5<0,
∴w随m的增大而减小,
∴m=75时,w最小=1125.
∴应买A种奖品75件,B种奖品25件,才能使总费用最少为1125元.
25.(2023秋 长治期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.
(1)如图1,连接CE,求证:△BCE是等边三角形;
(2)如图2,点M为CE上一点,连接BM,作等边△BMN,连接EN,求证:EN∥BC;
(3)如图3,点P为线段AD上一点,连接BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间的数量关系,并证明.
【解答】(1)证明:∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵BD是△ABC的角平分线,
∴∠DBA∠ABC=30°,
∴∠A=∠DBA,
∴AD=BD,
∵DE⊥AB,
∴AE=BE,
∴CEAB=BE,
∴△BCE是等边三角形;
(2)证明:∵△BCE与△MNB都是等边三角形,
∴BC=BE,BM=BN,∠EBC=∠MBN=60°,
∴∠CBM=∠EBN,
在△CBM和△EBN中,
,
∴△CBM≌△EBN(SAS),
∴∠BEN=∠BCM=60°,
∴∠BEN=∠EBC,
∴EN∥BC;
(3)解:DQ=AD+DP;理由如下:
延长BD至F,使DF=PD,连接PF,如图所示:
∵∠PDF=∠BDC=∠A+∠DBA=30°+30°=60°,
∴△PDF为等边三角形,
∴PF=PD=DF,∠F=60°,
∵∠PDQ=90°﹣∠A=60°,
∴∠F=∠PDQ=60°,
∴∠BDQ=180°﹣∠BDC﹣∠PDQ=60°,
∴∠BPQ=∠BDQ=60°,
∴∠Q=∠PBF,
在△PFB和△PDQ中,
,
∴△PFB≌△PDQ(AAS),
∴DQ=BF=BD+DF=BD+DP,
∵∠A=∠ABD,
∴AD=BD,
∴DQ=AD+DP.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末能力提升卷-2024-2025学年数学八年级上册苏科版
一.选择题(共8小题)
1.(2023秋 南充校级期末)下面是大疆科技、华为集团、太极股份和凤凰光学四个杰出科技企业的标志,其中是轴对称图形的是( )
A. B. C. D.
2.(2023秋 慈利县期末)下列各数中,不是无理数的是( )
A. B.π
C. D.0.1010010001
3.(2024春 韩城市期末)8的立方根是( )
A.±4 B.2 C.4 D.±2
4.(2023秋 文昌校级期末)下列函数(其中x是自变量)中,不是正比例函数的个数有( )
①y=﹣x;②y+2=2(x+1);③y=k2x(k是常数);④y2=x2.
A.1个 B.2个 C.3个 D.4个
5.(2023秋 东莞市校级期末)2002年国际数学家大会在北京召开,如图①是大会会标,会标中央图案是经过艺术处理的,它标志着中国古代数学的成就.如图②是我国古代数学家赵爽为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是( )
A.三角形内角和定理 B.三角形全等
C.勾股定理 D.轴对称图形
6.(2023秋 安徽期末)如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=3cm,CDBC,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0<t<10),连接DE,当△BDE是直角三角形时,t的值最多有( )个
A.1 B.2 C.3 D.4
7.(2023秋 阳城县期末)如图,等腰直角三角形DEF的斜边中点O与等腰直角三角形ABC的斜边中点重合,D,E两点分别在AB、BC上,若AB=4,AD=1,则△DEF的面积为( )
A.3 B.4 C.5 D.6
8.(2023秋 灵武市期末)在同一平面直角坐标系中,一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图象如图所示,则下列结论错误的是( )
A.y1随x的增大而增大
B.b<n
C.当x<2时,y1>y2
D.关于x,y的方程组的解为
二.填空题(共7小题)
9.(2024春 江都区期末)比较大小: .
10.(2023秋 金安区校级期末)在平面直角坐标系中,点P(2,2)到x轴的距离是 .
11.(2023秋 临潼区期末)如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若△ABC的周长26cm,△AEC的周长18cm,则AB的长为 .
12.(2023秋 蓬溪县期末)Rt△ABO在数轴上如图,点O在原点,OB=2,AB=1,以点O为圆心,OA为半径画弧,交数轴负半轴于点C,则点C所表示的数为 .
13.(2023秋 蜀山区期末)一次函数y=kx+b(k,b为常数且k≠0),若函数经过点(﹣2,0)和(0,1),则关于x的不等式kx+b>1的解集为 .
14.(2023秋 襄汾县期末)如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠ADE的度数为 .
15.(2023秋 迎江区校级期末)如图,在△ABC中,∠ABC=30°,,BC=2,点M在线段BC上运动(不包含点B),连接AM,将△ABM沿直线AM翻折得到△AB′M.
(1)当B′M⊥BC时,则∠BAM= .
(2)在点M运动过程中,点B′到直线BC距离的最大值是 .
三.解答题(共10小题)
16.(2023秋 廉江市校级期末).
17.(2023秋 裕安区校级期末)已知点P(a﹣3,a+1)解答下列各题:
(1)若点P在y轴上,试求出a的值;
(2)若Q(1,2),且PQ∥x轴,试求p的坐标.
18.(2023秋 仓山区校级期末)如图,BD平分∠ABC,∠1=∠2.求证:AD=CD.
19.(2023秋 平桥区校级期末)如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB于点F,且AC=EB.
(1)求证:△ACB≌△EBD;
(2)若DB=12,求AC的长.
20.(2023秋 金安区校级期末)△ABC在平面直角坐标系xOy中的位置如图所示,已知A(﹣2,3),B(﹣1,1),C(0,2),
(1)作△ABC关于y轴对称的图形△A1B1C1;
(2)将△A1B1C1向右平移4个单位长度,作出平移后的△A2B2C2.
21.(2023秋 平果市期末)如图,以等边△ABC的边AC为腰作等腰△ACD,连接BD,过点A作AE⊥BD交BC于点E,交DC的延长线于点F.
(1)求证:AE平分∠BAD;
(2)若∠AFD=∠BAC,CF=2,DF=7,求AF的长.
下面是小颖同学求AF长的过程,请将解题过程补充完整;
(2)解:如图所示,在FA上截取FG=FC,连接BF,CG,
∵∠AFD=∠BAC=60°,FG=FC,∴△FCG是等边三角形,
∴ .
∵△ABC是等边三角形,
∴BC=AC,∠ACB=∠GCF=60°,
∴ ,
在△ACG和△BCF中,
,
∴△ACG≌△BCF,
∴ .
由(1)知AF为BD的垂直平分线,
∴BF=FD,
∴ .
∴AF=AG+FG=DF+CF=7+2=9.
22.(2023秋 瑞金市期末)如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为20,求BC的长.
23.(2023秋 万安县期末)如图,直线y=2x+4与x轴交于点A,与y轴交于点B,点C是OB的中点.
(1)求点C的坐标;
(2)在x轴上找一点D,使得S△ACD=S△ABC,求点D的坐标;
(3)在x轴上是否存在一点P,使得△ABP是直角三角形?若存在,请写出点P的坐标;若不存在,请说明理由.
24.(2023秋 安庆期末)某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元,
(1)求A、B两种奖品单价各是多少元?
(2)学校计过购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍.设购买A种奖品m件,购买费用为w元,写出w(元)与m(件)之间的函数表达式,并求最少费用w的值.
25.(2023秋 长治期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.
(1)如图1,连接CE,求证:△BCE是等边三角形;
(2)如图2,点M为CE上一点,连接BM,作等边△BMN,连接EN,求证:EN∥BC;
(3)如图3,点P为线段AD上一点,连接BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间的数量关系,并证明.
期末能力提升卷-2024-2025学年数学八年级上册苏科版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8
答案 B C B B C C C C
一.选择题(共8小题)
1.(2023秋 南充校级期末)下面是大疆科技、华为集团、太极股份和凤凰光学四个杰出科技企业的标志,其中是轴对称图形的是( )
A. B. C. D.
【解答】解:选项A、C、D的图形均不能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形.
选项B的图形能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
故选:B.
2.(2023秋 慈利县期末)下列各数中,不是无理数的是( )
A. B.π
C. D.0.1010010001
【解答】解:由无理数的概念可知:...均是无理数,
是分数,不是无理数,
故选:C.
3.(2024春 韩城市期末)8的立方根是( )
A.±4 B.2 C.4 D.±2
【解答】解:∵23=8,∴,
故选:B.
4.(2023秋 文昌校级期末)下列函数(其中x是自变量)中,不是正比例函数的个数有( )
①y=﹣x;②y+2=2(x+1);③y=k2x(k是常数);④y2=x2.
A.1个 B.2个 C.3个 D.4个
【解答】解:①y=﹣x是正比例函数;
②y+2=2(x+1),整理得y=2x,是正比例函数;
③y=k2x(k是常数),当k=0时,不是函数,当k≠0时,是正比例函数;
④y2=x2,不是函数;
所以不是正比例函数的个数有2个,
故选:B.
5.(2023秋 东莞市校级期末)2002年国际数学家大会在北京召开,如图①是大会会标,会标中央图案是经过艺术处理的,它标志着中国古代数学的成就.如图②是我国古代数学家赵爽为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是( )
A.三角形内角和定理 B.三角形全等
C.勾股定理 D.轴对称图形
【解答】解:∵“弦图”是利用面积关系证明勾股定理的,
∴“弦图”解决的数学问题是:勾股定理.
故选:C.
6.(2023秋 安徽期末)如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=3cm,CDBC,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0<t<10),连接DE,当△BDE是直角三角形时,t的值最多有( )个
A.1 B.2 C.3 D.4
【解答】解:∵∠C=90°,BC=3cm,∠B=60°,
∴AB=2BC=6cm,
①当∠EDB=90°时,
∵BC=3cm,CDBC,
∴BD=2cm,
∵∠C=90°,
∴∠EDB=∠C,
∵∠B=∠B,
∴△BDE∽△BCA,
∴,
∴,
解得:BE=4,
即AE=6﹣4=2(cm),
当从A到E时,时间t=2秒,
当从A到B再到E时,时间t=6+4=10秒,
∵0<t<10,此时舍去;
②当∠BED=90°时,
∵∠DEB=∠C=90°,∠B=∠B,
∴△BED∽△BCA,
∴,
∴,
解得:BE=1(cm),
∴AE=5cm,
当从A到E时,时间t=5秒,
当从A到B再到E时,时间t=6+1=7(秒),
综合上述,时间t=2或5或7共3个,
故选:C.
7.(2023秋 阳城县期末)如图,等腰直角三角形DEF的斜边中点O与等腰直角三角形ABC的斜边中点重合,D,E两点分别在AB、BC上,若AB=4,AD=1,则△DEF的面积为( )
A.3 B.4 C.5 D.6
【解答】解:连接BO,EO,
∵△ABC是等腰直角三角形,O是斜边AC的中点,
∴OB⊥AC,OBAC,
∴OB=OA,
同理:OE⊥DF,OE=OD,
∵∠AOD+∠BOD=∠BOE+∠BOD=90°,
∴∠BOE=∠AOD,
在△OBE和△OAD中,
,
∴△OBE≌△OAD(SAS),
∴BE=AD=1,
∵BD=AB﹣AD=4﹣1=3,
∵∠DBE=90°,
∴DE,
∵△DEF是等腰直角三角形,
∴EF=DE,
∴△DEF的面积DE×EFDE2=5.
故选:C.
8.(2023秋 灵武市期末)在同一平面直角坐标系中,一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图象如图所示,则下列结论错误的是( )
A.y1随x的增大而增大
B.b<n
C.当x<2时,y1>y2
D.关于x,y的方程组的解为
【解答】解:A、y1随x的增大而增大,故选项A正确;
B、由图象可知,一次函数y1=ax+b(a≠0)的图象与y轴的交点在y2=mx+n(m≠0)的图象与y轴的交点的下方,即b<n,故选项B正确;
C、由图象可知:当x<2时,y1<y2,故选项C错误;
D、由图象可知,两条直线的交点为(2,3),
∴关于x,y的方程组的解为;
故选项D正确;
故选:C.
二.填空题(共7小题)
9.(2024春 江都区期末)比较大小: > .
【解答】解:∵,,18<12,
∴.
故答案为:>.
10.(2023秋 金安区校级期末)在平面直角坐标系中,点P(2,2)到x轴的距离是 2 .
【解答】解:点P(2,2)到x轴的距离是其纵坐标的绝对值,
所以点P(2,2)到x轴的距离为2,
故答案为:2.
11.(2023秋 临潼区期末)如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若△ABC的周长26cm,△AEC的周长18cm,则AB的长为 8cm .
【解答】解:∵AB的垂直平分线交AB于点D,交BC于点E,
∴AE=BE,
∵△ABC的周长是26cm,
∴BC+AB+AC=26(cm),
∵△AEC的周长18cm,
∴AC+AE+EC=18(cm),
∴BC+AC=18(cm),
∴AB=8(cm),
故答案为:8cm.
12.(2023秋 蓬溪县期末)Rt△ABO在数轴上如图,点O在原点,OB=2,AB=1,以点O为圆心,OA为半径画弧,交数轴负半轴于点C,则点C所表示的数为 .
【解答】解:由题意得,OB=2,AB=1,∠ABO=90°,OC=OA,
∴,
∴,
∵点C在点O左侧,
∴点C所表示的数为,
故答案为:.
13.(2023秋 蜀山区期末)一次函数y=kx+b(k,b为常数且k≠0),若函数经过点(﹣2,0)和(0,1),则关于x的不等式kx+b>1的解集为 x>0 .
【解答】解:如图所示,即为一次函数y=kx+b的函数图象,
由函数图象可知,当一次函数的函数值大于1时自变量的取值范围为x>0,
∴关于x的不等式kx+b>1的解集为x>0,
故答案为:x>0.
14.(2023秋 襄汾县期末)如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠ADE的度数为 70° .
【解答】解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,AB=AD,∠ADE=∠B,
∴∠EAC=∠DAB=40°,
∴△ABD中,∠B(180°﹣∠BAD)=70°,
∴∠ADE=∠B=70°,
故答案为:70°.
15.(2023秋 迎江区校级期末)如图,在△ABC中,∠ABC=30°,,BC=2,点M在线段BC上运动(不包含点B),连接AM,将△ABM沿直线AM翻折得到△AB′M.
(1)当B′M⊥BC时,则∠BAM= 15° .
(2)在点M运动过程中,点B′到直线BC距离的最大值是 .
【解答】解:(1)如图,
由折叠性质可知:∠B=∠B′=30°,∠AMB=∠AMB′,
∵∠AMB+∠AMB′+∠BMB′=360°,
∴∠AMB=∠AMB′=135°,
∵∠BAM+∠AMB+∠B=180°,
∴∠BAM=15°,
故答案为:15°;
(2)如图,AB′=AB,当垂足E在线段AB′上时,点B′到直线BC距离的最大;
∴∠AEM=∠B′EM=90°,
由折叠性质可知:∠BAM=∠B′AM,∠B=∠B′=30°,
∴∠BAE=60°,
∴∠EAM=∠BAM=∠B′=30°,
∴,
故答案为:.
三.解答题(共10小题)
16.(2023秋 廉江市校级期末).
【解答】解:原式=﹣2+1﹣(﹣8)+1
=﹣1+8+1
=8.
17.(2023秋 裕安区校级期末)已知点P(a﹣3,a+1)解答下列各题:
(1)若点P在y轴上,试求出a的值;
(2)若Q(1,2),且PQ∥x轴,试求p的坐标.
【解答】解:(1)∵点P(a﹣3,a+1)在y轴上,
∴a﹣3=0,
解得a=3;
(2)∵点P(a﹣3,a+1),Q(1,2),且PQ∥x轴,
∴a+1=2,
解得a=1,
∴a﹣3=1﹣3=﹣2,
∴P(﹣2,2).
18.(2023秋 仓山区校级期末)如图,BD平分∠ABC,∠1=∠2.求证:AD=CD.
【解答】证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠1=∠2,
∴180°﹣∠1=180°﹣∠2,
∴∠ADB=∠CDB,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(ASA),
∴AD=CD.
19.(2023秋 平桥区校级期末)如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB于点F,且AC=EB.
(1)求证:△ACB≌△EBD;
(2)若DB=12,求AC的长.
【解答】(1)证明:∵∠ACB=∠DBC=90°,DE⊥AB,
∴∠DEB+∠ABC=90°,∠A+∠ABC=90°,
∴∠DEB=∠A.
在△ACB和△EBD中,
,
∴△ACB≌△EBD(ASA);
(2)解:∵△ACB≌△EBD,
∴BC=DB,AC=EB.
∵E是BC的中点,
∴EBBC.
∵DB=12,BC=DB,
∴BC=12,
∴AC=EBBC=6.
20.(2023秋 金安区校级期末)△ABC在平面直角坐标系xOy中的位置如图所示,已知A(﹣2,3),B(﹣1,1),C(0,2),
(1)作△ABC关于y轴对称的图形△A1B1C1;
(2)将△A1B1C1向右平移4个单位长度,作出平移后的△A2B2C2.
【解答】解:(1)如图1,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
21.(2023秋 平果市期末)如图,以等边△ABC的边AC为腰作等腰△ACD,连接BD,过点A作AE⊥BD交BC于点E,交DC的延长线于点F.
(1)求证:AE平分∠BAD;
(2)若∠AFD=∠BAC,CF=2,DF=7,求AF的长.
下面是小颖同学求AF长的过程,请将解题过程补充完整;
(2)解:如图所示,在FA上截取FG=FC,连接BF,CG,
∵∠AFD=∠BAC=60°,FG=FC,∴△FCG是等边三角形,
∴ CG=CF .
∵△ABC是等边三角形,
∴BC=AC,∠ACB=∠GCF=60°,
∴ ∠ACG=60°﹣∠BCG=∠BCF ,
在△ACG和△BCF中,
,
∴△ACG≌△BCF,
∴ AG=BF .
由(1)知AF为BD的垂直平分线,
∴BF=FD,
∴ AG=DF .
∴AF=AG+FG=DF+CF=7+2=9.
【解答】(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,
∵△ACD是等腰三角形,
∴AC=AD,
∴AB=AD,即△ABD是等腰三角形,
∵AG⊥BD,
∴AG平分∠BAD,
∵点E是AG线段上的一点,即点A,G,E三点共线,
∴AE平分∠BAD;
(2)解:如图所示,在FA上截取FG=FC,连接BF,CG,
∵∠AFD=∠BAC=60°,FG=FC,
∴△FCG是等边三角形,
∴CG=CF,
∵△ABC是等边三角形,
∴BC=AC,∠ACB=∠GCF=60°,
∴∠ACG=60°﹣∠BCG=∠BCF,
在△ACG和△BCF中,
,
∴△ACG≌△BCF(SAS),
∴AG=BF,
由(1)可知AF为BD的垂直平分线,
∴BF=FD,
∴AG=DF,
∴AF=AG+FG=DF+CF=7+2=9.
故答案为:CG=CF,∠ACG=60°﹣∠BCG=∠BCF,AG=BF,AG=DF.
22.(2023秋 瑞金市期末)如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为20,求BC的长.
【解答】解:(1)∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣30°﹣50°=100°;
∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30°,
同理可得,∠FAC=∠ACB=50°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=100°﹣30°﹣50°=20°;
(2)∵△DAF的周长为20,
∴DA+DF+FA=20,
由(1)可知,DA=DB,FA=FC,
∴BC=DB+DF+FC=DA+DF+FA=20.
23.(2023秋 万安县期末)如图,直线y=2x+4与x轴交于点A,与y轴交于点B,点C是OB的中点.
(1)求点C的坐标;
(2)在x轴上找一点D,使得S△ACD=S△ABC,求点D的坐标;
(3)在x轴上是否存在一点P,使得△ABP是直角三角形?若存在,请写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵直线y=2x+4与x轴交于点A,与y轴交于点B,
当x=0时,y=4;当y=0时,x=﹣2,
∴B(0,4),A(﹣2,0),
∵点C是OB的中点,
∴C(0,2);
(2)∵OA=2,OC=2,BC=OB﹣OC=4﹣2=2,
∴S△ABC=BC OA 2×22,
∵S△ACD=S△ABC,
∴S△ACD=AD OC AD×22,
∴AD=2,
当点D在点A左侧时,OD=OA+AD=2+2=4,
∴D(﹣4,0),
当点D在点A右侧时,OD=OA﹣AD=2﹣2=0,
∴D(0,0),
综上,D(﹣4,0)或(0,0);
(3)存在,设点P的坐标为(m,0),
①∠APB=90°时,点P与原点重合,坐标为(0,0);
②∠ABP=90°时,则AP2=AB2+BP2,
∵AP=m+2,AB2=OA2+OB2=22+42=20,BP2=OB2+OP2=42+m2,
∴(m+2)2=20+42+m2,
解得m=8,
∴P(8,0),
综上,P(0,0)或(8,0).
24.(2023秋 安庆期末)某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元,
(1)求A、B两种奖品单价各是多少元?
(2)学校计过购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍.设购买A种奖品m件,购买费用为w元,写出w(元)与m(件)之间的函数表达式,并求最少费用w的值.
【解答】解(1)设A奖品的单价是x元,B奖品的单价是y元,由题意,得
,
解得,
答:A奖品的单价是10元,B奖品的单价是15元;
(2)由题意,得
w=10m+15(100﹣m)=﹣5m+1500
∴,
解得:70≤m≤75.
∵m是整数,
∴m=70,71,72,73,74,75.
∵w=﹣5m+1500,
∴k=﹣5<0,
∴w随m的增大而减小,
∴m=75时,w最小=1125.
∴应买A种奖品75件,B种奖品25件,才能使总费用最少为1125元.
25.(2023秋 长治期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.
(1)如图1,连接CE,求证:△BCE是等边三角形;
(2)如图2,点M为CE上一点,连接BM,作等边△BMN,连接EN,求证:EN∥BC;
(3)如图3,点P为线段AD上一点,连接BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间的数量关系,并证明.
【解答】(1)证明:∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵BD是△ABC的角平分线,
∴∠DBA∠ABC=30°,
∴∠A=∠DBA,
∴AD=BD,
∵DE⊥AB,
∴AE=BE,
∴CEAB=BE,
∴△BCE是等边三角形;
(2)证明:∵△BCE与△MNB都是等边三角形,
∴BC=BE,BM=BN,∠EBC=∠MBN=60°,
∴∠CBM=∠EBN,
在△CBM和△EBN中,
,
∴△CBM≌△EBN(SAS),
∴∠BEN=∠BCM=60°,
∴∠BEN=∠EBC,
∴EN∥BC;
(3)解:DQ=AD+DP;理由如下:
延长BD至F,使DF=PD,连接PF,如图所示:
∵∠PDF=∠BDC=∠A+∠DBA=30°+30°=60°,
∴△PDF为等边三角形,
∴PF=PD=DF,∠F=60°,
∵∠PDQ=90°﹣∠A=60°,
∴∠F=∠PDQ=60°,
∴∠BDQ=180°﹣∠BDC﹣∠PDQ=60°,
∴∠BPQ=∠BDQ=60°,
∴∠Q=∠PBF,
在△PFB和△PDQ中,
,
∴△PFB≌△PDQ(AAS),
∴DQ=BF=BD+DF=BD+DP,
∵∠A=∠ABD,
∴AD=BD,
∴DQ=AD+DP.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
