第四章 图形的相似 单元复习(含答案) 2024--2025学年北师大版九年级数学上册
文档属性
| 名称 | 第四章 图形的相似 单元复习(含答案) 2024--2025学年北师大版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 660.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-22 00:00:00 | ||
图片预览


文档简介
第四章 图形的相似 单元复习 2024--2025学年北师大版九年级数学上册
一、单选题
1.下列数中,能与6,9,10组成比例的数是( )
A.1 B.74 C.5.4 D.1.5
2.下列说法中不正确的是( )
A.相似多边形对应边的比等于相似比
B.相似多边形对应角平分线的比等于相似比
C.相似多边形周长的比等于相似比
D.相似多边形面积的比等于相似比
3.如图所示,长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下矩形与原矩形相似,那么剩下矩形的面积是( )
A.28cm2 B.27cm2 C.21cm2 D.20cm2
4.已知在中,,下列阴影部分的三角形与原不相似的是( )
A. B.
C. D.
5.如图,以点为位似中心,将放大得到若::,则的值为( )
A. B. C. D.
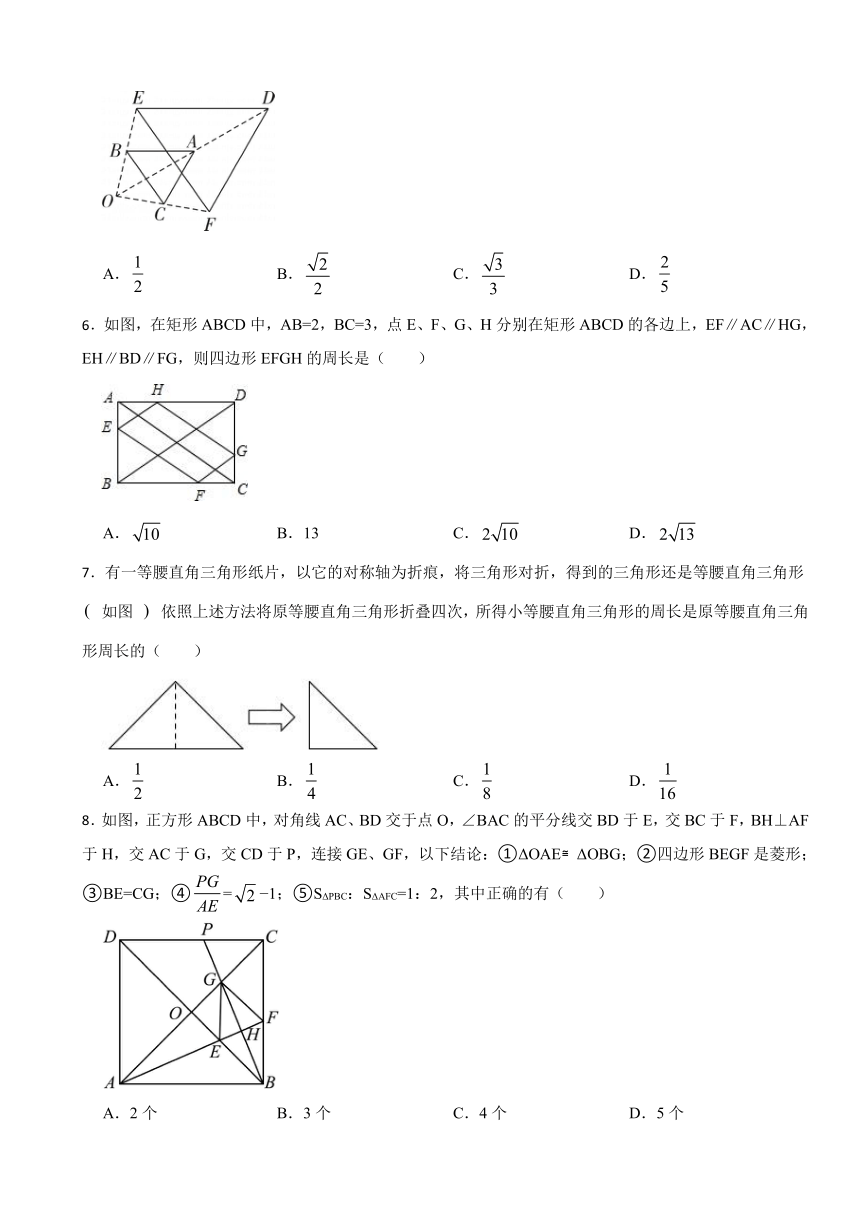
6.如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( )
A. B.13 C. D.
7.有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形 如图 依照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的( )
A. B. C. D.
8.如图,正方形ABCD中,对角线AC、BD交于点O,∠BAC的平分线交BD于E,交BC于F,BH⊥AF于H,交AC于G,交CD于P,连接GE、GF,以下结论:①ΔOAE ΔOBG;②四边形BEGF是菱形;③BE=CG;④= 1;⑤SΔPBC:SΔAFC=1:2,其中正确的有( )
A.2个 B.3个 C.4个 D.5个
9.如图,将矩形ABCD沿着GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,点E,O,F 在另一条直线上. 以下结论正确的是( )
A.△COF∽△CEG B.OC=3OF
C.AB:AD=4:3 D.GE=DF
10.如图,是矩形内的任意一点,连接,,,,得到,,,,设它们的面积分别是,,,,下列结论错误的是( )
A.若,则点在边的垂直平分线上
B.
C.若,,则的最小值为10
D.若,且,,则
二、填空题
11.如图,E是边AB上一点,连接AC、DE交于点F,,则 .
12.在同一时刻,身高1.6m的小强的影长是1.2m,旗杆的影长是15m,则旗杆高为 .
13.如图,在中,E是的中点,F是上的一点,,延长交的延长线于点G,若,则 .
14.某一时刻,小明测得一高为1m的竹竿的影长为0.8m,小李测得一棵树的影长为,那么这棵树的高是 .
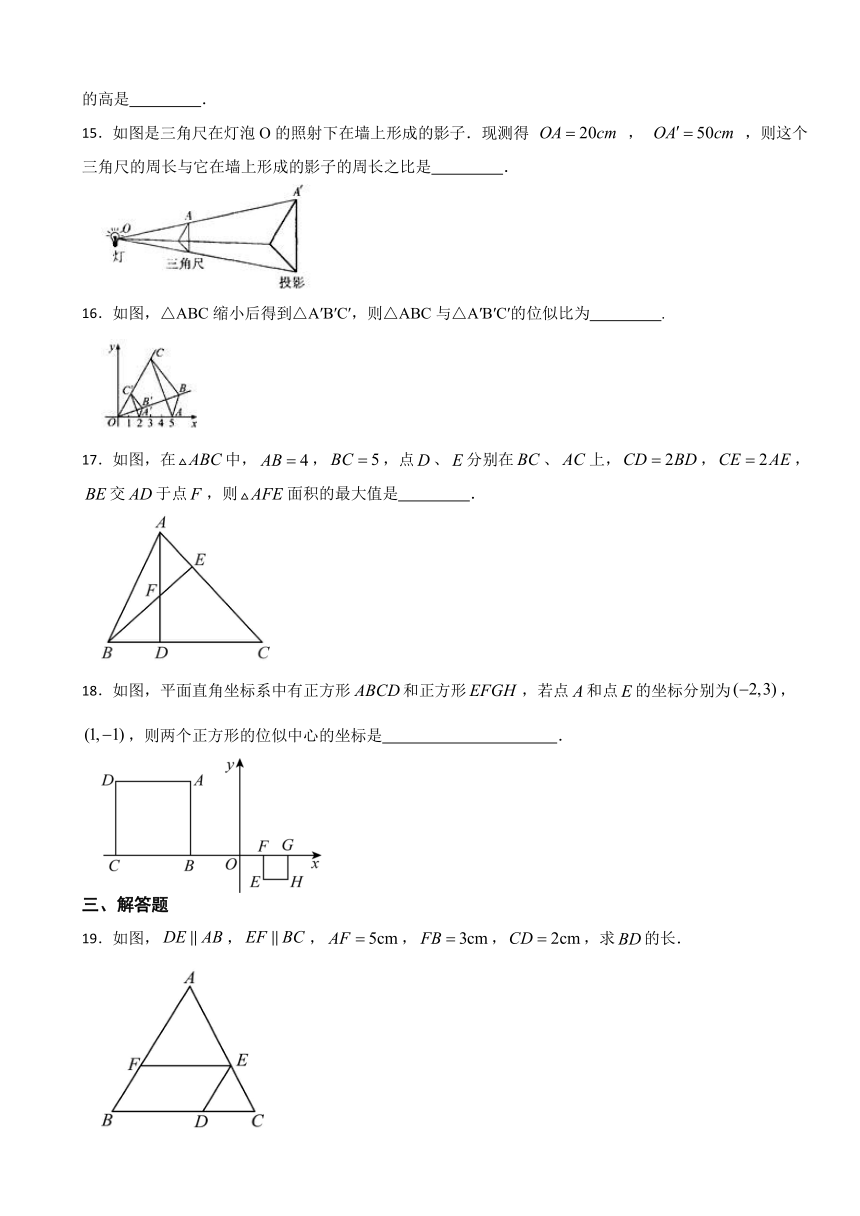
15.如图是三角尺在灯泡O的照射下在墙上形成的影子.现测得 , ,则这个三角尺的周长与它在墙上形成的影子的周长之比是 .
16.如图,△ABC缩小后得到△A′B′C′,则△ABC与△A′B′C′的位似比为 .
17.如图,在中,,,点、分别在、上,,,交于点,则面积的最大值是 .
18.如图,平面直角坐标系中有正方形和正方形,若点和点的坐标分别为,,则两个正方形的位似中心的坐标是 .
三、解答题
19.如图,,,,,,求的长.
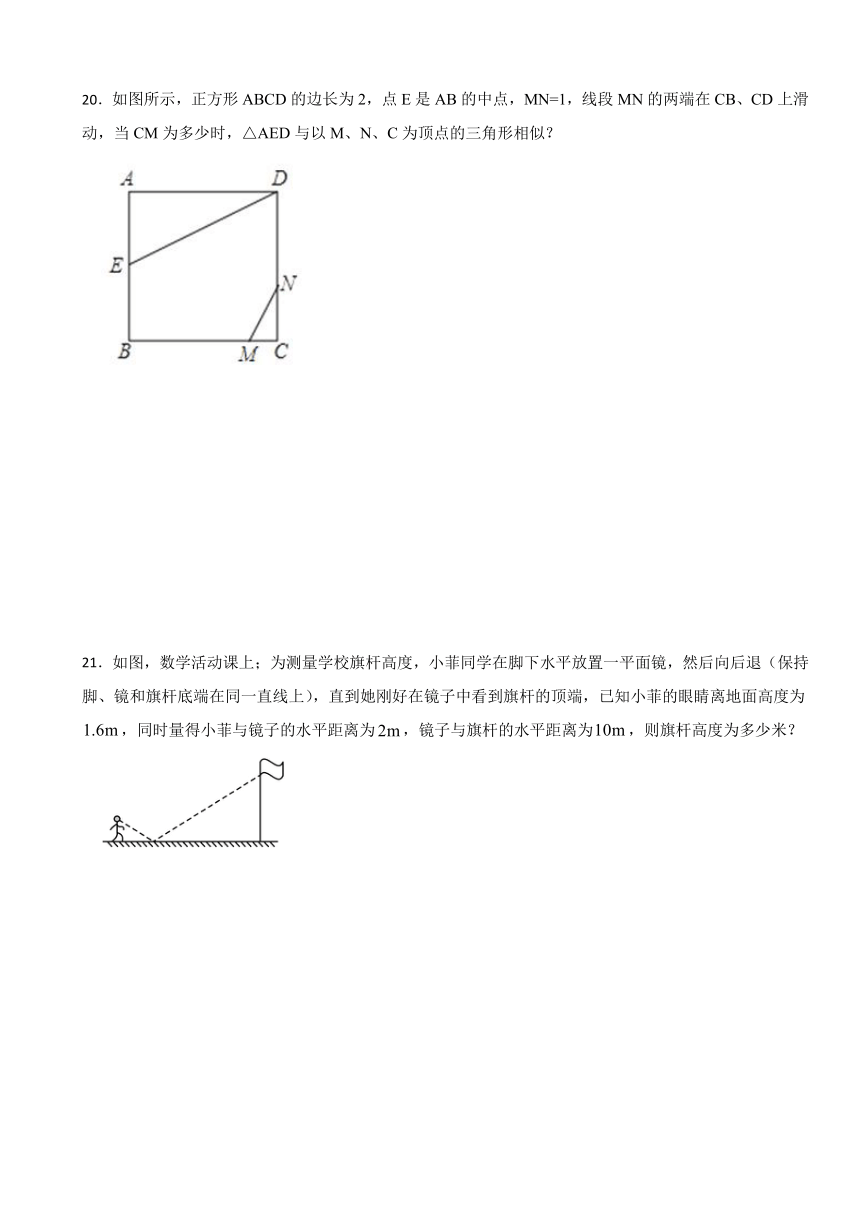
20.如图所示,正方形ABCD的边长为2,点E是AB的中点,MN=1,线段MN的两端在CB、CD上滑动,当CM为多少时,△AED与以M、N、C为顶点的三角形相似?
21.如图,数学活动课上;为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端,已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,则旗杆高度为多少米?
22.已知 是正方形 边 上任意一点,
(1) 将 沿 翻折至 ,
①如图 23-9①, 若 点恰好在对角线 上, , 求 的长;
②如图②, 若点 是 中点, , 射线 与 边交于点 , 求四边形 的面积.
(2) 如图③, 点 是边 上任意一点, 与 交于点 , 射线 与射线 交于点 , 求证: .
23.用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用.甲同学说:“当正方形的一边在最长边时,剪出的内接正方形最大”;乙同学说:“当正方形的一边在最短边上时,剪出的内接正方形最大”;丙同学说:“不确定,剪不出这样的正方形纸.”你认为谁说的有道理,请证明.(假设图中△ABC的三边a,b,c,且a>b>c,三边上的高分别记为ha,hb,hc)
24.如图所示,系列矩形纸张的规格特征是:①各矩形纸张都相似;②纸对裁后可以得到两张纸,纸对裁后可以得到两张纸,纸对裁后可以得到两张纸.
(1)填空:纸面积是纸面积的 倍,纸周长是纸周长的 倍.
(2)根据系列纸张的规格特征,求出该系列纸张的长与宽(长大于宽)之比.
(3)设1张纸张的重量为克,试求出1张纸张的质量.(用含的代数式表示)
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】B
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】
12.【答案】20
13.【答案】
14.【答案】12m
15.【答案】2:5
16.【答案】5∶2
17.【答案】
18.【答案】 或
19.【答案】
20.【答案】解:∵正方形ABCD的边长为2,点E是AB的中点,
∴∠A=90°,AB=AD=2,AE=AB=1,
∴DE= =,
分两种情况:
①CM与AE是对应边时,△AED∽△CMN,
∴,即,
解得:CM=;
②CM与AD是对应边时,△AED∽△CNM,
∴,即,
解得:CM=.
综上所述:当CM为或时,△AED与以M、N、C为顶点的三角形相似.
21.【答案】解:如图:
,,
,
,
,
,
即,
,
旗杆高度为8米.
22.【答案】(1)解:① 四边形 是正方形,
.
设 .
将 沿 翻折至 ,
.
.
, 即 ,
解得 , 即 .
②如图, 分别延长 交于点 ,
四边形 是正方形
.
.
点 中点,
.
,
解得 (负值已舍去).
易知 ,
.
. .
设 , 则
在 Rt 中, 由勾股定理得: ,
即 ,
解得 .
四边形 的面积
.
(2)证明: 设 ,
则 ,
.
四边形 是正方形,
.
.
.
易得 .
23.【答案】设△ABC的三条边上的对应高分别为ha,hb,hc,一边分别落在a,b,c上的内接正方形边长分别记为xa,xb,xc,
易得:△APN~△ABC,
∴ ,
∴xa= ,
同理xb= ,xc= ,
又设三角形ABC面积为s
∴xa﹣xb=
=
=
= (
= )
∵a>b,ha<b,
∴(b﹣a)(1﹣ )<0,
即xa﹣xb<0,
∴xa<xb,
同理:xb<xc,
∴xa<xb<xc.
∴乙同学说的正确.
24.【答案】(1)2;2
(2)解:设A1的长宽为m、n,则A2的长宽为n、,
∵两个矩形相似,
∴,
∴;
(3)解:由(1)可得对裁后的矩形重量是对裁前的,即克.
一、单选题
1.下列数中,能与6,9,10组成比例的数是( )
A.1 B.74 C.5.4 D.1.5
2.下列说法中不正确的是( )
A.相似多边形对应边的比等于相似比
B.相似多边形对应角平分线的比等于相似比
C.相似多边形周长的比等于相似比
D.相似多边形面积的比等于相似比
3.如图所示,长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下矩形与原矩形相似,那么剩下矩形的面积是( )
A.28cm2 B.27cm2 C.21cm2 D.20cm2
4.已知在中,,下列阴影部分的三角形与原不相似的是( )
A. B.
C. D.
5.如图,以点为位似中心,将放大得到若::,则的值为( )
A. B. C. D.
6.如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( )
A. B.13 C. D.
7.有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形 如图 依照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的( )
A. B. C. D.
8.如图,正方形ABCD中,对角线AC、BD交于点O,∠BAC的平分线交BD于E,交BC于F,BH⊥AF于H,交AC于G,交CD于P,连接GE、GF,以下结论:①ΔOAE ΔOBG;②四边形BEGF是菱形;③BE=CG;④= 1;⑤SΔPBC:SΔAFC=1:2,其中正确的有( )
A.2个 B.3个 C.4个 D.5个
9.如图,将矩形ABCD沿着GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,点E,O,F 在另一条直线上. 以下结论正确的是( )
A.△COF∽△CEG B.OC=3OF
C.AB:AD=4:3 D.GE=DF
10.如图,是矩形内的任意一点,连接,,,,得到,,,,设它们的面积分别是,,,,下列结论错误的是( )
A.若,则点在边的垂直平分线上
B.
C.若,,则的最小值为10
D.若,且,,则
二、填空题
11.如图,E是边AB上一点,连接AC、DE交于点F,,则 .
12.在同一时刻,身高1.6m的小强的影长是1.2m,旗杆的影长是15m,则旗杆高为 .
13.如图,在中,E是的中点,F是上的一点,,延长交的延长线于点G,若,则 .
14.某一时刻,小明测得一高为1m的竹竿的影长为0.8m,小李测得一棵树的影长为,那么这棵树的高是 .
15.如图是三角尺在灯泡O的照射下在墙上形成的影子.现测得 , ,则这个三角尺的周长与它在墙上形成的影子的周长之比是 .
16.如图,△ABC缩小后得到△A′B′C′,则△ABC与△A′B′C′的位似比为 .
17.如图,在中,,,点、分别在、上,,,交于点,则面积的最大值是 .
18.如图,平面直角坐标系中有正方形和正方形,若点和点的坐标分别为,,则两个正方形的位似中心的坐标是 .
三、解答题
19.如图,,,,,,求的长.
20.如图所示,正方形ABCD的边长为2,点E是AB的中点,MN=1,线段MN的两端在CB、CD上滑动,当CM为多少时,△AED与以M、N、C为顶点的三角形相似?
21.如图,数学活动课上;为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端,已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,则旗杆高度为多少米?
22.已知 是正方形 边 上任意一点,
(1) 将 沿 翻折至 ,
①如图 23-9①, 若 点恰好在对角线 上, , 求 的长;
②如图②, 若点 是 中点, , 射线 与 边交于点 , 求四边形 的面积.
(2) 如图③, 点 是边 上任意一点, 与 交于点 , 射线 与射线 交于点 , 求证: .
23.用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用.甲同学说:“当正方形的一边在最长边时,剪出的内接正方形最大”;乙同学说:“当正方形的一边在最短边上时,剪出的内接正方形最大”;丙同学说:“不确定,剪不出这样的正方形纸.”你认为谁说的有道理,请证明.(假设图中△ABC的三边a,b,c,且a>b>c,三边上的高分别记为ha,hb,hc)
24.如图所示,系列矩形纸张的规格特征是:①各矩形纸张都相似;②纸对裁后可以得到两张纸,纸对裁后可以得到两张纸,纸对裁后可以得到两张纸.
(1)填空:纸面积是纸面积的 倍,纸周长是纸周长的 倍.
(2)根据系列纸张的规格特征,求出该系列纸张的长与宽(长大于宽)之比.
(3)设1张纸张的重量为克,试求出1张纸张的质量.(用含的代数式表示)
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】B
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】
12.【答案】20
13.【答案】
14.【答案】12m
15.【答案】2:5
16.【答案】5∶2
17.【答案】
18.【答案】 或
19.【答案】
20.【答案】解:∵正方形ABCD的边长为2,点E是AB的中点,
∴∠A=90°,AB=AD=2,AE=AB=1,
∴DE= =,
分两种情况:
①CM与AE是对应边时,△AED∽△CMN,
∴,即,
解得:CM=;
②CM与AD是对应边时,△AED∽△CNM,
∴,即,
解得:CM=.
综上所述:当CM为或时,△AED与以M、N、C为顶点的三角形相似.
21.【答案】解:如图:
,,
,
,
,
,
即,
,
旗杆高度为8米.
22.【答案】(1)解:① 四边形 是正方形,
.
设 .
将 沿 翻折至 ,
.
.
, 即 ,
解得 , 即 .
②如图, 分别延长 交于点 ,
四边形 是正方形
.
.
点 中点,
.
,
解得 (负值已舍去).
易知 ,
.
. .
设 , 则
在 Rt 中, 由勾股定理得: ,
即 ,
解得 .
四边形 的面积
.
(2)证明: 设 ,
则 ,
.
四边形 是正方形,
.
.
.
易得 .
23.【答案】设△ABC的三条边上的对应高分别为ha,hb,hc,一边分别落在a,b,c上的内接正方形边长分别记为xa,xb,xc,
易得:△APN~△ABC,
∴ ,
∴xa= ,
同理xb= ,xc= ,
又设三角形ABC面积为s
∴xa﹣xb=
=
=
= (
= )
∵a>b,ha<b,
∴(b﹣a)(1﹣ )<0,
即xa﹣xb<0,
∴xa<xb,
同理:xb<xc,
∴xa<xb<xc.
∴乙同学说的正确.
24.【答案】(1)2;2
(2)解:设A1的长宽为m、n,则A2的长宽为n、,
∵两个矩形相似,
∴,
∴;
(3)解:由(1)可得对裁后的矩形重量是对裁前的,即克.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
