2.2法拉第电磁感应定律 课件(共37张PPT) 2024-2025学年人教版(2019)高中物理选择性必修第二册
文档属性
| 名称 | 2.2法拉第电磁感应定律 课件(共37张PPT) 2024-2025学年人教版(2019)高中物理选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 14.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-20 21:08:27 | ||
图片预览










文档简介
(共37张PPT)
2.2 法拉第电磁感应定律
人教版(2019)物理(选择性必修第二册)
第二章 电磁感应
目录
素养目标
01
课程导入
02
新课讲解
03
总结归纳
04
课堂练习
05
正确教育
素养目标
1.知道感应电动势的概念,会区分 的物理意义
2.理解法拉第电磁感应定律的内容和数学表达式
3.知道公式 E=Blvsinθ 的推导过程及适用条件
感应电流的大小是否与磁通量的变化有关呢?
穿过闭合导体回路的磁通量发生变化,闭合导体回路中就有感应电流。感应电流的大小跟哪些因素有关呢?
产生感应电流的条件
闭合电路
磁通量变化
新课讲解
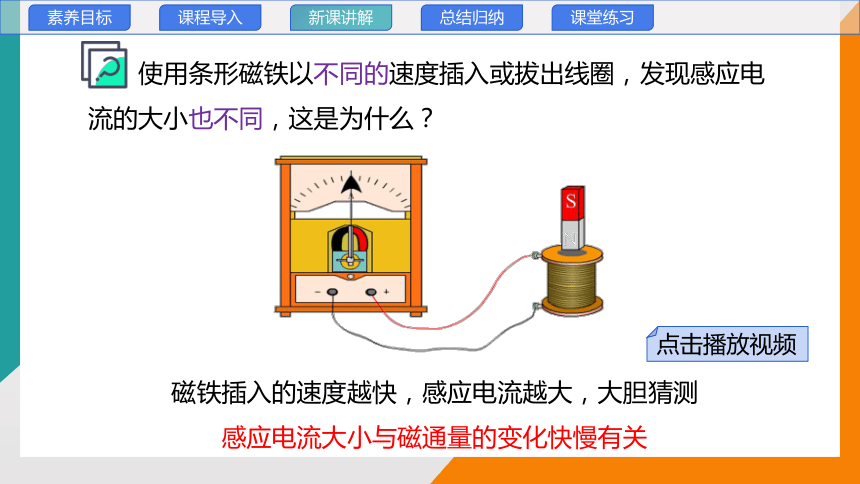
磁铁插入的速度越快,感应电流越大,大胆猜测
感应电流大小与磁通量的变化快慢有关
使用条形磁铁以不同的速度插入或拔出线圈,发现感应电流的大小也不同,这是为什么?
点击播放视频
体会感应电流大小的变化
返回
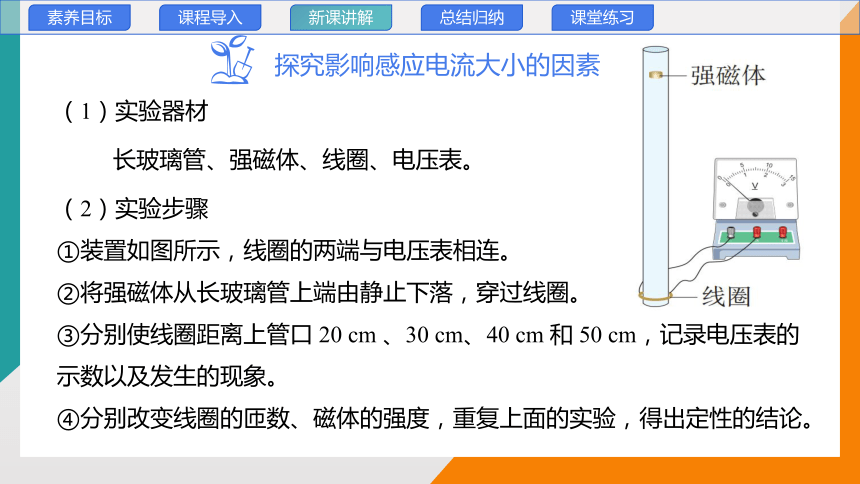
(1)实验器材
长玻璃管、强磁体、线圈、电压表。
(2)实验步骤
①装置如图所示,线圈的两端与电压表相连。
②将强磁体从长玻璃管上端由静止下落,穿过线圈。
③分别使线圈距离上管口 20 cm 、30 cm、40 cm 和 50 cm,记录电压表的示数以及发生的现象。
④分别改变线圈的匝数、磁体的强度,重复上面的实验,得出定性的结论。
探究影响感应电流大小的因素
条件 线圈匝数:200;磁铁个数:2个 下落高度 10cm 40cm
指针刻度
感应电流大小与磁铁在线圈中运动时间的关系
20
超出量程
感应电流大小
与磁铁在线圈中运动时间的关系?
感应电流大小与磁铁在线圈中运动时间成反比例关系
结论:
条件 线圈匝数:200;下落高度:30cm 磁铁个数 1 2
指针刻度
感应电流大小与磁体的强度的关系
15
30
感应电流大小是否与磁体的强度的关系?
感应电流大小与磁感应强度(磁铁个数)成正比例关系
结论:
条件 磁铁个数:2个;下落高度:30cm 线圈匝数 100 200
指针刻度
感应电流大小与线圈匝数的关系
15
30
感应电流大小是否与线圈匝数的关系?
感应电流大小与线圈匝数成正比例关系
结论:
重复上述实验多次,
可知,线圈距上管口距离越大,强磁体穿过线圈的速度越大,引起的磁通量变化越快,线圈两端的电压越大;线圈匝数越多、磁体越强,线圈两端的电压越大。
(4)实验结论:
磁通量变化越快,感应电动势越大,在同一电路中,感应电流越大;反之越小。
磁通量的变化就是磁通量的变化率,用 表示。
1.定义:在电磁感应现象中产生的电动势叫感应电动势
①产生感应电动势的那部分导体相当于电源
②产生条件:穿过电路的磁通量发生改变,与电路是否闭合无关
③方向判断:感应电动势的方向用楞次定律结合安培定则或右手定则判断
产生电动势的线圈相当于电源
感应电动势
如果电路不闭合虽然没有感应电流,但电动势依然存在。所以产生感应电动势为电磁感应现象的本质。
N
S
G
v
感应电动势大小
磁通量的变化率:
线圈的匝数n
电磁感应现象的本质
影响感应电动势大小的因素
闭合电路中感应电动势大小,跟穿过这一电路的磁通量的变化率 成正比。
1. 内容:
2.表达式:
1845年和1846年德国物理学家纽曼和韦伯先后在总结法拉第大量实验事实基础上提出了定量化的电磁感应定律,并用数学表达式的形式展现出来
①当各物理量单位都用国际单位时,k=1,则
②若线圈有n匝时,可以看成n个单匝线圈串联而成
3.感应电动势单位:
法拉第电磁感应定律
伏特(V),1 V=1 Wb/s
6、表达式 E=nΔΦ/Δt 的理解:
(1)n:线圈匝数
(2)ΔΦ/Δt:磁通量变化率(磁通量变化快慢),Φ-t图像中,斜率k=ΔΦ/Δt, 斜率k越大,感应电动势越大。与Φ、ΔΦ无直接关系,与n无关。
(3)ΔΦ:磁通量变化多少,与n无关
(4)Φ:磁感线条数多少,与n无关
该公式只求E感大小,E感方向(与内部I感方向相同)由楞次定律另行判断,求值时ΔΦ取绝对值,不涉及正负。
5、适用范围:所有电磁感应现象中的感应电动势求值
(1)一般为Δt时间内的平均感应电动势;
(2)当Δt→0时,表示瞬时感应电动势。
4、公式说明:
法拉第电磁感应定律
Φ大,ΔΦ不一定大
Φ大,ΔΦ/Δt不一定大
ΔΦ/Δt大小决定感应电动势的大小
磁感应强度变化
面积变化
Φ-t 图像上切线ΔΦ/Δt斜率表示
如图(a)所示的螺线管,匝数n=1 500,横截面积S=20 cm2,方向向右穿过螺线管的匀强磁场的磁感应强度按图(b)所示规律变。
(a)
(b)
(1)2 s内穿过线圈的磁通量的变化量是多少
(2)磁通量的变化率多大
(3)线圈中感应电动势的大小为多少
经典例题
【答案】(1)8×10-3 Wb (2)4×10-3 Wb/s (3)6 V
通过以上实验,你认为哪些因素影响了导线切割磁感线时电动势的大小?
如图所示,闭合电路中的一部分导体ab处于匀强磁场中,磁感应强度为B,两平行导轨的间距为L,导体ab以速度v匀速切割磁感线,其中B、L、v两两垂直,求产生的感应电动势
分析:回路在时间Δt 内增大的面积为:
ΔS=LvΔt
感应电动势为:
穿过回路的磁通量的变化为:
ΔΦ=BΔS
=BLvΔt
v 是相对于磁场的速度
适用条件:匀强磁场中,导线、B、v 相互垂直时
讨论:那要是B、L、v不垂直怎么计算呢?
× × × × × × × × × ×
× × × × × × × × × ×
G
a
b
v
a
b
如果将与B的方向夹角为θ速度按右图中所示分解在与磁场垂直和与磁场平行方向上,他们各自的产生电动势是多少?
①垂直于磁感线的分量:v1=vsinθ
②平行于磁感线的分量:v2=vcosθ
只有垂直于磁感线的分量切割磁感线,
才能产生感应电动势:
E=BLv1=Blvsinθ
θ=0时
平行:E=0
θ=90° 时
垂直:E=BLv
(无切割)
对切割有贡献
对切割无贡献
θ
v
B
注意:1.为切割磁感线的有效长度。
(垂直于、的两端口距离)
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
v
v
v
× × × ×
× × × ×
× × × ×
× × × ×
v
2. 是的特例,只适用于切割。
3. v为瞬时速度时, E为瞬时感应电动势;
v为平均速度时, E为平均感应电动势。
4.导体转动切割磁感线时的感应电动势:
(1)导体绕一端转动切割磁感线时:
(2)导体绕两端间某点转动切割磁感线时:
(3)导体绕两端延长线某点转动切割磁感线时:
(1)动生电动势大小原理:
(2)动生电动势方向:
右手定则
(3)非静电力来源:动生电动势所对应的非静电力是洛伦兹力沿导体棒方向的分力。
注意:动生电动势与洛伦兹力有关,但洛伦兹力始终不做功
动生电动势原理:由于导体运动切割磁感线而产生的电动势
× × × ×
× × × ×
× × × ×
+
+
+
C
D
+
-
V1
F2
F电
【例】如图所示,平行导轨间距为d,其左端接一个电阻R,匀强磁场的磁感应强度为B,方向垂直于平行金属导轨所在平面,一根金属棒与导轨成θ角放置,金属棒与导轨的电阻均不计。当金属棒沿垂直于棒的方向以恒定的速度v在导轨上滑行时,通过电阻R的电流大小是( )
D
法拉第电磁感应定律
法拉第电磁感应定律
导线切割磁感线时的感应电动势
感应电动势
(v⊥B)
(v⊥杆)
1.一根绝缘硬质细导线顺次绕成如图所示的线圈,其中大圆的面积为S1,小圆的面积均为S2。垂直线圈平面方向有一随时间t 变化的磁场,磁感应强度大小B=B0+kt,B0和k均为常量,则线圈中总的感应电动势大小为( )
A.
B.
C.
D.
C
答案:C
解析:由法拉第电磁感应定律可得大圆线圈产生的感应电动势为 ,每个小圆线圈产生的感应电动势均为 ,由线圈的绕线方式和楞次定律可知,4个小圆线圈产生的感应电动势方向相同,而大圆线圈产生的感应电动势方向与4个小圆线圈产生的感应电动势方向相反,所以线圈中总的感应电动势大小为 ,故选C。
2.如图甲所示,螺线管匝数n = 1000匝,横截面积S = 10 cm2,螺线管导线电阻r = 1Ω,电阻R = 9Ω,磁感应强度B的B-t图像如图乙所示(以向右为正方向),则( )
A.感应电动势为0.6V
B.感应电流为0.06A
C.电阻R两端的电压为6V
D.0~1s内感应电流的方向为从C点通过R流向A点
D
答案:D
解析:A.根据法拉第电磁感应定律
A错误;
B.根据闭合电路欧姆定律得感应电流为
B错误;
C.根据欧姆定律得电阻R两端的电压为
C错误;
D.根据楞次定律得0~1s内感应电流的方向为从C点通过R流向A点,D正确。
3.图甲为100匝面积为100cm2的圆形金属线圈处于匀强磁场中,磁场方向垂直线圈平面,t = 0时刻磁场
方向如图甲所示,磁感应强度B随
时间t变化的规律如图乙所示。下
列说法正确的是( )
A.0~2s内,线圈中感应电流的方向为顺时针
B.3s~4s内,线圈中感应电动势大小为0.08V
C.3s~4s和4s~5s内,线圈中感应电流方向相同
D.第5s内,线圈有扩张的趋势
C
答案:C
解析:A.0~2s内,磁通量增大,根据楞次定律可知,线圈中感应电流的方向为逆时针方向,故A错误;
B.3s~4s内,根据法拉第电磁感应定律有
故B错误; CD.3~4s,由题图可看出在该段时间内,磁场的方向垂直纸面向里且在减小,根据楞次定律可知,线框中感应电流方向沿顺时针方向;4~5s,由题图可看出在该段时间内,磁场的方向垂直纸面向外且在增大,根据楞次定律可知,线框中感应电流方向沿顺时针方向,线圈有缩小的趋势,故C正确,D错误;
4.舰载机返回航母甲板时有多种减速方式,如图所示,为一种电磁减速方式的简要模型。固定在水平面上足够长的平行光滑导轨,左端接有定值电阻,整个装置处在匀强磁场中。现有一舰载机可等效为垂直于导轨的导体棒ab,以一定初速度水平向右运动,导体棒和导轨的电阻不计。则导体棒运动过程中,其速度v、加速度a随运动时间t的关系图像可能正确的是( )
B
A
B
C
D
答案:B
解析:AB.导体棒切割磁感线,回路中出现感应电流,导体棒ab受到向左的安培力,向右减速运动,由
可知,由于导体棒速度减小,则加速度减小,所以导体棒做的是加速度越来越小的减速运动直至停止运动。故A错误;B正确;
CD.导体棒的最大加速度为
导体棒做加速度减小的减速运动,可知a-t图像的形状与v-t图像类似,为凹函数。故CD错误。
5.如图甲所示,100匝总阻值为0.3kΩ的圆形线圈两端M、N与一个阻值为1.2kΩ的电压表相连,其余电阻不计,线圈内有垂直纸面指向纸内方向的磁场,线圈中的磁通量在按图乙所示规律变化。下列说法正确的是( )
A.线圈中产生的感应电流沿顺时针方向
B.电压表的正接线柱接线圈的N端
C.线圈中磁通量的变化率为0.05Wb/s
D.电表的读数为40V
D
答案:D
解析:AB.根据楞次定律判断,线圈中产生的感应电流沿逆时针方向,所以电压表的正接线柱接线圈的M端,故AB错误;
C.由图乙知,线圈中磁通量的变化率为
故C错误;
D.感应电动势为
电表的读数为
故D正确。
2.2 法拉第电磁感应定律
人教版(2019)物理(选择性必修第二册)
第二章 电磁感应
目录
素养目标
01
课程导入
02
新课讲解
03
总结归纳
04
课堂练习
05
正确教育
素养目标
1.知道感应电动势的概念,会区分 的物理意义
2.理解法拉第电磁感应定律的内容和数学表达式
3.知道公式 E=Blvsinθ 的推导过程及适用条件
感应电流的大小是否与磁通量的变化有关呢?
穿过闭合导体回路的磁通量发生变化,闭合导体回路中就有感应电流。感应电流的大小跟哪些因素有关呢?
产生感应电流的条件
闭合电路
磁通量变化
新课讲解
磁铁插入的速度越快,感应电流越大,大胆猜测
感应电流大小与磁通量的变化快慢有关
使用条形磁铁以不同的速度插入或拔出线圈,发现感应电流的大小也不同,这是为什么?
点击播放视频
体会感应电流大小的变化
返回
(1)实验器材
长玻璃管、强磁体、线圈、电压表。
(2)实验步骤
①装置如图所示,线圈的两端与电压表相连。
②将强磁体从长玻璃管上端由静止下落,穿过线圈。
③分别使线圈距离上管口 20 cm 、30 cm、40 cm 和 50 cm,记录电压表的示数以及发生的现象。
④分别改变线圈的匝数、磁体的强度,重复上面的实验,得出定性的结论。
探究影响感应电流大小的因素
条件 线圈匝数:200;磁铁个数:2个 下落高度 10cm 40cm
指针刻度
感应电流大小与磁铁在线圈中运动时间的关系
20
超出量程
感应电流大小
与磁铁在线圈中运动时间的关系?
感应电流大小与磁铁在线圈中运动时间成反比例关系
结论:
条件 线圈匝数:200;下落高度:30cm 磁铁个数 1 2
指针刻度
感应电流大小与磁体的强度的关系
15
30
感应电流大小是否与磁体的强度的关系?
感应电流大小与磁感应强度(磁铁个数)成正比例关系
结论:
条件 磁铁个数:2个;下落高度:30cm 线圈匝数 100 200
指针刻度
感应电流大小与线圈匝数的关系
15
30
感应电流大小是否与线圈匝数的关系?
感应电流大小与线圈匝数成正比例关系
结论:
重复上述实验多次,
可知,线圈距上管口距离越大,强磁体穿过线圈的速度越大,引起的磁通量变化越快,线圈两端的电压越大;线圈匝数越多、磁体越强,线圈两端的电压越大。
(4)实验结论:
磁通量变化越快,感应电动势越大,在同一电路中,感应电流越大;反之越小。
磁通量的变化就是磁通量的变化率,用 表示。
1.定义:在电磁感应现象中产生的电动势叫感应电动势
①产生感应电动势的那部分导体相当于电源
②产生条件:穿过电路的磁通量发生改变,与电路是否闭合无关
③方向判断:感应电动势的方向用楞次定律结合安培定则或右手定则判断
产生电动势的线圈相当于电源
感应电动势
如果电路不闭合虽然没有感应电流,但电动势依然存在。所以产生感应电动势为电磁感应现象的本质。
N
S
G
v
感应电动势大小
磁通量的变化率:
线圈的匝数n
电磁感应现象的本质
影响感应电动势大小的因素
闭合电路中感应电动势大小,跟穿过这一电路的磁通量的变化率 成正比。
1. 内容:
2.表达式:
1845年和1846年德国物理学家纽曼和韦伯先后在总结法拉第大量实验事实基础上提出了定量化的电磁感应定律,并用数学表达式的形式展现出来
①当各物理量单位都用国际单位时,k=1,则
②若线圈有n匝时,可以看成n个单匝线圈串联而成
3.感应电动势单位:
法拉第电磁感应定律
伏特(V),1 V=1 Wb/s
6、表达式 E=nΔΦ/Δt 的理解:
(1)n:线圈匝数
(2)ΔΦ/Δt:磁通量变化率(磁通量变化快慢),Φ-t图像中,斜率k=ΔΦ/Δt, 斜率k越大,感应电动势越大。与Φ、ΔΦ无直接关系,与n无关。
(3)ΔΦ:磁通量变化多少,与n无关
(4)Φ:磁感线条数多少,与n无关
该公式只求E感大小,E感方向(与内部I感方向相同)由楞次定律另行判断,求值时ΔΦ取绝对值,不涉及正负。
5、适用范围:所有电磁感应现象中的感应电动势求值
(1)一般为Δt时间内的平均感应电动势;
(2)当Δt→0时,表示瞬时感应电动势。
4、公式说明:
法拉第电磁感应定律
Φ大,ΔΦ不一定大
Φ大,ΔΦ/Δt不一定大
ΔΦ/Δt大小决定感应电动势的大小
磁感应强度变化
面积变化
Φ-t 图像上切线ΔΦ/Δt斜率表示
如图(a)所示的螺线管,匝数n=1 500,横截面积S=20 cm2,方向向右穿过螺线管的匀强磁场的磁感应强度按图(b)所示规律变。
(a)
(b)
(1)2 s内穿过线圈的磁通量的变化量是多少
(2)磁通量的变化率多大
(3)线圈中感应电动势的大小为多少
经典例题
【答案】(1)8×10-3 Wb (2)4×10-3 Wb/s (3)6 V
通过以上实验,你认为哪些因素影响了导线切割磁感线时电动势的大小?
如图所示,闭合电路中的一部分导体ab处于匀强磁场中,磁感应强度为B,两平行导轨的间距为L,导体ab以速度v匀速切割磁感线,其中B、L、v两两垂直,求产生的感应电动势
分析:回路在时间Δt 内增大的面积为:
ΔS=LvΔt
感应电动势为:
穿过回路的磁通量的变化为:
ΔΦ=BΔS
=BLvΔt
v 是相对于磁场的速度
适用条件:匀强磁场中,导线、B、v 相互垂直时
讨论:那要是B、L、v不垂直怎么计算呢?
× × × × × × × × × ×
× × × × × × × × × ×
G
a
b
v
a
b
如果将与B的方向夹角为θ速度按右图中所示分解在与磁场垂直和与磁场平行方向上,他们各自的产生电动势是多少?
①垂直于磁感线的分量:v1=vsinθ
②平行于磁感线的分量:v2=vcosθ
只有垂直于磁感线的分量切割磁感线,
才能产生感应电动势:
E=BLv1=Blvsinθ
θ=0时
平行:E=0
θ=90° 时
垂直:E=BLv
(无切割)
对切割有贡献
对切割无贡献
θ
v
B
注意:1.为切割磁感线的有效长度。
(垂直于、的两端口距离)
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
v
v
v
× × × ×
× × × ×
× × × ×
× × × ×
v
2. 是的特例,只适用于切割。
3. v为瞬时速度时, E为瞬时感应电动势;
v为平均速度时, E为平均感应电动势。
4.导体转动切割磁感线时的感应电动势:
(1)导体绕一端转动切割磁感线时:
(2)导体绕两端间某点转动切割磁感线时:
(3)导体绕两端延长线某点转动切割磁感线时:
(1)动生电动势大小原理:
(2)动生电动势方向:
右手定则
(3)非静电力来源:动生电动势所对应的非静电力是洛伦兹力沿导体棒方向的分力。
注意:动生电动势与洛伦兹力有关,但洛伦兹力始终不做功
动生电动势原理:由于导体运动切割磁感线而产生的电动势
× × × ×
× × × ×
× × × ×
+
+
+
C
D
+
-
V1
F2
F电
【例】如图所示,平行导轨间距为d,其左端接一个电阻R,匀强磁场的磁感应强度为B,方向垂直于平行金属导轨所在平面,一根金属棒与导轨成θ角放置,金属棒与导轨的电阻均不计。当金属棒沿垂直于棒的方向以恒定的速度v在导轨上滑行时,通过电阻R的电流大小是( )
D
法拉第电磁感应定律
法拉第电磁感应定律
导线切割磁感线时的感应电动势
感应电动势
(v⊥B)
(v⊥杆)
1.一根绝缘硬质细导线顺次绕成如图所示的线圈,其中大圆的面积为S1,小圆的面积均为S2。垂直线圈平面方向有一随时间t 变化的磁场,磁感应强度大小B=B0+kt,B0和k均为常量,则线圈中总的感应电动势大小为( )
A.
B.
C.
D.
C
答案:C
解析:由法拉第电磁感应定律可得大圆线圈产生的感应电动势为 ,每个小圆线圈产生的感应电动势均为 ,由线圈的绕线方式和楞次定律可知,4个小圆线圈产生的感应电动势方向相同,而大圆线圈产生的感应电动势方向与4个小圆线圈产生的感应电动势方向相反,所以线圈中总的感应电动势大小为 ,故选C。
2.如图甲所示,螺线管匝数n = 1000匝,横截面积S = 10 cm2,螺线管导线电阻r = 1Ω,电阻R = 9Ω,磁感应强度B的B-t图像如图乙所示(以向右为正方向),则( )
A.感应电动势为0.6V
B.感应电流为0.06A
C.电阻R两端的电压为6V
D.0~1s内感应电流的方向为从C点通过R流向A点
D
答案:D
解析:A.根据法拉第电磁感应定律
A错误;
B.根据闭合电路欧姆定律得感应电流为
B错误;
C.根据欧姆定律得电阻R两端的电压为
C错误;
D.根据楞次定律得0~1s内感应电流的方向为从C点通过R流向A点,D正确。
3.图甲为100匝面积为100cm2的圆形金属线圈处于匀强磁场中,磁场方向垂直线圈平面,t = 0时刻磁场
方向如图甲所示,磁感应强度B随
时间t变化的规律如图乙所示。下
列说法正确的是( )
A.0~2s内,线圈中感应电流的方向为顺时针
B.3s~4s内,线圈中感应电动势大小为0.08V
C.3s~4s和4s~5s内,线圈中感应电流方向相同
D.第5s内,线圈有扩张的趋势
C
答案:C
解析:A.0~2s内,磁通量增大,根据楞次定律可知,线圈中感应电流的方向为逆时针方向,故A错误;
B.3s~4s内,根据法拉第电磁感应定律有
故B错误; CD.3~4s,由题图可看出在该段时间内,磁场的方向垂直纸面向里且在减小,根据楞次定律可知,线框中感应电流方向沿顺时针方向;4~5s,由题图可看出在该段时间内,磁场的方向垂直纸面向外且在增大,根据楞次定律可知,线框中感应电流方向沿顺时针方向,线圈有缩小的趋势,故C正确,D错误;
4.舰载机返回航母甲板时有多种减速方式,如图所示,为一种电磁减速方式的简要模型。固定在水平面上足够长的平行光滑导轨,左端接有定值电阻,整个装置处在匀强磁场中。现有一舰载机可等效为垂直于导轨的导体棒ab,以一定初速度水平向右运动,导体棒和导轨的电阻不计。则导体棒运动过程中,其速度v、加速度a随运动时间t的关系图像可能正确的是( )
B
A
B
C
D
答案:B
解析:AB.导体棒切割磁感线,回路中出现感应电流,导体棒ab受到向左的安培力,向右减速运动,由
可知,由于导体棒速度减小,则加速度减小,所以导体棒做的是加速度越来越小的减速运动直至停止运动。故A错误;B正确;
CD.导体棒的最大加速度为
导体棒做加速度减小的减速运动,可知a-t图像的形状与v-t图像类似,为凹函数。故CD错误。
5.如图甲所示,100匝总阻值为0.3kΩ的圆形线圈两端M、N与一个阻值为1.2kΩ的电压表相连,其余电阻不计,线圈内有垂直纸面指向纸内方向的磁场,线圈中的磁通量在按图乙所示规律变化。下列说法正确的是( )
A.线圈中产生的感应电流沿顺时针方向
B.电压表的正接线柱接线圈的N端
C.线圈中磁通量的变化率为0.05Wb/s
D.电表的读数为40V
D
答案:D
解析:AB.根据楞次定律判断,线圈中产生的感应电流沿逆时针方向,所以电压表的正接线柱接线圈的M端,故AB错误;
C.由图乙知,线圈中磁通量的变化率为
故C错误;
D.感应电动势为
电表的读数为
故D正确。
