6.3 向心加速度 课件 (共29张PPT) 2024-2025学年高中物理人教版(2019)必修第二册
文档属性
| 名称 | 6.3 向心加速度 课件 (共29张PPT) 2024-2025学年高中物理人教版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-20 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
第三节 向心加速度
第六章 圆周运动
目录
素养目标
01
课程导入
02
新课讲解
03
总结归纳
04
课堂练习
05
素养目标
1.知道匀速圆周运动中向心加速度大小的表达式。理解向心加速度与半径的关系,并会用来进行简单的计算
2.了解分析匀速圆周运动速度变化量时用到的极限思想
3.能根据问题情景选择合适的向心加速度的表达式
天宫二号空间实验室在轨飞行时,可认为它绕地球做匀速圆周运动。尽管线速度大小不变,但方向却时刻变化,因此,它运动的加速度一定不为0。那么,该如何确定它在轨飞行时加速度的方向和大小呢?
复习与
回顾
1.向心力的方向?
沿半径指向圆心,与速度方向垂直。
只改变线速度的方向不改变速度大小。
2.向心力的作用?
3.向心力的大小?
根据牛顿第二定律,物体的加速度方向跟合外力的方向相同
小球绕光滑桌面上的图钉做匀速圆周运动。
G
FN
F
新课讲解
O
v
v
v
线速度
大小
方向
不变
时刻变化
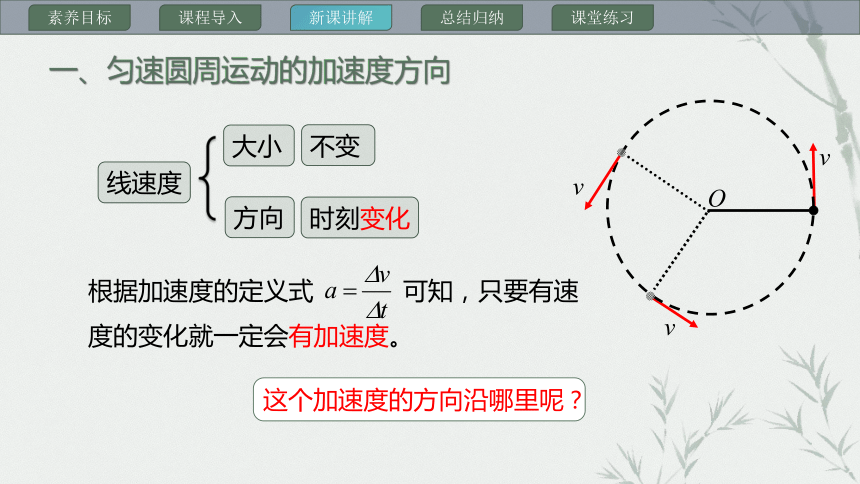
根据加速度的定义式 可知,只要有速度的变化就一定会有加速度。
这个加速度的方向沿哪里呢?
一、匀速圆周运动的加速度方向
一、匀速圆周运动的加速度方向
1.向心加速度:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度
4.物理意义:描述速度方向变化的快慢
2.符号:an
3.方向:始终指向圆心
5.说明:匀速圆周运动加速度的方向时刻改变,
所以匀速圆周运动不是匀变速运动,而是变加速运动。
v
an
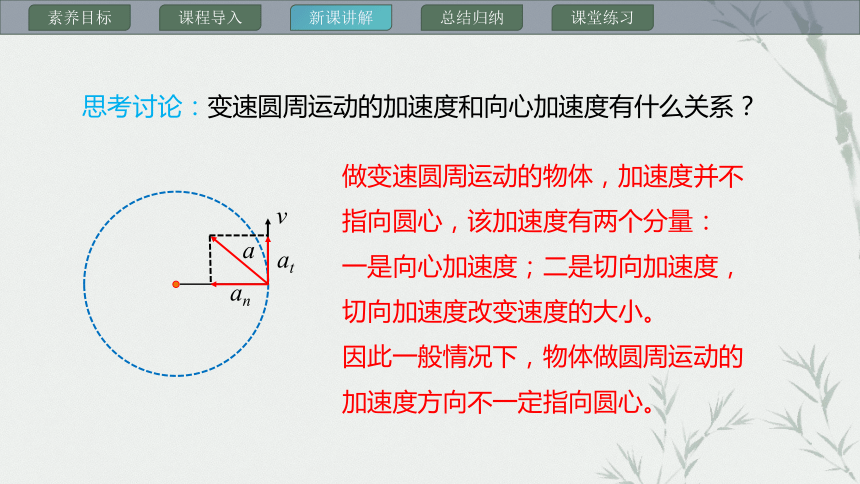
做变速圆周运动的物体,加速度并不指向圆心,该加速度有两个分量:
一是向心加速度;二是切向加速度,切向加速度改变速度的大小。
因此一般情况下,物体做圆周运动的加速度方向不一定指向圆心。
思考讨论:变速圆周运动的加速度和向心加速度有什么关系?
a
v
at
an
(传动)
(轴动)
根据
牛顿第二定律
物理意义:描述速度方向变化的快慢
单位:m/s2
二、匀速圆周运动的加速度大小
思考:对于向心加速度的公式,同学们有各自的看法。从 看,向心加速度与半径成反比;从a = ω2r看,向心加速度与半径成正比。这两个结论是否矛盾?
AB通过链条连接,属于传动装置,同一传动装置各轮边缘上线速度相等。所以适用“向心加速度与半径成反比”
BC 同在一根轴上,属于同轴转动装置,同轴转动轮上各点的角速度相等。所以适用“向心加速度与半径成正比
正确认识向心加速度的两种表达式
不矛盾:若角速度ω相同,则an与r成正比,如甲图;
若线速度v大小相同,则an与r成反比,如乙图
当ω一定时,a与r成正比
当v一定时,a与r成反比
(1)直线运动中的速度变化量:
v1
v2
Δv
v1
v2
Δv
拓展学习:用运动学的方法求向心加速度方向和大小
(2)曲线运动中的速度变化量:
v1
v2
A
B
v2
v1
Δv
(3)从几何角度推导向心加速度的大小:
如图甲所示,一物体沿着圆周运动,在 A、B 两点的速度分别为 vA、vB,可以分四步确定物体运动的加速度方向。
第一步,根据曲线运动的速度方向沿着切线方向,画出物体经过 A、B 两点时的速度方向,分别用 vA、vB 表示,如图甲所示。
第二步,平移 vA 至 B 点,如图乙所示。
第三步,根据矢量运算法则,做出物体由 A 点到 B 点的速度变化量 Δv,其方向由 vA 的箭头位置指向 vB 的箭头位置,如图丙所示。由于物体做匀速圆周运动,vA、vB 的大小相等,所以,Δv与 vA、vB 构成等腰三角形。
第四步,假设由 A 点到 B 点的时间极短,在匀速圆周运动的速度大小一定的情况下,A 点到 B 点的距离将非常小,作出此时的 Δv,如图丁所示。
仔细观察图丁,可以发现,此时,Δv与vA、vB都几乎垂直,因此Δv的方向几乎沿着圆周的半径,指向圆心。由于加速度a与Δv的方向是一致的,所以从运动学角度分析也可以发现:物体做匀速圆周运动时的加速度指向圆心。
所以
当Δt很小很小时,
所以
例题 如图所示,在长为 l 的细绳下端拴一个质量为 m 的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就沿圆锥面旋转,这样就成了一个圆锥摆。当绳子跟竖直方向的夹角为 θ 时,小球运动的向心加速度 an 的大小为多少?通过计算说明 :要增大夹角 θ,应该增大小球运动的角速度 ω。
经典例题
分析 由于小球在水平面内做圆周运动,向心加速度的方向始终指向圆心。可以根据受力分析,求出向心力的大小,进而求出向心加速度的大小。根据向心加速度公式,分析小球做圆周运动的角速度 ω 与夹角 θ 之间的关系。
解: 根据对小球的受力分析,可得小球的向心力Fn = mgtanθ
根据牛顿第二定律可得小球运动的向心加速度 an = Fn/m = gtan θ (1)
根据几何关系可知小球做圆周运动的半径 r=lsin θ (2)
把向心加速度公式 an=ω2r 和(2)式代入(1)式,可得 cosθ =
从此式可以看出,当小球运动的角速度增大时,夹角也随之增大。因此,要增大夹角θ,应该增大小球运动的角速度ω。
1.定义:匀速圆周运动的加速度
2.意义:描述速度方向变化的快慢
3.大小:
4.方向:始终指向圆心(时刻改变)
匀速圆周运动是变加速曲线运动
向心加速度
1.A、B在水平面内做匀速圆周运动,在相同时间内,它们通过的路程之比是4:3,运动方向改变的角度之比是3:2,则它们( )
A.线速度大小之比为3:4
B.角速度之比为3:2
C.圆周运动的半径之比为2:1
D.向心加速度大小之比为1:2
B
答案:B
解析:A.时间相同情况下,路程之比为4:3,根据 可知线速度之比为4:3,故A错误;B.时间相同情况下,角度改变之比为3:2,根据
可知角速度之比为3:2,故B正确;C.根据 ,可知半径之比为8:9,故C错误.D.由向心加速度公式 ,可知向心加速度之比为2:1,故D错误。故选B。
2.某同学拼装的玩具齿轮传动装置如图所示,图中四个齿轮自左向右的编号依次为1、2、3、4.它们的半径之比为3:6:3:4,其中齿轮1是主动轮,沿顺时针方向匀速转动。下列说法正确的是( )
A.齿轮4沿顺时针方向转动
B.齿轮1边缘与齿轮2边缘的线速度大小之比为
C.齿轮2边缘的向心加速度与齿轮3边缘的向心加速度大小之比为
D.齿轮3的转动周期与齿轮4的转动周期之比为
C
答案:C
解析:A.当齿轮1沿顺时针方向匀速转动时,齿轮2沿逆时针方向转动,齿轮3沿顺时针方向转动,齿轮4沿逆时针方向转动,故A错误;B.所有齿轮边缘的线速度大小都相等,齿轮1与齿轮2的线速度大小之比为 ,故B错误;C.根据 ,可知齿轮2边缘的向心加速度与齿轮3边缘的向心加速度大小之比为 ,故C正确;D.由
,可知齿轮3的转动周期与齿轮4的转动周期之比为 ,故D错误。故选C。
3.如图所示一种古老的舂米机.舂米时,稻谷放在石臼A中,横梁可以绕O转动,在横梁前端B处固定一舂米锤,脚踏在横梁另一端C点往下压时,舂米锤便向上抬起。然后提起脚,舂米锤就向下运动,击打A中的稻谷,使稻谷的壳脱落,稻谷变为大米。已知OC > OB,则在横梁绕O转动过程中( )
A.B、C的向心加速度相等
B.B、C的角速度关系满足
C.B、C的线速度关系满足
D.舂米锤击打稻谷时对稻谷的作用力大于稻谷对舂米锤的作用力
C
答案:C
解析:AB.由题图可知,B与C属于共轴转动,则它们的角速度是相等的,即 ,向心加速度 ,因OC > OB,可知C的向心加速度较大,故AB错误;C.由于OC > OB,由 可知C点的线速度大,故C正确;D.舂米锤对稻谷的作用力和稻谷对舂米锤的作用力是一对作用力与反作用力,二者大小相等,故D错误。故选C。
4.(多选)大型游乐装置“大摆锤”的简图如图所示,摆锤a和配重锤b分别固定在摆臂两端,并可绕摆臂上的转轴O在纸面内转动。若a、b到O的距离之比为2:1,在摆臂匀速转动的过程中,下列说法正确的是( )
A.a、b的线速度大小之比为2:1
B.a、b的角速度大小之比为1:2
C.a、b的向心加速度大小之比为2:1
D.a、b的向心加速度大小之比为1:4
AC
答案:AC
解析:a、b两点同轴转动,所以角速度相等,根据 ,可得a、b的线速度大小之比为 ,根据 ,可得a、b的向心加速度大小之比为 ,故选AC。
5.无级变速汽车变速箱的工作原理可以简化为如图所示的装置,两个相同锥体A、B水平放置,它们的中心轴分别与动力输入端和动力输出端连接,动力输入端的中心轴带动锥体A转动,锥体A带动钢带转动的同时,钢带在锥体上前后移动,改变转速比,实现变速。a、b是锥体上与钢带接触的两动点,不计钢带的形变且钢带所在的平面始终与两中心轴垂直,若保持动力输入端中心轴转速不变,则钢带由后向前运动的过程中( )
A.动点a、b的线速度相等且逐渐减小
B.锥体B的转速增大
C.汽车在减速
D.动点a、b的向心加速度大小之和减小
B
答案:B
解析:A.根据题意有动点 的线速度相等,有
钢带由后向前运动的过程中 增大,可得 增大,A错误;
BC.由于 ,有
解得
增大, 减小,可得 增大,汽车在加速,B正确,C错误;
D.根据 ,可得
由题意得 (定值)
故 增大,D错误。
故选B。
第三节 向心加速度
第六章 圆周运动
目录
素养目标
01
课程导入
02
新课讲解
03
总结归纳
04
课堂练习
05
素养目标
1.知道匀速圆周运动中向心加速度大小的表达式。理解向心加速度与半径的关系,并会用来进行简单的计算
2.了解分析匀速圆周运动速度变化量时用到的极限思想
3.能根据问题情景选择合适的向心加速度的表达式
天宫二号空间实验室在轨飞行时,可认为它绕地球做匀速圆周运动。尽管线速度大小不变,但方向却时刻变化,因此,它运动的加速度一定不为0。那么,该如何确定它在轨飞行时加速度的方向和大小呢?
复习与
回顾
1.向心力的方向?
沿半径指向圆心,与速度方向垂直。
只改变线速度的方向不改变速度大小。
2.向心力的作用?
3.向心力的大小?
根据牛顿第二定律,物体的加速度方向跟合外力的方向相同
小球绕光滑桌面上的图钉做匀速圆周运动。
G
FN
F
新课讲解
O
v
v
v
线速度
大小
方向
不变
时刻变化
根据加速度的定义式 可知,只要有速度的变化就一定会有加速度。
这个加速度的方向沿哪里呢?
一、匀速圆周运动的加速度方向
一、匀速圆周运动的加速度方向
1.向心加速度:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度
4.物理意义:描述速度方向变化的快慢
2.符号:an
3.方向:始终指向圆心
5.说明:匀速圆周运动加速度的方向时刻改变,
所以匀速圆周运动不是匀变速运动,而是变加速运动。
v
an
做变速圆周运动的物体,加速度并不指向圆心,该加速度有两个分量:
一是向心加速度;二是切向加速度,切向加速度改变速度的大小。
因此一般情况下,物体做圆周运动的加速度方向不一定指向圆心。
思考讨论:变速圆周运动的加速度和向心加速度有什么关系?
a
v
at
an
(传动)
(轴动)
根据
牛顿第二定律
物理意义:描述速度方向变化的快慢
单位:m/s2
二、匀速圆周运动的加速度大小
思考:对于向心加速度的公式,同学们有各自的看法。从 看,向心加速度与半径成反比;从a = ω2r看,向心加速度与半径成正比。这两个结论是否矛盾?
AB通过链条连接,属于传动装置,同一传动装置各轮边缘上线速度相等。所以适用“向心加速度与半径成反比”
BC 同在一根轴上,属于同轴转动装置,同轴转动轮上各点的角速度相等。所以适用“向心加速度与半径成正比
正确认识向心加速度的两种表达式
不矛盾:若角速度ω相同,则an与r成正比,如甲图;
若线速度v大小相同,则an与r成反比,如乙图
当ω一定时,a与r成正比
当v一定时,a与r成反比
(1)直线运动中的速度变化量:
v1
v2
Δv
v1
v2
Δv
拓展学习:用运动学的方法求向心加速度方向和大小
(2)曲线运动中的速度变化量:
v1
v2
A
B
v2
v1
Δv
(3)从几何角度推导向心加速度的大小:
如图甲所示,一物体沿着圆周运动,在 A、B 两点的速度分别为 vA、vB,可以分四步确定物体运动的加速度方向。
第一步,根据曲线运动的速度方向沿着切线方向,画出物体经过 A、B 两点时的速度方向,分别用 vA、vB 表示,如图甲所示。
第二步,平移 vA 至 B 点,如图乙所示。
第三步,根据矢量运算法则,做出物体由 A 点到 B 点的速度变化量 Δv,其方向由 vA 的箭头位置指向 vB 的箭头位置,如图丙所示。由于物体做匀速圆周运动,vA、vB 的大小相等,所以,Δv与 vA、vB 构成等腰三角形。
第四步,假设由 A 点到 B 点的时间极短,在匀速圆周运动的速度大小一定的情况下,A 点到 B 点的距离将非常小,作出此时的 Δv,如图丁所示。
仔细观察图丁,可以发现,此时,Δv与vA、vB都几乎垂直,因此Δv的方向几乎沿着圆周的半径,指向圆心。由于加速度a与Δv的方向是一致的,所以从运动学角度分析也可以发现:物体做匀速圆周运动时的加速度指向圆心。
所以
当Δt很小很小时,
所以
例题 如图所示,在长为 l 的细绳下端拴一个质量为 m 的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就沿圆锥面旋转,这样就成了一个圆锥摆。当绳子跟竖直方向的夹角为 θ 时,小球运动的向心加速度 an 的大小为多少?通过计算说明 :要增大夹角 θ,应该增大小球运动的角速度 ω。
经典例题
分析 由于小球在水平面内做圆周运动,向心加速度的方向始终指向圆心。可以根据受力分析,求出向心力的大小,进而求出向心加速度的大小。根据向心加速度公式,分析小球做圆周运动的角速度 ω 与夹角 θ 之间的关系。
解: 根据对小球的受力分析,可得小球的向心力Fn = mgtanθ
根据牛顿第二定律可得小球运动的向心加速度 an = Fn/m = gtan θ (1)
根据几何关系可知小球做圆周运动的半径 r=lsin θ (2)
把向心加速度公式 an=ω2r 和(2)式代入(1)式,可得 cosθ =
从此式可以看出,当小球运动的角速度增大时,夹角也随之增大。因此,要增大夹角θ,应该增大小球运动的角速度ω。
1.定义:匀速圆周运动的加速度
2.意义:描述速度方向变化的快慢
3.大小:
4.方向:始终指向圆心(时刻改变)
匀速圆周运动是变加速曲线运动
向心加速度
1.A、B在水平面内做匀速圆周运动,在相同时间内,它们通过的路程之比是4:3,运动方向改变的角度之比是3:2,则它们( )
A.线速度大小之比为3:4
B.角速度之比为3:2
C.圆周运动的半径之比为2:1
D.向心加速度大小之比为1:2
B
答案:B
解析:A.时间相同情况下,路程之比为4:3,根据 可知线速度之比为4:3,故A错误;B.时间相同情况下,角度改变之比为3:2,根据
可知角速度之比为3:2,故B正确;C.根据 ,可知半径之比为8:9,故C错误.D.由向心加速度公式 ,可知向心加速度之比为2:1,故D错误。故选B。
2.某同学拼装的玩具齿轮传动装置如图所示,图中四个齿轮自左向右的编号依次为1、2、3、4.它们的半径之比为3:6:3:4,其中齿轮1是主动轮,沿顺时针方向匀速转动。下列说法正确的是( )
A.齿轮4沿顺时针方向转动
B.齿轮1边缘与齿轮2边缘的线速度大小之比为
C.齿轮2边缘的向心加速度与齿轮3边缘的向心加速度大小之比为
D.齿轮3的转动周期与齿轮4的转动周期之比为
C
答案:C
解析:A.当齿轮1沿顺时针方向匀速转动时,齿轮2沿逆时针方向转动,齿轮3沿顺时针方向转动,齿轮4沿逆时针方向转动,故A错误;B.所有齿轮边缘的线速度大小都相等,齿轮1与齿轮2的线速度大小之比为 ,故B错误;C.根据 ,可知齿轮2边缘的向心加速度与齿轮3边缘的向心加速度大小之比为 ,故C正确;D.由
,可知齿轮3的转动周期与齿轮4的转动周期之比为 ,故D错误。故选C。
3.如图所示一种古老的舂米机.舂米时,稻谷放在石臼A中,横梁可以绕O转动,在横梁前端B处固定一舂米锤,脚踏在横梁另一端C点往下压时,舂米锤便向上抬起。然后提起脚,舂米锤就向下运动,击打A中的稻谷,使稻谷的壳脱落,稻谷变为大米。已知OC > OB,则在横梁绕O转动过程中( )
A.B、C的向心加速度相等
B.B、C的角速度关系满足
C.B、C的线速度关系满足
D.舂米锤击打稻谷时对稻谷的作用力大于稻谷对舂米锤的作用力
C
答案:C
解析:AB.由题图可知,B与C属于共轴转动,则它们的角速度是相等的,即 ,向心加速度 ,因OC > OB,可知C的向心加速度较大,故AB错误;C.由于OC > OB,由 可知C点的线速度大,故C正确;D.舂米锤对稻谷的作用力和稻谷对舂米锤的作用力是一对作用力与反作用力,二者大小相等,故D错误。故选C。
4.(多选)大型游乐装置“大摆锤”的简图如图所示,摆锤a和配重锤b分别固定在摆臂两端,并可绕摆臂上的转轴O在纸面内转动。若a、b到O的距离之比为2:1,在摆臂匀速转动的过程中,下列说法正确的是( )
A.a、b的线速度大小之比为2:1
B.a、b的角速度大小之比为1:2
C.a、b的向心加速度大小之比为2:1
D.a、b的向心加速度大小之比为1:4
AC
答案:AC
解析:a、b两点同轴转动,所以角速度相等,根据 ,可得a、b的线速度大小之比为 ,根据 ,可得a、b的向心加速度大小之比为 ,故选AC。
5.无级变速汽车变速箱的工作原理可以简化为如图所示的装置,两个相同锥体A、B水平放置,它们的中心轴分别与动力输入端和动力输出端连接,动力输入端的中心轴带动锥体A转动,锥体A带动钢带转动的同时,钢带在锥体上前后移动,改变转速比,实现变速。a、b是锥体上与钢带接触的两动点,不计钢带的形变且钢带所在的平面始终与两中心轴垂直,若保持动力输入端中心轴转速不变,则钢带由后向前运动的过程中( )
A.动点a、b的线速度相等且逐渐减小
B.锥体B的转速增大
C.汽车在减速
D.动点a、b的向心加速度大小之和减小
B
答案:B
解析:A.根据题意有动点 的线速度相等,有
钢带由后向前运动的过程中 增大,可得 增大,A错误;
BC.由于 ,有
解得
增大, 减小,可得 增大,汽车在加速,B正确,C错误;
D.根据 ,可得
由题意得 (定值)
故 增大,D错误。
故选B。
