概率初步解答题(含解析)--2024-2025学年人教版九年级数学上册期末专题训练
文档属性
| 名称 | 概率初步解答题(含解析)--2024-2025学年人教版九年级数学上册期末专题训练 |

|
|
| 格式 | docx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
概率初步解答题--2024-2025学年人教版九年级数学上册期末专题训练
1.太原市某校为了落实“五育”并举,提升学生的综合素养,在课外活动中开设了四个兴趣小组:A.跳长绳;B.篮球;C.书法;D.绘画.该校学生会围绕“你最喜欢的项目是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项).根据调查统计结果,绘制了如下两种不完整的统计图,请结合图中信息回答下列问题.
(1)本次共调查了________名学生,并将条形统计图补充完整.
(2)求篮球小组所对应扇形的圆心角度数.
(3)跳长绳小组的4名学生由3名男生和1名女生构成.从中随机抽取2名学生参加比赛.请用列表或画树状图的方法,求恰好抽到1名男生与1名女生的概率.
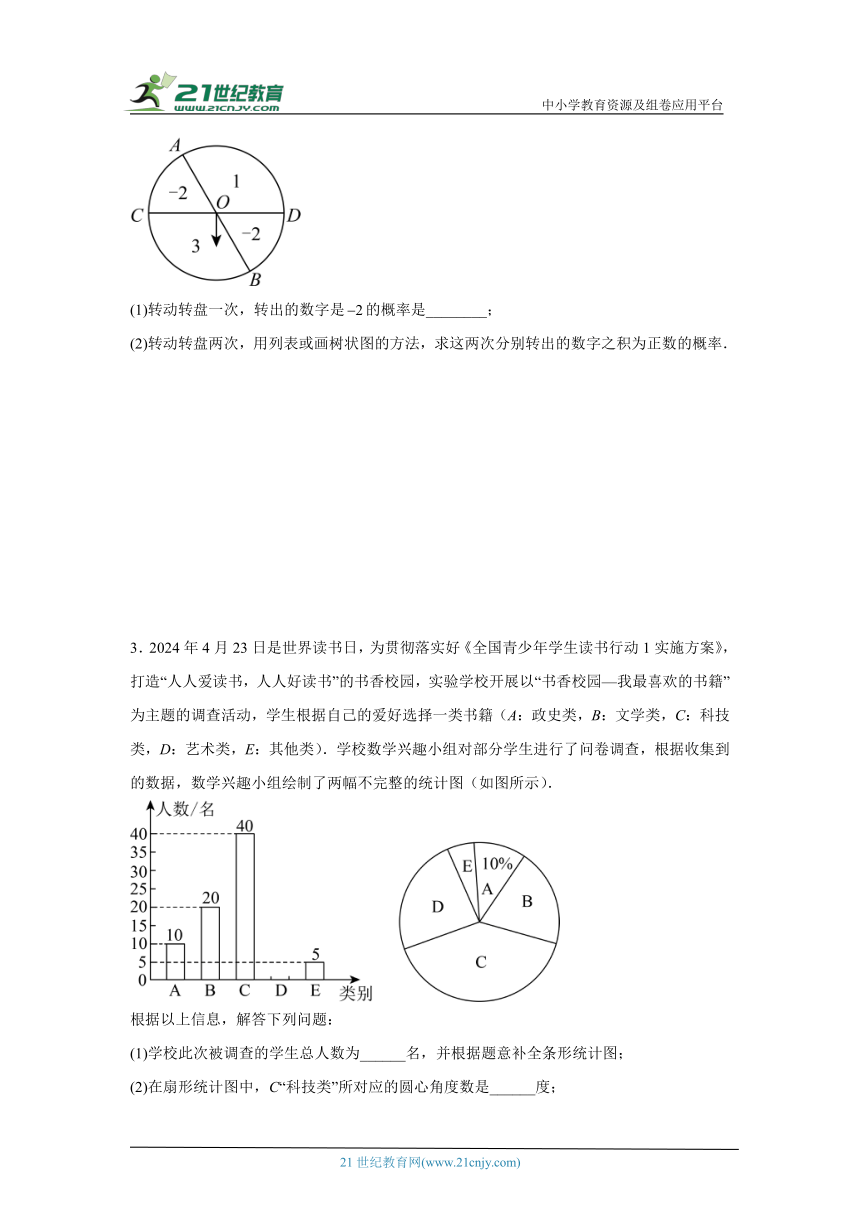
2.如图,一个可以自由转动的转盘,被它的两条直径分成了四个分别标有数字的扇形区域,,转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字.(若指针恰好停留在分界线上,则重新转一次)
(1)转动转盘一次,转出的数字是的概率是________;
(2)转动转盘两次,用列表或画树状图的方法,求这两次分别转出的数字之积为正数的概率.
3.2024年4月23日是世界读书日,为贯彻落实好《全国青少年学生读书行动1实施方案》,打造“人人爱读书,人人好读书”的书香校园,实验学校开展以“书香校园—我最喜欢的书籍”为主题的调查活动,学生根据自己的爱好选择一类书籍(A:政史类,B:文学类,C:科技类,D:艺术类,E:其他类).学校数学兴趣小组对部分学生进行了问卷调查,根据收集到的数据,数学兴趣小组绘制了两幅不完整的统计图(如图所示).
根据以上信息,解答下列问题:
(1)学校此次被调查的学生总人数为______名,并根据题意补全条形统计图;
(2)在扇形统计图中,C“科技类”所对应的圆心角度数是______度;
(3)学校数学兴趣小组中,甲同学从A,B,C三类书籍中随机选择一种,乙同学从B,C,D三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.
4.“青年大学习”是由共青团中央发起,广大青年参与,通过学习来提升自身理论水平、思维层次的行动.梦想从学习开始,事业从实践起步.某校为了解九年级学生学习“青年大学习”的情况,随机抽取部分九年级学生进行了问卷调查,按照调查结果,将学习情况分为优秀、良好、合格、较差四个等级.学校绘制了如下不完整的统计图,根据图中信息解答下列问题∶
(1)本次参与问卷调查的学生共有_________人,扇形统计图中“合格”所对应的百分比为_________;
(2)补全条形统计图;
(3)该校某班有4名同学(2名男同学,2名女同学)在调查中获得“优秀”等级,班主任将从这4名同学中随机选取2名同学,代表班级参加学校组织的“青年大学习”演讲比赛,请用列表或画树状图的方法,求所选两位同学恰好是1名男同学和1名女同学的概率.
5.2023年8月8日至20日,云南省第十六届运动会将在玉溪市举行,为全面发挥省运会在我省体育事业发展中的引领和示范作用,本届省运会进行了多项改革创新.其中大众组与上届相比,保留轮滑和棋牌项目,新增篮球、足球、射弩和工间操4个大项.某体育兴趣小组收集到了工间操、射弩、轮滑、棋牌四个项目的比赛规则,并制作了编号分别为A,B,C,D的4张卡片(如图,除图案和编号外,背面无其他差异),并将他们背面朝上洗匀后放在桌子上.
(1)从中随机抽取一张,抽到“射弩”的概率为 ;
(2)若甲同学从4张卡片中随机抽取1张不放回,乙同学再从余下的3张卡片中随机抽取1张,然后根据抽取的卡片讲述对应卡片上的比赛规则,请用列表法或画树状图法(树状图也称树形图)中的一种方法,求甲、乙两人中至少有一人讲述本届运动会新增项目的比赛规则的概率.
6.某教育部门为了解本地区中小学生参加家庭劳动时间的情况,随机抽取该地区1200名中小学生进行问卷调查,调查问卷和结果如下:
中小学生每周参加家庭劳动时间分为5组:第一组,第二组,第三组,第四组,第五组.对于每周参加家庭劳动时间不足的学生,影响他们每周参加家庭劳动的主要原因有:
A.没时间;B.家长不舍得;C.不喜欢;D.其他.请根据以上信息,解答下列问题:
(1)本次调查中,中小学生每周参加家庭劳动时间的中位数落在第_____组;
(2)求在本次被调查的中小学生中选择“不喜欢”的人数;
(3)在所调查的九年级一班学生中,有2名男生和2名女生,现需从这4名学生中抽取2名学生作进一步访谈调查,请用树状图或列表的方法,求所抽2名学生恰好是1名男生和1名女生概率.
7.在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间t(单位:小时).把调查结果分为四档,A档:;B档:;C档:;D档:.根据调查情况,给出了部分数据信息:
①A档和D档的所有数据是:7,7,7.5,10,7,10,7,7.5,7,7,10.5,10.5;
②图1和图2是两幅不完整的统计图.
根据以上信息解答问题:
(1)求本次调查的学生人数,并将图2补充完整;
(2)已知全校共1200名学生,请你估计全校B档的人数;
(3)学校要从D档的4名学生中随机抽取2名作读书经验分享,已知这4名学生,2名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.
8.为了响应市政府号召,某校开展了“创文明城市与我同行”活动周,活动周设置了“:文明礼仪,:生态环境,:交通安全,:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)在扇形统计图中,“”所在扇形的圆心角等于 度;
(3)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.
9.某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共 名.
(2)请将条形统计图补充完整,扇形统计图中“进取”所对应的圆心角是 .
(3)如果要在这5个主题中任选两个进行调查,用树状图或列表法,求恰好选到学生关注平等、感恩两个主题的概率.(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E)
10.某市利用各类灵活多样的宣传方式、各种宣传载体,全方位开展“国家反诈中心” 宣传推广工作,截止2023年底,注册人数已达216.39万人,某社区工作人员为调 查本社区居民对于“国家反诈中心”的了解情况,进行了一次问卷调查,本次问卷共设置10个问题,每题10分,问卷调查结束后,根据问卷结果分为A:非常了解(80-100分)、B:比较了解(60-80分)、C:基本了解(40-60分)、D:不太了解(0-40分)
四个等级并绘制了如下两幅不完整的统计图.
请根据如图提供的信息解答下列问题:
(1)扇形统计图中,A等级对应的扇形的圆心角度数为________,补全条形统计图;
(2)若该社区共有居民8000人,请你估计对于“国家反诈中心”非常了解的人数;
(3)为更好地开展“国家反诈中心”宜传推广工作,社区准备招募2名宜讲人员,现有问卷结果等级为A的4人报名,其中3人为一组居民,1人为二组居民,若从中随机选取2人,求选取的2人不是同一组居民的概率.
11.某超市抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖
(1)请用列表或树状图的方法,把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
12.南宁市某学校开展了“奋进万亿新征程,共筑强国强军梦”的主题研学活动.为了解学生参与情况,随机抽取部分学生对研学活动时长(用表示,单位:h)进行调查.经过整理,将数据分成四组(A组:;B组:;C组:;D组:),并绘制了如下不完整的条形统计图和扇形统计图.
(1)请补全条形统计图;
(2)扇形统计图中,的值为___________,A组对应的扇形圆心角的度数为_________;
(3)D组中有男、女生各两人,现从这四人中随机抽取两人进行研学宣讲,请用树状图或表格求所抽取的两人恰好是两名男生的概率.
13.3月14日是国际数学日,某校在“国际数学日”当天举行了丰富多彩的数学活动,其中游戏类活动有:.数字猜谜;.数独:.魔方;.24点游戏;.数字华容道.该校为了解学生对这五类数学游戏的喜爱情况,随机抽取部分学生进行了调查统计(每位学生必选且只能选一类),并根据调查结果,绘制了两幅不完整的统计图如图所示.
根据上述信息,解决下列问题.
(1)本次调查总人数为___________,并补全条形统计图:(要求在条形图上方注明人数)
(2)若该校有2000名学生,请估计该校参加魔方游戏的学生人数;
(3)该校从类中挑选出2名男生和2名女生,计划从这4名学生中随机抽取2名学生参加市青少年魔方比赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
14.为增强学生爱国意识,激发爱国情怀,某校9月开展了“喜迎二十大、永远跟党走、奋进新征程”主题教育活动,活动方式有:A.主题征文,B.书法绘画,C.红歌传唱,D.经典诵读.为了解最受学生喜爱的活动方式,现随机抽取若干名学生进行调查,并将调查结果绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)参与此次抽样调查的学生人数是_______,扇形统计图中A部分圆心角的度数是_______;
(2)请补全条形统计图;
(3)学校从1班,2班,3班,4班中随机选取两个班参加“红歌传唱”的活动,求恰好选中2班和3班的概率.
15.某校劳动实践基地共开设五门劳动实践课程,分别是:床铺整理,:衣物清洗,:手工制作、:简单烹饪、:绿植栽培;课程开设一段时间后,季老师采用抽样调查的方式在全校学生中开展了“我最喜欢的劳动实践课程”为主题的问卷调查.根据调查所收集的数我进行整理、绘制了如下两幅不完整的统计图.
根据图中信息,请回答下列问题:
(1)请将条形统计图补充完整,并直接写出“手工制作”对应的扇形圆心角度数;
(2)若该校共有名学生,请你估计全校最喜欢“绿植栽培”的学生人数;
(3)小兰同学从三门课程中随机选择一门参加劳动实践,小亮同学从三门课程中随机选择一门参加劳动实践,求两位同学选择相同课程的概率.
16.因国家对体育健康的重视程度不断提高,某校决定开展体育社团活动,分别有:A.足球社团,B.篮球社团,C.跑步社团,D.铅球社团,每位学生只能选其中一项作为社团活动.为了解学生对以上社团的参与情况,随机抽取部分学生进行了调查统计,并根据调查结果,绘制成如图所示的不完整的统计图:请根据图中信息,解答下列问题:
(1)本次一共调查了______名学生,图2中所在扇形的圆心角的度数为______;
(2)请补全条形统计图;
(3)甲、乙两位同学各随机选择一个社团参加,请用画树状图或列表的方法,求甲乙两位同学选择同一个社团的概率.
17.作为《黑神话 悟空》的创意来源之一,山西古建筑随着游戏的火爆收获无数关注,吸引大量游客前来旅游打卡,小军和小勇准备到山西旅游打卡,他们选了四处影点.门票价格分别为30元、50元、60元、100元,他们决定用转盘游戏决定地点.如图是一个可以自由转动的转盘,指针固定不动,转盘被分成了大小相同的4个扇形,并在每个扇形区域分别标上30元、50元、60元、100元.(当指针落在边界线上时,重新转动一次,直到指针指向某一区域内为止)
(1)若转动转盘一次,则指针落在30元区域的概率为______.
(2)小军和小勇每人转动转盘一次,当转盘停止时,记下各自指针所指区域内对应的金额,请用画树状图或列表法求两次所得金额之和小于100元的概率.
18.2024年10月20日上午7时30分,长沙马拉松暨全国半程马拉松锦标赛(第四站)鸣枪开跑,来自国内外的3万名跑友从贺龙体育中心东广场出发,用脚步丈量大美星城.本次赛事以“传递奔跑的力量”为主题,旨在增强全市民众科学健身意识,推动全民健身活动.本届赛事共设置马拉松,半程马拉松和欢乐跑三个项目.赛后随机抽取了部分参赛选手对本次赛事组织进行满意度评分调查,整理后得到下列不完整的图表:
等级 A B C D
分数段 90﹣100 80﹣89 70﹣79 60﹣69
频数 440 280 m 40
请根据表中提供的信息,解答下列问题:
(1)此次调查共抽取了 名选手,m= ,n= ;
(2)扇形统计图中,B等级所对应的扇形圆心角度数是 度;
(3)赛后全程马拉松男子组冠军和女子组冠军各一名;半程马拉松男子组冠军和女子组冠军各一名,欢乐跑没有设置冠亚军奖项.若从设置奖项的两个项目的男女冠军四人中随机抽取两人访谈,请用列表或画树状图的方法,求出恰好抽到全程马拉松女子组冠军和半程马拉松女子组冠军的概率.
19.在一个不透明的口袋里装有分别标注,,的个小球(小球除数字外,其余都相同),另有张背面完全一样、正面分别写有数字,,的卡片.现从口袋中任意摸出一个小球,再从这张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
(2)求这两次摸出的数字,至多有一次是“”的概率;
(3)小红和小莉做游戏,制定了游戏规则:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢这个游戏规则公平吗?请说明理由.
20.睡眠管理作为“五项管理”中的重要内容之一,也是学校教育电点关注的内容.某校为了解学生平均每天睡眠时间,随机抽取该校部分学生进行问卷调查,并将结果进行了统计和整理,绘制成如下统计表和不完整的统计图.
学生类别 学生平均每天睡眠时间单位:小时
A
B
C
D
E
(1)扇形统计图中表示C类学生平均每天睡眠时间的扇形的圆心角度数为______.
(2)请补全条形统计图.
(3)被抽取调查的E类4名学生中有2名女生,2名男生.从这4人中随机抽取2人进行电话回访,请用画树状图或列表的方法,求恰好抽到2名男生的概率.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)40,补全条形统计图如下:
(2)
(3)
【分析】本题考查了条形统计图和扇形统计图,及用列表法或树状图法求概率,准确理解题意,熟练掌握知识点是解题的关键.
(1)由A组人数及其所占百分比可得总人数,总人数减去A、B、D人数求出C组人数即可补全图形;
(2)用360度乘以篮球组人数所占比例即可;
(3)画树状图,共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果有6种,再由概率公式求解即可.
【详解】(1)解:本次调查总人数为(名),
C组人数为(名),
补全图形如下:
故答案为:40;
(2)解:,
故答案为:72;
(3)解:画树状图如下:
共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果共有6种,
∴刚好抽到1名男生与1名女生的概率为.
2.(1)
(2)
【分析】本题考查了用列表法和树状图法求概率的知识,熟练掌握列表法和树状图法是解题的关键.
(1)由题意可知,“”“”所占圆心角为,“”所占的圆心角共为,由计算可得转出数字是“”的概率;
(2)用列表法或树状图法得出所有可能的结果,再从中找到和为正数的结果数,然后利用概率公式求解即可.
【详解】(1)解:∵,
∴,,
∴“”和“”所占的扇形圆心角为, 个“”所占的扇形圆心角为,
∴转动转盘一次,转出的数字是的概率为;
故答案为:;
(2)解:树状图法:
由上图可知:所有可能的结果共种,其中数字之积为正数的有种,两次分别转出的数字之和为正数的概率为.
3.(1),见解析
(2)144
(3)
【分析】本题考查条形统计图与扇形统计图、画树状图或列表法求概率、概率公式.
(1)利用选择A类的学生人数除以其所占的百分比求得样本总量,再利用总人数减去其他类的学生人数求得D类的学生人数,再补全条形统计图即可;
(2)利用C类的学生人数除以样本的总人数求得其所占的百分比,再乘以即可求解;
(3)画树状图可得共有9种等可能的结果,其中甲乙两位同学选择相同类别书籍有2种等可能的结果,再利用概率公式求解即可.
【详解】(1)解:被调查学生总人数:(名),
的人数(名),
补全条形统计图如下:
故答案为:100;
(2)解:C“科技类”所对应的圆心角度数是,
故答案为:144;
(3)解:画树状图如下:
共有9种等可能的结果,其中甲乙两位同学选择相同类别书籍的结果有2种,
∴甲乙两位同学选择相同类别书籍的概率为.
4.(1)80,
(2)见详解
(3)
【分析】本题主要考查了条形统计图、扇形统计图、列举法求概率等知识,通过条形统计图和扇形统计图获得所需信息是解题关键.
(1)利用调查学生中“优秀”等级学生人数除以其占比,即可求得本次参与问卷调查的学生总数;利用“合格”等级学生人数除以所调查学生总数乘以,即可求得扇形统计图中“合格”所对应的百分比;
(2)首先求得学习情况为“良好”的学生人数,然后补画条形统计图即可;
(3)根据题意作出树状图,结合树状图可知,共有12种等可能的结果,其中所选两位同学恰好是1名男同学和1名女同学的结果有8种,即可获得答案.
【详解】(1)解:(人),
即本次参与问卷调查的学生共有80人,
,
即扇形统计图中“合格”所对应的百分比为.
故答案为:80,;
(2)参与调查的学生中,学习情况为“良好”的学生人数为(人),
故可补全条形统计图,如下所示:
(3)根据题意,作出树状图如下,
由树状图可知,共有12种等可能的结果,其中所选两位同学恰好是1名男同学和1名女同学的结果有8种,
所以,所选两位同学恰好是1名男同学和1名女同学的概率为.
5.(1)
(2)
【分析】本题考查用列表法或画树状图法求概率,熟练掌握概率=所求情况数与总情况数之比.
(1)根据概率公式求解即可;
(2)用列表法求解即可.
【详解】(1)解:因为从A、B、C、D中随机选一项,共有4种等可能结果,故恰好选中“射弩”的概率是;
故答案为:;
(2)解:列表分析如下:
甲 乙 A B C D
A
B
C
D
∵共有12种等可能的结果,其中甲、乙两人中至少有一人讲述本届运动会新增项目的比赛规则的有10种情况,
∴甲、乙两人中至少有一人讲述本届运动会新增项目的比赛规则的概率:.
6.(1)二
(2)在本次被调查的中小学生中选择“不喜欢”的人数为175人
(3)
【分析】本题考查的是频数分布直方图和扇形统计图的知识和概率公式、画树状图或列表格求概率,解题的关键是读懂频数分布直方图和利用统计图获取信息和掌握求概率的方法.
(1)由中位数的定义即可得出结论;
(2)用1200乘“不喜欢”所占百分比即可;
(3)画树状图即可求解;
【详解】(1)解:由统计图可知,抽取的这1200名学生每周参加家庭劳动时间的中位数为第600个和第601个数据的平均数,
,故中位数落在第二组;
故答案为:二;
(2)解:(人).
在本次被调查的中小学生中选择“不喜欢”的人数为175人.
(3)解:列树状图如解图:
共有12种等可能的结果,其中恰好是1名男生和1名女生的结果有8种,
(恰好是1名男生和1名女生).
7.(1)40人,补全图形见解析
(2)480人
(3)
【分析】本题考查条形统计图以及树状图法,注意结合题意中“写出所有可能的结果”的要求,使用列举法,注意按一定的顺序列举,做到不重不漏.
(1)用A档人数除以所占百分比即可得到总人数;用总人数减去A档,B档和D档人数,即可得到C档人数,从而可补全条统计图;
(2)先求出B档所占百分比,再乘以1200即可得到结论;
(3)分别用,,,表示四名同学,然后通过画树状图表示出所有等可能的结果数,再用概率公式求解即可.
【详解】(1)解:由①可知,A档有8人;本次调查人数是:(人);
∴C档人数是:(人),
补充完整图2如图:
(2)(人)
答:全校B档的人数为480人,
(3)用,表示2名来自八年级的学生,,表示2名来自九年级的学生,
所有的等可能的结果数有12个,抽到的2名学生来自不同年级的结果数有8个,
∴抽到的2名学生来自不同年级的概率.
8.(1)
(2)
(3)
【分析】()用组人数除以它的百分比即可求解;
()用乘以组人数的占比即可求解;
()画出树状图,根据树状图解答即可求解;
本题考查了扇形统计图和条形统计图,用树状图或列表法求概率,掌握以上知识点是解题的关键.
【详解】(1)解:本次随机调查的学生人数是;
故答案为:;
(2)解:在扇形统计图中,“”所在扇形的圆心角,
答案为:;
(3)解:画树状图如图所示:
由树状图可得,共有种等可能的结果,其中小明和小华恰好选中同一个主题活动的结果有种,
∴小明和小华恰好选中同一个主题活动的概率为.
9.(1)280
(2)补图见解析,
(3)
【分析】本题考查了补全条形统计图,圆心角的度数,运用列表或树状图求概率,解决此题的关键是读懂题意,根据图表得到需要的信息.
(1)根据“平等”的人数除以占的百分比得到调查的学生总数即可;
(2)求出“互助”与“进取”的学生数,补全条形统计图,求出“进取”占的圆心角度数即可;
(3)列表或画树状图得出所有等可能的情况数,找出恰好选到“B”与“C”的情况数,即可求出所求的概率.
【详解】(1)解:(名),
答:这次调查的学生共有280名,
故答案为:280;
(2)解:(名),(名),
补全条形统计图,如图所示,
根据题意得:,,
答:“进取”所对应的圆心角是,
故答案为:;
(3)解:用树状图为:
共有20种等可能的结果,恰好选到“B”和“C”有2种,
∴恰好选到“进取”和“感恩”两个主题的概率是.
10.(1),图见详解
(2)对于“国家反诈中心”非常了解的人数约2400人
(3)选取的2人不是同一组居民的概率为
【分析】(1)用条形统计图中C的人数除以扇形统计图中C的百分比求出问卷调查的人数,再用条形统计图中A的人数除以问卷调查的人数再乘以即可得A等级对应的人数所占百分比;求出B等级的人数,补全条形统计图即可.
(2)根据用样本估计总体,用8000乘以样本中A等级对应的人数所占百分比,即可得出答案.
(3)画树状图得出所有等可能的结果数以及选取的2人不是同一组居民的结果数,再利用概率公式可得出答案.
【详解】(1)解:问卷调查的人数为(人),
∴扇形统计图中,A等级对应的人数所占百分比为,
∴A等级对应的扇形的圆心角度数为.
故答案为:.
B等级的人数为(人).
补全条形统计图如图所示.
(2)解:(人).
答:对于“国家反诈中心”非常了解的人数约2400人.
(3)解:将3个一组居民分别记为A,B,C,1个二组居民记为D,
画树状图如下:
共有12种等可能的结果,其中选取的2人不是同一组居民的结果有6种,
∴选取的2人不是同一组居民的概率为.
【点睛】本题考查列表法与树状图法、条形统计图、扇形统计图、用样本估计总体,能够读懂统计图,掌握列表法与树状图法以及用样本估计总体是解答本题的关键.
11.(1)详见解析
(2)
【分析】本题主要考查了用列表法和树状图法求概率等知识点,
(1)首先根据题意画出表格,然后由表格即可求得所有等可能的结果;
(2)由(1)知,所有可能出现的结果一共有16种,然后根据概率公式进行解答即可;
解答此类问题的关键是明确题意,写出所有的可能情况,求出相应的概率.
【详解】(1)解:列表得,
1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
由列表可知,所有可能出现的结果一共有16种;
(2)解:由(1)知,所有可能出现的结果一共有16种,这些结果出现的可能性相同,其中两次所得数字之和为8、6、5的结果有8种,
∴抽奖一次中奖的概率为:,
答:抽奖一次能中奖的概率为.
12.(1)见解析
(2)32,
(3)
【分析】本题考查了列表法与树状图法,条形统计图和扇形统计图关联.
(1)用组的人数除以它所占的百分比得到调查的总人数,然后求出组的人数,从而补全统计图;
(2)用组的人数除以总人数,求出,再用乘以组所占的百分比,从而得出组对应的扇形圆心角的度数;
(3)画树状图展示所有12种等可能的结果数,找出所选的两人恰好是两名男生的结果数,然后利用概率公式求解.
【详解】(1)解:抽取的总人数有:(人),
组的人数有:(人),
补全统计图如下:
(2)解:,即;
组对应的扇形圆心角的度数为:;
故答案为:32,;
(3)解:画树状图为:
共有12种等可能的结果数,其中所选的两人恰好是两名男生的结果数为2,
所以所选的两人恰好是两名男生的概率.
13.(1),见解析
(2)估计该校参加魔方游戏的学生人数为人
(3)恰好抽到1名男生和1名女生的概率为
【分析】本题考查了条形统计图与扇形统计图相关联,用样本估计总体,画树状图法求概率,掌握相关知识点是解题关键.
(1)根据选择B类的学生人数和所占百分比,求出调查总人数,再求出选择D类的学生人数,补全条形统计图即可;
(2)用学校人数乘以选择C类的学生人数的占比,即可求解;
(3)利用画树状图法求解即可.
【详解】(1)解:本次调查总人数为(人),
选择D类的学生人数为(人),
补全条形统计图如下:
(2)解:(人),
答:估计该校参加魔方游戏的学生人数约为人;
(3)解:画树状图如下图:
由树状图可知,共有种情况,其中恰好抽到1名男生和1名女生的情况有种,
恰好抽到1名男生和1名女生的概率为.
14.(1)40,
(2)详见解析
(3)
【分析】本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或事件B的概率.也考查了统计图.
(1)由C类型人数及其所占百分比可得总人数,用乘以A类型人数所占比例即可;
(2)根据(1)的结果即可补全条形统计图;
(3)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【详解】(1)解:总人数(人),
A类型人数(人)
扇形统计图中A部分圆心角的度数为,
故答案为40,;
(2)解:补全条形统计图如图所示,
(3)解:将1班,2班,3班,4班分别记为1,2,3,4.
根据题意,列表如下:
班级 1 2 3 4
1
2
3
4
如表,所有可能发生的结果共有12种,并且它们发生的可能性相等,其中恰好选中2班和3班的有2种,
恰好选中2班和3班的概率是.
15.(1)补充条形统计图见解析,
(2)人
(3)
【分析】()根据选择“”的人数及比例求出总人数,总人数乘以占的比例求得“”的人数,总人数减去其他类别的人数求得“”的人数,据此即可将条形统计图补充完整,再用乘以“”占的比例即为“手工制作”对应的扇形圆心角度数;
()利用样本估计总体思想求解;
()通过列表或画树状图列出所有等可能的情况,再从中找出符合条件的情况数,再利用概率公式计算即可;
本题考查了条形统计图和扇形统计图,利用样本估计总体,利用画树状图或者列表法求概率,解题的关键是将条形统计图与扇形统计图的信息进行关联,掌握画树状图或者列表法求概率的原理.
【详解】(1)解:参与调查的总人数为:人,
∴“”的人数人,
∴“”的人数人,
补充条形统计图如图:
“手工制作”对应的扇形圆心角度数;
(2)解:,
答:估计全校最喜欢“绿植栽培”的学生人数为人;
(3)解:画树状图如下:
由图可知,共有种等可能的情况,其中两位同学选择相同课程的情况有种,
∴甲乙两位同学选择相同课程的概率为.
16.(1)50,
(2)见解析
(3)
【分析】本题考查的是用树状图法求概率、条形统计图和扇形统计图等知识.
(1)由B的人数除以所占百分比得出此次调查一共随机抽取的学生人数,依次去求出选D的人数、选C的人数,即可解决问题;
(2)根据(1)中的求解即可补全条形统计图;
(3)画树状图,共有16种等可能的结果,其中甲乙两位同学选择同一个社团的结果有4种,再由概率公式求解即可.
【详解】(1)解:本次调查一共随机抽取的学生人数为:(名)
∴D的人数为:(名),
∴C的人数为:(名),
∴图2中所在扇形的圆心角的度数为,
故答案为:50,
(2)补全条形统计图如下:
(3)解:画树状图如下:
共有16种等可能的结果,其中甲乙两位同学选择同一个社团的结果有4种,
∴甲乙两位同学选择同一个社团的概率为.
17.(1)
(2)
【分析】本题考查了概率的应用,掌握树状图或列表法是解题关键.
(1)根据概率的定义即可求解;
(2)画出树状图确定全部可能结果以及满足条件的情况,即可求解.
【详解】(1)解:∵转盘被分成了大小相同的4个扇形,
∴若转动转盘一次,则指针落在30元区域的概率为:,
故答案为:;
(2)解:画出树状图如下:
30元 50元 60元 100元
30元 60元 80元 90元 130元
50元 80元 100元 110元 150元
60元 90元 110元 120元 160元
100元 130元 150元 160元 200元
共有16种机会均等的结果,其中两次所得金额之和小于100元的情况有5种.
∴两次所得金额之和小于100元的概率为.
18.(1)800,40,5
(2)126
(3)
【分析】本题考查了列表法求概率,频数分布表以及扇形统计图;
(1)根据等级的人数除以占比得出总人数,进而求得的值;
(2)根据等级的占比乘以,即可求解;
(3)设四个项目的冠军分别为,根据列表法求概率,即可求解.
【详解】(1)解:依题意,名选手,,
∴
故答案为:,,.
(2)扇形统计图中,等级所对应的扇形圆心角度数是,
故答案为:.
(3)解:设全程马拉松男子组冠军、全程马拉松女子组冠军、半程马拉松男子组冠军、半程马拉松女子组冠军分别为,列表如下,
A B C D
A AB AC AD
B BA BC BD
C CA CB CD
D DA DB DC
共有12种等可能结果,其中恰好抽到全程马拉松女子组冠军和半程马拉松女子组冠军的有2种情形,
∴恰好抽到全程马拉松女子组冠军和半程马拉松女子组冠军的概率为
19.(1),,,,,,,,
(2)
(3)不公平,理由见解析
【分析】本题考查游戏的公平性及概率的计算,
(1)画出树状图,然后写出所有的等可能结果;
(2)根据(1)中的结果,再根据概率公式解答即可;
(3)根据概率公式分别计算出小红赢的概率和小莉赢的概率,再进行比较即可;
解题的关键是掌握:概率=所求情况数与总情况数之比;概率相等就公平,否则就不公平.
【详解】(1)解:画树状图如下:
共有9种等可能结果,分别是,,,,,,,,;
(2)由(1)知,至多有一次是""的情况有种,
∴(至多有一次是""),
∴至多有一次是“”的概率是;
(3)卡片上的数字是球上数字的整数倍的有,,,,共种情况,
∴小红赢的概率是,小莉赢的概率是,
∵,
∴此规则不公平,小莉获胜的概率大.
20.(1)
(2)见解析
(3)
【分析】本题考查统计图表,利用树状图法求概率,从统计图表中有效的获取信息,是解题的关键:
(1)类学生人数除以所占的比例求出总人数,360度乘以类学生所占的比例求出圆心角的度数;
(2)求出D类的人数,补全条形图即可;
(3)画出树状图,利用概率公式进行计算即可.
【详解】(1)解:(人);
;
故答案为:;
(2)D类的人数为(人),
补全条形统计图,如图,
(3)画树状图如下:
共有12种等可能结果,其中两人恰好是2名男生的结果有2种.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
概率初步解答题--2024-2025学年人教版九年级数学上册期末专题训练
1.太原市某校为了落实“五育”并举,提升学生的综合素养,在课外活动中开设了四个兴趣小组:A.跳长绳;B.篮球;C.书法;D.绘画.该校学生会围绕“你最喜欢的项目是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项).根据调查统计结果,绘制了如下两种不完整的统计图,请结合图中信息回答下列问题.
(1)本次共调查了________名学生,并将条形统计图补充完整.
(2)求篮球小组所对应扇形的圆心角度数.
(3)跳长绳小组的4名学生由3名男生和1名女生构成.从中随机抽取2名学生参加比赛.请用列表或画树状图的方法,求恰好抽到1名男生与1名女生的概率.
2.如图,一个可以自由转动的转盘,被它的两条直径分成了四个分别标有数字的扇形区域,,转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字.(若指针恰好停留在分界线上,则重新转一次)
(1)转动转盘一次,转出的数字是的概率是________;
(2)转动转盘两次,用列表或画树状图的方法,求这两次分别转出的数字之积为正数的概率.
3.2024年4月23日是世界读书日,为贯彻落实好《全国青少年学生读书行动1实施方案》,打造“人人爱读书,人人好读书”的书香校园,实验学校开展以“书香校园—我最喜欢的书籍”为主题的调查活动,学生根据自己的爱好选择一类书籍(A:政史类,B:文学类,C:科技类,D:艺术类,E:其他类).学校数学兴趣小组对部分学生进行了问卷调查,根据收集到的数据,数学兴趣小组绘制了两幅不完整的统计图(如图所示).
根据以上信息,解答下列问题:
(1)学校此次被调查的学生总人数为______名,并根据题意补全条形统计图;
(2)在扇形统计图中,C“科技类”所对应的圆心角度数是______度;
(3)学校数学兴趣小组中,甲同学从A,B,C三类书籍中随机选择一种,乙同学从B,C,D三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.
4.“青年大学习”是由共青团中央发起,广大青年参与,通过学习来提升自身理论水平、思维层次的行动.梦想从学习开始,事业从实践起步.某校为了解九年级学生学习“青年大学习”的情况,随机抽取部分九年级学生进行了问卷调查,按照调查结果,将学习情况分为优秀、良好、合格、较差四个等级.学校绘制了如下不完整的统计图,根据图中信息解答下列问题∶
(1)本次参与问卷调查的学生共有_________人,扇形统计图中“合格”所对应的百分比为_________;
(2)补全条形统计图;
(3)该校某班有4名同学(2名男同学,2名女同学)在调查中获得“优秀”等级,班主任将从这4名同学中随机选取2名同学,代表班级参加学校组织的“青年大学习”演讲比赛,请用列表或画树状图的方法,求所选两位同学恰好是1名男同学和1名女同学的概率.
5.2023年8月8日至20日,云南省第十六届运动会将在玉溪市举行,为全面发挥省运会在我省体育事业发展中的引领和示范作用,本届省运会进行了多项改革创新.其中大众组与上届相比,保留轮滑和棋牌项目,新增篮球、足球、射弩和工间操4个大项.某体育兴趣小组收集到了工间操、射弩、轮滑、棋牌四个项目的比赛规则,并制作了编号分别为A,B,C,D的4张卡片(如图,除图案和编号外,背面无其他差异),并将他们背面朝上洗匀后放在桌子上.
(1)从中随机抽取一张,抽到“射弩”的概率为 ;
(2)若甲同学从4张卡片中随机抽取1张不放回,乙同学再从余下的3张卡片中随机抽取1张,然后根据抽取的卡片讲述对应卡片上的比赛规则,请用列表法或画树状图法(树状图也称树形图)中的一种方法,求甲、乙两人中至少有一人讲述本届运动会新增项目的比赛规则的概率.
6.某教育部门为了解本地区中小学生参加家庭劳动时间的情况,随机抽取该地区1200名中小学生进行问卷调查,调查问卷和结果如下:
中小学生每周参加家庭劳动时间分为5组:第一组,第二组,第三组,第四组,第五组.对于每周参加家庭劳动时间不足的学生,影响他们每周参加家庭劳动的主要原因有:
A.没时间;B.家长不舍得;C.不喜欢;D.其他.请根据以上信息,解答下列问题:
(1)本次调查中,中小学生每周参加家庭劳动时间的中位数落在第_____组;
(2)求在本次被调查的中小学生中选择“不喜欢”的人数;
(3)在所调查的九年级一班学生中,有2名男生和2名女生,现需从这4名学生中抽取2名学生作进一步访谈调查,请用树状图或列表的方法,求所抽2名学生恰好是1名男生和1名女生概率.
7.在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间t(单位:小时).把调查结果分为四档,A档:;B档:;C档:;D档:.根据调查情况,给出了部分数据信息:
①A档和D档的所有数据是:7,7,7.5,10,7,10,7,7.5,7,7,10.5,10.5;
②图1和图2是两幅不完整的统计图.
根据以上信息解答问题:
(1)求本次调查的学生人数,并将图2补充完整;
(2)已知全校共1200名学生,请你估计全校B档的人数;
(3)学校要从D档的4名学生中随机抽取2名作读书经验分享,已知这4名学生,2名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.
8.为了响应市政府号召,某校开展了“创文明城市与我同行”活动周,活动周设置了“:文明礼仪,:生态环境,:交通安全,:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)在扇形统计图中,“”所在扇形的圆心角等于 度;
(3)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.
9.某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共 名.
(2)请将条形统计图补充完整,扇形统计图中“进取”所对应的圆心角是 .
(3)如果要在这5个主题中任选两个进行调查,用树状图或列表法,求恰好选到学生关注平等、感恩两个主题的概率.(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E)
10.某市利用各类灵活多样的宣传方式、各种宣传载体,全方位开展“国家反诈中心” 宣传推广工作,截止2023年底,注册人数已达216.39万人,某社区工作人员为调 查本社区居民对于“国家反诈中心”的了解情况,进行了一次问卷调查,本次问卷共设置10个问题,每题10分,问卷调查结束后,根据问卷结果分为A:非常了解(80-100分)、B:比较了解(60-80分)、C:基本了解(40-60分)、D:不太了解(0-40分)
四个等级并绘制了如下两幅不完整的统计图.
请根据如图提供的信息解答下列问题:
(1)扇形统计图中,A等级对应的扇形的圆心角度数为________,补全条形统计图;
(2)若该社区共有居民8000人,请你估计对于“国家反诈中心”非常了解的人数;
(3)为更好地开展“国家反诈中心”宜传推广工作,社区准备招募2名宜讲人员,现有问卷结果等级为A的4人报名,其中3人为一组居民,1人为二组居民,若从中随机选取2人,求选取的2人不是同一组居民的概率.
11.某超市抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖
(1)请用列表或树状图的方法,把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
12.南宁市某学校开展了“奋进万亿新征程,共筑强国强军梦”的主题研学活动.为了解学生参与情况,随机抽取部分学生对研学活动时长(用表示,单位:h)进行调查.经过整理,将数据分成四组(A组:;B组:;C组:;D组:),并绘制了如下不完整的条形统计图和扇形统计图.
(1)请补全条形统计图;
(2)扇形统计图中,的值为___________,A组对应的扇形圆心角的度数为_________;
(3)D组中有男、女生各两人,现从这四人中随机抽取两人进行研学宣讲,请用树状图或表格求所抽取的两人恰好是两名男生的概率.
13.3月14日是国际数学日,某校在“国际数学日”当天举行了丰富多彩的数学活动,其中游戏类活动有:.数字猜谜;.数独:.魔方;.24点游戏;.数字华容道.该校为了解学生对这五类数学游戏的喜爱情况,随机抽取部分学生进行了调查统计(每位学生必选且只能选一类),并根据调查结果,绘制了两幅不完整的统计图如图所示.
根据上述信息,解决下列问题.
(1)本次调查总人数为___________,并补全条形统计图:(要求在条形图上方注明人数)
(2)若该校有2000名学生,请估计该校参加魔方游戏的学生人数;
(3)该校从类中挑选出2名男生和2名女生,计划从这4名学生中随机抽取2名学生参加市青少年魔方比赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
14.为增强学生爱国意识,激发爱国情怀,某校9月开展了“喜迎二十大、永远跟党走、奋进新征程”主题教育活动,活动方式有:A.主题征文,B.书法绘画,C.红歌传唱,D.经典诵读.为了解最受学生喜爱的活动方式,现随机抽取若干名学生进行调查,并将调查结果绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)参与此次抽样调查的学生人数是_______,扇形统计图中A部分圆心角的度数是_______;
(2)请补全条形统计图;
(3)学校从1班,2班,3班,4班中随机选取两个班参加“红歌传唱”的活动,求恰好选中2班和3班的概率.
15.某校劳动实践基地共开设五门劳动实践课程,分别是:床铺整理,:衣物清洗,:手工制作、:简单烹饪、:绿植栽培;课程开设一段时间后,季老师采用抽样调查的方式在全校学生中开展了“我最喜欢的劳动实践课程”为主题的问卷调查.根据调查所收集的数我进行整理、绘制了如下两幅不完整的统计图.
根据图中信息,请回答下列问题:
(1)请将条形统计图补充完整,并直接写出“手工制作”对应的扇形圆心角度数;
(2)若该校共有名学生,请你估计全校最喜欢“绿植栽培”的学生人数;
(3)小兰同学从三门课程中随机选择一门参加劳动实践,小亮同学从三门课程中随机选择一门参加劳动实践,求两位同学选择相同课程的概率.
16.因国家对体育健康的重视程度不断提高,某校决定开展体育社团活动,分别有:A.足球社团,B.篮球社团,C.跑步社团,D.铅球社团,每位学生只能选其中一项作为社团活动.为了解学生对以上社团的参与情况,随机抽取部分学生进行了调查统计,并根据调查结果,绘制成如图所示的不完整的统计图:请根据图中信息,解答下列问题:
(1)本次一共调查了______名学生,图2中所在扇形的圆心角的度数为______;
(2)请补全条形统计图;
(3)甲、乙两位同学各随机选择一个社团参加,请用画树状图或列表的方法,求甲乙两位同学选择同一个社团的概率.
17.作为《黑神话 悟空》的创意来源之一,山西古建筑随着游戏的火爆收获无数关注,吸引大量游客前来旅游打卡,小军和小勇准备到山西旅游打卡,他们选了四处影点.门票价格分别为30元、50元、60元、100元,他们决定用转盘游戏决定地点.如图是一个可以自由转动的转盘,指针固定不动,转盘被分成了大小相同的4个扇形,并在每个扇形区域分别标上30元、50元、60元、100元.(当指针落在边界线上时,重新转动一次,直到指针指向某一区域内为止)
(1)若转动转盘一次,则指针落在30元区域的概率为______.
(2)小军和小勇每人转动转盘一次,当转盘停止时,记下各自指针所指区域内对应的金额,请用画树状图或列表法求两次所得金额之和小于100元的概率.
18.2024年10月20日上午7时30分,长沙马拉松暨全国半程马拉松锦标赛(第四站)鸣枪开跑,来自国内外的3万名跑友从贺龙体育中心东广场出发,用脚步丈量大美星城.本次赛事以“传递奔跑的力量”为主题,旨在增强全市民众科学健身意识,推动全民健身活动.本届赛事共设置马拉松,半程马拉松和欢乐跑三个项目.赛后随机抽取了部分参赛选手对本次赛事组织进行满意度评分调查,整理后得到下列不完整的图表:
等级 A B C D
分数段 90﹣100 80﹣89 70﹣79 60﹣69
频数 440 280 m 40
请根据表中提供的信息,解答下列问题:
(1)此次调查共抽取了 名选手,m= ,n= ;
(2)扇形统计图中,B等级所对应的扇形圆心角度数是 度;
(3)赛后全程马拉松男子组冠军和女子组冠军各一名;半程马拉松男子组冠军和女子组冠军各一名,欢乐跑没有设置冠亚军奖项.若从设置奖项的两个项目的男女冠军四人中随机抽取两人访谈,请用列表或画树状图的方法,求出恰好抽到全程马拉松女子组冠军和半程马拉松女子组冠军的概率.
19.在一个不透明的口袋里装有分别标注,,的个小球(小球除数字外,其余都相同),另有张背面完全一样、正面分别写有数字,,的卡片.现从口袋中任意摸出一个小球,再从这张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
(2)求这两次摸出的数字,至多有一次是“”的概率;
(3)小红和小莉做游戏,制定了游戏规则:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢这个游戏规则公平吗?请说明理由.
20.睡眠管理作为“五项管理”中的重要内容之一,也是学校教育电点关注的内容.某校为了解学生平均每天睡眠时间,随机抽取该校部分学生进行问卷调查,并将结果进行了统计和整理,绘制成如下统计表和不完整的统计图.
学生类别 学生平均每天睡眠时间单位:小时
A
B
C
D
E
(1)扇形统计图中表示C类学生平均每天睡眠时间的扇形的圆心角度数为______.
(2)请补全条形统计图.
(3)被抽取调查的E类4名学生中有2名女生,2名男生.从这4人中随机抽取2人进行电话回访,请用画树状图或列表的方法,求恰好抽到2名男生的概率.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)40,补全条形统计图如下:
(2)
(3)
【分析】本题考查了条形统计图和扇形统计图,及用列表法或树状图法求概率,准确理解题意,熟练掌握知识点是解题的关键.
(1)由A组人数及其所占百分比可得总人数,总人数减去A、B、D人数求出C组人数即可补全图形;
(2)用360度乘以篮球组人数所占比例即可;
(3)画树状图,共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果有6种,再由概率公式求解即可.
【详解】(1)解:本次调查总人数为(名),
C组人数为(名),
补全图形如下:
故答案为:40;
(2)解:,
故答案为:72;
(3)解:画树状图如下:
共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果共有6种,
∴刚好抽到1名男生与1名女生的概率为.
2.(1)
(2)
【分析】本题考查了用列表法和树状图法求概率的知识,熟练掌握列表法和树状图法是解题的关键.
(1)由题意可知,“”“”所占圆心角为,“”所占的圆心角共为,由计算可得转出数字是“”的概率;
(2)用列表法或树状图法得出所有可能的结果,再从中找到和为正数的结果数,然后利用概率公式求解即可.
【详解】(1)解:∵,
∴,,
∴“”和“”所占的扇形圆心角为, 个“”所占的扇形圆心角为,
∴转动转盘一次,转出的数字是的概率为;
故答案为:;
(2)解:树状图法:
由上图可知:所有可能的结果共种,其中数字之积为正数的有种,两次分别转出的数字之和为正数的概率为.
3.(1),见解析
(2)144
(3)
【分析】本题考查条形统计图与扇形统计图、画树状图或列表法求概率、概率公式.
(1)利用选择A类的学生人数除以其所占的百分比求得样本总量,再利用总人数减去其他类的学生人数求得D类的学生人数,再补全条形统计图即可;
(2)利用C类的学生人数除以样本的总人数求得其所占的百分比,再乘以即可求解;
(3)画树状图可得共有9种等可能的结果,其中甲乙两位同学选择相同类别书籍有2种等可能的结果,再利用概率公式求解即可.
【详解】(1)解:被调查学生总人数:(名),
的人数(名),
补全条形统计图如下:
故答案为:100;
(2)解:C“科技类”所对应的圆心角度数是,
故答案为:144;
(3)解:画树状图如下:
共有9种等可能的结果,其中甲乙两位同学选择相同类别书籍的结果有2种,
∴甲乙两位同学选择相同类别书籍的概率为.
4.(1)80,
(2)见详解
(3)
【分析】本题主要考查了条形统计图、扇形统计图、列举法求概率等知识,通过条形统计图和扇形统计图获得所需信息是解题关键.
(1)利用调查学生中“优秀”等级学生人数除以其占比,即可求得本次参与问卷调查的学生总数;利用“合格”等级学生人数除以所调查学生总数乘以,即可求得扇形统计图中“合格”所对应的百分比;
(2)首先求得学习情况为“良好”的学生人数,然后补画条形统计图即可;
(3)根据题意作出树状图,结合树状图可知,共有12种等可能的结果,其中所选两位同学恰好是1名男同学和1名女同学的结果有8种,即可获得答案.
【详解】(1)解:(人),
即本次参与问卷调查的学生共有80人,
,
即扇形统计图中“合格”所对应的百分比为.
故答案为:80,;
(2)参与调查的学生中,学习情况为“良好”的学生人数为(人),
故可补全条形统计图,如下所示:
(3)根据题意,作出树状图如下,
由树状图可知,共有12种等可能的结果,其中所选两位同学恰好是1名男同学和1名女同学的结果有8种,
所以,所选两位同学恰好是1名男同学和1名女同学的概率为.
5.(1)
(2)
【分析】本题考查用列表法或画树状图法求概率,熟练掌握概率=所求情况数与总情况数之比.
(1)根据概率公式求解即可;
(2)用列表法求解即可.
【详解】(1)解:因为从A、B、C、D中随机选一项,共有4种等可能结果,故恰好选中“射弩”的概率是;
故答案为:;
(2)解:列表分析如下:
甲 乙 A B C D
A
B
C
D
∵共有12种等可能的结果,其中甲、乙两人中至少有一人讲述本届运动会新增项目的比赛规则的有10种情况,
∴甲、乙两人中至少有一人讲述本届运动会新增项目的比赛规则的概率:.
6.(1)二
(2)在本次被调查的中小学生中选择“不喜欢”的人数为175人
(3)
【分析】本题考查的是频数分布直方图和扇形统计图的知识和概率公式、画树状图或列表格求概率,解题的关键是读懂频数分布直方图和利用统计图获取信息和掌握求概率的方法.
(1)由中位数的定义即可得出结论;
(2)用1200乘“不喜欢”所占百分比即可;
(3)画树状图即可求解;
【详解】(1)解:由统计图可知,抽取的这1200名学生每周参加家庭劳动时间的中位数为第600个和第601个数据的平均数,
,故中位数落在第二组;
故答案为:二;
(2)解:(人).
在本次被调查的中小学生中选择“不喜欢”的人数为175人.
(3)解:列树状图如解图:
共有12种等可能的结果,其中恰好是1名男生和1名女生的结果有8种,
(恰好是1名男生和1名女生).
7.(1)40人,补全图形见解析
(2)480人
(3)
【分析】本题考查条形统计图以及树状图法,注意结合题意中“写出所有可能的结果”的要求,使用列举法,注意按一定的顺序列举,做到不重不漏.
(1)用A档人数除以所占百分比即可得到总人数;用总人数减去A档,B档和D档人数,即可得到C档人数,从而可补全条统计图;
(2)先求出B档所占百分比,再乘以1200即可得到结论;
(3)分别用,,,表示四名同学,然后通过画树状图表示出所有等可能的结果数,再用概率公式求解即可.
【详解】(1)解:由①可知,A档有8人;本次调查人数是:(人);
∴C档人数是:(人),
补充完整图2如图:
(2)(人)
答:全校B档的人数为480人,
(3)用,表示2名来自八年级的学生,,表示2名来自九年级的学生,
所有的等可能的结果数有12个,抽到的2名学生来自不同年级的结果数有8个,
∴抽到的2名学生来自不同年级的概率.
8.(1)
(2)
(3)
【分析】()用组人数除以它的百分比即可求解;
()用乘以组人数的占比即可求解;
()画出树状图,根据树状图解答即可求解;
本题考查了扇形统计图和条形统计图,用树状图或列表法求概率,掌握以上知识点是解题的关键.
【详解】(1)解:本次随机调查的学生人数是;
故答案为:;
(2)解:在扇形统计图中,“”所在扇形的圆心角,
答案为:;
(3)解:画树状图如图所示:
由树状图可得,共有种等可能的结果,其中小明和小华恰好选中同一个主题活动的结果有种,
∴小明和小华恰好选中同一个主题活动的概率为.
9.(1)280
(2)补图见解析,
(3)
【分析】本题考查了补全条形统计图,圆心角的度数,运用列表或树状图求概率,解决此题的关键是读懂题意,根据图表得到需要的信息.
(1)根据“平等”的人数除以占的百分比得到调查的学生总数即可;
(2)求出“互助”与“进取”的学生数,补全条形统计图,求出“进取”占的圆心角度数即可;
(3)列表或画树状图得出所有等可能的情况数,找出恰好选到“B”与“C”的情况数,即可求出所求的概率.
【详解】(1)解:(名),
答:这次调查的学生共有280名,
故答案为:280;
(2)解:(名),(名),
补全条形统计图,如图所示,
根据题意得:,,
答:“进取”所对应的圆心角是,
故答案为:;
(3)解:用树状图为:
共有20种等可能的结果,恰好选到“B”和“C”有2种,
∴恰好选到“进取”和“感恩”两个主题的概率是.
10.(1),图见详解
(2)对于“国家反诈中心”非常了解的人数约2400人
(3)选取的2人不是同一组居民的概率为
【分析】(1)用条形统计图中C的人数除以扇形统计图中C的百分比求出问卷调查的人数,再用条形统计图中A的人数除以问卷调查的人数再乘以即可得A等级对应的人数所占百分比;求出B等级的人数,补全条形统计图即可.
(2)根据用样本估计总体,用8000乘以样本中A等级对应的人数所占百分比,即可得出答案.
(3)画树状图得出所有等可能的结果数以及选取的2人不是同一组居民的结果数,再利用概率公式可得出答案.
【详解】(1)解:问卷调查的人数为(人),
∴扇形统计图中,A等级对应的人数所占百分比为,
∴A等级对应的扇形的圆心角度数为.
故答案为:.
B等级的人数为(人).
补全条形统计图如图所示.
(2)解:(人).
答:对于“国家反诈中心”非常了解的人数约2400人.
(3)解:将3个一组居民分别记为A,B,C,1个二组居民记为D,
画树状图如下:
共有12种等可能的结果,其中选取的2人不是同一组居民的结果有6种,
∴选取的2人不是同一组居民的概率为.
【点睛】本题考查列表法与树状图法、条形统计图、扇形统计图、用样本估计总体,能够读懂统计图,掌握列表法与树状图法以及用样本估计总体是解答本题的关键.
11.(1)详见解析
(2)
【分析】本题主要考查了用列表法和树状图法求概率等知识点,
(1)首先根据题意画出表格,然后由表格即可求得所有等可能的结果;
(2)由(1)知,所有可能出现的结果一共有16种,然后根据概率公式进行解答即可;
解答此类问题的关键是明确题意,写出所有的可能情况,求出相应的概率.
【详解】(1)解:列表得,
1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
由列表可知,所有可能出现的结果一共有16种;
(2)解:由(1)知,所有可能出现的结果一共有16种,这些结果出现的可能性相同,其中两次所得数字之和为8、6、5的结果有8种,
∴抽奖一次中奖的概率为:,
答:抽奖一次能中奖的概率为.
12.(1)见解析
(2)32,
(3)
【分析】本题考查了列表法与树状图法,条形统计图和扇形统计图关联.
(1)用组的人数除以它所占的百分比得到调查的总人数,然后求出组的人数,从而补全统计图;
(2)用组的人数除以总人数,求出,再用乘以组所占的百分比,从而得出组对应的扇形圆心角的度数;
(3)画树状图展示所有12种等可能的结果数,找出所选的两人恰好是两名男生的结果数,然后利用概率公式求解.
【详解】(1)解:抽取的总人数有:(人),
组的人数有:(人),
补全统计图如下:
(2)解:,即;
组对应的扇形圆心角的度数为:;
故答案为:32,;
(3)解:画树状图为:
共有12种等可能的结果数,其中所选的两人恰好是两名男生的结果数为2,
所以所选的两人恰好是两名男生的概率.
13.(1),见解析
(2)估计该校参加魔方游戏的学生人数为人
(3)恰好抽到1名男生和1名女生的概率为
【分析】本题考查了条形统计图与扇形统计图相关联,用样本估计总体,画树状图法求概率,掌握相关知识点是解题关键.
(1)根据选择B类的学生人数和所占百分比,求出调查总人数,再求出选择D类的学生人数,补全条形统计图即可;
(2)用学校人数乘以选择C类的学生人数的占比,即可求解;
(3)利用画树状图法求解即可.
【详解】(1)解:本次调查总人数为(人),
选择D类的学生人数为(人),
补全条形统计图如下:
(2)解:(人),
答:估计该校参加魔方游戏的学生人数约为人;
(3)解:画树状图如下图:
由树状图可知,共有种情况,其中恰好抽到1名男生和1名女生的情况有种,
恰好抽到1名男生和1名女生的概率为.
14.(1)40,
(2)详见解析
(3)
【分析】本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或事件B的概率.也考查了统计图.
(1)由C类型人数及其所占百分比可得总人数,用乘以A类型人数所占比例即可;
(2)根据(1)的结果即可补全条形统计图;
(3)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【详解】(1)解:总人数(人),
A类型人数(人)
扇形统计图中A部分圆心角的度数为,
故答案为40,;
(2)解:补全条形统计图如图所示,
(3)解:将1班,2班,3班,4班分别记为1,2,3,4.
根据题意,列表如下:
班级 1 2 3 4
1
2
3
4
如表,所有可能发生的结果共有12种,并且它们发生的可能性相等,其中恰好选中2班和3班的有2种,
恰好选中2班和3班的概率是.
15.(1)补充条形统计图见解析,
(2)人
(3)
【分析】()根据选择“”的人数及比例求出总人数,总人数乘以占的比例求得“”的人数,总人数减去其他类别的人数求得“”的人数,据此即可将条形统计图补充完整,再用乘以“”占的比例即为“手工制作”对应的扇形圆心角度数;
()利用样本估计总体思想求解;
()通过列表或画树状图列出所有等可能的情况,再从中找出符合条件的情况数,再利用概率公式计算即可;
本题考查了条形统计图和扇形统计图,利用样本估计总体,利用画树状图或者列表法求概率,解题的关键是将条形统计图与扇形统计图的信息进行关联,掌握画树状图或者列表法求概率的原理.
【详解】(1)解:参与调查的总人数为:人,
∴“”的人数人,
∴“”的人数人,
补充条形统计图如图:
“手工制作”对应的扇形圆心角度数;
(2)解:,
答:估计全校最喜欢“绿植栽培”的学生人数为人;
(3)解:画树状图如下:
由图可知,共有种等可能的情况,其中两位同学选择相同课程的情况有种,
∴甲乙两位同学选择相同课程的概率为.
16.(1)50,
(2)见解析
(3)
【分析】本题考查的是用树状图法求概率、条形统计图和扇形统计图等知识.
(1)由B的人数除以所占百分比得出此次调查一共随机抽取的学生人数,依次去求出选D的人数、选C的人数,即可解决问题;
(2)根据(1)中的求解即可补全条形统计图;
(3)画树状图,共有16种等可能的结果,其中甲乙两位同学选择同一个社团的结果有4种,再由概率公式求解即可.
【详解】(1)解:本次调查一共随机抽取的学生人数为:(名)
∴D的人数为:(名),
∴C的人数为:(名),
∴图2中所在扇形的圆心角的度数为,
故答案为:50,
(2)补全条形统计图如下:
(3)解:画树状图如下:
共有16种等可能的结果,其中甲乙两位同学选择同一个社团的结果有4种,
∴甲乙两位同学选择同一个社团的概率为.
17.(1)
(2)
【分析】本题考查了概率的应用,掌握树状图或列表法是解题关键.
(1)根据概率的定义即可求解;
(2)画出树状图确定全部可能结果以及满足条件的情况,即可求解.
【详解】(1)解:∵转盘被分成了大小相同的4个扇形,
∴若转动转盘一次,则指针落在30元区域的概率为:,
故答案为:;
(2)解:画出树状图如下:
30元 50元 60元 100元
30元 60元 80元 90元 130元
50元 80元 100元 110元 150元
60元 90元 110元 120元 160元
100元 130元 150元 160元 200元
共有16种机会均等的结果,其中两次所得金额之和小于100元的情况有5种.
∴两次所得金额之和小于100元的概率为.
18.(1)800,40,5
(2)126
(3)
【分析】本题考查了列表法求概率,频数分布表以及扇形统计图;
(1)根据等级的人数除以占比得出总人数,进而求得的值;
(2)根据等级的占比乘以,即可求解;
(3)设四个项目的冠军分别为,根据列表法求概率,即可求解.
【详解】(1)解:依题意,名选手,,
∴
故答案为:,,.
(2)扇形统计图中,等级所对应的扇形圆心角度数是,
故答案为:.
(3)解:设全程马拉松男子组冠军、全程马拉松女子组冠军、半程马拉松男子组冠军、半程马拉松女子组冠军分别为,列表如下,
A B C D
A AB AC AD
B BA BC BD
C CA CB CD
D DA DB DC
共有12种等可能结果,其中恰好抽到全程马拉松女子组冠军和半程马拉松女子组冠军的有2种情形,
∴恰好抽到全程马拉松女子组冠军和半程马拉松女子组冠军的概率为
19.(1),,,,,,,,
(2)
(3)不公平,理由见解析
【分析】本题考查游戏的公平性及概率的计算,
(1)画出树状图,然后写出所有的等可能结果;
(2)根据(1)中的结果,再根据概率公式解答即可;
(3)根据概率公式分别计算出小红赢的概率和小莉赢的概率,再进行比较即可;
解题的关键是掌握:概率=所求情况数与总情况数之比;概率相等就公平,否则就不公平.
【详解】(1)解:画树状图如下:
共有9种等可能结果,分别是,,,,,,,,;
(2)由(1)知,至多有一次是""的情况有种,
∴(至多有一次是""),
∴至多有一次是“”的概率是;
(3)卡片上的数字是球上数字的整数倍的有,,,,共种情况,
∴小红赢的概率是,小莉赢的概率是,
∵,
∴此规则不公平,小莉获胜的概率大.
20.(1)
(2)见解析
(3)
【分析】本题考查统计图表,利用树状图法求概率,从统计图表中有效的获取信息,是解题的关键:
(1)类学生人数除以所占的比例求出总人数,360度乘以类学生所占的比例求出圆心角的度数;
(2)求出D类的人数,补全条形图即可;
(3)画出树状图,利用概率公式进行计算即可.
【详解】(1)解:(人);
;
故答案为:;
(2)D类的人数为(人),
补全条形统计图,如图,
(3)画树状图如下:
共有12种等可能结果,其中两人恰好是2名男生的结果有2种.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
