第二十六章 反比例函数 专项训练(含答案) 2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 第二十六章 反比例函数 专项训练(含答案) 2024-2025学年人教版九年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 658.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-22 21:44:31 | ||
图片预览



文档简介
第二十六章反比例函数专项训练 2024-2025学年人教版九年级数学下册
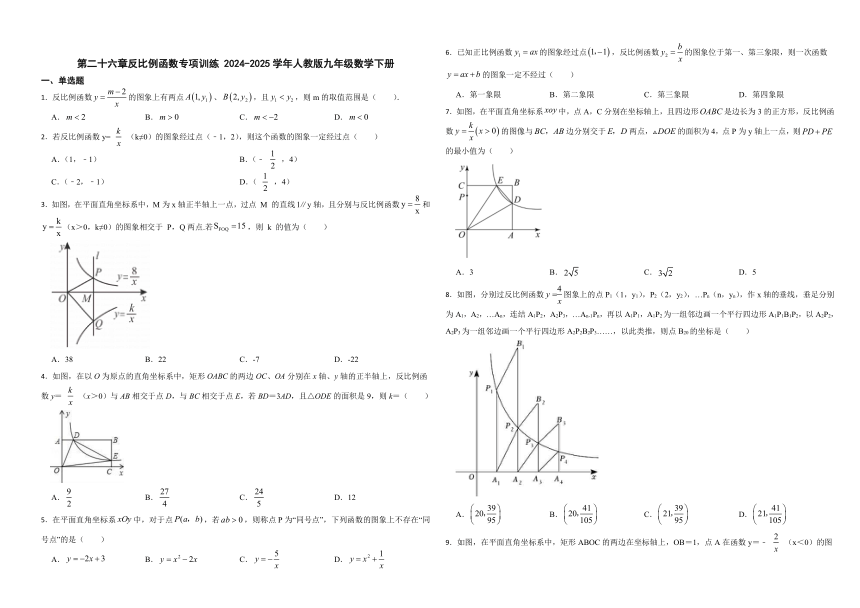
一、单选题
1.反比例函数的图象上有两点、,且,则m的取值范围是( ).
A. B. C. D.
2.若反比例函数y= (k≠0)的图象经过点(﹣1,2),则这个函数的图象一定经过点( )
A.(1,﹣1) B.(﹣ ,4)
C.(﹣2,﹣1) D.( ,4)
3.如图,在平面直角坐标系中,M为x轴正半轴上一点,过点 M 的直线l∥y轴,且分别与反比例函数和 (x>0,k≠0)的图象相交于 P,Q两点.若,则 k 的值为( )
A.38 B.22 C.-7 D.-22
4.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y= (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
A. B. C. D.12
5.在平面直角坐标系中,对于点,若,则称点P为“同号点”,下列函数的图象上不存在“同号点”的是( )
A. B. C. D.
6.已知正比例函数的图象经过点,反比例函数的图象位于第一、第三象限,则一次函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图,在平面直角坐标系中,点A,C分别在坐标轴上,且四边形是边长为3的正方形,反比例函数的图像与边分别交于两点,的面积为4,点P为y轴上一点,则的最小值为( )
A.3 B. C. D.5
8.如图,分别过反比例函数图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn),作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An-1Pn,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3……,以此类推,则点B20的坐标是( )
A. B. C. D.
9.如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=﹣ (x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y= (x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
A. B. C. D.
10.如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y 上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )
A.2.5 B.3 C.3.5 D.4
二、填空题
11.若点 、 在反比例函数 图象上,则 、 大小关系是 .
12.已知反比例函数(m为常数,)图象的两个分支分布在第二、四象限,则m的取值范围是 .
13.若反比例函数y1=,y2=﹣,当1≤x≤3时,函数y1的最大值是a,函数y2的最大值是b,则ab= .
14.如图,已知在平面直角坐标系中,点P在反比例函数图象上,点B为y轴负半轴上一点,连结交x轴于点A,点C为x轴负半轴上一点,连结和.若,,且的面积为3,则k的值是 .
15.如图,点A在反比例函数的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为4,则k= .
16.如图,一定质量的氧气,其体积V()是密度ρ()的反比例函数,其图象如图,当时的氧气的体积 .
17.如图,点A是反比例函数的图象上一点,轴交x轴于点B,, .
三、解答题
18.如图,已知,是一次函数的图象与反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出不等式的解集.
19.如图,直线与双曲线 交于点和点,与 y轴交于点A,求点A的坐标.
20.某小组进行漂洗实验,每次漂洗的衣服量和添加洗衣粉量固定不变.实验发现,当每次漂洗用水量(升)一定时,衣服中残留的洗衣粉量(克)与漂洗次数(次)满足(为常数),已知当使用5升水,漂洗1次后,衣服中残留洗衣粉2克.
(1)求的值.
(2)如果每次用水5升,要求漂洗后残留的洗衣粉量小于0.8克,求至少漂洗多少次?
(3)现将20升水等分成次()漂洗,要使残留的洗衣粉量降到0.5克,求每次漂洗用水多少升?
21.如图,一次函数(为常数,)的图象与反比例函数为常数,的图象在第一象限交于点,与轴交于点.
(1)求一次函数和反比例函数的解析式.
(2)点在轴上,是以为腰的等腰三角形,请直接写出点的坐标.
22.如下图,反比例函数与一次函数的图象都经过点和点,以为边作正方形(点A、B、C、D逆时针排列).
(1)求m的值和一次函数的解析式.
(2)求点C的坐标.
(3)将正方形平移得到正方形,在平移过程中,使点A的对应顶点M始终在第一象限内且在反比例函数的图象上(点M与点A不重合),当正方形与正方形的重叠部分为正方形时,求重叠正方形的边长.
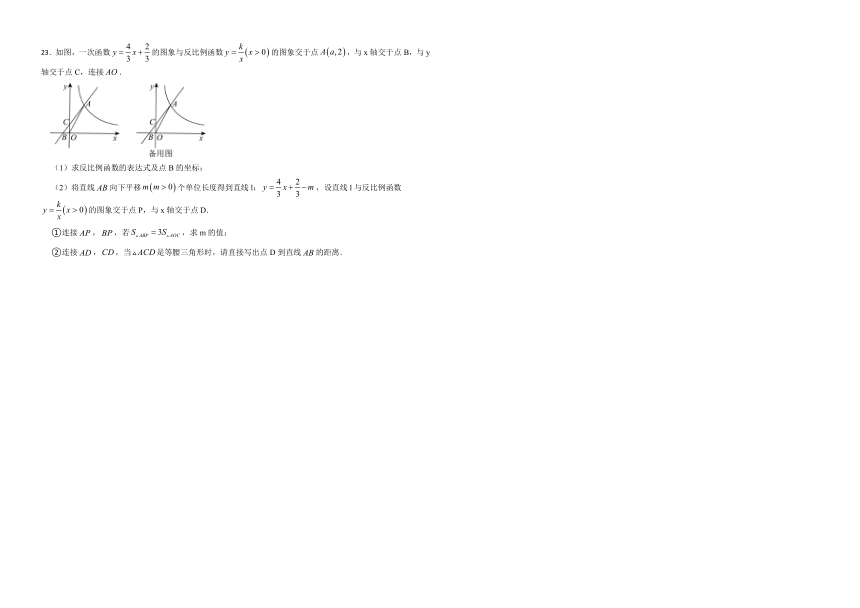
23.如图,一次函数的图象与反比例函数的图象交于点,与x轴交于点B,与y轴交于点C,连接.
(1)求反比例函数的表达式及点B的坐标;
(2)将直线向下平移个单位长度得到直线l:,设直线l与反比例函数的图象交于点P,与x轴交于点D.
①连接,,若,求m的值;
②连接,,当是等腰三角形时,请直接写出点D到直线的距离.
答案解析部分
1.【答案】A
2.【答案】B
【解析】【解答】解:将点(﹣1,2)代入y= 得,2=﹣ ,
解得k=﹣2,
∴反比例函数的解析式为y=﹣ ,
当x=﹣ 时,y=4.
故答案为:B.
【分析】将点(﹣1,2)代入反比例函数解析式求得k的值,然后对各个选项进行判断即可.
3.【答案】D
【解析】【解答】解:∵l∥y轴,
∴l⊥x轴,
∵直线l分别与反比例函数和 的图象相交于 P,Q两点,
∴S△POM=×8=4,S△OMQ=|k|,
∵S△POM+S△OMQ=S△POQ=15
∴4+|k|=15,
∴k=±22,
∵的图象经过第四象限,
∴k<0,
∴k=-22.
故答案为:D.
【分析】易得l⊥x轴,从而由反比例函数k的几何意义可得S△POM=×8=4,S△OMQ=|k|,进而根据S△POM+S△OMQ=S△POQ建立方程求出k的值,再结合函数所在的象限即可得出答案.
4.【答案】C
【解析】【解答】解:∵四边形OCBA是矩形,
∴AB=OC,OA=BC,
设B点的坐标为(a,b),
∵BD=3AD,
∴D( ,b),
∵点D,E在反比例函数的图象上,
∴ =k,∴E(a, ),
∵S△ODE=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣ ﹣ k﹣ (b﹣ )=9,
∴k= ,
故答案为:C.
【分析】所给的三角形面积等于长方形面积减去三个直角三角形的面积,然后即可求出B的横纵坐标的积即是反比例函数的比例系数.
5.【答案】C
【解析】【解答】解:由题意,图象经过第一和第三象限的函数都是满足条件的,
函数的图象在二、四象限,不满足条件,
故答案为:C.
【分析】由题意,图象经过第一和第三象限的函数都是满足条件的,据此判断即可.
6.【答案】C
【解析】【解答】解:∵正比例函数y1=ax的图象经过点(1,-1),
∴a=-1,
∵ 反比例函数的图象位于第一、第三象限 ,
∴b>0,
∴一次函数y=ax+b的图象经过一、二、四象限,即该函数的图象一定不会经过第三象限,
故A、B、D三个选项都是错误的,不符合题意;只有C选项正确,符合题意.
故答案为:C.
【分析】将点(1,-1)代入正比例函数y1=ax可求出a=-1,根据反比例函数的图象与系数的关系,由反比例函数的图象位于第一、第三象限,得b>0,进而根据一次函数的图象与系数的关系:y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象限;当a>0,b<0时,图象过一、三、四象限;当a>0,b=0时,图象过一、三象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限,当a<0,b=0时,图象过二、四象限,即可判断得出答案.
7.【答案】B
【解析】【解答】正方形的边长是3,
点的横坐标和点的纵坐标为3,
,,,
,,
的面积为,
,
或(舍去),
,,
作关于轴的对称点,连接交轴于,则的长的最小值,
,
,,
,
即的最小值为,
故选:B.
【分析】本题考查反比例函数的系数的几何意义,轴对称中最小距离问题,勾股定理,正方形的性质.根据正方形的边长是3,据此可推出点的横坐标和点的纵坐标为3,求得,,,进而可求出BE和BD,利用三角形的面积公式可列方程,解方程可求出k的值,进而可求出点D和点E的坐标:,,作关于轴的对称点,连接交轴于,则的长的最小值,利用勾股定理可求出,进而可求出答案.
8.【答案】D
【解析】【解答】解:点 P1(1,y1),P2(2,y2)在反比例函数图象上 ,
,
,
四边形是平行四边形,
,
点B1的纵坐标是:,即B1(2,6),
同理可得,点B2的纵坐标为:,即,
点B3的纵坐标为:,
...
点Bn的横坐标为:,纵坐标为:,
.
故答案为:D.
【分析】根据反比例函数图象上点的坐标特征求得点 P1 、 P2 的纵坐标,由平行四边形的性质得到B1、 B2的坐标,以此类推得到规律并求出点B20的坐标.
9.【答案】C
【解析】【解答】解:∵OB=1,AB⊥OB,点A在函数 (x<0)的图象上,
∴当x= 1时,y=2,
∴A( 1,2).
∵此矩形向右平移3个单位长度到 的位置,
∴B1(2,0),
∴A1(2,2).
∵点A1在函数 (x>0)的图象上,
∴k=4,
∴反比例函数的解析式为 ,O1(3,0),
∵C1O1⊥x轴,
∴当x=3时,
∴P
故答案为:C.
【分析】先求出A点坐标,再根据图形平移的性质得出A1点的坐标,故可得出反比例函数的解析式,把O1点的横坐标代入即可得出结论.
10.【答案】C
【解析】【解答】解:设点D(m, ),
如图所示,过点D作x轴的垂线交CE于点G,过点A过x轴的平行线交DG于点H,过点A作AN⊥x轴于点N,
∵∠GDC+∠DCG=90°,∠GDC+∠HDA=90°,
∴∠HDA=∠GCD,
又AD=CD,∠DHA=∠CGD=90°,
∴△DHA≌△CGD(AAS),
∴HA=DG,DH=CG,
同理△ANB≌△DGC(AAS),
∴AN=DG=1=AH,则点G(m, -1),CG=DH,
AH=-1-m=1,解得:m=-2,
故点G(-2,-4),D(-2,-3),H(-2,1),
则点E(- ,-4),GE= ,
CE=CG-GE=DH-GE=4- =3.5,
故答案为:C.
【分析】根据反比例函数图象上的点的坐标特点设点D(m, ),如图所示,过点D作x轴的垂线交CE于点G,过点A过x轴的平行线交DG于点H,过点A作AN⊥x轴于点N,根据同角的余角相等得出∠HDA=∠GCD,从而利用AAS判断出△DHA≌△CGD,根据全等三角形的性质得出HA=DG,DH=CG,同理△ANB≌△DGC,推出AN=DG=1=AH,故G(m, -1),CG=DH,从而列出方程,求解算出m的值得出G,D,H三点的坐标,进而得出点E的坐标,根据两点间的距离公式得出GE的长,最后根据CE=CG-GE=DH-GE即可算出答案。
11.【答案】
【解析】【解答】解:∵反比例函数y=
中,k=1>0,∴此函数图象的两个分支分别为与一、三象限,且在每一象限内y随x的增大而减小.
∵﹣2<﹣1<0,
∴A、B两点都在第三象限的分支上,
∴y1>y2.
故答案为:y1>y2.
【分析】反比例函数
,图象在一、三象限,且在每一象限内y随x的增大而减小,则先比较横坐标的大小,确定所在的象限,从而可判断函数值的大小.
12.【答案】
13.【答案】
【解析】【解答】解:∵ 反比例函数y1=中自变量系数2>0,
∴图象的两支分布在第一、三象限,且在每一个象限内,y随x的增大而减小,
∵当1≤x≤3时,函数y1的最大值是a,
∴当x=1时,函数最大值a=2;
∵ 反比例函数y2=﹣中自变量系数-3<0,
∴图象的两支分布在第二、四象限,且在每一个象限内,y随x的增大而增大,
∵当1≤x≤3时,函数y2的最大值是b,
∴当x=3时,函数最大值b=-1;
∴ab=2-1=.
故答案为:.
【分析】反比例函数中,当k>0时,图象的两支分布在第一、三象限,且在每一个象限内,y随x的增大而减小;当k<0时,图象的两支分布在第二、四象限,且在每一个象限内,y随x的增大而增大,据此可求出a、b的值,进而再根据负整数指数幂的性质计算可得答案.
14.【答案】-3
【解析】【解答】解:过P作PD⊥x轴,如下图:
∵PA=PC,PD⊥AC;
∴
∵ ,
∴AD=OA,
在
∴(ASA),
∴AD=OA,PD=OB,
设OA=a,OB=b,
则A(-a,0),B(0,-b),AC=2a,
∴P(-2a,b),
∵的面积为3 ,
∴
∴
化简得:,
∵P(-2a,b)在
∴k=-2ab=-3,
故答案为:-3.
【分析】过P作PD⊥x轴,证明,得OA=OC=AD,设OA=a,OB=b,来表示A、B坐标及AC长度,继而得到P点坐标,根据 的面积为3 得到a和b的关系,根据P在反比例函数上,将P代入解析式,求得k
15.【答案】16
【解析】【解答】解:∵C是OB的中点,∴△AOC和△ABC的面积相等,
∴△AOB的面积是4×2=8
即
∴
∴k=16
故答案为:16
【分析】k为A点横纵坐标的乘积,A在第一象限,横纵坐标的值分别和OB和AB相等,所以k=OB×AB
16.【答案】6
17.【答案】3
18.【答案】(1),
(2)或
19.【答案】
20.【答案】(1)
(2)3次
(3)5升
21.【答案】(1)一次函数的解析式为,反比例函数的解析式为
(2)或或
22.【答案】(1),
(2)
(3)
23.【答案】(1)反比例函数的表达式为,点B的坐标为
(2)①;②当是等腰三角形时,点D到直线AB的距离为或
一、单选题
1.反比例函数的图象上有两点、,且,则m的取值范围是( ).
A. B. C. D.
2.若反比例函数y= (k≠0)的图象经过点(﹣1,2),则这个函数的图象一定经过点( )
A.(1,﹣1) B.(﹣ ,4)
C.(﹣2,﹣1) D.( ,4)
3.如图,在平面直角坐标系中,M为x轴正半轴上一点,过点 M 的直线l∥y轴,且分别与反比例函数和 (x>0,k≠0)的图象相交于 P,Q两点.若,则 k 的值为( )
A.38 B.22 C.-7 D.-22
4.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y= (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
A. B. C. D.12
5.在平面直角坐标系中,对于点,若,则称点P为“同号点”,下列函数的图象上不存在“同号点”的是( )
A. B. C. D.
6.已知正比例函数的图象经过点,反比例函数的图象位于第一、第三象限,则一次函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图,在平面直角坐标系中,点A,C分别在坐标轴上,且四边形是边长为3的正方形,反比例函数的图像与边分别交于两点,的面积为4,点P为y轴上一点,则的最小值为( )
A.3 B. C. D.5
8.如图,分别过反比例函数图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn),作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An-1Pn,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3……,以此类推,则点B20的坐标是( )
A. B. C. D.
9.如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=﹣ (x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y= (x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
A. B. C. D.
10.如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y 上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )
A.2.5 B.3 C.3.5 D.4
二、填空题
11.若点 、 在反比例函数 图象上,则 、 大小关系是 .
12.已知反比例函数(m为常数,)图象的两个分支分布在第二、四象限,则m的取值范围是 .
13.若反比例函数y1=,y2=﹣,当1≤x≤3时,函数y1的最大值是a,函数y2的最大值是b,则ab= .
14.如图,已知在平面直角坐标系中,点P在反比例函数图象上,点B为y轴负半轴上一点,连结交x轴于点A,点C为x轴负半轴上一点,连结和.若,,且的面积为3,则k的值是 .
15.如图,点A在反比例函数的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为4,则k= .
16.如图,一定质量的氧气,其体积V()是密度ρ()的反比例函数,其图象如图,当时的氧气的体积 .
17.如图,点A是反比例函数的图象上一点,轴交x轴于点B,, .
三、解答题
18.如图,已知,是一次函数的图象与反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出不等式的解集.
19.如图,直线与双曲线 交于点和点,与 y轴交于点A,求点A的坐标.
20.某小组进行漂洗实验,每次漂洗的衣服量和添加洗衣粉量固定不变.实验发现,当每次漂洗用水量(升)一定时,衣服中残留的洗衣粉量(克)与漂洗次数(次)满足(为常数),已知当使用5升水,漂洗1次后,衣服中残留洗衣粉2克.
(1)求的值.
(2)如果每次用水5升,要求漂洗后残留的洗衣粉量小于0.8克,求至少漂洗多少次?
(3)现将20升水等分成次()漂洗,要使残留的洗衣粉量降到0.5克,求每次漂洗用水多少升?
21.如图,一次函数(为常数,)的图象与反比例函数为常数,的图象在第一象限交于点,与轴交于点.
(1)求一次函数和反比例函数的解析式.
(2)点在轴上,是以为腰的等腰三角形,请直接写出点的坐标.
22.如下图,反比例函数与一次函数的图象都经过点和点,以为边作正方形(点A、B、C、D逆时针排列).
(1)求m的值和一次函数的解析式.
(2)求点C的坐标.
(3)将正方形平移得到正方形,在平移过程中,使点A的对应顶点M始终在第一象限内且在反比例函数的图象上(点M与点A不重合),当正方形与正方形的重叠部分为正方形时,求重叠正方形的边长.
23.如图,一次函数的图象与反比例函数的图象交于点,与x轴交于点B,与y轴交于点C,连接.
(1)求反比例函数的表达式及点B的坐标;
(2)将直线向下平移个单位长度得到直线l:,设直线l与反比例函数的图象交于点P,与x轴交于点D.
①连接,,若,求m的值;
②连接,,当是等腰三角形时,请直接写出点D到直线的距离.
答案解析部分
1.【答案】A
2.【答案】B
【解析】【解答】解:将点(﹣1,2)代入y= 得,2=﹣ ,
解得k=﹣2,
∴反比例函数的解析式为y=﹣ ,
当x=﹣ 时,y=4.
故答案为:B.
【分析】将点(﹣1,2)代入反比例函数解析式求得k的值,然后对各个选项进行判断即可.
3.【答案】D
【解析】【解答】解:∵l∥y轴,
∴l⊥x轴,
∵直线l分别与反比例函数和 的图象相交于 P,Q两点,
∴S△POM=×8=4,S△OMQ=|k|,
∵S△POM+S△OMQ=S△POQ=15
∴4+|k|=15,
∴k=±22,
∵的图象经过第四象限,
∴k<0,
∴k=-22.
故答案为:D.
【分析】易得l⊥x轴,从而由反比例函数k的几何意义可得S△POM=×8=4,S△OMQ=|k|,进而根据S△POM+S△OMQ=S△POQ建立方程求出k的值,再结合函数所在的象限即可得出答案.
4.【答案】C
【解析】【解答】解:∵四边形OCBA是矩形,
∴AB=OC,OA=BC,
设B点的坐标为(a,b),
∵BD=3AD,
∴D( ,b),
∵点D,E在反比例函数的图象上,
∴ =k,∴E(a, ),
∵S△ODE=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣ ﹣ k﹣ (b﹣ )=9,
∴k= ,
故答案为:C.
【分析】所给的三角形面积等于长方形面积减去三个直角三角形的面积,然后即可求出B的横纵坐标的积即是反比例函数的比例系数.
5.【答案】C
【解析】【解答】解:由题意,图象经过第一和第三象限的函数都是满足条件的,
函数的图象在二、四象限,不满足条件,
故答案为:C.
【分析】由题意,图象经过第一和第三象限的函数都是满足条件的,据此判断即可.
6.【答案】C
【解析】【解答】解:∵正比例函数y1=ax的图象经过点(1,-1),
∴a=-1,
∵ 反比例函数的图象位于第一、第三象限 ,
∴b>0,
∴一次函数y=ax+b的图象经过一、二、四象限,即该函数的图象一定不会经过第三象限,
故A、B、D三个选项都是错误的,不符合题意;只有C选项正确,符合题意.
故答案为:C.
【分析】将点(1,-1)代入正比例函数y1=ax可求出a=-1,根据反比例函数的图象与系数的关系,由反比例函数的图象位于第一、第三象限,得b>0,进而根据一次函数的图象与系数的关系:y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象限;当a>0,b<0时,图象过一、三、四象限;当a>0,b=0时,图象过一、三象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限,当a<0,b=0时,图象过二、四象限,即可判断得出答案.
7.【答案】B
【解析】【解答】正方形的边长是3,
点的横坐标和点的纵坐标为3,
,,,
,,
的面积为,
,
或(舍去),
,,
作关于轴的对称点,连接交轴于,则的长的最小值,
,
,,
,
即的最小值为,
故选:B.
【分析】本题考查反比例函数的系数的几何意义,轴对称中最小距离问题,勾股定理,正方形的性质.根据正方形的边长是3,据此可推出点的横坐标和点的纵坐标为3,求得,,,进而可求出BE和BD,利用三角形的面积公式可列方程,解方程可求出k的值,进而可求出点D和点E的坐标:,,作关于轴的对称点,连接交轴于,则的长的最小值,利用勾股定理可求出,进而可求出答案.
8.【答案】D
【解析】【解答】解:点 P1(1,y1),P2(2,y2)在反比例函数图象上 ,
,
,
四边形是平行四边形,
,
点B1的纵坐标是:,即B1(2,6),
同理可得,点B2的纵坐标为:,即,
点B3的纵坐标为:,
...
点Bn的横坐标为:,纵坐标为:,
.
故答案为:D.
【分析】根据反比例函数图象上点的坐标特征求得点 P1 、 P2 的纵坐标,由平行四边形的性质得到B1、 B2的坐标,以此类推得到规律并求出点B20的坐标.
9.【答案】C
【解析】【解答】解:∵OB=1,AB⊥OB,点A在函数 (x<0)的图象上,
∴当x= 1时,y=2,
∴A( 1,2).
∵此矩形向右平移3个单位长度到 的位置,
∴B1(2,0),
∴A1(2,2).
∵点A1在函数 (x>0)的图象上,
∴k=4,
∴反比例函数的解析式为 ,O1(3,0),
∵C1O1⊥x轴,
∴当x=3时,
∴P
故答案为:C.
【分析】先求出A点坐标,再根据图形平移的性质得出A1点的坐标,故可得出反比例函数的解析式,把O1点的横坐标代入即可得出结论.
10.【答案】C
【解析】【解答】解:设点D(m, ),
如图所示,过点D作x轴的垂线交CE于点G,过点A过x轴的平行线交DG于点H,过点A作AN⊥x轴于点N,
∵∠GDC+∠DCG=90°,∠GDC+∠HDA=90°,
∴∠HDA=∠GCD,
又AD=CD,∠DHA=∠CGD=90°,
∴△DHA≌△CGD(AAS),
∴HA=DG,DH=CG,
同理△ANB≌△DGC(AAS),
∴AN=DG=1=AH,则点G(m, -1),CG=DH,
AH=-1-m=1,解得:m=-2,
故点G(-2,-4),D(-2,-3),H(-2,1),
则点E(- ,-4),GE= ,
CE=CG-GE=DH-GE=4- =3.5,
故答案为:C.
【分析】根据反比例函数图象上的点的坐标特点设点D(m, ),如图所示,过点D作x轴的垂线交CE于点G,过点A过x轴的平行线交DG于点H,过点A作AN⊥x轴于点N,根据同角的余角相等得出∠HDA=∠GCD,从而利用AAS判断出△DHA≌△CGD,根据全等三角形的性质得出HA=DG,DH=CG,同理△ANB≌△DGC,推出AN=DG=1=AH,故G(m, -1),CG=DH,从而列出方程,求解算出m的值得出G,D,H三点的坐标,进而得出点E的坐标,根据两点间的距离公式得出GE的长,最后根据CE=CG-GE=DH-GE即可算出答案。
11.【答案】
【解析】【解答】解:∵反比例函数y=
中,k=1>0,∴此函数图象的两个分支分别为与一、三象限,且在每一象限内y随x的增大而减小.
∵﹣2<﹣1<0,
∴A、B两点都在第三象限的分支上,
∴y1>y2.
故答案为:y1>y2.
【分析】反比例函数
,图象在一、三象限,且在每一象限内y随x的增大而减小,则先比较横坐标的大小,确定所在的象限,从而可判断函数值的大小.
12.【答案】
13.【答案】
【解析】【解答】解:∵ 反比例函数y1=中自变量系数2>0,
∴图象的两支分布在第一、三象限,且在每一个象限内,y随x的增大而减小,
∵当1≤x≤3时,函数y1的最大值是a,
∴当x=1时,函数最大值a=2;
∵ 反比例函数y2=﹣中自变量系数-3<0,
∴图象的两支分布在第二、四象限,且在每一个象限内,y随x的增大而增大,
∵当1≤x≤3时,函数y2的最大值是b,
∴当x=3时,函数最大值b=-1;
∴ab=2-1=.
故答案为:.
【分析】反比例函数中,当k>0时,图象的两支分布在第一、三象限,且在每一个象限内,y随x的增大而减小;当k<0时,图象的两支分布在第二、四象限,且在每一个象限内,y随x的增大而增大,据此可求出a、b的值,进而再根据负整数指数幂的性质计算可得答案.
14.【答案】-3
【解析】【解答】解:过P作PD⊥x轴,如下图:
∵PA=PC,PD⊥AC;
∴
∵ ,
∴AD=OA,
在
∴(ASA),
∴AD=OA,PD=OB,
设OA=a,OB=b,
则A(-a,0),B(0,-b),AC=2a,
∴P(-2a,b),
∵的面积为3 ,
∴
∴
化简得:,
∵P(-2a,b)在
∴k=-2ab=-3,
故答案为:-3.
【分析】过P作PD⊥x轴,证明,得OA=OC=AD,设OA=a,OB=b,来表示A、B坐标及AC长度,继而得到P点坐标,根据 的面积为3 得到a和b的关系,根据P在反比例函数上,将P代入解析式,求得k
15.【答案】16
【解析】【解答】解:∵C是OB的中点,∴△AOC和△ABC的面积相等,
∴△AOB的面积是4×2=8
即
∴
∴k=16
故答案为:16
【分析】k为A点横纵坐标的乘积,A在第一象限,横纵坐标的值分别和OB和AB相等,所以k=OB×AB
16.【答案】6
17.【答案】3
18.【答案】(1),
(2)或
19.【答案】
20.【答案】(1)
(2)3次
(3)5升
21.【答案】(1)一次函数的解析式为,反比例函数的解析式为
(2)或或
22.【答案】(1),
(2)
(3)
23.【答案】(1)反比例函数的表达式为,点B的坐标为
(2)①;②当是等腰三角形时,点D到直线AB的距离为或
