27.1.3圆周角 课时作业(含简单答案)2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.1.3圆周角 课时作业(含简单答案)2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 379.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-21 19:20:36 | ||
图片预览


文档简介
3.圆周角
@预习导航
1.圆周角的概念
圆周角: ,并且两边都与圆 的角叫做圆周角.
推 导:半圆或直径所对的圆周角都相等,都等于90°( ).
2.圆周角定理
定 理:在同圆或等圆中,同弧或等弧所对的圆周角 ,都等于该弧所对的圆心角的 ;相等的圆周角所对的弧相等.
3.圆内接多边形
定 义:如果一个圆经过一个多边形的各顶点,这个圆就叫做这个多边形的 ,这个多边形叫做这个圆的 .
4.圆周角定理引出的重要结论
推 论1:90°的圆周角所对的弦是 .
推 论2:圆内接四边形的对角 .
拓 展:圆内接四边形的一个外角等于它的内对角.
思路转换:在同圆或等圆中,圆心角相等 圆周角相等 弧相等 弦相等 弦心距相等,这是连结角、弧、弦关系的重要途径.
@归类探究
类型之一 圆周角定理的证明
求证:圆周角的度数等于它所对弧上的圆心角度数的一半.
类型之二 圆周角定理及推论的运用
如图,点A、B、C在☉O上,∠ACB=54°,则∠ABO的度数是( )
A.54° B.27°
C.36° D.108°
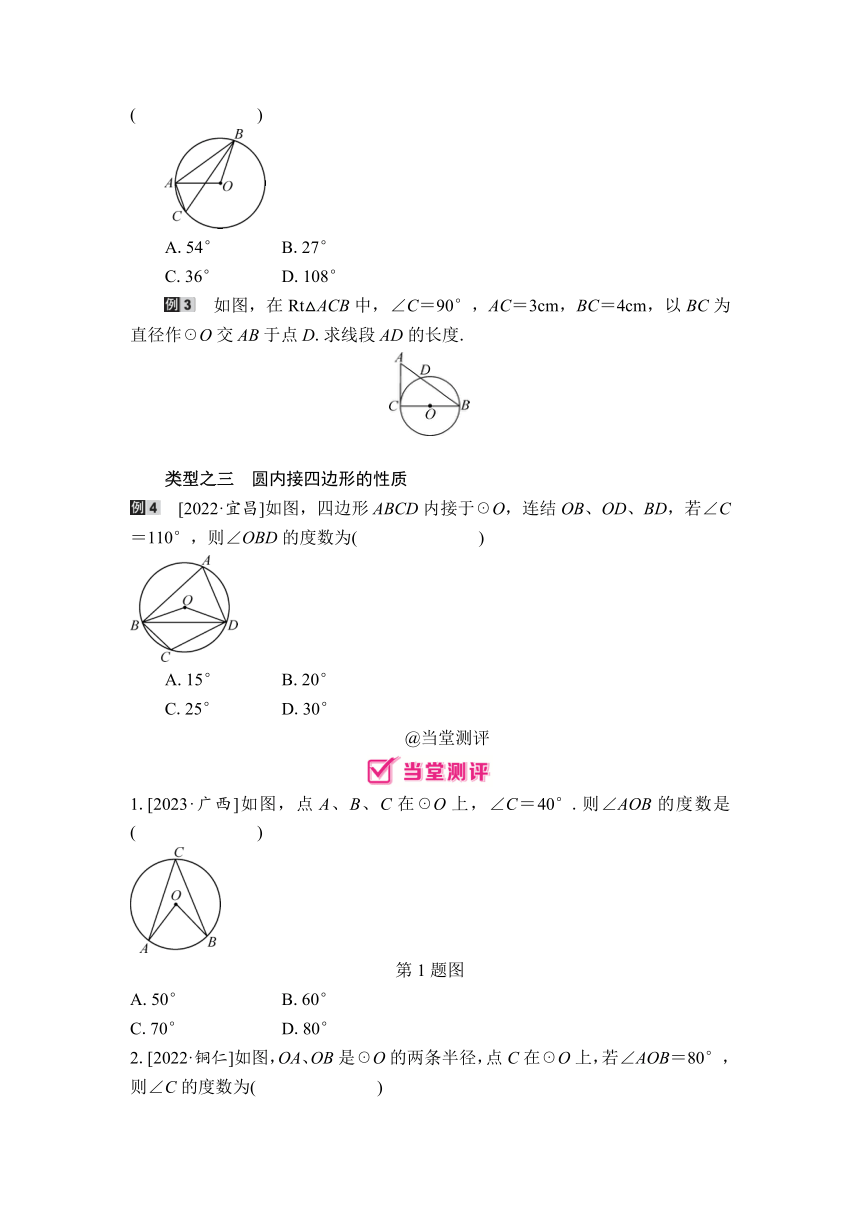
如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作☉O交AB于点D.求线段AD的长度.
类型之三 圆内接四边形的性质
[2022·宜昌]如图,四边形ABCD内接于☉O,连结OB、OD、BD,若∠C=110°,则∠OBD的度数为( )
A.15° B.20°
C.25° D.30°
@当堂测评
1.[2023·广西]如图,点A、B、C在☉O上,∠C=40°.则∠AOB的度数是( )
第1题图
A.50° B.60°
C.70° D.80°
2.[2022·铜仁]如图,OA、OB是☉O的两条半径,点C在☉O上,若∠AOB=80°,则∠C的度数为( )
第2题图
A.30° B.40°
C.50° D.60°
3.[2023·枣庄]如图,在☉O中,弦AB、CD相交于点P.若∠A=48°,∠APD=80°,则∠B的度数为( )
第3题图
A.32° B.42°
C.48° D.52°
4.[2023·绍兴]如图,四边形ABCD内接于☉O,若∠D=100°,则∠B的度数是 .
第4题图
@分层训练
1.如图,☉O是△ABC的外接圆,AC是☉O的直径,点P在☉O上,若∠ACB=40°,则∠BPC的度数是( )
第1题图
A.40° B.45°
C.50° D.55°
2.如图,在☉O中,若点C是的中点,则图中与∠BAC相等的角(∠BAC除外)有( )
第2题图
A.2个 B.3个
C.4个 D.5个
3.[2023·随州]如图,在☉O中,OA⊥BC,∠AOB=60°,则∠ADC的度数为 .
4.[2023·宁夏]如图,四边形ABCD内接于☉O,延长AD至点E,已知∠AOC=140°,那么∠CDE= °.
5.[2023·株洲]如图所示,点A、B、C是☉O上不同的三点,点O在△ABC的内部,连结BO、CO,并延长线段BO交线段AC于点D.若∠A=60°,∠OCD=40°,则∠ODC= 度.
第5题图
6.如图,在☉O中,AE是直径,半径OC垂直于弦AB,垂足为点D,连结BE.若AB=2,CD=1,则BE的长是 .
第6题图
7.如图,在以AB为直径的☉O中,点C为圆上的一点,=3,弦CD⊥AB于点E,弦AF交CE于点H,交BC于点G.若点H是AG的中点,则∠CBF的度数为( )
A.18° B.21°
C.22.5° D.30°
8.如图,四边形ABCD是☉O的内接四边形,AD与BC的延长线交于点E,∠DCB=100°,∠B=50°.求证:△CDE是等腰三角形.
9.[2022·广东]如图,四边形ABCD内接于☉O,AC为☉O的直径,∠ADB=∠CDB.
(1)试判断△ABC的形状,并给出证明;
(2)若AB=,AD=1,求CD的长度.
10.(推理能力)如图,四边形ABCD是☉O的内接四边形,AC⊥BD,OF⊥AB,垂足分别是点E、F.
(1)直接写出OF与CD的数量关系 ,并证明你的结论;
(2)若AB=2,CD=1,求☉O的半径.
3.圆周角
【预习导航】
1.顶点在圆上 相交 直角 2.相等 一半 3.外接圆 内接多边形 4.直径 互补
【归类探究】
【例1】略
【例2】C
【例3】AD=cm.
【例4】B
【当堂测评】
1.D 2.B 3.A 4.80°
【分层训练】
1.C 2.B 3.30° 4.70 5.80 6.6 7.C
8.略
9.(1)△ABC是等腰直角三角形.证明略.
(2)CD=
10.(1)OF=CD.证明略.
(2)☉O的半径为.
。
@预习导航
1.圆周角的概念
圆周角: ,并且两边都与圆 的角叫做圆周角.
推 导:半圆或直径所对的圆周角都相等,都等于90°( ).
2.圆周角定理
定 理:在同圆或等圆中,同弧或等弧所对的圆周角 ,都等于该弧所对的圆心角的 ;相等的圆周角所对的弧相等.
3.圆内接多边形
定 义:如果一个圆经过一个多边形的各顶点,这个圆就叫做这个多边形的 ,这个多边形叫做这个圆的 .
4.圆周角定理引出的重要结论
推 论1:90°的圆周角所对的弦是 .
推 论2:圆内接四边形的对角 .
拓 展:圆内接四边形的一个外角等于它的内对角.
思路转换:在同圆或等圆中,圆心角相等 圆周角相等 弧相等 弦相等 弦心距相等,这是连结角、弧、弦关系的重要途径.
@归类探究
类型之一 圆周角定理的证明
求证:圆周角的度数等于它所对弧上的圆心角度数的一半.
类型之二 圆周角定理及推论的运用
如图,点A、B、C在☉O上,∠ACB=54°,则∠ABO的度数是( )
A.54° B.27°
C.36° D.108°
如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作☉O交AB于点D.求线段AD的长度.
类型之三 圆内接四边形的性质
[2022·宜昌]如图,四边形ABCD内接于☉O,连结OB、OD、BD,若∠C=110°,则∠OBD的度数为( )
A.15° B.20°
C.25° D.30°
@当堂测评
1.[2023·广西]如图,点A、B、C在☉O上,∠C=40°.则∠AOB的度数是( )
第1题图
A.50° B.60°
C.70° D.80°
2.[2022·铜仁]如图,OA、OB是☉O的两条半径,点C在☉O上,若∠AOB=80°,则∠C的度数为( )
第2题图
A.30° B.40°
C.50° D.60°
3.[2023·枣庄]如图,在☉O中,弦AB、CD相交于点P.若∠A=48°,∠APD=80°,则∠B的度数为( )
第3题图
A.32° B.42°
C.48° D.52°
4.[2023·绍兴]如图,四边形ABCD内接于☉O,若∠D=100°,则∠B的度数是 .
第4题图
@分层训练
1.如图,☉O是△ABC的外接圆,AC是☉O的直径,点P在☉O上,若∠ACB=40°,则∠BPC的度数是( )
第1题图
A.40° B.45°
C.50° D.55°
2.如图,在☉O中,若点C是的中点,则图中与∠BAC相等的角(∠BAC除外)有( )
第2题图
A.2个 B.3个
C.4个 D.5个
3.[2023·随州]如图,在☉O中,OA⊥BC,∠AOB=60°,则∠ADC的度数为 .
4.[2023·宁夏]如图,四边形ABCD内接于☉O,延长AD至点E,已知∠AOC=140°,那么∠CDE= °.
5.[2023·株洲]如图所示,点A、B、C是☉O上不同的三点,点O在△ABC的内部,连结BO、CO,并延长线段BO交线段AC于点D.若∠A=60°,∠OCD=40°,则∠ODC= 度.
第5题图
6.如图,在☉O中,AE是直径,半径OC垂直于弦AB,垂足为点D,连结BE.若AB=2,CD=1,则BE的长是 .
第6题图
7.如图,在以AB为直径的☉O中,点C为圆上的一点,=3,弦CD⊥AB于点E,弦AF交CE于点H,交BC于点G.若点H是AG的中点,则∠CBF的度数为( )
A.18° B.21°
C.22.5° D.30°
8.如图,四边形ABCD是☉O的内接四边形,AD与BC的延长线交于点E,∠DCB=100°,∠B=50°.求证:△CDE是等腰三角形.
9.[2022·广东]如图,四边形ABCD内接于☉O,AC为☉O的直径,∠ADB=∠CDB.
(1)试判断△ABC的形状,并给出证明;
(2)若AB=,AD=1,求CD的长度.
10.(推理能力)如图,四边形ABCD是☉O的内接四边形,AC⊥BD,OF⊥AB,垂足分别是点E、F.
(1)直接写出OF与CD的数量关系 ,并证明你的结论;
(2)若AB=2,CD=1,求☉O的半径.
3.圆周角
【预习导航】
1.顶点在圆上 相交 直角 2.相等 一半 3.外接圆 内接多边形 4.直径 互补
【归类探究】
【例1】略
【例2】C
【例3】AD=cm.
【例4】B
【当堂测评】
1.D 2.B 3.A 4.80°
【分层训练】
1.C 2.B 3.30° 4.70 5.80 6.6 7.C
8.略
9.(1)△ABC是等腰直角三角形.证明略.
(2)CD=
10.(1)OF=CD.证明略.
(2)☉O的半径为.
。
