27.2.3切线 第2课时 切线长定理和三角形的内切圆 课时作业(含简单答案)2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.2.3切线 第2课时 切线长定理和三角形的内切圆 课时作业(含简单答案)2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 333.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-21 19:22:48 | ||
图片预览


文档简介
3.切 线 第2课时 切线长定理和三角形的内切圆
@预习导航
1.切线长定理
切线长:圆的切线上某一点与 之间的线段的长叫做这点到圆的切线长.
切线长定理:过圆外一点所画的圆的两条切线,它们的 相等,这一点和圆心的连线平分这两条 的夹角.
常用结论:如图所示,OP⊥AB.
相似三角形:△OAP∽△ODA∽△ADP.
相等的线段:PA=PB,OA=OB,AD=BD.
相等的角:∠OPA=∠OPB,∠POA=∠POB,∠PAB=∠PBA,∠OAB=∠OBA,∠OAP=∠OBP=∠ODA=∠ODB=90°.
2.三角形的内切圆、内心
定 义:与三角形 叫做三角形的内切圆,这个三角形叫做圆的外切三角形.
内 心:三角形的 的圆心叫做三角形的内心,三角形的内心是三角形 的交点.
3.三角形内心的性质
内心性质:(1)三角形内心到三边的距离相等;
(2)三角形内心与顶点的连线平分三角形内角;
(3)三角形内心一定在三角形的内部.
三角形的面积:已知△ABC的面积为S,内切圆半径为r,三边长为a、b、c,则有S=(a+b+c)r.
直角三角形内切圆半径:r=(其中a、b为直角边长,c为斜边长).
@归类探究
类型之一 切线长定理的运用
如图,PA、PB是☉O的切线,切点分别是A、B,Q为上一点,过点Q作☉O的切线,分别交PA、PB于E、F两点.已知PA=12cm,∠P=70°.求:
(1)△PEF的周长;
(2)∠EOF的度数.
【点悟】 (1)当点Q在上移动时,△PEF的周长不随Q点的移动而变化.(2)求此类三角形的周长,通常利用切线长定理进行线段的等价代换.
类型之二 三角形的内切圆
如图,☉O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DEF=45°.连结BO并延长交AC于点G,AB=4,AG=2.求:
(1)∠A的度数;
(2)☉O的半径.
@当堂测评
1.如图,☉O是△ABC的内切圆,则点O是△ABC的( )
第1题图
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
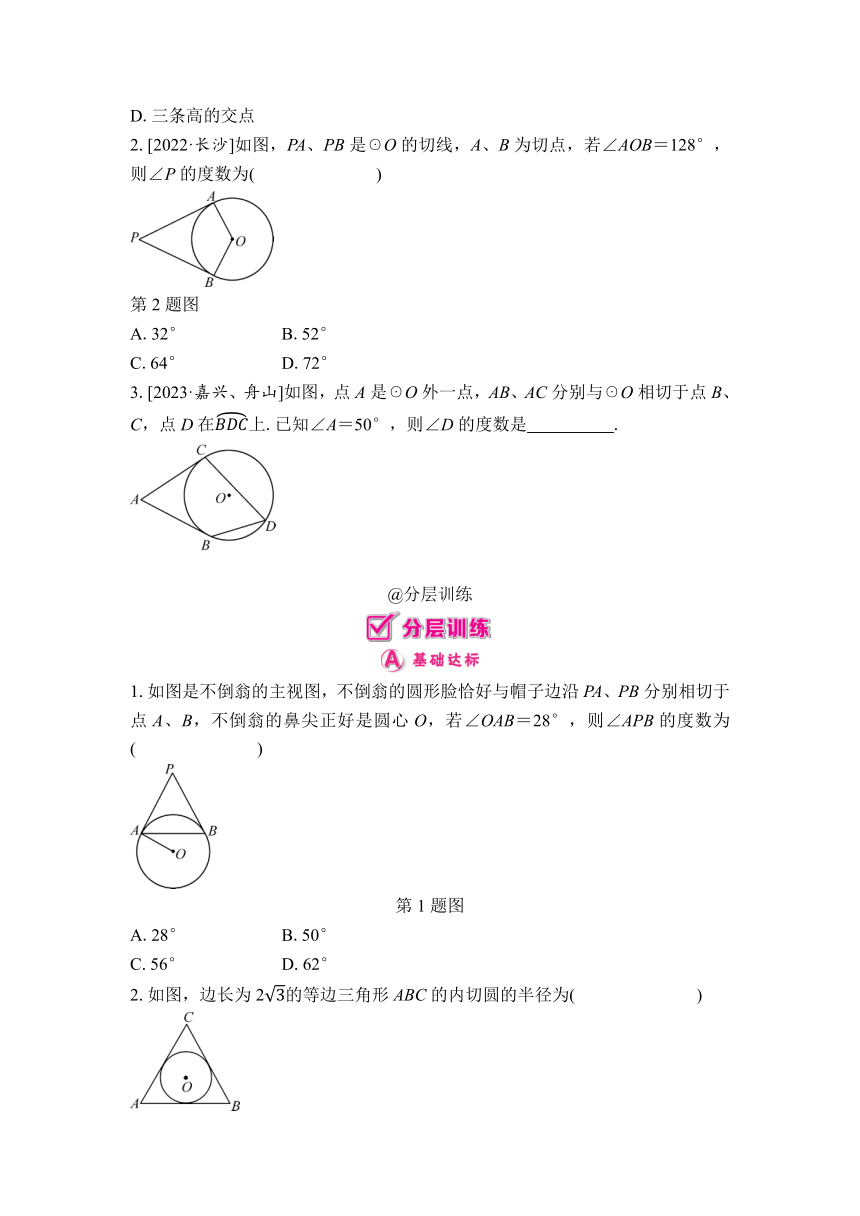
2.[2022·长沙]如图,PA、PB是☉O的切线,A、B为切点,若∠AOB=128°,则∠P的度数为( )
第2题图
A.32° B.52°
C.64° D.72°
3.[2023·嘉兴、舟山]如图,点A是☉O外一点,AB、AC分别与☉O相切于点B、C,点D在上.已知∠A=50°,则∠D的度数是 .
@分层训练
1.如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为( )
第1题图
A.28° B.50°
C.56° D.62°
2.如图,边长为2的等边三角形ABC的内切圆的半径为( )
第2题图
A.1 B.
C.2 D.2
3.如图,已知PA、PB切☉O于点A、B,C是劣弧AB上一动点,过点C作☉O的切线交PA于点M,交PB于点N.已知∠P=56°,则∠MON的度数是( )
A.56° B.60°
C.62° D.不可求
4.[2023·泰安]为了测量一个圆形光盘的半径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=4cm,则这张光盘的半径是 cm.(精确到0.1cm;参考数据:≈1.73)
5.如图,△ABC的内切圆☉O分别与AB、AC、BC相切于点D、E、F.若∠C=90°,AC=6,BC=8,则☉O的半径等于 .
6.如图,PA和PB是☉O的切线,点A和点B是切点,AC是☉O的直径.已知∠P=40°,求∠ACB的度数.
7.[2022·株洲]中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是:一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切),如图所示.
第7题图
问题:此图中,正方形的一条对角线AB与☉O相交于点M、N(点N在点M的右上方),若AB的长度为10丈,☉O的半径为2丈,则BN的长度为 丈.
8.如图,等边三角形ABC内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边△ABC的内心成中心对称,则圆中的黑色部分的面积与△ABC的面积之比是 .
第8题图
9.[2024·常德月考]已知PA、PB分别切☉O于A、B,E为劣弧AB上一点,过E点的切线交PA于点C,交PB于点D.
(1)若PA=6,求△PCD的周长;
(2)若∠P=50°,求∠DOC.
10.(推理能力)如图,在△ABC中,AB=AC,☉O是△ABC的内切圆,它与AB、BC、CA分别相切于点D、E、F.
(1)求证:BE=CE;
(2)若∠A=90°,AB=AC=2,求☉O的半径.
第2课时 切线长定理和三角形的内切圆
【预习导航】
1.切点 切线长 切线 2.各边都相切的圆 内切圆 三条内角平分线
【归类探究】
【例1】(1)C△PEF=24cm.
(2)∠EOF=55°.
【例2】(1)∠A=90°.
(2)☉O的半径为.
【当堂测评】
1.B 2.B 3.65°
【分层训练】
1.C 2.A 3.C 4.6.9 5.2
6.∠ACB=70°. 7.(8-2) 8.
9.(1)C△PCD=12. (2)∠COD=65°.
10.(1)略 (2)☉O的半径是2-.
。
@预习导航
1.切线长定理
切线长:圆的切线上某一点与 之间的线段的长叫做这点到圆的切线长.
切线长定理:过圆外一点所画的圆的两条切线,它们的 相等,这一点和圆心的连线平分这两条 的夹角.
常用结论:如图所示,OP⊥AB.
相似三角形:△OAP∽△ODA∽△ADP.
相等的线段:PA=PB,OA=OB,AD=BD.
相等的角:∠OPA=∠OPB,∠POA=∠POB,∠PAB=∠PBA,∠OAB=∠OBA,∠OAP=∠OBP=∠ODA=∠ODB=90°.
2.三角形的内切圆、内心
定 义:与三角形 叫做三角形的内切圆,这个三角形叫做圆的外切三角形.
内 心:三角形的 的圆心叫做三角形的内心,三角形的内心是三角形 的交点.
3.三角形内心的性质
内心性质:(1)三角形内心到三边的距离相等;
(2)三角形内心与顶点的连线平分三角形内角;
(3)三角形内心一定在三角形的内部.
三角形的面积:已知△ABC的面积为S,内切圆半径为r,三边长为a、b、c,则有S=(a+b+c)r.
直角三角形内切圆半径:r=(其中a、b为直角边长,c为斜边长).
@归类探究
类型之一 切线长定理的运用
如图,PA、PB是☉O的切线,切点分别是A、B,Q为上一点,过点Q作☉O的切线,分别交PA、PB于E、F两点.已知PA=12cm,∠P=70°.求:
(1)△PEF的周长;
(2)∠EOF的度数.
【点悟】 (1)当点Q在上移动时,△PEF的周长不随Q点的移动而变化.(2)求此类三角形的周长,通常利用切线长定理进行线段的等价代换.
类型之二 三角形的内切圆
如图,☉O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DEF=45°.连结BO并延长交AC于点G,AB=4,AG=2.求:
(1)∠A的度数;
(2)☉O的半径.
@当堂测评
1.如图,☉O是△ABC的内切圆,则点O是△ABC的( )
第1题图
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
2.[2022·长沙]如图,PA、PB是☉O的切线,A、B为切点,若∠AOB=128°,则∠P的度数为( )
第2题图
A.32° B.52°
C.64° D.72°
3.[2023·嘉兴、舟山]如图,点A是☉O外一点,AB、AC分别与☉O相切于点B、C,点D在上.已知∠A=50°,则∠D的度数是 .
@分层训练
1.如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为( )
第1题图
A.28° B.50°
C.56° D.62°
2.如图,边长为2的等边三角形ABC的内切圆的半径为( )
第2题图
A.1 B.
C.2 D.2
3.如图,已知PA、PB切☉O于点A、B,C是劣弧AB上一动点,过点C作☉O的切线交PA于点M,交PB于点N.已知∠P=56°,则∠MON的度数是( )
A.56° B.60°
C.62° D.不可求
4.[2023·泰安]为了测量一个圆形光盘的半径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=4cm,则这张光盘的半径是 cm.(精确到0.1cm;参考数据:≈1.73)
5.如图,△ABC的内切圆☉O分别与AB、AC、BC相切于点D、E、F.若∠C=90°,AC=6,BC=8,则☉O的半径等于 .
6.如图,PA和PB是☉O的切线,点A和点B是切点,AC是☉O的直径.已知∠P=40°,求∠ACB的度数.
7.[2022·株洲]中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是:一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切),如图所示.
第7题图
问题:此图中,正方形的一条对角线AB与☉O相交于点M、N(点N在点M的右上方),若AB的长度为10丈,☉O的半径为2丈,则BN的长度为 丈.
8.如图,等边三角形ABC内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边△ABC的内心成中心对称,则圆中的黑色部分的面积与△ABC的面积之比是 .
第8题图
9.[2024·常德月考]已知PA、PB分别切☉O于A、B,E为劣弧AB上一点,过E点的切线交PA于点C,交PB于点D.
(1)若PA=6,求△PCD的周长;
(2)若∠P=50°,求∠DOC.
10.(推理能力)如图,在△ABC中,AB=AC,☉O是△ABC的内切圆,它与AB、BC、CA分别相切于点D、E、F.
(1)求证:BE=CE;
(2)若∠A=90°,AB=AC=2,求☉O的半径.
第2课时 切线长定理和三角形的内切圆
【预习导航】
1.切点 切线长 切线 2.各边都相切的圆 内切圆 三条内角平分线
【归类探究】
【例1】(1)C△PEF=24cm.
(2)∠EOF=55°.
【例2】(1)∠A=90°.
(2)☉O的半径为.
【当堂测评】
1.B 2.B 3.65°
【分层训练】
1.C 2.A 3.C 4.6.9 5.2
6.∠ACB=70°. 7.(8-2) 8.
9.(1)C△PCD=12. (2)∠COD=65°.
10.(1)略 (2)☉O的半径是2-.
。
