27.4 正多边形和圆 课时作业(含简单答案)2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.4 正多边形和圆 课时作业(含简单答案)2024-2025学年数学华东师大版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 331.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-21 19:24:19 | ||
图片预览


文档简介
27.4 正多边形和圆
@预习导航
1.正多边形
定 义:各 相等,各 也相等的多边形叫做正多边形.
2.正多边形与圆的关系
规 律:把圆分成n(n≥3)等份,依次连结各分点所得的多边形是圆的内接正n边形.
关 系:任何正多边形都有一个 和 .
3.正多边形的有关概念
中 心:正多边形的外接圆(或内切圆)的 叫做正多边形的中心.
半 径:正多边形的 的半径叫做正多边形的半径.
边心距:正多边形的中心到正多边形的一边的 叫做正多边形的边心距.
中心角:正多边形每一边所对的外接圆的 叫做正多边形的中心角.
说 明:在由正n边形外接圆半径R、内切圆半径r、边长的一半组成的Rt△OAT中,有一锐角为.这一基本图形是解决正多边形问题的关键.
4.正多边形的画法
原 理:由于在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,因此可以用等分圆心角的方法来等分圆周,画正多边形.
方 法:等分圆周有两种方法:①用 等分;②用 等分.
@归类探究
类型之一 正多边形的有关计算
如图,有一个亭子,它的地基是外接圆的半径为4m的正六边形,求地基的周长和面积.(≈1.732,结果保留小数点后一位)
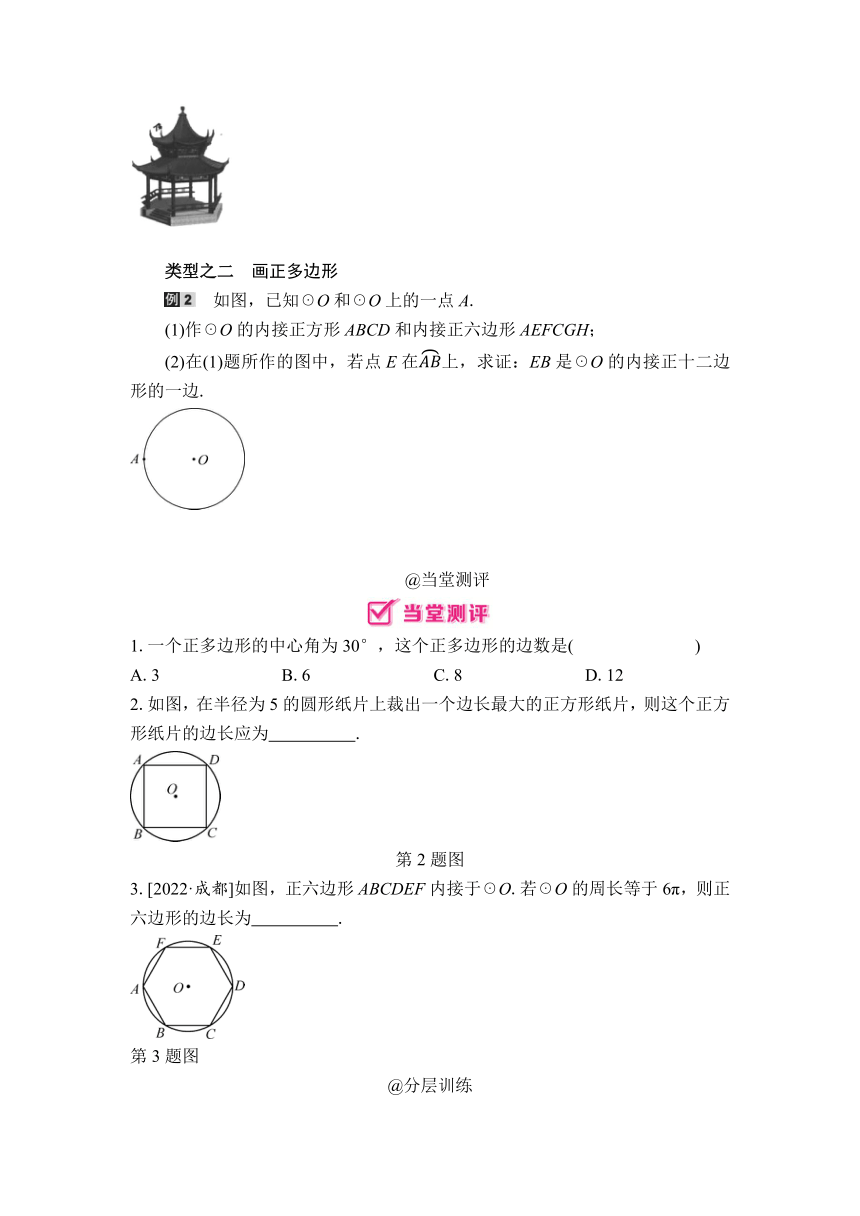
类型之二 画正多边形
如图,已知☉O和☉O上的一点A.
(1)作☉O的内接正方形ABCD和内接正六边形AEFCGH;
(2)在(1)题所作的图中,若点E在上,求证:EB是☉O的内接正十二边形的一边.
@当堂测评
1.一个正多边形的中心角为30°,这个正多边形的边数是( )
A.3 B.6 C.8 D.12
2.如图,在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为 .
第2题图
3.[2022·成都]如图,正六边形ABCDEF内接于☉O.若☉O的周长等于6π,则正六边形的边长为 .
第3题图
@分层训练
1.如图,等边三角形ABC和正方形ADEF都内接于☉O,则AD∶AB=( )
A.2∶ B.∶
C.∶ D.∶2
2.[2023·福建]刘徽在《九章算术注》中提到了“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,得到了圆周率π的近似值为3.1416.如图,☉O的半径为1,以圆内接正六边形面积近似估计☉O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为( )
A. B.2
C.3 D.2
3.如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口b=3cm,则螺帽的边长a= cm.
4.[2023·内江]如图,正六边形ABCDEF内接于☉O,点P在上,点Q是的中点,则∠CPQ的度数为 .
5.[2023·衡阳]如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 .
6.在半径为2的圆中,其内接正三角形、正四边形、正六边形的边心距之比为 .
7.图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图2,AE是☉O的直径,用直尺和圆规作☉O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).
8.如图1,小吴同学在陶艺课上为八角花盆制作圆形托盘.已知八角花盆底部截面是一个正八边形(如图2),请根据下列信息解决问题.
(1)求八角花盆底部截面正八边形一个内角的度数;
(2)若八角花盆底部截面正八边形的边长是16cm,小吴同学制作的圆形托盘半径是22cm,问:这个托盘是否适用于此八角花盆?(图3中边长的数据为近似值,供选用)
9.(推理能力)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答问题.
作法:如图2,①作直径AF;
②以F为圆心,FO为半径作圆弧,与☉O交于点M、N;
③连结AM、MN、NA.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗?请说明理由.
(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连结这些分点,得到正n边形,求n的值.
(4)应用:如图3,将5个全等的等腰三角形拼成内外两个大小不同的正五边形图案,设小正五边形边长为1,则大正五边形的边长为 .
图3
27.4 正多边形和圆
【预习导航】
1.边 角 2.外接圆 内切圆 3.圆心 外接圆 距离 圆心角 4.量角器 圆规
【归类探究】
【例1】亭子地基的周长为24m.地基的面积为41.6m2.
【例2】略
【当堂测评】
1.D 2.5 3.3
【分层训练】
1.B 2.C 3. 4.45° 5.10 6.1∶∶
7.略
8.(1)正八边形的一个内角为135°.
(2)这个托盘适用于此八角花盆.
9.(1)∠ABC=108°.
(2)△AMN是正三角形.理由略.
(3)n的值是15.
(4)
。
@预习导航
1.正多边形
定 义:各 相等,各 也相等的多边形叫做正多边形.
2.正多边形与圆的关系
规 律:把圆分成n(n≥3)等份,依次连结各分点所得的多边形是圆的内接正n边形.
关 系:任何正多边形都有一个 和 .
3.正多边形的有关概念
中 心:正多边形的外接圆(或内切圆)的 叫做正多边形的中心.
半 径:正多边形的 的半径叫做正多边形的半径.
边心距:正多边形的中心到正多边形的一边的 叫做正多边形的边心距.
中心角:正多边形每一边所对的外接圆的 叫做正多边形的中心角.
说 明:在由正n边形外接圆半径R、内切圆半径r、边长的一半组成的Rt△OAT中,有一锐角为.这一基本图形是解决正多边形问题的关键.
4.正多边形的画法
原 理:由于在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,因此可以用等分圆心角的方法来等分圆周,画正多边形.
方 法:等分圆周有两种方法:①用 等分;②用 等分.
@归类探究
类型之一 正多边形的有关计算
如图,有一个亭子,它的地基是外接圆的半径为4m的正六边形,求地基的周长和面积.(≈1.732,结果保留小数点后一位)
类型之二 画正多边形
如图,已知☉O和☉O上的一点A.
(1)作☉O的内接正方形ABCD和内接正六边形AEFCGH;
(2)在(1)题所作的图中,若点E在上,求证:EB是☉O的内接正十二边形的一边.
@当堂测评
1.一个正多边形的中心角为30°,这个正多边形的边数是( )
A.3 B.6 C.8 D.12
2.如图,在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为 .
第2题图
3.[2022·成都]如图,正六边形ABCDEF内接于☉O.若☉O的周长等于6π,则正六边形的边长为 .
第3题图
@分层训练
1.如图,等边三角形ABC和正方形ADEF都内接于☉O,则AD∶AB=( )
A.2∶ B.∶
C.∶ D.∶2
2.[2023·福建]刘徽在《九章算术注》中提到了“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,得到了圆周率π的近似值为3.1416.如图,☉O的半径为1,以圆内接正六边形面积近似估计☉O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为( )
A. B.2
C.3 D.2
3.如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口b=3cm,则螺帽的边长a= cm.
4.[2023·内江]如图,正六边形ABCDEF内接于☉O,点P在上,点Q是的中点,则∠CPQ的度数为 .
5.[2023·衡阳]如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 .
6.在半径为2的圆中,其内接正三角形、正四边形、正六边形的边心距之比为 .
7.图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图2,AE是☉O的直径,用直尺和圆规作☉O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).
8.如图1,小吴同学在陶艺课上为八角花盆制作圆形托盘.已知八角花盆底部截面是一个正八边形(如图2),请根据下列信息解决问题.
(1)求八角花盆底部截面正八边形一个内角的度数;
(2)若八角花盆底部截面正八边形的边长是16cm,小吴同学制作的圆形托盘半径是22cm,问:这个托盘是否适用于此八角花盆?(图3中边长的数据为近似值,供选用)
9.(推理能力)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答问题.
作法:如图2,①作直径AF;
②以F为圆心,FO为半径作圆弧,与☉O交于点M、N;
③连结AM、MN、NA.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗?请说明理由.
(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连结这些分点,得到正n边形,求n的值.
(4)应用:如图3,将5个全等的等腰三角形拼成内外两个大小不同的正五边形图案,设小正五边形边长为1,则大正五边形的边长为 .
图3
27.4 正多边形和圆
【预习导航】
1.边 角 2.外接圆 内切圆 3.圆心 外接圆 距离 圆心角 4.量角器 圆规
【归类探究】
【例1】亭子地基的周长为24m.地基的面积为41.6m2.
【例2】略
【当堂测评】
1.D 2.5 3.3
【分层训练】
1.B 2.C 3. 4.45° 5.10 6.1∶∶
7.略
8.(1)正八边形的一个内角为135°.
(2)这个托盘适用于此八角花盆.
9.(1)∠ABC=108°.
(2)△AMN是正三角形.理由略.
(3)n的值是15.
(4)
。
