第27章 圆 质量评估(含简单答案)2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 第27章 圆 质量评估(含简单答案)2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 387.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-21 00:00:00 | ||
图片预览


文档简介
第27章 圆 质量评估
一、选择题(共10小题,每小题3分,共30分)
1.已知圆的半径是5cm,如果圆心到直线的距离是5cm,那么该直线和圆的位置关系是( )
A.相交 B.相切 C.相离 D.内含
2.如图,已知点A、B、C在☉O上,C为的中点.若∠BAC=35°,则∠AOB等于( )
A.140° B.120° C.110° D.70°
3.如图,圆拱桥的拱顶C到水面AB的距离CD=8m,桥拱半径OC=5m,则水面宽AB为( )
第3题图
A.4m B.5m C.6m D.8m
4.如图,四边形ABCD内接于☉O,AC、BD为对角线,BD经过圆心O.若∠BAC=40°,则∠DBC的度数为( )
第4题图
A.40° B.50° C.60° D.70°
5.如图是高铁线路在转向处所设计的圆曲线(即圆弧)示意图,高铁列车在转弯时的曲线起点为A,曲线终点为B,过点A、B的两条切线相交于点C,列车在从A到B行驶的过程中转角α为60°.若圆曲线的半径OA=1.5km,则这段圆曲线的长为( )
第5题图
A.km B.km
C.km D.km
6.如图,AB是☉O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是( )
第6题图
A.AE⊥DE B.AE∥OD
C.DE=OD D.∠BOD=50°
7.如图,PA、PB为☉O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交☉O于点D.下列结论不一定成立的是( )
第7题图
A.△BPA为等腰三角形 B.AB与PD相互垂直平分
C.点A、B都在以PO为直径的圆上 D.PC为△BPA的边AB上的中线
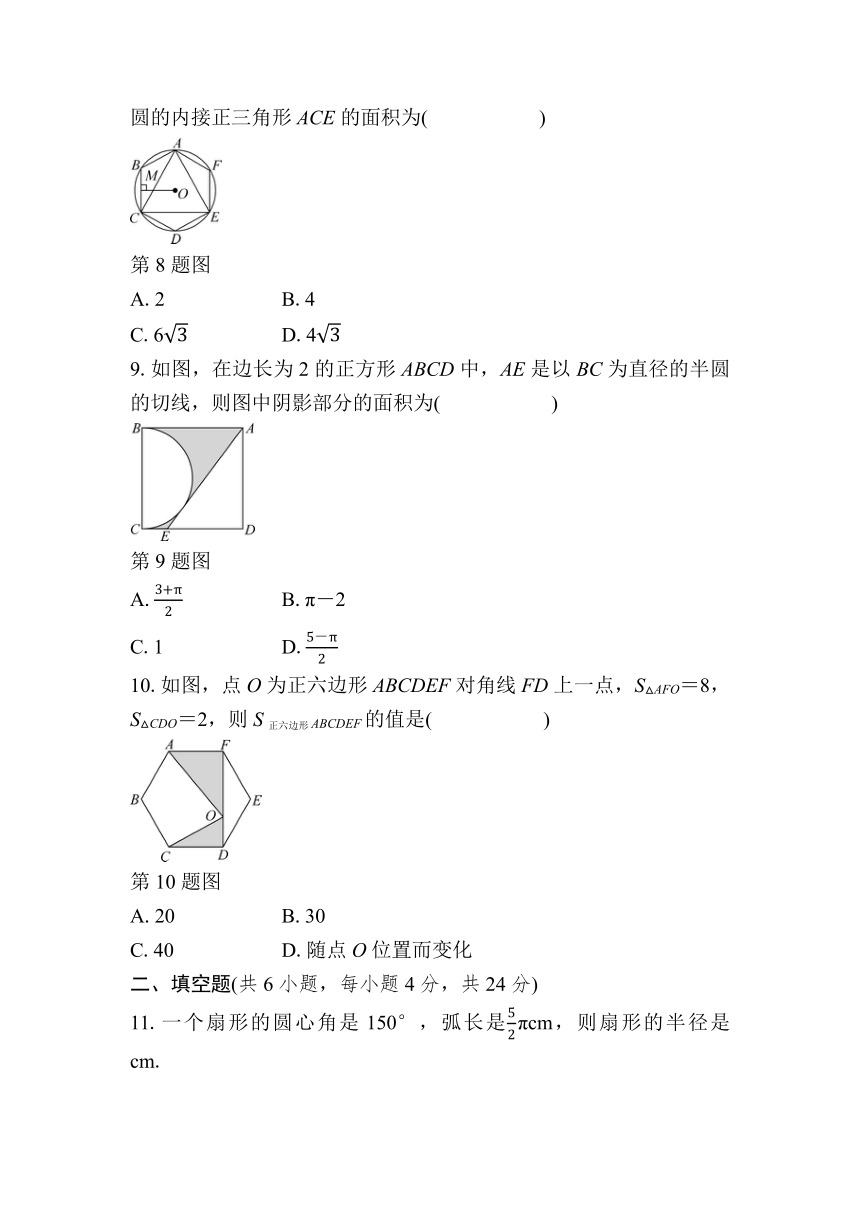
8.如图,已知☉O的内接正六边形ABCDEF的边心距OM=2,则该圆的内接正三角形ACE的面积为( )
第8题图
A.2 B.4
C.6 D.4
9.如图,在边长为2的正方形ABCD中,AE是以BC为直径的半圆的切线,则图中阴影部分的面积为( )
第9题图
A. B.π-2
C.1 D.
10.如图,点O为正六边形ABCDEF对角线FD上一点,S△AFO=8,S△CDO=2,则S正六边形ABCDEF的值是( )
第10题图
A.20 B.30
C.40 D.随点O位置而变化
二、填空题(共6小题,每小题4分,共24分)
11.一个扇形的圆心角是150°,弧长是πcm,则扇形的半径是 cm.
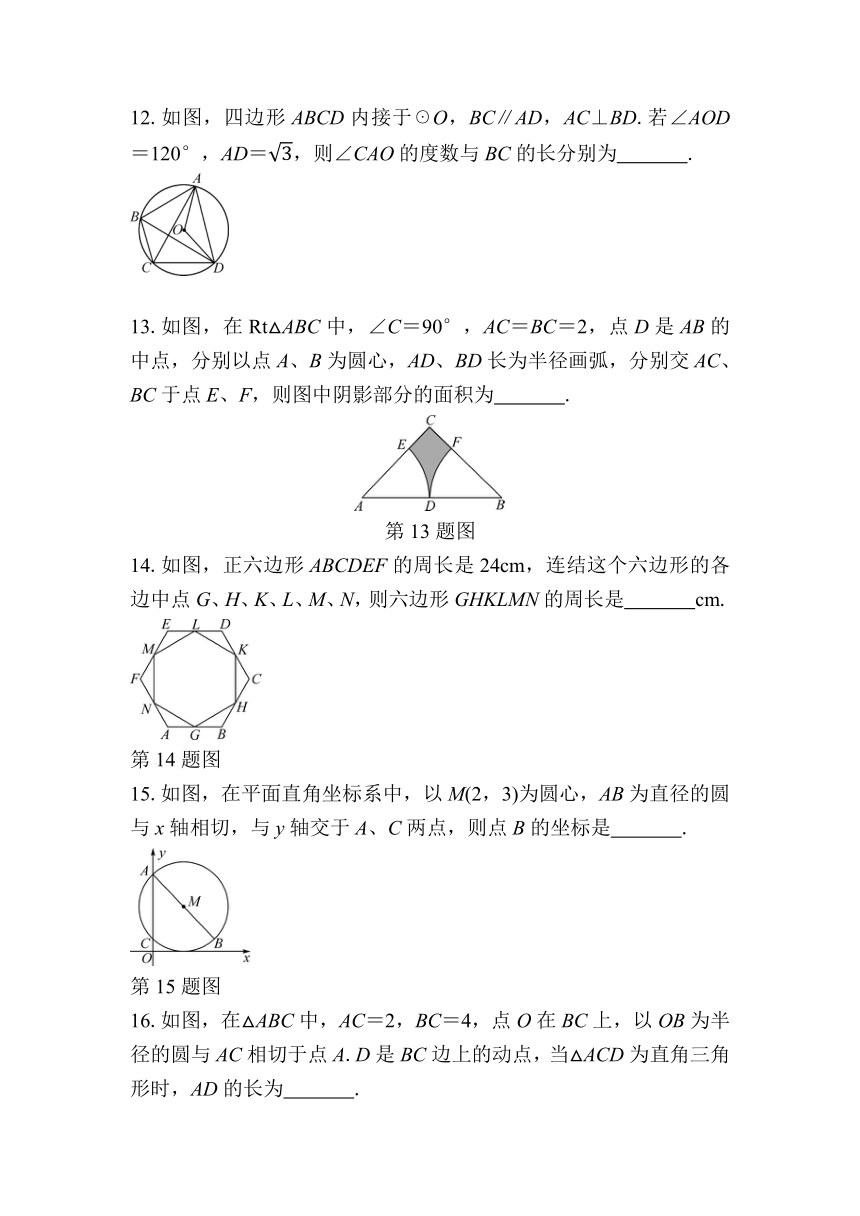
12.如图,四边形ABCD内接于☉O,BC∥AD,AC⊥BD.若∠AOD=120°,AD=,则∠CAO的度数与BC的长分别为 .
13.如图,在Rt△ABC中,∠C=90°,AC=BC=2,点D是AB的中点,分别以点A、B为圆心,AD、BD长为半径画弧,分别交AC、BC于点E、F,则图中阴影部分的面积为 .
第13题图
14.如图,正六边形ABCDEF的周长是24cm,连结这个六边形的各边中点G、H、K、L、M、N,则六边形GHKLMN的周长是 cm.
第14题图
15.如图,在平面直角坐标系中,以M(2,3)为圆心,AB为直径的圆与x轴相切,与y轴交于A、C两点,则点B的坐标是 .
第15题图
16.如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A.D是BC边上的动点,当△ACD为直角三角形时,AD的长为 .
第16题图
三、解答题(共6小题,共96分)
17.(12分)如图,四边形ABCD内接于☉O,D是弧AC的中点,延长BC到点E,使CE=AB,连结BD、ED.
第17题图
(1)求证:BD=ED.
(2)若∠ABC=60°,AD=5,则☉O的直径为 .
18.(16分)如图,AB是☉O的直径,C、D为☉O上的点,且BC∥OD,过点D作DE⊥AB于点E.
第18题图
(1)求证:BD平分∠ABC;
(2)若BC=4,DE=3,求☉O的半径.
19.(16分)如图,在△ABC中,AB=4,∠C=64°,以AB为直径的☉O与AC相交于点D,E为上一点,且∠ADE=40°.
第19题图
(1)求的长;
(2)若∠EAD=76°,求证:CB为☉O的切线.
20.(16分)如图,在Rt△AOB中,∠ABO=90°,∠OAB=30°,以点O为圆心,OB为半径的圆交BO的延长线于点C,过点C作OA的平行线,交☉O于点D,连结AD.
第20题图
(1)求证:AD为☉O的切线;
(2)若OB=2,求的长.
21.(18分)如图,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为1的☉A与OM相切于点B,连结BA并延长交☉A于点D,交ON于点E.
(1)求证:ON是☉A的切线;
(2)若∠MON=60°,求图中阴影部分的面积.(结果保留π)
22.(18分)【探究】如图1,△ABC是等边三角形,它内接于☉O,点D是上任意一点(不与点B、C重合),连结BD、CD,求证:BD+CD=AD.
小明分析后发现,如图2,将△ACD绕点A顺时针旋转60°得到△ABE,再证明D、B、E三点共线,从而得到等边三角形ADE,进而证得BD+CD=AD.
下面是小明的部分证明过程:
证明:∵△ACD绕点A顺时针旋转60°得到△ABE,
∴∠ACD=∠ABE.
∵∠ACD+∠ABD=180°,
∴∠ABE+∠ABD=180°,
∴D、B、E三点共线.
请你补全余下的证明过程.
【应用】如图1,△ABC是等边三角形,它内接于☉O,点D是上任意一点(不与点B、C重合),连结BD、CD.若BD=2CD=2,则四边形ABDC的面积为 .
图1
【拓展】如图3,等腰直角三角形ABC内接于☉O,∠BAC=90°,点D在☉O上且位于直线BC下方,若☉O的半径为2,则四边形ABDC的周长的最大值为 .
图3
第27章质量评估
1.B 2.A 3.D 4.B 5.B 6.C 7.B 8.D
9.D 10.B 11.3 12.15°,1 13.2- 14.12
15.(4,3-) 16.或
17.(1) (2)10
18.(1)略 (2)☉O的半径为.
19.(1)的长为. (2)略
20.(1)略 (2)的长为.
21.(1)略 (2)S阴影=-π.
22.【探究】略 【应用】 【拓展】8
。
一、选择题(共10小题,每小题3分,共30分)
1.已知圆的半径是5cm,如果圆心到直线的距离是5cm,那么该直线和圆的位置关系是( )
A.相交 B.相切 C.相离 D.内含
2.如图,已知点A、B、C在☉O上,C为的中点.若∠BAC=35°,则∠AOB等于( )
A.140° B.120° C.110° D.70°
3.如图,圆拱桥的拱顶C到水面AB的距离CD=8m,桥拱半径OC=5m,则水面宽AB为( )
第3题图
A.4m B.5m C.6m D.8m
4.如图,四边形ABCD内接于☉O,AC、BD为对角线,BD经过圆心O.若∠BAC=40°,则∠DBC的度数为( )
第4题图
A.40° B.50° C.60° D.70°
5.如图是高铁线路在转向处所设计的圆曲线(即圆弧)示意图,高铁列车在转弯时的曲线起点为A,曲线终点为B,过点A、B的两条切线相交于点C,列车在从A到B行驶的过程中转角α为60°.若圆曲线的半径OA=1.5km,则这段圆曲线的长为( )
第5题图
A.km B.km
C.km D.km
6.如图,AB是☉O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是( )
第6题图
A.AE⊥DE B.AE∥OD
C.DE=OD D.∠BOD=50°
7.如图,PA、PB为☉O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交☉O于点D.下列结论不一定成立的是( )
第7题图
A.△BPA为等腰三角形 B.AB与PD相互垂直平分
C.点A、B都在以PO为直径的圆上 D.PC为△BPA的边AB上的中线
8.如图,已知☉O的内接正六边形ABCDEF的边心距OM=2,则该圆的内接正三角形ACE的面积为( )
第8题图
A.2 B.4
C.6 D.4
9.如图,在边长为2的正方形ABCD中,AE是以BC为直径的半圆的切线,则图中阴影部分的面积为( )
第9题图
A. B.π-2
C.1 D.
10.如图,点O为正六边形ABCDEF对角线FD上一点,S△AFO=8,S△CDO=2,则S正六边形ABCDEF的值是( )
第10题图
A.20 B.30
C.40 D.随点O位置而变化
二、填空题(共6小题,每小题4分,共24分)
11.一个扇形的圆心角是150°,弧长是πcm,则扇形的半径是 cm.
12.如图,四边形ABCD内接于☉O,BC∥AD,AC⊥BD.若∠AOD=120°,AD=,则∠CAO的度数与BC的长分别为 .
13.如图,在Rt△ABC中,∠C=90°,AC=BC=2,点D是AB的中点,分别以点A、B为圆心,AD、BD长为半径画弧,分别交AC、BC于点E、F,则图中阴影部分的面积为 .
第13题图
14.如图,正六边形ABCDEF的周长是24cm,连结这个六边形的各边中点G、H、K、L、M、N,则六边形GHKLMN的周长是 cm.
第14题图
15.如图,在平面直角坐标系中,以M(2,3)为圆心,AB为直径的圆与x轴相切,与y轴交于A、C两点,则点B的坐标是 .
第15题图
16.如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A.D是BC边上的动点,当△ACD为直角三角形时,AD的长为 .
第16题图
三、解答题(共6小题,共96分)
17.(12分)如图,四边形ABCD内接于☉O,D是弧AC的中点,延长BC到点E,使CE=AB,连结BD、ED.
第17题图
(1)求证:BD=ED.
(2)若∠ABC=60°,AD=5,则☉O的直径为 .
18.(16分)如图,AB是☉O的直径,C、D为☉O上的点,且BC∥OD,过点D作DE⊥AB于点E.
第18题图
(1)求证:BD平分∠ABC;
(2)若BC=4,DE=3,求☉O的半径.
19.(16分)如图,在△ABC中,AB=4,∠C=64°,以AB为直径的☉O与AC相交于点D,E为上一点,且∠ADE=40°.
第19题图
(1)求的长;
(2)若∠EAD=76°,求证:CB为☉O的切线.
20.(16分)如图,在Rt△AOB中,∠ABO=90°,∠OAB=30°,以点O为圆心,OB为半径的圆交BO的延长线于点C,过点C作OA的平行线,交☉O于点D,连结AD.
第20题图
(1)求证:AD为☉O的切线;
(2)若OB=2,求的长.
21.(18分)如图,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为1的☉A与OM相切于点B,连结BA并延长交☉A于点D,交ON于点E.
(1)求证:ON是☉A的切线;
(2)若∠MON=60°,求图中阴影部分的面积.(结果保留π)
22.(18分)【探究】如图1,△ABC是等边三角形,它内接于☉O,点D是上任意一点(不与点B、C重合),连结BD、CD,求证:BD+CD=AD.
小明分析后发现,如图2,将△ACD绕点A顺时针旋转60°得到△ABE,再证明D、B、E三点共线,从而得到等边三角形ADE,进而证得BD+CD=AD.
下面是小明的部分证明过程:
证明:∵△ACD绕点A顺时针旋转60°得到△ABE,
∴∠ACD=∠ABE.
∵∠ACD+∠ABD=180°,
∴∠ABE+∠ABD=180°,
∴D、B、E三点共线.
请你补全余下的证明过程.
【应用】如图1,△ABC是等边三角形,它内接于☉O,点D是上任意一点(不与点B、C重合),连结BD、CD.若BD=2CD=2,则四边形ABDC的面积为 .
图1
【拓展】如图3,等腰直角三角形ABC内接于☉O,∠BAC=90°,点D在☉O上且位于直线BC下方,若☉O的半径为2,则四边形ABDC的周长的最大值为 .
图3
第27章质量评估
1.B 2.A 3.D 4.B 5.B 6.C 7.B 8.D
9.D 10.B 11.3 12.15°,1 13.2- 14.12
15.(4,3-) 16.或
17.(1) (2)10
18.(1)略 (2)☉O的半径为.
19.(1)的长为. (2)略
20.(1)略 (2)的长为.
21.(1)略 (2)S阴影=-π.
22.【探究】略 【应用】 【拓展】8
。
