第五章 平行四边形 专项训练 三角形中位线的应用模型(含答案)
文档属性
| 名称 | 第五章 平行四边形 专项训练 三角形中位线的应用模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 12.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-22 09:56:36 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
专项训练 三角形中位线的应用模型
类型一 连接两中点或第三边,构造三角形中位线
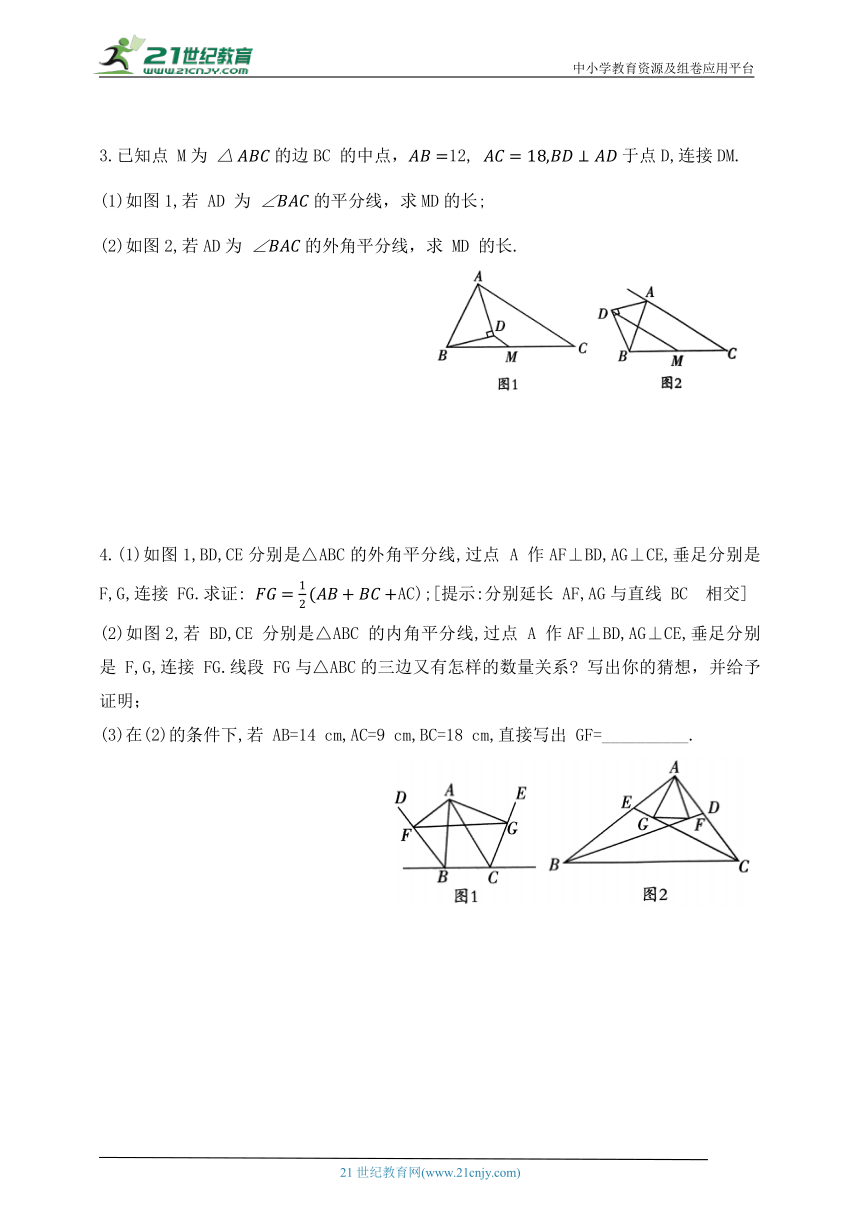
1.如图1,已知点 E,F,G,H 分别为四边形ABCD 的边AB,BC,CD,DA 的中点,连接EF,FG,GH,HE.
(1)求证:四边形 EFGH 是平行四边形(提示:可连接AC或BD);
(2)在电脑上用适当的应用程序画出图1,然后用鼠标拖动点 D,当点 D 在原四边形ABCD 的内部或外部时,图1 依次变为图2、图3.图 2、图 3 中四边形 EFGH 还是平行四边形吗 选择其中之一说明理由.
类型二 利用角平分线+垂直,延长补形造全等,构造三角形中位线
2.如图所示,在四边形 ABCD 中, ∥BD 平分E,F 分别是BD,AC的中点.
求证:
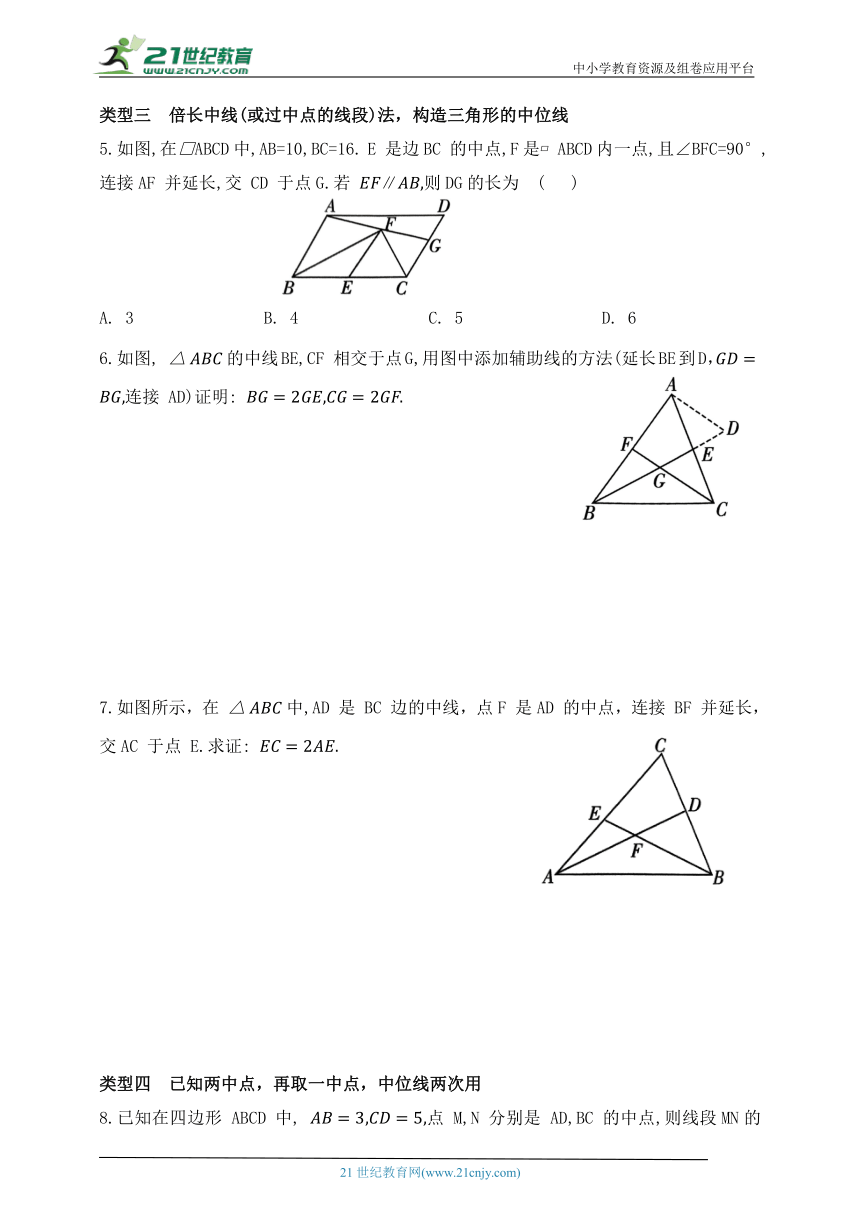
3.已知点 M为 的边BC 的中点,12, 于点D,连接DM.
(1)如图1,若 AD 为 的平分线,求MD的长;
(2)如图2,若AD为 的外角平分线,求 MD 的长.
4.(1)如图1,BD,CE分别是△ABC的外角平分线,过点 A 作AF⊥BD,AG⊥CE,垂足分别是 F,G,连接 FG.求证: AC);[提示:分别延长 AF,AG与直线 BC 相交]
(2)如图2,若 BD,CE 分别是△ABC 的内角平分线,过点 A 作AF⊥BD,AG⊥CE,垂足分别是 F,G,连接 FG.线段 FG与△ABC的三边又有怎样的数量关系 写出你的猜想,并给予证明;
(3)在(2)的条件下,若 AB=14 cm,AC=9 cm,BC=18 cm,直接写出 GF=__________.
类型三 倍长中线(或过中点的线段)法,构造三角形的中位线
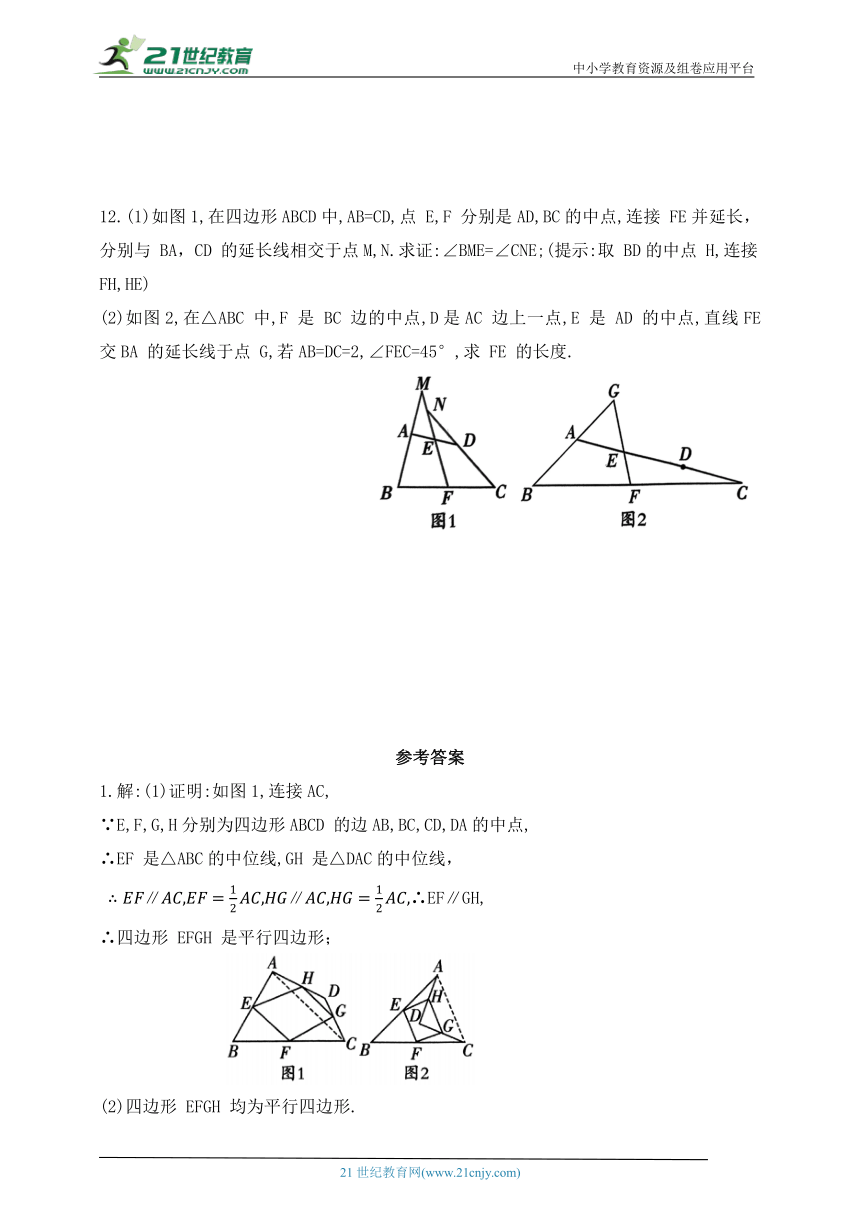
5.如图,在□ABCD中,AB=10,BC=16. E 是边BC 的中点,F是 ABCD内一点,且∠BFC=90°,连接AF 并延长,交 CD 于点G.若 ∥则DG的长为 ( )
A. 3 B. 4 C. 5 D. 6
6.如图, 的中线BE,CF 相交于点G,用图中添加辅助线的方法(延长BE到D,连接 AD)证明:
7.如图所示,在 中,AD 是 BC 边的中线,点F 是AD 的中点,连接 BF 并延长,交AC 于点 E.求证:
类型四 已知两中点,再取一中点,中位线两次用
8.已知在四边形 ABCD 中, 点 M,N 分别是 AD,BC 的中点,则线段MN的取值范围是 ( )
第8题图 第9题图
9.在四边形 ABCD 中,对角线 且AC=4,BD=8,E,F分别是边AB,CD的中点,则
类型五 已知两边相等,取中点,利用中位线构造等腰三角形
10.如图所示,在 中,点D,E分别为AB,AC上的点,且. 点 M,N 分别是BE,CD的中点.过MN的直线交AB于点 P,交 AC 于点 Q,线段 AP,AQ 相等吗 为什么
11.已知:如图,在四边形 ABCD 中,对角线点 E,F 为AB,CD中点,连接EF,交 BD,AC 于点 P,Q,求证:
12.(1)如图1,在四边形ABCD中,AB=CD,点 E,F 分别是AD,BC的中点,连接 FE并延长,分别与 BA,CD 的延长线相交于点M,N.求证:∠BME=∠CNE;(提示:取 BD的中点 H,连接FH,HE)
(2)如图2,在△ABC 中,F 是 BC 边的中点,D是AC 边上一点,E 是 AD 的中点,直线FE交BA 的延长线于点 G,若AB=DC=2,∠FEC=45°,求 FE 的长度.
参考答案
1.解:(1)证明:如图1,连接AC,
∵E,F,G,H分别为四边形ABCD 的边AB,BC,CD,DA的中点,
∴EF 是△ABC的中位线,GH 是△DAC的中位线,
∥∥∴EF∥GH,
∴四边形 EFGH 是平行四边形;
(2)四边形 EFGH 均为平行四边形.
证明(以图2为例):如图2,连接AC.在△BAC中,∵E,F 分别为AB,BC的中点,
∥
在△DAC中,∵H,G分别为AD,CD的中点,
∥∴EF∥GH.
∴四边形 EFGH 是平行四边形.
2.证明:(1)∵AD∥BC,∴∠ADB=∠DBC.
∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ADB=∠ABD.∴AB=AD,
∵点E是BD的中点,∴AE⊥BD;
(2)延长AE交BC 于点 M,
∵AD∥BM,∴∠ADB=∠DBM.
在△ADE和△MBE中, ∴△ADE≌△MBE(ASA),∴AD=BM,AE=EM.
∵点F是AC的中点, ∥
3.解:(1)如图1,延长BD 交AC于点E,
∵AD为∠BAC的平分线,BD⊥AD,∴∠BAD=∠EAD,∠ADB=∠ADE,
∵AD=AD,∴△ABD≌△AED(ASA),∴BD=DE,AB=AE=12,
∴CE=AC=AE=18-12=6.1
又∵点M 为△ABC的边 BC 的中点,∴DM 是△BCE的中位线,
(2)如图2,延长BD,CA,相交于点 E,
∵AD为∠BAC的外角平分线,BD⊥AD,
由(1),得BD=DE,AB=AE=12,∴CE=AC+AE=18+12=30,
又∵M为△ABC的边BC 的中点,∴DM是△BCE的中位线,
4.解:(1)证明:如图1,延长AF,AG 交直线BC于点M,N,
∵AF⊥BD,BD平分∠ABM,∴∠AFB=∠BFM,∠ABF=∠MBF,
在△ABF和△MBF中, ∴△ABF≌△MBF(ASA),
∴MB=AB,∴AF=MF,
同理,得CN=AC,AG=NG,∴FG是△AMN的中位线,
(2)猜想:
证明:如图2,延长AG,AF,与直线 BC 相交于点M,N,
同理(1),得△ABF≌△NBF,∴NB=AB,AF=NF,
同理,得CM=AC,AG=MG,
(3)由(2),得
故答案为
5. B
6.证明: ∴FG是△ABD的中位线,
∥
在△AED和△CEG中,
7.证明:如图,过点 D作DG∥AC交BE于点G.
∵AD是BC 边的中线,∴点 D 是BC的中点,∴BD=CD,
∵F是AD的中点,∴DF=AF.
∵DG∥AC,且AD是BC 边上的中线,∴DG是△BEC的中位线,
∵DG∥AC,∴∠FDG=∠FAE,
在△FDG和△FAE中, ∴△FDG≌△FAE(ASA),
∴DG=AE, 即EC=2AE.
8. B
9.2 解析:如图,取 BC的中点G,连接EG,FG,
∵E,F分别是边AB,CD的中点,
∴EG∥AC且 FG∥BD且
∵AC⊥BD,∴EG⊥FG,
10.解:AP=AQ.理由如下:
如图所示,取 BC的中点 H,连接MH,NH.
∵点 M,H分别为 BE,BC的中点,∴MH∥EC,且
∵点 N,H分别为CD,BC的中点,∴NH∥BD,且
∵BD=CE,∴MH=NH,∴∠HMN=∠HNM.
∵MH∥EC,∴∠HMN=∠PQA,同理,得∠HNM=∠QPA,
∴∠QPA=∠PQA,∴△APQ为等腰三角形,∴AP=AQ.
11.证明:取 BC中点G,连接EG,FG,
∵点 E,G分别为AB,BC的中点,∥
∴∠FEG=∠OQP,同理,得 ∥∴∠EFG=∠OPQ,
∵AC=BD,∴EG=FG,∴∠FEG=∠EFG,∴∠OPQ=∠OQP.
12.解:(1)证明:连接BD,取DB的中点H,连接EH,FH,
∵点 E,H分别是AD,BD的中点,∥∴∠BME=∠HEF,
∵点 F,H 分别是BC,BD的中点,∥∴∠CNE=∠HFE,
∵AB=CD,∴HE=FH,∴∠HEF=∠HFE,∴∠BME=∠CNE;
(2)连接 BD,取 DB 的中点 H,连接 EH,FH,
∵点E,F分别是 AD,BC的中点,H 是BD的中点,
∥∴∠HFE=∠FEC=45°,
∵AB=CD=2,∴HF=HE=1,∴∠HEF=∠HFE=45°,
∴∠EHF=180°-∠HFE-∠HEF=90°,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
专项训练 三角形中位线的应用模型
类型一 连接两中点或第三边,构造三角形中位线
1.如图1,已知点 E,F,G,H 分别为四边形ABCD 的边AB,BC,CD,DA 的中点,连接EF,FG,GH,HE.
(1)求证:四边形 EFGH 是平行四边形(提示:可连接AC或BD);
(2)在电脑上用适当的应用程序画出图1,然后用鼠标拖动点 D,当点 D 在原四边形ABCD 的内部或外部时,图1 依次变为图2、图3.图 2、图 3 中四边形 EFGH 还是平行四边形吗 选择其中之一说明理由.
类型二 利用角平分线+垂直,延长补形造全等,构造三角形中位线
2.如图所示,在四边形 ABCD 中, ∥BD 平分E,F 分别是BD,AC的中点.
求证:
3.已知点 M为 的边BC 的中点,12, 于点D,连接DM.
(1)如图1,若 AD 为 的平分线,求MD的长;
(2)如图2,若AD为 的外角平分线,求 MD 的长.
4.(1)如图1,BD,CE分别是△ABC的外角平分线,过点 A 作AF⊥BD,AG⊥CE,垂足分别是 F,G,连接 FG.求证: AC);[提示:分别延长 AF,AG与直线 BC 相交]
(2)如图2,若 BD,CE 分别是△ABC 的内角平分线,过点 A 作AF⊥BD,AG⊥CE,垂足分别是 F,G,连接 FG.线段 FG与△ABC的三边又有怎样的数量关系 写出你的猜想,并给予证明;
(3)在(2)的条件下,若 AB=14 cm,AC=9 cm,BC=18 cm,直接写出 GF=__________.
类型三 倍长中线(或过中点的线段)法,构造三角形的中位线
5.如图,在□ABCD中,AB=10,BC=16. E 是边BC 的中点,F是 ABCD内一点,且∠BFC=90°,连接AF 并延长,交 CD 于点G.若 ∥则DG的长为 ( )
A. 3 B. 4 C. 5 D. 6
6.如图, 的中线BE,CF 相交于点G,用图中添加辅助线的方法(延长BE到D,连接 AD)证明:
7.如图所示,在 中,AD 是 BC 边的中线,点F 是AD 的中点,连接 BF 并延长,交AC 于点 E.求证:
类型四 已知两中点,再取一中点,中位线两次用
8.已知在四边形 ABCD 中, 点 M,N 分别是 AD,BC 的中点,则线段MN的取值范围是 ( )
第8题图 第9题图
9.在四边形 ABCD 中,对角线 且AC=4,BD=8,E,F分别是边AB,CD的中点,则
类型五 已知两边相等,取中点,利用中位线构造等腰三角形
10.如图所示,在 中,点D,E分别为AB,AC上的点,且. 点 M,N 分别是BE,CD的中点.过MN的直线交AB于点 P,交 AC 于点 Q,线段 AP,AQ 相等吗 为什么
11.已知:如图,在四边形 ABCD 中,对角线点 E,F 为AB,CD中点,连接EF,交 BD,AC 于点 P,Q,求证:
12.(1)如图1,在四边形ABCD中,AB=CD,点 E,F 分别是AD,BC的中点,连接 FE并延长,分别与 BA,CD 的延长线相交于点M,N.求证:∠BME=∠CNE;(提示:取 BD的中点 H,连接FH,HE)
(2)如图2,在△ABC 中,F 是 BC 边的中点,D是AC 边上一点,E 是 AD 的中点,直线FE交BA 的延长线于点 G,若AB=DC=2,∠FEC=45°,求 FE 的长度.
参考答案
1.解:(1)证明:如图1,连接AC,
∵E,F,G,H分别为四边形ABCD 的边AB,BC,CD,DA的中点,
∴EF 是△ABC的中位线,GH 是△DAC的中位线,
∥∥∴EF∥GH,
∴四边形 EFGH 是平行四边形;
(2)四边形 EFGH 均为平行四边形.
证明(以图2为例):如图2,连接AC.在△BAC中,∵E,F 分别为AB,BC的中点,
∥
在△DAC中,∵H,G分别为AD,CD的中点,
∥∴EF∥GH.
∴四边形 EFGH 是平行四边形.
2.证明:(1)∵AD∥BC,∴∠ADB=∠DBC.
∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ADB=∠ABD.∴AB=AD,
∵点E是BD的中点,∴AE⊥BD;
(2)延长AE交BC 于点 M,
∵AD∥BM,∴∠ADB=∠DBM.
在△ADE和△MBE中, ∴△ADE≌△MBE(ASA),∴AD=BM,AE=EM.
∵点F是AC的中点, ∥
3.解:(1)如图1,延长BD 交AC于点E,
∵AD为∠BAC的平分线,BD⊥AD,∴∠BAD=∠EAD,∠ADB=∠ADE,
∵AD=AD,∴△ABD≌△AED(ASA),∴BD=DE,AB=AE=12,
∴CE=AC=AE=18-12=6.1
又∵点M 为△ABC的边 BC 的中点,∴DM 是△BCE的中位线,
(2)如图2,延长BD,CA,相交于点 E,
∵AD为∠BAC的外角平分线,BD⊥AD,
由(1),得BD=DE,AB=AE=12,∴CE=AC+AE=18+12=30,
又∵M为△ABC的边BC 的中点,∴DM是△BCE的中位线,
4.解:(1)证明:如图1,延长AF,AG 交直线BC于点M,N,
∵AF⊥BD,BD平分∠ABM,∴∠AFB=∠BFM,∠ABF=∠MBF,
在△ABF和△MBF中, ∴△ABF≌△MBF(ASA),
∴MB=AB,∴AF=MF,
同理,得CN=AC,AG=NG,∴FG是△AMN的中位线,
(2)猜想:
证明:如图2,延长AG,AF,与直线 BC 相交于点M,N,
同理(1),得△ABF≌△NBF,∴NB=AB,AF=NF,
同理,得CM=AC,AG=MG,
(3)由(2),得
故答案为
5. B
6.证明: ∴FG是△ABD的中位线,
∥
在△AED和△CEG中,
7.证明:如图,过点 D作DG∥AC交BE于点G.
∵AD是BC 边的中线,∴点 D 是BC的中点,∴BD=CD,
∵F是AD的中点,∴DF=AF.
∵DG∥AC,且AD是BC 边上的中线,∴DG是△BEC的中位线,
∵DG∥AC,∴∠FDG=∠FAE,
在△FDG和△FAE中, ∴△FDG≌△FAE(ASA),
∴DG=AE, 即EC=2AE.
8. B
9.2 解析:如图,取 BC的中点G,连接EG,FG,
∵E,F分别是边AB,CD的中点,
∴EG∥AC且 FG∥BD且
∵AC⊥BD,∴EG⊥FG,
10.解:AP=AQ.理由如下:
如图所示,取 BC的中点 H,连接MH,NH.
∵点 M,H分别为 BE,BC的中点,∴MH∥EC,且
∵点 N,H分别为CD,BC的中点,∴NH∥BD,且
∵BD=CE,∴MH=NH,∴∠HMN=∠HNM.
∵MH∥EC,∴∠HMN=∠PQA,同理,得∠HNM=∠QPA,
∴∠QPA=∠PQA,∴△APQ为等腰三角形,∴AP=AQ.
11.证明:取 BC中点G,连接EG,FG,
∵点 E,G分别为AB,BC的中点,∥
∴∠FEG=∠OQP,同理,得 ∥∴∠EFG=∠OPQ,
∵AC=BD,∴EG=FG,∴∠FEG=∠EFG,∴∠OPQ=∠OQP.
12.解:(1)证明:连接BD,取DB的中点H,连接EH,FH,
∵点 E,H分别是AD,BD的中点,∥∴∠BME=∠HEF,
∵点 F,H 分别是BC,BD的中点,∥∴∠CNE=∠HFE,
∵AB=CD,∴HE=FH,∴∠HEF=∠HFE,∴∠BME=∠CNE;
(2)连接 BD,取 DB 的中点 H,连接 EH,FH,
∵点E,F分别是 AD,BC的中点,H 是BD的中点,
∥∴∠HFE=∠FEC=45°,
∵AB=CD=2,∴HF=HE=1,∴∠HEF=∠HFE=45°,
∴∠EHF=180°-∠HFE-∠HEF=90°,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
