人教版五年级上册数学第1课时 植树问题(1)课件(共18张PPT)
文档属性
| 名称 | 人教版五年级上册数学第1课时 植树问题(1)课件(共18张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-22 11:34:51 | ||
图片预览







文档简介
(共18张PPT)
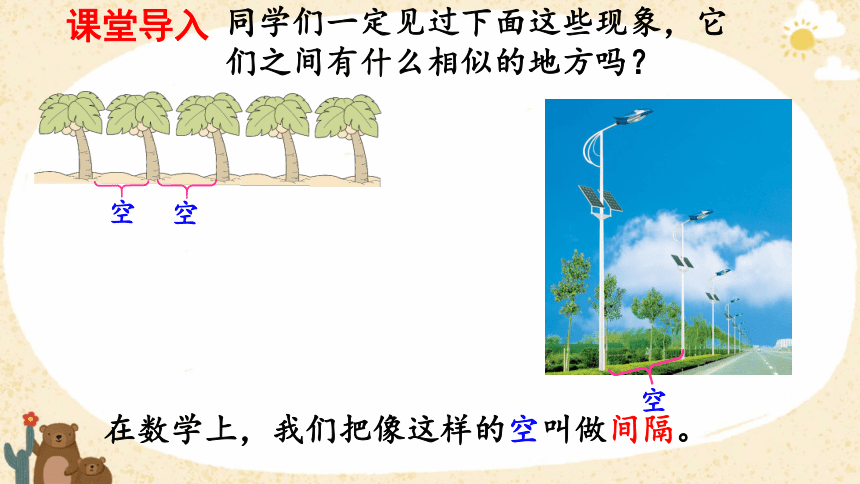
同学们一定见过下面这些现象,它们之间有什么相似的地方吗?
空
空
空
在数学上,我们把像这样的空叫做间隔。
课堂导入
人教版数学五年级(上)
第1课时 植树问题(1)
数学广角
7
1. 发现植树棵数与间隔数之间的关系。
2.理解间隔数与棵数之间的规律并运用规律解决问题。
学习目标
新知探究
1
同学们在全长 100 m 的小路一边植树,每隔 5 m 栽一棵(两端要栽)。一共要栽多少棵树?
(教材第106页例1)
从题目中你获得了哪些条件?
要求什么问题?
“一边”“两端要栽” “每隔 5 m”各是什么意思?
100 m 太长了,可以先用简单的数试试。
对吗?检验一下。
每隔 5 m 栽 1 棵,共栽 100÷5=20(棵)。
1
同学们在全长 100 m 的小路一边植树,每隔 5 m 栽一棵(两端要栽)。一共要栽多少棵树?
小组合作:探究100 m的小路要栽多少棵树?
合作要求
1. 先各自画画示意图,看看10m、20 m长的 小路一边可以栽几棵树?想一想25m、30 m、35 m呢?
2. 组内交流,说说自己的想法和发现,并记录下来。
3. 归纳小结,准备全班汇报。
10 m可以栽几棵树?
5 m
10 m
5 m
有2个间隔,能栽3(棵)树;
20 m可以栽几棵树?
5 m
20 m
5 m
5 m
5 m
有4个间隔,能栽5(棵)树;
5 m
25 m
5 m
5 m
5 m
有5个间隔,能栽6(棵)树。
5 m
25 m可以栽几棵树?
总路长 间隔数/个 植树棵数
10m
20 m
25 m
30 m
35 m
4
5
5
6
6
7
7
8
+1
+1
+1
你发现了什么规律?不画图,你能完成下表吗?
+1
2
+1
3
交流小结:你发现了什么规律?
在一条路线上植树(两端都栽)的问题:
①总长÷间距=间隔数
②间隔数+1=棵数
间隔数×间距=总长 间距=总长÷间隔数
棵树-1=间隔数
1
同学们在全长 100 m 的小路一边植树,每隔 5 m 栽一棵(两端要栽)。一共要栽多少棵树?
间隔数:100 ÷ 5 = 20(个)
植树棵数:20 + 1 =21(棵)
答:一共要栽21棵树。
学校有一条长为60 m的小道,计划在道路一旁栽树,每隔3 m栽一棵。
想:小道长( )m,每隔( )m栽一棵,有( )个间隔。
如果两端都要栽树,那么一共要栽( )棵树。
60
21
20
3
1.填一填。
2. 工人们正在架设电线杆,相邻两根的距离是200 m。 在总长 3000 m 的笔直路上,一共要架设多少根电线杆(两端都架设)?
如果把电线杆看作树,那么这道题也是植树问题。
3000÷200 = 15(个)
15+1 = 16(根)
答:一共要架设16根电线杆。
(教材第109页第3题)
(教材第109页第1题)
3. 马路一边栽了 25 棵梧桐树。如果每两棵梧桐中间栽一棵银杏树,一共要栽多少棵银杏树?
25 - 1 = 24(棵)
答:一共要栽 24 棵银杏树。
把银杏树就当成两棵树之间的间隔,这样就可根据“植数棵树-1=间隔数” 来解答。
4. 5路公共汽车行驶路线全长12 km,相邻两站之间的路程都是1 km。一共设有多少个车站?
12÷1 = 12(个)
12+1 = 13(个)
答:一共设有13个车站。
假如一个车站就是一棵树,这也是植树问题。
(教材第109页第2题)
可以把一盏路灯看作一棵树,当做植树问题来解答。
(教材第107页“做一做”)
5. 在一条全长2 km的街道两旁安装路灯(两端也要安装),每隔50 m安一盏。一共要安装多少盏路灯?
2000÷50+ 1 = 41(盏)
2 km = 2000 m
41×2 = 82(盏)
答:一共要安装82盏路灯。
这节课你有什么收获?
在一条路线上植树(两端都栽)
1.间隔数=总路长÷植株间距,
植树棵数=间隔数+1。
2.公路安装路灯、架设电线杆、设置站点、排队、
上楼梯等,都可以看成植树问题来解答。
课堂小结
同学们一定见过下面这些现象,它们之间有什么相似的地方吗?
空
空
空
在数学上,我们把像这样的空叫做间隔。
课堂导入
人教版数学五年级(上)
第1课时 植树问题(1)
数学广角
7
1. 发现植树棵数与间隔数之间的关系。
2.理解间隔数与棵数之间的规律并运用规律解决问题。
学习目标
新知探究
1
同学们在全长 100 m 的小路一边植树,每隔 5 m 栽一棵(两端要栽)。一共要栽多少棵树?
(教材第106页例1)
从题目中你获得了哪些条件?
要求什么问题?
“一边”“两端要栽” “每隔 5 m”各是什么意思?
100 m 太长了,可以先用简单的数试试。
对吗?检验一下。
每隔 5 m 栽 1 棵,共栽 100÷5=20(棵)。
1
同学们在全长 100 m 的小路一边植树,每隔 5 m 栽一棵(两端要栽)。一共要栽多少棵树?
小组合作:探究100 m的小路要栽多少棵树?
合作要求
1. 先各自画画示意图,看看10m、20 m长的 小路一边可以栽几棵树?想一想25m、30 m、35 m呢?
2. 组内交流,说说自己的想法和发现,并记录下来。
3. 归纳小结,准备全班汇报。
10 m可以栽几棵树?
5 m
10 m
5 m
有2个间隔,能栽3(棵)树;
20 m可以栽几棵树?
5 m
20 m
5 m
5 m
5 m
有4个间隔,能栽5(棵)树;
5 m
25 m
5 m
5 m
5 m
有5个间隔,能栽6(棵)树。
5 m
25 m可以栽几棵树?
总路长 间隔数/个 植树棵数
10m
20 m
25 m
30 m
35 m
4
5
5
6
6
7
7
8
+1
+1
+1
你发现了什么规律?不画图,你能完成下表吗?
+1
2
+1
3
交流小结:你发现了什么规律?
在一条路线上植树(两端都栽)的问题:
①总长÷间距=间隔数
②间隔数+1=棵数
间隔数×间距=总长 间距=总长÷间隔数
棵树-1=间隔数
1
同学们在全长 100 m 的小路一边植树,每隔 5 m 栽一棵(两端要栽)。一共要栽多少棵树?
间隔数:100 ÷ 5 = 20(个)
植树棵数:20 + 1 =21(棵)
答:一共要栽21棵树。
学校有一条长为60 m的小道,计划在道路一旁栽树,每隔3 m栽一棵。
想:小道长( )m,每隔( )m栽一棵,有( )个间隔。
如果两端都要栽树,那么一共要栽( )棵树。
60
21
20
3
1.填一填。
2. 工人们正在架设电线杆,相邻两根的距离是200 m。 在总长 3000 m 的笔直路上,一共要架设多少根电线杆(两端都架设)?
如果把电线杆看作树,那么这道题也是植树问题。
3000÷200 = 15(个)
15+1 = 16(根)
答:一共要架设16根电线杆。
(教材第109页第3题)
(教材第109页第1题)
3. 马路一边栽了 25 棵梧桐树。如果每两棵梧桐中间栽一棵银杏树,一共要栽多少棵银杏树?
25 - 1 = 24(棵)
答:一共要栽 24 棵银杏树。
把银杏树就当成两棵树之间的间隔,这样就可根据“植数棵树-1=间隔数” 来解答。
4. 5路公共汽车行驶路线全长12 km,相邻两站之间的路程都是1 km。一共设有多少个车站?
12÷1 = 12(个)
12+1 = 13(个)
答:一共设有13个车站。
假如一个车站就是一棵树,这也是植树问题。
(教材第109页第2题)
可以把一盏路灯看作一棵树,当做植树问题来解答。
(教材第107页“做一做”)
5. 在一条全长2 km的街道两旁安装路灯(两端也要安装),每隔50 m安一盏。一共要安装多少盏路灯?
2000÷50+ 1 = 41(盏)
2 km = 2000 m
41×2 = 82(盏)
答:一共要安装82盏路灯。
这节课你有什么收获?
在一条路线上植树(两端都栽)
1.间隔数=总路长÷植株间距,
植树棵数=间隔数+1。
2.公路安装路灯、架设电线杆、设置站点、排队、
上楼梯等,都可以看成植树问题来解答。
课堂小结
